Next Article in Journal
Analysis of the Control Effect of Bacillus amyloliquefaciens C4 Wettable Powder on Potato Bacterial Wilt Caused by Ralstonia solanacearum
Previous Article in Journal
Energy Saving Technologies and Practices in Facility Agriculture in Cold Regions
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Agronomy
Volume 15
Issue 1
10.3390/agronomy15010205
agronomy-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Winter Wheat Yield Prediction Using Satellite Remote Sensing Data and Deep Learning Models

by
Hongkun Fu
1,
Jian Lu
1,
Jian Li
2,*,
Wenlong Zou
2,
Xuhui Tang
2,
Xiangyu Ning
3 and
Yue Sun
3
1
College of Agriculture, Jilin Agricultural University, Changchun 130118, China
2
College of Information Technology, Jilin Agricultural University, Changchun 130118, China
3
Northeast Institute of Geography and Agroecology, Chinese Academy of Sciences, Changchun 130102, China
*
Author to whom correspondence should be addressed.
Agronomy 2025, 15(1), 205; https://doi.org/10.3390/agronomy15010205
Submission received: 4 December 2024 / Revised: 11 January 2025 / Accepted: 15 January 2025 / Published: 16 January 2025
(This article belongs to the Section Precision and Digital Agriculture)
Browse Figures
Versions Notes

Abstract

:
Accurate crop yield prediction is crucial for formulating agricultural policies, guiding agricultural management, and optimizing resource allocation. This study proposes a method for predicting yields in China’s major winter wheat-producing regions using MOD13A1 data and a deep learning model which incorporates an Improved Gray Wolf Optimization (IGWO) algorithm. By adjusting the key parameters of the Convolutional Neural Network (CNN) with IGWO, the prediction accuracy is significantly enhanced. Additionally, the study explores the potential of the Green Normalized Difference Vegetation Index (GNDVI) in yield prediction. The research utilizes data collected from March to May between 2001 and 2010, encompassing vegetation indices, environmental variables, and yield statistics. The results indicate that the IGWO-CNN model outperforms traditional machine learning approaches and standalone CNN models in terms of prediction accuracy, achieving the highest performance with an R2 of 0.7587, an RMSE of 593.6 kg/ha, an MAE of 486.5577 kg/ha, and an MAPE of 11.39%. The study finds that April is the optimal period for early yield prediction of winter wheat. This research validates the effectiveness of combining deep learning with remote sensing data in crop yield prediction, providing technical support for precision agriculture and contributing to global food security and sustainable agricultural development.

1. Introduction

Wheat (Triticum aestivum L.) is one of the most important food crops globally, providing the primary source of nutrition for humans and serving as a key energy substance for animal feed [1]. Winter wheat production currently faces severe challenges: on the one hand, the global population continues to increase; on the other hand, extreme and severe weather occur frequently, introducing numerous unpredictable factors into agricultural production [2]. Consequently, wheat production has garnered significant attention. Obtaining accurate winter wheat yield information is crucial for agricultural managers, operators, and for agricultural insurance claims [3]. An accurate prediction of winter wheat yield before harvest would greatly benefit production practices and decision-making.
In the process of large-scale yield prediction, traditional methods typically require substantial manpower, materials, and resources, and they are limited to predicting yields over relatively small areas [4]. However, with the continuous development of remote sensing technology and the launch of various satellites, new opportunities have arisen for our research [5]. These advancements now allow us to obtain comprehensive data on crop growth and environmental conditions, making it feasible to predict yields over large areas [6]. Early prediction is particularly crucial as it enables researchers and producers to make timely decisions. Current early prediction methods can be categorized into two main types: process-based crop growth models and empirical statistical models [7]. Process-based models require the collection of extensive data throughout the crop growth cycle, including meteorological information, crop genotype details, soil characteristics, and field management practices. This demand for a substantial amount of data can be challenging to fulfill in a timely and accurate manner during large-scale field surveys [8].
In contrast, empirical statistical models predict yield by establishing complex relationships between crop yield and related variables. These models are generally easier to operate and have therefore been widely adopted in forecasting [9]. This simple empirical model is actually a linear model, which shows good performance by establishing a linear relationship between field yield components (number of ears per unit area, number of grains per ear, and thousand-grain weight) and yield. However, field yield prediction often involves complex nonlinear relationships, necessitating substantial computing power for accurate calculations [10]. To address these challenges, machine learning and deep learning methods have demonstrated significant advantages [11]. In numerous experiments, these algorithms have accurately revealed the complex relationships between vegetation indices (such as GNDVI), climate change, and yield [12]. Many studies have employed multiple remote sensing-based indicators for regression analysis with crop yield [13]. For instance, some studies have achieved good results in predicting corn yield through the application of machine learning and deep learning models [14].
In deep learning models, parameter adjustment directly impacts the algorithm’s accuracy. Manual parameter tuning is not only time-consuming but also often fails to achieve high-precision results [15]. To address this challenge, optimization algorithms have been introduced. These algorithms automatically adjust parameters through numerous simulation experiments, ensuring that the model parameters attain an optimal state [16]. Furthermore, the incorporation of optimization algorithms significantly enhances the model’s stability and generalization ability. Optimization algorithms encompass various aspects, such as solving optimization problems, improving efficiency, handling complexity, and tackling large-scale issues [17,18]. In a study by Guo et al. [19], the Improved Particle Swarm Optimization Algorithm (IPSO)-BPNN was employed to predict winter wheat yield in the Guanzhong Plain of China. The results demonstrated a significant improvement in prediction accuracy, further validating the immense potential of optimization algorithms in the field of yield forecasting. The Improved Gray Wolf Optimizer (IGWO) has exhibited excellent performance in numerous prediction tasks [20]. Belonging to the category of swarm intelligence-based algorithms [21], IGWO boasts powerful global optimization capabilities, efficient search performance, precise parameter optimization, and reliable dynamic adjustment strategies [22]. Since the IGWO had not yet been extensively applied to crop yield forecasting, and specifically, the IGWO with Convolutional Neural Networks (CNN), the IGWO-CNN model, had not been utilized to predict winter wheat yield, we elected to assess the predictive performance of the IGWO-CNN model using a dataset encompassing ten years.
This study utilized satellite data in conjunction with the deep learning model incorporating the IGWO algorithm to predict the yield of winter wheat in China’s Huang-Huai-Hai region, the middle and lower reaches of the Yangtze River region, and the northwest wheat region.
This paper’s research encompasses the following three aspects: Evaluating the effectiveness of the IGWO-CNN model in predicting winter wheat yield; comparing the predictive capabilities of machine learning models and deep learning models; and exploring the optimal advancing prediction period for winter wheat yield. We anticipate that these results will provide robust technical support for the advancement of precision agriculture technology, thereby making significant contributions to global food security and promoting sustainable agricultural development.

2. Materials and Methods

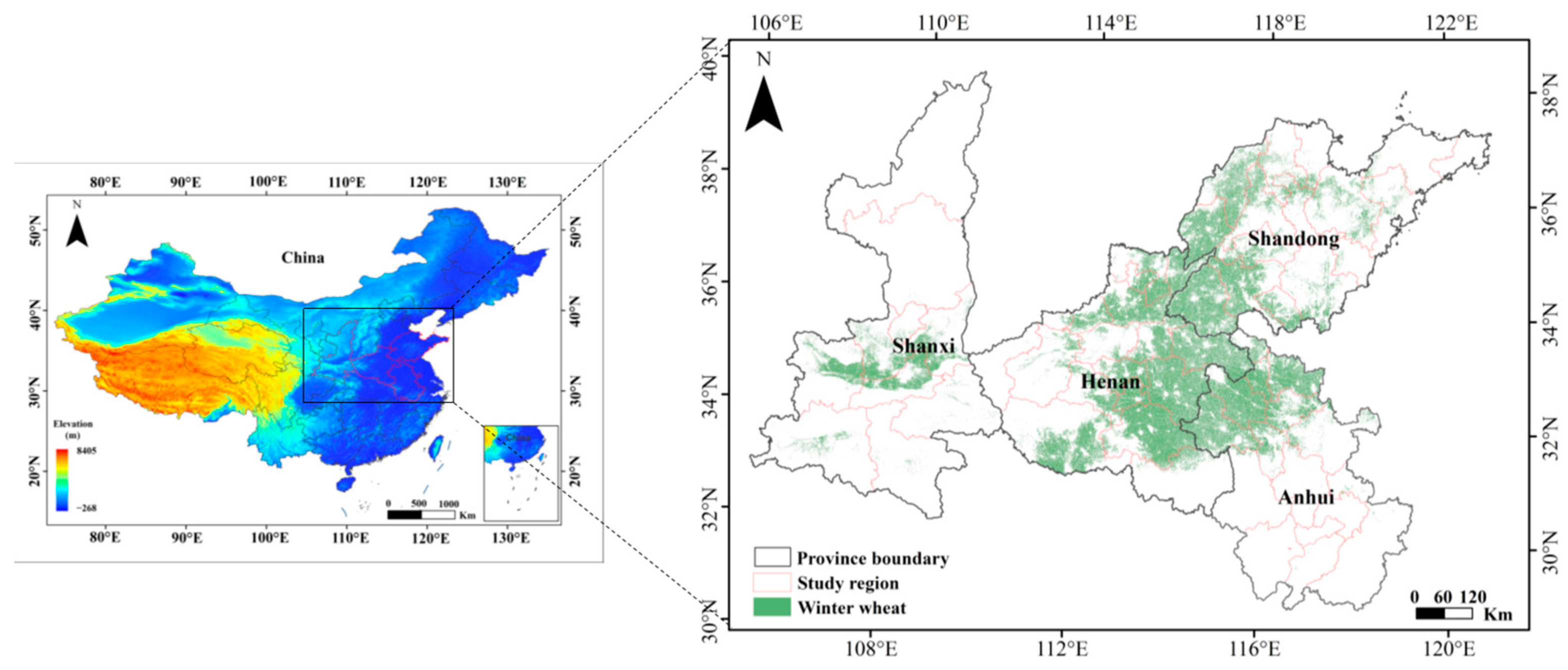
2.1. Study Area

The study area encompasses China’s Huang-Huai-Hai wheat region, the middle and lower reaches of the Yangtze River wheat region, and the Northwest wheat region, spanning four major provinces for winter wheat cultivation: Henan, Shandong, Anhui, and Shaanxi. Each of these wheat-growing regions exhibits unique climatic conditions. The wheat-growing areas in the Huang-Huai-Hai region feature a warm temperate monsoon climate, characterized by cold and dry winters, hot and rainy summers, and occasional severe spring droughts. The wheat fields located in the middle and lower reaches of the Yangtze River are influenced by a north subtropical humid monsoon climate, with mild winters and moderate rainfall, followed by hot summers with abundant precipitation. Precipitation is generally plentiful and relatively evenly distributed throughout the year. In the Northwest wheat region, the climate of Shaanxi Province is particularly diverse. The southern part of Shaanxi has a northern subtropical climate that is humid and rainy, whereas Guanzhong and most areas in northern Shaanxi have a warm temperate climate that is semi-humid or semi-arid. Despite the varying climatic conditions across these wheat-growing regions, they all offer suitable temperatures, sufficient rainfall, and adequate sunlight, providing an optimal environment for wheat growth. Winter wheat is typically sown in autumn and harvested in May of the following year. In the winter wheat-growing regions, following the harvest, crops such as corn are often cultivated as subsequent plantings. As illustrated in Figure 1, winter wheat is primarily distributed in central Shaanxi Province, most of Henan Province, central and southern Shandong Province, and northern Anhui Province.

2.2. Data

In this study, we selected winter wheat data from March, April, and May within the study area, encompassing the entire growth cycle of winter wheat from the jointing stage to maturity. During this period, winter wheat was in its active growth phase. The data collected during this timeframe encompassed vegetation indices, environmental variables, winter wheat distribution maps, and municipal-level winter wheat yield statistics (Table 1). Utilizing these data, we investigated the relationships between winter wheat yield, crop growth status, and environmental factors. To identify the month with the highest prediction accuracy in our experiment, we resampled all datasets to a 500 m resolution and adjusted the vegetation indices and environmental data to monthly averages. We applied the winter wheat planting area mask and calculated the average value for each municipality. The data download and processing for this study were conducted on the Google Earth Engine (GEE) platform.
With the application of modern tools such as remote sensing (RS), Geographic Information Systems (GIS), Artificial Intelligence (AI), and deep learning [23], early crop planting mapping has been facilitated, laying the groundwork for yield prediction. We adopted an early mapping technology for winter wheat in China, which relies on Landsat and Sentinel satellite imagery [24], boasting a spatial resolution of 30 m.
To ensure the accuracy of yield data, we obtained winter wheat yield data from 2001 to 2010 from the Statistics Bureaus of Shaanxi Province (https://tjj.shaanxi.gov.cn/), Henan Province (https://tjj.henan.gov.cn/), Shandong Province (https://tjj.shandong.gov.cn/), and Anhui Province (https://tjj.ah.gov.cn/). To guarantee the representativeness of the experimental results, we collected yield data from 58 cities and regions across these provinces. During the data screening process, we excluded winter wheat yield data that fell outside the theoretical value range or exhibited any discontinuity over the ten-year period, thus ensuring the accuracy of subsequent analyses.
To predict yield using remote sensing data, we selected vegetation indices (VIs) from the MOD13A1 product. Vegetation indices are crucial indicators of plant growth, enabling us to assess the health, vigor, and photosynthetic activity of crops. Specifically, we chose several vegetation indices, namely the Normalized Difference Vegetation Index (NDVI) [25], the Green Normalized Difference Vegetation Index (GNDVI) [26], the Difference Water Index (NDWI) [27], the Enhanced Vegetation Index (EVI), and the Ratio Vegetation Index (RVI) [28].
Vegetation indices directly reflect the growth status of crops, while environmental changes exert a direct influence on plant growth. The primary environmental factors that we considered include precipitation, evapotranspiration, and drought conditions. To facilitate our study, we selected the following environmental variables: precipitation accumulation (PR) [29], actual evapotranspiration (AET) [30], Palmer Drought Severity Index (PDSI) [31], climate water deficit (DEF) [32], downwelling shortwave radiation (SRAD) [33], Temperature Minimum (TMMN) [34], Temperature Maximum (TMMX) [35], Vapor Pressure Deficit (VPD) [36], and Vapor Pressure (VAP) [37].

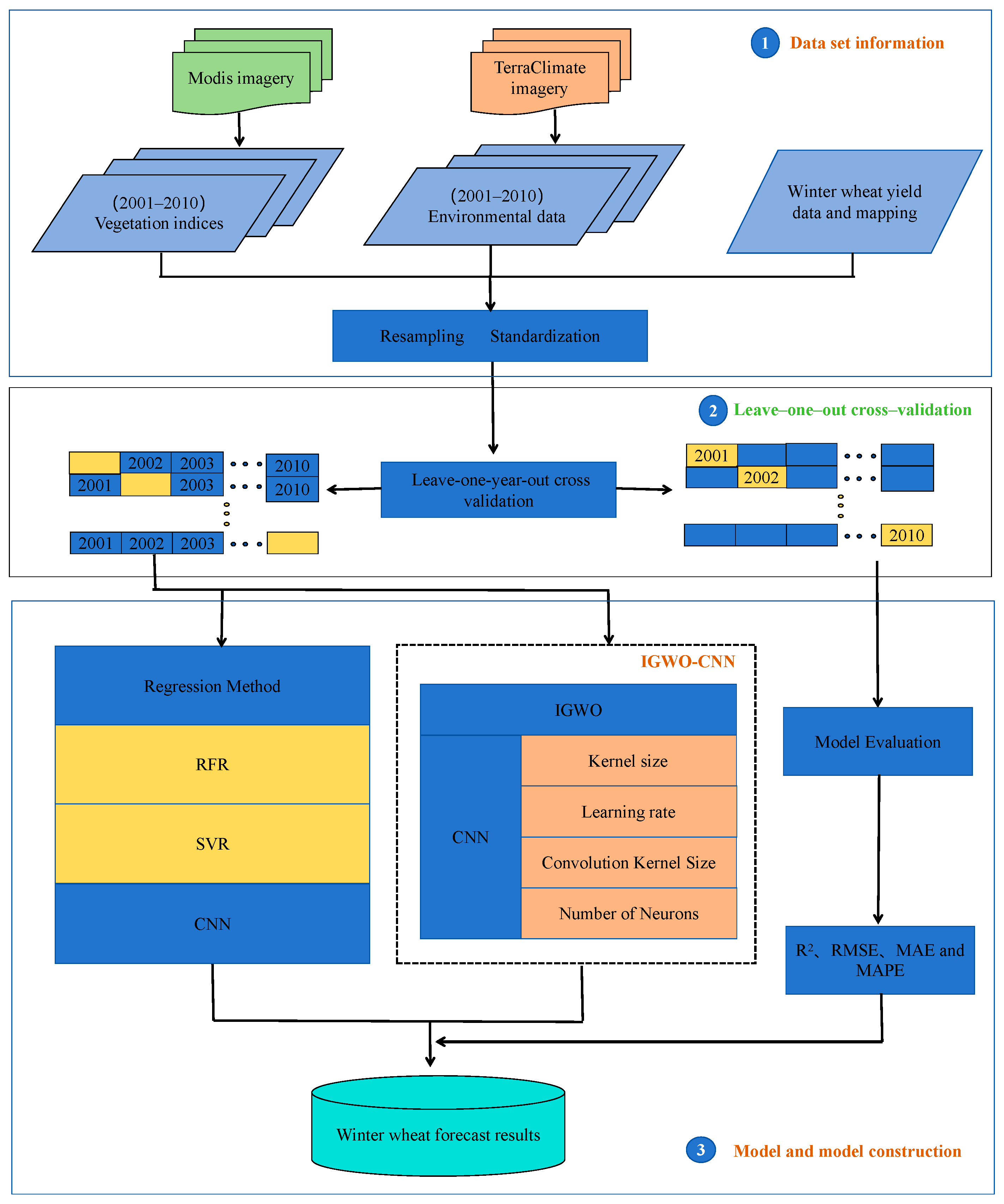
2.3. Methods

We enhanced the deep learning model by employing deep learning as a framework and incorporating the IGWO algorithm to optimize key parameters, including the learning rate, convolution kernel size, batch size, and number of neurons. To better evaluate the performance of the IGWO-CNN model, it was compared with RFR, SVR, KNN, and CNN.

2.3.1. Models

In this study, we compared three machine learning models: Random Forest Regression (RFR), Support Vector Machine Regression (SVR), and K-Nearest Neighbor (KNN) algorithm.
RFR is widely used in prediction tasks owing to its ability to capture nonlinear relationships among variables, and it has demonstrated exceptional performance in managing complex datasets [38]. During the training phase, the model constructs multiple decision trees and calculates their average to obtain the final prediction result.
SVR, a machine learning technique based on supervised learning, is extensively applied in regression analysis [39]. It adopts a linear approach to learn from training data and address nonlinear problems. In our study, the SVR model employed the Radial Basis Function (RBF) kernel [40].
The KNN algorithm involves using a distance metric to identify the K most similar or closest samples in the training set for a given test sample that requires prediction [41]. In regression tasks, the predicted value is calculated as the average of the target variable values of the K neighbors [42].
We chose CNN (Figure 2) as the deep learning model for comparison.
The framework of the CNN model is a one-dimensional convolutional neural network designed for processing one-dimensional array data [43]. The input dimensions of the CNN layer are configured to align with the number of features in the remote sensing data (10). The CNN model comprises a total of nine one-dimensional convolutional layers. The first layer utilizes 64 convolution kernels of size 3 to capture local features of the data; the second layer employs 128 convolution kernels of size 3 to capture more complex data features; and the third layer uses 512 convolution kernels of size 3 to further refine the feature extraction. To enhance model efficiency and mitigate memory consumption, the number of convolution kernels in subsequent layers is reduced: the fourth layer reverts to 64 convolution kernels, while the fifth and sixth layers utilize 128 and 512 convolution kernels, respectively. The configurations of the seventh to ninth layers mirror the preceding ones. This design aids in reducing model complexity and the risk of overfitting, enabling the model to focus more on key features. Additionally, a maximum pooling layer (with a pool size of 2) is incorporated into the model to diminish the feature dimension, followed by a flattening layer that converts the multi-dimensional output of the convolutional layers into a one-dimensional array for input to the fully connected layer. Lastly, two fully connected layers are utilized to produce the final prediction results [44].
In initial experiments, we observed that key hyperparameters such as learning rate, convolution kernel size, batch size, and number of neurons required frequent adjustment to achieve optimal performance of the CNN model [45]. To address this challenge, we introduced the IGWO algorithm, which optimizes these parameters by simulating the social hierarchy behavior of gray wolves—defining different levels of wolves (α wolves, β wolves, and δ wolves) that represent optimal solutions, suboptimal solutions, and average solutions, respectively, facilitating efficient convergence to the global optimal solution. To ensure comprehensive coverage of the search space, we established both a parent population and a child population, using the prediction accuracy of the CNN as the criterion for evaluating each solution. This approach not only intuitively reflects the model’s performance but also provides a clear direction for algorithm optimization. We set the population size to 70 individuals and the maximum number of iterations for the algorithm to 80, balancing the relationship between computational resources and search accuracy. Furthermore, we specified detailed settings for the four hyperparameters: learning rate (ranging from 0.0001 to 0.01), convolution kernel size (set to 2 or 3), batch size (ranging from 16 to 512), and number of neurons (ranging from 1 to 512). In the model, we incorporated an adaptive adjustment mechanism and a reverse learning strategy based on local optimality [46], effectively avoiding the issue of early convergence and enhancing global search capability. By augmenting the influence of secondary leader wolves, IGWO also improves information sharing and decision-making processes.
Based on the IGWO algorithm framework proposed by [47], this study successfully applied it to hyperparameter optimization of the CNN model, significantly improving the model’s prediction performance on practical application datasets. The aforementioned code was executed within a Python environment. All parameters are listed in Table 2.

2.3.2. Verification Method

We use the one-year validation method to accurately predict winter wheat yields. This method has the advantages of comprehensive data utilization, accurate model evaluation, high applicability and flexibility, and strong practicality. We utilized a dataset spanning from 2001 to 2010, where nine years of data were used for model training and the remaining one year of data were reserved for testing, with this process being repeated ten times.

2.3.3. Performance Evaluation

In terms of model evaluation, four indicators are used to compare the accuracy of the estimated predicted yield with the observed yield of winter wheat. These indicators are the coefficient of determination ( R 2 ), root mean square error (RMSE), mean absolute error (MAE), and mean absolute percentage error (MAPE). The calculation methods for these indicators are as follows:
R 2 = 1 − ∑ i = 1 n ( y i − y ^ i ) 2 ∑ i = 1 n ( y i − y ¯ ) 2
R M S E = 1 n ∑ i = 1 n ( y i − y ^ i ) 2
M A P E = 1 n ∑ i = 1 n ( y i − y ^ i y i )
M A E = 1 n ∑ i = 1 n ( y i − y ^ i )
R2 and RMSE are widely used metrics in forecasting. The closer the R2 value is to 1, the higher the prediction accuracy of the model, indicating a better fit [48]. Similarly, a smaller RMSE indicates better model stability, as it represents the square root of the average of squared differences between predicted and actual values. In addition to this, we also considered MAE and MAPE for accuracy evaluation. MAE, which is the average of the absolute differences between predicted and actual values, provides an overall measure of the model’s error [49]. A lower MAE indicates a more accurate model. MAPE, on the other hand, is a commonly used indicator that measures the percentage difference between the predicted and actual values, providing a relative measure of forecast accuracy [50]. By analyzing these four indicators together, we can gain a more comprehensive evaluation of the model’s performance.
As shown in Figure 3, we present the satellite remote sensing data and the machine learning and deep learning model framework used for winter wheat yield prediction.

3. Results

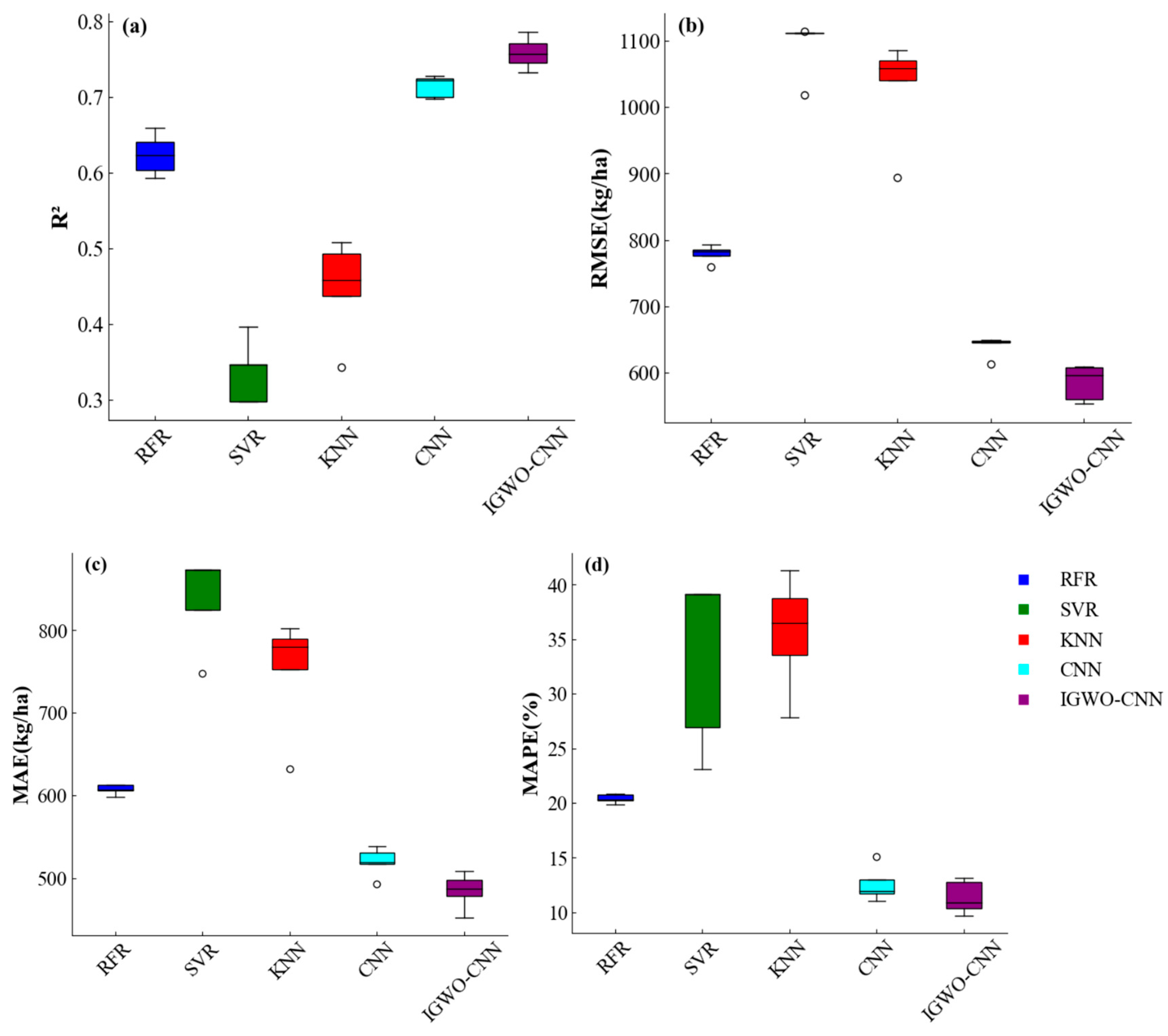
3.1. Experimental Results and Analysis

In this study, the relationship between winter wheat yield and various vegetation indices as well as environmental variables was analyzed using the Pearson correlation coefficient. The results of this analysis are presented in Figure 4. Among the indices examined, all were positively correlated with winter wheat yield except for PR, which exhibited a negative correlation. Notably, GNDVI, an improved version of NDVI, demonstrated the highest correlation (0.83). GNDVI is particularly sensitive to changes in crop chlorophyll content and can accurately distinguish different concentrations of chlorophyll in plants. NDVI, which is used to assess vegetation growth status and coverage, had a correlation of 0.77 with winter wheat yield. EVI is highly sensitive to soil background changes and is suitable for monitoring the ecological environment conducive to crop growth; its correlation was also strong (0.77). RVI, a sensitive indicator of green plants, showed a correlation of 0.69. PR, representing accumulated precipitation and reflecting the moisture content of the crop environment, was negatively correlated (−0.59). AET, which reflects the amount of water consumed by crops through transpiration and soil evaporation, had a correlation of 0.60. PDSI, a standardized drought index that considers multiple meteorological factors such as precipitation, temperature, and soil moisture, had a correlation of 0.56. DEF, an important indicator for evaluating the moisture conditions of the crop growth environment, showed a correlation of 0.58. SRAD, which affects the photosynthesis capacity of crops and indirectly reflects surface temperature and water evaporation, had a correlation of 0.64. Based on these results, we decided to remove indices with low correlations and those with high inter-correlations to avoid redundancy. Consequently, NDWI, TMMX, TMMN, VPD, and VAP were eliminated from further analysis.

3.2. Prediction Results for Winter Wheat Yield Using Different Models

We utilized vegetation indices and environmental data to predict winter wheat yields in the Huang-Huai-Hai wheat region, the middle and lower reaches of the Yangtze River wheat region, and the Northwest wheat region. The prediction performances of five different models, namely RFR, SVR, KNN, CNN, and IGWO-CNN, were evaluated. When analyzing the relationship between winter wheat vegetation indices, environmental data, and yield, the test results of these five models indicated that the R2 value ranged from 0.3371 to 0.7587, the RMSE value ranged from 593.6 to 1093.1 kg/ha, the MAE value ranged from 486.6 to 838.4 kg/ha, and the MAPE value ranged from 11.4% to 33.5%. By comparing and analyzing Figure 5a–d, we observed that the two deep learning models, CNN and IGWO-CNN, generally outperformed the other three machine learning models (RFR, SVR, and KNN) in terms of accuracy. Among the deep learning models, IGWO-CNN exhibited a higher R2 value than CNN, while its RMSE, MAE, and MAPE values were lower, indicating that the IGWO-CNN model had the best overall prediction performance. Specifically, the IGWO-CNN model achieved the highest accuracy (R2 = 0.7587, RMSE = 593.6 kg/ha, MAE = 486.6 kg/ha, and MAPE = 11.4%). In contrast, among the three machine learning models, the SVR model had the lowest accuracy (R2 = 0.3371, RMSE = 1093.1 kg/ha, MAE = 838.4 kg/ha, and MAPE = 33.5%), suggesting that SVR is relatively weaker in predicting the relationship between actual and observed yields.

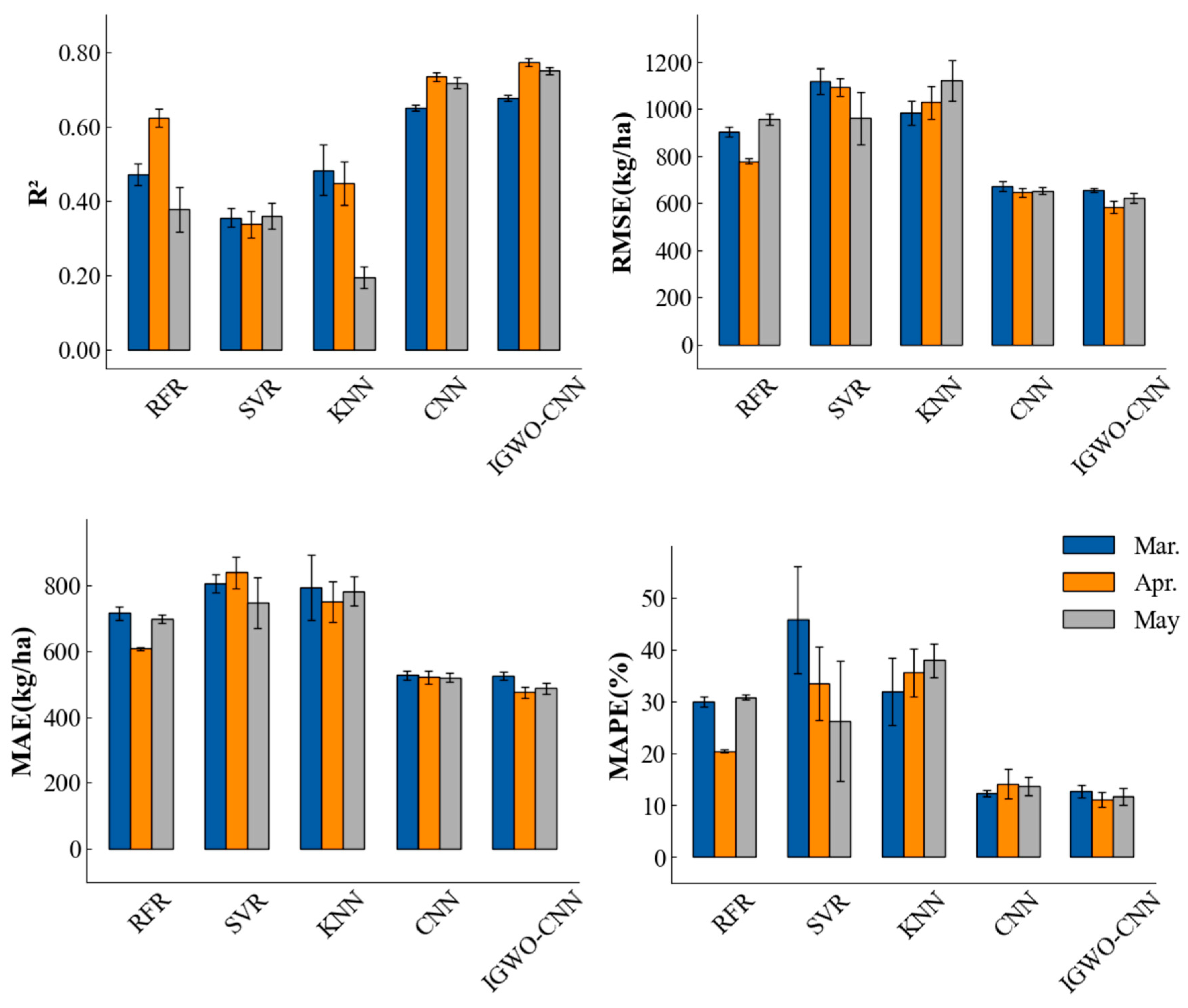
3.3. Comparison of Winter Wheat Yield Forecasts in Different Months

We used data from March, April, and May to predict the yield of winter wheat in the study area and determined the optimal period for early prediction by comparing the yield prediction results obtained from these three months. By comparing the prediction results for each month, it was further confirmed that the deep learning models outperform the machine learning model in terms of R2, RMSE, MAE, and MAPE. Additionally, the prediction results of the deep learning model exhibited greater stability. As illustrated in Figure 6, the error of the deep learning model is significantly lower than that of the machine learning model. When comparing RMSE and MAE values, the errors of the RFR, CNN, and IGWO-CNN models were found to be smaller. Through the above analysis, it is evident that the IGWO-CNN model demonstrates superior prediction performance. Furthermore, when comparing the forecast results for March, April, and May, the forecast results of the RFR, CNN, and IGWO-CNN models in April were significantly better than those in March and May.

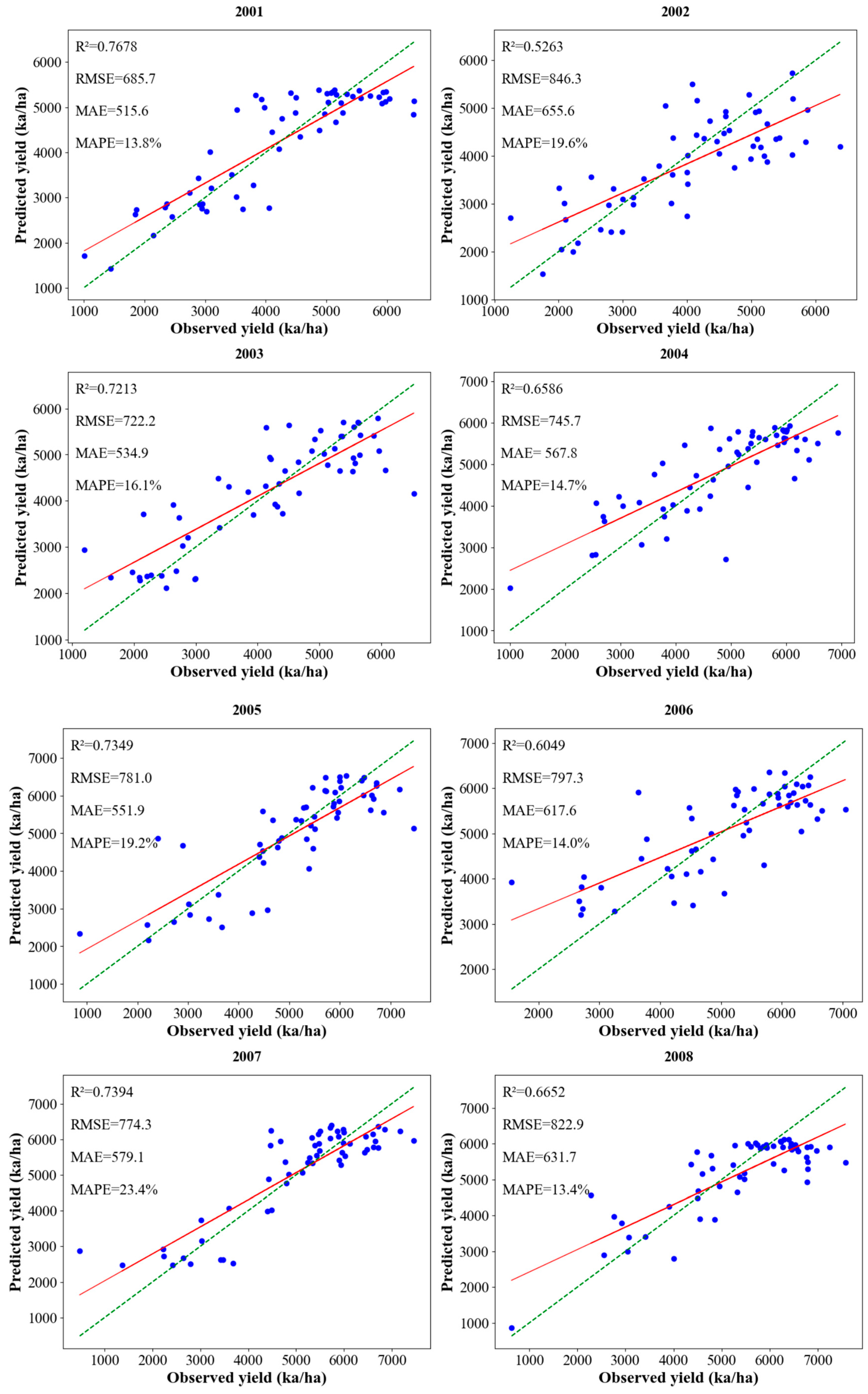
3.4. Comparison of Prediction Results in Different Years Based on IGWO-CNN Model

Figure 7 depicts the correlation between the measured yield and the predicted yield of winter wheat for each year using the IGWO-CNN model with the leave-one-year-out method. To assess the prediction accuracy of the measured versus predicted yield, a y = x diagonal line has been included in the figure. The proximity of the data points in Figure 7 to this diagonal line serves as an indicator: the closer a point lies to the y = x line, the higher the concordance between the predicted yield and the measured yield. By analyzing the predicted output for the decade spanning from 2001 to 2010, we observed that, with the exception of 2002, the prediction accuracy for the other years was above 0.6. Specifically, in the years 2001, 2003, 2005, 2007, and 2009, the prediction results were optimal, with accuracy levels surpassing 0.7. The points representing the measured and predicted yields were evenly and densely distributed around the y = x line. This indicates that the predictions were highly accurate and reliable during these years, as the closeness of the points to the y = x line suggests a strong correlation between the predicted and actual yields. Among these five years, the best linear fitting effect was observed in 2007, with an R2 value of 0.7394, RMSE of 774.3, MAE of 579.1, and MAPE of 23.4%. This may be attributed to two factors: firstly, we incorporated multiple feature extractions when constructing the model and discarded some unimportant features in the process; secondly, the incorporation of the optimization algorithm significantly enhanced the model’s predictive capability.

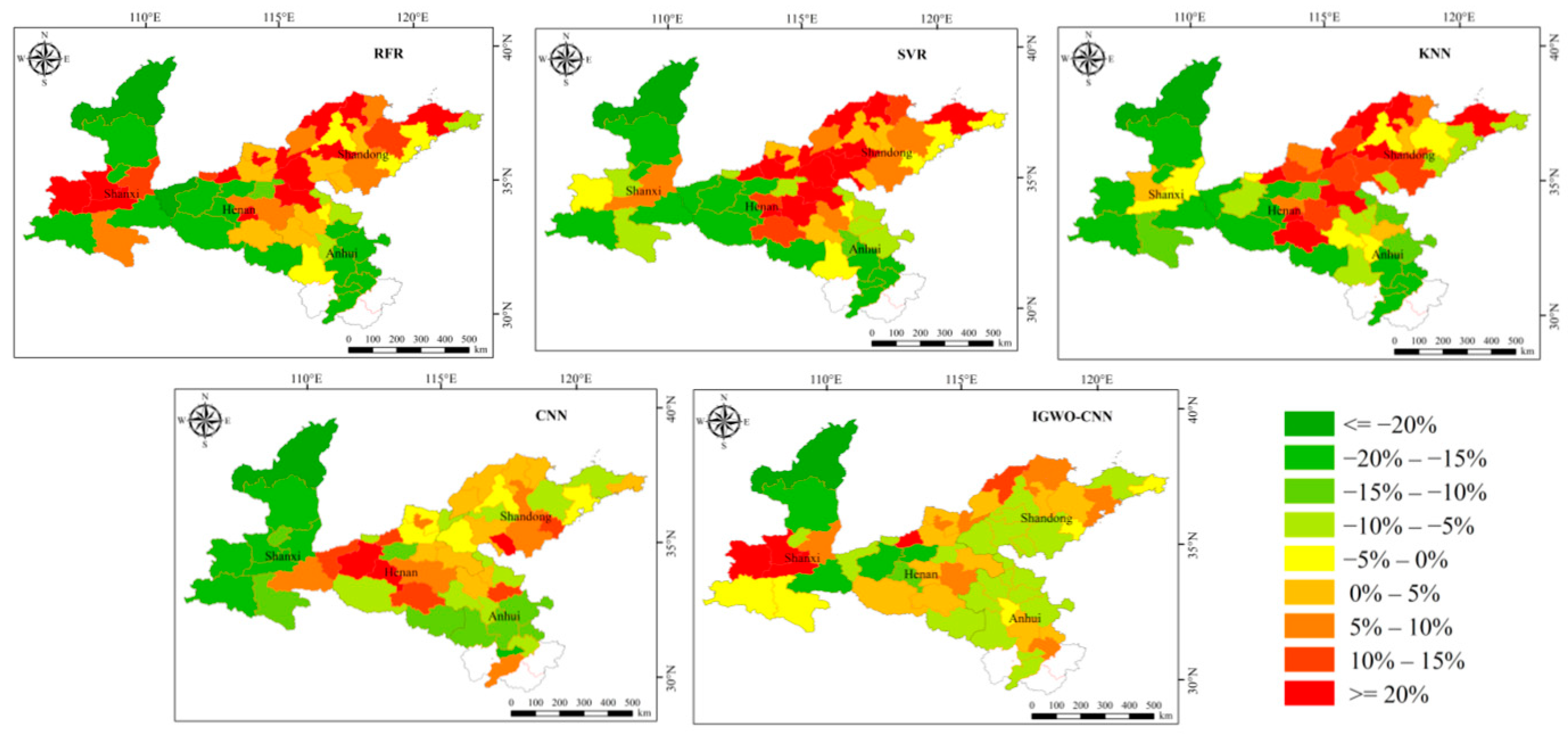
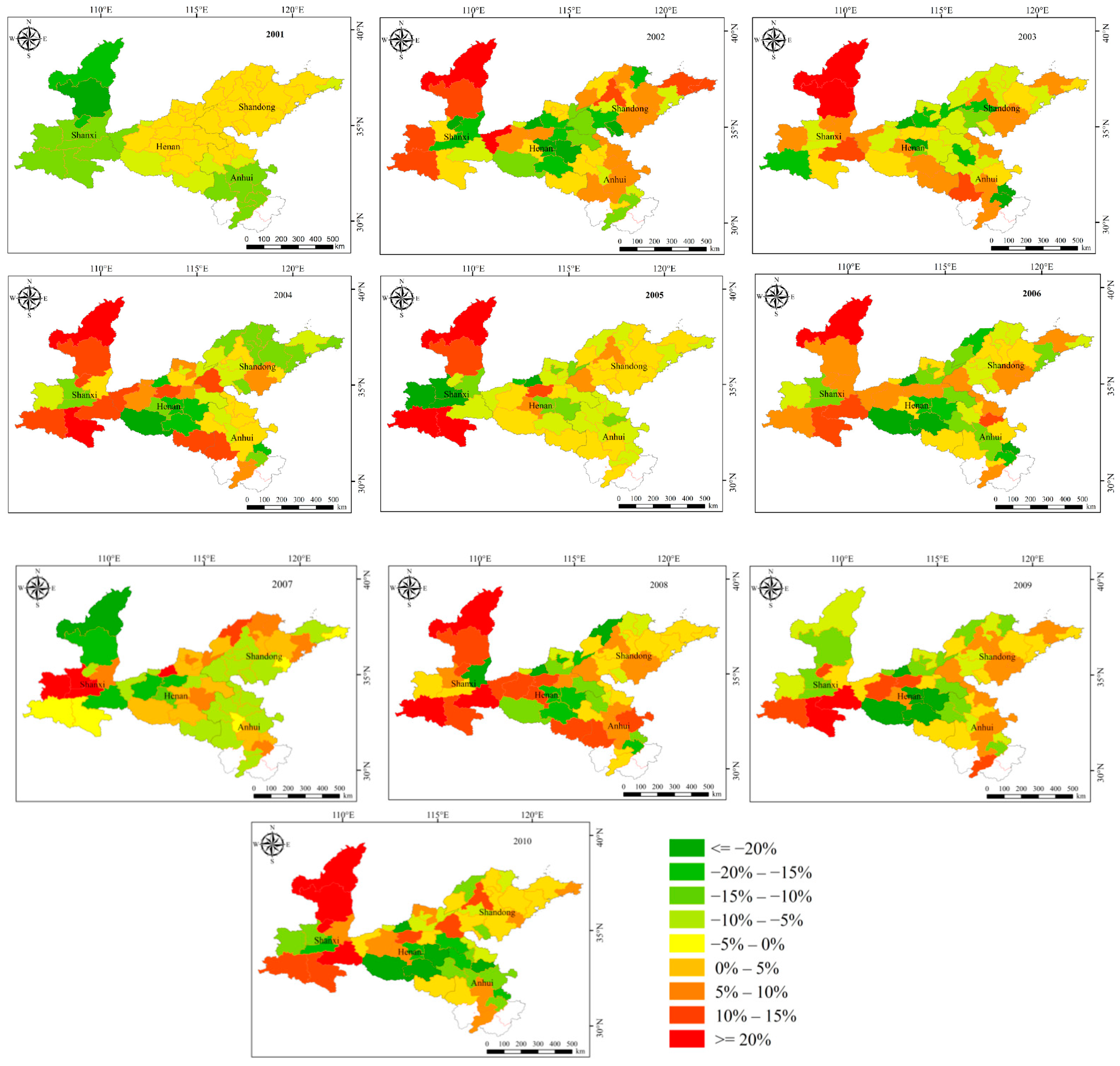
3.5. Spatial Distribution and Error Analysis of Winter Wheat Yield Forecast

We used five models to map the spatial distribution of winter wheat yield in the study area, as depicted in Figure 8. By combining official statistical data from 2001 to 2010, we found that the prediction results for 2007 were the most accurate. Therefore, we focused on comparing the predictions of the five models for the spatial distribution of winter wheat yield in 2007. Observing the data presented in the figure, it is evident that cities with higher winter wheat yields are primarily concentrated in Shandong Province, Anhui Province, and Henan Province. Conversely, cities with lower winter wheat production are mainly located in Shaanxi Province. We further analyzed the predicted yield data and plotted error graphs for the five models, as shown in Figure 9. The results indicated that the CNN and IGWO-CNN models exhibit the smallest prediction errors, with the IGWO-CNN model performing the best. The IGWO-CNN model tended to slightly underestimate the yields, but the error is minimal, and its prediction results are the closest to the statistical data. This excellent performance may be attributed to the incorporation of the optimization algorithm. In contrast, the prediction results of RFR, SVR, and KNN show a tendency to overestimate yields in high-producing areas and underestimate yields in low-producing areas. Additionally, the error analysis reveals that the RFR, SVR, and KNN models have larger errors compared to the IGWO-CNN model.
Based on the outstanding performance of the IGWO-CNN model, we plotted the spatial distribution of predicted winter wheat production from 2001 to 2010 to analyze its generalization ability in prediction. As shown in Figure 10, the overall trend of winter wheat production over the past decade has been on the rise. However, in 2002, most high-yield areas saw a significant drop in production, possibly due to environmental changes. By analyzing the error map (Figure 11), we observed a notable tendency to overestimate production in Shaanxi Province. Aside from a few years and cities where prediction errors were larger, the model’s overall performance is satisfactory, further validating the generalization capability of the IGWO-CNN model. In light of its performance, it is clear that the IGWO-CNN model possesses great potential for mining the relationship between vegetation indices, environmental data, and yield.

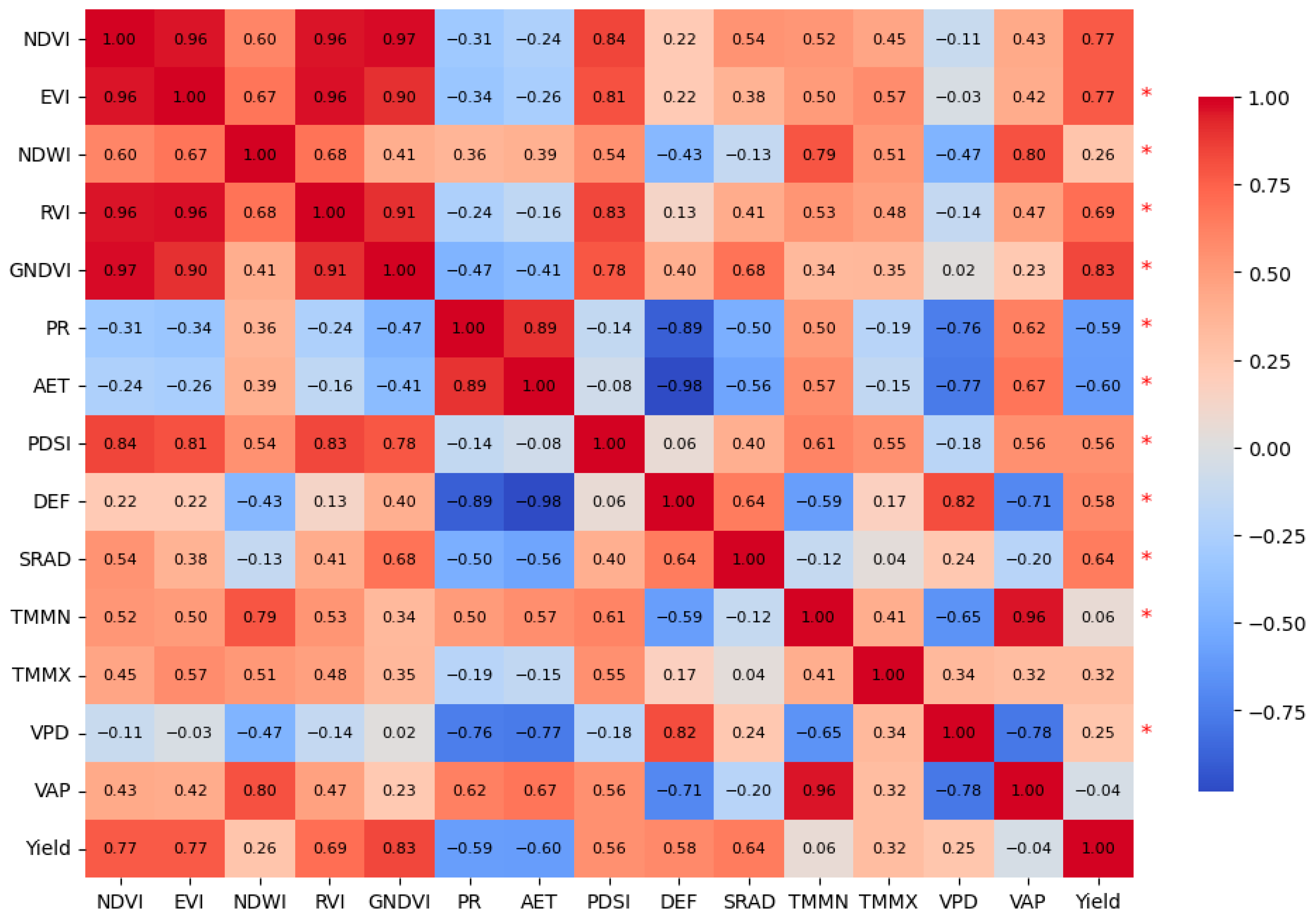
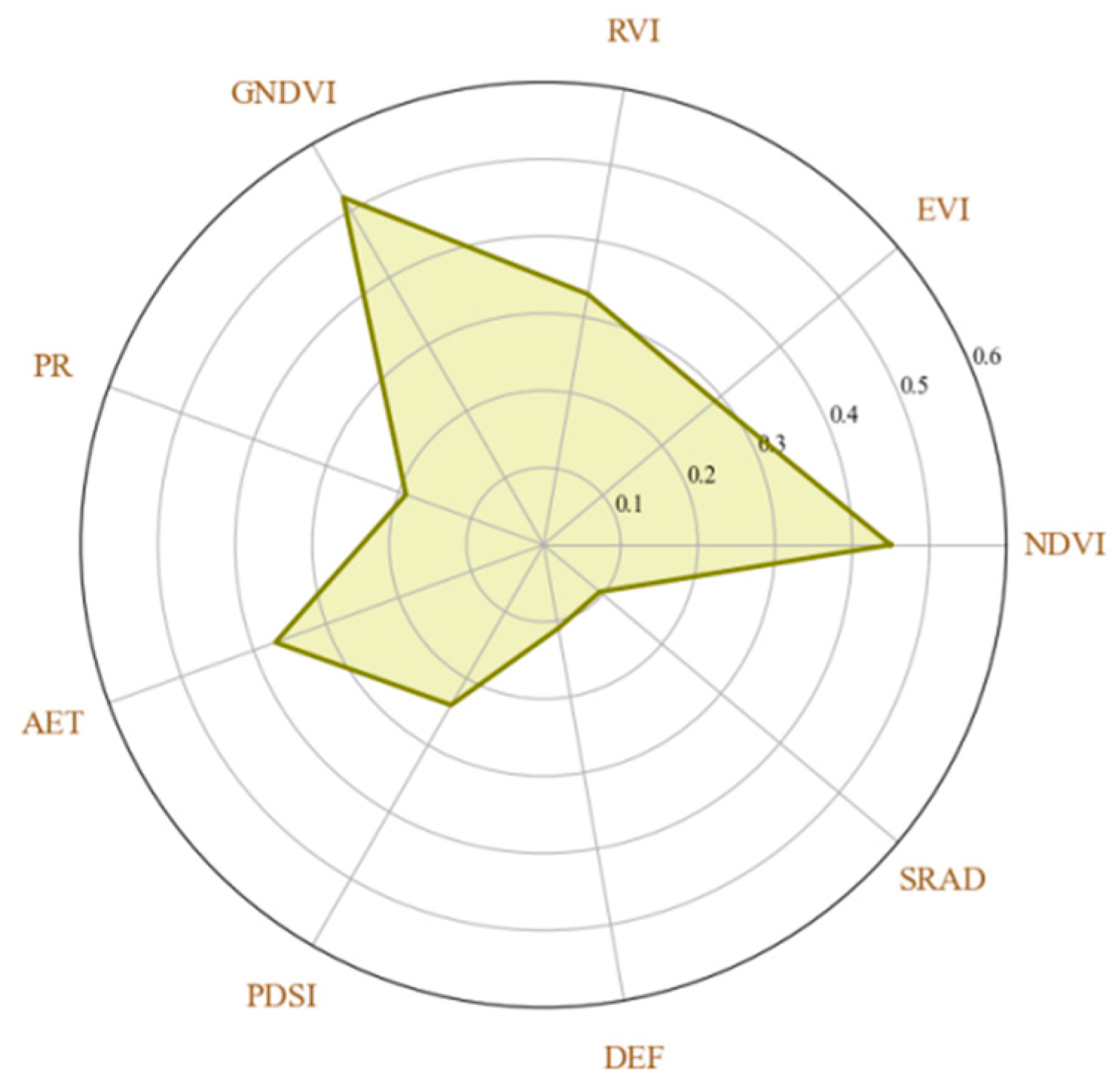
3.6. Importance of Individual Indicators in Yield Estimation

We aimed to thoroughly analyze the contribution of each indicator to winter wheat yield prediction within the IGWO-CNN model. A wind rose diagram (Figure 12) was employed to elucidate the significance of vegetation indices and environmental variables in predicting winter wheat yield. The diagram clearly depicts the weight of each factor in the prediction model, allowing for an intuitive understanding of their impact on the forecasted winter wheat yield. Our analysis revealed that GNDVI made the most substantial contribution to the forecasting process, with an importance score of 0.5204, further affirming its pivotal role in winter wheat yield forecasting. The second most influential indicator was NDVI, which scored 0.4523 in importance. NDVI primarily reflects changes in crop biomass, which, in turn, mirror the production capacity and health status of the crop. Additionally, among the environmental data, AET and PDSI exhibited the highest contributions, with importance scores of 0.3712 and 0.2461, respectively, highlighting the crucial role of environmental factors in the prediction process.

4. Discussion

In this study, we employed a method that integrates the IGWO algorithm with the CNN model, resulting in a significant improvement in prediction accuracy during the forecasting process and offering new insights into complex agricultural data analysis [51]. Compared with standalone convolutional neural network learning models, this framework demonstrates superior performance in terms of prediction accuracy, generalization, and global search capabilities [52]. The combination of the IGWO algorithm with the CNN model exhibited the highest accuracy ( R 2 = 0.7587, RMSE = 593.6, MAE = 486.6, and MAPE = 11.4%). This represents a 6.15% increase in accuracy compared to the CNN model alone, while the RMSE, MSE, and MAPE decreased by 7.34%, 6.37%, and 9.40%, respectively. Furthermore, when compared with the conventional machine learning SVR model, our approach significantly improved prediction accuracy and model stability, with notable reductions in RMSE, MSE, and MAPE. The performance of our winter wheat yield prediction model was markedly better than that of traditional machine learning models and single deep learning models, aligning with the findings of previous studies [53].
The improvement in prediction accuracy can largely be attributed to the core strength of deep learning models, which lie in their ability to learn hierarchical data features [54]. Multi-layer neural networks possess potent capabilities, enabling them to recognize patterns and features at various levels of abstraction, ranging from simple to complex [11,55]. Through layer-by-layer processing, they gradually develop a profound understanding of the data [56]. In the subsequent phases of CNN model development, we reduced the number of convolution kernels to decrease model complexity, mitigate the risk of overfitting, and focus on the most critical features rather than on all features [57]. Additionally, we incorporated the IGWO algorithm to iteratively update model parameters and identify the optimal set [58]. During experimentation, parameters were fine-tuned to achieve the best possible configuration, ensuring the model maintained optimal performance. This not only enhanced prediction accuracy but also improved the interpretability of the influencing factors.
We used the best-performing model, IGWO-CNN, to analyze the winter wheat yield forecast period. To enhance the accuracy of the experiment, most of China’s winter wheat planting areas and the important period of yield formation from March to May were selected for research [59]. This period encompasses the jointing stage through to the harvest stage of winter wheat. Extensive experimental results indicate that the winter wheat yield forecast is most accurate in April (Figure 5). Around mid-to-late April, winter wheat is in its flowering period, and the correlation coefficient between the forecast for April and the actual yield value is the highest. This finding aligns with the study by Zhuang, Zhang, Cheng, Han, Luo, Zhang, Cao, Zhang, He, Xu, and Tao [59], as the growth during the flowering period directly affects the later fruiting rate of winter wheat. At this time, winter wheat growth reaches its peak [60]. Additionally, physiological indicators, such as chlorophyll content, become easier to monitor. Chlorophyll reflects the photosynthesis capacity of crops to a certain extent and also serves as an indicator of crop grain growth [61].
In this study, we compared and analyzed the average error spatial distribution map with the predicted spatial distribution map. It can be observed from Figure 8 that models tend to overestimate the yield when predicting the yield. The southwestern part of Henan tends to be overestimated in the RF and KNN model predictions, while the central part of Shaanxi and most of Anhui tend to be overestimated in the CNN model predictions. However, there is a tendency for the SVR model predictions to be underestimated in northeastern Henan and southwestern Shandong. The IGWO-CNN model is consistent with the actual output in most areas, especially in most regions of Henan and Shandong, where it is basically consistent with the measured values. The fact that RF, KNN, and CNN all tend to overestimate in these models may be attributed to certain differences in planting methods and varieties of winter wheat across different regions during yield prediction, which in turn limit the predictive ability of the model [62,63].
From the comparative analysis of Figure 9 and Figure 10, we found that the winter wheat production in 2001 and 2002 exhibit an underestimated trend. The linear analysis of each year presented in Figure 6 indicated that the prediction accuracy for 2002 was particularly low. To delve into the reasons behind this phenomenon, we began by examining environmental parameters. These parameters encompassed precipitation, temperature, and soil moisture within the winter wheat’s growing environment. After analyzing a substantial amount of environmental data from 2002, we discovered a severe drought in April, and, upon consulting the statistical yearbook, found that the winter temperature in 2002 was 1.5–1.3 °C higher than the average temperature for the same period in other years. Continuous rainfall over a large area in May subsequently posed significant challenges to the winter wheat harvest. This series of environmental changes ultimately impacted the final winter wheat yield. Furthermore, extreme climate conditions led to substantial deviations in forecasts [64]. The yield forecast for winter wheat from 2003 to 2009 demonstrated an increasing trend, which was consistent with the trend observed in the measured yield. In 2010, the yield in some areas experienced a notable decline, attributable to drought during the critical growth period of winter wheat. Nonetheless, the yield of winter wheat in certain local areas still exhibited a slight increase in 2010, thanks to the improvement of irrigation facilities and the expansion of irrigated areas in recent years [65], which have mitigated the adverse effects of drought on crop growth.

5. Conclusions

This paper proposes a CNN model integrated with the IGWO algorithm. Furthermore, by comparing various models, including Random Forest Regression (RFR), Support Vector Machine Regression (SVR), K-Nearest Neighbors (KNN), CNN, and the proposed IGWO-CNN, we observe that the R2 values range from 0.3371 to 0.7587, the Root Mean Square Errors (RMSE) range from 593.6 to 1093.1 kg/ha, the Mean Absolute Errors (MAE) range from 486.6 to 838.4 kg/ha, and the Mean Absolute Percentage Errors (MAPE) range from 11.4% to 33.5%. Among these models, the IGWO-CNN model exhibits significant advantages in prediction accuracy, with an R2 value of 0.7587, an RMSE of 593.6 kg/ha, an MAE of 486.6 kg/ha, and a MAPE of 11.4%.
Through an in-depth analysis of various vegetation indices and environmental variables based on data from 2001 to 2010, the spatial distribution and error analysis of the IGWO-CNN model further confirm its robustness and generalization capability in predicting winter wheat yield. These results strongly indicate that the IGWO-CNN model possesses stable performance, high accuracy, and is suitable for practical applications in winter wheat yield prediction.
Looking ahead, we plan to further explore the IGWO-CNN model and apply it to yield predictions for other crops and regions. Additionally, we aim to investigate yield predictions at a finer spatial resolution.

Author Contributions

Conceptualization, H.F. and J.L. (Jian Li); methodology, H.F. and J.L. (Jian Lu); software, H.F. and J.L. (Jian Lu); validation, H.F., J.L. (Jian Lu), and X.N.; formal analysis, H.F. and X.T.; investigation, H.F. and Y.S.; resources, H.F. and X.T.; data curation, H.F. and W.Z.; writing—original draft preparation, H.F. and J.L. (Jian Li); writing—review and editing, H.F., W.Z., and J.L. (Jian Li); visualization, H.F. and X.N.; supervision, W.Z. and X.N.; project administration, W.Z. and X.N.; funding acquisition, J.L. (Jian Li). All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Changchun Science and Technology Development Program, grant number 21ZGN26 and by the Jilin Province Science and Technology Development Program, grant number 20230508026RC.

Data Availability Statement

The datasets generated and analyzed during the current study are available from the corresponding author upon reasonable request. These datasets are not publicly accessible as they are subject to ongoing research and contain information that has not yet been fully disseminated.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Gupta, R.; Meghwal, M.; Prabhakar, P.K. Bioactive compounds of pigmented wheat (Triticum aestivum): Potential benefits in human health. Trends Food Sci. Technol. 2021, 110, 240–252. [Google Scholar] [CrossRef]
  2. Omotoso, A.B.; Letsoalo, S.; Olagunju, K.O.; Tshwene, C.S.; Omotayo, A.O. Climate change and variability in sub-Saharan Africa: A systematic review of trends and impacts on agriculture. J. Clean. Prod. 2023, 414, 137487. [Google Scholar] [CrossRef]
  3. Nordmeyer, E.F.; Danne, M.; Musshoff, O. Can satellite-retrieved data increase farmers’ willingness to insure against drought?—Insights from Germany. Agric. Syst. 2023, 211, 103718. [Google Scholar] [CrossRef]
  4. Ali, A.; Hussain, T.; Tantashutikun, N.; Hussain, N.; Cocetta, G. Application of Smart Techniques, Internet of Things and Data Mining for Resource Use Efficient and Sustainable Crop Production. Agriculture 2023, 13, 397. [Google Scholar] [CrossRef]
  5. Casagli, N.; Intrieri, E.; Tofani, V.; Gigli, G.; Raspini, F. Landslide detection, monitoring and prediction with remote-sensing techniques. Nat. Rev. Earth Environ. 2023, 4, 51–64. [Google Scholar] [CrossRef]
  6. Sheikh, M.; Iqra, F.; Ambreen, H.; Pravin, K.A.; Ikra, M.; Chung, Y.S. Integrating artificial intelligence and high-throughput phenotyping for crop improvement. J. Integr. Agric. 2024, 23, 1787–1802. [Google Scholar] [CrossRef]
  7. Clark, R.; Dahlhaus, P.; Robinson, N.; Larkins, J.-a.; Morse-McNabb, E. Matching the model to the available data to predict wheat, barley, or canola yield: A review of recently published models and data. Agric. Syst. 2023, 211, 103749. [Google Scholar] [CrossRef]
  8. Kumar, R.; Agrawal, N. Analysis of multi-dimensional Industrial IoT (IIoT) data in Edge–Fog–Cloud based architectural frameworks: A survey on current state and research challenges. J. Ind. Inf. Integr. 2023, 35, 100504. [Google Scholar] [CrossRef]
  9. Hai, A.; Bharath, G.; Patah, M.F.A.; Daud, W.M.A.W.; Rambabu, K.; Show, P.; Banat, F. Machine learning models for the prediction of total yield and specific surface area of biochar derived from agricultural biomass by pyrolysis. Environ. Technol. Innov. 2023, 30, 103071. [Google Scholar] [CrossRef]
  10. Luo, L.; Sun, S.; Xue, J.; Gao, Z.; Zhao, J.; Yin, Y.; Gao, F.; Luan, X. Crop yield estimation based on assimilation of crop models and remote sensing data: A systematic evaluation. Agric. Syst. 2023, 210, 103711. [Google Scholar] [CrossRef]
  11. Ahmed, S.F.; Alam, M.S.B.; Hassan, M.; Rozbu, M.R.; Ishtiak, T.; Rafa, N.; Mofijur, M.; Shawkat Ali, A.B.M.; Gandomi, A.H. Deep learning modelling techniques: Current progress, applications, advantages, and challenges. Artif. Intell. Rev. 2023, 56, 13521–13617. [Google Scholar] [CrossRef]
  12. Naghdyzadegan Jahromi, M.; Zand-Parsa, S.; Razzaghi, F.; Jamshidi, S.; Didari, S.; Doosthosseini, A.; Pourghasemi, H.R. Developing machine learning models for wheat yield prediction using ground-based data, satellite-based actual evapotranspiration and vegetation indices. Eur. J. Agron. 2023, 146, 126820. [Google Scholar] [CrossRef]
  13. Arshad, S.; Kazmi, J.H.; Javed, M.G.; Mohammed, S. Applicability of machine learning techniques in predicting wheat yield based on remote sensing and climate data in Pakistan, South Asia. Eur. J. Agron. 2023, 147, 126837. [Google Scholar] [CrossRef]
  14. Dhaliwal, D.S.; Williams, M.M. Sweet corn yield prediction using machine learning models and field-level data. Precis. Agric. 2024, 25, 51–64. [Google Scholar] [CrossRef]
  15. Mütter, F.; Berger, C.; Königshofer, B.; Höber, M.; Hochenauer, C.; Subotić, V. Artificial intelligence for solid oxide fuel cells: Combining automated high accuracy artificial neural network model generation and genetic algorithm for time-efficient performance prediction and optimization. Energy Convers. Manag. 2023, 291, 117263. [Google Scholar] [CrossRef]
  16. Vigya; Shiva, C.K.; Vedik, B.; Raj, S.; Mahapatra, S.; Mukherjee, V. A novel chaotic chimp sine cosine algorithm part-II: Automatic generation control of complex power system. Chaos Solitons Fractals 2023, 173, 113673. [Google Scholar] [CrossRef]
  17. Bian, K.; Priyadarshi, R. Machine learning optimization techniques: A Survey, classification, challenges, and Future Research Issues. Arch. Comput. Methods Eng. 2024, 31, 4209–4233. [Google Scholar] [CrossRef]
  18. Han, W.; Gu, Q.; Gu, H.; Xia, R.; Gao, Y.; Zhou, Z.; Luo, K.; Fang, X.; Zhang, Y. Design of Chili Field Navigation System Based on Multi-Sensor and Optimized TEB Algorithm. Agronomy 2024, 14, 2872. [Google Scholar] [CrossRef]
  19. Tian, H.; Wang, P.; Tansey, K.; Zhang, S.; Zhang, J.; Li, H. An IPSO-BP neural network for estimating wheat yield using two remotely sensed variables in the Guanzhong Plain, PR China. Comput. Electron. Agric. 2020, 169, 105180. [Google Scholar] [CrossRef]
  20. Hatta, N.M.; Zain, A.M.; Sallehuddin, R.; Shayfull, Z.; Yusoff, Y. Recent studies on optimisation method of Grey Wolf Optimiser (GWO): A review (2014–2017). Artif. Intell. Rev. 2019, 52, 2651–2683. [Google Scholar] [CrossRef]
  21. Castillo-García, G.; Morán-Fernández, L.; Bolón-Canedo, V. Feature selection for domain adaptation using complexity measures and swarm intelligence. Neurocomputing 2023, 548, 126422. [Google Scholar] [CrossRef]
  22. Bardhan, A.; Biswas, R.; Kardani, N.; Iqbal, M.; Samui, P.; Singh, M.P.; Asteris, P.G. A novel integrated approach of augmented grey wolf optimizer and ANN for estimating axial load carrying-capacity of concrete-filled steel tube columns. Constr. Build. Mater. 2022, 337, 127454. [Google Scholar] [CrossRef]
  23. Md-Tahir, H.; Mahmood, H.S.; Husain, M.; Khalil, A.; Shoaib, M.; Ali, M.; Ali, M.M.; Tasawar, M.; Khan, Y.A.; Awan, U.K.; et al. Localized Crop Classification by NDVI Time Series Analysis of Remote Sensing Satellite Data; Applications for Mechanization Strategy and Integrated Resource Management. AgriEngineering 2024, 6, 2429–2444. [Google Scholar] [CrossRef]
  24. Dong, J.; Fu, Y.; Wang, J.; Tian, H.; Fu, S.; Niu, Z.; Han, W.; Zheng, Y.; Huang, J.; Yuan, W. Early-season mapping of winter wheat in China based on Landsat and Sentinel images. Earth Syst. Sci. Data 2020, 12, 3081–3095. [Google Scholar] [CrossRef]
  25. Cihlar, J.; St.-Laurent, L.; Dyer, J.A. Relation between the normalized difference vegetation index and ecological variables. Remote Sens. Environ. 1991, 35, 279–298. [Google Scholar] [CrossRef]
  26. Kyratzis, A.C.; Skarlatos, D.P.; Menexes, G.C.; Vamvakousis, V.F.; Katsiotis, A. Assessment of Vegetation Indices Derived by UAV Imagery for Durum Wheat Phenotyping under a Water Limited and Heat Stressed Mediterranean Environment. Front. Plant Sci. 2017, 8, 1114. [Google Scholar] [CrossRef]
  27. Gao, B.-c. NDWI—A normalized difference water index for remote sensing of vegetation liquid water from space. Remote Sens. Environ. 1996, 58, 257–266. [Google Scholar] [CrossRef]
  28. Huete, A.R. A soil-adjusted vegetation index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
  29. Gregow, E.; Saltikoff, E.; Albers, S.; Hohti, H. Precipitation accumulation analysis–assimilation of radar-gauge measurements and validation of different methods. Hydrol. Earth Syst. Sci. 2013, 17, 4109–4120. [Google Scholar] [CrossRef]
  30. Hadadi, F.; Moazenzadeh, R.; Mohammadi, B. Estimation of actual evapotranspiration: A novel hybrid method based on remote sensing and artificial intelligence. J. Hydrol. 2022, 609, 127774. [Google Scholar] [CrossRef]
  31. Amirhajloo, S.; Gheysari, M.; Shayannejad, M.; Shirvani, M. Selection of the best nitrogen fertilizer management scenario in wheat based on Palmer drought severity index with an environmental perspective. Eur. J. Agron. 2023, 151, 126980. [Google Scholar] [CrossRef]
  32. Grossman, J.J. Phenological physiology: Seasonal patterns of plant stress tolerance in a changing climate. New Phytol. 2023, 237, 1508–1524. [Google Scholar] [CrossRef] [PubMed]
  33. Hao, H.; Yao, J.; Chen, Y.; Xu, J.; Li, Z.; Duan, W.; Ismail, S.; Wang, G. Ecological transitions in Xinjiang, China: Unraveling the impact of climate change on vegetation dynamics (1990–2020). J. Geogr. Sci. 2024, 34, 1039–1064. [Google Scholar] [CrossRef]
  34. Kakhani, N.; Rangzan, M.; Jamali, A.; Attarchi, S.; Alavipanah, S.K.; Mommert, M.; Tziolas, N.; Scholten, T. SSL-SoilNet: A Hybrid Transformer-Based Framework with Self-Supervised Learning for Large-Scale Soil Organic Carbon Prediction. IEEE Trans. Geosci. Remote Sens. 2024, 62, 4509915. [Google Scholar] [CrossRef]
  35. Yang, F.; Zhang, D.; Zhang, Y.; Zhang, Y.; Han, Y.; Zhang, Q.; Zhang, Q.; Zhang, C.; Liu, Z.; Wang, K. Prediction of corn variety yield with attribute-missing data via graph neural network. Comput. Electron. Agric. 2023, 211, 108046. [Google Scholar] [CrossRef]
  36. Noguera, I.; Vicente-Serrano, S.M.; Peña-Angulo, D.; Domínguez-Castro, F.; Juez, C.; Tomás-Burguera, M.; Lorenzo-Lacruz, J.; Azorin-Molina, C.; Halifa-Marín, A.; Fernández-Duque, B.; et al. Assessment of vapor pressure deficit variability and trends in Spain and possible connections with soil moisture. Atmos. Res. 2023, 285, 106666. [Google Scholar] [CrossRef]
  37. Guo, W.; Huang, S.; Huang, Q.; She, D.; Shi, H.; Leng, G.; Li, J.; Cheng, L.; Gao, Y.; Peng, J. Precipitation and vegetation transpiration variations dominate the dynamics of agricultural drought characteristics in China. Sci. Total Environ. 2023, 898, 165480. [Google Scholar] [CrossRef] [PubMed]
  38. Guo, J.; Zan, X.; Wang, L.; Lei, L.; Ou, C.; Bai, S. A random forest regression with Bayesian optimization-based method for fatigue strength prediction of ferrous alloys. Eng. Fract. Mech. 2023, 293, 109714. [Google Scholar] [CrossRef]
  39. Roy, A.; Chakraborty, S. Support vector machine in structural reliability analysis: A review. Reliab. Eng. Syst. Saf. 2023, 233, 109126. [Google Scholar] [CrossRef]
  40. Ngu, J.C.Y.; Yeo, W.S.; Thien, T.F.; Nandong, J. A comprehensive overview of the applications of kernel functions and data-driven models in regression and classification tasks in the context of software sensors. Appl. Soft Comput. 2024, 164, 111975. [Google Scholar] [CrossRef]
  41. Wang, A.X.; Chukova, S.S.; Nguyen, B.P. Ensemble k-nearest neighbors based on centroid displacement. Inf. Sci. 2023, 629, 313–323. [Google Scholar] [CrossRef]
  42. Agrawal, P.; Gnanaprakash, R.; Dhawane, S.H. Prediction of Biodiesel Yield Employing Machine Learning: Interpretability Analysis via Shapley Additive Explanations. Fuel 2024, 359, 130516. [Google Scholar] [CrossRef]
  43. Yang, Y.; Zhang, Y.; Cheng, Y.; Lei, Z.; Gao, X.; Huang, Y.; Ma, Y. Using one-dimensional convolutional neural networks and data augmentation to predict thermal production in geothermal fields. J. Clean. Prod. 2023, 387, 135879. [Google Scholar] [CrossRef]
  44. Guo, Z.; Yang, C.; Wang, D.; Liu, H. A novel deep learning model integrating CNN and GRU to predict particulate matter concentrations. Process Saf. Environ. Prot. 2023, 173, 604–613. [Google Scholar] [CrossRef]
  45. Singh, P.; Chaudhury, S.; Panigrahi, B.K. Hybrid MPSO-CNN: Multi-level Particle Swarm optimized hyperparameters of Convolutional Neural Network. Swarm Evol. Comput. 2021, 63, 100863. [Google Scholar] [CrossRef]
  46. Gad, A.G.; Houssein, E.H.; Zhou, M.; Suganthan, P.N.; Wazery, Y.M. Damping-Assisted Evolutionary Swarm Intelligence for Industrial IoT Task Scheduling in Cloud Computing. IEEE Internet Things J. 2024, 11, 1698–1710. [Google Scholar] [CrossRef]
  47. Yu, X.; Hu, Z. A multi-strategy driven reinforced hierarchical operator in the grey wolf optimizer for feature selection. Inf. Sci. 2024, 677, 120924. [Google Scholar] [CrossRef]
  48. Nguyen, T.; Kashani, A.; Ngo, T.; Bordas, S. Deep neural network with high-order neuron for the prediction of foamed concrete strength. Comput.-Aided Civ. Infrastruct. Eng. 2019, 34, 316–332. [Google Scholar] [CrossRef]
  49. Friedman, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
  50. Ghimire, S.; Deo, R.C.; Casillas-Pérez, D.; Salcedo-Sanz, S. Efficient daily electricity demand prediction with hybrid deep-learning multi-algorithm approach. Energy Convers. Manag. 2023, 297, 117707. [Google Scholar] [CrossRef]
  51. Huo, D.; Malik, A.W.; Ravana, S.D.; Rahman, A.U.; Ahmedy, I. Mapping smart farming: Addressing agricultural challenges in data-driven era. Renew. Sustain. Energy Rev. 2024, 189, 113858. [Google Scholar] [CrossRef]
  52. Jalali, S.M.J.; Ahmadian, S.; Khodayar, M.; Khosravi, A.; Shafie-khah, M.; Nahavandi, S.; Catalão, J.P.S. An advanced short-term wind power forecasting framework based on the optimized deep neural network models. Int. J. Electr. Power Energy Syst. 2022, 141, 108143. [Google Scholar] [CrossRef]
  53. Abou Houran, M.; Salman Bukhari, S.M.; Zafar, M.H.; Mansoor, M.; Chen, W. COA-CNN-LSTM: Coati optimization algorithm-based hybrid deep learning model for PV/wind power forecasting in smart grid applications. Appl. Energy 2023, 349, 121638. [Google Scholar] [CrossRef]
  54. Hashemi, M.G.Z.; Tan, P.-N.; Jalilvand, E.; Wilke, B.; Alemohammad, H.; Das, N.N. Yield estimation from SAR data using patch-based deep learning and machine learning techniques. Comput. Electron. Agric. 2024, 226, 109340. [Google Scholar] [CrossRef]
  55. Zheng, H.; Zheng, Z.; Hu, R.; Xiao, B.; Wu, Y.; Yu, F.; Liu, X.; Li, G.; Deng, L. Temporal dendritic heterogeneity incorporated with spiking neural networks for learning multi-timescale dynamics. Nat. Commun. 2024, 15, 277. [Google Scholar] [CrossRef] [PubMed]
  56. Phiphitphatphaisit, S.; Surinta, O. Multi-layer adaptive spatial-temporal feature fusion network for efficient food image recognition. Expert Syst. Appl. 2024, 255, 124834. [Google Scholar] [CrossRef]
  57. Jonathan, A.L.; Cai, D.; Ukwuoma, C.C.; Nkou, N.J.J.; Huang, Q.; Bamisile, O. A radiant shift: Attention-embedded CNNs for accurate solar irradiance forecasting and prediction from sky images. Renew. Energy 2024, 234, 121133. [Google Scholar] [CrossRef]
  58. Yuan, C.; Zhao, D.; Heidari, A.A.; Liu, L.; Chen, Y.; Chen, H. Polar lights optimizer: Algorithm and applications in image segmentation and feature selection. Neurocomputing 2024, 607, 128427. [Google Scholar] [CrossRef]
  59. Zhuang, H.; Zhang, Z.; Cheng, F.; Han, J.; Luo, Y.; Zhang, L.; Cao, J.; Zhang, J.; He, B.; Xu, J.; et al. Integrating data assimilation, crop model, and machine learning for winter wheat yield forecasting in the North China Plain. Agric. For. Meteorol. 2024, 347, 109909. [Google Scholar] [CrossRef]
  60. Fischer, T.; Gonzalez, F.G.; Miralles, D.J. Breeding for increased grains/m2 in wheat crops through targeting critical period duration: A review. Field Crops Res. 2024, 316, 109497. [Google Scholar] [CrossRef]
  61. Zhang, B.; Gu, L.; Dai, M.; Bao, X.; Sun, Q.; Zhang, M.; Qu, X.; Li, Z.; Zhen, W.; Gu, X. Estimation of grain filling rate of winter wheat using leaf chlorophyll and LAI extracted from UAV images. Field Crops Res. 2024, 306, 109198. [Google Scholar] [CrossRef]
  62. Lu, J.; Fu, H.; Tang, X.; Liu, Z.; Huang, J.; Zou, W.; Chen, H.; Sun, Y.; Ning, X.; Li, J. GOA-optimized deep learning for soybean yield estimation using multi-source remote sensing data. Sci. Rep. 2024, 14, 7097. [Google Scholar] [CrossRef] [PubMed]
  63. Li, J.; He, Z.; Zhou, G.; Yan, S.; Zhang, J. DeepAT: A Deep Learning Wheat Phenotype Prediction Model Based on Genotype Data. Agronomy 2024, 14, 2756. [Google Scholar] [CrossRef]
  64. Chen, L.; Zhong, X.; Li, H.; Wu, J.; Lu, B.; Chen, D.; Xie, S.-P.; Wu, L.; Chao, Q.; Lin, C.; et al. A machine learning model that outperforms conventional global subseasonal forecast models. Nat. Commun. 2024, 15, 6425. [Google Scholar] [CrossRef]
  65. Xue, S.; Fang, Z.; van Riper, C.; He, W.; Li, X.; Zhang, F.; Wang, T.; Cheng, C.; Zhou, Q.; Huang, Z.; et al. Ensuring China’s food security in a geographical shift of its grain production: Driving factors, threats, and solutions. Resour. Conserv. Recycl. 2024, 210, 107845. [Google Scholar] [CrossRef]
Agronomy 15 00205 g001
Figure 1. Map of 2010 Research Area with Cultivated Winter Wheat: Green Indicates Masked Areas.
Figure 1. Map of 2010 Research Area with Cultivated Winter Wheat: Green Indicates Masked Areas.
Agronomy 15 00205 g001
Agronomy 15 00205 g002
Figure 2. Network architecture of the CNN model enhanced with improved Gray Wolf Optimizer for winter wheat yield prediction.
Figure 2. Network architecture of the CNN model enhanced with improved Gray Wolf Optimizer for winter wheat yield prediction.
Agronomy 15 00205 g002
Agronomy 15 00205 g003
Figure 3. Framework for winter wheat yield prediction integrating satellite remote sensing and machine/deep learning models.
Figure 3. Framework for winter wheat yield prediction integrating satellite remote sensing and machine/deep learning models.
Agronomy 15 00205 g003
Agronomy 15 00205 g004
Figure 4. Inter–Variable and yield correlation heatmap with significance indicators. The * indicates that the correlation coefficient (r) has a p–value less than 0.001, which suggests a very high level of statistical significance for that particular correlation.
Figure 4. Inter–Variable and yield correlation heatmap with significance indicators. The * indicates that the correlation coefficient (r) has a p–value less than 0.001, which suggests a very high level of statistical significance for that particular correlation.
Agronomy 15 00205 g004
Agronomy 15 00205 g005
Figure 5. Comparison of predictive performance among five models using (a) R2, (b) RMSE, (c) MAE, and (d) MAEP metrics; white circles indicate errors.
Figure 5. Comparison of predictive performance among five models using (a) R2, (b) RMSE, (c) MAE, and (d) MAEP metrics; white circles indicate errors.
Agronomy 15 00205 g005
Agronomy 15 00205 g006
Figure 6. R2, RMSE, MAE, and MAEP metrics of winter wheat yield prediction models across different periods (2001–2010), evaluated at county scale using leave–one–year–out validation. error bars represent standard error of the mean across validation folds.
Figure 6. R2, RMSE, MAE, and MAEP metrics of winter wheat yield prediction models across different periods (2001–2010), evaluated at county scale using leave–one–year–out validation. error bars represent standard error of the mean across validation folds.
Agronomy 15 00205 g006
Agronomy 15 00205 g007aAgronomy 15 00205 g007b
Figure 7. Comparison of observed and IGWO-CNN model predicted winter wheat yields from 2001 to 2010. Dotted line represents 1:1 line, red line indicates trend line.
Figure 7. Comparison of observed and IGWO-CNN model predicted winter wheat yields from 2001 to 2010. Dotted line represents 1:1 line, red line indicates trend line.
Agronomy 15 00205 g007aAgronomy 15 00205 g007b
Agronomy 15 00205 g008
Figure 8. Spatial pattern of winter wheat yield predictions for 2007 based on RFR, SVR, KNN, CNN, and IGWO-CNN models.
Figure 8. Spatial pattern of winter wheat yield predictions for 2007 based on RFR, SVR, KNN, CNN, and IGWO-CNN models.
Agronomy 15 00205 g008
Agronomy 15 00205 g009
Figure 9. Mean errors of winter wheat yield prediction in 2007 using RFR, SVR, KNN, CNN, and IGWO-CNN.
Figure 9. Mean errors of winter wheat yield prediction in 2007 using RFR, SVR, KNN, CNN, and IGWO-CNN.
Agronomy 15 00205 g009
Agronomy 15 00205 g010
Figure 10. Spatial distribution of winter wheat yield predictions using the IGWO-CNN model from 2001 to 2010.
Figure 10. Spatial distribution of winter wheat yield predictions using the IGWO-CNN model from 2001 to 2010.
Agronomy 15 00205 g010
Agronomy 15 00205 g011
Figure 11. Mean errors of winter wheat yield prediction from 2001 to 2010 by IGWO-CNN.
Figure 11. Mean errors of winter wheat yield prediction from 2001 to 2010 by IGWO-CNN.
Agronomy 15 00205 g011
Agronomy 15 00205 g012
Figure 12. Importance of individual indicators obtained through SHAP analysis of the IGWO-CNN model.
Figure 12. Importance of individual indicators obtained through SHAP analysis of the IGWO-CNN model.
Agronomy 15 00205 g012
Table 1. Sources of data.
Table 1. Sources of data.
DataVariableTemporal ResolutionSpatial ResolutionSource
Vegetation indicesNDVI, EVI, NDWI, RVI, GNDVI16-day500 mMOD13A1 Version 6.1 product
Environmental dataPR, AET, PDSI, DEF, SRAD, TMMN, TMMX, VPD, VAPMonthly1 kmTerraClimate datasets
Winter wheat yield and planting areaPlanting areaYear30 mhttps://doi.org/10.5194/essd-12-3081-2020
(accessed on 23 June 2024)
Yield data for winter wheatYearCityhttps://tjj.henan.gov.cn/
(accessed on 23 June 2024)
YearCityhttps://tjj.shaanxi.gov.cn/
(accessed on 26 June 2024)
YearCityhttps://tjj.shandong.gov.cn/
(accessed on 26 June 2024)
YearCityhttps://tjj.ah.gov.cn/
(accessed on 26 June 2024)
Table 2. Hyperparameters tested and selected for each model.
Table 2. Hyperparameters tested and selected for each model.
ModelHyperparameterSelected Value
RFRn_estimators200
min_samples_leaf2
random_state2
SVRKerneRBF
gamma0.00001
Epsilon0.001
Regularization Parameter (C)1000
KNNn_neighbors5
weightsUniform
algorithmAuto
leaf_size30
p2
CNNfilters64, 128, 512
kernel_size3
dense_layers2
dense_neurons32
learning_rate0.0006
loss_functionMse
batch_size256
epochs1000
IGWO-CNNfilters64, 128, 512
kernel_size2
dense_layers2
dense_neurons70
learning_rate0.001
loss_functionMse
batch_size512
epochs1000
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Fu, H.; Lu, J.; Li, J.; Zou, W.; Tang, X.; Ning, X.; Sun, Y. Winter Wheat Yield Prediction Using Satellite Remote Sensing Data and Deep Learning Models. Agronomy 2025, 15, 205. https://doi.org/10.3390/agronomy15010205

AMA Style

Fu H, Lu J, Li J, Zou W, Tang X, Ning X, Sun Y. Winter Wheat Yield Prediction Using Satellite Remote Sensing Data and Deep Learning Models. Agronomy. 2025; 15(1):205. https://doi.org/10.3390/agronomy15010205

Chicago/Turabian Style

Fu, Hongkun, Jian Lu, Jian Li, Wenlong Zou, Xuhui Tang, Xiangyu Ning, and Yue Sun. 2025. "Winter Wheat Yield Prediction Using Satellite Remote Sensing Data and Deep Learning Models" Agronomy 15, no. 1: 205. https://doi.org/10.3390/agronomy15010205

APA Style

Fu, H., Lu, J., Li, J., Zou, W., Tang, X., Ning, X., & Sun, Y. (2025). Winter Wheat Yield Prediction Using Satellite Remote Sensing Data and Deep Learning Models. Agronomy, 15(1), 205. https://doi.org/10.3390/agronomy15010205

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop