Prediction of Greenhouse Microclimatic Parameters Using Building Transient Simulation and Artificial Neural Networks

Abstract

In the realm of agricultural advancement, the relentless quest for agricultural efficiency amidst the vagaries of climate change has positioned greenhouse technology as a linchpin for secure and sustainable food production. The precise management of greenhouse microclimatic conditions i.e., the ability to accurately predict and maintain ideal temperature and relative humidity, is crucial for enhancing plant growth and health, optimizing resource use, and ensuring sustainable agricultural practices. However, maintaining optimal microclimatic conditions is a significant challenge due to the dynamic nature of external environmental influences. This study aims to address the critical need for advanced predictive tools that can enhance the control and management of greenhouse microclimates, thereby supporting sustainable agricultural practices and food security. Our research introduces a novel integration of building transient simulation (TRNSYS) and artificial neural networks (ANNs) to predict temperature and relative humidity inside a greenhouse across the calendar year, based on external atmospheric conditions. The TRNSYS model meticulously simulates the greenhouse’s thermal load, incorporating real-world data to ensure a high level of accuracy in describing the facility’s dynamic behavior. Our ANN model, composed of three layers, underwent optimization to identify the ideal number of neurons, learning rates, and epochs, settling on a model configuration that minimized prediction errors. The evaluation metrics, including root mean square error (RMSE) and mean absolute error (MAE), demonstrated the model’s effectiveness, with an RMSE of 0.3166 °C for temperature and 5.9% for relative humidity, and MAE values of 0.1002° and 3.4%, respectively. These findings underscore the model’s potential as a powerful tool for greenhouse climate control, offering substantial benefits in terms of energy efficiency, resource optimization, and overall sustainability in agriculture. By leveraging detailed dynamic simulations and advanced neural network algorithms, this study contributes significantly to the field of precision agriculture, presenting a novel approach to managing greenhouse environments in the face of changing climatic conditions.

1. Introduction

The advent of glass and plastic greenhouses has significantly advanced agricultural productivity by offering controlled environments that protect plants from extreme weather while managing essential conditions like air temperature, humidity, and CO₂ levels [1,2,3,4,5]. These innovations are vital in areas with sub-optimal climate conditions, extending cultivation periods beyond traditional growing seasons. However, the variability of these parameters, influenced by stochastic external climatic conditions, challenges the stability and efficiency of greenhouse microclimates.

Historically, these structures have transitioned from simple protective enclosures to complex systems, meticulously managing internal climates to enhance plant growth and extend growing seasons [6]. Contemporary greenhouse operations are increasingly reliant on innovative methods to improve energy efficiency and microclimate control. The integration of technologies such as passive cooling and heating systems, renewable energy sources, and dynamic modeling of internal environments reflects a shift towards sustainable practices that align with global sustainability goals. Enhancing energy efficiency in greenhouses has centered on integrating renewable energy sources such as solar and geothermal systems for heating [7,8,9,10]. Similarly, innovative cooling strategies, such as the utilization of rock beds, have demonstrated the potential to maintain lower temperatures within polyethylene tunnel-type greenhouses, providing a sustainable alternative to conventional cooling methods [4]. These developments highlight the ongoing need for advanced systems capable of dynamic environmental control.

Recent advancements in artificial neural networks (ANNs) have shown substantial promise in predicting essential microclimatic parameters, allowing for more responsive adjustments to internal greenhouse conditions based on external climatic changes [11,12,13]. This study aims to refine these predictive capabilities by developing and validating an ANN model using data from a TRNSYS simulation of existing greenhouse structures [14,15,16,17,18,19,20,21]. This model is expected to enhance the operational effectiveness and energy efficiency of greenhouses by accurately forecasting temperature and relative humidity variations [22,23,24]. Furthermore, the interaction between internal and external climatic conditions necessitates the use of comprehensive models that account for unpredictable environmental factors, which can significantly impact thermal dynamics and plant growth [25,26,27,28,29,30,31]. By enhancing the predictability and control of temperature and relative humidity, the proposed model aims to contribute effectively to sustainable agricultural practices.

Our methodology builds on previous work by incorporating detailed simulations that consider the intricate energy dynamics within greenhouses, such as solar radiation and energy transfer through construction materials [32,33,34,35]. By integrating insights from established studies on passive and active greenhouse heating in southern Europe, we aim to tailor our model to real-world applications, ensuring its relevance across different climatic conditions [4]. In summary, this research leverages cutting-edge machine learning techniques to tackle the complex challenges of greenhouse climate management. By developing a robust ANN model that effectively predicts and manages microclimatic conditions, this study contributes to the broader goals of sustainable agriculture, maximizing productivity while minimizing environmental impact and resource use [36,37,38,39].

2. Materials and Methods

This study was conducted in a greenhouse in the region of Šabac municipality in Serbia. The “Farmakom MB” greenhouse, located in Debrc, near the main road from Šabac to Obrenovac, close to the Sava River, is ideally situated for production in a protected area using geothermal water energy for heating. This location is particularly suitable due to its mild winters and not so pronounced low temperatures, and also because of the large number of geothermal water sources with satisfactory temperatures that the region is rich in. The facility covers a total area of 4.2 hectares, with dimensions of 365 m in length, 115 m in width, and 6.5 m in height, featuring a double-foil envelope composed of 3 to 5 layers, between which air is constantly blown to form a 15 cm thick air layer maintained at overpressure.

The space inside the greenhouse is divided into 8 units of 0.5 hectares each. In the technical section, there is no heating system, and the temperature is maintained solely by sunlight passing through the roof domes. A special area with controlled conditions, completely isolated from the rest of the greenhouse, is designated for seedling preparation, where set parameters of temperature and relative humidity are maintained throughout the year. The rest of the facility is divided into four interconnected areas without any barriers, which further complicates the control of conditions for plant cultivation, both in terms of maintaining defined atmospheric conditions and potentially isolating plants from the occurrence of possible diseases. In the central part of the greenhouse, there are water tanks for irrigation, pumps that deliver geothermal water for heating, and tanks with artificial nutrition for plants. Throughout the year, the facility produces vegetable crops, mostly tomatoes, and to a lesser extent peppers, cucumbers, and lettuce during the winter period.

To validate both models, TRNSYS Type 56 and ANNs, various types of data were collected from sensors located in the greenhouse used for controlling thermal conditions. Temperature and humidity sensors were installed at three different heights—0.5 m, 2 m, and 4 m—across five rows in length and five columns in width, totaling 25 sensors at each height (3 × 25). Measurements were conducted using sets of WatchDog Data Loggers Model 150 Temp/RH and a WatchDog Data Logger Model 450, with a temperature accuracy of ±0.6 °C and relative humidity accuracy of ±3%. Additionally, solar energy was measured at the 2 m height using two solarimeters connected to a WatchDog Data Logger Model 450. These solarimeters have a measuring range of 1–1250 W/m², with a precision of ±5%. The measurement interval was set to every hour.

2.1. TRNSYS Generalized Thermal Load Model

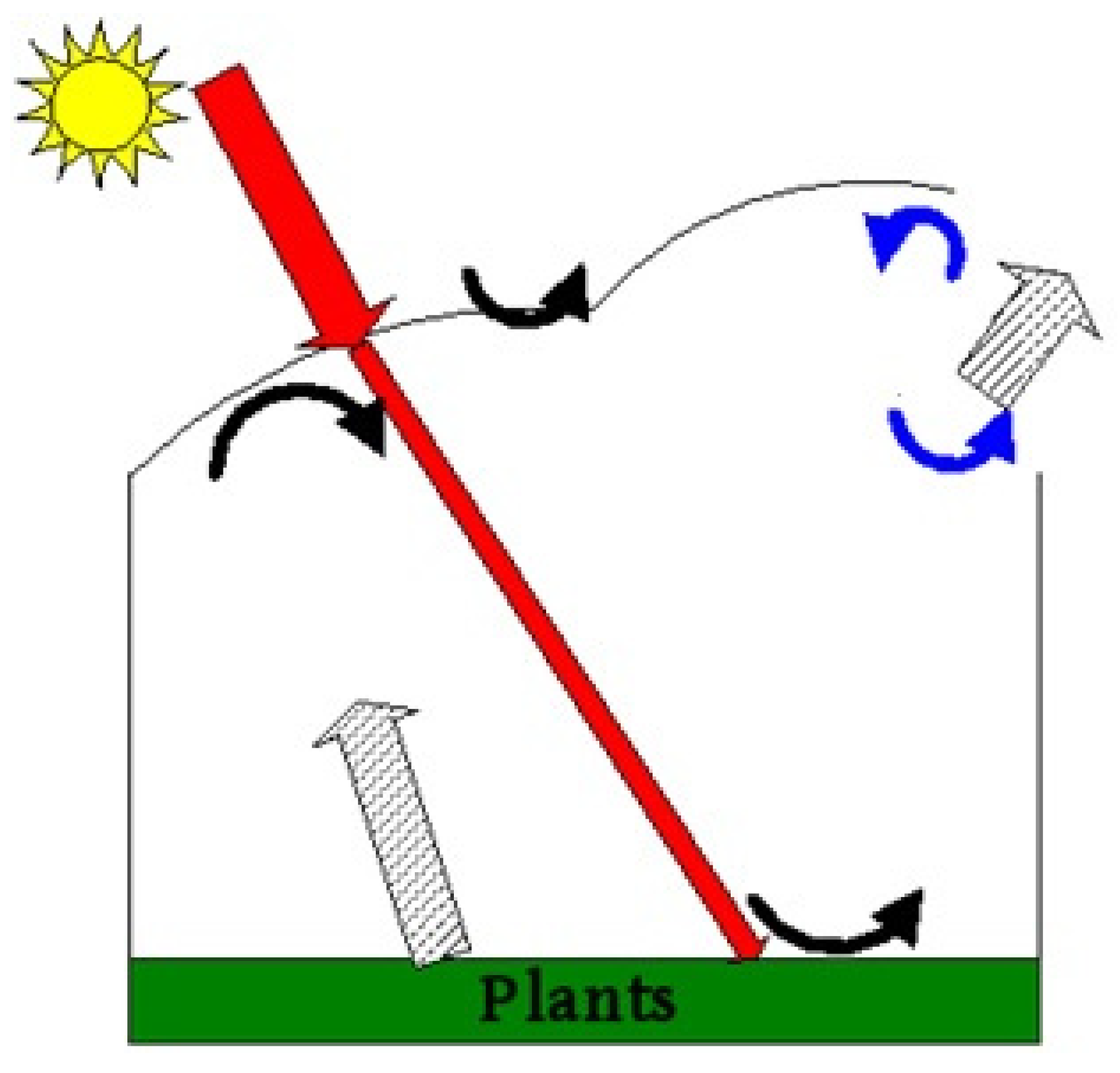
In defining the mathematical model of greenhouse thermal load, three components play an important role: plants inside the space, air in the building, and covering material. Unlike conventional buildings, a greenhouse has a transparent film whose role is to allow transmission of solar radiation, which is then absorbed by soil and plants. To understand the energy flow inside a greenhouse, as shown in Figure 1, it is necessary to introduce the following preconditions in order to reduce complexity:

-

External atmospheric parameters remain constant during the time step calculation (hourly values of outside air parameters do not change).

-

There is no condensation inside the building, or in the inner surfaces of film.

-

Change in temperature and relative humidity inside the building is uniform.

Heat flux, which is transmitted by convection into the air of the building, can be expressed by the following equation [21,35,36]:

$$\dot{q}={\dot{q}}_{surf,i}+{\dot{q}}_{inf,i}+{\dot{q}}_{vent,i }+{\dot{q}}_{gain,i}+{\dot{q}}_{wall,i} \left[\frac{W}{m^2}\right]$$

(1)

where ${\dot{q}}_{surf,i}$ heat flux transmitted by convection from soil into air, ${\dot{q}}_{inf,i}$ losses due to infiltration, ${\dot{q}}_{vent,i }$ losses due to ventilation, ${\dot{q}}_{gain,i}$ thermal load due to internal sources of energy in the building, and ${\dot{q}}_{wall,i}$ heat flux delivered by convection from the walls of the building film into air.

The heat flux delivered by radiation to the inner surface of the building film, ${\dot{q}}_{wall,r,i}$, can be represented by the following equation [35]:

$${\dot{q}}_{wall,r,i}={\dot{q}}_{sol,i}+{\dot{q}}_{long,i}+{\dot{q}}_{plant,i} \left[\frac{W}{m^2}\right]$$

(2)

where ${\dot{q}}_{sol,i}$ represents shortwave solar radiation that has passed through the film of the building and is directly absorbed by the inner surfaces,${\dot{q}}_{long,i}$ denotes longwave solar radiation exchanged between the adjacent inner surfaces of the film, and ${\dot{q}}_{plant,i}$ is the heat flux from plants towards the inner surfaces of the film of the building.

The energy balance for the film itself can be expressed by [35]:

$${\dot{q}}_{wall,i}+{\dot{q}}_{wall,o}+{\dot{q}}_{wall,r,i}+{\dot{q}}_{sky,o}=0$$

(3)

where ${\dot{q}}_{wall,i}$ is the heat flux that is by convection transmitted from the inside air to the film of the building, ${\dot{q}}_{wall,o}$ is the heat flux that is by convection transmitted from the outside air to the film of the building, and ${\dot{q}}_{sky,o}$ is the heat flux of radiation between the sky and the outer surface of the covering. The heat flux delivered by radiation to the inner surface of the building film, ${\dot{q}}_{wall,r,i}$, is defined in Equation (2).

To better determine the dynamic thermal behavior of the building and monitor the dependance of the thermal load on changes in external environmental parameters, heat transfer coefficients for both the outside and inside films of the building were dynamically modeled. To calculate the heat transfer coefficient on the outside film of the building, the reduced wind speed relative to the normal of the described surface must be determined [37]:

• surface located in direction of wind flow:

$$\begin{gathered} v_l=0.25 · v ; v>2 m/s \\ {v}_l=0.5 ; v<2 m/s \end{gathered}$$

(4)

• surface located in the leeward, oriented opposite to the direction of wind flow:

$$v_l=0.3+0.5·v$$

(5)

where $v_l$ signifies the local wind velocity towards the observed surface, and $v$ signifies the wind speed.

The forced convection heat transfer coefficient due to air flow over the outer surface is denoted by [37]:

$${\alpha }_{sp}=3.5+5.6·v_l$$

(6)

The heat transfer coefficient on the inner film surfaces of the building depends on the combined convection, which occurs in the boundary layer adjacent to the surface. This depends on whether the surface is vertical or horizontal, the temperature differences between the inner surface and the air in the observed zone, and the number of changes of air inside the zone. Validation of the TRNSYS model was conducted based on measured temperature values during the heating period, when parameters of the interior space conditions were monitored. 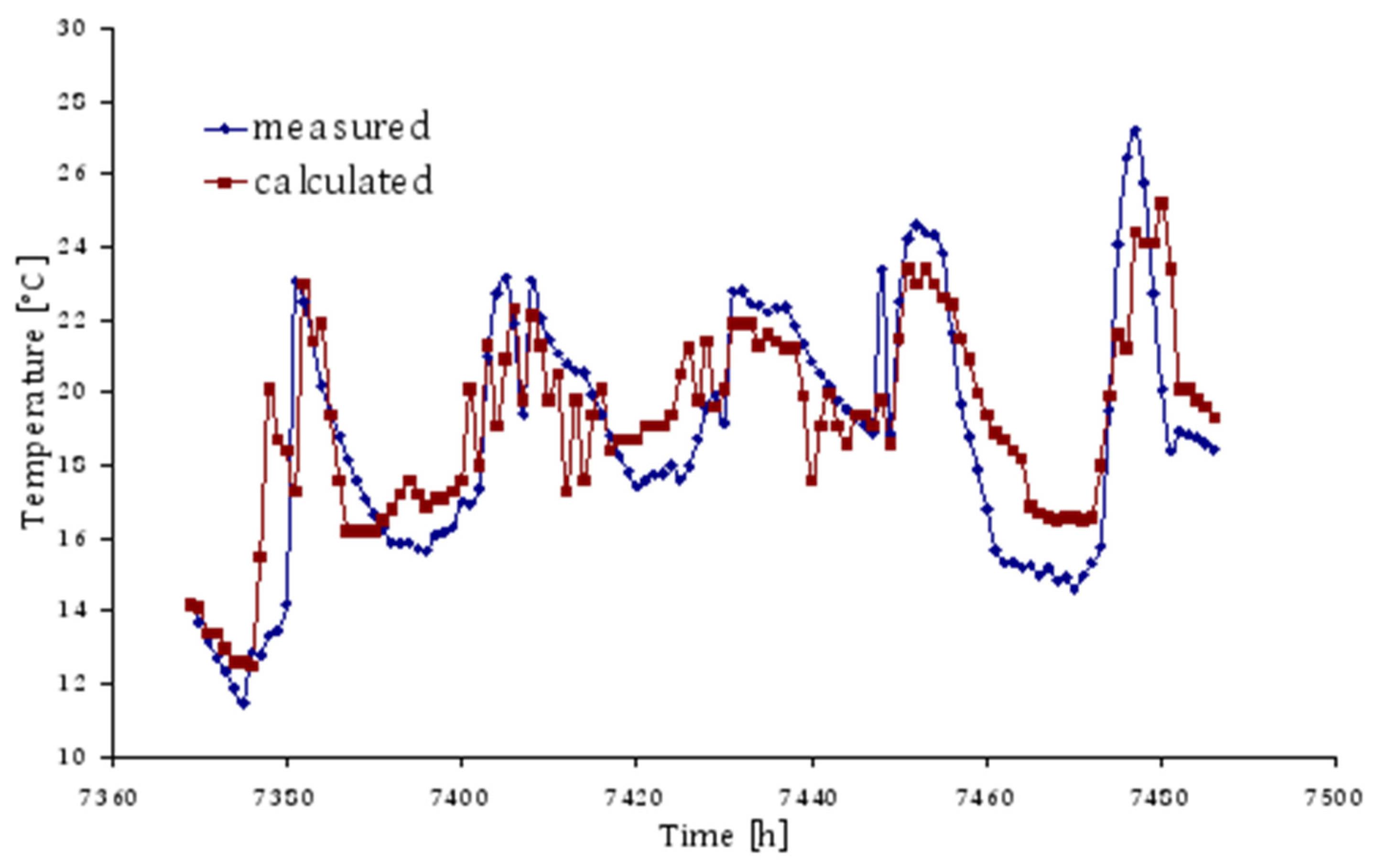Figure 2, for five selected days in November, shows a comparison of the air temperature in the house obtained by numerical simulation with the measured values.

The simulation results match well with the measured values, indicating that the model is well positioned. It can be further improved by determining the optimal amount of fresh air introduced into the building through natural ventilation to create favorable conditions for plant growth during the period from October to May.

Relevant meteorological data required for defining the model of the heating and energy system in the greenhouse and their examination through dynamic simulations were obtained from the typical meteorological year for the given location (TMY). A typical meteorological year consists of data collected over a period of 10 years and represents average values for a location, so they can be used as relevant data in determining the thermal behavior of the building. TMY includes values of dry and wet bulb temperatures, relative and absolute humidity, wind speed and direction, precipitation percentage, and other data for all 8760 h of the year. Extreme values that can occur in real conditions throughout the year, such as extremely low temperatures in winter and high temperatures in summer, can be separately analyzed. According to the data processed from the TMY for the location of Šabac, the change in air temperature is shown in Figure 3. It is clearly observed that in the winter period, extremely low temperatures are not pronounced, which favorably affects the heat losses of the building, especially at night. The minimum temperature according to the TMY in the winter period is about −10 °C, and the maximum in the summer period goes up to 35 °C. In the summer period, higher external air temperatures adversely affect the increase in temperature inside the greenhouse, and thereby the maintenance of plants.

2.2. Greenhouse Condition

The space inside the greenhouse spans 4.2 hectares and is divided into three sections. One section includes technical rooms for staff offices, sanitary facilities, and four chambers for seed germination and cooling. This technical section lacks a heating system, relying solely on solar radiation that penetrates through the roof domes. Another distinct area, completely isolated from the rest, is specially designed for preparation of seedlings where required temperature and relative humidity parameters are meticulously maintained throughout the year. The remainder of the building is split into four interconnected zones without any barriers, complicating the control of plant growth conditions both in terms of maintaining defined atmospheric conditions and isolating plants from potential disease outbreaks. In the greenhouse’s central area, irrigation tanks and pumps deliver geothermal water for heating and feeding plant nutrition tanks. Vegetable crops, such as tomatoes, peppers, cucumbers, and lettuce (during the winter), are cultivated all year around.

The existing heating system consists of plastic tubes arranged vertically at several levels to cover the zone where the plants grow (Figure 4). The system operates with a geothermal energy capacity of 22 L/s, with water heated to 53 °C. As the water circulates through the heating system, it cools to 15 °C before being discharged into a nearby river. The available heat flux for heating amounts to 2855kW. Inside the plant growing zone, a 20m³ tank stores water that is piped throughout the growing area. The geothermal heating system is regulated to maintain night temperature at 17 °C, and day temperature at 20 °C.

There is no forced ventilation system in the greenhouse. The absence of a system adversely affects not only the high temperatures caused by solar radiation during summer but also the air quality and the CO₂ levels needed for plant growth development. In summer, natural ventilation is employed to cool the space; the roof domes open when internal temperatures exceed a specified threshold and close automatically when wing speeds surpass 35 km/h during rainfall or other meteorological events to ensure structural safety. During summer, the domes are predominantly open, while in winter, they are open for several hours daily to ensure fresh air intake. The recommendation for minimum fresh air flow for effective ventilation, providing sufficient CO₂, is between 2 and 3 air changes per hour (ACH).

The greenhouse is covered with two five-layer foil covers separated by a 15 cm air layer, maintained under slight overpressure to preserve its shape. However, the foil’s condition is poor and irregularly maintained, leading to soiling that reduces solar flux and increases infiltration rate. This issue is particularly problematic during the winter nights when, despite the relatively high ambient temperatures in recent years, the heating system fails to maintain the set indoor temperature of 20 °C, dropping to 17 °C instead.

2.3. Artificial Neutral Network Structure

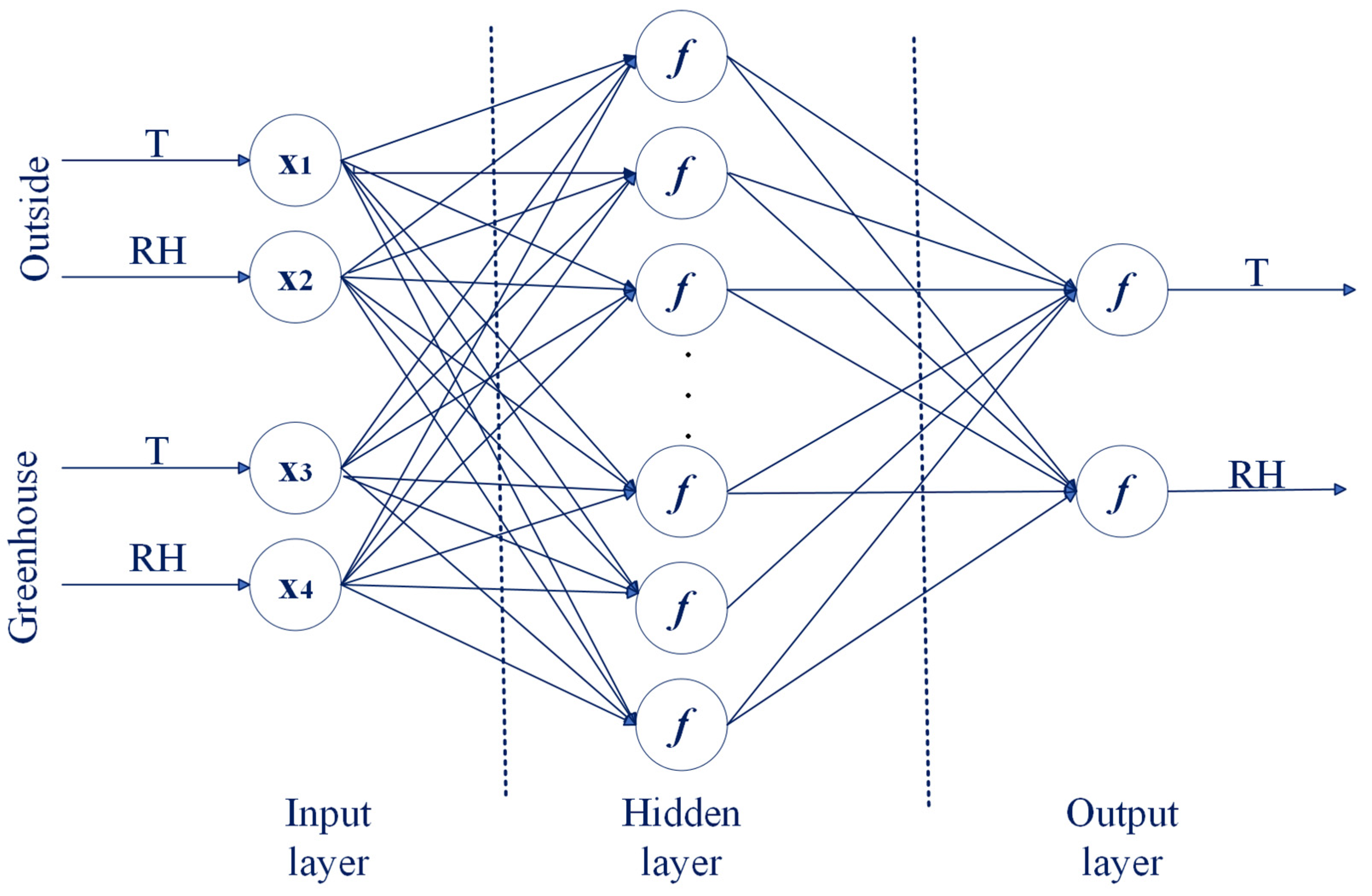
The training and testing dataset for the model were constructed using data from TRNSYS simulations and real meteorological data for the specified location. The dataset comprised 8760 data points, split into training and testing sets in an 80:20 ratio. Validation data sets were selected from measured data in the greenhouse on specific days during the heating period. The back-propagation algorithm, a supervised learning technique, was utilized for modeling with hidden layers to enhance the prediction rate of the model (Figure 5). The ANNs demonstrated exceptional performance, with each neuron calculating the weight factor in two stages. The Levenberg–Marqardt algorithm [38] was employed as the learning technique.

The input layer consisted of four neurons, based on the assumption that the predicted values of microclimatic parameters–temperature and relative humidity—could be enhanced with real-time external conditions. Given that the thermal load structure of a greenhouse is significantly more complex than that of residential buildings due to specific internal gains, the ANN model aims to predict microclimatic parameters in a more straightforward manner. The output layer contained two neurons for the optimal internal temperature and relative humidity. The number of hidden layers and neurons is a crucial factor for model accuracy. Similar studies typically use one hidden layer with the number of neurons determined from sum of input and output neurons [18] or based on an array of n/2, n, 2n, 2n + 1 [39]. In the study, the optimization of the number of neurons, learning rate, and number of epochs was conducted to find the optimal model that would exhibit the highest accuracy and the least losses compared to the initial model. The chosen model configurations are displayed in

Table 1. Configurations of the chosen models in simulations with relevant parameters.

Model	ANNs Neurons Scheme	Learning Rate	Epoch
M01	4-2-2	0.02	200
M02	4-3-2
M03	4-4-2
M04	4-5-2
M05	4-6-2
M06	4-7-2
M07	4-8-2
M08	4-9-2
M09	4-10-2
M10	4-6-2	0.018	200
M11			300
M12		0.0079	200
M13			300

.

Model validation was not only performed using the original dataset but was also based on measured real data from the greenhouse, thereby providing a performance measure given by the linear correlation coefficient, coefficient of determination, mean absolute error, and mean square error [32]. The double validation was essential because the original dataset was also derived from predictions obtained from the TRNSYS simulation, aiming to demonstrate the effectiveness of both prediction models.

The performance measure typically includes the linear correlation coefficient (r), coefficient of determination (R²), mean absolute error (MAE), and root mean square error (RMSE) [13]:

$$r=\frac{n\sum \widehat{y}y-\left(\sum \widehat{y}\right)\left(\sum y\right)}{\sqrt{n\left(\sum {\widehat{y}}^2\right)-{\left(\sum \widehat{y}\right)}^2}\sqrt{n\left(\sum y^2\right)-{\left(\sum y\right)}^2}}$$

(7)

$$R^2=1-\frac{{\sum }_{i=1}^n{\left(y_i-{\widehat{y}}_i\right)}^2}{{\sum }_{i=1}^n{\left(y_i-{\overline{y}}_i\right)}^2}$$

(8)

$$MAE=\frac{1}{n}\sum _{i=1}^n\left|{\widehat{y}}_i-y_i\right|$$

(9)

$$RMSE=\sqrt{\sum _{i=1}^n\left[\frac{\left({\widehat{y}}_i-{ y_i}^2\right)}{n}\right]}$$

(10)

where ŷ is the predicted value, y is the measured value, y is the mean of measured variables, and n is the number of data points.

3. Results and Discussion

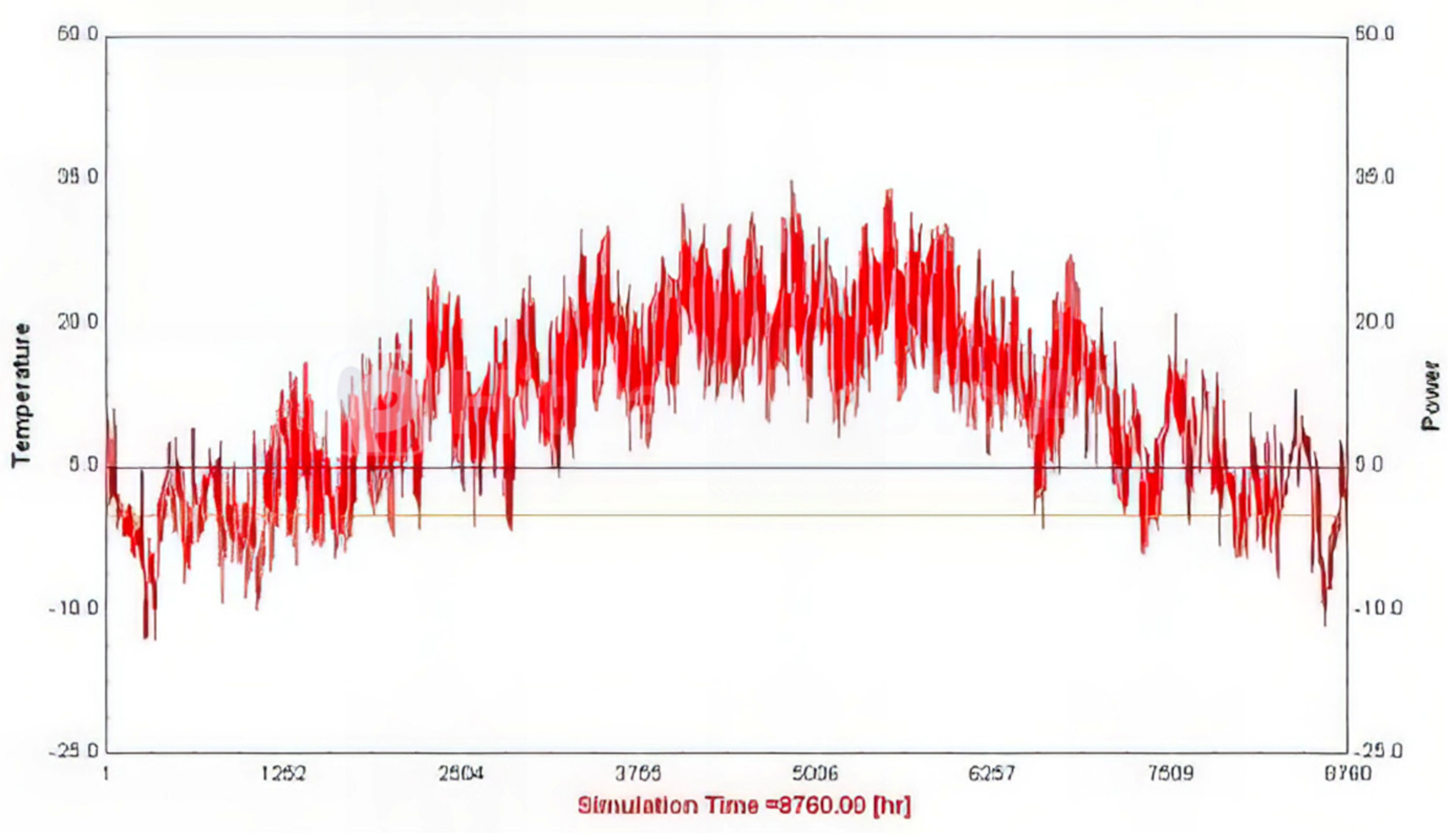
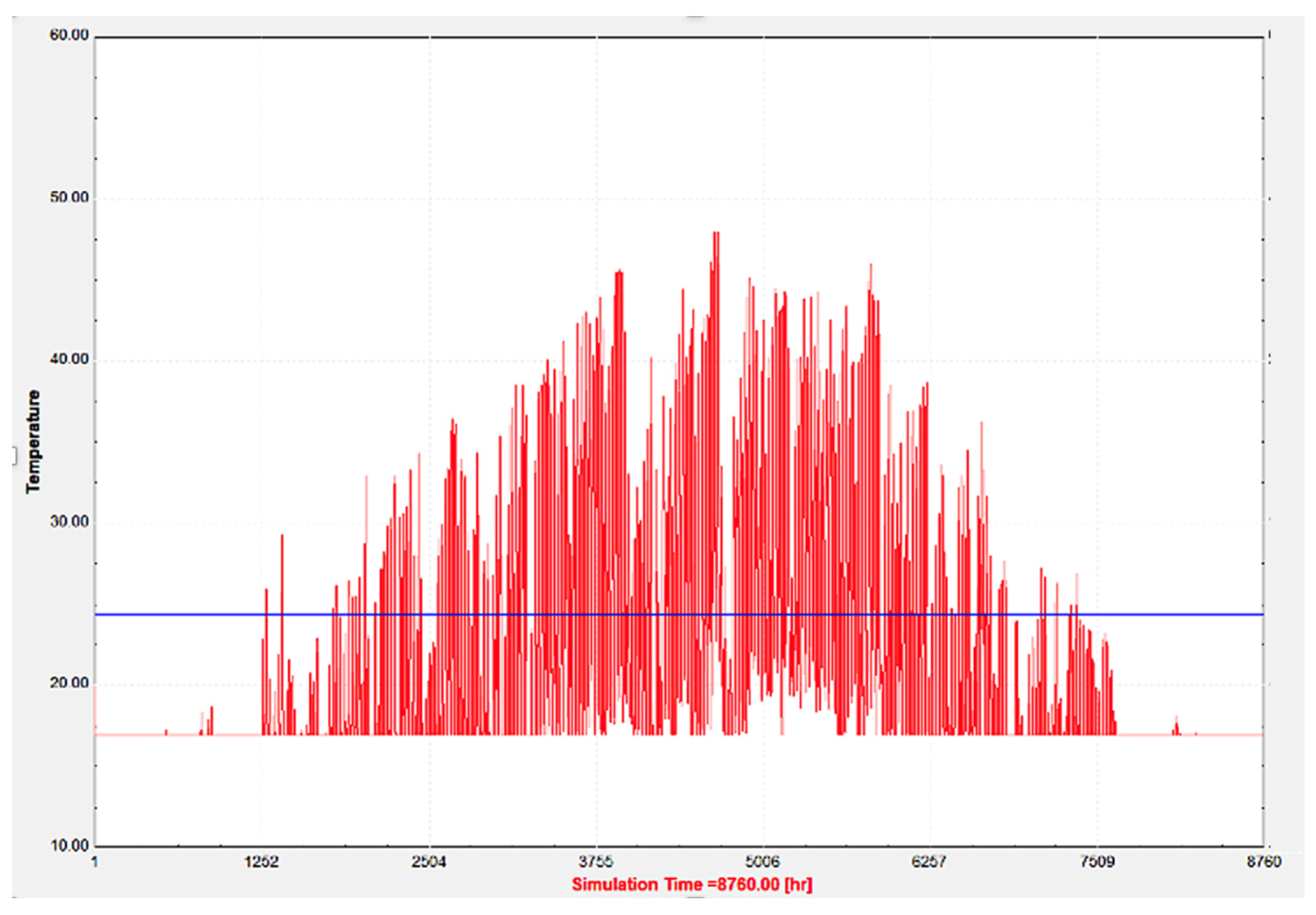
The TRNSYS model’s dynamic simulation for the described greenhouse was conducted in accordance with the procedures outlined in Section 2.1. As previously mentioned, this model is highly complex and requires precise specifications of the entire system including covering, heating, ventilation, air conditioning, infiltration, and internal load. This greenhouse simulation is more intricate than standard simulations due to the dynamic interactions between various internal and external environment parameters. The primary objective of this paper is to demonstrate a possibility of a development of a robust ANN model, which is capable to provide accurate predictions, based on mentioned complex interactions.. The variations in internal temperatures derived from the TRNSYS simulation are depicted in Figure 6.

During the heating period, the TRNSYS model demonstrated a strong correlation with the observed data. The model predicted higher temperatures during the summer due to the absence of a mechanical ventilation system. Minimal adjustments to the ACH led to deviations from the measured greenhouse temperatures, primarily due to the manual adjustment of side panels to increase airflow and decrease internal temperature.

The ANN model employed a multi-layer perceptron network with a single hidden layer containing neurons that utilized a hyperbolic tangential activation function, and an output layer composed of two neurons with a linear activation function. The model’s complexity and effectiveness in predicting internal conditions were assessed by varying the number of neurons in the hidden layer, the learning rate, and the number of epochs, as detailed in Table 1.

The initial phase of determining the best training algorithm involved adjusting the number of neurons, as per the settings described.

Table 2. Variation of RMSE, MAE, and R2 values for different ANN models.

Model	R2		MAE		RMSE
	Temperature	RH	Temperature	RH	Temperature	RH
M01	0.8177	0.9957	0.1818	0.0043	0.4264	0.0653
M02	0.8147	0.9954	0.1848	0.0045	0.4230	0.0675
M03	0.8233	0.9957	0.1763	0.0043	0.4199	0.0656
M04	0.8256	0.9957	0.1740	0.0043	0.4171	0.0655
M05	0.8326	0.9955	0.1670	0.0044	0.4083	0.0666
M06	0.8096	0.9954	0.1902	0.0046	0.4361	0.0680
M07	0.8079	0.9944	0.1919	0.0056	0.4380	0.0750
M08	0.8174	0.9943	0.1824	0.4271	0.4271	0.0757
M09	0.8126	0.9946	0.1871	0.0053	0.4326	0.0731

presents the performance analysis using RMSE, where the M05 model yielded the best outcomes for temperature differences and relative humidity consistency.

Based on RMSE and MAE, model M13 showed superior prediction capabilities, as evidenced in

Table 3. Variation of RMSE, MAE, and R2 values for different ANN models.

Model	R2		MAE		RMSE
	Temperature	RH	Temperature	RH	Temperature	RH
M10	0.8141	0.9947	0.1857	0.0053	0.4301	0.0729
M11	0.8654	0.9956	0.1345	0.0043	0.3667	0.0660
M12	0.8829	0.9962	0.1169	0.0037	0.3420	0.0610
M13	0.8997	0.9966	0.1002	0.0034	0.3166	0.0587

, suggesting that it can accurately predict the indoor air parameters based on data derived from TMY I and TRNSYS simulations.

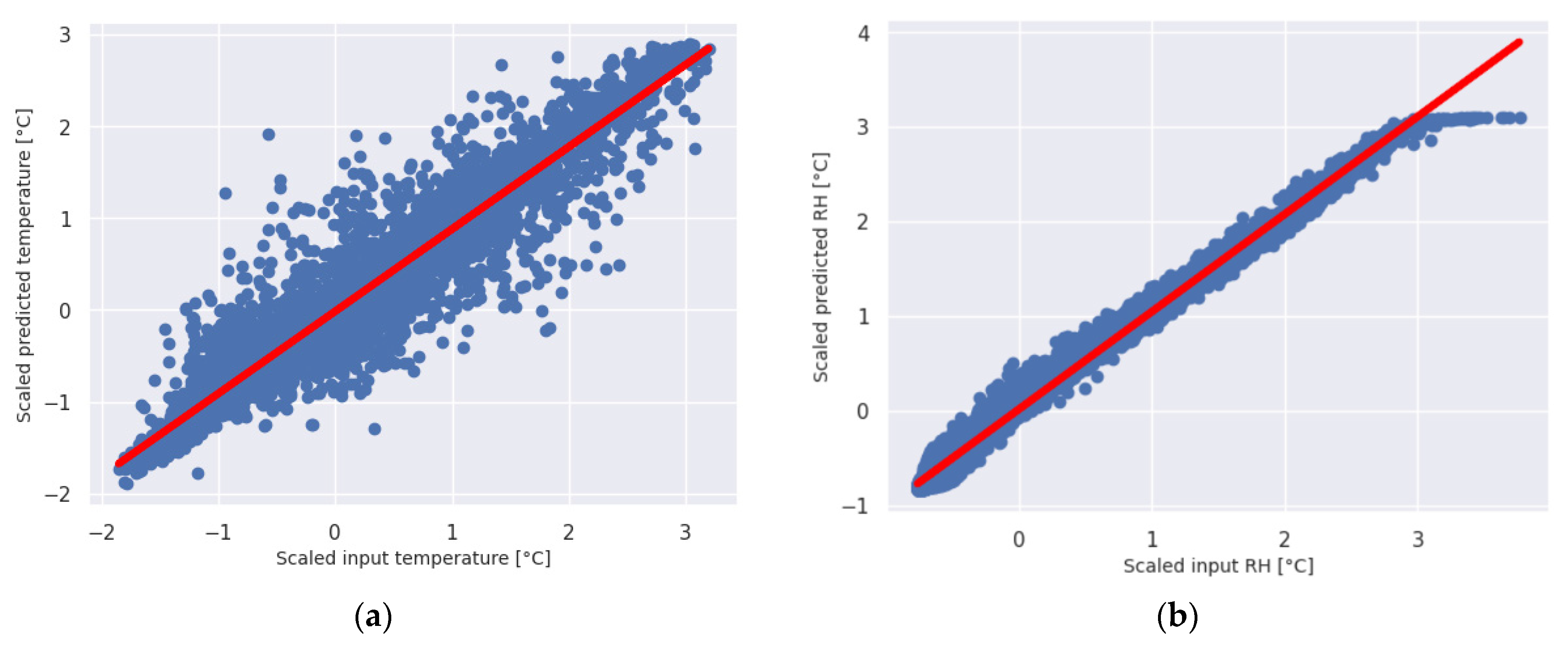
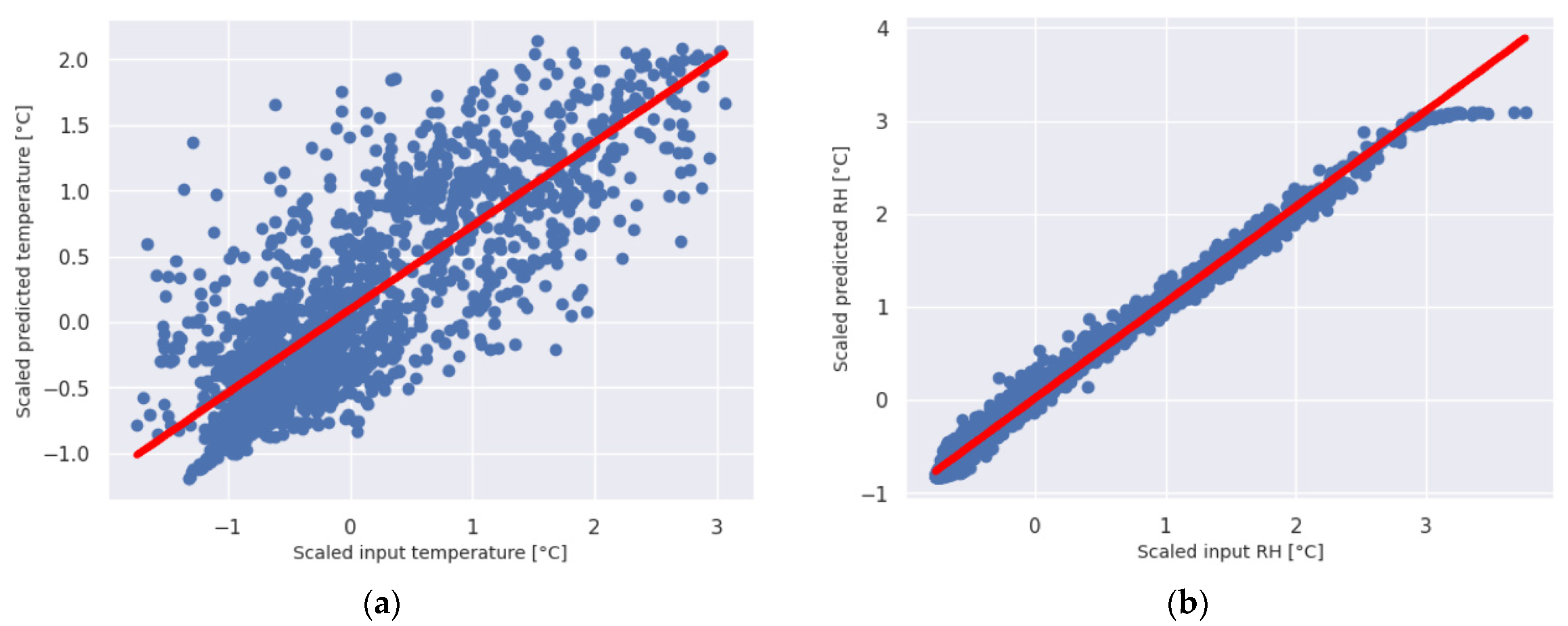
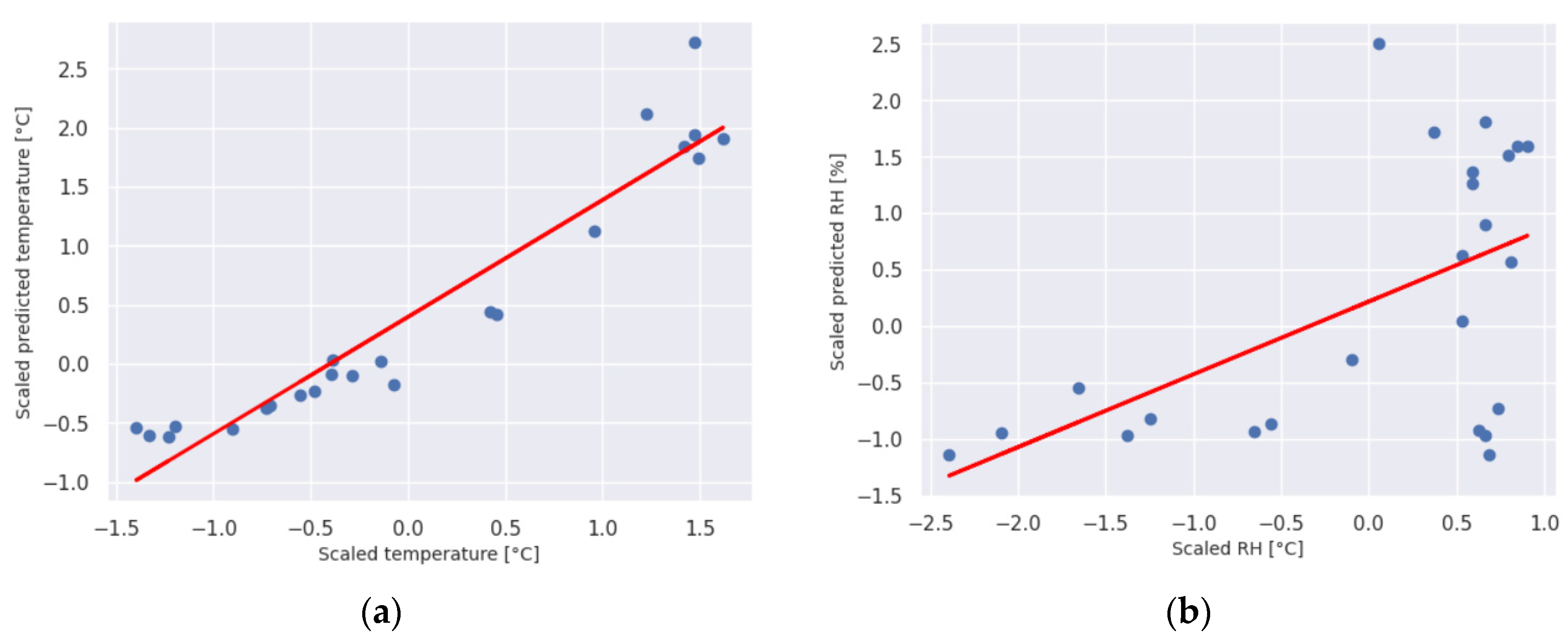
Figure 7 and Figure 8 illustrate the relationship between predicted and TRNSYS-obtained data for the training and testing datasets, respectively. The favorable comparisons indicate that model M13 aligns well with real-world data, potentially replacing the need for more complex modeling approaches.

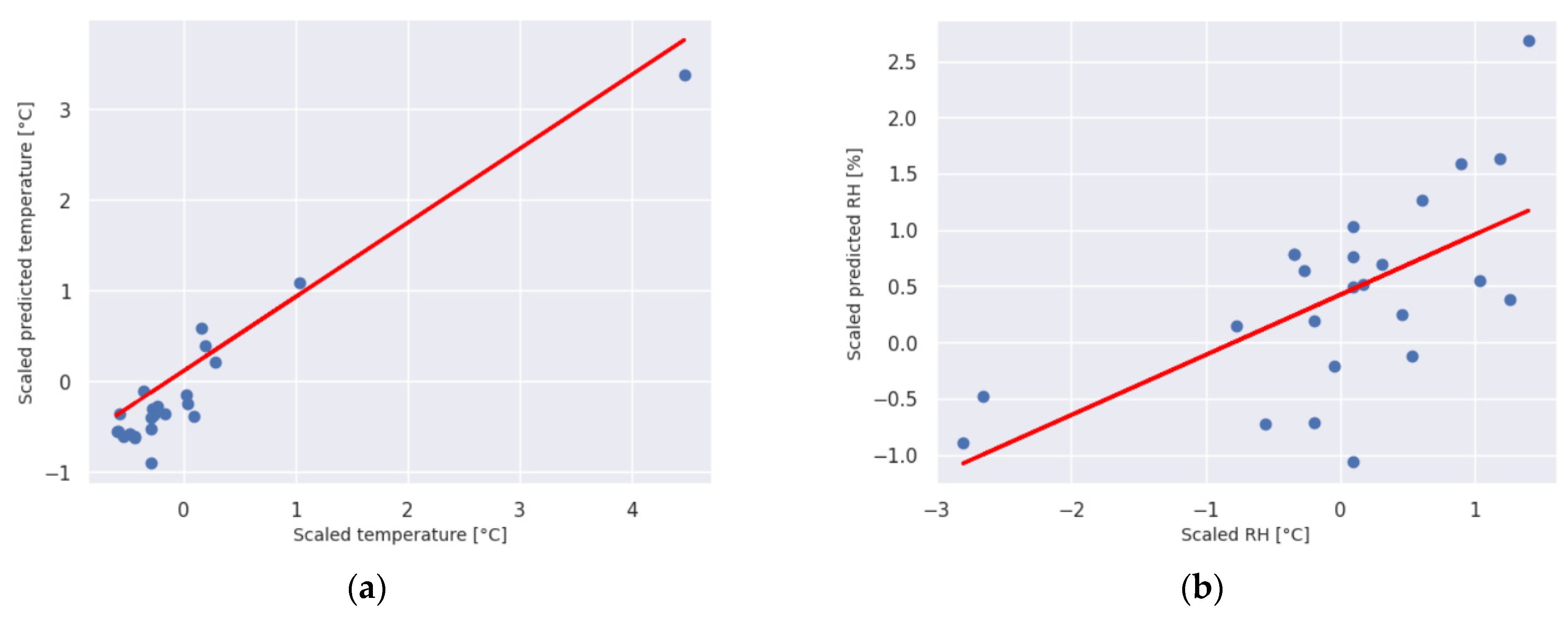
As the TRNSYS model is constructed using detailed information about the structure of the object, its orientation, and all other significant internal features, the predicted values for temperature and relative humidity are highly dependent on all these parameters within such a complex object. The accuracy of the TRNSYS model’s dynamic behavior is contingent upon the precision of the data entered in Type 56. A major challenge with the studied greenhouse is the lack of mechanical ventilation and inadequate natural ventilation, which, in combination with a dewing system, significantly impacts the relative humidity inside the greenhouse. To further validate the model, four days during the heating season (from 4 November to 4 December 2022) characterized by weaker ventilation, were selected. This reduced ventilation was influenced by external conditions such as high wind speeds, which necessitated the closing of the domes. The validation results these days are presented in Figure 9, Figure 10, Figure 11 and Figure 12 and

Table 4. Differences between the input data and the data obtained by prediction.

Data	Parameter	Equation	Adj.R2
train	Temperature	y = 0.7708× + 0.0186	0.681
	Relative humidity	y = 1.022× + 0.0105	0.989
test	Temperature	y = 0.8961× − 0.0151	0.903
	Relative humidity	y = 1.003× + 0.00187	0.997

.

The temperature within the greenhouse is primarily determined by the complex thermal load of the object: conduction through the coverings, convection at the external and internal surfaces, and solar radiation—both transmitted and absorbed by internal surfaces and reflected. The actual measured data aligns relatively well with the predicted values, with adjusted R² values ranging from 0.681 to 0.989. This demonstrates that data obtained from a typical meteorological year, as well as simulations of the physical load, can effectively substitute for the actual measurements for long-term temperature prediction in greenhouses. Variations in relative humidity are mainly due to deviations in real conditions on selected days from the predicted model of natural ventilation. For instance, strong winds led to the domes being closed, and consequently, the moisture model did align perfectly with the selected moisture settings in the TRNSYS model, resulting in reduced accuracy of the model. However, the trend of correlation between the data was still maintained.

4. Conclusions

This study explored the viability of using an artificial neural network (ANN) model to predict mean temperature and relative humidity in a greenhouse environment. By employing dynamic simulations based on meteorological data from 2007 to 2021, we investigated whether a simplified ANN model could effectively replace a more complex dynamic model traditionally used for these purposes.

The hypothesis proposes that if the ANN model accurately predicts greenhouse microclimates, then the model’s predictions on test data and real measurements should demonstrate high accuracy and low error rates. In practice, the study showed that the model consistently produced satisfactory accuracy in predicting changes in mean temperature and relative humidity, particularly within the plant cultivation areas of the greenhouse. This confirmed our expectation that a complex dynamic model of the greenhouse’s thermal load could be effectively simplified into an ANN model, which not only met but often exceeded the accuracy levels of traditional modeling approaches, especially in periods of stable environmental conditions.

The application of ANN provided deep insights into the non-linear relationships between various microclimatic factors, including temperature, humidity, wind speed and direction, and direct and indirect radiation effects. Despite the challenges posed by the lack of mechanical ventilation in the simulated setup, which introduced some variability, the ANN model’s predictions remained robust. Statistical analyses using RMSE and MAE confirmed the model’s efficacy, demonstrating its capability to reflect true microclimatic conditions accurately.

While the results were promising, they also highlighted the potential for further enhancing the model’s accuracy and applicability by incorporating more complex data inputs and extending the network’s architecture. Future research could benefit from including additional data points and expanding the complexity of the neural network to better manage the dynamic nature of greenhouse environments. This advancement suggests that ANN models could be increasingly used to optimize environmental conditions within greenhouses, potentially improving crop yield and resource efficiency.