Abstract
Aside from plant breeding and agricultural inputs, understanding and interpreting the Genotype × Environment (G × E) interaction has contributed significantly to the increase in wheat yield. In Central Macedonia, Greece, fifteen commercially important durum wheat cultivars and one landrace were tested in six cultivation environments classified into high- and low- productivity environments. This study aimed to identify the most productive and stable durum wheat genotypes across Mediterranean farming systems through a comparative examination of genotype plus genotype by environment (GGE) biplot alongside fifteen parametric and non-parametric stability models. In the organic (low productivity) environment, cultivar Zoi and the landrace Lemnos showed remarkable results, indicating a potential solution for biological agriculture. For the late-sowing (low productivity) environment, some widespread varieties such as Mexicali-81, Meridiano, and Maestrale had excellent performance, showing potential to overcome more adverse conditions during critical grain filling periods such as higher air temperature and deficient soil moisture, i.e., conditions that correlate with climate change. Evaluation of genotypes in all environments for a combination of high yield and stable production, showed that the best genotypes were G8 (Simeto), G2 (Canavaro), and G12 (Elpida). In the subgroup with the three high-productivity environments, G12 (Elpida), G8 (Simeto), and G6 (Mexicali-81) were the best genotypes, followed by G2 (Canavaro), while in the low-productivity subgroup, the G2 (Canavaro), G13 (Zoi) and G8 (Simeto) genotypes were the best.
1. Introduction
The global population is expected to grow approximately 1% in the coming years, and the global use of major agricultural commodities, including wheat, is expected to grow by 1.1% due to both population growth and per capita growth in demand [1]. Global wheat production in 2022/23 is estimated at 770 million tonnes and is expected to rise to 840 million tonnes [1], of which durum wheat (Triticum durum Desf.) has an average production of approximately 40 million tonnes [2]. The increase in global cereal production results from increased yield, considering the limited potential for the availability of more arable land. However, environmental concerns and policies (e.g., the EU Green Deal) could negatively affect the yield in some places [1]. This increases the need to sustain and even increase the yield of field crops more sustainably, exploiting available techniques and agricultural practices that contribute to an efficient increase in productivity.
Originating from the Levant, where it was first domesticated, durum wheat was an essential cultivar for Greeks, Phoenicians, Romans, and all Mediterranean countries, which until 1955 planted local landraces [2]. Durum wheat holds substantial economic significance due to its distinctive attributes and the food products, notably pasta. It serves as a crucial energy source, offering diverse vitamins, minerals, and other essential nutritional compounds vital for human dietary requirements [3]. Over the last few decades, researchers have conducted many breeding programs. New genotypes produced by these breeding programs have to be evaluated in multi-environmental trials; AMMI analysis then needs to be conducted to group the genotypes being assessed into the most suitable environments [4]. Although innovations in the field of genetics have had the ultimate effect of increasing the yield [5], classical breeding programs are still important and, along with the use of new techniques and technologies, could continue to provide new cultivars of durum wheat [6]. Multi-location trials are also necessary to identify the most suitable genotypes for the target locations.
G × E interaction involving genotype performance changes across different environments and can complicate the identification of superior genotypes. This phenomenon is known as the crossover concept [7]. The ultimate target remains to identify the genotype that produces high and stable yields in various environments; this can then be put forth as a superior selection with high adaptability [4,8]. Genotypes with confirmed high grain yields and stability under certain environmental conditions could be used as parental lines in breeding programs in locations with similar conditions [9]. Various statistical tools have been developed to address G × E interpretation and crop stability and are classified into two categories based on their statistical properties: parametric and non-parametric measures. Commonly used parametric models are the variance of deviations from regression () [10], the stability variance () [11], the coefficient of variability () [12], and the stability measure [13] from AMMI analysis [14]. Concerning the non-parametric statistics, many models have been suggested, including Si by Nassaar and Huehn [15] and NPi by Thennarasu [16], which are based on similar genotype ranks across environments (stable genotypes), with genotypes that display similar ranks across environments assumed to be stable. Parametric and non-parametric statistical methods may approach stability differently. These approaches introduce two distinct facets of stability: the “static” or “biological” and the “agronomic” or “dynamic” [17]. In terms of the static aspect, a genotype is considered stable when it maintains a consistent yield across various environments. However, none of these methods comprehensively explain genotype performance across diverse environments [18].
AMMI and GGE biplot analyses were used to visualize the results of the interactions between genotypes and environments. These analyses aim to identify varieties that perform above the average and are stable in multiple environments and, second, suggest using varieties with low stability in particular environments by exploiting their adaptability under specific environmental conditions [19]. The GGE biplot model [7,20] offers a comprehensive visual assessment of the entire genotype–environment interaction, presenting a biplot that encapsulates both average yield performance and stability. GGE effectively filters out the noise originating from the environmental main effect (E) and highlights the two crucial components: genotype effects (G) and G × E interactions. The genotype’s value is visually represented using scores obtained from principal component analysis. Genotypes positioned closer to the performance line are deemed more stable compared with those located farther away. Moreover, the model quantifies a genotype’s distance from the “ideal genotype”, which represents the one with the highest mean performance and absolute stability, effectively occupying the central position within a series of concentric cycles. Although such an ideal genotype is rarely found in practice, it is a reference point for evaluating genotypes. The concentric circles, centered on the ideal genotype, facilitate the visualization of the relative distances between all and ideal genotypes. The plot distance between any given genotype and the ideal genotype can be used to measure its desirability [7,20].
Abiotic components that describe an environment are the non-living factors that affect the growth of living organisms, like plants, which grow in the ecosystem. Climatic parameters like rain, precipitation, and temperature are significant factors that characterize an environment [21]. Additionally, wind conditions, moisture, and light are some characteristics of the environment that affect grain yield [22]. Furthermore, soil parameters, like pH [21] and salinity [22], affect the adaptability of specific cereal genotypes. In summary, an agricultural system incorporates all the parameters mentioned above, which can affect crop growth and biomass accumulation and turn a percentage of biomass into seed production. Similarly, the agronomical practices adopted affect productivity and the efficient use of resources, biomass accumulation, and eventually higher grain yield. As a result, agricultural systems where different farming practices are applied are considered different environments.
In the last years, the Genotype (G) × Environment (E) interaction has been escalated to a triple interaction that includes the Management (M) factor, which is considered a third factor [5], or in some cases, is incorporated into the Environment factor. Identifying the ideal sowing window for durum wheat is now an essential management practice with a principal role in high yield, which is highly associated with the grain-filling period [23]. Similarly, the agronomical practices adopted affect productivity and the efficient use of resources, biomass accumulation, and, eventually, grain yield. As a result, agricultural systems where different farming practices are applied can represent different environments [24]. Nitrogen fertilization is another management practice crucial for grain yield and quality. The interaction between genotype and N availability should be exploited to produce durum wheat, a crop with quality requirements [25]. Unlike other cereal crops, durum wheat cultivation is not currently investigated for plant density, so this question is solved. Regarding irrigation, more and more countries in the Mediterranean region and in other areas where durum wheat is cultivated with supplemental irrigation focus their research and the strategy of their breeding programs on drought-tolerant genotypes in a period where intense climatic events are escalating [26,27].
This study aimed to identify the most productive and stable genotypes across Mediterranean farming systems, including biological and low/high productivity farming systems, through a comparative examination of the yield and analyses of the GGE biplot alongside fifteen parametric and non-parametric stability models.
2. Materials and Methods
2.1. Plant Material and Environments
Experiments were performed during the 2021–2022 growing season. Fifteen commercially available cultivars and one traditional landrace (shown in Table 1) were evaluated in six environments (three low and three high-productivity environments; Table 2). These genotypes were selected based on their popularity among growers, potential for high yields, and commercial value.

Table 1.
The present study used a list of genotypes (name, origin, genealogy, and release date).

Table 2.
Details of the six environments used to study G × E interactions of durum wheat genotypes.
The six environments that were evaluated were:
- E1: Thermi-Typical fertilization/Typical date of sowing (middle of November). In the typical fertilization (total N amount of 150 kg ha−1), one-third was applied before sowing (ammonium phosphate 20-10-0) and two-thirds at full tillering stage (Zadok 29) (ammonium nitrate 33.5-0-0). It is characterized as a low-productivity environment.
- E2: Thermi-organic field with no fertilization/Typical date of sowing (middle of November). It is characterized as a low-productivity environment.
- E3: Thermi-late sowing. Typical fertilization (described above) and late sowing i.e., end of January. It is characterized as a low-productivity environment.
- E4: Splitting N in top-dress application: splitting one-third (ammonium phosphate 20-10-0) before sowing, one-third (ammonium nitrate 33.5-0-0) at full tillering (Zadok 29), and one-third during the first node (Zadok 31).
- E5: Nea Gonia (Typical fertilization and date of sowing as described above).
- E6: Sindos (Typical fertilization and date of sowing as described above).
2.2. Experimental Design
Experimental trials were conducted in all environments using Randomized Complete Block Design (RCBD) of plot size, with four replicates. Each genotype was sowed in an area of 12 square meters (8 m × 1.5 m) comprising six rows with 0.25 m row-to-row distance. Details on soil/climatic data and agronomical practices, like the dates of sowing and fertilizer application, are presented in Table 2 and Table S1. Weedcide (6% pinoxaden and 1.55% clonquintocet-mexyl) was applied except for the biological field. The grain yield from each plot, reported in metric tonnes per hectare (t/ha), was standardized to a moisture content of 14%.
2.3. Statistical Analysis
Genotypes (G) and environments (E) were fixed treatment effects. Two-way ANOVA (Table 3) was performed for all environments (6), high-yielding environments (3), and low-yielding environments (3). The mean performances of grain yield (ton/ha) for all the genotypes in the environments (3 for high-yielding and 3 for low-yielding) are presented in Table 4. Two-way ANOVA (Table 3) was performed for all environments (6), high-yielding environments (3), and low-yielding environments (3), and the effects of the interaction between genotype and environment (6 for all, 3 for high-yielding, and 3 for low-yielding) on the yield are presented in Table 4. The Shapiro–Wilk test was used to check the normal distribution of variables, whereas Levene’s test was used to check the ANOVA assumptions for equality of the error variances and residual normality [30]. Differences between genotypes were identified using a post hoc Duncan test. To assess the contribution of each source of variation on the variability in yield, the ANOVA treatment sum of squares (SS) was partitioned into three components (SS of G, SS of E, and SS of G × E), and the broad sense heritability coefficient (H2) was calculated [31]. Spearman’s rank correlation coefficients were also computed and assessed for their significance at three probability levels: 0.001 (indicating a strong correlation), 0.01 (indicating a moderate correlation), and 0.05 (indicating a weak correlation). The above-mentioned statistical analyses were conducted using IBM’s SPSS package v. 23 (IBM Corp., Armonk, NY, USA, 2015).

Table 3.
Analysis of variance (ANOVA) between grain yields of sixteen genotypes of durum wheat in all environments (6), high-yielding environments (3), and low-yielding environments (3).

Table 4.
Effect of genotype on yield (ton.ha−1) in six different environments (3 low-yielding environments, three high-yielding environments, and over fields).
2.3.1. Parametric
Wricke’s ecovalence, Wi2
Wricke [32] introduced the concept of ecovalence, which represents the contribution of each genotype to the sum of squares of genotype–environment (GE) interactions. The ecovalence (Wi) of the ith genotype is calculated by squaring its interaction with the environments and then summing this value across all environments.
Shukla’s stability variance, σ2i
In 1972, Shukla [11] proposed the stability variance of genotype i, defined as its variance across environments after accounting for the main effects of environmental means. Based on this statistic, genotypes with the lowest values are the most stable.
Deviation from regression, S2di
In addition to slope regression, the variance of deviations from the regression (S2di) has been suggested as one of the most used parameters for selecting stable genotypes. Genotypes with S2di = 0 would be the most stable, while S2di > 0 would indicate lower stability across all environments [10].
Coefficient of variance, CVi
Francis and Kannenberg (1987) [12] suggested the coefficient of variation, which serves as a stability statistic. It combines the coefficient of variation (CV), mean yield, and environmental variance (EV).
Kang’s rank-sum KR
Kang’s rank-sum method [33] employs yield and σ2i (variance) as selection criteria. This parameter accords equal weight to yield and stability statistics in identifying high-yielding and stable genotypes. The genotype with the highest yield and the lowest σ2i is assigned a rank of one. Next, the yield and stability variance ranks for each genotype are combined.
GE variance component θ(i)
This statistic represents a modified measure of stability. It involves removing the ith genotype from the entire dataset and calculating the variance of the remaining subset’s genotype–environment interaction (GEI). This GEI variance serves as the stability index for the ith genotype. This statistic shows that genotypes with higher values are more stable.
AMMI’s stability value, ,
The AMMI models [14] were implemented using the GenStat (13th edition) statistical package [34], which is reliant on the first and second principal component (PC) scores—namely PC1 (representing the interaction of the first PCA) and PC2 (representing the interaction of the second PCA)—and calculated using the following equation, according to Purchase [13].
where SS is the sum of squares. The genotype with the smallest value was regarded as the most stable.
Genotype superiority, ,
The calculation of genotype superiority [35], denoted as , involved determining the mean square distance between the genotype and the maximum response:
Here, Ymax represents the maximum response observed among all genotypes in the given environment (j).
Yij: the yield of the ith cultivar grown in the jth location.
e: the number of locations.
The key takeaway is that the smallest value indicates the better genotype.
2.3.2. Non-Parametric Statistics
Nassar and Huhn’s statistics S(1), S(2), S(3), S(6)
Huhn [36] and Nassar and Huhn [15] proposed 4 non-parametric statistics for assessing genotype stability:
- S(1): Represents the mean of the absolute rank differences of genotypes across all tested environments.
- S(2): Represents the variance among the ranks across all tested environments.
- S(3): Represents the sum of the absolute deviation for each genotype relative to the mean of ranks.
- S(6): Represents the sum of squares of rank for each genotype relative to the mean of ranks.
The mean yield data must be transformed into ranks for each genotype and environment to calculate these stability measures. Genotypes with similar ranks across environments are deemed to be stable. A lower value for these statistics indicates higher stability for a particular genotype.
Thennarasu’s statistics NP(1), NP(2), NP(3), NP(4)
These four stability statistics were introduced by Thennarasu [16]. They are derived from the ranks of adjusted means of genotypes in each environment. When these statistics give low values, it indicates high stability.
where rij* is the rank of the ith genotype in the jth environment based on adjusted data, and are mean and median ranks, respectively, for adjusted values, and Mdi are the mean and median ranks of the ith genotype in the jth environment, respectively. and are the mean and median ranks obtained from the unadjusted data.
The GGE biplot model is based on singular value decomposition of the first two principal components:
where is the measured mean of genotype i in environment j, μ is the grand mean, is the main effect of environment j, and are the singular values for the first and second principal components (PC1 and PC2, respectively), and are eigenvectors of genotype i for PC1 and PC2, and are eigenvectors of environment j for PC1 and PC2, is the residual associated with genotype i in environment j.
3. Results
3.1. Analysis of Variance and Mean Performance
Based on the ANOVA (Table 3) for all the environments, the grain yield of durum wheat was significantly affected by environment, genotype, and their interaction (p < 0.001 for all effects). Even the partial ANOVA of high-yielding environments (E4–E6) and low-yielding environments (E1–E3) indicated that both G, E, and their interaction significantly affected the yield. Another interesting finding from this analysis is that for all environments, the highest percentage of variation was explained by G × E (43%), followed by E (41.7%) and G (15.3%). However, in low-yielding environments, E, G × E, and G were more similar, explaining 39%, 37.2%, and 23.3% of the variation, respectively. In the case of high-yielding environments, the G × E interaction explained 51.9% of the variation, G explained 46.6%, and E explained 1.5%.
The studied durum wheat genotypes across the environments showed significant imprints of productivity (Table 4). Based on the results from all the examined environments, G5 had the highest grain yield (3.77 ton.ha−1), followed by G6 (3.61 ton.ha−1), G8 (3.47 ton.ha−1), G12 (3.37 ton.ha−1), and G2 (3.33 ton.ha−1); however, there were no statistically significant differences between these best-performing genotypes. The genotypes with the lowest overall productivity were G1 (2.31 ton.ha−1), G9 (2.76 ton.ha−1), G16 (2.76 ton.ha−1), and G11 (2.78 ton.ha−1).
The results of the productivity of the genotypes in each environment are particularly interesting. In the case of E1 (low-yielding environment), G8 (4.31 ton.ha−1), G13 (4.13 ton.ha−1), and G3 (4.13 ton.ha−1) had the highest yields, but with no significant differences between them, while genotypes G1 (1.55 ton.ha−1) and G10 (2.15 ton.ha−1) recorded the lowest yields. In E2, an organic low-yielding environment, G13 (2.75 ton.ha−1), G1 (2.64 ton.ha−1), G5 (2.62 ton.ha−1), G2 (2.46 ton.ha−1), and G4 (4.40 ton.ha−1) gave the highest yields, with no statistically significant differences between them. The lowest grain yields were recorded for G6 (1.73 ton.ha−1) and G10 (1.84 ton.ha−1). In E3, a late-sowing low-yielding environment, G6 (3.08 ton.ha−1) had the highest grain production, with significant differences compared with all the other genotypes, followed by G3 (2.71 ton.ha−1) and G5 (2.67 ton.ha−1). Genotypes G1 (1.98 ton.ha) and G16 (1.98 ton.ha−1) recorded the lowest grain yields. In E4, a high-yielding environment, G14 had the highest grain production (5.27 ton.ha−1), with statistically significant differences compared with all the other genotypes, i.e., G2 (4.56 ton.ha−1), G6 (4.46 ton.ha−1), G11 (4.41 ton.ha−1), and G16 (4.31 ton.ha−1), followed by a very good performance and no statistically significant differences between them. In this environment, the lowest grain yields were recorded for G1 (2.27 ton.ha−1) and G9 (2.58 ton.ha−1). In E5, a high-yielding environment, G5 had the highest grain production (5.73 ton.ha−1), with statistically significant differences compared with all the other genotypes, i.e., G4 (4.62 ton.ha−1), G3 (4.43 ton.ha−1), G12 (4.30 ton.ha−1), G6 (4.10 ton.ha−1), and G2 (4.06 ton.ha−1), which had no statistically significant differences between them, while genotype G15 (2.43 ton.ha−1) had the lowest grain yield. Finally, in E6, a high-yielding environment, genotypes G5 (5.73 ton.ha−1), G6 (5.24 ton.ha−1), G12 (4.30 ton.ha−1), G10 (4.01 ton.ha−1), and G4 (3.96 ton.ha−1) recorded high grain yields, while genotypes G11 (2.12 ton.ha−1) and G1 (2.19 ton.ha−1) had low grain yields.
3.2. AMMI and GGE Biplot Analyses
Based on AMMI data analysis, two mega-environments, including all six environments (three low-productivity and three high-productivity fields), were identified, as depicted in Figure 1. E1, E2, and E3 form the first mega-environment, representing the low-productivity environments, while E4, E5, and E6 form the second mega-environment, representing the high-productivity environments. Based on the position of the two environment subgroups, genotypes such as G1 and G9 are better suited to low-productivity environments, while genotypes such as G14, G6, G5, and G12 are better adapted to high-productivity environments.
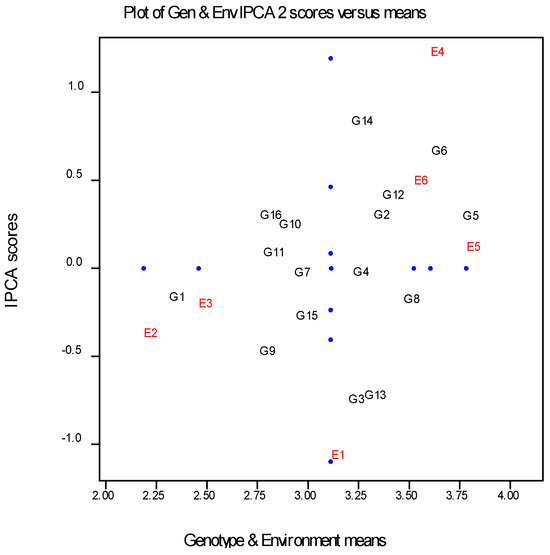
Figure 1.
AMMI biplot analysis (E = Environments, G = Genotypes) of E and G groupings.
Combined and partial GGE biplot analyses explained 73.06% (Figure 2), 92.42% (Figure 3), and 92.48% (Figure 4) of the total variability in all, low-, and high-productivity environments, respectively. Genotypes G6 and G12 were very close to the stability line in the combined analysis of all the environments.
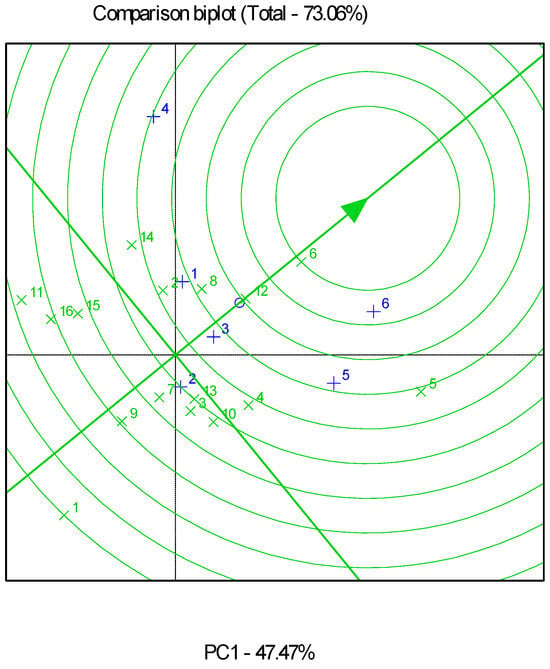
Figure 2.
Genotype and genotype by environment (GGE) biplot for grain yields of the sixteen genotypes evaluated in six environments (analysis of all environments). The “×” sign corresponds to genotypes, and the “+” sign corresponds to environments.
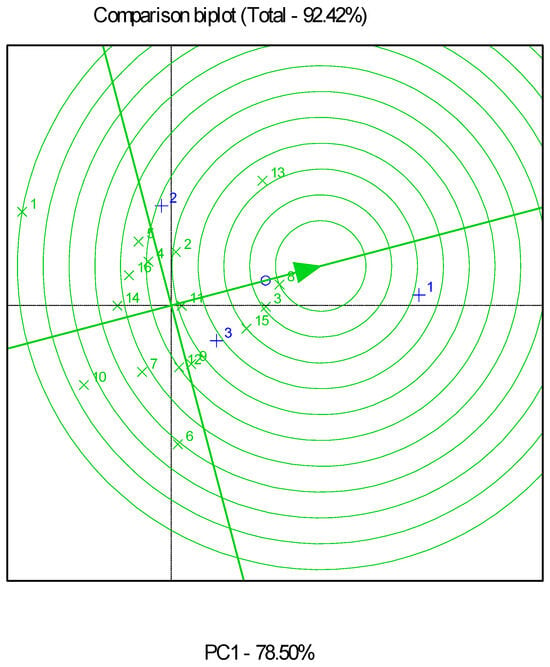
Figure 3.
Genotype and genotype by environment (GGE) biplot for grain yields of the sixteen genotypes evaluated in three low-productivity environments. The “×” sign corresponds to genotypes, and the “+” sign corresponds to environments.
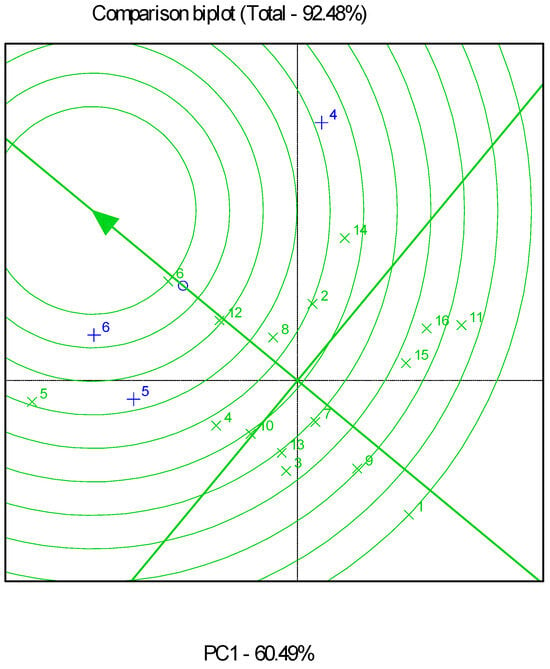
Figure 4.
Genotype and genotype by environment (GGE) biplot for grain yields of the sixteen genotypes evaluated in three high-productivity environments. The “×” sign corresponds to genotypes, and the “+” sign corresponds to environments.
The GGE biplot identified G8 as the best-performing genotype for the low-productivity fields, which also showed high stability. G3 and G15 followed, with inferior productivity and stability. As for the high-productivity environments, GGE biplot analysis indicated that G6 was the genotype closest to the ideal, as it had the best performance and high stability. This was followed by G12 and G5, with the latter showing comparatively low stability.
3.3. Prominent Genotypes Based on Multiple Stability Parameters
Several parametric and non-parametric indices were calculated to evaluate the genotypes based on their adoption in different environments. Table 5 displays the genotypes found in each index’s first five and last five positions based on the ranking for each respective statistic. In the total evaluation of all environments, G8, G2, and G7 dominated the top 5 ranking, with frequencies of 18/18, 16/18, and 13/18, respectively, identifying them as the most stable genotypes. For the bottom five rankings, G11 and G1 had the worst positions, with frequencies of 18/18 and 14/18, respectively. In the subgroup with the three high-productivity environments, G12, G8, and G6 were the genotypes with the highest presence in the top 5 ranking, with frequencies of 16/18, 16/18, and 12/16, respectively. In the bottom five ranking, G16 and G11 had frequencies of 16/18 for all indices, followed by G3 with 12/18. For the low-productivity subgroup, G2, G9, and G13 were the genotypes with the highest presence in the top 5 rankings, with frequencies of 17/18, 14/18, and 10/18, respectively. Considering the bottom five ranking, genotypes G11 and G10 each had a high frequency of 15/18, followed by G5 (14/18) and G3 (11/18).

Table 5.
Genotypes were categorized into the top 5 and bottom five groups based on both mean yield and stability measures of genotype superiority using the GGE biplot. The classification considered parametric measures (ASVi, Pi, σ2i, CVi, s2di, Wi2, KR and θ(i)) as well as non-parametric measures (S(1), S(2), S(3), S(4), NP(1), NP(2), NP(3), and NP(4)).
Table 6 displays the rank correlations between the statistical measures assessed across the six environments. The mean grain yield demonstrates a strong positive correlation with measures of GGE, , KR, S(3), S(6), NP(2), NP(3), and NP(4). Among the statistical measurements that were estimated, GGE biplot, , and consider yield and G × E interaction for cultivar evaluation, while the remaining statistical measures mainly consider stability. GGE analysis, , and KR were strongly and positively correlated, but had no correlation found with . Moreover, strong positive correlations were recorded for: (1) σ2i with all except S(3) and S(6), (2) CVi with s2di, (3) Wi2 with all except S(3), S(6), and NP(4), (4) θ(i) with all except S(3), S(6), and NP(4), (5) S(1) with S(2) and NP(4), (6) S(2) with S(3) and NP(1), (7) S(3) with S(6), NP(1), NP(2), NP(3), and NP(4), (8) S(6) with NP(2), NP(3), and NP(4), and (9) between NP(2), NP(3), and NP(4).

Table 6.
Spearman’s rank correlation coefficients were computed between the statistics for mean yield, cultivar superiority on the GGE biplot, parametric measures (ASVi, Pi, σ2i, CVi, s2di, Wi2, KR and θ(i)), and non-parametric measures (S(1), S(2), S(3), S(4), NP(1), NP(2), NP(3), and NP(4)).
4. Discussion
Durum wheat stands as the predominant cereal crop in the Mediterranean basin. Environmental and climatic elements, with notable sensitivity to water availability and elevated temperatures during the grain-filling period, can significantly affect the productivity of durum wheat [6,37,38]. Limited water availability and adverse conditions underline the significance of identifying the most productive and stable genotypes across different Mediterranean farming systems. Selection of the most appropriate crop variety stands out as the most cost-effective and efficient method for enhancing the productivity of a Mediterranean agricultural system. This strategic choice enables increased and more consistent production outcomes without a parallel rise in production costs, thereby maximizing resource utilization. In this multi-environment trial, durum wheat varieties such as Meridiano (G5), Mexicali-81 (G6), Simeto (G8), Elpida (G12), and Canavaro (G2) had mean grain yield productivities ranging from 3.33 to 3.77 ton.ha−1 based on the total evaluation of all environments, an outcome that was more or less expected. In the case of low-productivity environments, Mexicali-81 (G6) and Simeto (G8) were high-performing genotypes, although the relatively new varieties Maestrale (G3) and Zoi (G13), released in 2004 and 2011, respectively, also had high productivity. With tonnage above 5.00 tonnes per hectare, Meridiano (G5), Mexicali-81 (G6), and Thraki (G14) had high grain yield production in the high-productivity environments.
In parallel, the adoption of organic farming is on the rise globally. The European Commission (EC) has set an ambitious goal of converting a minimum of 25% of the European Union’s agricultural land to organic farming by 2030 [39]. However, the challenge is that modern commercial varieties are better suited for high-input farming, leaving a gap in cultivars adaptable to organic or low-input agriculture. One potential solution to this issue in wheat farming could be found in landraces, as they have demonstrated remarkable adaptability and productivity in low-input farming systems or under organic conditions. In our research, the landrace Limnos G1 exhibited high productivity (2.64 ton.ha−1) in the organic environment (E2) and ranked among the top three most productive cultivars; thus, proposing the cultivation of the Limnos landrace in organic farming systems could be a viable option. Furthermore, integrating landraces into agricultural systems has the added benefit of contributing to biodiversity expansion. This is particularly significant in wheat breeding, as landraces play a crucial role in reducing the genetic erosion of cultivated wheat. By broadening the genetic base in breeding programs, landraces provide essential traits that help crops cope with the challenges of changing environments, such as those influenced by climate change [40,41]. In the context of an autogamous crop like wheat, landraces represent a mix of pure lines. This characteristic can lead to the development of genetically stable genotypes or commercial cultivars relatively quickly, making them suitable for organic or low-input environments. Numerous successful examples exist where intensive breeding programs incorporating effective plant selection under ultra-low plant densities have harnessed the variations in landraces/cultivars in wheat [42,43] and other autogamous species [44,45].
The timing of sowing stands out as a critical factor influencing cereal production and quality, as emphasized by McLeod et al. [46]. The ideal sowing period typically falls around November in the Mediterranean Basin countries. Despite this, farmers frequently face challenges, leading to delayed sowing attributed to excessively wet or dry soil conditions. Notably, delaying sowing beyond the optimal agronomically recommended period often decreases yield [46] since it exposes durum wheat crops to potentially adverse conditions such as high air temperature and deficient soil moisture during the critical period of anthesis and grain filling. This situation becomes particularly relevant when considering climate change projections, as Porter and Gawith hypothesized [47]; therefore, evaluating cultivars in late-sowing environments becomes crucial. In Environment 3 (E3), characterized by late-sowing and low yields, Mexicali-81 (G6) exhibited the highest grain production, showing significant differences from all the other genotypes. Following closely were Meridiano (G5) and Maestrale (G3), with Meridiano (G5) also demonstrating notable performance.
Based on Simmonds [48], genotypes contributed 25–40%, the environment contributed 30–60%, and G × E interaction contributed the remaining 15–25%; thus, multi-environment field evaluation is a necessary practice that has been followed for the selection of high-yield best-adapted genotypes for many types of cereals cultivated for their grains, including durum wheat [49] and other species such as barley [50] where kernel yield is significant. Moreover, considering the effect of G × E on wheat yield per ha increase [48], the study of this parameter is of high importance since genotype rank changes from one environment to another. However, the concept of crossover interaction hampers the discovery of superior genotypes [51]. Several statistical tools have been proposed for G × E interpretation and the study of crop stability. However, a complete visual evaluation of all G × E interaction aspects is possible with the GGE biplot model [7,52].
This study aimed to compare the utilization of the GGE biplot alongside fifteen parametric and non-parametric stability models in assessing durum wheat genotypes. Another target of the study was the identification of the most productive and stable genotypes across different Mediterranean farming systems, including biological and low/high productivity farming systems. The statistical metrics mentioned above can be categorized into two main groups. The first set considers the inherent genetic characteristics (G) and the interactions between genotypes and their respective environments (GE). Consequently, they offer a comprehensive assessment considering yield performance and genotype stability under varying conditions. Conversely, the second set of statistics emphasizes genotype–environment interactions (GE) while primarily focusing on stability as a critical factor in genotype evaluation. A supplementary but essential parameter for evaluating a genotype is its stability under different environmental conditions. The stability statistics indicated that, in general, in the overall evaluation, Simeto (G8), Canavaro (G2), Monastir (G7), and M. Aurelio (G4) were the most stable genotypes across different environmental conditions, while Anna (G11) and Limnos (G1) had significant fluctuations in their performance across the different environments. In the low-performing environments, Canavaro (G2) and Svevo (G9) were the most stable genotypes, while Anna (G11) and Vendeta (G10) had the lowest stability. In the high-yielding environments, Elpida (G12), Simeto (G8), and Mexicali-81 (G6) showed the highest stability. On the contrary, Sifnos (G16) and Anna (G11) were exceptionally unstable. Adapting specific genotypes to high- and low-yielding environments is a valuable tool for evaluating varieties [53]. Selection of the most suitable genotype and fertilizer application is now considered a precision farming component [54].
All statistical tools that consider both G and G × E, including GGE biplot, Pi, and KR, were strongly correlated with each other and yield, apart from . Similar results in other environmental evaluations of wheat were found by Smutna et al. [53]. These findings align with prior research indicating that these tools contribute to the agronomic concept of stability [18,55]. was positively correlated with σ2i, CVi, s2di, Wi2, and θ(i), parameters that do not correlate with yield, thus demoting the highest yielding genotypes. Similar results were found by other wheat researchers [53]. Moreover, the Si, Npi, and CVi statistics are influenced by both yield and stability. Consequently, they promote genotypes that display typical stability and may not excel under optimal conditions [18,56].
Extensive crossover genotype–environment (GE) interactions imply that the current genotype evaluation procedures may not accurately reflect the prevailing conditions. However, utilizing the GGE biplot has proven efficacious in facilitating the straightforward identification of superior genotypes. The GGE biplot model comprehensively considers both genotypic (G) and genotype–environment (GE) interactions, presenting a graphical representation that serves as a valuable methodology for assessing the adaptability and stability of genotypes across diverse environments. This approach offers a visual and integrated evaluation of performance and stability [7,20,24,52].
GGE biplot analysis of all environments, which evaluated both average yield performance and stability, indicated that Mexicali-81 (G6) and Elpida (G12) are the varieties closest to the ideal genotype. Simeto (G8) and Maestrale (G3) had good performance in the low-yielding environments, while Mexicali-81 (G6) and Elpida (G12) were the varieties closest to the ideal genotype in the high-yielding environments, validating the results of the evaluation of all the environments. GGE biplot analysis has been used to evaluate genotypes in wheat, with successful results [57] and adoption to heat stress and irrigation environments [58]. Considering both performance and stability through visual analysis constitutes a significant advantage, instilling confidence in the agronomists in the decision-making process of promoting superior genotypes. Consequently, this approach aids breeders in identifying genotypes that merit release for cultivation.
Evaluation of all environments for a combination of high yield and stable production showed that the best genotypes were G8 (Simeto), G2 (Canavaro), and G12 (Elpida). Similarly, G12 (Elpida), G8 (Simeto), and G6 (Mexicali-81) were the best genotypes in the subgroup with the three high-productivity environments, followed by G2 (Canavaro), while G2 (Canavaro), G13 (Zoi), and G8 (Simeto) were the best genotypes in the low-productivity environment subgroup.
5. Conclusions
Evaluation of sixteen durum wheat genotypes in six multi-environmental trials confirmed that a detailed study of the Genotype × Environment interaction could increase the yield of durum wheat farming systems. The stability models used in the study resulted in a diverse ranking of genotypes. A very interesting result was that many statistical tools that consider both G and G × E, such as GGE biplot, Pi, and KR, showed strong correlations with each other and with yield. This aided in the identification of the most suitable genotypes. This statistical set centered on the agronomic aspect of stability. On the other hand, statistical parameters focusing on the statical aspect of stability, such as , σ2i, Cvi, s2di, Wi2, KR, and θ(i), downplayed the significance of the highest yielding genotypes. Ultimately, the GGE biplot proved to be a highly effective statistical tool for assessing the worth of wheat genotypes in terms of both specific and general adaptation. It achieved this while preserving yield capacity and providing graphical representations. An interesting outcome emerged regarding the landrace Lemnos, suggesting its potential use in organic agriculture. Finally, our study revealed that some commercial cultivars exhibited better performance under late-sowing conditions, indicating their tolerance of more adverse conditions during the critical grain filling period, such as higher air temperature and deficient soil moisture, i.e., conditions correlated with climate change.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/agronomy14010102/s1, Table S1. Location, type of differentiation, and cultivation information for the six environments.
Author Contributions
Conceptualization, E.N., A.A. and I.M.; methodology, E.N., N.T., I.S., N.K., E.V., E.K., F.P., S.D., A.A. and I.M.; validation, E.N., N.T., I.S., N.K. and I.M.; formal analysis, E.N., N.K. and I.M.; investigation, E.N., N.T., I.S., N.K., E.V., E.K., F.P., S.D., A.A. and I.M.; resources, E.N., N.T., I.S., N.K., E.V., E.K., F.P., S.D., A.A. and I.M.; data curation, E.N. and I.M.; writing—original draft preparation, E.N., N.T., I.S., N.K., E.V., E.K., F.P., S.D., A.A. and I.M.; writing—review and editing, E.N., N.T., I.S., N.K., E.V., E.K., F.P., S.D., A.A. and I.M.; visualization, E.N., N.T., I.S., N.K., E.V., E.K., F.P., S.D., A.A. and I.M.; supervision, E.N. and I.M.; project administration, I.M. and A.A.; funding acquisition, I.M. and A.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research was implemented in the framework of the GrWheat research project (project code MIS 5072523), which was co-funded by the European Union and Greek National Funds through the Operational Program Competitiveness, Entrepreneurship and Innovation, under the call Research-Create-Innovate.
Data Availability Statement
Data are only available on request due to privacy restrictions.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- OECD; FAO. OECD-FAO Agricultural Outlook 2022–2031; OECD: Paris, France, 2022. [Google Scholar]
- Martínez-Moreno, F.; Solís, I.; Noguero, D.; Blanco, A.; Özberk, İ.; Nsarellah, N.; Elias, E.; Mylonas, I.; Soriano, J.M. Durum Wheat in the Mediterranean Rim: Historical Evolution and Genetic Resources. Genet. Resour. Crop Evol. 2020, 67, 1415–1436. [Google Scholar] [CrossRef]
- Grant, C.; Cubadda, F.; Carcea, M.; Pogna, N.E.; Gazza, L. CHAPTER 7—Vitamins, Minerals, and Nutritional Value of Durum Wheat11Cynthia Grant Is an Employee of Agriculture and Agri-Food Canada. ©Her Majesty the Queen in Right of Canada, as Represented by the Minister of Agriculture and Agri-Food Canada. In Durum Wheat, 2nd ed.; Sissons, M., Abecassis, J., Marchylo, B., Carcea, M., Eds.; AACC International Press: St. Paul, MN, USA, 2012; pp. 125–137. ISBN 978-1-891127-65-6. [Google Scholar]
- Crossa, J.; Fox, P.N.; Pfeiffer, W.H.; Rajaram, S.; Gauch, H.G. AMMI Adjustment for Statistical Analysis of an International Wheat Yield Trial. Theor. Appl. Genet. 1991, 81, 27–37. [Google Scholar] [CrossRef] [PubMed]
- Beres, B.L.; Rahmani, E.; Clarke, J.M.; Grassini, P.; Pozniak, C.J.; Geddes, C.M.; Porker, K.D.; May, W.E.; Ransom, J.K. A Systematic Review of Durum Wheat: Enhancing Production Systems by Exploring Genotype, Environment, and Management (G × E × M) Synergies. Front. Plant Sci. 2020, 11, 568657. [Google Scholar] [CrossRef] [PubMed]
- Xynias, I.N.; Mylonas, I.; Korpetis, E.G.; Ninou, E.; Tsaballa, A.; Avdikos, I.D.; Mavromatis, A.G. Durum Wheat Breeding in the Mediterranean Region: Current Status and Future Prospects. Agronomy 2020, 10, 432. [Google Scholar] [CrossRef]
- Yan, W. Singular-Value Partitioning in Biplot Analysis of Multienvironment Trial Data. Agron. J. 2002, 94, 990–996. [Google Scholar] [CrossRef]
- Li, W.; Yan, Z.-H.; Wei, Y.-M.; Lan, X.-J.; Zheng, Y.-L. Evaluation of Genotype × Environment Interactions in Chinese Spring Wheat by the AMMI Model, Correlation and Path Analysis. J. Agron. Crop Sci. 2006, 192, 221–227. [Google Scholar] [CrossRef]
- Roostaei, M.; Jafarzadeh, J.; Roohi, E.; Nazary, H.; Rajabi, R.; Mohammadi, R.; Khalilzadeh, G.R.; Seif, F.; Mirfatah, S.M.M.; Amiri, S.S.; et al. Genotype × Environment Interaction and Stability Analyses of Grain Yield in Rainfed Winter Bread Wheat. Exp. Agric. 2022, 58, e37. [Google Scholar] [CrossRef]
- Eberhart, S.A.; Russell, W.A. Stability Parameters for Comparing Varieties1. Crop Sci. 1966, 6, 36–40. [Google Scholar] [CrossRef]
- Shukla, G.K. Some Statistical Aspects of Partitioning Genotype-Environmental Components of Variability. Heredity 1972, 29, 237–245. [Google Scholar] [CrossRef]
- Francis, T.R.; Kannenberg, L.W. Yield Stability Studies in Short-Season maize. I. A. descriptive method for grouping genotypes. Can. J. Plant Sci. 1978, 58, 1029–1034. [Google Scholar] [CrossRef]
- Purchase, J.L.; Hatting, H.; van Deventer, C.S. Genotype × Environment Interaction of Winter Wheat (Triticum aestivum L.) in South Africa: II. Stability Analysis of Yield Performance. S. Afr. J. Plant Soil 2000, 17, 101–107. [Google Scholar] [CrossRef]
- Gauch, H.G. Model Selection and Validation for Yield Trials with Interaction. Biometrics 1988, 44, 705–715. [Google Scholar] [CrossRef]
- Nassar, R.; Hühn, M. Studies on Estimation of Phenotypic Stability: Tests of Significance for Nonparametric Measures of Phenotypic Stability. Biometrics 1987, 43, 45–53. [Google Scholar] [CrossRef]
- Thennarasu, K. On Certain Non-Parametric Procedures for Studying Genotype-Environment Interactions and Yield Stability. Ph.D. Thesis, IARI, Division of Agricultural Statistics, New Delhi, India, 1995. [Google Scholar]
- Becker, H.C.; Léon, J. Stability Analysis in Plant Breeding. Plant Breed. 1988, 101, 1–23. [Google Scholar] [CrossRef]
- Mohammadi, R.; Amri, A. Comparison of Parametric and Non-Parametric Methods for Selecting Stable and Adapted Durum Wheat Genotypes in Variable Environments. Euphytica 2008, 159, 419–432. [Google Scholar] [CrossRef]
- Saeidnia, F.; Taherian, M.; Nazeri, S.M. Graphical Analysis of Multi-Environmental Trials for Wheat Grain Yield Based on GGE-Biplot Analysis under Diverse Sowing Dates. BMC Plant Biol. 2023, 23, 198. [Google Scholar] [CrossRef] [PubMed]
- Yan, W.; Kang, M.S.; Ma, B.; Woods, S.; Cornelius, P.L. GGE Biplot vs. AMMI Analysis of Genotype-by-Environment Data. Crop Sci. 2007, 47, 643–653. [Google Scholar] [CrossRef]
- Katsenios, N.; Sparangis, P.; Leonidakis, D.; Katsaros, G.; Kakabouki, I.; Vlachakis, D.; Efthimiadou, A. Effect of Genotype × Environment Interaction on Yield of Maize Hybrids in Greece Using AMMI Analysis. Agronomy 2021, 11, 479. [Google Scholar] [CrossRef]
- Farokhzadeh, S.; Shahsavand Hassani, H.; Mohammadi-Nejad, G.; Zinati, Z. Evaluation of Grain Yield Stability of Tritipyrum as a Novel Cereal in Comparison with Triticale Lines and Bread Wheat Varieties through Univariate and Multivariate Parametric Methods. PLoS ONE 2022, 17, e0274588. [Google Scholar] [CrossRef]
- Padovan, G.; Martre, P.; Semenov, M.A.; Masoni, A.; Bregaglio, S.; Ventrella, D.; Lorite, I.J.; Santos, C.; Bindi, M.; Ferrise, R.; et al. Understanding Effects of Genotype × Environment × Sowing Window Interactions for Durum Wheat in the Mediterranean Basin. Field Crops Res. 2020, 259, 107969. [Google Scholar] [CrossRef]
- Gao, F.-C.; Yan, H.-D.; Gao, Y.; Huang, Y.; Li, M.; Song, G.-L.; Ren, Y.-M.; Li, J.-H.; Jiang, Y.-X.; Tang, Y.-J.; et al. Interpretation of Genotype-Environment-Sowing Date/Plant Density Interaction in Sorghum [Sorghum bicolor (L.) Moench] in Early Mature Regions of China. Front. Plant Sci. 2022, 13, 1008198. [Google Scholar] [CrossRef] [PubMed]
- Ben Mariem, S.; González-Torralba, J.; Collar, C.; Aranjuelo, I.; Morales, F. Durum Wheat Grain Yield and Quality under Low and High Nitrogen Conditions: Insights into Natural Variation in Low- and High-Yielding Genotypes. Plants 2020, 9, 1636. [Google Scholar] [CrossRef] [PubMed]
- Ayed, S.; Bouhaouel, I.; Othmani, A.; Bassi, F.M. Use of Wild Relatives in Durum Wheat (Triticum turgidum L. Var. Durum Desf.) Breeding Program: Adaptation and Stability in Context of Contrasting Environments in Tunisia. Agronomy 2021, 11, 1782. [Google Scholar] [CrossRef]
- Mohammadi, R.; Amri, A. Genotype × Environment Interaction for Durum Wheat Grain Yield and Selection for Drought Tolerance in Irrigated and Droughted Environments in Iran. J. Crop Sci. Biotechnol. 2011, 14, 265–274. [Google Scholar] [CrossRef]
- Beck, H.E.; Zimmermann, N.E.; McVicar, T.R.; Vergopolan, N.; Berg, A.; Wood, E.F. Present and Future Köppen-Geiger Climate Classification Maps at 1-Km Resolution. Sci. Data 2018, 5, 180214. [Google Scholar] [CrossRef] [PubMed]
- Peel, M.C.; Finlayson, B.L.; McMahon, T.A. Updated World Map of the Köppen-Geiger Climate Classification. Hydrol. Earth Syst. Sci. 2007, 11, 1633–1644. [Google Scholar] [CrossRef]
- Kozak, M.; Piepho, H.-P. What’s Normal Anyway? Residual Plots Are More Telling than Significance Tests When Checking ANOVA Assumptions. J. Agron. Crop Sci. 2018, 204, 86–98. [Google Scholar] [CrossRef]
- Yumpu.com Principles of Plant Genetics and Breeding. Available online: https://www.yumpu.com/en/document/view/5679061/principles-of-plant-genetics-and-breeding (accessed on 10 December 2023).
- Wricke, G. Evaluation Method for Recording Ecological Differences in Field Trials. Z. Pflanzenzücht 1962, 47, 92–96. [Google Scholar]
- Kang, M.S. A Rank-Sum Method for Selecting High-Yielding, Stable Corn Genotypes. Cereal Res. Commun. 1988, 16, 113–115. [Google Scholar]
- Payne, R. Genstat. Wiley Interdiscip. Rev. Comput. Stat. 2009, 1, 255–258. [Google Scholar] [CrossRef]
- Lin, C.S.; Binns, M.R. A Method of Analyzing Cultivar × Location × Year Experiments: A New Stability Parameter. Theor. Appl. Genet. 1988, 76, 425–430. [Google Scholar] [CrossRef] [PubMed]
- Huehn, M. Nonparametric Measures of Phenotypic Stability. Part 1: Theory. Euphytica 1990, 47, 189–194. [Google Scholar] [CrossRef]
- Rezzouk, F.Z.; Gracia-Romero, A.; Kefauver, S.C.; Nieto-Taladriz, M.T.; Serret, M.D.; Araus, J.L. Durum Wheat Ideotypes in Mediterranean Environments Differing in Water and Temperature Conditions. Agric. Water Manag. 2022, 259, 107257. [Google Scholar] [CrossRef]
- Sabella, E.; Aprile, A.; Negro, C.; Nicolì, F.; Nutricati, E.; Vergine, M.; Luvisi, A.; De Bellis, L. Impact of Climate Change on Durum Wheat Yield. Agronomy 2020, 10, 793. [Google Scholar] [CrossRef]
- European Commission Organic Action Plan. Available online: https://agriculture.ec.europa.eu/farming/organic-farming/organic-action-plan_en (accessed on 16 November 2023).
- Abu-Zaitoun, S.Y.; Chandrasekhar, K.; Assili, S.; Shtaya, M.J.; Jamous, R.M.; Mallah, O.B.; Nashef, K.; Sela, H.; Distelfeld, A.; Alhajaj, N.; et al. Unlocking the Genetic Diversity within A Middle-East Panel of Durum Wheat Landraces for Adaptation to Semi-Arid Climate. Agronomy 2018, 8, 233. [Google Scholar] [CrossRef]
- Mylonas, I.; Stavrakoudis, D.; Katsantonis, D.; Korpetis, E. Chapter 1—Better Farming Practices to Combat Climate Change. In Climate Change and Food Security with Emphasis on Wheat; Ozturk, M., Gul, A., Eds.; Academic Press: Cambridge, MA, USA, 2020; pp. 1–29. ISBN 978-0-12-819527-7. [Google Scholar]
- Ninou, E.G.; Mylonas, I.G.; Tsivelikas, A.; Ralli, P.; Dordas, C.; Tokatlidis, I.S. Wheat Landraces Are Better Qualified as Potential Gene Pools at Ultraspaced Rather than Densely Grown Conditions. Sci. World J. 2014, 2014, 957472. [Google Scholar] [CrossRef] [PubMed]
- Ninou, E.; Mylonas, I.; Karagianni, I.; Michailidou, S.; Tsivelikas, A.; Sistanis, I.; Avdikos, I.; Korpetis, E.; Papathanasiou, F. Utilization of Intra-Cultivar Variation for Grain Yield and Protein Content within Durum Wheat Cultivars. Agriculture 2022, 12, 661. [Google Scholar] [CrossRef]
- Ninou, E.; Papathanasiou, F.; Vlachostergios, D.N.; Mylonas, I.; Kargiotidou, A.; Pankou, C.; Papadopoulos, I.; Sinapidou, E.; Tokatlidis, I. Intense Breeding within Lentil Landraces for High-Yielding Pure Lines Sustained the Seed Quality Characteristics. Agriculture 2019, 9, 175. [Google Scholar] [CrossRef]
- Koutsika-Sotiriou, M.; Mylonas, I.G.; Ninou, E.; Traka-Mavrona, E. The Cultivation Revival of a Landrace: Pedigree and Analytical Breeding. Euphytica 2010, 176, 15–24. [Google Scholar] [CrossRef]
- McLeod, J.G.; Campbell, C.A.; Dyck, F.B.; Vera, C.L. Optimum Seeding Date for Winter Wheat in Southwestern Saskatchewan. Agron. J. 1992, 84, 86–90. [Google Scholar] [CrossRef]
- Porter, J.R.; Gawith, M. Temperatures and the Growth and Development of Wheat: A Review. Eur. J. Agron. 1999, 10, 23–36. [Google Scholar] [CrossRef]
- Simmonds, N.W. Genotype (G), Environment (E) and G Components of Crop Yields. Exp. Agric. 1981, 17, 355–362. [Google Scholar] [CrossRef]
- Al-Sayaydeh, R.; Shtaya, M.J.; Qubbaj, T.; Al-Rifaee, M.K.; Alabdallah, M.A.; Migdadi, O.; Gammoh, I.A.; Al-Abdallat, A.M. Performance and Stability Analysis of Selected Durum Wheat Genotypes Differing in Their Kernel Characteristics. Plants 2023, 12, 2664. [Google Scholar] [CrossRef] [PubMed]
- Pour-Aboughadareh, A.; Barati, A.; Koohkan, S.A.; Jabari, M.; Marzoghian, A.; Gholipoor, A.; Shahbazi-Homonloo, K.; Zali, H.; Poodineh, O.; Kheirgo, M. Dissection of Genotype-by-Environment Interaction and Yield Stability Analysis in Barley Using AMMI Model and Stability Statistics. Bull. Natl. Res. Cent. 2022, 46, 19. [Google Scholar] [CrossRef]
- Baker, R.J. Tests for crossover genotype-environmental interactions. Can. J. Plant Sci. 1988, 68, 405–410. [Google Scholar] [CrossRef]
- Yan, W. GGEbiplot—A Windows Application for Graphical Analysis of Multienvironment Trial Data and Other Types of Two-Way Data. Agron. J. 2001, 93, 1111–1118. [Google Scholar] [CrossRef]
- Smutná, P.; Mylonas, I.; Tokatlidis, I.S. The Use of Stability Statistics to Analyze Genotype × Environments Interaction in Rainfed Wheat Under Diverse Agroecosystems. Int. J. Plant Prod. 2021, 15, 261–271. [Google Scholar] [CrossRef]
- Bojtor, C.; Mousavi, S.M.N.; Illés, Á.; Széles, A.; Nagy, J.; Marton, C.L. Stability and Adaptability of Maize Hybrids for Precision Crop Production in a Long-Term Field Experiment in Hungary. Agronomy 2021, 11, 2167. [Google Scholar] [CrossRef]
- Kebede, A.; Getahun, A. Adaptability and Stability Analysis of Groundnut Genotypes Using AMMI Model and GGE-Biplot. J. Crop Sci. Biotechnol. 2017, 20, 343–349. [Google Scholar] [CrossRef]
- Akcura, M.; Kaya, Y.; Taner, S.; Ayranci, R. Parametric Stability Analyses for Grain Yield of Durum Wheat. Plant Soil Environ. 2006, 52, 254–261. [Google Scholar] [CrossRef]
- Bosi, S.; Negri, L.; Fakaros, A.; Oliveti, G.; Whittaker, A.; Dinelli, G. GGE Biplot Analysis to Explore the Adaption Potential of Italian Common Wheat Genotypes. Sustainability 2022, 14, 897. [Google Scholar] [CrossRef]
- Bishwas, K.C.; Poudel, M.R.; Regmi, D. AMMI and GGE Biplot Analysis of Yield of Different Elite Wheat Line under Terminal Heat Stress and Irrigated Environments. Heliyon 2021, 7, e07206. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).