Abstract
The electrostatic spray technology can significantly improve the utilization rate of liquid medicine under the operation characteristics of unmanned aerial vehicles (UAVs) with small load and low spray volume. To explore the settlement law of electrostatic droplets, further improve the amount of droplets deposited in target crops, and reduce the loss of missing target, this study adopted the method of combining numerical simulation and high-speed photography to study the movement characteristics of electrostatic droplets of UAV induction conical electrostatic nozzle. Based on the droplet spatial dynamics theory, a user-defined function and volume of fluid (UDF-VOF) multiphase spray model is established to simulate the trajectory of electrostatic droplet. TEMA software is used to analyze the droplet motion image under electrostatic field, and the characteristic parameters, such as trajectory and velocity are obtained. Theoretical analysis and spray test results show that the main factors affecting electrostatic droplet settlement are charging voltage, droplet falling distance, and airflow velocity. The optimal charging voltage of electrostatic droplet is 14 kv, the maximum charge-mass ratio is 1.04 mC/kg, and the average particle size is 209.77 μm. The numerical simulation results show that spray height, charging voltage, and lateral wind speed have significant effects on droplet sedimentation. The results of high-speed camera analysis show that the induced electric field causes the droplet to adsorb the target crop, resulting in the droplet movement trajectory deflection.
1. Introduction
Large amounts of pesticides are lost in surrounding areas due to the spray drift that results in health risks and environmental contamination. To improve drift reduction efforts in the crop protection field, researchers have been developing new spraying technologies to maximize the adsorption effect and increase the efficacy of crop protection products. In the operation of plant protection machinery, about 30% of pesticides are lost, and the other 50–60% of pesticide droplets fall into the earth after settlement, causing environmental pollution [1,2]. For a long time, ground plant protection machinery has been the main method of pesticide spraying in China, which is characterized by a large amount of pesticide spraying and low utilization rate, resulting in serious problems, such as pesticide waste, environmental pollution, poor economic benefits, and pesticide residues in food [3,4,5]. With the development of modern plant protection spraying technology, the combination of electrostatic spraying technology and aviation spraying technology has solved many problems in traditional ground spraying. Electrostatic spraying technology is a new application technology developed on the basis of droplet control technology and ultra-low volume spraying theory and practice. It has the characteristics of “electrostatic surround effect”; therefore, more droplets can be deposited in the central location of the target and the utilization rate of pesticides can be improved [6,7,8]. Compared with conventional spraying technology, electrostatic spraying can realize directional spraying, improve the utilization rate of pesticide, and save the cost of application. According to statistics, the effective utilization rate of pesticides using high-quality electrostatic spraying technology reaches 50–60% [9]. Agricultural aviation electrostatic spray technology, as one of the contents of China’s development of precision agricultural aviation application technology, has positive significance for the effective use of pesticides and the reduction in environmental pollution [10]. With the gradual application of agricultural aviation electrostatic spraying technology, researchers have conducted a series of explorations [11,12,13]. Ru et al. [14] designed a special aviation spray system for XY8D UAV, and proved that the deposition and coverage rates of the droplet in different parts of target crops were significantly increased by the aviation electrostatic spray through field spraying experiments of rice. Assuno et al. [15] and Zhang et al. [16] both proved that the aviation electrostatic spraying technology has the effect of reducing droplet drift and increasing droplet deposition.
It can be seen that the current research on aviation electrostatic spraying mainly focuses on the compatibility design and operation effect of the spraying machine and spraying system. In fact, it is the most direct and effective way to understand the characteristics of electrostatic spraying and grasp its advantages, in order to study the trajectory of charged droplet in the process of settling. Therefore, it is necessary to strengthen the research on the relationship between the trajectory of electrostatic droplet and the settlement law. Some researchers have used computational fluid dynamics (CFD) to simulate the motion trajectory of droplets and the internal state of the nozzle [17,18,19,20,21], but the influence of electrostatic field on the motion trajectory of electrostatic droplets is rarely involved. Relevant scholars conducted laboratory tests to intuitively analyze the movement track of droplets, and used relevant testing instruments to initially describe the movement state, deposition behavior, and distribution characteristics of the spray flow field of droplets [22,23,24,25]. However, the relevant testing instruments mainly test the parameters related to the movement of droplets, rather than directly observe the movement track of droplets, and the numerical calculation results have a large deviation from the experiment. Especially in [24], the spray characteristics including droplets size and velocity under different electrostatic voltages are investigated systemically, and its result concludes that the electrostatic force could assuredly affect the movement characteristics for small size droplets; however, the actual movement track and change pattern of droplet are not shown. In other words, non-visual studies reach conclusions that lack verifiable evidence. Therefore, it is necessary to establish a numerical model of the movement trajectory of charged droplet based on theoretical analysis and verify the simulation results using an intuitive high-speed camera. In this paper, a multiphase flow numerical model for the trajectory of electrostatic droplet is established by combining simulation analysis with experimental verification. High-speed photography technology is used to obtain the trajectory image of electrostatic droplets and verify the influence relationship between the trajectory of charged droplet and the settlement law. This study is used to improve the utilization rate of pesticides and optimize the operating parameters of UAV electrostatic spraying technology.
2. Materials and Methods
2.1. Materials and Equipment
The electrostatic spraying system used in this test was the induction conical electrostatic nozzle and its charging device of YG20-6 six-rotor plant protection UAV (Heilongjiang Bayi Agricultural University College of Engineering, Heilongjiang, China), as shown in Figure 1. The electrode diameter of the electrostatic nozzle is 40 mm, the width is 17 mm, the spray conical angle is 80°, the nozzle size is 2 mm, the initial motion speed of the droplet is 20 m/s, and the particle size range is 150–350 μm. (According to the ISO 25358-2018 standard ‘Crop protection equipment-Droplet-size spectra from atomizers-Measurement and classification’, the nozzle droplet particle size can be defined as Fine). Herein, the test spray liquid is tap water and the laboratory potted rice (East Farmers 426) is the test plant (BBCH 20-29 period), with leaf blade length of 10–30 cm and width of 1–2 cm.
Figure 1.
YG20-6 six-rotor plant protection UAV and induction conical electrostatic nozzle.
The 6485 picoammeter (accuracy ±0.5%) and JA31002 precision electronic balance (accuracy 0.001 g) were used for the charge-mass ratio test (Key Laboratory of Plant Protection Engineering, Jiangsu, China). The droplet charge-mass ratio test of charging voltage is set to 6–20 kv, spray time is set to 60 s, and spray pressure is set to 0.2 MPa. The liquid pressure is monitored by the Chinese Suxun SUX 90A-0-10 MPa diffusion silicon pressure sensor. The particle size of electrostatic droplets is tested by the Winner318 laser particle size analyzer, with the accuracy of 0.001 μm (Jinan Micro Nano Technology Co., Ltd. Shandong, China). Each experiment is repeated three times and the results are averaged.
The PCO Dimax CS3 camera (PCO Co., Ltd., German) and its supporting equipment are used for tracking the experiments of electrostatic droplets, as shown in Figure 2. The specific parameters are shown in Table 1.
Figure 2.
Induction conical aerostatic nozzle and its charging device of Y5-B fixed-wing aircraft.
Table 1.
Main features index of high-speed camera.
The target is placed directly below the electrostatic nozzle, and the shooting position of the camera is at the same level as the target. As shown in Figure 3, the camera and light source angles were adjusted, and a clear field of view is selected in the area near the leaf deposition of fog drops for shooting. The test environment is a dark room without the influence of cross wind. The spray pressure is set at 0.2 MPa, the charging voltage is set at 0 and 14 kv, respectively, and the spray height is set at 1.5 m. After the spray is stabilized, the camera begins to shoot. The shooting speed is set at 4000 frames per second and the resolution is 1080 × 960. After shooting, the images are saved to the corresponding format of image processing and analyzed by TEMA 2D analysis software (high-precision motion software developed by the Swedish company Image-System) [26].
Figure 3.
Test shooting area. 点 means point.
2.2. Numerical Simulation of Motion Characteristics of Electrostatic Droplet
2.2.1. Boundary Condition Setting
The maximum calculation volume of the simulation test is 5 × 3 × 4 m. The simulated temperature was set at 23° and the humidity at 40%. By changing the spray height, lateral wind speed, and charged voltage, the movement trajectory of droplets under different conditions are simulated, respectively. The numerical simulation equation follows three conservation laws, namely, energy conservation, mass conservation, and momentum conservation. It is assumed that the behavior of electrostatic particles does not affect the formation of electric field, the continuous phase is air, the dispersed phase is particles, the air density is 1.225 (kg·m−3), the viscosity coefficient is 1.7894 × 10−5 (Pa·S), and the maximum charge is 6.7 × 10−8 (mC). By constructing the potential field and differentiating it, the field strength is obtained. Therefore, the Laplace equation of electrostatic potential (UDS) is as follows [27]:
where φ is the electrostatic potential (v).
The electric field E generated by the electrostatic potential is:
The force F of the electric field acting on the particle is:
where E is the electric field generated by the electrostatic potential (N/C) and q is the particle charge (C).
The force of the electric field on the particle is proportional to the spatial gradient of the electrostatic potential. The continuous trajectory of particle movement after a certain time can be obtained by simulation analysis.
2.2.2. Grid Partitioning
The center of the electrode was set as the origin of coordinates, and the final fluid domain was established including six parts: Electrode, inlet, outlet, top surface, ground, and side. The number of nodes in the three directions is set to 50, 60, and 30, respectively. The steam content at the outlet was used as the index to test the grid independence. The total number of grids reached 456,909 when the outlet water vapor content did not change. The mesh mass unit is 0.4, which meets the compliance standard, as shown in Figure 4. In the computational domains for the cross wind stage of simulation, the airflows were created along the X direction. The two ends in the X direction were set as the velocity-inlet and pressure-outlet. The other boundaries for the sides, top, and bottom were set as a no-slip wall.
Figure 4.
Grid partitioning of fluid domain.
2.2.3. Electric Field UDF Setting
At the initial stage of calculation, the flow field is set as the steady state, and the gravity direction is selected as −9.8 (kg·m−2). Under the control of turbulent k-e model, the fluid inlet is set as the velocity inlet and the fluid outlet as the pressure outlet. The side and top are symmetric boundaries, and the residual curve is obtained by parallel calculation, as shown in Figure 5. After the residual calculation converges, it shows that the state of single-phase flow is convergent. Then, the convergent single-phase flow field is considered as the initial field of dynamical proton model (DPM), and the serial is used to set the DPM model in FLUENT. After the DPM model is set up, the potential field is constructed. Different charging voltages of 0, 14, and 20 kv, respectively were set to the electrodes. The droplet density is set to 998.2 (kg·cm−3). Since the strength of the electric field is uncertain, it is obtained by taking the derivative of the electric potential. In this paper, the electrostatic field is programmed with MATLAB to obtain the field intensity in three directions, and the electric field force is obtained by multiplying with the charge quantity. Algorithm 1 is provided in the paper.
| Algorithm 1 CFD droplet trajectory electric field programming |
| #include “udf.h” |
| #include “dpm.h” |
| #include “sg.h” |
| #include “surf.h” |
| #define q0 2.0/* charge [C]/[Kg] */ |
| DEFINE_ADJUST(calc, domain) |
| { |
| #if !RP_HOST |
| Thread *t; |
| cell_t c; |
| face_t f; |
| thread_loop_c(t,domain) |
| { |
| /* E = -grad(phi) */ |
| C_UDMI(c,t,0) = -C_UDSI_G(c,t,0)[0];/* E_x */ |
| C_UDMI(c,t,1) = -C_UDSI_G(c,t,0)[1];/* E_y */ |
| C_UDMI(c,t,2) = -C_UDSI_G(c,t,0)[2];/* E_z */ |
| } |
| thread_loop_f (t,domain) |
| { |
| if (NULL != THREAD_STORAGE(t,SV_UDS_I(0)) && |
| NULL != T_STORAGE_R_NV(t,SV_UDSI_G(0))) |
| { |
| begin_c_loop(f,t) |
| { |
| /* this is for post processing purpuses */ |
| F_UDMI(f,t,0) = - C_UDSI_G(F_C0(f,t),t->t0,0)[0]; |
| F_UDMI(f,t,1) = - C_UDSI_G(F_C0(f,t),t->t0,0)[1]; |
| F_UDMI(f,t,2) = - C_UDSI_G(F_C0(f,t),t->t0,0)[2]; |
| DEFINE_DPM_BODY_FORCE(particle_body_force, p, i) |
| { |
| #if !RP_HOST |
| cell_t c = RP_CELL(&(p->cCell)); |
| Thread *t = RP_THREAD(&(p->cCell)); |
| if ( i==0) |
| { |
| bforce=q0*exp(-0.0097*P_TIME(p))*C_UDMI(c,t,0); /* q*Ex */ |
| } |
| else if (i==1) |
| { |
| bforce = q0*exp(-0.0097*P_TIME(p))*C_UDMI(c,t,1);/* q*Ey */ |
| } |
| else |
| { |
| bforce = q0*exp(-0.0097*P_TIME(p))*C_UDMI(c,t,2);/* q*Ez */ |
| } |
| /* an acceleration should be returned m/s2 or q*E is [C/kg]*[V/m] this is [N]/[Kg] */ |
| #endif |
| } |
Figure 5.
UDF calculation result.
The UDF function is used to embed the obtained electric field intensity into the CFD software, in order to complete the electro-hydraulic coupling. The UDF calculation result is shown in Figure 5.
2.2.4. Simulation Model Verification
As shown in Figure 6, to verify the reliability of the model, the spray pressure is set at 0.2 Mpa for simulation. The spray conical angle of 75° is obtained by the simulation experiment. Under the same spray conditions, the spray conical angle of 77° is obtained by the high-speed camera test, which indicates that the model has a good agreement. As shown in Figure 7, the droplet particle size distribution range obtained in the simulation is 150–350 μm. The distribution trend of the simulation results is the same as the test results.
Figure 6.
Simulation and test results of spray conical angle.
Figure 7.
Simulation results of droplet particle size.
2.2.5. Experiment Design
The influence factors of spray height, charging voltage, and lateral wind speed were used to simulate the droplet trajectory. To simulate the spray height of the movement characteristics of droplets, the influence of lateral wind speed is set to 0 m/s, charging voltage is set to 0 kv, and the spray height is set to 1–3 m. To simulate the charging voltage of the movement characteristics of droplets, the influence of lateral wind speed is set to 0 m/s, charging voltage is set to 0–20 kv, and the spray height is set to 3 m. To simulate the lateral wind speed of the movement characteristics of droplets, the influence of lateral wind speed is set to 0–2 m/s, charging voltage is set to 0 kv, and the spray height is set to 1 m. After determining the influence of various factors on the droplet movement track, the spray height is set as 3 m and the lateral wind speed is set as 2 m/s. The motion characteristics of electrostatic droplets and non-electrostatic droplets under the optimal charging voltage were analyzed.
3. Results and Discussion
3.1. Charge-Mass Ratio of Electrostatic Droplets Analysis
The measurement results of the droplet charge-mass ratio under different charging voltages are shown in Figure 8. The charge-mass ratio reaches the maximum of 1.04 mC/kg when the charging voltage is 14 kv. The charge-mass ratio does not increase with the increase in charging voltage when the charging voltage exceeds 14 kv. At this time, the voltage corresponding to the maximum charge-mass ratio is the limit operating voltage of the electrostatic nozzle.
Figure 8.
Charge-mass ratio of electrostatic droplets.
3.2. Particle Size of Electrostatic Droplets Analysis
The measurement results of droplet particle size under different charging voltages are shown in Figure 9. The droplet size has no clear change when the charging voltage is less than 10 kv. The droplet particle size reaches the minimum value of 209.77 μm when the charging voltage is 14 kv. The droplet size is refined by an induced electric field. However, the particle size of the droplet will not decrease all the time, which reaches the electric charge limit of the electrostatic nozzle.
Figure 9.
Particle size of electrostatic droplets.
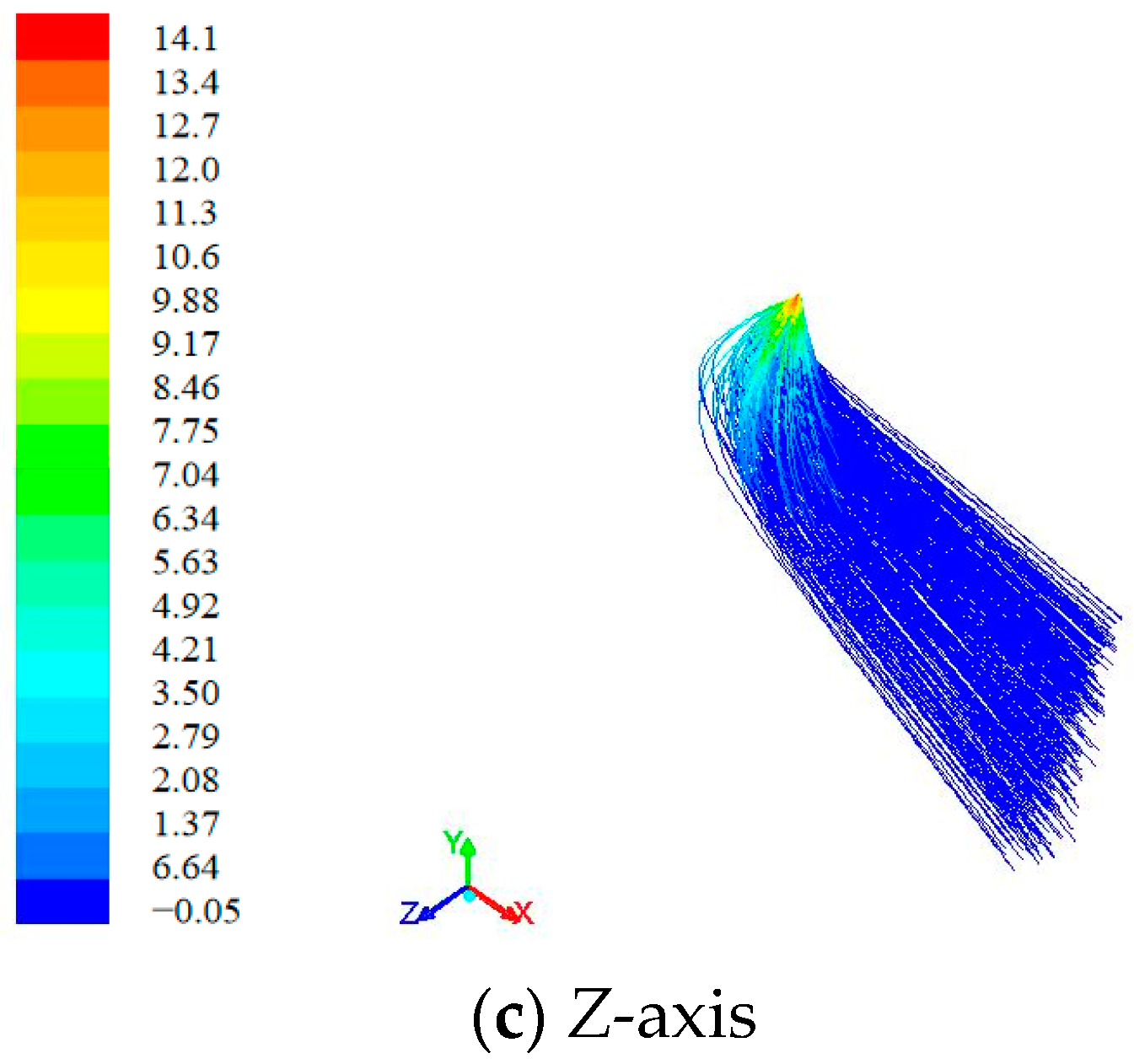
3.3. Numerical Simulation Analysis
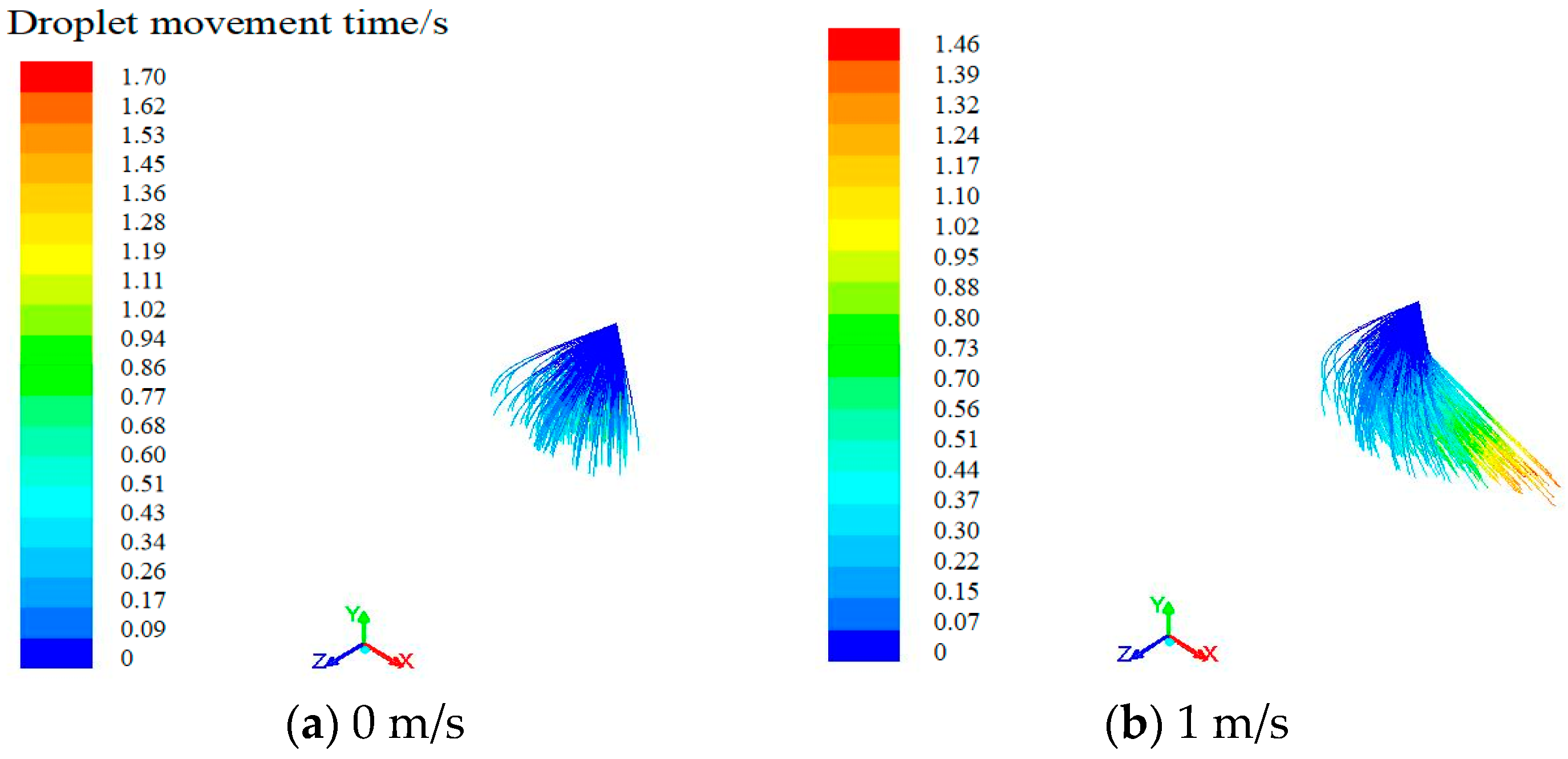
3.3.1. Droplets Movement Trajectory at Different Spray Heights
As shown in Figure 10, the droplet movement trajectory is proportional to the change in spray height. The maximum stagnation times of droplet particles are 1.70, 3.22, and 5.55 s. With the increase in spray height, the movement time of droplets increases and the movement speed of droplets decreases. The droplet distribution is uniform and the spray flow field presents a regular conical spray when the spray height is 1 m. The results show that the spray height of 1 m is suitable for the droplets movement under this condition. The droplets are in the process of settling when the spray height is 3 m. With the increase in moving distance, the droplet trajectory will not be deflected and the large area of diffuse drift phenomenon will not occur under the condition of no wind.
Figure 10.
Droplets movement trajectory at different spray heights.
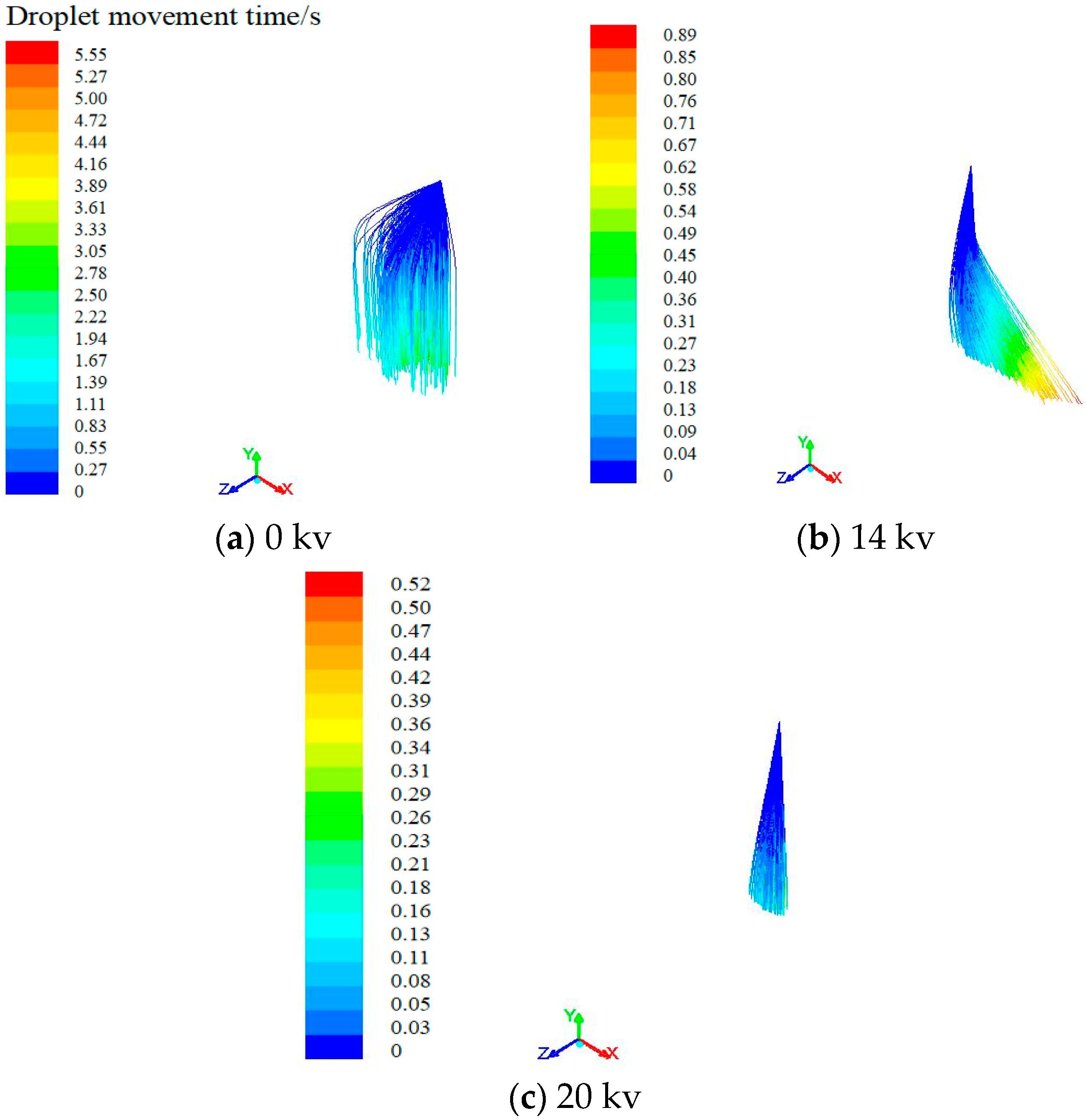
3.3.2. Droplets Movement Trajectory at Different Charging Voltages
As shown in Figure 11, the movement trajectory of droplet changed significantly after charging. With the increase in charging voltage, the deflection degree of droplet trajectory increases and then decreases gradually. The droplet trajectory will be deflected to a large extent when the charging voltage is 14 kv. However, the deflection of the trajectory is very small when the charging voltage is increased to 20 kv. The results show that the charging voltage has a significant effect on the trajectory of the droplet, and the amount of charge in the droplet determines the deflection degree of the trajectory of the droplet.
Figure 11.
Droplets movement trajectory at different charging voltages.
3.3.3. Droplets Movement Trajectory at Different Lateral Winds
As shown in Figure 12, the droplets movement trajectory is proportional to the change in lateral wind. With the increase in lateral wind speed, the maximum retention time of particles is 1.70, 1.46, and 1.33 s. Under the condition of no lateral wind, the droplets movement trajectory naturally falls. With the increase in lateral wind, the droplets movement trajectory was not abnormal at the beginning. However, after settling for a certain distance, the trajectory gradually deflects when approaching the target, and deflection increases with the lateral wind.
Figure 12.
Droplets movement trajectory at different lateral winds.
3.3.4. Motion Characteristics of Charged Droplet Comparative Analysis
The motion trajectory and velocity distribution of droplets on the X, Y, and Z axes are shown in Figure 13 and Figure 14. Under the conditions of lateral wind speed of 2 m/s and charging voltage of 14 kv, the distribution range of non-electrostatic droplets is 5 × 3 × 2.36 m and the distribution range of electrostatic droplets is 4.37 × 3 × 1.86 m. The results show that the distribution range of droplets under charge is smaller than the ordinary droplets. In addition, the drift of droplets decreases and the effective deposition increases. Under the condition of lateral wind, the electrostatic deflection of droplets position is 2.56–2.71 m in the vertical direction and the electrostatic deflection of droplets position is 1.05–1.2 m in the horizontal direction. The results showed that the lateral wind affected the overall movement trend of droplets, but the inductive charging of charged droplets effectively improved the ability to resist the invasion of lateral wind.
Figure 13.
The trajectory of non-electrostatic droplets in the axes of X, Y, and Z.
Figure 14.
The trajectory of electrostatic droplets in the axes of X, Y, and Z.
As shown in Figure 15 and Figure 16, the velocity distribution of non-electrostatic droplets in the X, Y, and Z axes were 12.7–0.034 m/s, 19.8–0.472 m/s, 14.1–0.045 m/s and the velocity distribution of electrostatic droplets in the X, Y, and Z axes were 23.1–0.387 m/s, 19.9–1.81 m/s, 23.2–0.198 m/s. The results show that the movement velocity of electrostatic droplets is greater than the non-electrostatic droplets, and the movement velocity of droplets decreases with the increase in time.
Figure 15.
The velocity of non-electrostatic droplets in the axes of X, Y, and Z.
Figure 16.
The velocity of electrostatic droplets in the axes of X, Y, and Z.
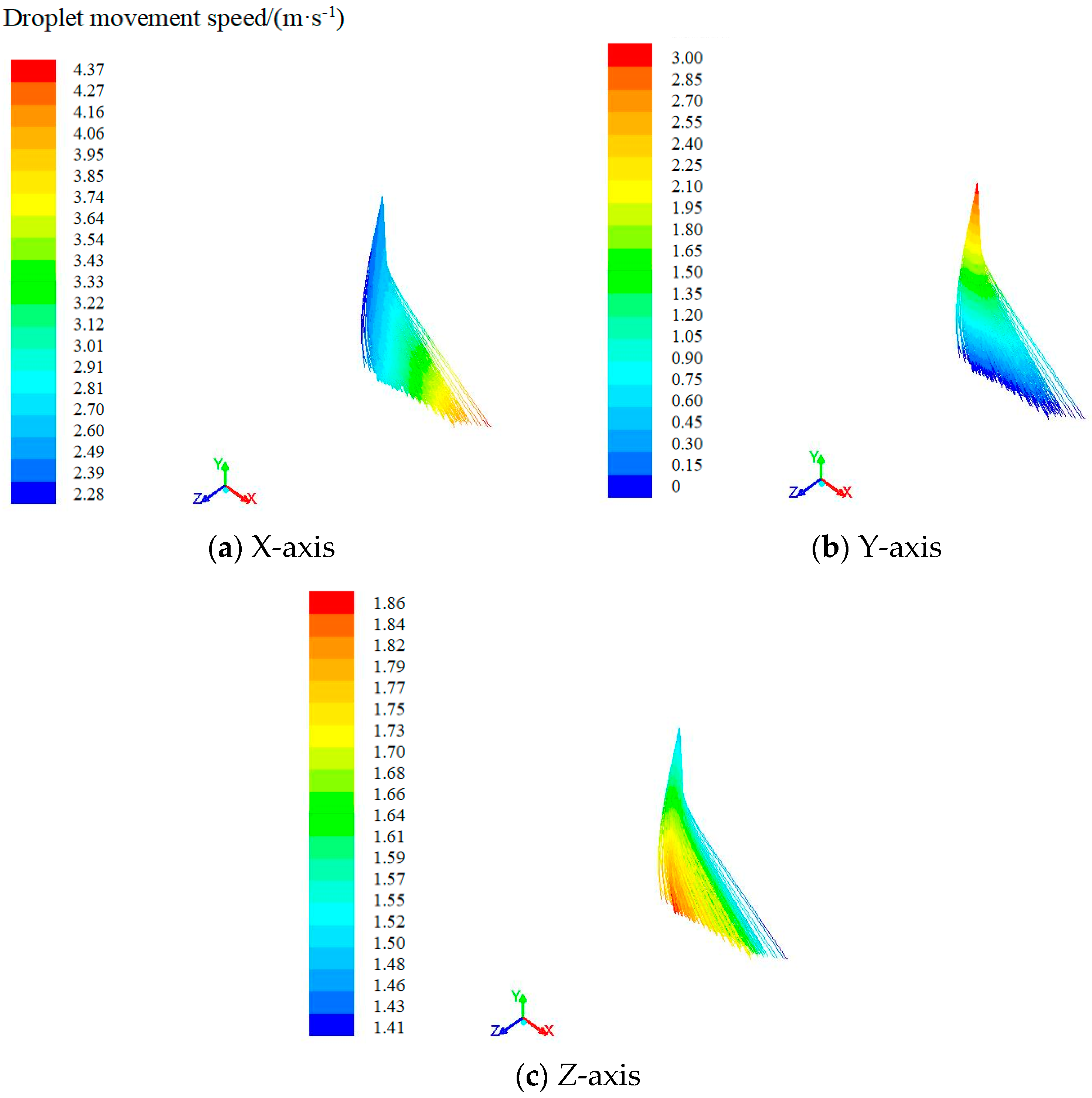
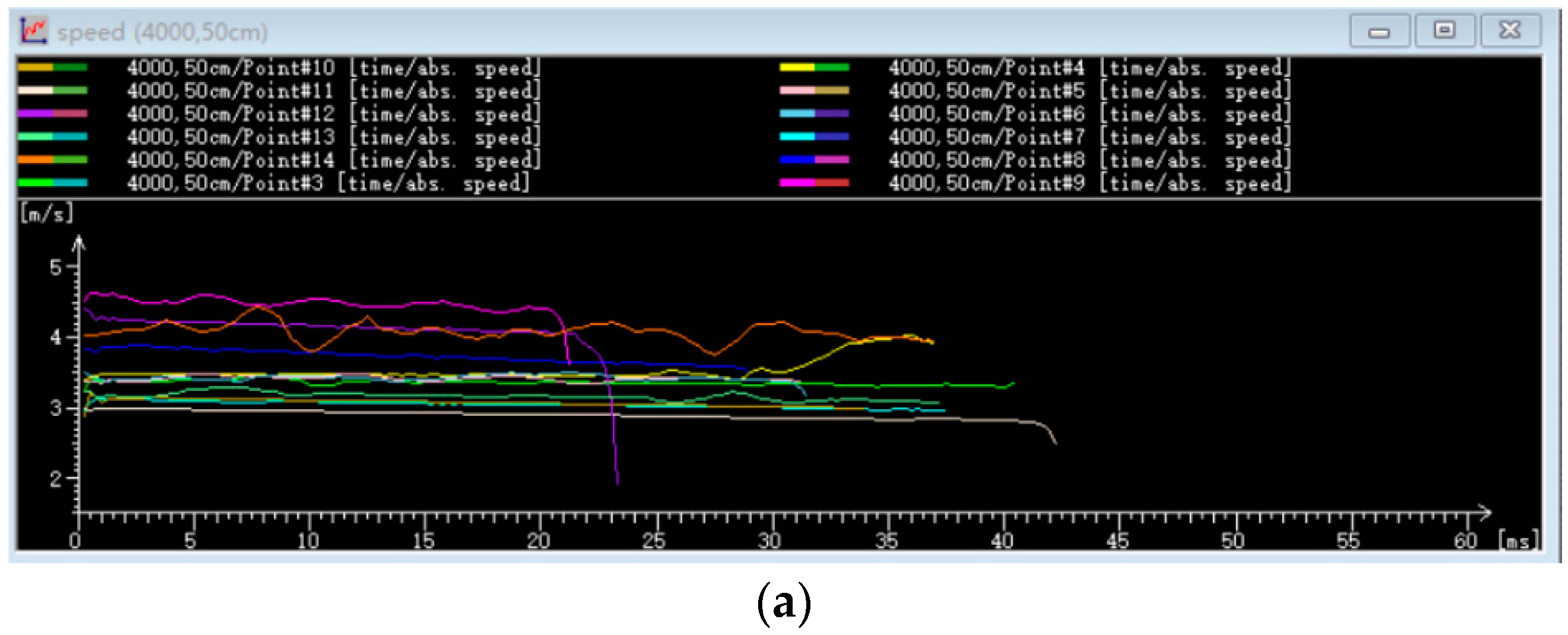
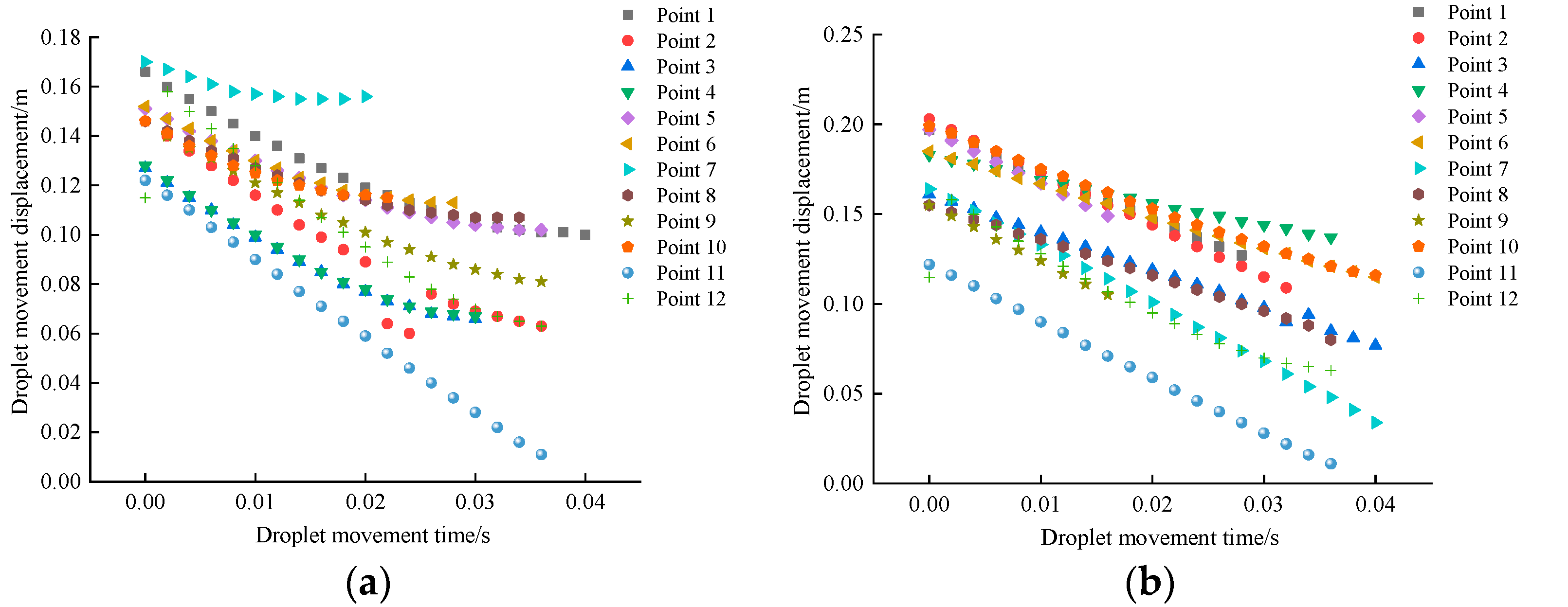
3.4. Droplet Motion Characteristics by High-Speed Camera Technology Analysis
The motion trajectory of electrostatic droplets based on the high-speed camera technology is tracked, as shown in Figure 17.
Figure 17.
Motion trajectory of electrostatic droplets based on the high-speed camera technology.
TEMA software and SPSS19.0 software were used to collect data and analyze the 12 data points. Results of the tracking of droplets by TEMA software analysis are shown in Figure 18 and Figure 19.
Figure 18.
Tracking of droplets by TEMA software analysis: (a) Non-electrostatic droplets; (b) electrostatic droplets.
Figure 19.
Speed of droplets by TEMA software analysis: (a) Non-electrostatic droplets; (b) electrostatic droplets.
According to the analysis results of high-speed photography, electrostatic droplets complete the settling motion under the action of space electric field, generate the induced electric field when approaching the target, and the droplets begin to adsorb the target. The tracked electrostatic droplets move in the direction of the target as a whole, and the speed increases slowly. As the droplet approached the target, its velocity increased continuously. The results confirmed that the droplet accelerated motion under the action of the induced electric field, and electrostatic adsorption with the test target occurred, in which the trajectory of the droplet was deflected.
Figure 20.
Motion displacement characteristic of droplets by SPSS analysis: (a) Non-electrostatic droplets; (b) electrostatic droplets.
Figure 21.
Motion speed characteristic of droplets by SPSS analysis: (a) Non-electrostatic droplets; (b) electrostatic droplets.
As shown in Table 2, the diameter of the selected droplets can be calculated by the software.
Table 2.
The diameter of the selected droplets.
In the whole spray field, with the increase in time and distance, the distribution range of droplets in the horizontal direction becomes larger. The non-electrostatic droplets distribution range is 0–0.18 m and the electrostatic droplets distribution range is 0–0.22 m. The movement velocity of non-electrostatic droplets range is 1.5–4 m/s, and the movement velocity fluctuation of most droplets is very small. The results show that the droplet moves at a constant speed in this region and maintains a stable state after atomization. Under the combined action of space electric field and induced electric field, the electrostatic droplet can adsorb the target blade, and its velocity range is 2.8–4.5 m/s. This result is consistent with the field operation of Assuno et al. [15] and Zhang et al. [16].
The phenomenon of electrostatic surround is characteristic of electrostatic spray [7,8]. At present, there are few studies that can accurately capture this phenomenon. Most researchers use numerical simulation to predict the trajectory of fog droplets [17,18,19]. In this paper, we identify and track the electrostatic droplets in the flow field of electrostatic spray by combining CFD simulation and high-speed photography. This research method can verify the simulation results. The simulation analysis and high-speed photography are consistent with the motion trajectory of the droplet. The above results show the electrostatic surround between electrostatic droplets and target crop leaves. The results verify the actual spraying effect of Ru et al. [14]. The experimental algorithm has been presented in the attachment. The study revealed the relationship between the motion law of electrostatic droplets and the effect of deposition, and provided a new method for further studying the electrostatic spray technology.
4. Conclusions
This study was motivated by attaining a detailed understanding of charged droplet motion characteristics for multi-rotor electrostatic plant protection UAVs, and then making recommendations for the formulation of spray strategies. The method of numerical simulation and high-speed camera tracking was used to identify and track droplets in the electrostatic spray flow field. The droplet trajectory model was established to reveal the relationship between the droplet trajectory and the settlement law. The research conclusions are as follows:
(1) The main factors affecting electrostatic droplets settlement are charging voltage, droplet falling distance, and lateral wind velocity. In the falling process, the particle size and the decrease range of droplets increase after charging. Static electricity assist in improving the distribution uniformity of droplets.
(2) The multiphase flow coupled electrostatic spray model based on the UDF-VOF method can well describe the droplet movement trajectory under the action of multiple factors. The induced electric field causes the droplet to adsorb the target crop, resulting in the deflection of the trajectory. In addition, further work will focus on the influence mechanism of rotor wind field, electrostatic droplet, and crop interaction on the canopy deposition.
(3) The motion characteristics of electrostatic droplet were tracked by the high-speed camera technology. The results confirmed the adsorption between electrostatic droplets and target crops. The intensity of the induced electric field was quantified. Compared with the non-electrostatic droplet, the distribution range and velocity of electrostatic droplet are increased.
Author Contributions
J.H. and C.L. conceived the idea of the experiment; M.Z. and C.L. performed the field test; Q.L. and C.L. analyzed the data; J.H., C.L., Y.L., Q.L., S.Z. and W.Z. wrote and revised the paper. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Key Research and Development Program Project of China (No. 2017YFC1601905-04), Heilongjiang Province Natural Science Outstanding Youth Project (No. YQ2019E032), and Heilongjiang Province Applied Technology Research and Development Program Project (No. GA21B003). We also give special thanks to the support of National Soybean Industry Technology System Post Expert Foundation of China (No. CARS-04-PS30) funded by the China Agriculture Research System of MOF and MARA.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Liu, X.; Song, L.; Cui, H.; Liu, Y.; Liu, X.; Wu, M. Decoupling on influence of air droplets stress and canopy porosity change on deposition performance in air-assisted spray. Chin. Soc. Agric. Mach. 2021, 52, 117–126, 137. (In Chinese) [Google Scholar]
- Lan, Y.; Chen, S. Current status and trends of plant protection UAV and its spraying technology in China. Int. J. Precis. Agric. Aviat. 2018, 1, 1–9. [Google Scholar] [CrossRef]
- Lan, Y.; Chen, S.; Fritz, B.K. Current status and future trends of precision agricultural aviation technologies. Int. J. Agric. Biol. Eng. 2017, 10, 1–17. [Google Scholar]
- Zhang, D.; Lan, Y.; Chen, L.; Wang, X.; Liang, D. Current status and future trends of agricultural aerial spraying technology in China. Trans. Chin. Soc. Agric. Mach. 2014, 45, 53–59. (In Chinese) [Google Scholar]
- Lan, Y.; Chen, S.; Deng, J.; Zhou, Z.; Ouyang, F. Development situation and problem analysis of plant protection unmanned aerial vehicle in China. Int. J. Agric. Biol. Eng. 2019, 10, 18–30. [Google Scholar]
- Martin, D.; Latheef, M. Aerial electrostatic spray deposition and canopy penetraion in cotton. J. Electrost. 2017, 90, 38–44. [Google Scholar] [CrossRef]
- Martin, D.; Latheef, M.; López, J. Electrostatically charged aerial application improved spinosad deposition on early season cotton. J. Electrost. 2019, 97, 121–125. [Google Scholar] [CrossRef]
- Patel, M.; Praveen, B.; Sahoo, H.; Patel, B.; Kumar, A.; Singh, M. An advance air-induced air-assisted electrostatic nozzle with enhanced performance. Comput. Electron. Agric. 2017, 135, 280–288. [Google Scholar] [CrossRef]
- Cunha, J.; Barizon, R.; Ferracini, V. Spray drift and caterpilar and stink bug control from aerial applications with electrostatic charge and atomizer on soybean crop. Eng. Agric. 2017, 37, 1163–1170. [Google Scholar]
- Zhou, L.; Zhang, L.; Xue, X. Research progress and application status of electrostatic pesticide spray technology. Trans. CSAE 2018, 34, 1–11. (In Chinese) [Google Scholar]
- Wang, S.; Li, X.; Zhou, H. Design and experiment of an aerial electrostatic spraying system for unmanned agricultural aircraft systems. Appl. Eng. Agric. 2020, 36, 955–962. [Google Scholar] [CrossRef]
- Post, S.; Roten, R. A review of the effects of droplet size and flow rate on the chargeability of spray droplets in electrostatic agricultural sprays. Trans. ASABE 2018, 61, 1243–1248. [Google Scholar] [CrossRef]
- Zhao, D.; Lan, Y.; Shen, W. Development of a charge transfer space loop to improve adsorption performance in aerial electrostatic spray. Int. J. Agric. Biol. Eng. 2020, 13, 50–55. [Google Scholar] [CrossRef]
- Ru, Y.; Jin, L.; Jia, Z. Design and experiment on electrostatic spraying system for unmanned aerial vehicle. Trans. CSAE 2015, 31, 42–47. [Google Scholar]
- Assuno, H.; Cunha, J.; Silva, S. Spray deposition on maize using an electrostatic sprayer. Eng. Agrícola 2020, 40, 503–510. [Google Scholar] [CrossRef]
- Zhang, W.; Hou, Y.; Liu, X. Wind tunnel experimental study on droplet drift reduction by a conical electrostatic nozzle for pesticide spraying. Int. J. Agric. Biol. Eng. 2017, 10, 87–94. [Google Scholar]
- Krinke, T.; Deppert, K.; Magnusson, M. Microscopic of the deposition of nanoparticles from the gas phase. J. Aerosol Sci. 2002, 33, 1341–1359. [Google Scholar] [CrossRef]
- Colbert, S.; Colmcross, A. A computer simulation for predicting electrostatic spray coating patterns. Powder Technol. 2005, 151, 77–86. [Google Scholar] [CrossRef]
- Dastourani, H.; Jahannama, M.; Eslami-Majd, A. A physical insight into electrospray process in cone-jet mode: Role of operating parameters. Int. J. Heat Fluid Flow 2018, 70, 315–335. [Google Scholar] [CrossRef]
- Xue, X.; Lan, Y.; Sun, Z.; Chang, C.; Hoffmann, W.C. Develop an unmanned aerial vehicle based automatic aerial spraying system. Comput. Electron. Agric. 2016, 128, 58–66. [Google Scholar] [CrossRef]
- Liu, C.; Hu, J.; Li, Y.; Zhao, S.; Li, Q.; Zhang, W. Numerical Simulation on Air-Liquid Transient Flow and Regression Model on Air-Liquid Ratio of Air Induction Nozzle. Agronomy 2023, 13, 248. [Google Scholar] [CrossRef]
- Wang, J.; Xu, W.; Wen, J. Numerical simulation on gas-liquid phase flow of large-scale plant protection unmanned aerial vehicle spraying. Trans. Chin. Soc. Agric. Mach. 2017, 48, 62–69. (In Chinese) [Google Scholar]
- Mark, N.; Malay, M.; Robert, C. Predicting particle trajectories on an electrodynamic screen-theory and experiment. J. Electrost. 2013, 71, 185–188. [Google Scholar]
- Wang, Z.; Zhang, Y.; Guo, T. Experimental study on size and velocity of charged droplets. Procedia Eng. 2015, 126, 522–526. [Google Scholar] [CrossRef]
- Kwek, J.; Heng, D.; Lee, S. High speed imaging with electrostatic charge monitoring to track powder deagglomeration upon impact. J. Aerosol Sci. 2013, 65, 77–87. [Google Scholar] [CrossRef]
- Frej, D.; Jaśkiewicz, M. Comparison of Volunteers’ Head Displacement with Computer Simulation—Crash Test with Low Speed of 20 km/h. Sensors 2022, 22, 9720. [Google Scholar] [CrossRef]
- Yang, P.; Wang, Z.; Liang, Z.; Liang, H.; Yang, Y. Molecular dynamics study of electric field acting on water surface potential. Chem. J. 2019, 77, 1045–1053. (In Chinese) [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).