Abstract
Maize is one of the important grain crops grown globally, and growth will directly affect its yield and quality, so it is important to monitor maize growth efficiently and non-destructively. To facilitate the use of unmanned aerial vehicles (UAVs) for maize growth monitoring, comprehensive growth indicators for maize monitoring based on multispectral remote sensing imagery were established. First of all, multispectral image data of summer maize canopy were collected at the jointing stage, and meanwhile, leaf area index (LAI), relative chlorophyll content (SPAD), and plant height (VH) were measured. Then, the comprehensive growth monitoring indicators CGMICV and CGMICR for summer maize were constructed by the coefficient of variation method and the CRITIC weighting method. After that, the CGMICV and CGMICR prediction models were established by the partial least-squares (PLSR) and sparrow search optimization kernel extremum learning machine (SSA-KELM) using eight typical vegetation indices selected. Finally, a comparative analysis was performed using ground-truthing data, and the results show: (1) For CGMICV, the R2 and RMSE of the model built by SSA-KELM are 0.865 and 0.040, respectively. Compared to the model built by PLSR, R2 increased by 4.5%, while RMSE decreased by 0.3%. For CGMICR, the R2 and RMSE of the model built by SSA-KELM are 0.885 and 0.056, respectively. Compared to the other model, R2 increased by 4.6%, and RMSE decreased by 2.8%. (2) Compared to the models by single indicator, among the models constructed based on PLSR, the CGMICR model had the highest R2. In the models constructed based on SSA-KELM, the R2 of models by the CGMICR and CGMICV were larger than that of the models by SPAD (R2 = 0.837), while smaller than that of the models by LAI (R2 = 0.906) and models by VH (R2 = 0.902). In summary, the comprehensive growth monitoring indicators prediction model established in this paper is effective and can provide technical support for maize growth monitoring.
1. Introduction
Maize is one of the most important crops grown globally and accounts for the highest proportion of the global cereal market. Ensuring maize production is of great significance in guaranteeing global economic development and food security [1]. The growth of maize is an important data source for early yield estimation, and its final yield can be predicted to a certain extent. Sujan Sapkota et al. [2] used a drone equipped with a multispectral camera to obtain the canopy spectral information of maize plants, and successfully monitored the growth and yield estimation of maize by using multiple growth parameters such as maize plant height, biomass, and leaf area index combined with vegetation index. Therefore, real-time and effective monitoring of field corn growth is of great significance in guiding field management [3]. In maize growth monitoring research, many parameters characterize maize growth [4,5,6,7], such as aboveground biomass, chlorophyll content, leaf area index, plant height, and leaf nitrogen content. In the study, three growth indicators, leaf area index (LAI, total plant leaf area per unit land area as a multiple of land area), relative chlorophyll content (SPAD, relative proportions of chlorophyll content in different samples), and plant height (VH, distance from the base of the plant to the top of the main stem, i.e., between the growing points of the main stem), were selected to initiate research and analysis of summer maize growth monitoring.
The leaf area index (LAI) is an important basis for characterizing the canopy structure and growth of crops, and is one of the most important parameters for evaluating crop growth conditions [8]. Ma JW et al. [9] constructed and validated a winter wheat LAI prediction model by combining four methods (GPR, artificial neural network (ANN), partial least-squares regression (PLSR), and spectral index (SI), with hyperspectral data), and the results showed the best results for ANN and GPR. Hang YH et al. [10] explored the use of spectral features, texture index, and crop cover to construct LAI estimation models through UAV remote sensing data, and the results showed that the combination of the three types of indices to construct multiple stepwise regression and artificial neural network models estimated LAI with the best accuracy. Tao HL et al. [11] used a UAV with a hyperspectral camera, and used stepwise regression analysis (SWR) and PLSR methods to predict AGB and LAI using vegetation index, red edge parameters, and their combinations, respectively. The results showed that the PLSR algorithm had the best effect in predicting AGB and LAI by combining the vegetation index with the red edge parameters. Chlorophyll (SPAD) is the main pigment that converts light energy into chemical energy and is the driving force behind photosynthesis in plants [12]. Qiao L et al. [13] utilized multispectral remote sensing images of maize captured by drones during the tasseling stage. They observed a significant linear correlation between near-ground vegetation indices and maize canopy chlorophyll content under medium and low crop coverage. For high coverage, a noticeable nonlinear correlation emerged, and the model for monitoring chlorophyll content, established based on partial least-squares regression (PLSR), demonstrated the best performance. Guo Y [14] and team identified optimal combinations of drone spectral indices and texture indices using the SRM model. Applying support vector machine (SVM) and random forest (RF) models, they estimated maize SPAD values, with the SVM model yielding the most optimal predictive results. Plant height (VH), as an important indicator of crop growth, can be used to indirectly obtain crop biomass [15], and can also be used to predict crop yield in conjunction with vegetation index and canopy cover [16]. Bending et al. [17] obtained visible-light data of barley based on a UAV-mounted digital camera. By constructing a CMS, they realized the accurate extraction of crop height and established a barley plant height estimation model. Xu YF et al. [18] constructed 22 multispectral vegetation indices with image spectral reflectance features, and selected three different machine learning algorithms to establish a plant height monitoring model for winter wheat. The results showed that the optimal prediction model for plant height was the MLR-VH model. Under normal circumstances, a single growth indicator characterizes the physiological information status of crops in a certain aspect. The data belong to the ‘point’ data in essence, and to a certain extent, they cannot represent the overall growth situation of crops, the use of multiple indicators, and the relationship between them to establish a comprehensive growth monitoring indicator (CGMI), which is of practical significance for remote sensing monitoring of crop growth.
Comprehensive growth monitoring indicators can be modeled according to different assignment methods, and the commonly used assignment method is the equalization method. Pei HJ et al. [19] synthesized five indicators reflecting wheat growth, including leaf area index, leaf chlorophyll content, plant nitrogen content, plant water content, and biomass, into a single growth indicator according to equal weights, and combined wheat growth by combining with partial least-squares regression, and achieved a high-precision model. This method did not take into account the contribution of a single indicator to the integrated growth monitoring indicator and simply constructed each indicator into a composite indicator according to equal weights. Although the above studies have good predictive capabilities, most of them are limited to using a single growth indicator to predict crop growth, or simply constructing a comprehensive growth indicator without considering the contribution of each indicator to crop growth, which makes them constructed from the prediction model has certain limitations. Considering the different degrees of importance of each indicator in the comprehensive growth monitoring indicators and the non-uniformity of the scale of each indicator, the coefficient of variation method and the CRITIC weighting method were used to try to construct the comprehensive growth monitoring indicators (CGMI).
In the study, we used summer maize multispectral image data to establish a crop growth monitoring model, and comparatively analyzed the correlation between comprehensive growth monitoring indices and individual indices and vegetation index. The main objectives include: (1) use of the coefficient of variation method and CRITIC weighting method to weight chlorophyll content, leaf area index, and plant height according to their contribution to the overall growth, and construct comprehensive growth monitoring indices respectively; (2) analysis of the correlation of comprehensive growth monitoring indicators and individual indicators with vegetation indices; (3) use of the PLSR and SSA-KELM algorithms to construct a comprehensive growth monitoring indicator prediction model, followed by analysis in comparison with a single growth indicator prediction model.
2. Materials and Methods
2.1. Overview of the Experimental Area
The experimental area was situated in China’s first tractor company limited intelligent agriculture demonstration farm in Yiyang County, Luoyang City, Henan Province, China, at coordinates 112°37′11.72″ E, 34°47′79.03″ N, belonging to the temperate continental monsoon-type climate. The area where the geographical coordinates are located is shown in Figure 1. The terrain in the experimental field was flat. The maize variety in this experiment was Zheng Dan 958, which was planted in rotation with wheat. The planting density is 67,000 plants m−2, the row spacing is 0.6 m, and the plant spacing is 0.2 m. Its management methods, such as irrigation, fertilization, pest, and weed control, were the same as those of local conventional farmland.
Figure 1.
Geographical location of China’s first tractor company limited intelligent agriculture demonstration farm.
2.2. UAV Data Acquisition and Preprocessing
This study utilized a DJI Phantom 4 drone (DJI, Shenzhen, China) to collect multispectral remote sensing data of summer maize, equipped with an integrated multispectral imaging system consisting of one visible-light camera and five multispectral cameras (blue, green, red, red edge, and near-infrared). The experiment took place on 22 July 2022, from 10:00 to 12:00 during the summer maize jointing stage, with stable light intensity, clear weather, and no wind.
Before image acquisition, flight routes were planned using mapping software (DJI Terra, V3.9.4, DJI, Shenzhen, China), and spectral image collection followed the planned routes. The drone flew at a height of 70 m, with the sensor lens pointing vertically downward and an 85% overlap rate in both longitudinal and lateral directions. The flight direction was north-south, with a speed of 3.5 m/s.
For reflectance calibration, a calibration reflectance panel was placed on the ground in the experimental area before and after image acquisition. The drone, manually controlled, hovered 2 m directly above the calibration panel to capture spectral images, obtaining standard reflectance values for the test.
Import the gathered multispectral images into Pix4D Mapper software (from Pix4D, V4.4.12, Lausanne, Switzerland) for preprocessing to derive the reflectance spectrum of summer corn within the sampling point ROI region (illustrated as the box in Figure 2). The primary steps encompass (1) ortho-image processing; (2) calibration using reflectance board DN values, generating stitched images; (3) geometric correction with concurrently obtained high-definition digital images as references; (4) choosing the necessary ROI region pertinent to this study; (5) deriving the average reflectance spectrum within the ROI, representing the summer corn’s reflectance spectrum within that specific ROI region. For this study, 20 experimental ROI regions, each measuring 10 m × 5 m, are chosen based on growth gradients. Of the data, 70% is designated as the training set (70 plants of maize), while the remaining 30% forms the validation set (30 plants of maize).

Figure 2.
ROI regional distribution map [20].
2.3. Field Data Acquisition
Growth indicators are time-sensitive [21]. Ground-truthing data, mainly including relative chlorophyll content, leaf area index, and plant height, were synchronously collected on the same day that summer maize multispectral remote sensing data were acquired.
- (1)
- Measurement of Relative Chlorophyll Content
In this experiment, a portable SPAD-502Plus chlorophyll meter (Konica Minolta, Tokyo, Japan) was used for SPAD determination. Five maize plants were selected in each experimental area according to the five-point sampling method, avoiding leaf veins to collect the SPAD values of the three parts of the ear leaves of each maize plant, the root, the middle of the leaf, and the tip of the leaf. Each part was repeated twice, and the average of the six times’ data was taken as the SPAD value of the plant [22]. The mean SPAD value of 5 plants in the experimental area was calculated as the relative chlorophyll content of maize plants in that area.
- (2)
- Determination of Leaf Area Index
In this experiment, leaf area index data were collected using the aspect ratio method. Measure summer maize leaf length and maximum leaf width with a tape measure. Five maize plants were selected from each experimental area according to the five-point sampling method, and the and of their leaves were measured, and each part was repeated three times to take the average value [23]. The mean LAI value of five plants in the experimental area was calculated as the LAI of maize plants in the area. The LAI calculation formula is as follows:
where is the maize leaf area conversion factor with a value of 0.75, is the planting density (plants m−2), is the total number of leaves (pieces) of the th plant, and is the number of plants measured.
- (3)
- Maize Height Measurement
Five maize plants were selected in each ROI area according to the five-point sampling method, and the vertical distance from the ground to the highest point of the plant was measured physically using a tape measure with the plant’s leaves naturally spread. Measurements were repeated three times for each plant to take the average value. The average heights of the five maize plants in the experimental area were taken as the plant height of the maize in that area.
2.4. Comprehensive Growth Indicator Construction
Based on the importance of relative chlorophyll content, leaf area index, and plant height in the comprehensive growth monitoring indicator of summer maize, the Comprehensive growth monitoring indicator (CGMI) of maize was constructed. For this reason, in this study, the CRITIC weighting method was used in this study to determine the weights of the three indicators, and the weights of LAI, SPAD, and VH were A, B, and C. This led to the establishment of the comprehensive growth monitoring indicator CGMICR.
The CRITIC weighting method is an objective method of assigning weights based on the volatility of data [24]. Its basic idea lies in two indicators, which are volatility (contrast strength) and conflict (correlation) indicators. Volatility is expressed using the standard deviation. If the larger the standard deviation of the data indicates greater volatility, the higher the weight will be. Conflict is expressed using the correlation coefficient table. If the value of the correlation coefficient between the indicators is larger, it means that there is more similarity between the indicators, and the smaller the conflict, then its weight will be lower.
- (1)
- Data Normalization
To eliminate the influence of different scales on the evaluation results, it is necessary to normalize the indicators. The normalization formula is as follows:
where denotes the value of the th evaluation indicator for the th sample, denotes the minimum value in the th indicator, denotes the maximum value in the th indicator, and denotes the data normalized to the th indicator.
- (2)
- Calculation of Indicator Volatility
In the CRITIC weighting method, a larger standard deviation indicates that the indicator is more volatile and more informative, and more weight should be given to the indicator.
where denotes the mean of the th indicator, and denotes the standard deviation of the th indicator is the volatility of that indicator.
- (3)
- Calculation of Conflicting Indicators
The conflict between indicators is expressed using the correlation coefficient; the stronger the correlation between an indicator and other indicators, the less conflict there is between the indicator and other indicators, reflecting more of the same information, and the more repetitive the content of the evaluation that can be embodied, which to a certain extent weakens the intensity of the evaluation of the indicator, and the weight assigned to the indicator should be reduced.
where denotes the correlation matrix of the indicator, denote the th indicator and the th indicator, denotes the correlation coefficient between the th indicator and the th indicator, and denotes the number of indicators.
- (4)
- Calculation of the Information Content of the Indicator
- (5)
- Calculation of Objective Weights for Indicators
- (6)
- Comprehensive Growth Monitoring Indicator CGMICR
The CRITIC weight method was used to derive A, B, and C as 0.331, 0.390, and 0.279, respectively, and the comprehensive growth monitoring indicator CGMICR was constructed. The expression of CGMICR is as follows:
where is the normalized LAI value, is the normalized SPAD value, and is the normalized VH value.
2.5. Selection of Vegetation Indices
In the initial stage of the study, the correlation analysis between a single band and the maize growth indicator showed that the correlation between the single band and the maize growth indicator was low, which was similar to the results of previous studies [25,26]. Therefore, the vegetation index was used to predict the growth of maize. The vegetation index (VI) changes through the combination of reflectance in different bands, which weakens the interference of background and other factors on the spectral characteristics of vegetation to a certain extent, and helps to improve the accuracy of remote sensing data to express crop growth. [27]. To better reflect the information contained in CGMI, this study extracted the spectral reflectance of 20 ROI regions from the spliced raw images and constructed vegetation indices by linear or nonlinear combinations. Eight vegetation indices with high relevance and wide application were selected: Green Ratio Vegetation Index (GRVI), Green Optimal Soil-Adjusted Vegetation Index (GOSAVI), Optimal Vegetation Index (VIopt), Normalized Difference Vegetation Index (NVI), Green Difference Vegetation Index (GDVI), Ratio Vegetation Index (RVI), Normalized Difference Vegetation Index (NDVI), Vegetation Index (RVI), Green Normalized Difference Vegetation Index (GNDVI), and Canopy Chlorophyll Content Index (CCCI). The formula for calculating the vegetation indices is shown in Table 1.

Table 1.
Vegetation indices and its calculation formula [20].
2.6. Model Construction
In this study, kernel-based extreme learning machine based on sparrow search algorithm optimization (SSA-KELM) was used to construct a comprehensive growth monitoring model.
Kernel-based extreme learning machine (KELM) is an improved algorithm based on ELM, and combined with the kernel function, KELM guarantees good generalization ability and faster learning speed based on retaining the advantages of ELM to improve the prediction performance of the model [35]. The predictive performance of KELM is significantly influenced by the regularization coefficient C and kernel function parameter S. Inadequate parameter optimization ability and poor local search capabilities can result in convergence on local optima, leading to low prediction accuracy. The SSA-KELM model optimizes the regularization coefficient C and kernel function parameter S using the sparrow search algorithm, enhancing the model’s predictive capability. To further select the regularization coefficient C and kernel function parameter S, the fitness function is designed as the training set’s mean squared error (MSE):
where is the estimated value, is the measured value, and is the number of samples.
The fitness function selects the post-training MSE. A smaller MSE indicates a higher alignment between predicted and original data. The final optimization yields the best regularization coefficient C and kernel function parameter S. Using these optimized values, the network is trained on the testing dataset [20]. The flowchart of the SSA-KELM algorithm is shown in Figure 3.
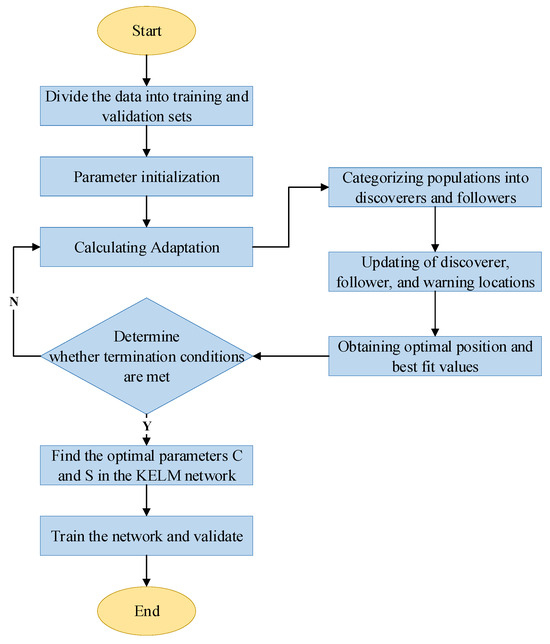
Figure 3.
Flow chart of SSA-optimized KELM algorithm.
2.7. Experimental Comparison Methods
2.7.1. Coefficient of Variation Method
The coefficient of variation method was selected as the comparison method of the CRITIC weight method. The coefficient of variation method is based on the evaluation of the degree of variation of the indicator value reflected in the amount of information to determine the weight of the indicator. That is, the weight of the indicator with the changes in the value of the indicator changes is a dynamic and objective method of assigning weights, and the results of its ascertainment of the weight are not subject to the influence of the outline [36]. In this study, the coefficient of variation method was used as the comparison method of the CRITIC weight method, and the weights of LAI, SPAD, and VH were determined to be A, B, and C, respectively, and a comprehensive growth monitoring indicator CGMICV was established.
- (1)
- The data normalization process is the same as the CRITIC weight method;
- (2)
- Calculation of the coefficient of variation.
- (3)
- Calculation of Indicator Weights
- (4)
- Comprehensive Growth Monitoring Indicator CGMICV
The coefficient of variation method was used to derive A, B, and C as 0.440, 0.202, and 0.358, respectively, and the comprehensive growth monitoring indicator CGMICV was constructed, and the expression of CGMICV is as follows:
where is the normalized LAI value, is the normalized SPAD value, and is the normalized VH value.
2.7.2. Partial Least-Squares Regression (PLSR) Method
PLSR is a technique aimed at identifying the optimal fitting function for a dataset by minimizing the sum of squared errors. It blends statistical methods like correlation analysis, principal component analysis, and multiple linear regression, effectively addressing issues related to data covariance [37]. Xie P et al. [38] used PLSR and PSO-SVM algorithms to compare and establish a hyperspectral quantitative inversion model of soil selenium content. Fu HY et al. [39] used PLSR, SVM, RF, and other modeling methods to construct the estimation models of relative chlorophyll content, leaf area index, and leaf relative water content of ramie, respectively, and proposed a more suitable dynamic monitoring method for physical and chemical traits of ramie in the field. In comparison to multivariate linear regression algorithms, PLSR can establish a multivariate linear model when the independent variables have multicollinearity and a limited number of sample points, ensuring predictive accuracy. In contrast to principal component analysis, partial least squares not only absorb the idea of extracting information from the explanatory variables in principal component analysis but also pay attention to the problem of explaining the dependent variable by the independent variables, which is ignored in the principal component analysis [40].
2.8. Model Evaluation Methodology
In the study, three indicators, coefficient of determination (R2), root mean square error (RMSE), and mean relative error (MRE) were used to judge the prediction effect of the model, and the specific formulas are shown below. R2 indicates the degree of fit between the predicted value and the measured value, and RMSE reflects the degree of deviation between the predicted value and the measured value. The more R2 tends to be close to 1, the smaller RMSE is, indicating that the model predicts better. MRE is used to describe the error between the model prediction result and the actual value to evaluate the model stability. The smaller the MRE is, the more stable the model is.
where denotes the predicted value, denotes the mean of the predicted value, denotes the measured value, denotes the mean of the measured value, and denotes the number of samples.
3. Results and Discussion
3.1. Correlation Analysis of Different Vegetation Indices with Combined Growth Indicators and Single Growth Indicators
The Pearson significance test was chosen to correlate the composite growth monitoring indicators CGMICV, CGMICR, and the individual growth indicators that make up the composite growth monitoring indicators with the eight vegetation indices in turn. The correlations are shown in Table 2.

Table 2.
The correlation of vegetation indices with growth indicators.
All the growth indicators showed a positive correlation with each vegetation index. Comparing and analyzing the single growth indicators, the correlation between the growth indicator VH and the vegetation index was the strongest. All of them were significantly correlated at the 0.01 level, and the correlation coefficients r were all greater than 0.6. The correlation between the SPAD indicator and the eight vegetation indices was generally low, and the correlation with the vegetation index CCCI was the highest, reaching 0.601.
In constructing the comprehensive growth monitoring indicators, the correlation between the comprehensive growth monitoring indicators CGMICV and CGMICR and the vegetation index was generally lower than that of the VH indicators due to the simultaneous consideration of the three single growth indicators and the assignment of weights to each of them, with the lower correlation between the SPAD indicators and the vegetation index. For the composite growth monitoring indicator CGMICV, the vegetation indices GOSAVI, VIopt, NDVI, GNDVI, CCCI, and CGMICV were significantly correlated at the 0.01 level, whereas GRVI, GDVI, RVI, and CGMICV were significantly correlated at the 0.05 level, and the correlation coefficients r were all greater than 0.5. For the comprehensive growth monitoring indicator CGMICR, the correlation coefficients between the eight selected vegetation indices and CGMICR were all greater than 0.6, which is a strong correlation, and all of them were significantly correlated at the 0.01 level.
3.2. Construction and Testing of the CGMI Model for Comprehensive Growth Monitoring Indicators
3.2.1. Construction and Testing of the CGMICV Monitoring Model
The PLSR and SSA-KELM algorithms combined with eight vegetation indices were used for model construction and prediction analysis of the comprehensive growth monitoring indicators CGMICV and CGMICR. The effect of the prediction model of CGMICV built based on PLSR and SSA-KELM is shown in Table 3, and the linear fitting comparison between its predicted and measured values is shown in Figure 4.

Table 3.
Comparison of results from CGMICV prediction models based on PLSR and SSA-KELM.
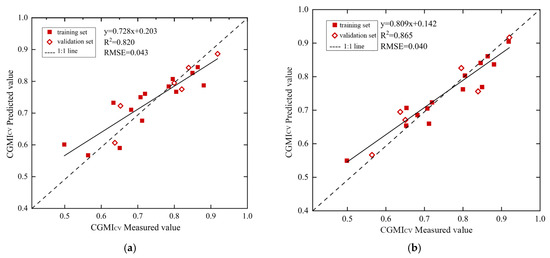
Figure 4.
Relationship between predicted and measured values of the CGMICV models based on PLSR and SSA-KELM: (a) PLSR-CGMICV predictive model; (b) SSA-KELM-CGMICV predictive model.
For the PLSR model, the R2 of the training set was 0.820, the RMSE was 0.043, the validation set decreased by 0.004, the RMSE increased by 0.005 from the prediction set R2, and the prediction effect decreased slightly. For the SSA-KELM model, the training set has an R2 of 0.865 and an RMSE of 0.040, and the validation set has an increase of 0.006 and an increase of 0.005 in the RMSE over the prediction set, with a small increase in accuracy but an increased in prediction error. Overall, the SSA-KELM model increased the R2 of the training set by 0.045 and decreased the RMSE by 0.003 compared to the PLSR model, while the validation set increased the R2 by 0.055 and decreased the RMSE by 0.003. The prediction of both the training set and validation set of the SSA-KELM model is better than that of the PLSR model.
3.2.2. Construction and Testing of the CGMICR Monitoring Model
The prediction results of the CGMICR prediction model based on PLSR and SSA-KELM are shown in Table 4, and the linear fit comparison of its predicted and measured values is shown in Figure 5.

Table 4.
Comparison of results from CGMICR prediction models based on PLSR and SSA-KELM.
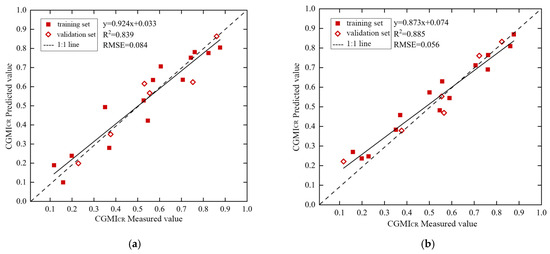
Figure 5.
Relationship between predicted and measured values of the CGMICR models based on PLSR and SSA-KELM: (a) PLSR-CGMICR predictive model; (b) SSA-KELM-CGMICR predictive model.
For the PLSR model, the RMSE was 0.084 for both the training and validation sets, and the validation set had an increase of 0.001 in R2 over the training set, with essentially the same prediction effect. For the SSA-KELM model, the R2 of the training set was 0.885, the RMSE was 0.056, and the validation set had an increase of 0.004 in R2 and an increase of 0.002 in RMSE compared to the training set, with a decreased in the fitting effect but a smaller overall difference. In summary, the model built by SSA-KELM increased R2 by 0.046 and decreased RMSE by 0.028 for the training set and increased R2 by 0.049 and decreased RMSE by 0.026 for the validation set compared to the PLSR model. The prediction effect of both training and validation sets of the SSA-KELM model is better than the PLSR model.
Comparing and analyzing the comprehensive growth monitoring indicators CGMICV and CGMICR, the prediction effect of the CGMICR model is better than that of the CGMICV model because of the CRITIC weighting method, compared with the coefficient of variation method, not only takes into account the fluctuation of each evaluation index, but also involves the conflict between different indexes, and it can more realistically reflect the crop’s growth situation.
3.3. Stability Analysis of the Comprehensive Growth Monitoring Indicator Model
When constructing a nonlinear model, the presence of multicollinearity among independent variables can significantly undermine the reliability of model testing and yield unstable analytical outcomes. To assess the stability of the CGMI monitoring model, training and validation sets mirroring the modeling proportions were meticulously chosen. Subsequently, the CGMICV and CGMICR regression models, constructed using PLSR and SSA-KELM methodologies, respectively, underwent rigorous testing in 100 random runs. The average mean relative error (MRE) across the 100 prediction results were calculated. The results are shown in Figure 6.

Figure 6.
Predictive effects of CGMI models constructed based on PLSR and SSA-KELM: (a) prediction effects of CGMICV models; (b) prediction effects of CGMICR models.
The fluctuation range of the average relative errors of the CGMICV models constructed by different algorithms varies less, and the fluctuation range of the average relative error of the PLSR-CGMICV model is from 8.2% to 24.0%, with a median of 17.4% and a mean of 17.3%. The fluctuation range of the average relative error of the SSA-KELM-CGMICV model is from 6.5% to 22.1%, with a median of 12.7% and a mean of 12.9%. The overall average relative error is smaller than PLSR-CGMICV, which indicates that the SSA-KELM-CGMICV model is more stable.
The PLSR-CGMICR model’s average relative error fluctuates from 6.8% to 20.0%, with a median of 12.8% and a mean of 13.0%. The SSA-KELM-CGMICR model’s average relative error fluctuates from 2.7% to 11.9%, which is reduced compared to that of PLSR-CGMICR, with a median of 7.2% and a mean of 7.1%, which likewise indicates the greater stability of modeling using SSA-KELM.
3.4. Discussions
3.4.1. Comparative Analysis of the Predictive Effects of Different Growth Indicators
To verify the effect of the prediction model for the comprehensive growth monitoring indicators, the prediction model was constructed using PLSR and SSA-KELM methods for leaf area index (LAI), relative chlorophyll content (SPAD), and plant height (VH) sequentially, and the results of the model prediction are shown in Table 5.

Table 5.
Comparison of all growth indicator prediction models based on PLSR and SSA-KELM.
For all growth indicators, the R2 of the SSA-KELM model is greater than that of the PLSR model. Among all the models constructed using a single growth indicator, the SSA-KELM-LAI model had the best prediction effect, with an R2 of 0.906, which is 8.5% higher than that of PLSR-LAI. The R2 of the SSA-KELM-VH model is 0.902, which is 6.8% higher than that predicted by PLSR-VH. The accuracy of the SSA-KELM-SPAD model is low, and the R2 is 0837, which is 10.5% higher than that predicted by PLSR-VH. Among all the models constructed using the comprehensive growth monitoring indicators, the CGMICR monitoring model was better than the CGMICV monitoring model, with SSA-KELM-CGMICR achieving the best monitoring effect (R2 = 0.885). The reason is that when constructing the comprehensive growth monitoring indicators, the CRITIC weighting method, compared with the coefficient of variation method, not only takes into account the influence of the volatility of the evaluation indicators on the weights but also involves the conflicting nature between different indicators. Therefore, the weights of LAI and VH are appropriately reduced, and the weight of SPAD is increased, which improved the prediction effect of the constructed CGMICR model compared with that of CGMICV. However, the sensitivity of SPAD to multispectral information is relatively weak in this stage, and increasing the weights of SPAD also weakened the monitoring ability of CGMICR.
3.4.2. Stability Analysis of Predictive Models for Different Growth Indicators
The PLSR and SSA-KELM methods were used to test the regression model of a single growth indicator for 100 random runs in sequence, and the average relative error (MRE) of the 100 prediction results was counted and analyzed in comparison with the stability of the CGMI monitoring model. Since the modeling effect of all indicators using the PLSR algorithm is lower than the modeling effect of the SSA-KELM algorithm, only the stability of SSA-KELM algorithm modeling is discussed this time. The stability results of the predictive models constructed based on SSA-KELM for all the growth indicators are shown in Table 6.

Table 6.
Stability comparison of all growth indicator prediction models constructed based on SSA-KELM.
Compared with the monitoring models of single growth indicators constituting CGMI, the stability of the CGMICV and CGMICR models is smaller than that of the SPAD model, mainly because the error fluctuation range of the LAI indicator is large, which leads to the larger error fluctuation range of CGMICV and CGMICR. The stability of the CGMICV and CGMICR models was greater than that of the LAI and VH models because a single growth indicator has limitations and can only simply reflect a certain physiological information of the crop, which is essentially a ‘point’ of data and cannot uniformly reflect the overall characteristics of the crop. Zhai LT et al. [41] inverted the nitrogen content, chlorophyll content, and water content of winter wheat based on the PLSR model, the R2 of single index inversion was 0.72, 0.31, 0.61, respectively, and the R2 of comprehensive index inversion was 0.75. The results showed that the inversion effect of the comprehensive index model was better than that of a single index, and the results of this study were similar to the present study. In summary, compared with the single growth indicator, the comprehensive growth monitoring indicator has a better prediction effect. Compared with the comprehensive growth monitoring indicator CGMICV and CGMICR, the error fluctuation range, median error and mean value of the error of the CGMICR model are smaller than those of the CGMICV model, which indicates that the comprehensive growth monitoring indicator CGMICR has better stability.
However, this experiment only discussed the growth of maize at the jointing stage, which is a more vigorous stage of maize growth and development, and also the stage of low crop cover, which will have a certain impact on the results of the experiment. As the growth cycle progresses, further research and analysis are needed to monitor the growth of maize plants during different growth stages, such as the staminate stage, silking stage, and grouting stage after the jointing stage, to achieve more accurate monitoring of maize plant growth.
4. Conclusions
In the study, modeling prediction analysis of comprehensive summer maize growth was conducted based on UAV multispectral image data, and the main conclusions are as follows:
- (1)
- The comprehensive growth monitoring indicators CGMICV and CGMICR constructed using the coefficient of variation method and the CRITIC weighting method were both positively correlated with the vegetation index. The correlation coefficients between CGMICR and the vegetation index were both greater than the correlation coefficients between CGMICV and CGMICR.
- (2)
- A comprehensive growth monitoring indicator model based on SSA-KELM was established. For CGMICV, the model R2 was 0.871, and the RMSE was 0.045; for CGMICR, the model R2 was 0.889, and the RMSE was 0.058, which shows that the model built by SSA-KELM-CGMICR is more stable and more effective.
- (3)
- Based on the CGMICV and CGMICR monitoring models built by PLSR, the monitoring effect of the PLSR-CGMICV model is lower than that of the PLSR-CGMICR model, and both of them are lower than that of the model constructed by SSA-KELM. In summary, the model constructed based on SSA-KELM has a better monitoring effect.
Author Contributions
Conceptualization, H.M., J.J. and H.C.; Methodology, H.M., X.L., H.C. and N.L.; Software, X.L. and H.C.; Validation, H.M., X.L. and H.C.; Formal analysis, H.M., X.L. and H.C.; Investigation, H.M. and X.L.; Resources, H.M., X.L. and N.L.; Data curation, H.M. and X.L.; Writing—Original Draft Preparation, H.M.; Writing—Review and Editing, H.M., X.L. and H.C.; Visualization, H.M.; Supervision, Y.S. and C.Y.; Project Administration, J.J., H.C. and Y.S.; Funding Acquisition, J.J. and H.C. All authors have read and agreed to the published version of the manuscript.
Funding
Major Science and Technology Project of Henan Province (No. 221100110800), Longmen Laboratory Major Projects (No. 231100220200); Postgraduate Education Reform Project of Henan Province (No. 2021SJGLX138Y). The present research was supported by the 2020 Training Plan for Young Backbone Teachers in Colleges and Universities of Henan Province (No. 2020GGJS075); Henan Provincial University Science and Technology Innovation Talent Support Program (No. 23HASTIT020); Henan Provincial Science and Technology Research Project (No. 222102110067).
Data Availability Statement
The data that support the findings of this study are available on request from the corresponding author.
Conflicts of Interest
Author Nana Li was employed by the company Caterpillar Mechanical Components. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Yu, Y.; Jiang, Z.H.; Wang, G.J.; Kattel, G.R.; Chuai, X.W.; Shang, Y.; Zou, Y.F.; Miao, L.J. Disintegrating the impact of climate change on maize yield from human management practices in China. Agric. For. Meteorol. 2022, 327, 109235. [Google Scholar] [CrossRef]
- Sapkota, S.; Paudyal, D.R. Growth Monitoring and Yield Estimation of Maize Plant Using Unmanned Aerial Vehicle (UAV) in a Hilly Region. Sensors 2023, 23, 5432. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.Y.; Yang, H.; Li, X.X.; Zheng, Y.J.; Yan, H.J.; Li, N. Corn growth monitoring based on visible spectrum remote sensing by unmanned aerial vehicle (UAV). Spectrosc. Spectr. Anal. 2021, 41, 265–270. [Google Scholar]
- Wu, B.F.; Zhang, F.; Liu, C.L.; Zhang, L.; Luo, Z.M. An integrated method for crop condition monitoring. J. Remote Sens. 2004, 8, 498–514. [Google Scholar]
- Li, Z.N. Study on indicators for remote sensing monitoring of winter wheat growth. Chin. Acad. Agric. Sci. 2010, 33, 74–82. [Google Scholar]
- Meng, J.H. Study on Indicators for Remote Sensing Monitoring of Crop Growth. Ph.D. Thesis, Graduate School of the Chinese Academy of Sciences (Institute of Remote Sensing Applications), Beijing, China, 2006; pp. 1–12. [Google Scholar]
- Zhao, J.; Pan, F.J.; Xiao, X.; Hu, L.B.; Wang, X.L.; Yan, Y.; Zhang, S.L.; Tian, B.Q.; Yu, H.L.; Lan, Y.B. Summer Maize Growth Estimation Based on Near-Surface Multi-Source Data. Agronomy 2023, 13, 532. [Google Scholar] [CrossRef]
- He, J.; Wang, L.G.; Guo, Y.; Zhang, Y.; Yang, X.Z.; Liu, T.; Zhang, H.L. Estimation of maize LAI based on multi-spectral remote sensing by unmanned aerial vehicle (UAV). J. Big Data Agric. 2021, 3, 20–28. [Google Scholar]
- Ma, J.W.; Wang, L.J.; Chen, P.F. Comparing Different Methods for Wheat LAI Inversion Based on Hyperspectral Data. Agriculture 2022, 12, 1353. [Google Scholar] [CrossRef]
- Hang, Y.H.; Su, H.; Yu, Z.Y.; Liu, H.J.; Guan, H.X.; Kong, F.C. Estimation of Rice Leaf Area Index Combining Spectral and Textural Characteristics and Coverage of Unmanned Aerial Vehicles. J. Agric. Eng. 2021, 37, 64–71. [Google Scholar]
- Tao, H.; Feng, H.; Xu, L.; Miao, M.; Long, H.; Yue, J.; Li, Z.; Yang, G.; Yang, X.; Fan, L. Estimation of crop growth parameters using UAV-based hyperspectral remote sensing data. Sensors 2020, 20, 1296. [Google Scholar] [CrossRef]
- Trawczynski, C. Assessment of the nutrition of potato plants with nitrogen according to the NNI test and SPAD indicator. J. Elem. 2019, 24, 687–700. [Google Scholar] [CrossRef]
- Qiao, L.; Tang, W.J.; Gao, D.H.; Zhao, R.M.; An, L.L.; Li, M.Z.; Sun, H.; Song, D. UAV-based chlorophyll content estimation by evaluating vegetation index responses under different crop coverages. Comput. Electron. Agric. 2022, 196, 106775. [Google Scholar] [CrossRef]
- Guo, Y.H.; Chen, S.Z.; Li, X.X.; Cunha, M.; Jayavelu, S.; Cammarano, D.; Fu, Y.S. Machine Learning-Based Approaches for Predicting SPAD Values of Maize Using Multi-Spectral Images. Remote Sens. 2022, 14, 1337. [Google Scholar] [CrossRef]
- Gil-Docampo, M.L.; Arza-García, M.; Ortiz-Sanz, J.; Martínez-Rodríguez, S.; Marcos-Robles, J.L.; Sánchez-Sastre, L.F. Above-ground biomass estimation of arable crops using UAV-based SfM photogrammetry. Geocarto International. 2020, 35, 687–699. [Google Scholar] [CrossRef]
- Belton, D.; Helmholz, P.; Long, J.; Zerihun, A. Crop Height Monitoring Using a Consumer-Grade Camera and UAV Technology. PFG-J. Photogramm. Remote Sens. Geoinf. Sci. 2019, 87, 249–262. [Google Scholar] [CrossRef]
- Bendig, J.; Yu, K.; Aasen, H.; Bolten, A.; Bennertz, S.; Broscheit, J.; Gnyp, M.L.; Bareth, G. Combining UAV-based plant height from crop surface models, visible, and near-infrared vegetation indices for biomass monitoring in barley. Int. J. Appl. Earth Obs. Geoinf. 2015, 39, 79–87. [Google Scholar] [CrossRef]
- Xu, Y.F. Parameter Inversion and Integrated Growth Monitoring of Winter Wheat Based on Multi-Spectral Remote Sensing by Unmanned Aerial Vehicle (UAV). Master’s Thesis, Anhui University of Science and Technology, Huainan, China, 2022; pp. 39–52. [Google Scholar]
- Pei, H.J.; Feng, H.K.; Li, C.C.; Jin, X.L.; Li, Z.H.; Yang, G.J. Unmanned aerial remote sensing monitoring of winter wheat growth based on comprehensive indicators. J. Agric. Eng. 2017, 33, 74–82. [Google Scholar]
- Ji, J.T.; Li, N.N.; Cui, H.W.; Li, Y.C.; Zhao, X.B.; Zhang, H.L.; Ma, H. Study on Monitoring SPAD Values for Multispatial Spatial Vertical Scales of Summer Maize Based on UAV Multispectral Remote Sensing. Agriculture 2023, 13, 1004. [Google Scholar] [CrossRef]
- Brewer, K.; Clulow, A.; Sibanda, M.; Gokool, S.; Naiken, V.; Mabhaudhi, T. Predicting the Chlorophyll Content of Maize over Phenotyping as a Proxy for Crop Health in Smallholder Farming Systems. Remote Sens. 2022, 14, 518. [Google Scholar] [CrossRef]
- Zhang, S.M.; Zhao, G.X.; Lang, K.; Su, B.W.; Chen, X.N.; Xi, X.; Zhang, H.B. Integrated Satellite, Unmanned Aerial Vehicle (UAV) and Ground Inversion of the SPAD of Winter Wheat in the Reviving Stage. Sensors 2019, 19, 1485. [Google Scholar] [CrossRef]
- Zhang, X.; Tao, S.Y.; Zhang, M. Inversion of leaf area index of spring maize from FY-3B satellite based on LSTM algorithm. J. Jilin Univ. 2022, 52, 2071–2080. [Google Scholar]
- Zhang, L.J.; Zhang, X. Weighted clustering method based on improved CRITIC method. Stat. Decis.-Mak. 2015, 22, 65–68. [Google Scholar]
- Zhou, Q.; Wang, J.J.; Huo, Z.Y.; Liu, C.; Wang, W.; Ding, L. UAV multispectral remote sensing estimation of SPAD values in wheat canopy at different growth stages. Spectrosc. Spectr. Anal. 2023, 43, 1912–1920. [Google Scholar]
- Huang, W.; Guan, Q.; Luo, J.; Zhang, J.; Zhao, J.; Liang, D.; Huang, L.; Zhang, D. New optimized spectral indices for identifying and monitoring winter wheat diseases. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2516–2524. [Google Scholar] [CrossRef]
- Hirooka, Y.; Homma, K.; Shiraiwa, T. Parameterization of the vertical distribution of leaf area index (LAI) in rice (Oryza sativa L.) using a plant canopy analyzer. Sci. Rep. 2018, 8, 6387. [Google Scholar] [CrossRef]
- Marin, D.B.; Ferraz, G.A.E.S.; Guimarães, P.H.S.; Schwerz, F.; Santana, L.S.; Barbosa, B.D.S.; Barata, R.A.P.; Faria, R.D.; Dias, J.E.L.; Conti, L.; et al. Remotely Piloted Aircraft and Random Forest in the Evaluation of the Spatial Variability of Foliar Nitrogen in Coffee Crop. Remote Sens. 2021, 13, 1471. [Google Scholar] [CrossRef]
- Zhou, X.F.; Zhang, J.C.; Chen, D.M.; Huang, Y.B.; Kong, W.P.; Yuan, L.; Ye, H.C.; Huang, W.J. Assessment of leaf chlorophyll content models for winter wheat using Landsat-8 multispectral remote sensing data. Remote Sens. 2020, 12, 2574. [Google Scholar] [CrossRef]
- Jiang, J.; Johansen, K.; Stanschewski, C.S.; Wellman, G.; Mousa, M.A.A.; Fiene, G.M.; Asiry, K.A.; Tester, M.; McCabe, M.F. Phenotyping a diversity panel of quinoa using UAV-retrieved leaf area index, SPAD-based chlorophyll and a random forest approach. Precis. Agric. 2022, 23, 961–983. [Google Scholar] [CrossRef]
- Motohka, T.; Nasahara, K.N.; Oguma, H.; Tsuchida, S. Applicability of Green-Red Vegetation Index for Remote Sensing of Vegetation Phenology. Remote Sens. 2010, 2, 2369–2387. [Google Scholar] [CrossRef]
- Deng, L.; Mao, Z.H.; Li, X.J.; Hu, Z.W.; Duan, F.Z.; Yan, Y.N. UAV-based multispectral remote sensing for precision agriculture: A comparison between different cameras. ISPRS J. Photogramm. Remote Sens. 2018, 146, 124–136. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, H.; Niu, Y.; Han, W. Mapping maize water stress based on UAV multispectral remote sensing. Remote Sens. 2019, 11, 605. [Google Scholar] [CrossRef]
- Shu, M.Y.; Fei, S.P.; Zhang, B.Y.; Yang, X.H.; Guo, Y.; Li, B.G.; Ma, Y.T. Application of UAV Multisensor Data and Ensemble Approach for High-Throughput Estimation of Maize Phenotyping Traits. Plant Phenomics 2022, 2022, 11. [Google Scholar] [CrossRef]
- Zhao, L.; Zhao, X.; Li, Y.; Shi, Y.; Zhou, H.; Li, X.; Wang, X.; Xing, X. Applicability of hybrid bionic optimization models with kernel-based extreme learning machine algorithm for predicting daily reference evapotranspiration: A case study in arid and semiarid regions, China. Environ. Sci. Pollut. Res. Int. 2022, 30, 22396–22412. [Google Scholar] [CrossRef] [PubMed]
- Tao, Z.F.; Ge, L.L.; Chen, H.Y. A class of non-negative variable weight combination prediction methods based on sliding window. Control. Decis.-Mak. 2020, 35, 1446–1452. [Google Scholar]
- Wu, Q.; Sun, H.; Li, M.Z.; Song, Y.Y.; Zhang, Y.E. Research on accurate segmentation and chlorophyll diagnosis method for multispectral images of maize crops. Spectrosc. Spectr. Anal. 2015, 35, 178–183. [Google Scholar]
- Xie, P.; Wang, Z.H.; Xiao, B.; Cao, H.-l.; Huang, Y.; Su, W.-l. Hyperspectral quantitative inversion of soil selenium content based on sCARS-PSO-SVM. Spectrosc. Spectr. Anal. 2023, 43, 3599–3606. [Google Scholar]
- Fu, H.Y.; Wang, W.; Lu, J.N.; Yue, Y.K.; Cui, G.X.; Yu, W. Estimation of ramie physicochemical property based on UAV multispectral remote sensing and machine learning. Trans. Chin. Soc. Agric. Mach. 2023, 54, 194–200. [Google Scholar]
- Liu, T.; Zhang, H.; Wang, Z.Y.; He, C.; Zhang, Q.G.; Jiao, Y.Z. Estimation of leaf area index and chlorophyll content in wheat using unmanned aerial vehicle multispectral estimation. J. Agric. Eng. 2021, 37, 65–72. [Google Scholar]
- Zhai, L.T.; Wei, F.Y.; Feng, H.K.; Li, C.C.; Yang, G.J. Winter wheat growth monitoring based on integrated indicators. Jiangsu Agric. Sci. 2020, 48, 244–249. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).