Understanding the Effect of Seasonal Climate Variability on the Salinity in Unsaturated Agricultural Soil
Abstract
:1. Introduction
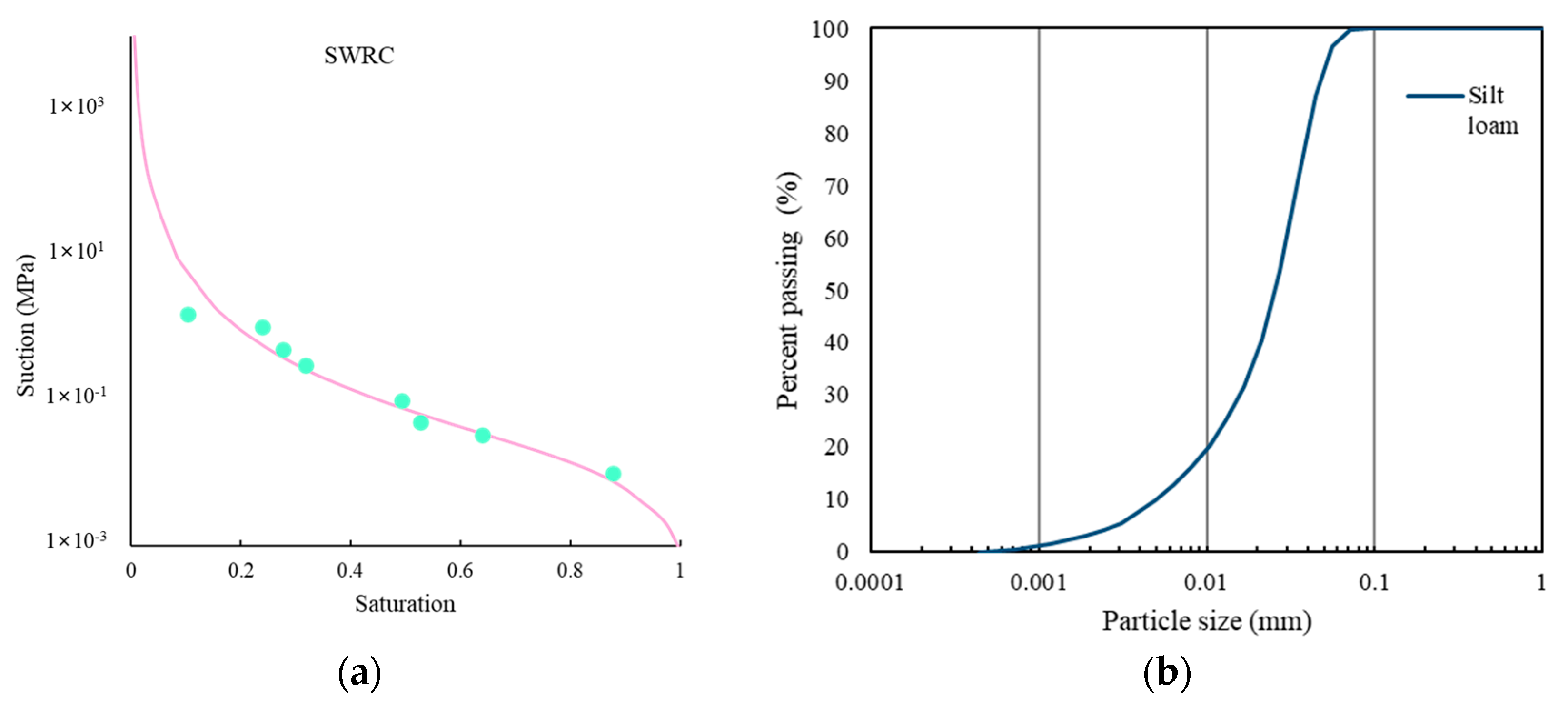
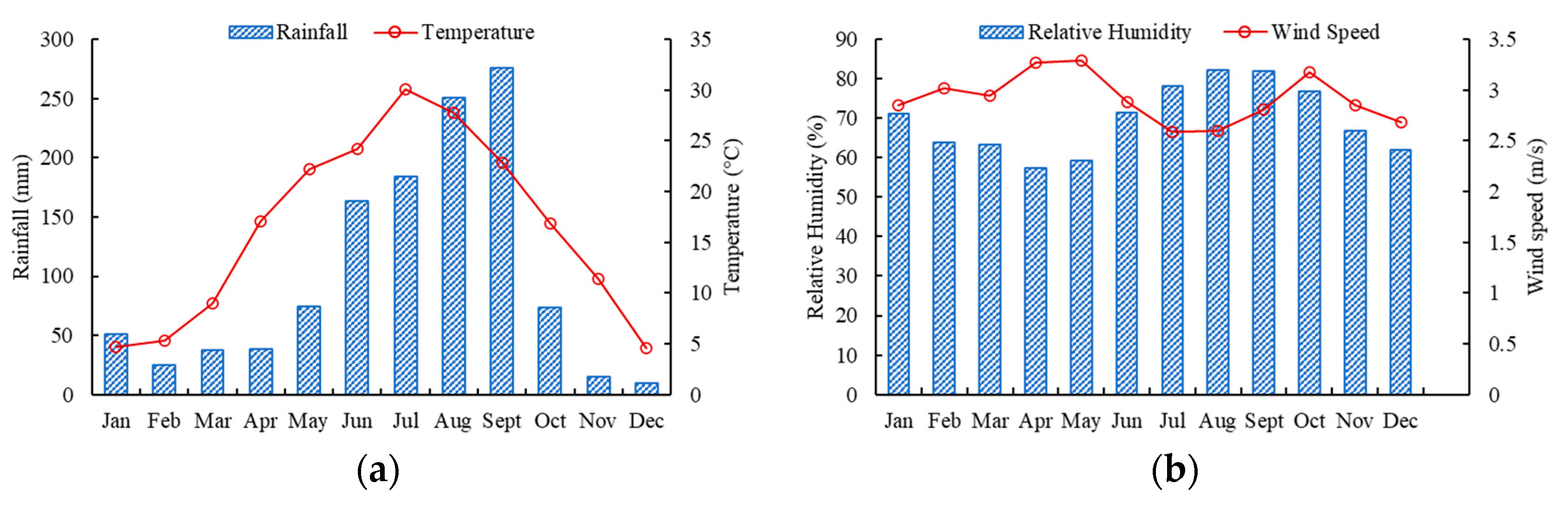
2. Experimental Site
3. Method and Model
3.1. Cases Simulated
3.2. FE Model and Initial Conditions
3.3. Simulation of Salt Transport
3.4. Climate Boundary Condition
4. Results
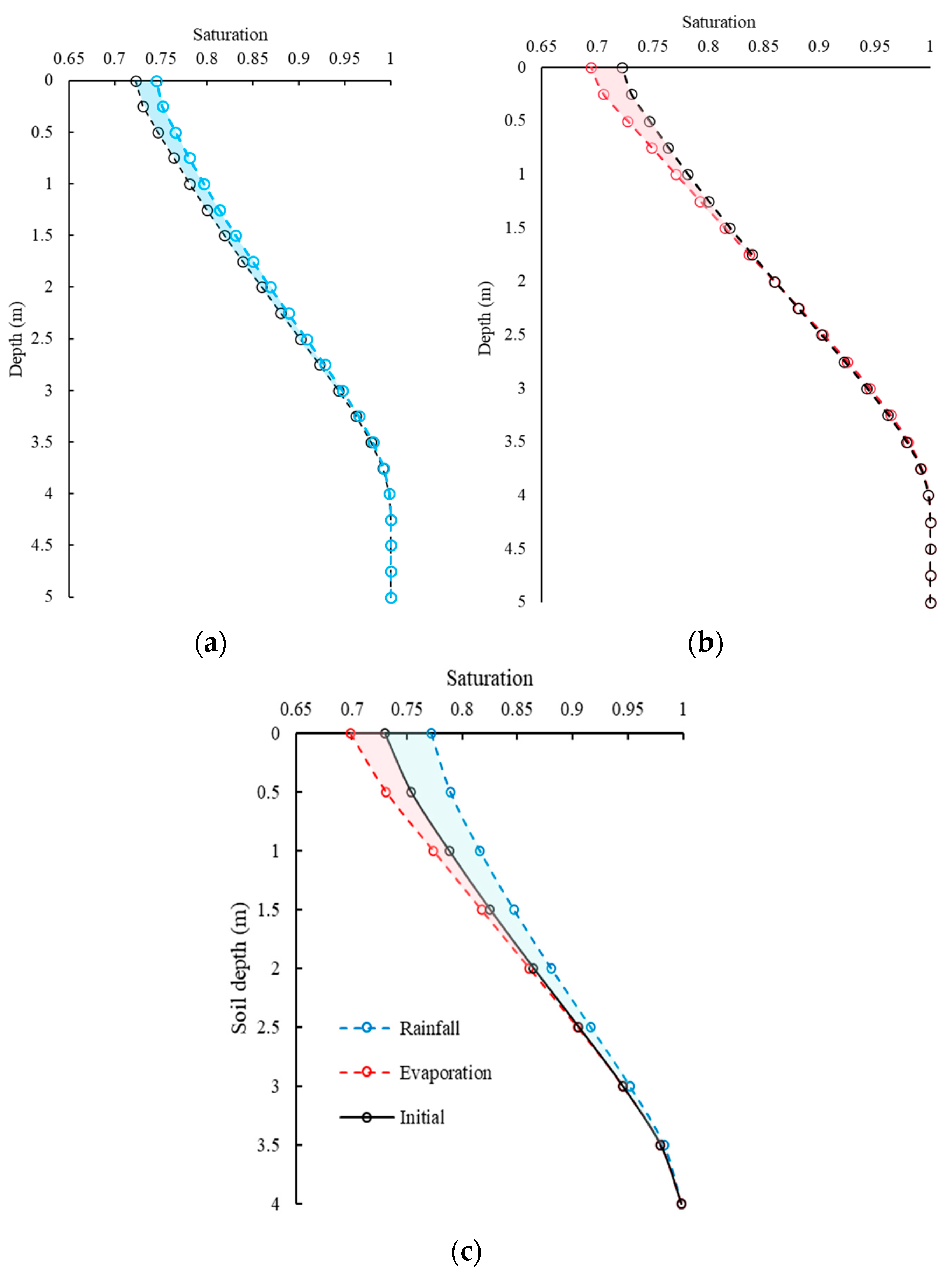
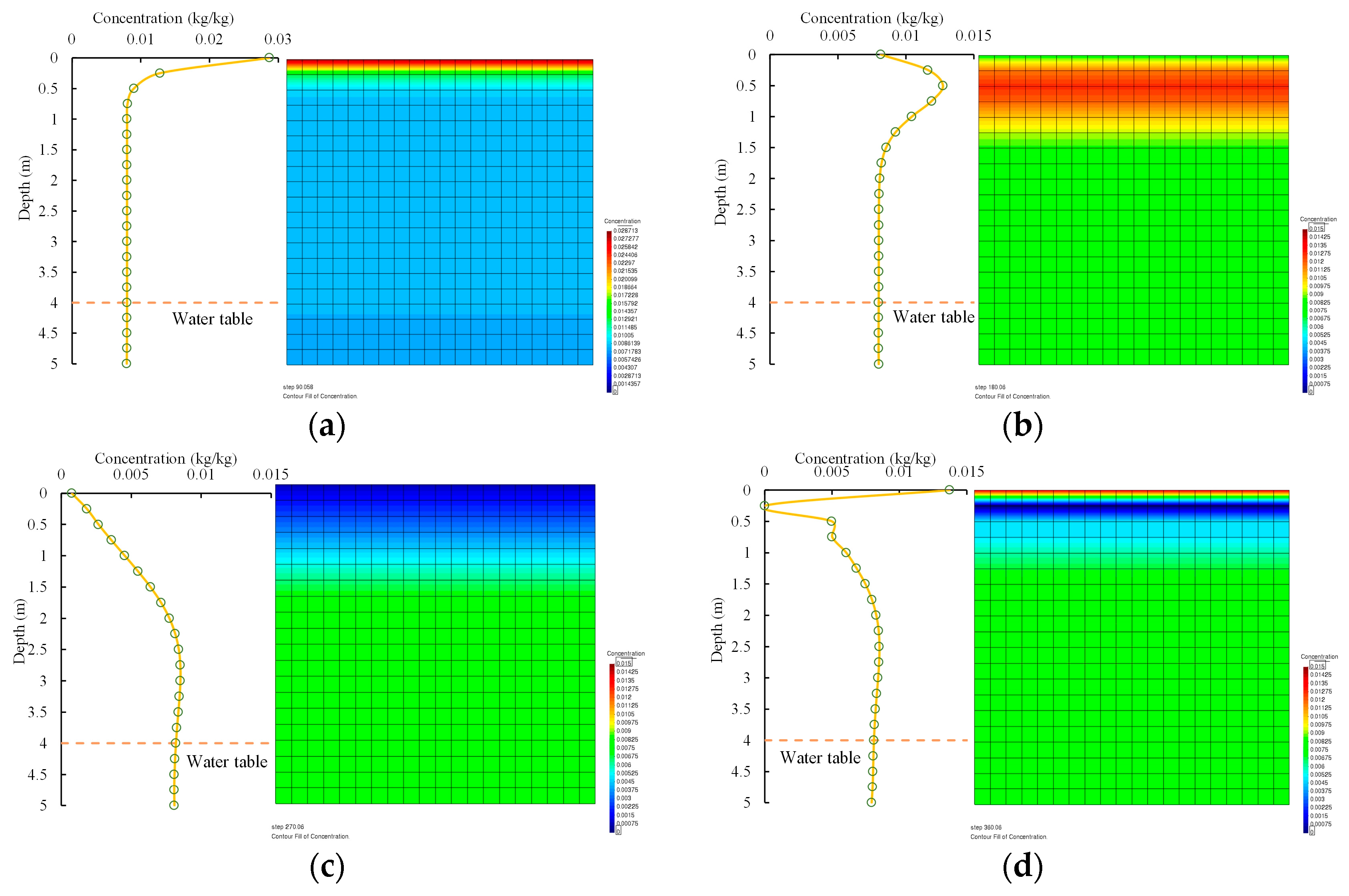
4.1. Understanding Salt Transport Caused by Rain and Evaporation
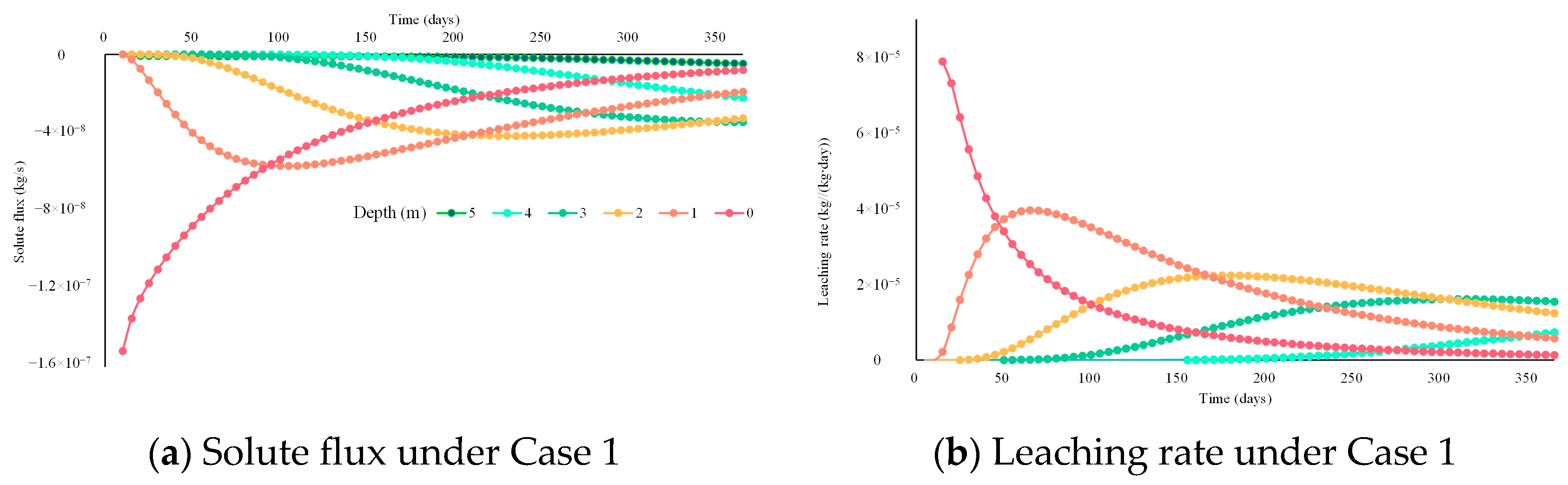
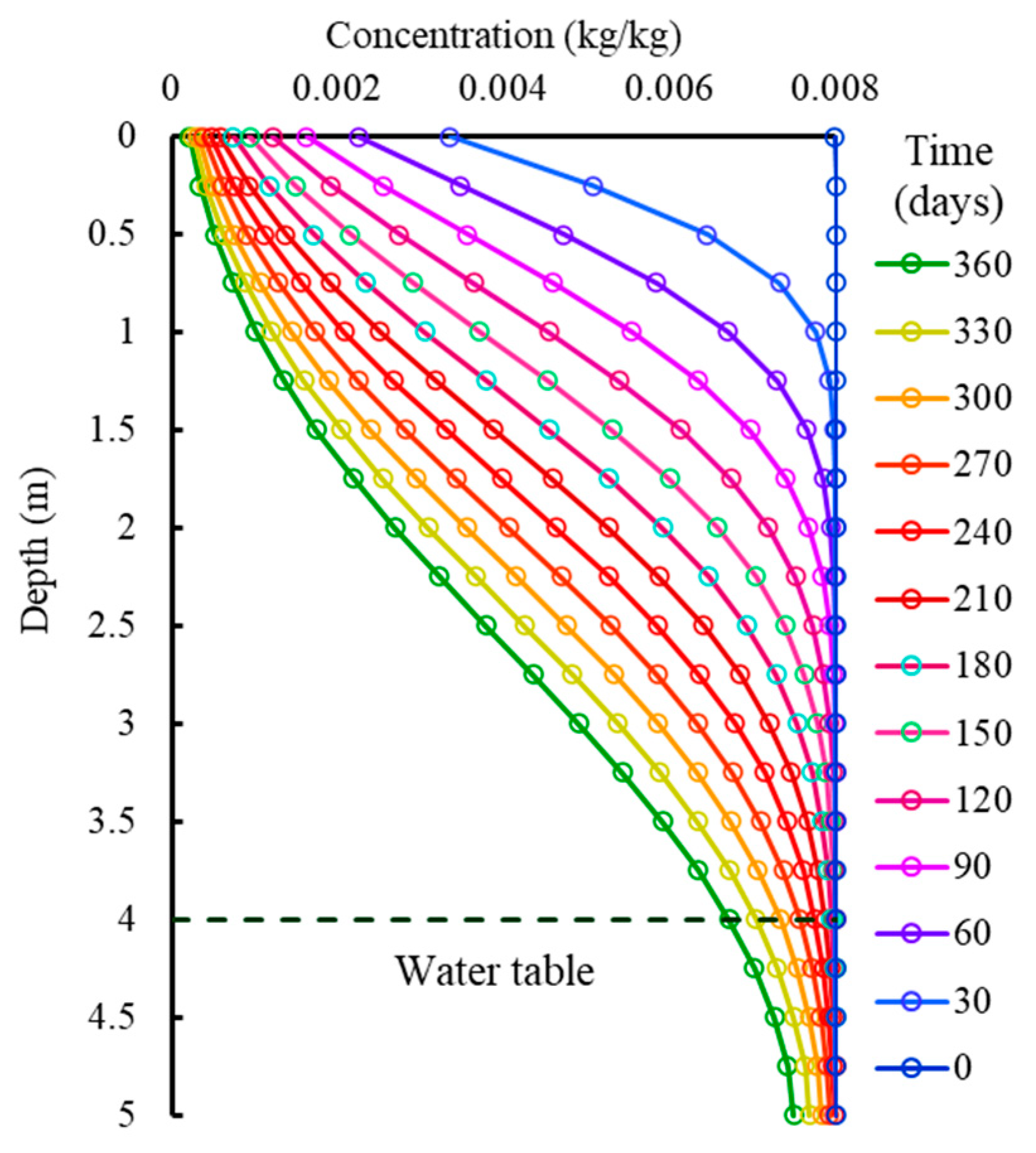
4.1.1. Salt Leaching by Rainfall
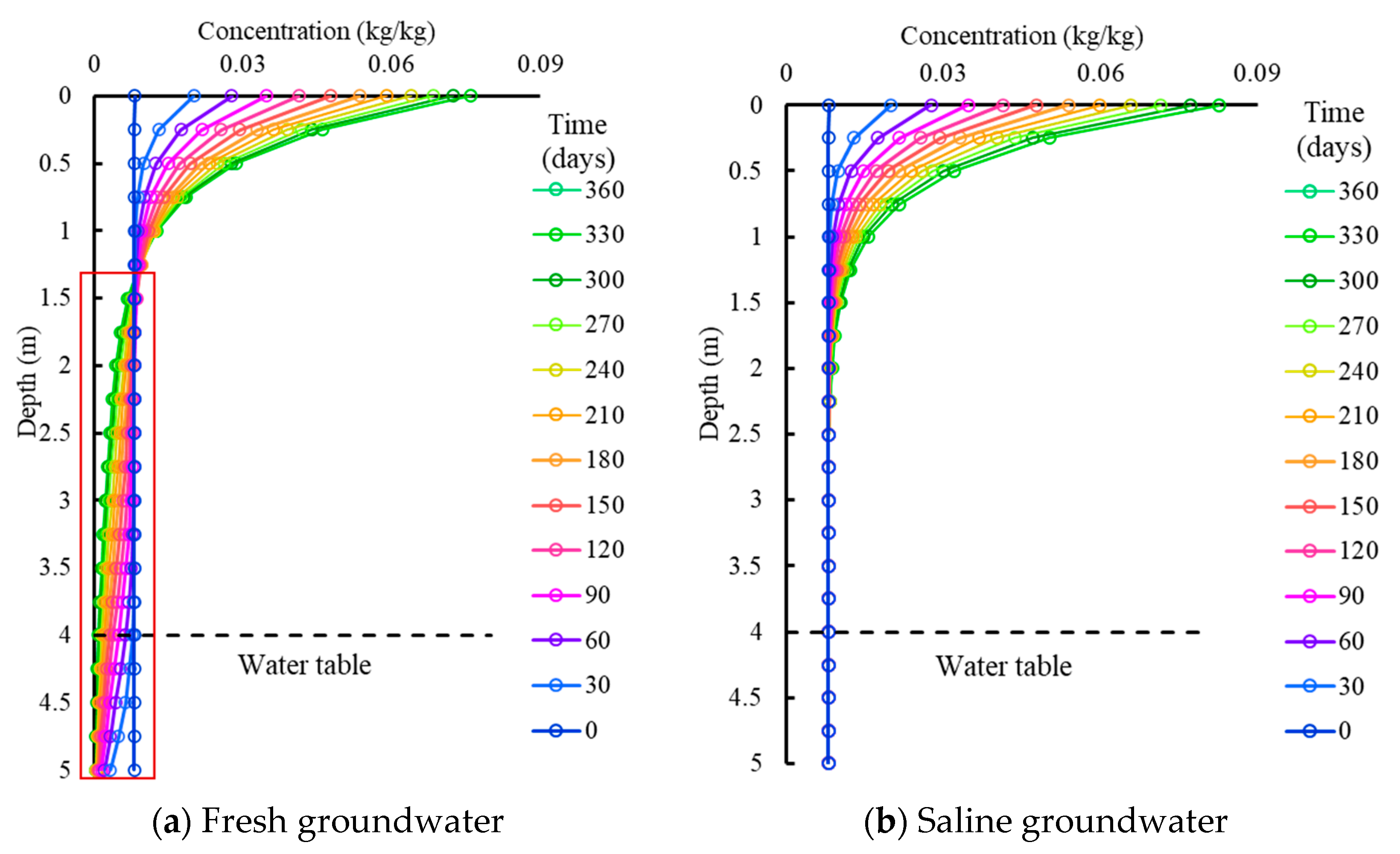
4.1.2. Salt Accumulation by Evaporation
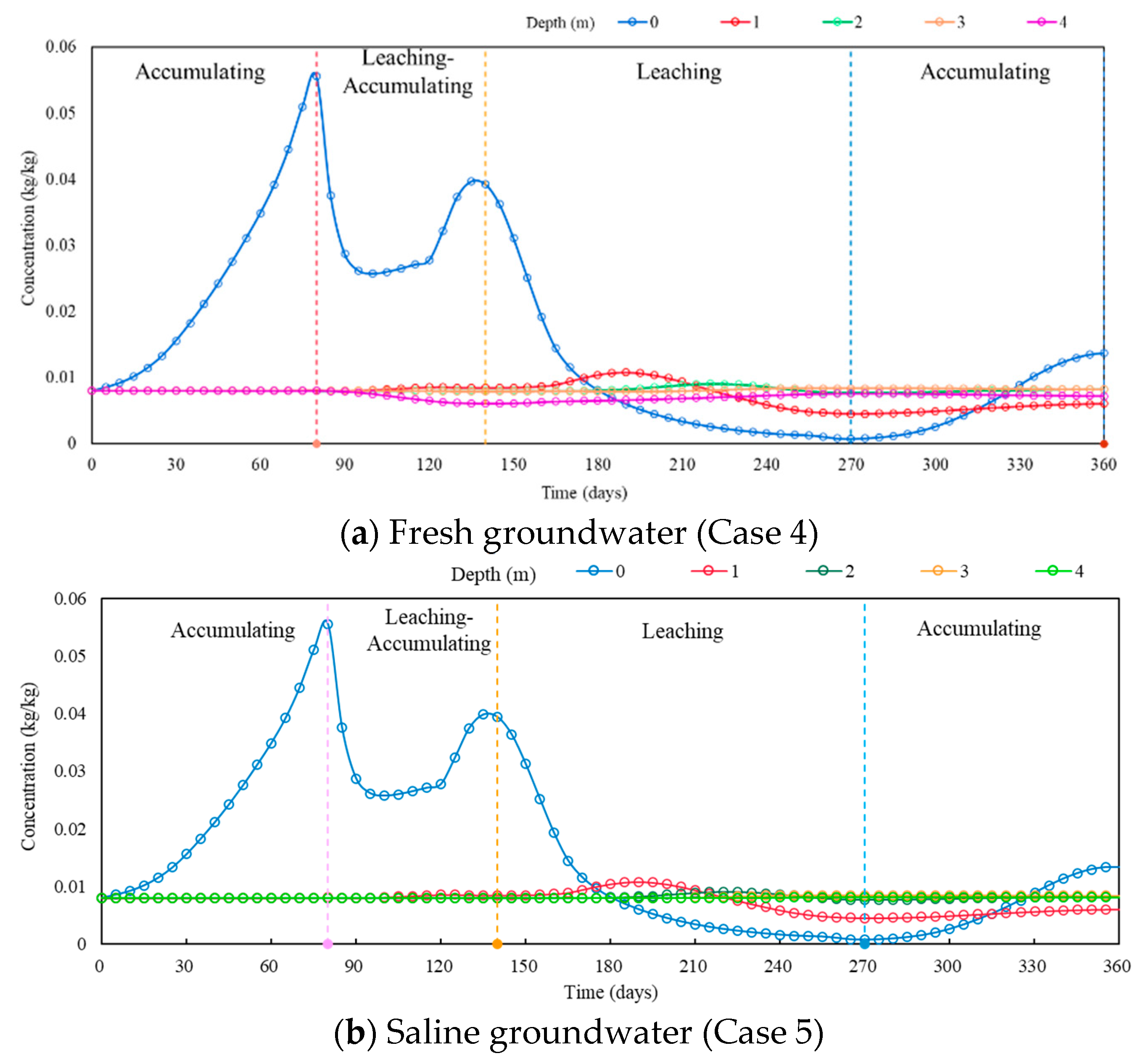
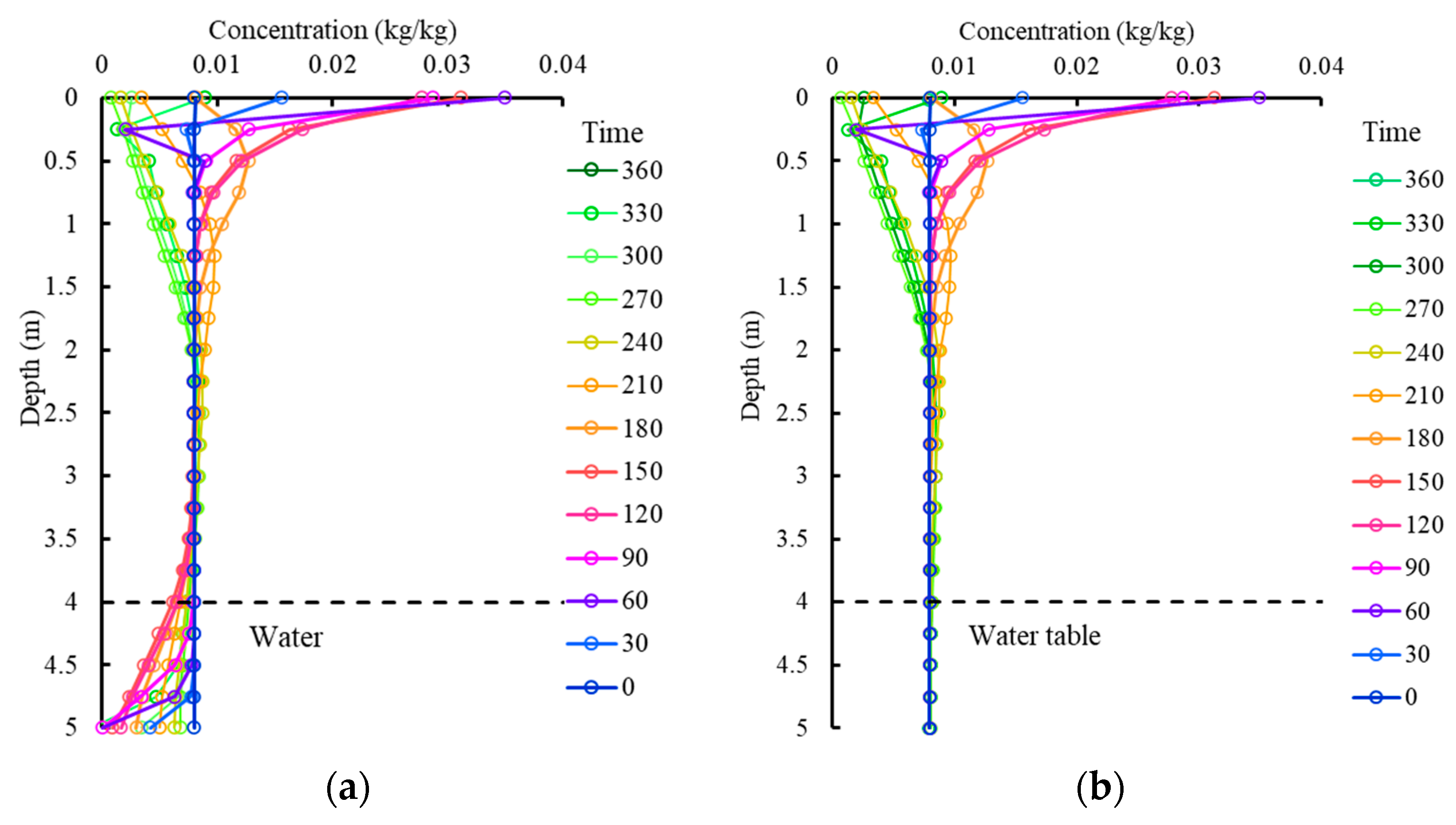
4.2. Effect of Climate Action on Salinity Distribution
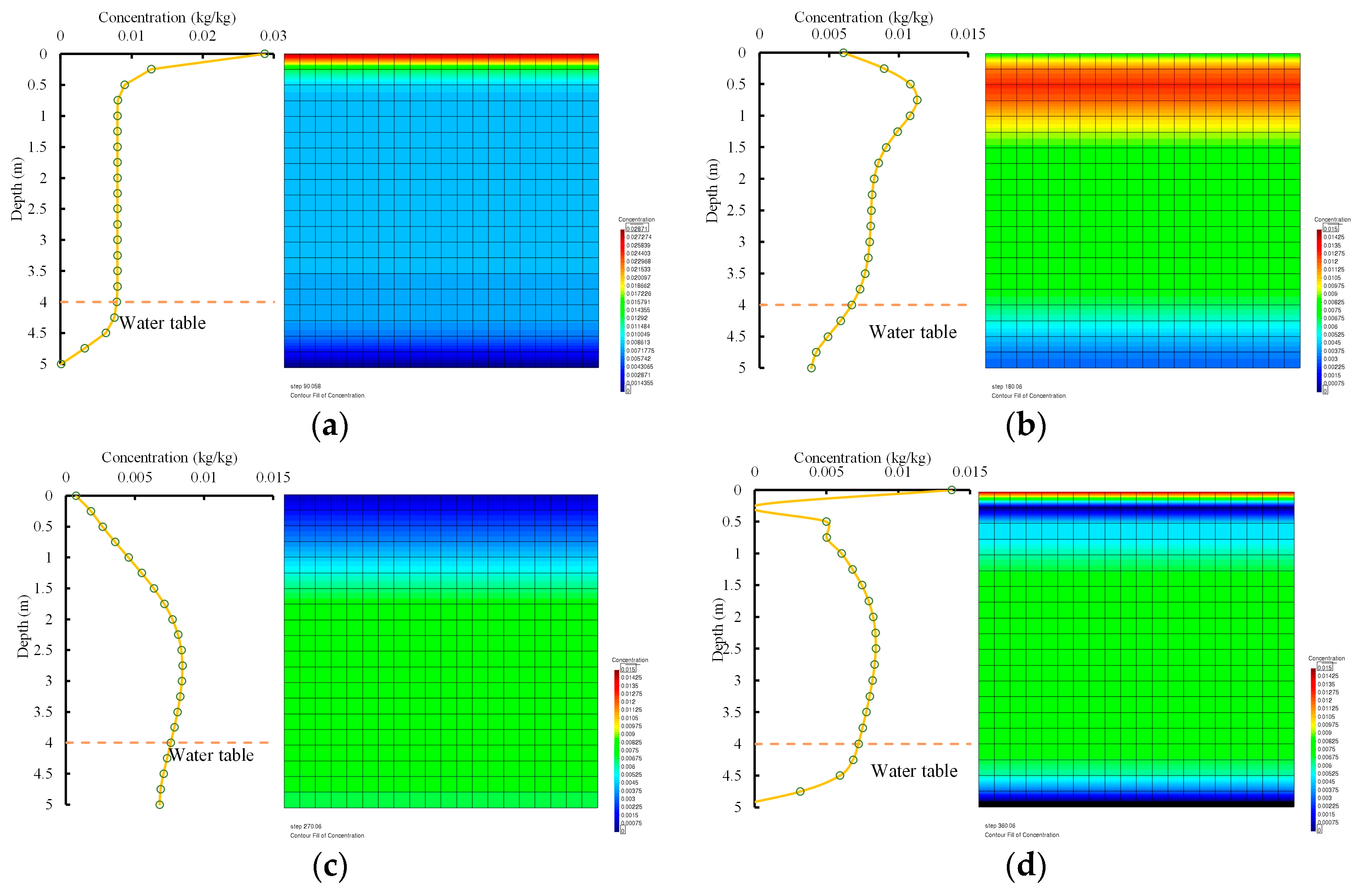
4.2.1. One-Year Simulation
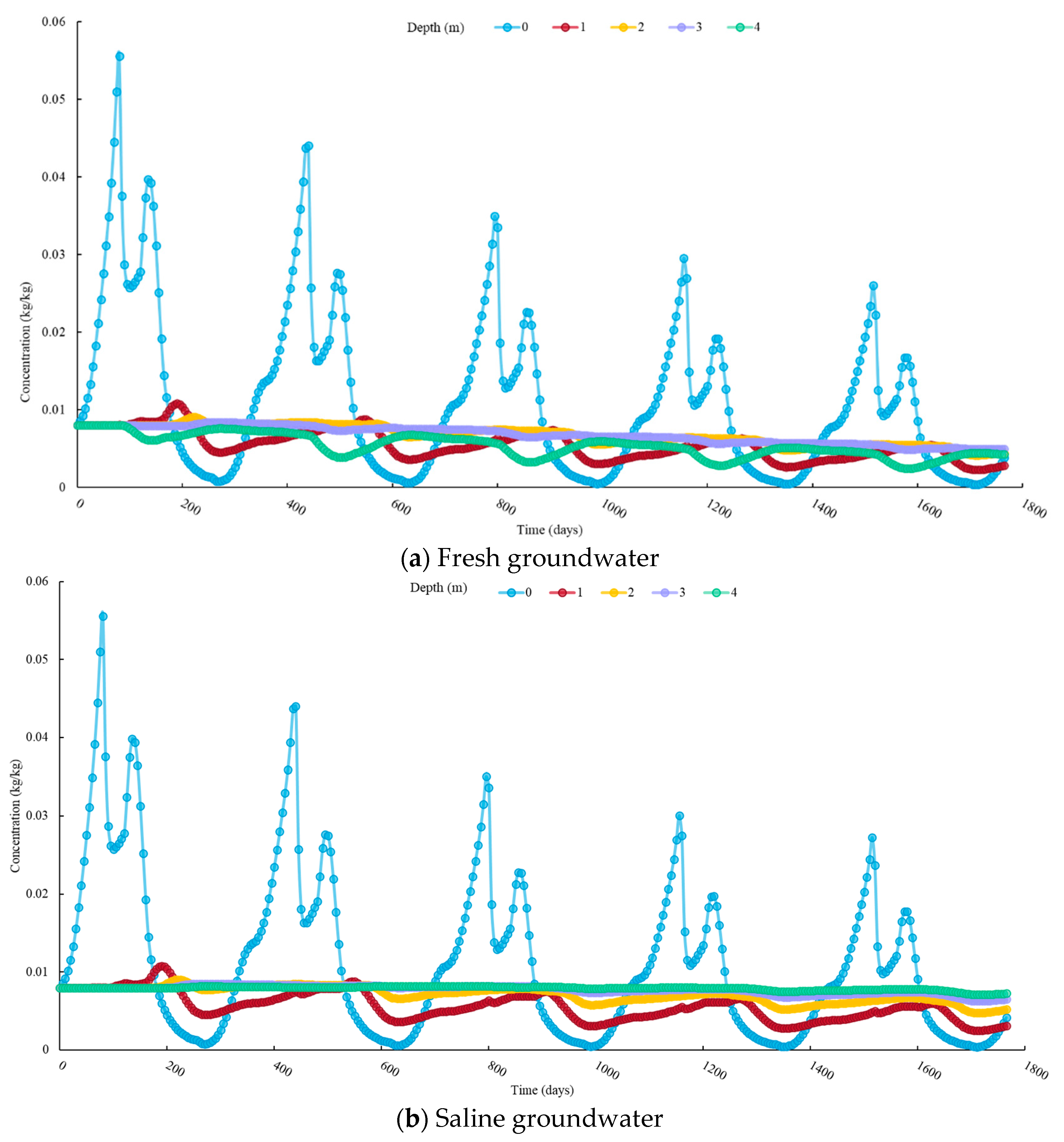
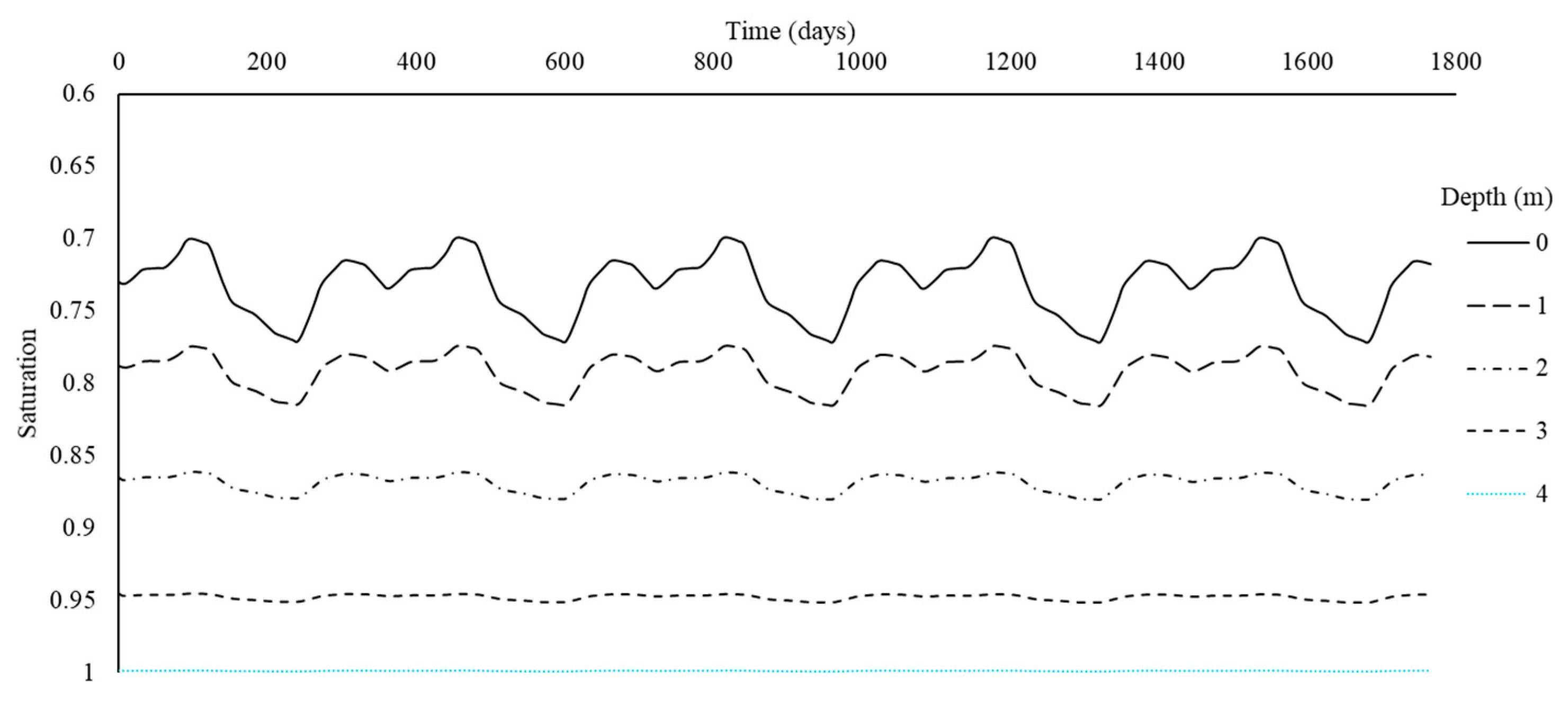
4.2.2. Study for 5 Years
5. Discussion
6. Conclusions
- (1)
- Rainfall at the surface induced a downward flow pattern in the unsaturated zone that led to a salt leaching process with nonlinear efficiency. Due to evaporation, the water moves upwards transporting salt to the surface, and therefore the soil salinity above the evaporation front can be remarkably higher. The significant change in salt concentration under rainfall and evaporation would enhance the salt diffusion and dispersion, thus reducing leaching/accumulating efficiency. The soil salinity beneath the evaporation front remained steady with saline groundwater and decreased with evaporation with fresh groundwater.
- (2)
- The seasonal climate had a significant effect on the soil salinity redistribution in the vadose zone. The model can compute the salt accumulation process during the dry season and the salt leaching process during the wet season. Salt decreased fast for the first three years (i.e., the highest value decreased from 0.055 to 0.033 kg/kg), but decreased slower for the last two years (i.e., the highest value decreased from 0.033 to 0.026 kg/kg). The salt leaching efficiency decreased with time under natural climate action. Fresh groundwater supplements would be helpful to leach the salt in the unsaturated zone.
- (3)
- The soil salt content and saturation on the surface had a significant response to the climate condition changes. It is very important to fully consider the seasonal climate variability for the future study of unsaturated soil salt distribution and transport. Further experiments on the combination of the numerical model and natural monitoring are needed to gain additional information on irrigation and drainage management. The use of Code_Bright in the investigation of solute transport in the unsaturated zone provides a theoretical basis for numerical analysis applications for coupled thermo-chemo-hydro–mechanical problems in agricultural engineering.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Shackelford, C.D. Geoenvironmental Engineering. In Reference Module in Earth Systems and Environmental Sciences; Elsevier: Amsterdam, The Netherlands, 2013; pp. 1–29. [Google Scholar] [CrossRef]
- Corwin, D.L. Climate change impacts on soil salinity in agricultural areas. Eur. J. Soil Sci. 2021, 72, 842–862. [Google Scholar] [CrossRef]
- Singh, A. Salinization and drainage problems of agricultural land. Irrig. Drain. 2020, 69, 844–853. [Google Scholar] [CrossRef]
- Iost, S.; Landgraf, D.; Makeschin, F. Chemical soil properties of reclaimed marsh soil from Zhejiang Province P.R. China. Geoderma 2007, 142, 245–250. [Google Scholar] [CrossRef]
- Liu, C.; Xu, J.M.; Ding, N.F.; Fu, Q.L.; Guo, B.; Lin, Y.C.; Li, H.; Li, N. The effect of long-term reclamation on enzyme activities and microbial community structure of saline soil at Shangyu, China. Environ. Earth Sci. 2013, 69, 151–159. [Google Scholar] [CrossRef]
- Tian, B.; Wu, W.; Yang, Z.; Zhou, Y. Drivers, trends, and potential impacts of long-term coastal reclamation in China from 1985 to 2010. Estuar. Coast. Shelf Sci. 2016, 170, 83–90. [Google Scholar] [CrossRef]
- Li, S.; Luo, W.; Jia, Z.; Tang, S.; Chen, C. The effect of natural rainfall on salt leaching under watertable management. L. Degrad. Dev. 2018, 29, 1953–1961. [Google Scholar] [CrossRef]
- Gran, M.; Carrera, J.; Massana, J.; Saaltink, M.W.; Olivella, S.; Ayora, C.; Lloret, A. Dynamics of water vapor flux and water separation processes during evaporation from a salty dry soil. J. Hydrol. 2011, 396, 215–220. [Google Scholar] [CrossRef]
- Liu, D.; She, D.; Mu, X. Water flow and salt transport in bare saline-sodic soils subjected to evaporation and intermittent irrigation with saline/distilled water. L. Degrad. Dev. 2019, 30, 1204–1218. [Google Scholar] [CrossRef]
- Yan, S.F.; Yu, S.E.; Wu, Y.B.; Pan, D.F.; She, D.L.; Ji, J. Seasonal Variations in Groundwater Level and Salinity in Coastal Plain of Eastern China Influenced by Climate. J. Chem. 2015. [Google Scholar] [CrossRef]
- Okur, B.; Örçen, N. Chapter 12—Soil Salinization and Climate Change; Prasad, M.N.V., Pietrzykowski, M., Eds.; Elsevier: Amsterdam, The Netherlands, 2020; pp. 331–350. [Google Scholar] [CrossRef]
- He, B.; Cai, Y.; Ran, W.; Jiang, H. Spatial and seasonal variations of soil salinity following vegetation restoration in coastal saline land in eastern China. Catena 2014, 118, 147–153. [Google Scholar] [CrossRef]
- Geng, X.; Boufadel, M.C. Numerical modeling of water flow and salt transport in bare saline soil subjected to evaporation. J. Hydrol. 2015, 524, 427–438. [Google Scholar] [CrossRef]
- Zhang, C.; Li, L.; Lockington, D. Numerical study of evaporation-induced salt accumulation and precipitation in bare saline soils: Mechanism and feedback. Water Resour. Res. 2014, 50, 8084–8106. [Google Scholar] [CrossRef]
- Yang, T.; Šimůnek, J.; Mo, M.; Mccullough-Sanden, B.; Shahrokhnia, H.; Cherchian, S.; Wu, L. Assessing salinity leaching efficiency in three soils by the HYDRUS-1D and -2D simulations. Soil Tillage Res. 2019, 194. [Google Scholar] [CrossRef]
- Mao, W.; Zhu, Y.; Wu, J.; Ye, M.; Yang, J. Modelling the salt accumulation and leaching processes in arid agricultural areas with a new mass balance model. J. Hydrol. 2020, 591, 125329. [Google Scholar] [CrossRef]
- Olivella, S.; Gens, A.; Carrera, J.; Alonso, E.E. Numerical formulation for a simulator (CODE_BRIGHT) for the coupled analysis of saline media. Eng. Comput. 1996, 13, 87–112. [Google Scholar] [CrossRef]
- Dongli, S.; Dongdong, L.; Jiajia, M.; Agbna, G.H.D. Hydrological responses on saline-sodic soil slopes in a coastal reclamation area of China. Catena 2016, 144, 130–140. [Google Scholar] [CrossRef]
- Liu, D.; She, D. Sodicity effects on hydrological processes of sodic soil slopes under simulated rainfall. Hydrol. Process. 2017, 31, 981–994. [Google Scholar] [CrossRef]
- Wang, H.; She, D.; Fei, Y.; Tang, S. Synergic effects of biochar and polyacrylamide amendments on the mechanical properties of silt loam soil under coastal reclamation in China. Catena 2019, 182, 104152. [Google Scholar] [CrossRef]
- van Genuchten, M.T. Closed-Form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Biavati, G.; Horányi, A.; Muñoz Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Rozum, I.; et al. ERA5 Monthly Averaged Data on Single Levels from 1979 to Present, ERA5 Monthly Averaged Data on Single Levels from 1959 to Present. 2019. Available online: https://www.ecmwf.int/en/forecasts/dataset/ecmwf-reanalysis-v5 (accessed on 21 October 2023).
- Rose, D.A.; Konukcu, F.; Gowing, J.W. Effect of watertable depth on evaporation and salt accumulation from saline groundwater. Aust. J. Soil Res. 2005, 43, 565–573. [Google Scholar] [CrossRef]
- Ahmad, M.U.D.; Bastiaanssen, W.G.M.; Feddes, R.A. Sustainable use of groundwater for irrigation: A numerical analysis of the subsoil water fluxes. Irrig. Drain. 2002, 51, 227–241. [Google Scholar] [CrossRef]
- Hunt, A.G.; Skinner, T.E.; Ewing, R.P.; Ghanbarian-Alavijeh, B. Dispersion of solutes in porous media. Eur. Phys. J. B 2011, 80, 411–432. [Google Scholar] [CrossRef]
- Campbell, G.S.; Norman, J.M. An Introduction to Environmental Biophysics, An Introduction to Environmental Biophysics; Springer: New York, NY, USA, 1998. [Google Scholar] [CrossRef]
- Yu, X.; Dan, H.-C.; Xin, P. Method for Improving Leaching Efficiency of Coastal Subsurface Drainage Systems. J. Irrig. Drain. Eng. 2018, 144, 04018019. [Google Scholar] [CrossRef]
- Wang, S.; Song, X.; Wang, Q.; Xiao, G.; Wang, Z.; Liu, X.; Wang, P. Shallow groundwater dynamics and origin of salinity at two sites in salinated and water-deficient region of North China Plain, China. Environ. Earth Sci. 2012, 66, 729–739. [Google Scholar] [CrossRef]
- Adrover, M.; Moyà, G.; Vadell, J. Seasonal and depth variation of soil chemical and biological properties in alfalfa crops irrigated with treated wastewater and saline groundwater. Geoderma 2017, 286, 54–63. [Google Scholar] [CrossRef]
- Hongde, W.; Dongli, S.; Yipeng, Z.; Donghao, M. Unsaturated soil shear strength of agricultural soils influenced by reclaimed sequences in coastal China. Eur. J. Soil Sci. 2022, 73, e13237. [Google Scholar] [CrossRef]
- Yang, Y.; Zhu, Y.; Wu, J.; Mao, W.; Ye, M.; Yang, J. Development and application of a new package for MODFLOW-LGR-MT3D for simulating regional groundwater and salt dynamics with subsurface drainage systems. Agric. Water Manag. 2022, 260, 107330. [Google Scholar] [CrossRef]
- Eswar, D.; Karuppusamy, R.; Chellamuthu, S. Drivers of Soil Salinity and Their Correlation with Climate Change. Curr. Opin. Env. Sustain. 2021, 50, 310–318. [Google Scholar] [CrossRef]
- Grieve, C.M.; Grattan, S.R.; Maas, E.V. Chapter 13 Plant Salt Tolerance. Agric. Salin. Assess. Manag. 2012, 71, 405–459. [Google Scholar] [CrossRef]


| Parameters | Case 1 (Rainfall) | Cases 2 and 3 (Evaporation) | Cases 4 and 5 (Climate) | ||
|---|---|---|---|---|---|
| T (°C) | 25 | 25 | Climate data See Figure 3 | ||
| Pga (MPa) | 0.1 | 0.1 | |||
| HR (%) | 68% | 68% | |||
| P (mm) | 1010 | 0 | |||
| va (m/s) | 3.15 | 3.15 | |||
| Groundwater salinity (kg/kg) | 0 | 0 | 0.008 | 0 | 0.008 |
| Constitutive Laws | Model | Material Parameters | Legend |
|---|---|---|---|
| Liquid advective flux (Darcy law) | k = 5.5 × 10−13 m2 μl = 0.89 MPa s ρl = 1 g/cm3 g = 9.8 m/s2 | ql: liquid flow k: intrinsic permeability μl: liquid viscosity ρl: liquid density g: gravity Pl: liquid pressure | |
| Water retention curve [21] | λ = 0.3631 P0 = 0.03 MPa Srl = 0.017 Sls = 1 | Se: degree of saturation Sls: maximum saturation Srl: residual saturation Pg: gas pressure P0: pressure for a measured T λ: shape function | |
| Liquid flow | λ = 0.3631 | krl: coefficient for liquid relative permeability λ: constant | |
| Diffusive fluxes of vapor | D = 5.9 × 10−6 m2/s n = 2.3 Pg = 1 × 105 Pa | : diffusion coefficient of vapor in gas phase Pg: gas pressure T: Temperature | |
| Diffusive fluxes of salt | D = 2.59 × 10−9 m2/s Q = 24,530 J/mol | : diffusion coefficient of salt in liquid (m2/s) D: constant Q: constant | |
| Dispersive fluxes of mass [25] | dl = 0.5 m dt = 0.05 m | : dispersion coefficient of salt in liquid dl and dt: longitudinal and transverse dispersivity for solutes in liquid phase | |
| Conductive flux of heat [26] | λsolid = 2 W/mK λliq = 0.6 W/mK λgas = 0.024 W/mK | ic: conductive heat flux λ: thermal conductivity ϕ: porosity |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; She, D.; Cardoso, R. Understanding the Effect of Seasonal Climate Variability on the Salinity in Unsaturated Agricultural Soil. Agronomy 2023, 13, 2802. https://doi.org/10.3390/agronomy13112802
Wang H, She D, Cardoso R. Understanding the Effect of Seasonal Climate Variability on the Salinity in Unsaturated Agricultural Soil. Agronomy. 2023; 13(11):2802. https://doi.org/10.3390/agronomy13112802
Chicago/Turabian StyleWang, Hongde, Dongli She, and Rafaela Cardoso. 2023. "Understanding the Effect of Seasonal Climate Variability on the Salinity in Unsaturated Agricultural Soil" Agronomy 13, no. 11: 2802. https://doi.org/10.3390/agronomy13112802
APA StyleWang, H., She, D., & Cardoso, R. (2023). Understanding the Effect of Seasonal Climate Variability on the Salinity in Unsaturated Agricultural Soil. Agronomy, 13(11), 2802. https://doi.org/10.3390/agronomy13112802







