Mapping Soil Organic Matter Content Based on Feature Band Selection with ZY1-02D Hyperspectral Satellite Data in the Agricultural Region
Abstract
:1. Introduction
2. Materials
2.1. Study Area
2.2. Gathering and Preparation of the Soil Samples
2.3. Hyperspectral Satellite Data Acquisition, Pre-Processing, and First Derivative Processing
3. Methods
3.1. Characteristic Spectral Band Selection
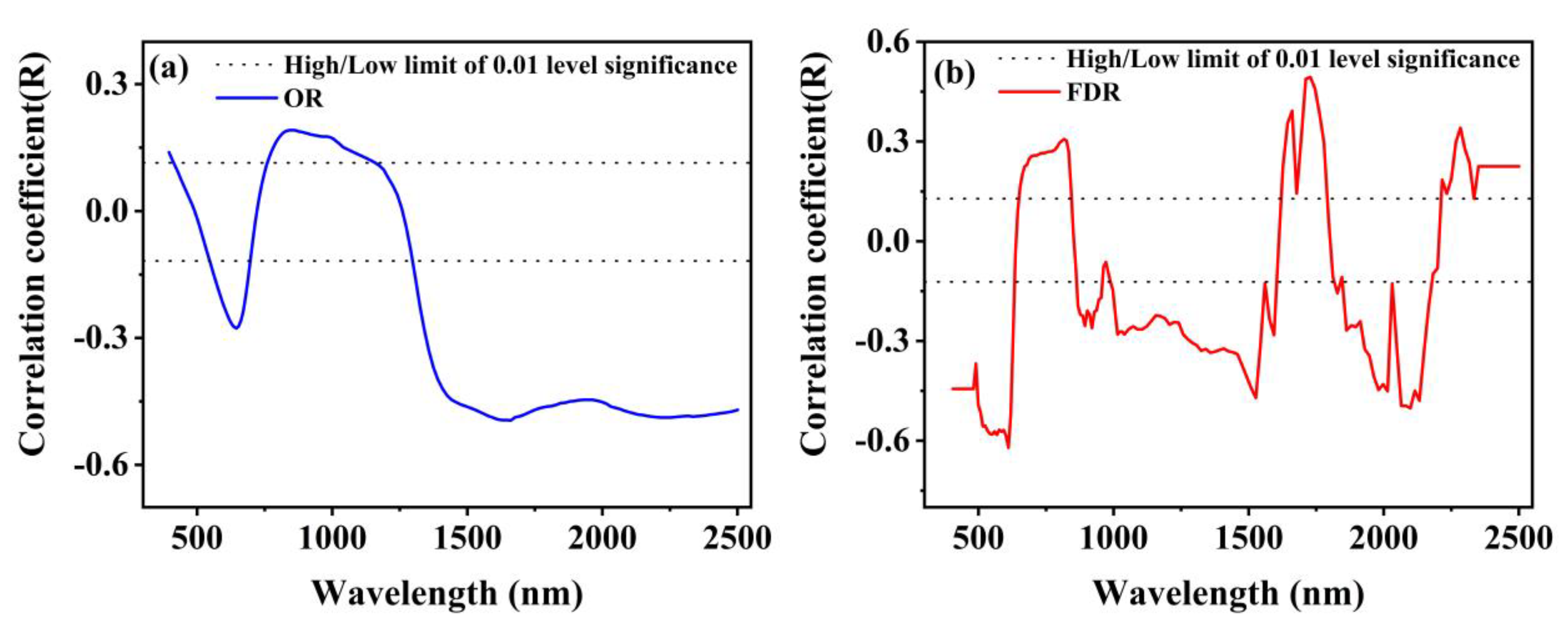
3.1.1. Correlation Coefficient (CC)
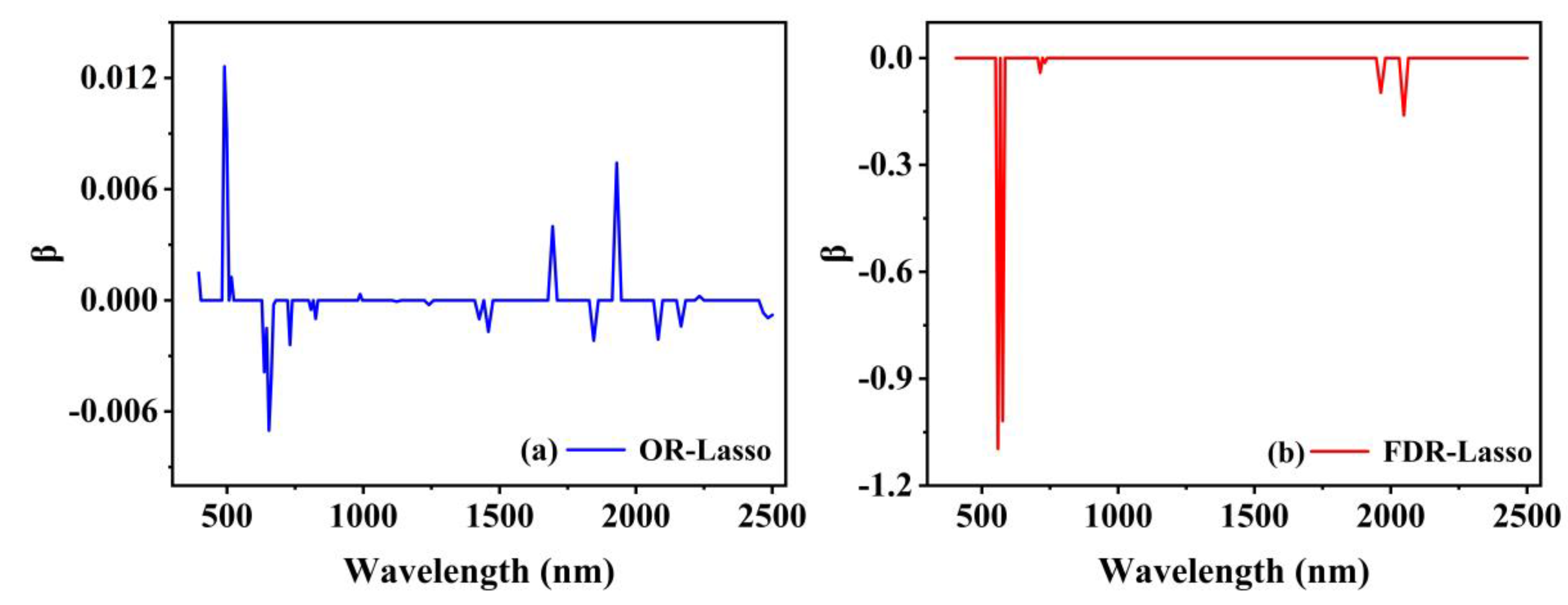
3.1.2. Least Absolute Shrinkage and Selection Operator (Lasso)
3.2. Prediction Models
3.2.1. Multiple Linear Regression (MLR)
3.2.2. Partial Least Squares Regression (PLSR)
3.2.3. Random Forest (RF)
3.3. Model Accuracy Evaluation
3.4. Model Stability Evaluation
4. Results
4.1. Statistical Description of SOM Content
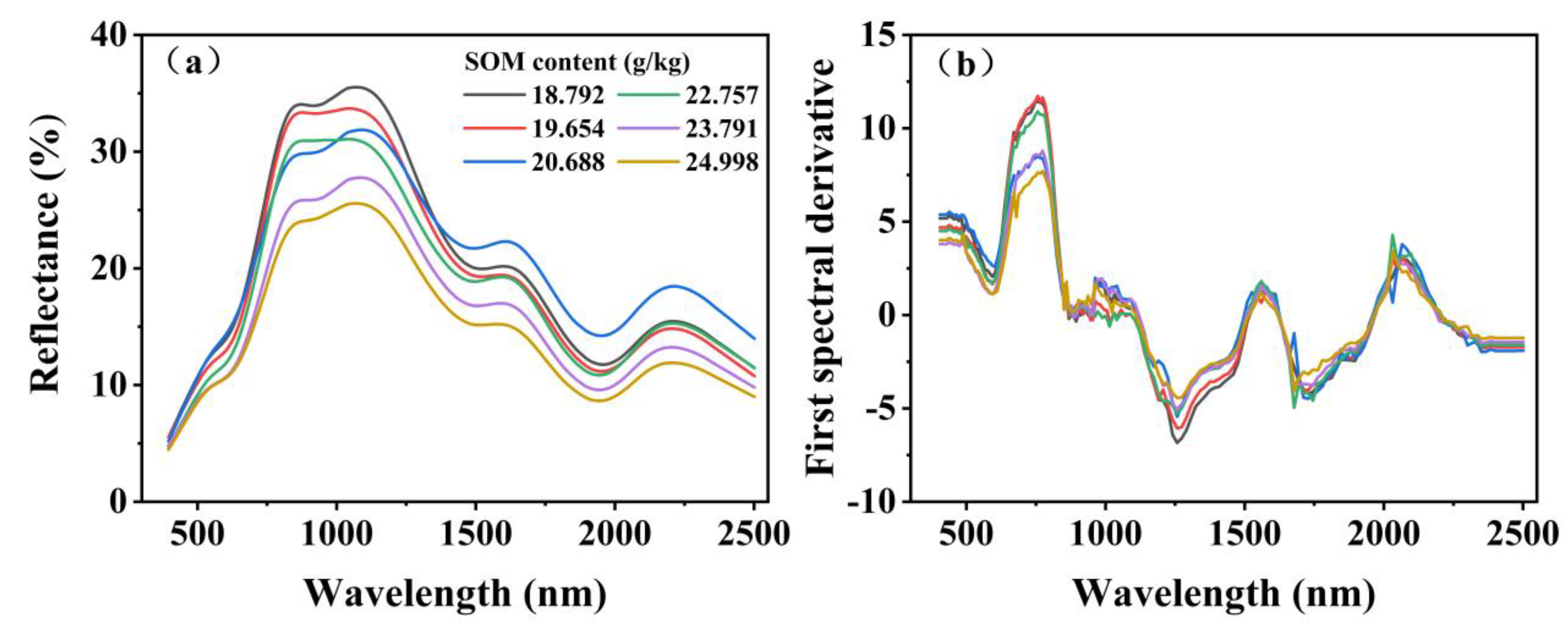
4.2. Spectral Reflectance Characteristics of Soil Samples
4.2.1. Original Reflectance (OR)
4.2.2. First Derivative Reflectance (FDR)
4.3. Characteristic Spectral Band Selection
4.3.1. CC Characteristic Band Choice
4.3.2. Lasso Characteristic Spectral Band Choice
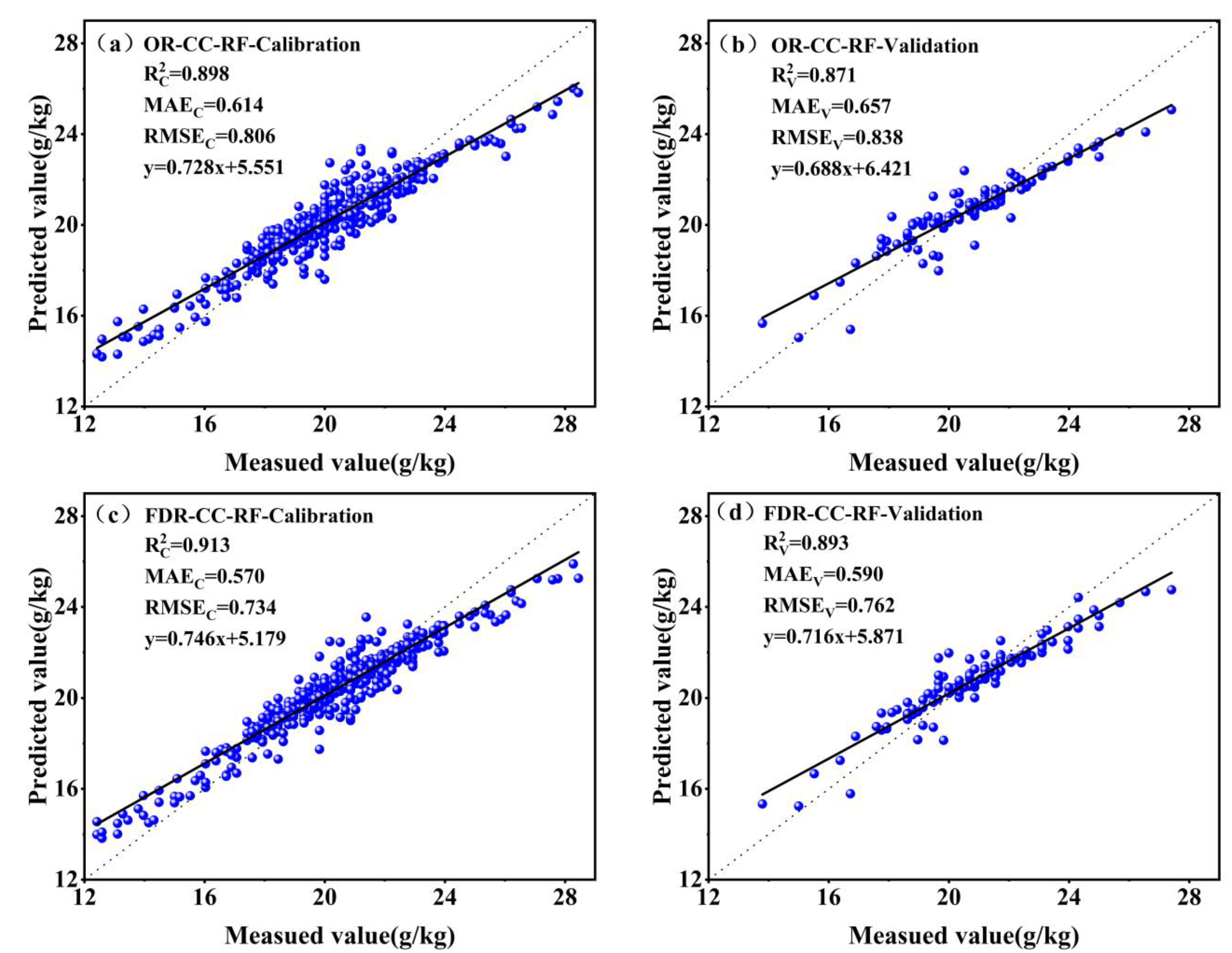
4.4. The Results of Prediction Models
5. Discussion
5.1. Benefits of FDR Processing
5.2. Benefits of Lasso Feature Band Selection
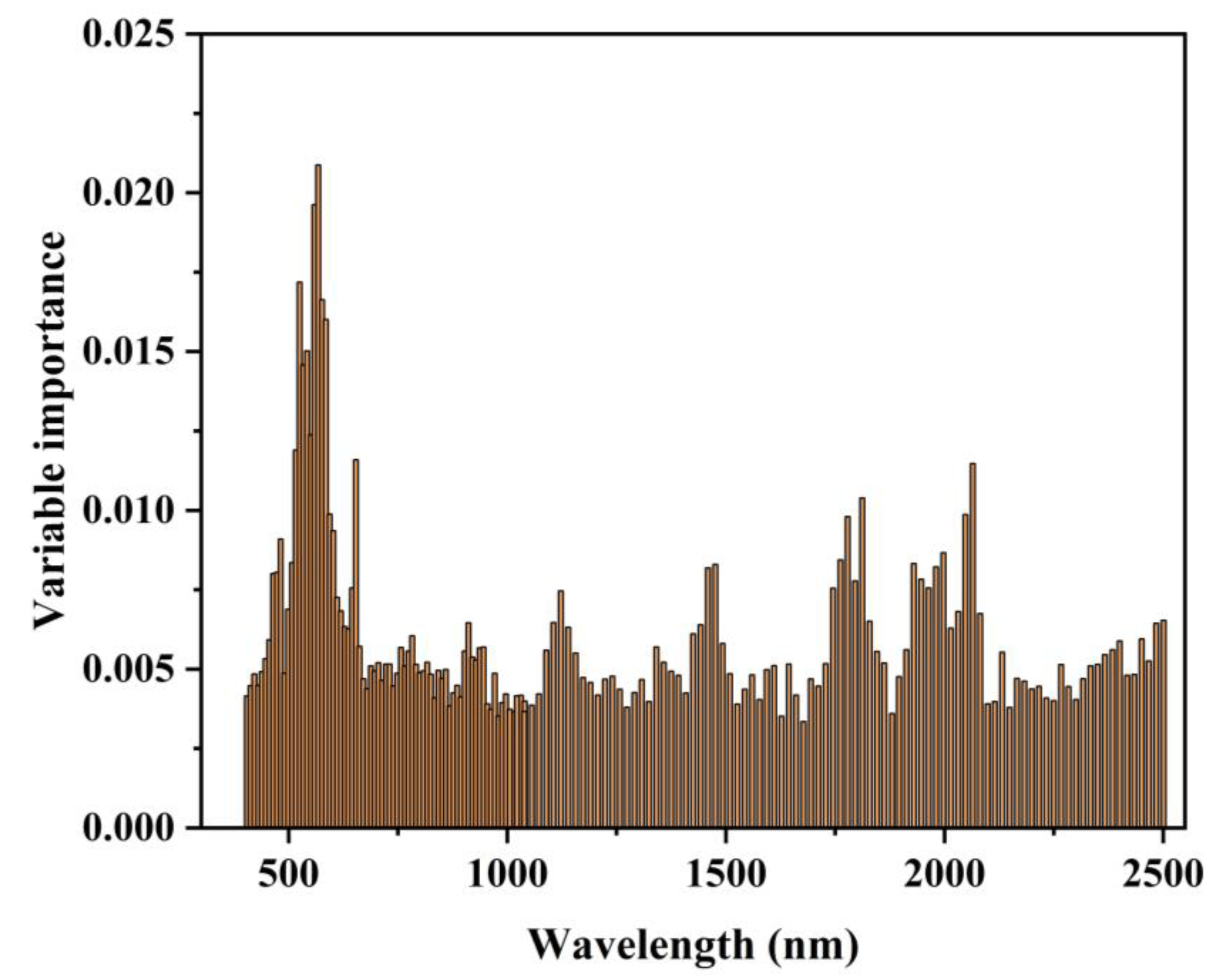
5.3. Importance Analysis of RF Model Input Variables
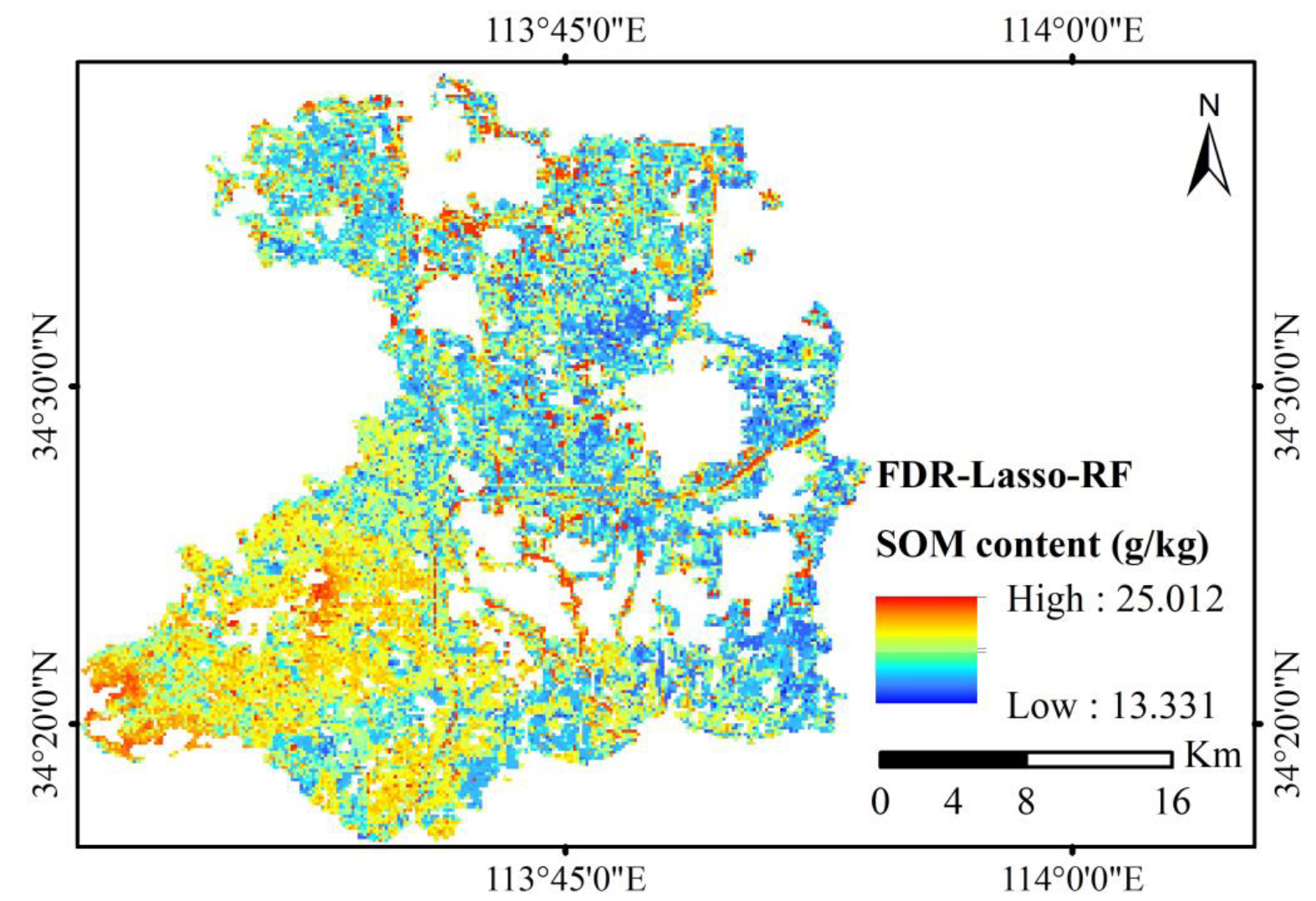
5.4. Optimal Model SOM Mapping
6. Conclusions
- (1)
- In comparison to OR, FDR treatment can increase model fitting accuracy by emphasizing SOM spectral characteristic information in the soil spectrum.
- (2)
- The Lasso feature selection method can effectively extract the SOM feature and spectral bands, reduce the data dimension, highlight key information, and enhance model estimation capabilities.
- (3)
- The RF model provides excellent SOM content prediction and model stability. The FDR-Lasso-RF model is the best prediction model, with R2 = 0.921, MAEV = 0.512 g/kg, and RMSEV = 0.645 g/kg in its validation set.
- (4)
- Hyperspectral satellite data make up for the lack of large-scale observation of laboratory hyperspectral data and provide a feasible method for rapid, large-scale, and accurate prediction and mapping of SOM content in agricultural areas.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhao, Y.; Xu, X.; Tian, K.; Huang, B.; Hai, N. Comparison of sampling schemes for the spatial prediction of soil organic matter in a typical black soil region in China. Environ. Earth Sci. 2016, 75, 4. [Google Scholar] [CrossRef]
- Tian, J.; Lu, S.; Fan, M.; Li, X.; Kuzyakov, Y. Labile soil organic matter fractions as influenced by non-flooded mulching cultivation and cropping season in rice–wheat rotation. Eur. J. Soil Biol. 2013, 56, 19–25. [Google Scholar] [CrossRef]
- Liu, J.; Dong, Z.; Xia, J.; Wang, H.; Xie, J. Estimation of soil organic matter content based on CARS algorithm coupled with random forest. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2021, 258, 119823. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Shang, K.; Xiao, C.; Wang, C.; Tang, H. Spectral Index for Mapping Topsoil Organic Matter Content Based on ZY1-02D Satellite Hyperspectral Data in Jiangsu Province, China. ISPRS Int. J. Geo-Inf. 2022, 11, 111. [Google Scholar] [CrossRef]
- Rossel, R.A.V.; Webster, R. Predicting soil properties from the Australian soil visible-near infrared spectroscopic database. Eur. J. Soil Sci. 2012, 63, 848–860. [Google Scholar] [CrossRef]
- Wei, L.; Yuan, Z.; Wang, Z.; Zhao, L.; Zhang, Y.; Lu, X.; Cao, L. Hyperspectral Inversion of Soil Organic Matter Content Based on a Combined Spectral Index Model. Sensors 2020, 20, 2777. [Google Scholar] [CrossRef]
- Gruba, P.; Socha, J.; Błońska, E.; Lasota, J. Effect of variable soil texture, metal saturation of soil organic matter (SOM) and tree species composition on spatial distribution of SOM in forest soils in Poland. Sci. Total Environ. 2015, 521–522, 90–100. [Google Scholar] [CrossRef]
- Caddeo, A.; Marras, S.; Sallustio, L.; Spano, D.; Sirca, C. Soil organic carbon in Italian forests and agroecosystems: Estimating current stock and future changes with a spatial modelling approach. Agric. For. Meteorol. 2019, 278, 107654. [Google Scholar] [CrossRef]
- Shi, T.; Liu, H.; Chen, Y.; Wang, J.; Wu, G. Estimation of arsenic in agricultural soils using hyperspectral vegetation indices of rice. J. Hazard. Mater. 2016, 308, 243–252. [Google Scholar] [CrossRef]
- Yu, Q.; Yao, T.; Lu, H.; Feng, W.; Xue, Y.; Liu, B. improving estimation of soil organic matter content by combining Landsat 8 OLI images and environmental data: A case study in the river valley of the southern Qinghai-Tibet Plateau. Comput. Electron. Agric. 2021, 185, 106144. [Google Scholar] [CrossRef]
- Nawar, S.; Mouazen, A.M. Optimal sample selection for measurement of soil organic carbon using on-line vis-NIR spectroscopy. Comput. Electron. Agric. 2018, 151, 469–477. [Google Scholar] [CrossRef]
- Allory, V.; Cambou, A.; Moulin, P.; Schwartz, C.; Cannavo, P.; Vidal-Beaudet, L.; Barthès, B.G. Quantification of soil organic carbon stock in urban soils using visible and near infrared reflectance spectroscopy (VNIRS) in situ or in laboratory conditions. Sci. Total Environ. 2019, 686, 764–773. [Google Scholar] [CrossRef] [PubMed]
- Xie, S.; Li, Y.; Wang, X.; Liu, Z.; Ma, K.; Ding, L. Research on estimation models of the spectral characteristics of soil organic matter based on the soil particle size. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2021, 260, 119963. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Shang, K.; Xu, Y. Analysis of Sensitive Spectral Characteristics of Farmland Soil Organic Matter Content Based on Ahsi/zy1-02d Data. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Brussels, Belgium, 11–16 July 2021. [Google Scholar] [CrossRef]
- Luo, C.; Zhang, X.; Meng, X.; Zhu, H.; Ni, C.; Chen, M.; Liu, H. Regional mapping of soil organic matter content using multitemporal synthetic Landsat 8 images in Google Earth Engine. Catena 2022, 209, 105842. [Google Scholar] [CrossRef]
- De Santana, F.B.; de Souza, A.M.; Poppi, R.J. Green methodology for soil organic matter analysis using a national near infrared spectral library in tandem with learning machine. Sci. Total Environ. 2019, 658, 895–900. [Google Scholar] [CrossRef]
- Knox, N.M.; Grunwald, S.; McDowell, M.L.; Bruland, G.L.; Myers, D.B.; Harris, W.G. Modelling soil carbon fractions with visible near-infrared (VNIR) and mid-infrared (MIR) spectroscopy. Geoderma 2015, 239–240, 229–239. [Google Scholar] [CrossRef]
- Liu, H.; Bao, Y.; Meng, X.; Cui, Y.; Zhang, A.; Liu, Y.; Wang, D. Inversion of soil organic matter based on GF-5 images under different noise reduction methods. Trans. Chin. Soc. Agric. Eng. 2020, 36, 90–98. [Google Scholar] [CrossRef]
- Gu, X.; Wang, Y.; Sun, Q.; Yang, G.; Zhang, C. Hyperspectral inversion of soil organic matter content in cultivated land based on wavelet transform. Comput. Electron. Agric. 2019, 167, 105053. [Google Scholar] [CrossRef]
- Xie, S.; Ding, F.; Chen, S.; Wang, X.; Li, Y.; Ma, K. Prediction of soil organic matter content based on characteristic band selection method. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2022, 273, 120949. [Google Scholar] [CrossRef]
- Zhai, M. Inversion of organic matter content in wetland soil based on Landsat 8 remote sensing image. J. Vis. Commun. Image Represent. 2019, 64, 102645. [Google Scholar] [CrossRef]
- Dou, X.; Wang, X.; Liu, H.; Zhang, X.; Cui, Y. Prediction of soil organic matter using multi-temporal satellite images in the Songnen Plain, China. Geoderma 2019, 356, 113896. [Google Scholar] [CrossRef]
- Vaudour, E.; Gomez, C.; Lagacherie, P.; Loiseau, T.; Arrouays, D. Temporal mosaicking approaches of Sentinel-2 images for extending topsoil organic carbon content mapping in croplands. Int. J. Appl. Earth Obs. Geoinf. 2021, 96, 102277. [Google Scholar] [CrossRef]
- Castaldi, F.; Palombo, A.; Santini, F.; Pascucci, S.; Pignatti, S.; Casa, R. Evaluation of the potential of the current and forthcoming multispectral and hyperspectral imagers to estimate soil texture and organic carbon. Remote Sens. Environ. 2016, 179, 54–65. [Google Scholar] [CrossRef]
- Meng, X.; Bao, Y.; Liu, J.; Liu, H.; Kong, F. Regional soil organic carbon prediction model based on a discrete wavelet analysis of hyperspectral satellite data. ITC J. 2020, 89, 102111. [Google Scholar] [CrossRef]
- Viscarra Rossel, R.A.; Cattle, S.R.; Ortega, A.; Fouad, Y. In situ measurements of soil colour, mineral composition and clay content by vis–NIR spectroscopy. Geoderma 2009, 150, 253–266. [Google Scholar] [CrossRef]
- Dotto, A.C.; Dalmolin, R.S.D.; Caten, A.T.; Grunwald, S. A systematic study on the application of scatter-corrective and spectral-derivative preprocessing for multivariate prediction of soil organic carbon by Vis-NIR spectra. Geoderma 2018, 314, 262–274. [Google Scholar] [CrossRef]
- Vašát, R.; Kodešová, R.; Klement, A.; Borůvka, L. Simple but efficient signal pre-processing in soil organic carbon spectroscopic estimation. Geoderma 2017, 298, 46–53. [Google Scholar] [CrossRef]
- Zhang, Z.; Ding, J.; Zhu, C.; Wang, J. Combination of efficient signal pre-processing and optimal band combination algorithm to predict soil organic matter through visible and near-infrared spectra. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2020, 240, 118553. [Google Scholar] [CrossRef] [PubMed]
- Swierenga, H.; Wülfert, F.; De Noord, O.E.; De Weijer, A.P.; Smilde, A.K.; Buydens, L.M.C. Development of robust calibration models in near infra-red spectrometric applications. Anal. Chim. Acta 2000, 411, 121–135. [Google Scholar] [CrossRef]
- Galvão, R.K.H.; Araújo, M.C.U.; Silva, E.C.; José, G.E.; Soares, S.F.C.; Paiva, H.M. Short Report Cross-Validation for the Selection of Spectral Variables Using the Successive Projections Algorithm. J. Braz. Chem. Soc. 2007, 18, 1580–1584. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression Shrinkage and Selection via the Lasso. J. R. Stat. Soc. Ser. B 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Wang, K.; Yang, S.; Guo, C.; Bian, X. Spectral Variable Selection Methods Based on LASSO Algorithm. J. Instrum. Anal. 2022, 41, 398–402. [Google Scholar] [CrossRef]
- Li, D.; Chen, X.; Peng, Z.; Chen, S.; Chen, W.; Han, L.; Li, Y. Prediction of soil organic matter content in a litchi orchard of South China using spectral indices. Soil Tillage Res. 2012, 123, 78–86. [Google Scholar] [CrossRef]
- Press, W.H.; Teukolsky, S.A. Savitzky-Golay Smoothing Filters. Comput. Phys. 1990, 4, 669. [Google Scholar] [CrossRef]
- Tsai, F.; Philpot, W. Derivative Analysis of Hyperspectral Data. Remote Sens. Environ. 1998, 66, 41–51. [Google Scholar] [CrossRef]
- Tsai, F.; Philpot, W.D. A derivative-aided hyperspectral image analysis system for land-cover classification. IEEE Trans. Geosci. Remote Sens. 2002, 40, 416–425. [Google Scholar] [CrossRef]
- Minhoni, R.T.D.A.; Scudiero, E.; Zaccaria, D.; Saad, J.C.C. Multitemporal satellite imagery analysis for soil organic carbon assessment in an agricultural farm in southeastern Brazil. Sci. Total Environ. 2021, 784, 147216. [Google Scholar] [CrossRef]
- Yu, L.; Hong, Y.; Gen, L.; Zhou, Y.; Zhu, Q.; Cao, J.; Nie, Y. Hyperspectral estimation of soil organic matter content based on partial least squares regression. Trans. Chin. Soc. Agric. Eng. 2015, 31, 103–109. [Google Scholar] [CrossRef]
- Shen, L.; Gao, M.; Yan, J.; Li, Z.; Leng, P.; Yang, Q.; Duan, S. Hyperspectral Estimation of Soil Organic Matter Content using Different Spectral Preprocessing Techniques and PLSR Method. Remote Sens. 2020, 12, 1206. [Google Scholar] [CrossRef] [Green Version]
- Demattê, J.A.M.; Ramirez-Lopez, L.; Marques, K.P.P.; Rodella, A.A. Chemometric soil analysis on the determination of specific bands for the detection of magnesium and potassium by spectroscopy. Geoderma 2017, 288, 8–22. [Google Scholar] [CrossRef]
- Jakab, G.; Rieder, Á.; Vancsik, A.V.; Szalai, Z. Soil organic matter characterisation by photometric indices or photon correlation spectroscopy: Are they comparable? Hung. Geogr. Bull. 2018, 67, 109–120. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, F.; Kung, H.; Johnson, V.C. New methods for improving the remote sensing estimation of soil organic matter content (SOMC) in the Ebinur Lake Wetland National Nature Reserve (ELWNNR) in northwest China. Remote Sens. Environ. 2018, 218, 104–118. [Google Scholar] [CrossRef]
- Yu, X.; Liu, Q.; Wang, Y.; Liu, X.; Liu, X. Evaluation of MLSR and PLSR for estimating soil element contents using visible/near-infrared spectroscopy in apple orchards on the Jiaodong peninsula. Catena 2016, 137, 340–349. [Google Scholar] [CrossRef]
- Zhang, D.; Zhao, Y.; Qing, K.; Zhao, N.; Yang, Y. Influence of spectral transformation methods on nutrient content inversion accuracy by hyperspectral remote sensing in black soil. Trans. Chin. Soc. Agric. Eng. 2018, 34, 141–147. [Google Scholar] [CrossRef]
- Dai, F.; Zhou, Q.; Lv, Z.; Wang, X.; Liu, G. Spatial prediction of soil organic matter content integrating artificial neural network and ordinary kriging in Tibetan Plateau. Ecol. Indic. 2014, 45, 184–194. [Google Scholar] [CrossRef]
- Mehmood, T.; Liland, K.H.; Snipen, L.; Sæbø, S. A review of variable selection methods in Partial Least Squares Regression. Chemom. Intell. Lab. Syst. 2012, 118, 62–69. [Google Scholar] [CrossRef]
- Vohland, M.; Ludwig, M.; Thiele-Bruhn, S.; Ludwig, B. Quantification of Soil Properties with Hyperspectral Data: Selecting Spectral Variables with Different Methods to Improve Accuracies and Analyze Prediction Mechanisms. Remote Sens. 2017, 9, 1103. [Google Scholar] [CrossRef]
- Rossel, R.A.V.; Behrens, T. Using data mining to model and interpret soil diffuse reflectance spectra. Geoderma 2010, 158, 46–54. [Google Scholar] [CrossRef]
- Galvao, L.S.I.S.; Vitorello, I. Variability of Laboratory Measured Soil Lines of Soils from Southeastern Brazil. Remote Sens. Environ. 1998, 63, 166–181. [Google Scholar] [CrossRef]




| Satellite Payloads | ZY-1-02D |
|---|---|
| Launch Time | 12 December 2019 |
| Number of Bands | 76 (VNIR), 90 (SWIR) |
| Spectral Range (nm) | 400–2500 |
| Spectral Resolution (nm) | 10 (VNIR), 20 (SWIR) |
| Spatial Resolution (m) | 30 |
| Swath Width (km) | 60 |
| Revisit Cycle (d) | 3 |
| Set | N | Max (g/kg) | Min (g/kg) | Mean (g/kg) | SD (g/kg) | CV (%) |
|---|---|---|---|---|---|---|
| Whole set | 539 | 28.446 | 12.413 | 20.316 | 2.501 | 12.309 |
| Calibration set | 431 | 28.446 | 12.413 | 20.195 | 2.527 | 12.513 |
| Validation set | 108 | 27.412 | 13.792 | 20.797 | 2.344 | 11.271 |
| Spectral | Number of Bands | Wavelength Range (nm) | Maximum Correlation Band (nm) | Correlation Coefficient R |
|---|---|---|---|---|
| OR | 133 | 400–413, 551–697 | 1661 | −0.495 |
| 766–1157, 1308–2500 | ||||
| FDR | 149 | 405–628, 654–843 | 611 | −0.621 |
| 868–954, 988–1594 | ||||
| 1627–1779, 1829 | ||||
| 1862–2166, 2216–2500 |
| Method | Number of Bands | Wavelength (nm) |
|---|---|---|
| OR-Lasso | 27 | 400, 490–500, 516, 636–671, 722–731, 808, 825, 988, 1123 |
| 1241, 1425, 1459, 1695, 1846, 1930, 2082, 2166, 2233 | ||
| 2468–2500 | ||
| FDR-Lasso | 6 | 559, 567, 714, 731, 1964, 2048 |
| Model | Method | Calibration Set | Validation Set | ||||
|---|---|---|---|---|---|---|---|
| (g/kg) | (g/kg) | (g/kg) | (g/kg) | ||||
| MLR | OR | 0.646 | 1.166 | 1.503 | 0.256 | 1.751 | 2.203 |
| OR-CC | 0.616 | 1.203 | 1.564 | 0.239 | 1.712 | 2.159 | |
| OR-Lasso | 0.453 | 1.471 | 1.863 | 0.296 | 1.536 | 1.925 | |
| FDR | 0.625 | 1.202 | 1.545 | 0.200 | 1.789 | 2.279 | |
| FDR-CC | 0.601 | 1.242 | 1.594 | 0.172 | 1.821 | 2.315 | |
| FDR-Lasso | 0.414 | 1.508 | 1.929 | 0.385 | 1.409 | 1.799 | |
| PLSR | OR | 0.330 | 1.598 | 2.066 | 0.307 | 1.528 | 1.942 |
| OR-CC | 0.312 | 1.618 | 2.094 | 0.298 | 1.528 | 1.954 | |
| OR-Lasso | 0.316 | 1.611 | 2.083 | 0.448 | 1.337 | 1.704 | |
| FDR | 0.316 | 1.599 | 2.087 | 0.286 | 1.540 | 1.972 | |
| FDR-CC | 0.317 | 1.599 | 2.087 | 0.285 | 1.539 | 1.972 | |
| FDR-Lasso | 0.393 | 1.525 | 1.963 | 0.411 | 1.369 | 1.761 | |
| RF | OR | 0.900 | 0.603 | 0.797 | 0.880 | 0.633 | 0.807 |
| OR-CC | 0.898 | 0.614 | 0.806 | 0.871 | 0.657 | 0.838 | |
| OR-Lasso | 0.908 | 0.601 | 0.764 | 0.901 | 0.537 | 0.721 | |
| FDR | 0.913 | 0.567 | 0.743 | 0.897 | 0.582 | 0.750 | |
| FDR-CC | 0.913 | 0.570 | 0.734 | 0.893 | 0.590 | 0.762 | |
| FDR-Lasso | 0.923 | 0.553 | 0.701 | 0.921 | 0.512 | 0.645 | |
| Model | Method | Calibration Set | Validation Set |
|---|---|---|---|
| RF | OR | 0.160 | 0.302 |
| OR-CC | 0.157 | 0.291 | |
| OR-Lasso | 0.156 | 0.309 | |
| FDR | 0.162 | 0.305 | |
| FDR-CC | 0.160 | 0.296 | |
| FDR-Lasso | 0.167 | 0.307 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, H.; Zhang, R.; Dai, W.; Zhou, X.; Zhang, D.; Yang, Y.; Cui, J. Mapping Soil Organic Matter Content Based on Feature Band Selection with ZY1-02D Hyperspectral Satellite Data in the Agricultural Region. Agronomy 2022, 12, 2111. https://doi.org/10.3390/agronomy12092111
Guo H, Zhang R, Dai W, Zhou X, Zhang D, Yang Y, Cui J. Mapping Soil Organic Matter Content Based on Feature Band Selection with ZY1-02D Hyperspectral Satellite Data in the Agricultural Region. Agronomy. 2022; 12(9):2111. https://doi.org/10.3390/agronomy12092111
Chicago/Turabian StyleGuo, Hengliang, Rongrong Zhang, Wenhao Dai, Xiaowen Zhou, Dujuan Zhang, Yaohuan Yang, and Jian Cui. 2022. "Mapping Soil Organic Matter Content Based on Feature Band Selection with ZY1-02D Hyperspectral Satellite Data in the Agricultural Region" Agronomy 12, no. 9: 2111. https://doi.org/10.3390/agronomy12092111
APA StyleGuo, H., Zhang, R., Dai, W., Zhou, X., Zhang, D., Yang, Y., & Cui, J. (2022). Mapping Soil Organic Matter Content Based on Feature Band Selection with ZY1-02D Hyperspectral Satellite Data in the Agricultural Region. Agronomy, 12(9), 2111. https://doi.org/10.3390/agronomy12092111




