Applying Spatial Statistical Analysis to Ordinal Data for Soybean Iron Deficiency Chlorosis
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Sets
2.2. Analytic Methods
2.2.1. Model 1: Ordinary Least Squares (OLS) without Range and Row Covariates
2.2.2. Model 2: Ordinary Least Square (OLS) with Range and Row
2.2.3. Model 3: Moving Grid Adjustment
2.2.4. Model 4: Spatial Autoregressive Lag Model
2.2.5. Model 5: Spatial Autoregressive Error Model
2.2.6. Model 6: Spatial Durbin Mixed Model
2.2.7. Model 7: AR1 by AR1 via ASReml-R
2.2.8. Model 8: P-spline Mixed Model via SpATS
2.2.9. Performance Metrics to Compare the Models
2.3. Heatmap and Lagrange Multiplier Test
2.3.1. Kruskal-Wallis Test and Multiple Comparisons of Models
2.3.2. Relative Efficiency (RE)
2.3.3. Effective Dimension (ED)
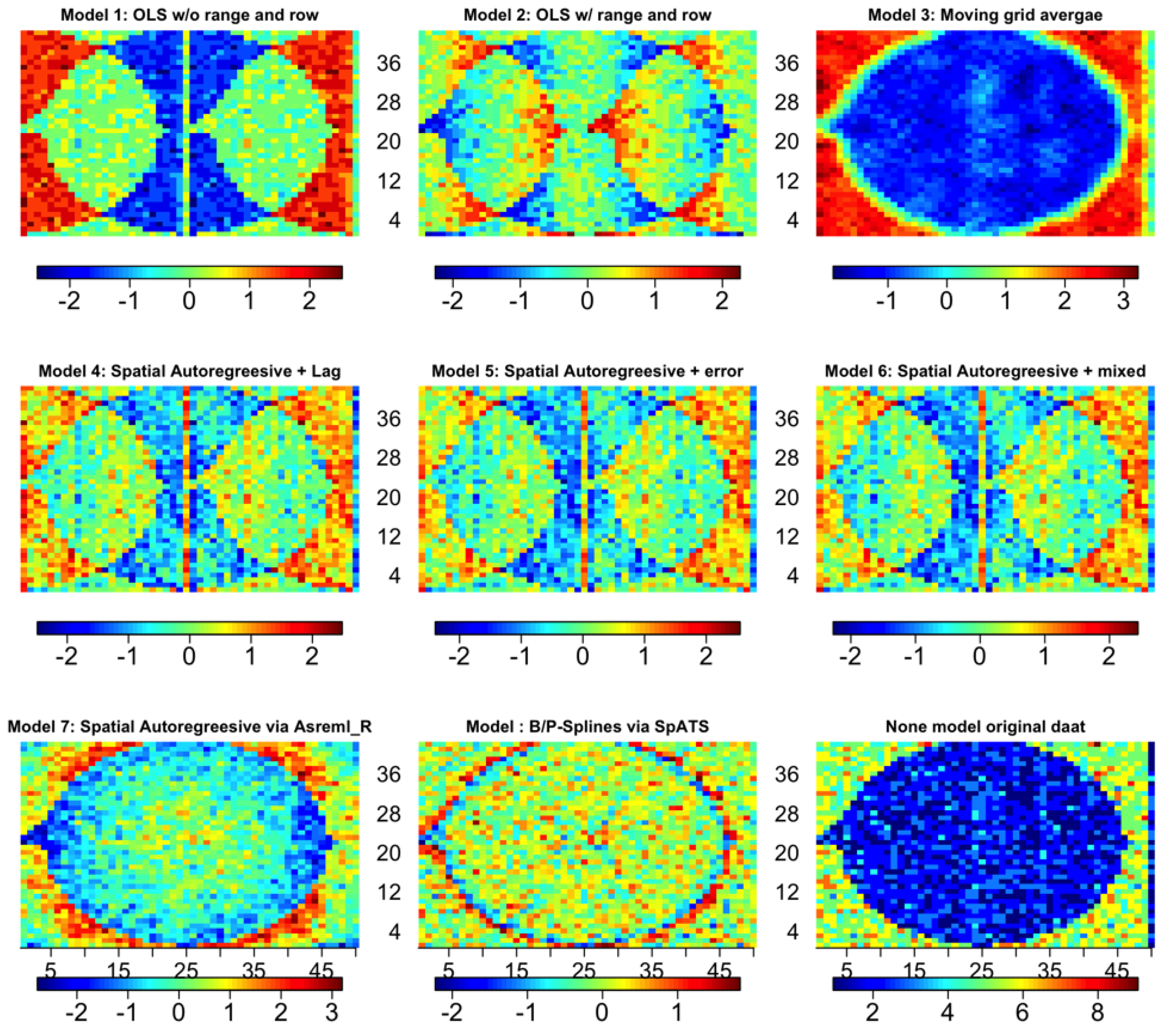
3. Results and Discussion
3.1. Results from the P-spline Model SpATS
3.2. Spatial Effective Dimension (ED) and Importance of Surface Trend by F(row):F(range)
3.3. Variance Components Analysis and Importance of Surface Trend by F(row):F(range)
3.4. Comparison Metrics among the Eight Models
3.5. Relative Efficiency (RE) of the Spatial Autoregressive (SAR) Analyses
3.6. Lagrange Multiplier Test (LMT)
3.7. Statistical Experimental Design for Spatial Analysis versus Breeding Practice
3.8. IDC Hill Plot Size and Spatial Variation
3.9. The Tensor Product Penalized Splines May Perform Better for Continuous Data Type than for Ordinal Data Type
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Acronym | Term | Definition |
|---|---|---|
| AIC | Akaike information criterion | A mathematical method for evaluating how well a model fits the data |
| AR1 | first-order autoregressive | The order of an autoregression is the number of immediately preceding values in the series that are used to predict the value at present |
| AR2 | second-order autoregressive | The order of an autoregression is the number of preceding 2 values in the series that are used to predict the value at present |
| EDs | effective dimension | A parameter to measure the complexity of the spatial model. A larger number indicates more variables in the model |
| IDC | iron deficiency chlorosis | A nutrient deficiency with yellowing symptoms of the soybean foliage and stunting of the plant |
| METs | multiple environmental trials (METs) analysis | Statistical method to estimate genotypes by environments |
| mvngGrAd | moving grid adjustment | Mvnggrad package allows performing a moving grid adjustment in plant breeding field trials |
| LMT | Lagrange multiplier test | LMT fits a linear regression model to examine whether the fitted model is significant |
| OLR | ordinary least squares | A linear least-squares method for estimating the unknown parameters in a linear regression model |
| RCBD | randomized complete block design | Standard design for agricultural experiments where similar experimental units are grouped into blocks or replicate |
| RE | relative efficiency | It was used to compare experimental design efficiency |
| RRV | Red River Valley | North American region that is drained by the Red River and is soybean IDC-prone |
| RSE | residual standard error | To measure how well a regression model fits a dataset |
| SAR | geospatial autoregressive regression | A group of models to adjust geospatial variations |
| SpATS | spatial analysis of field trials with splines | Field variation and autocorrelation adjustment model |
| Spdep | spatial dependence | R package to analyze spatial autocorrelation |
References
- Lin, S.F.; Baumer, J.S.; Ivers, D.; de Cianzio, S.R.; Shoemaker, R.C. Field and nutrient solution tests measure similar mechanisms controlling iron deficiency chlorosis in soybean. Crop Sci. 1998, 38, 254–259. [Google Scholar] [CrossRef]
- Goos, R.J.; Johnson, B.E. A comparison of three methods for reducing iron-deficiency chlorosis in soybean. Agron. J. 2000, 92, 1135–1139. [Google Scholar] [CrossRef]
- YChart. US Soybeans Acres Planted. Available online: https://ycharts.com/indicators/us_soybeans_acres_planted (accessed on 10 July 2020).
- Froehlich, D.M.; Niebur, W.S.; Fehr, W.R. Yield reduction from iron deficiency chlorosis in soybeans. In Agronomy Abstracts; American Society of Agronomy: Madison, WI, USA, 1980; pp. 54–55. [Google Scholar]
- Hansen, N.C.; Schmitt, M.A.; Anderson, J.E.; Strock, J.S. Iron deficiency of soybean in the upper midwest and associated soil properties. Agron. J. 2003, 95, 1595–1601. [Google Scholar] [CrossRef]
- Hansen, N.C.; Jolley, V.D.; Naeve, S.L.; Goos, R.J. Iron deficiency of soybean in the north central us and associated soil properties. Soil Sci. Plant Nutr. 2004, 50, 983–987. [Google Scholar] [CrossRef]
- Niebur, W.S.; Fehr, W.R. Agronomic evaluation of soybean genotypes resistant to iron-deficiency chlorosis. Crop Sci. 1981, 21, 551–554. [Google Scholar] [CrossRef]
- Cianzio, S.R.d.; Fehr, W.R.; Anderson, I.C. Genotypic evaluation for iron deficiency chlorosis in soybeans by visual scores and chlorophyll concentration. Crop Sci. 1979, 19, 644–646. [Google Scholar] [CrossRef]
- Gaspar, P. Management of Soybeans on Soils Prone to Iron Deficiency Chlorosis. Available online: https://www.pioneer.com/us/agronomy/iron_deficiency_chlorosis.html#IntroductionofIronDeficiencyChlorosis_1 (accessed on 1 September 2019).
- Spehar, C.R. Field screening of soya bean (glycine-max (l) merrill) germplasm for aluminum tolerance by the use of augmented design. Euphytica 1994, 76, 203–213. [Google Scholar] [CrossRef]
- Clarke, G.P.Y.; Stefanova, K.T. Optimal design for early-generation plant-breeding trials with unreplicated or partially replicated test lines. (report). Aust. N. Z. J. Stat. 2011, 53, 461. [Google Scholar] [CrossRef]
- Williams, E.R.; John, J.A.; Whitaker, D. Construction of more flexible and efficient p-rep designs. Aust. N. Z. J. Stat. 2014, 56, 89–96. [Google Scholar] [CrossRef]
- Moehring, J.; Williams, E.R.; Piepho, H.P. Efficiency of augmented p-rep designs in multi-environmental trials. Theor. Appl. Genet. 2014, 127, 1049–1060. [Google Scholar] [CrossRef]
- Williams, E.; Piepho, H.P.; Whitaker, D. Augmented p-rep designs. Biom. J. 2011, 53, 19–27. [Google Scholar] [CrossRef] [PubMed]
- Piepho, H.P.; Buchse, A.; Truberg, B. On the use of multiple lattice designs and alpha-designs in plant breeding trials. Plant Breed. 2006, 125, 523–528. [Google Scholar] [CrossRef]
- Yau, S.K. Efficiency of alpha-lattice designs in international variety yield trials of barley and wheat. J. Agric. Sci. 1997, 128, 5–9. [Google Scholar] [CrossRef]
- Anselin, L.; Rey, S.J. Perspectives on Spatial Data Analysis; Advances in Spatial Science, The Regional Science Series; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Mobley, L.R.; Root, E.; Anselin, L.; Lozano-Gracia, N.; Koschinsky, J. Spatial analysis of elderly access to primary care services. Int. J. Health Geogr. 2006, 5, 19. [Google Scholar] [CrossRef][Green Version]
- Anselin, L. How (not) to lie with spatial statistics. Am. J. Prev. Med. 2006, 30, S3–S6. [Google Scholar] [CrossRef]
- Anselin, L.; Florax, R.J.G.M.; Rey, S.J. Advances in Spatial Econometrics: Methodology, Tools and Applications; Springer: Berlin/Heidelberg, Germany, 2004; p. xxii. 513p. [Google Scholar]
- Anselin, L. Spatial Econometrics. In A Companion to Theoretical Econometrics; Blackwell Publishing Ltd.: Hoboken, NJ, USA, 2003; p. xvii. 709p. [Google Scholar]
- Ugrinowitsch, C.; Fellingam, G.W.; Ricard, M.D. Limitations of ordinary least square models in analyzing repeated measures data. Med. Sci. Sports Exerc. 2004, 36, 2144–2148. [Google Scholar] [CrossRef]
- Clarke, F.R.; Baker, R.J.; Depauw, R.M. Moving mean and least-squares smoothing for analysis of grain-yield data. Crop Sci. 1994, 34, 1479–1483. [Google Scholar] [CrossRef]
- Rosielle, A.A. Comparison of lattice designs, check plots, and moving means in wheat breeding trials. Euphytica 1980, 29, 129–133. [Google Scholar] [CrossRef]
- Townleysmith, T.F.; Hurd, E.A. Use of moving means in wheat yield trials. Can. J. Plant Sci. 1973, 53, 447–450. [Google Scholar] [CrossRef]
- Diers, B.W.; Voss, B.K.; Fehr, W.R. Moving-mean analysis of field-tests for iron efficiency of soybean. Crop Sci. 1991, 31, 54–56. [Google Scholar] [CrossRef]
- Mak, C.; Harvey, B.L.; Berdahl, J.D. Evaluation of control plots and moving means for error control in barley nurseries. Crop Sci. 1978, 18, 870–873. [Google Scholar] [CrossRef]
- Technow, F. R Package mvngGrAd: Moving Grid Adjustment in Plant Breeding Field Trials. R package version 0.1. Available online: https://mran.microsoft.com/snapshot/2016-01-22/web/packages/mvngGrAd/mvngGrAd.pdf (accessed on 20 July 2022).
- Dormann, E.; Wokrina, T. Anisotropy and spatial restriction of conduction electron diffusion in perylene radical cation salt. Synth. Met. 1997, 86, 2183–2184. [Google Scholar] [CrossRef]
- Lado, B.; Matus, I.; Rodriguez, A.; Inostroza, L.; Poland, J.; Belzile, F.; del Pozo, A.; Quincke, M.; Castro, M.; von Zitzewitz, J. Increased Genomic Prediction Accuracy in Wheat Breeding Through Spatial Adjustment of Field Trial Data. G3-Genes Genomes Genet. 2013, 3, 2105–2114. [Google Scholar] [CrossRef] [PubMed]
- Tobler, W.R. Smooth pycnophylactic interpolation for geographical regions. J. Am. Stat. Assoc. 1979, 74, 519–530. [Google Scholar] [CrossRef]
- Dormann, C.F. Effects of incorporating spatial autocorrelation into the analysis of species distribution data. Glob. Ecol. Biogeogr. 2007, 16, 129–138. [Google Scholar] [CrossRef]
- Gleeson, A.C.; Cullis, B.R. Residual maximum-likelihood (reml) estimation of a neighbor model for field experiments. Biometrics 1987, 43, 277–288. [Google Scholar] [CrossRef]
- Cullis, B.R.; Gleeson, A.C. Spatial-analysis of field experiments-an extension to 2 dimensions. Biometrics 1991, 47, 1449–1460. [Google Scholar] [CrossRef]
- Hu, X.Y.; Spilke, J. Comparison of various spatial models for the analysis of cultivar trials. N. Z. J. Agric. Res. 2009, 52, 277–287. [Google Scholar] [CrossRef]
- Wilkinson, G.N.; Eckert, S.R.; Hancock, T.W.; Mayo, O. Nearest neighbour (NN) analysis of field experiments. J. R. Stat. Soc. Ser. B-Stat. Methodol. 1983, 45, 151–211. [Google Scholar] [CrossRef]
- Piepho, H.P.; Richter, C.; Williams, E. Nearest neighbour adjustment and linear variance models in plant breeding trials. Biom. J. 2008, 50, 164–189. [Google Scholar] [CrossRef]
- Ainsley, A.E.; Dyke, G.V.; Jenkyn, J.F. Inter-plot interference and nearest-neighbor analysis of field experiments. J. Agric. Sci. 1995, 125, 1–9. [Google Scholar] [CrossRef]
- Federer, W.T. Recovery of interblock, intergradient, and intervariety information in incomplete block and lattice rectangle designed experiments. Biometrics 1998, 54, 471–481. [Google Scholar] [CrossRef][Green Version]
- Kempton, R.; Mead, R.; Engel, B.; ter Braak, C.J.F.; Nelder, J.A.; Morton, R.; Green, P.; Molenberghs, G.; Basford, K.; Longford, N.T.; et al. The analysis of designed experiments and longitudinal data by using smoothing splines-Discussion. J. R. Stat. Soc. Ser. C-Appl. Stat. 1999, 48, 300–311. [Google Scholar]
- Gilmour, A.R.; Cullis, B.R.; Verbyla, A.P. Accounting for Natural and Extraneous Variation in the Analysis of Field Experiments. J. Agric. Biol. Environ. Stat. 1997, 2, 269–293. [Google Scholar] [CrossRef]
- Stefanova, K.T.; Smith, A.B.; Cullis, B.R. Enhanced Diagnostics for the Spatial Analysis of Field Trials. J. Agric. Biol. Environ. Stat. 2009, 14, 392–410. [Google Scholar] [CrossRef]
- Dhrymes, P. Introductory Econometrics by Phoebus Dhrymes, 1st ed.; Imprint; Springer International Publishing: Cham, Switzerland, 2017. [Google Scholar]
- Cappa, E.P.; Cantet, R.J.C. Bayesian estimation of a surface to account for a spatial trend using penalized splines in an individual-tree mixed model. Can. J. For. Res.-Rev. Can. De Rech. For. 2007, 37, 2677–2688. [Google Scholar] [CrossRef]
- Cappa, E.P.; Lstiburek, M.; Yanchuk, A.D.; El-Kassaby, Y.A. Two-dimensional penalized splines via Gibbs sampling to account for spatial variability in forest genetic trials with small amount of information available. Silvae Genet. 2011, 60, 25–35. [Google Scholar] [CrossRef][Green Version]
- Rodríguez-Álvarez, M.X.; Boer, M.P.; van Eeuwijk, F.A.; Eilers, P.H.C. Spatial Models for Field Trials. arXiv 2016, arXiv:1607.08255. [Google Scholar]
- Velazco, J.G.; Rodriguez-Alvarez, M.X.; Boer, M.P.; Jordan, D.R.; Eilers, P.H.C.; Malosetti, M.; van Eeuwijk, F.A. Modelling spatial trends in sorghum breeding field trials using a two-dimensional P-spline mixed model. Theor. Appl. Genet. 2017, 130, 1375–1392. [Google Scholar] [CrossRef]
- Chen, Y. New approaches for calculating Moran’s index of spatial autocorrelation. PLoS ONE 2013, 8, e68336. [Google Scholar] [CrossRef]
- Frank, E.; Harrell, J. Regression Modeling Strategies, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2015; p. 582. [Google Scholar]
- Bivand, R.S. Applied Spatial Data Analysis with R by Roger S. Bivand, Edzer Pebesma, Virgilio Gómez-Rubio, 2nd ed.; Imprint; Springer: New York, NY, USA, 2013. [Google Scholar]
- Bivand, R.; Piras, G. Comparing Implementations of Estimation Methods for Spatial Econometrics. J. Stat. Softw. 2015, 63, 1–36. [Google Scholar] [CrossRef]
- Butler, D.G.; Cullis, B.R.; Gilmour, A.R.; Gogel, B.G.; Thompson, R. ASReml-R Reference Manual Version 4; VSN International Ltd.: Hemel Hempstead, UK, 2017. [Google Scholar]
- Rodríguez-Álvarez, M. Correcting for spatial heterogeneity in plant breeding experiments with P-splines. Spat. Stat. 2018, 23, 52–71. [Google Scholar] [CrossRef]
- Bivand, R. Implementing Spatial Data Analysis Software Tools in R. Geogr. Anal. 2006, 38, 23–40. [Google Scholar] [CrossRef]
- Baltagi, B.H.; Liu, L. Testing for random effects and spatial lag dependence in panel data models. Stat. Probab. Lett. 2008, 78, 3304–3306. [Google Scholar] [CrossRef]
- Anselin, L.; Moreno, R. Properties of tests for spatial error components. Reg. Sci. Urban Econ. 2003, 33, 595–618. [Google Scholar] [CrossRef]
- Bekti, R. Sutikno. Spatial Durbin model to identify influential factors of diarrhea. J. Math. Stat. 2012, 8, 396–402. [Google Scholar]
- Dormann, C.F.; McPherson, J.M.; Araújo, M.B.; Bivand, R.; Bolliger, J.; Carl, G.; Davies, R.G.; Hirzel, A.; Jetz, W.; Kissling, W.D.; et al. Methods to Account for Spatial Autocorrelation in the Analysis of Species Distributional Data: A Review. Ecography 2007, 30, 609–628. [Google Scholar] [CrossRef]
- Butler, D.G.; Cullis, B.R.; Gilmour, A.R.; Gogel, B.J. Mixed Models for S Language Environments ASReml-R Reference Manual; Department of Primary Industries and Fisheries: Brisbane, Australia, 2009.
- Lee, D.J.; Durban, M.; Eilers, P. Efficient two-dimensional smoothing with P-spline ANOVA mixed models and nested bases. Comput. Stat. Data Anal. 2013, 61, 22–37. [Google Scholar] [CrossRef]
- Ebeling, H.; White, D.A.; Rangarajan, F.V.N. ASMOOTH: A simple and efficient algorithm for adaptive kernel smoothing of two-dimensional imaging data. Mon. Not. R. Astron. Soc. 2006, 368, 65–73. [Google Scholar] [CrossRef]
- Gareth, J.; Daniela, W.; Trevor, H.; Robert, T. An Introduction to Statistical Learning with Applications in R, 1st ed.; Imprint; Springer: New York, NY, USA, 2013. [Google Scholar]
- Fortin, M.-J.; Dale, M.R.T. Spatial autocorrelation in ecological studies: A legacy of solutions and myths. Geogr. Anal. 2009, 41, 392. [Google Scholar] [CrossRef]
- Bivand, R.; Müller, W.G.; Reder, M. Power calculations for global and local Moran’s I. Comput. Stat. Data Anal. 2009, 53, 2859–2872. [Google Scholar] [CrossRef]
- Clewer, A.G.; Scarisbrick, D.H. Practical Statistics and Experimental Design for Plant and Crop Science; John Wiley & Sons: Chichester, UK; New York, NY, USA, 2001. [Google Scholar]
- Nychka, D. Tools for Spatial Data. 2016. Available online: http://www.image.ucar.edu/fields/ (accessed on 1 August 2022). [CrossRef]
- Ostertagova, E.; Ostertag, O.; Kováč, J. Methodology and application of the Kruskal-Wallis test. In Applied Mechanics and Materials; Trans Tech Publications Ltd.: Wollerau, Switzerland, 2014; pp. 115–120. [Google Scholar]
- de Mendiburu, F.; de Mendiburu, M.F. Package ‘agricolae’. R Package Version 2019. Available online: https://CRAN.R-project.org/package=agricolae (accessed on 20 July 2022).
- Abd El-Mohsen, A.A.; Abo-Hegazy, S.R.E. Comparing the Relative Efficiency of Two Experimental Designs in Wheat Field Trials. Egypt. J. Plant Breed. 2013, 17, 1–17. [Google Scholar] [CrossRef]
- Rodríguez-Álvarez, M.X.; Lee, D.-J.; Kneib, T.; Durbán, M.; Eilers, P. Fast smoothing parameter separation in multidimensional generalized P-splines: The SAP algorithm. Stat. Comput. 2015, 25, 941–957. [Google Scholar] [CrossRef]
- Mead, R.; Gilmour, S.G.; Mead, A. Statistical Principles for the Design of Experiments. Introduction; Cambridge University Press: Cambridge, UK, 2012; pp. 3–8. [Google Scholar]
- Knorzer, H.; Hartung, K.; Piepho, H.P.; Lewandowski, I. Assessment of variability in biomass yield and quality: What is an adequate size of sampling area for miscanthus? Glob. Change Biol. Bioenergy 2013, 5, 572–579. [Google Scholar] [CrossRef]
- Casler, M.D. Finding Hidden Treasure: A 28-Year Case Study for Optimizing Experimental Designs. Commun. Biometry Crop Sci. 2013, 8, 23–28. [Google Scholar]
- Sripathi, R.; Conaghan, P.; Grogan, D.; Casler, M.D. Spatial Variability Effects on Precision and Power of Forage Yield Estimation. Crop Sci. 2017, 57, 1383–1393. [Google Scholar] [CrossRef]



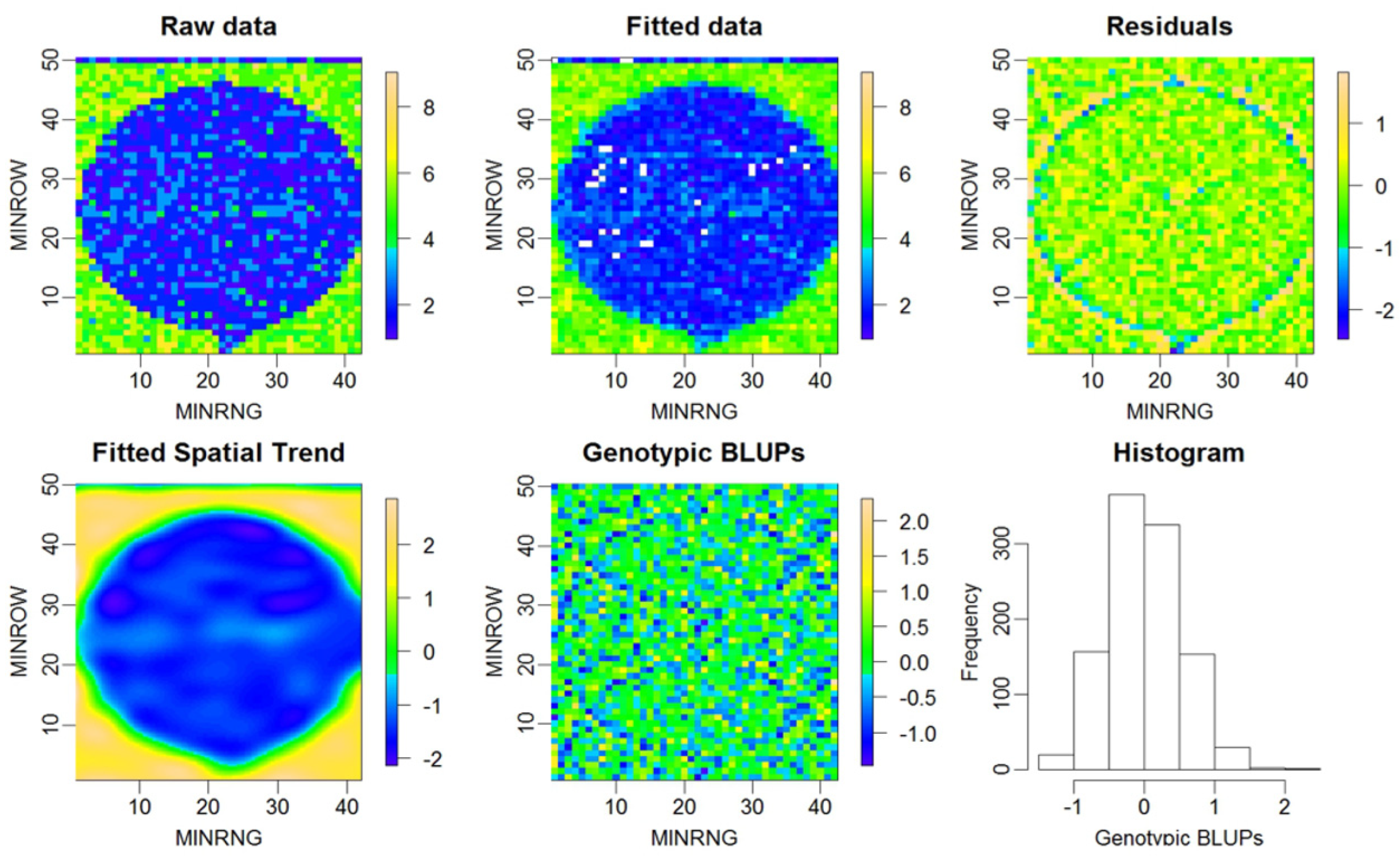
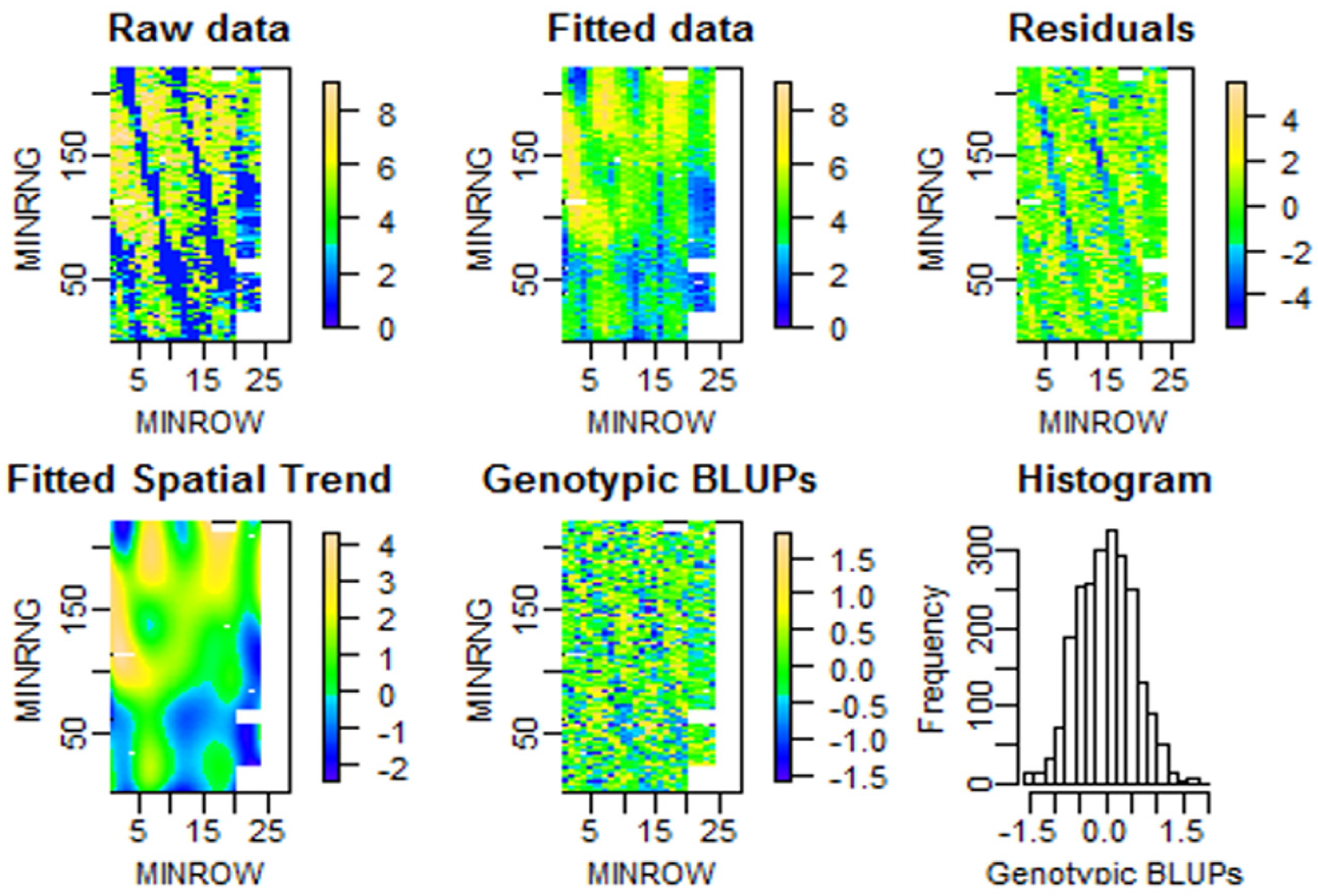
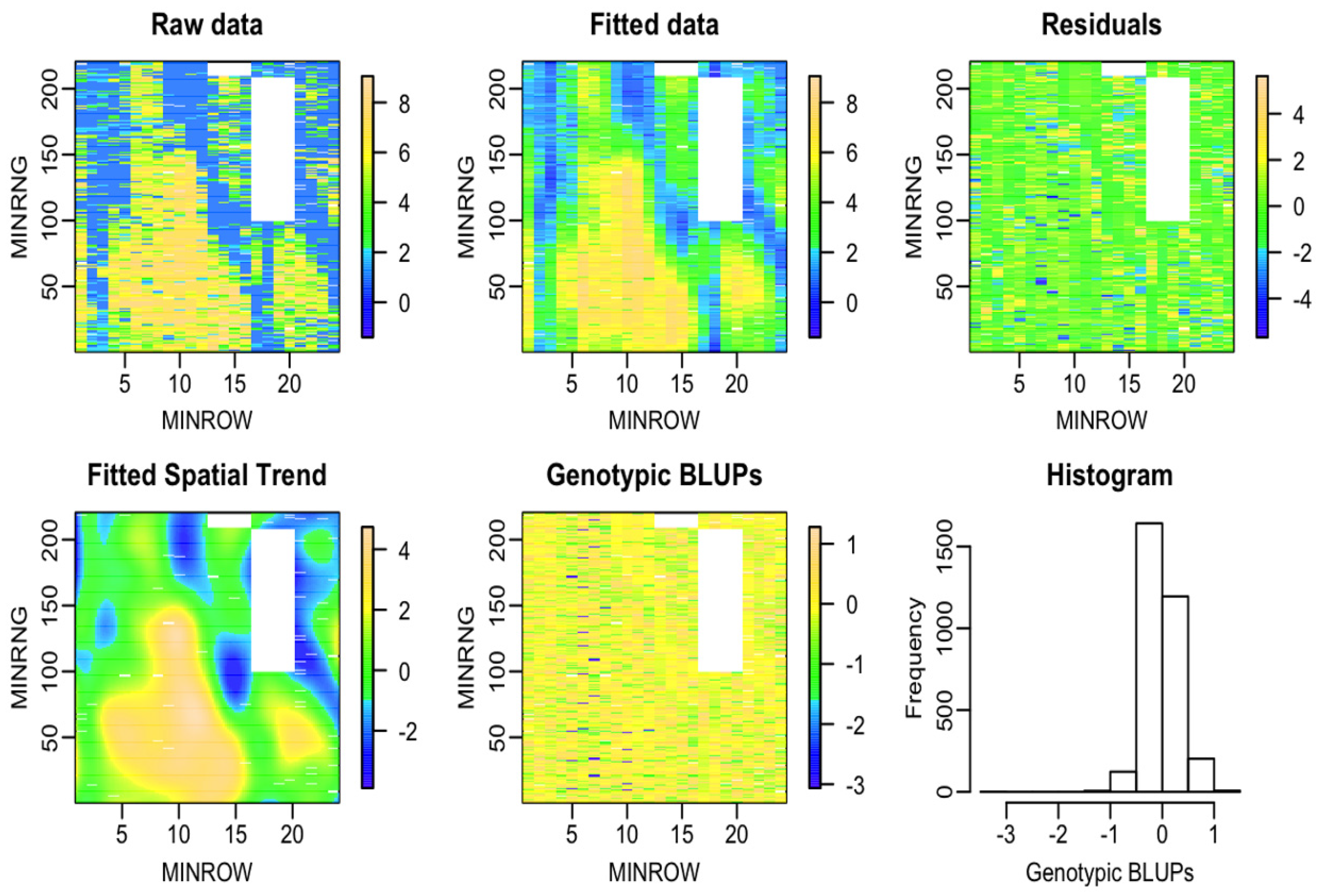
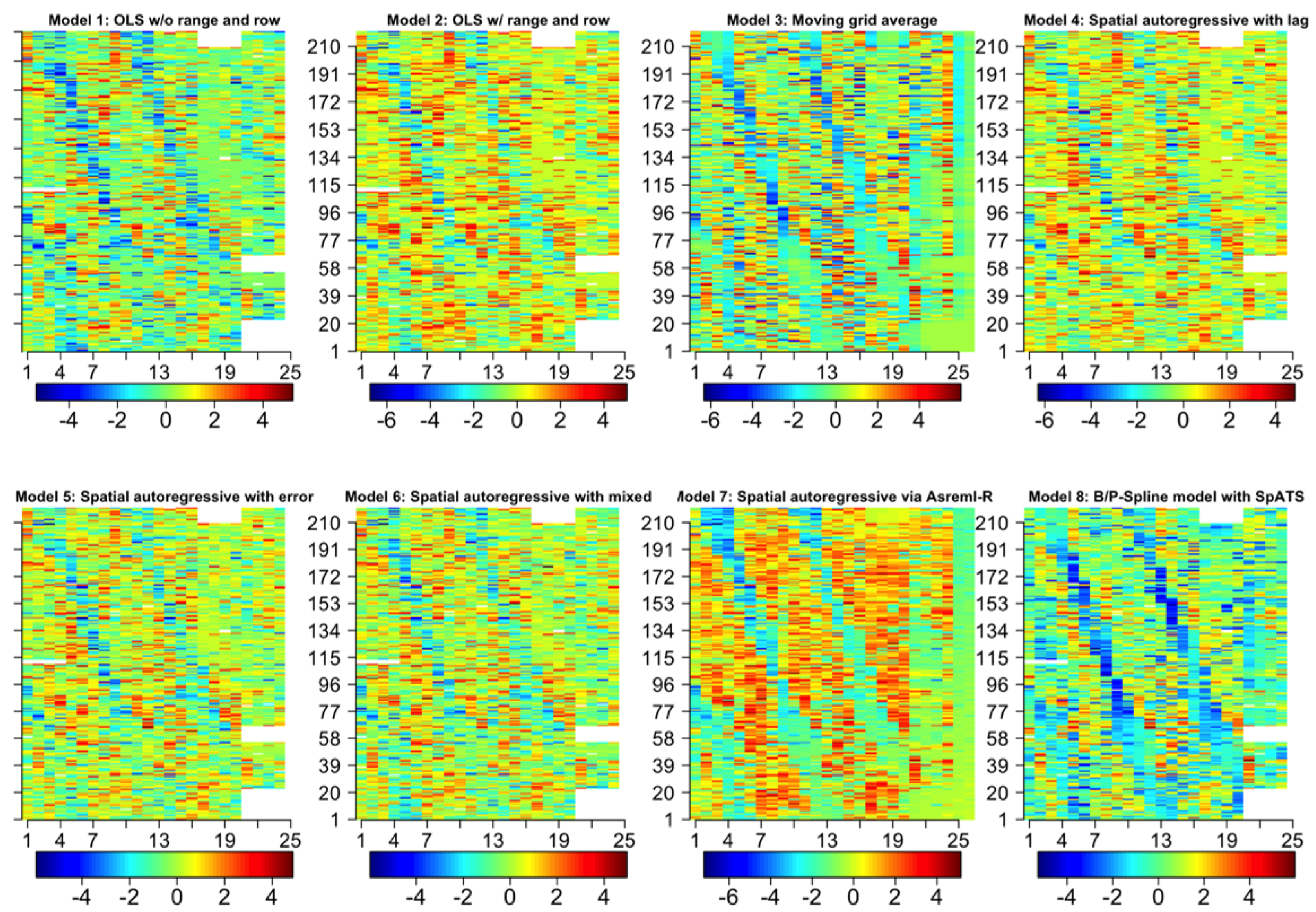
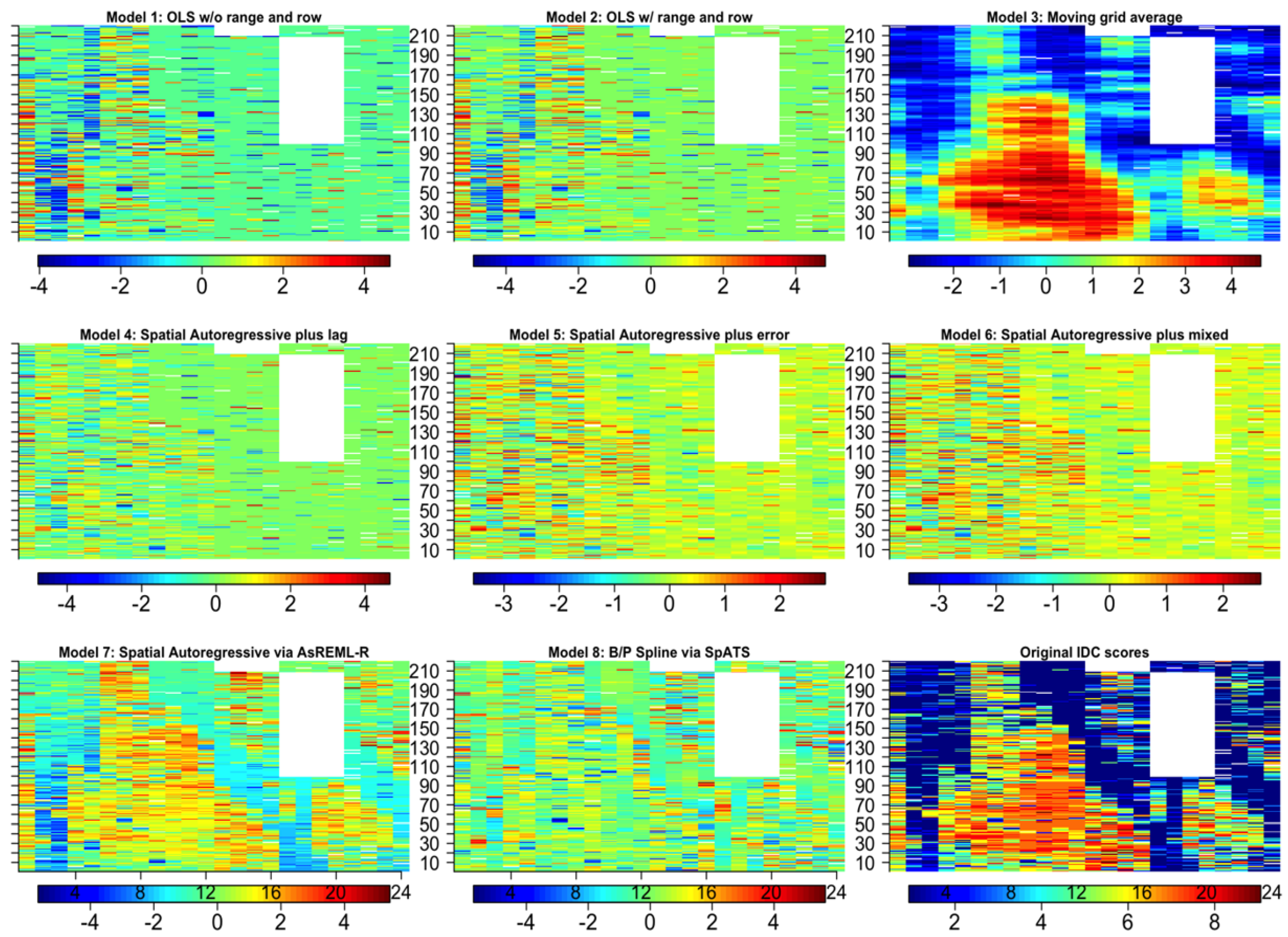

| Dataset Name | Exp. Design | No. Rows | No. Range | No. Entries | Ave No. Replicates | No. Plots | Data Sources | Spatial correction |
|---|---|---|---|---|---|---|---|---|
| Dataset 1 | RCBD | 50 | 42 | 1050 | 2.00 | 2100 | Simulated | Corrected |
| Dataset 2 | α-lattice | 220 | 26 | 2774 | 1.83 | 5074 | Iowa | Corrected |
| Dataset 3 | α-lattice | 24 | 220 | 2652 | 1.79 | 5280 | Minnesota | Corrected |
| Dataset 4 | α-lattice | 110 | 56 | 2719 | 1.88 | 5124 | RRV | No |
| Dataset 5 | α-lattice | 100 | 60 | 2407 | 1.81 | 4362 | Nebraska | No |
| Total | 504 | 404 | 11,602 | 1.84 | 21,401 |
| Variance Component | Variance | Distribution | Percentage of SD (%) |
|---|---|---|---|
| Location SD | 1.5 | Normal | 14.42 |
| Experiment SD | 0.5 | Poisson | 4.81 |
| Line SD | 2.1 | Normal | 20.19 |
| Range SD | 0.2 | Normal | 1.92 |
| Row SD | 1.0 | Normal | 9.62 |
| Rep SD | 0.1 | Normal | 0.96 |
| Pattern_SD | 3.8 | Normal | 36.54 |
| Residual | 1.2 | Normal | 11.54 |
| Model Name | Model No | Spatial Term | R Package | Reference |
|---|---|---|---|---|
| OLS w/o RR | M1 | None | RMS | [49] |
| OLS w/RR | M2 | None | RMS | [49] |
| MovingGrid | M3 | Mean of grid | mvngGrAd | [28] |
| SAR + lag | M4 | Lag | spdep | [50] |
| SAR + error | M5 | Error | spdep | [50] |
| SAR Durbin | M6 | Lag+ Error | spatialreg | [51] |
| ASReml AR1 | M7 | AR1(range): AR1(row) | ASReml-R | [52] |
| B/P-Spline | M8 | psanova(range, row) | SpATS | [53] |
| Variables Name | Data Set 1 | Data Set 2 | Data Set 3 | |||
|---|---|---|---|---|---|---|
| EDs | EDm | EDs | EDm | EDs | EDm | |
| Range | 10.1 | 42 | 0.0 | 220 | 24.6 | 221 |
| Row | 41.1 | 50 | 13.9 | 28 | 17.6 | 24 |
| Row:Range | 1.0 | 1 | 1.0 | 1 | 1.0 | 1 |
| F(Range) | 3.0 | 11 | 7.0 | 11 | 5.8 | 11 |
| F(Row) | 2.3 | 11 | 6.6 | 11 | 3.3 | 11 |
| F(Range):Row | 0.0 | 11 | 6.5 | 11 | 5.8 | 11 |
| Range:F(Row) | 1.8 | 11 | 1.6 | 11 | 10.0 | 11 |
| F(Range):F(Row) | 83.3 | 121 | 28.9 | 36 | 79.7 | 121 |
| % F(Range):F(Row) | 58.42 | 46.90 | 44.12 | 10.94 | 53.92 | 29.44 |
| Total | 142.6 | 258 | 65.5 | 329 | 147.8 | 411 |
| Variables | Type | Data Set 1 | Data Set 2 | Data Set 3 | Mean | |||
|---|---|---|---|---|---|---|---|---|
| Var | % Var | Var | % Var | Var | % Var | % Var | ||
| LINCD | R | 0.43 | 0.10 | 0.71 | 0.01 | 0.46 | 0.05 | 0.05 |
| Range | R | 0.01 | 0.00 | 0.00 | 0.00 | 0.02 | 0.00 | 0.00 |
| Row | R | 0.07 | 0.02 | 0.20 | 0.00 | 0.78 | 0.08 | 0.03 |
| f(RANGE) | S | 4.97 | 1.15 | 39.05 | 0.59 | 13.09 | 1.39 | 1.04 |
| f(ROW) | S | 55.63 | 12.89 | 223.32 | 3.39 | 14.92 | 1.58 | 5.95 |
| f(RANGE):ROW | S | 0.31 | 0.07 | 352.16 | 5.34 | 32.58 | 3.45 | 2.95 |
| RANGE:f(ROW) | S | 0.55 | 0.13 | 66.26 | 1.00 | 737.68 | 78.13 | 26.42 |
| f(RANGE):f(ROW) | S | 369.15 | 85.56 | 5912.83 | 89.63 | 142.97 | 15.14 | 63.44 |
| Residual | R | 0.34 | 0.08 | 2.61 | 0.04 | 1.67 | 0.18 | 0.10 |
| total | 431.47 | 100.00 | 6597.15 | 100.00 | 944.18 | 100.00 | 100.00 | |
| Models Compared | R2 Values | AIC Values | Residual SE * | Moran’s I Index | p-Value of Moran’s I | Prediction Accuracy I | Prediction Accuracy II |
|---|---|---|---|---|---|---|---|
| OLS w/o RR | 0.5200 | 8978 | 1.7590 | 0.5151 | 2.2 × 10−16 | 0.7200 | 0.6882 |
| OLS w/RR | 0.6862 | 6630 | 1.0060 | 0.5159 | 2.2 × 10−16 | 0.9200 | 0.6192 |
| MovingGrid | 0.3409 | 261 | 1.0631 | 0.9492 | 2.2 × 10−16 | 0.6246 | 0.6246 |
| SAR + lag | 0.6580 | 7794 | 0.8476 | 0.4575 | 2.2 × 10−16 | 0.8846 | 0..4146 |
| SAR + error | 0.6811 | 7658 | 0.8017 | 0.4599 | 2.2 × 10−16 | 0.8977 | 0.4279 |
| SAR + mixed | 0.6780 | 7646 | 0.7771 | 0.0349 | 0.02179 | 0.9052 | 0.4422 |
| ASReml AR1 | 0.7289 | 2325 ** | 0.6364 | 0.2681 | 2.2 × 10−16 | 0.8538 | 0.3581 |
| P-Spline | 0.8931 | 10,065 | 0.5582 | 0.0748 | 5.21 × 10−7 | 0.9473 | 0.5124 |
| Models Compared | R2 Value | AIC Value | RSE Value | Moran’s I Index | P-Value Moran’s I | Prediction Accuracy 1 | Prediction Accuracy 2 |
|---|---|---|---|---|---|---|---|
| OLS w/o RR | 0.666 | 22,657 | 1.937 | 0.2148 | 2.2 × 10−16 | 0.9428 | 0.8295 |
| OLS w/RR | 0.648 | 22,793 | 1.923 | 0.2131 | 2.2 × 10−16 | 0.9429 | 0.8283 |
| MovingGrid | 0.385 | 6788 | 1.8094 | 0.8664 | 2.2 × 10−16 | 0.5839 | 0.7426 |
| SAR + lag | 0.685 | 22,521 | 1.3458 | 0.1655 | 2.2 × 10−16 | 0.8356 | 0.5540 |
| SAR + error | 0.715 | 22,479 | 1.3080 | 0.1518 | 2.2 × 10−16 | 0.8457 | 0.5752 |
| SAR + mixed | 0.701 | 22,581 | 1.3408 | 0.1778 | 2.2 × 10−16 | 0.9486 | 0.8435 |
| ASReml AR1 | 0.555 | 14,689 | 1.6765 | 0.3962 | 2.2 × 10−16 | 0.8088 | 0.5033 |
| B/P-Spline | 0.565 | 50,678 | 1.6156 | 0.2639 | 2.2 × 10−16 | 0.7636 | 0.4636 |
| Model Compared | R2 Value | AIC Value | RSE Value | Moran’s I Index | P-Value of Moran’s I | Prediction Accuracy 1 | Prediction Accuracy 2 |
|---|---|---|---|---|---|---|---|
| OLS w/o RR | 0.8390 | 20,298 | 1.8440 | 0.1456 | 2.2 × 10−16 | 0.9534 | 0.8020 |
| OLS w/RR | 0.8442 | 20,145 | 1.8150 | 0.1358 | 2.2 × 10−16 | 0.9541 | 0.8033 |
| MovingGrid | 0.5685 | 5204 | 1.6790 | 0.9306 | 2.2 × 10−16 | 0.6569 | 0.4049 |
| SAR + lag | 0.9076 | 18,251 | 0.7852 | 0.0220 | 0.2330 | 0.9672 | 0.8471 |
| SAR + error | 0.9450 | 17,283 | 0.6059 | 0.0568 | 4.5 × 10−8 | 0.9723 | 0.8654 |
| SAR + mixed | 0.9491 | 17,180 | 0.5827 | 0.0826 | 1.8 × 10−15 | 0.9746 | 0.8753 |
| ASReml AR1 | 0.6399 | 12,603 | 1.5503 | 0.4233 | 2.2 × 10−16 | 0.8448 | 0.5004 |
| B/P-Spline | 0.7494 | 41,241 | 1.2935 | 0.1169 | 2.2 × 10−16 | 0.8684 | 0.5732 |
| Model Name | Model Number | RSE Rank | Least Significant Differences (LSD) Tests |
|---|---|---|---|
| OLS w/o RR | M1 | 21.67 | a |
| OLS w/RR | M2 | 17.67 | ab |
| MovingGrid | M3 | 16.00 | abc |
| ASReml AR1 | M7 | 12.00 | bcd |
| B/P-Spline | M8 | 9.33 | cd |
| SAR + lag | M4 | 9.33 | cd |
| SAR + error | M5 | 7.33 | d |
| SAR + mixed | M6 | 6.67 | d |
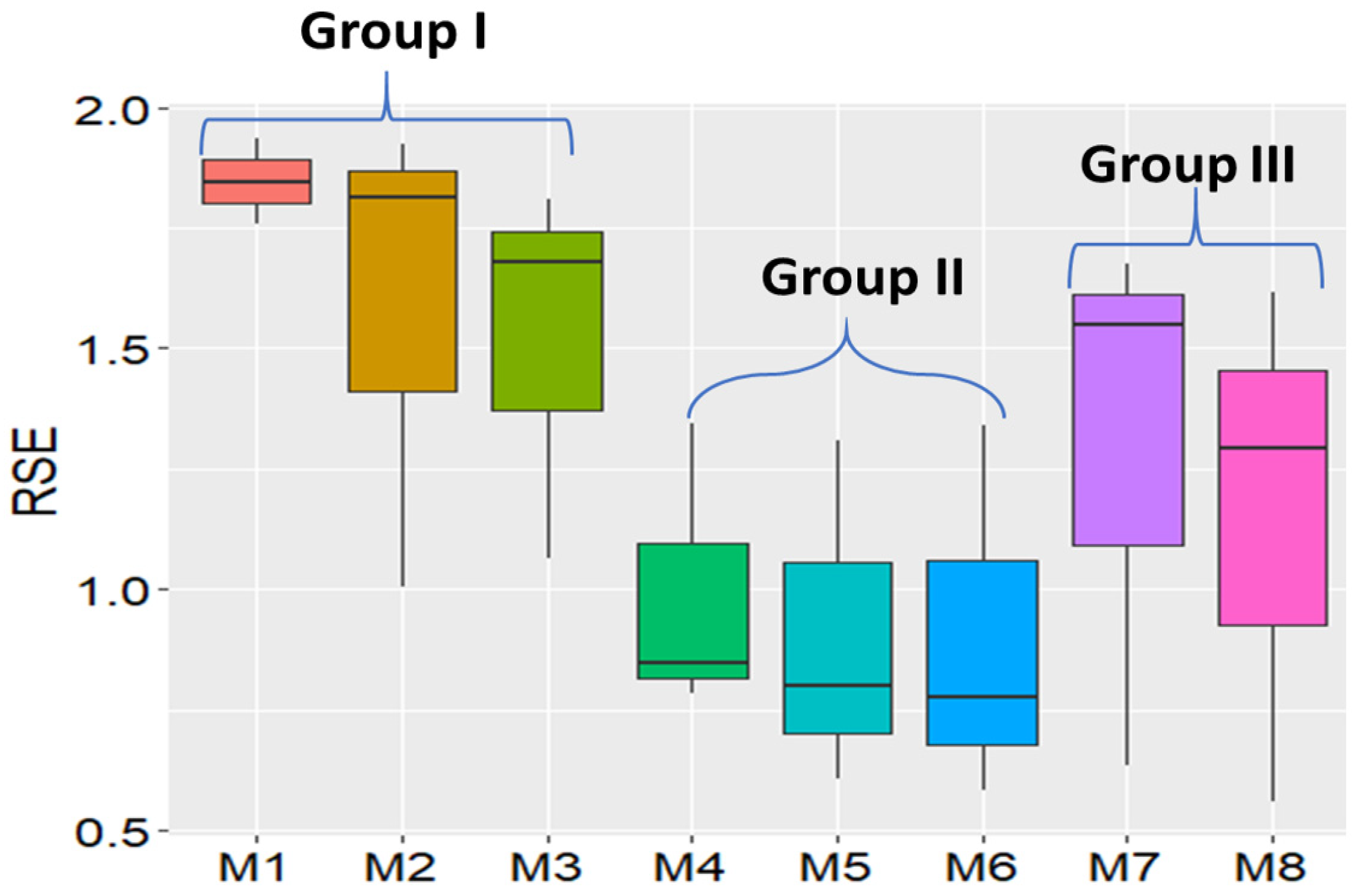
| Model Group Pairs | Mean of 1st Group | Mean of 2nd Group | Mean Difference | t-Test Stats | p-Values |
|---|---|---|---|---|---|
| Groups I vs. II | 1.78 | 0.66 | 1.12 | −6.3367 | 0.00039 |
| Groups I vs. III | 1.78 | 1.42 | 0.36 | −2.0133 | 0.08396 |
| Groups II vs. III | 0.66 | 1.42 | −0.76 | 3.5051 | 0.00993 |
| Model Name | Model Number | Mean RSE | RE to Model 1 (%) | RE to Model 2 (%) |
|---|---|---|---|---|
| OLS w/o RR | M1 | 1.8467 | 100.00 | 85.63 |
| OLS w/RR | M2 | 1.5813 | 136.37 | 100.00 |
| MovingGrid | M3 | 1.5172 | 148.15 | 104.23 |
| ASReml AR1 | M7 | 1.2877 | 205.65 | 122.80 |
| SAR + lag | M4 | 0.9929 | 345.94 | 159.27 |
| B/P-Spline | M8 | 1.1558 | 255.29 | 136.82 |
| SAR + error | M5 | 0.9052 | 416.19 | 174.69 |
| SAR + mixed | M6 | 0.9002 | 420.82 | 175.66 |
| Spatial Models | Variables Tested | Model Categories | Dependence Estimates |
|---|---|---|---|
| SAR + error | Error dependence | Spatial error model | 2730.3 |
| RLMerr | Lag variance except for LMerr | Error + possible lag | 108.98 |
| SAR + lag | Lagged variable | Spatial lag model | 2728.1 |
| RLMlag | Error variance except for LMlag | Lag + error model | 106.75 |
| SAR + mixed | Both error and lag model | Spatial Durbin mixed | 2837.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Z.; Cannon, S.B.; Beavis, W.D. Applying Spatial Statistical Analysis to Ordinal Data for Soybean Iron Deficiency Chlorosis. Agronomy 2022, 12, 2095. https://doi.org/10.3390/agronomy12092095
Xu Z, Cannon SB, Beavis WD. Applying Spatial Statistical Analysis to Ordinal Data for Soybean Iron Deficiency Chlorosis. Agronomy. 2022; 12(9):2095. https://doi.org/10.3390/agronomy12092095
Chicago/Turabian StyleXu, Zhanyou, Steven B. Cannon, and William D. Beavis. 2022. "Applying Spatial Statistical Analysis to Ordinal Data for Soybean Iron Deficiency Chlorosis" Agronomy 12, no. 9: 2095. https://doi.org/10.3390/agronomy12092095
APA StyleXu, Z., Cannon, S. B., & Beavis, W. D. (2022). Applying Spatial Statistical Analysis to Ordinal Data for Soybean Iron Deficiency Chlorosis. Agronomy, 12(9), 2095. https://doi.org/10.3390/agronomy12092095









