Abstract
Knowledge about pasture growth rates is crucial for optimizing forage use efficiencies in intensively managed pasture and silage-based dairy systems, enabling optimized cutting/grazing times for high yields with high forage quality. The aim of this study was to parameterise a simple model, GrasProg, for predicting pasture growth in an intensively managed dairy production system under a cut-and-carry management. For this, pasture crop-growth rates were measured over a period of two years (2016 and 2017) at five contrasting sites in Schleswig-Holstein, Northern Germany. The pastures received nitrogen (N) fertilizer at a rate of 280 kg N ha−1 and were cut on a four-week interval. Average annual dry matter (DM) yields ranged from 10.9 to 11.6 t/ha for the three different locations. The DM accumulation simulated by GrasProg matched actual measurements over the varying intervals well (R2 = 0.65; RMSE = 49.5 g DM m−2; and NSE = 0.44). Two model parameters were adjusted within the vegetation period, namely, the relative growth rate, a proxy of the number of generative tillers, and the initial biomass at the start of each growth period, a proxy for the tillering density. Both predicted and measured pasture growth rates showed the same typical seasonal pattern, with high growth rates in spring, followed by decreasing growth rates to the end of the vegetation period. These good calibration statistics, with adjusting of only two model parameters, for the different sites and different climatic conditions mean that GrasProg can be used to identify optimum grazing or cutting strategies, with optimal yield and forage quality.
1. Introduction
Intensive dairy-production systems in temperate climates, based on genetic selection for high per-animal production levels have traditionally relied on high proportions of maize silage and concentrated feed [1,2,3]. These systems, however, face increasing societal and political pressure to improve animal welfare [4], as well as environmental performance [5]. As a result, pasture-based production systems are currently experiencing a renaissance in promoting positive animal welfare, as well as reduced environmental impacts and additional ecosystem services [6]. In temperate regions of Europe, grasslands are covering more than one third of the agricultural area [7], and in Germany with a similar 28% share [8]. In Schleswig-Holstein, the most northern state in Germany, permanent grassland accounts for 58% of the total area used for forage production in dairying, with the majority being under a cut-and-carry system [8].
Studies have revealed that full-grazing strategies with a low share of supplementary feeding, as is common in Ireland, Australia, and New Zealand, have the lowest costs per unit of dry-matter intake, and the use of a high share of home-grown forages has the lowest feeding cost per liter of milk. Such grazing strategies are reliant on favorable environmental conditions, including mild temperatures in winter and summer, adequate and evenly distributed precipitation, as well as fertile soils [9], as found in Northwest Europe. While pasture growth in autumn and winter is temperature-limited in this region, climate change and the associated extension of the effective vegetation period for pasture growth is likely to increase forage supply from grassland [10].
While it is known that improved grazing management allows for better control of herbage growth with positive effects on production [11], the past lack of interest in pasture-based dairying in Europe has led to a knowledge gap and experience in optimal pasture management [2,11]. This includes grazing or cutting intervals, as well as tactical fertilizer and manure applications, which improve nutrient management in grassland systems, and, as such, reduce adverse environmental effects. As feeding costs are a large part of the direct costs for dairy systems, optimized grassland management to better control herbage growth, as well as prediction of herbage growth, is essential, not only for economic reasons, but also for the increasing societal pressure for resource-saving and animal welfare-oriented production.
Several studies have shown that pasture-based systems can be economically competitive with confinement systems [12,13], while also increasing the ecosystem services from dairy farming [14]. Although milk production per cow is often lower in pasture-based systems, lower feed costs [15] combined with high milk yields per ha [14] and other economic factors mean that grazing systems can represent a competitive husbandry and feeding alternative from an economic perspective, while also meeting the demand for resource-conserving and animal welfare-oriented production.
Pasture growth rates (kg DM ha−1 day−1) and, thus, the fodder supply are characterized by maximum rates in spring during the reproductive development of the grass tillers, followed by a subsequent morpho-physiological and drought-related summer depression [16,17]. In the subsequent vegetative stage, after a short recovering due to a second seasonal peak in tillering [18], growth rates decrease steadily until the end of the vegetation period, with large inter- and intra-annual fluctuations depending on temperature, and water and nutrient availability [17]. These phenological and weather-related DM growth rates are a key challenge in pasture management, as a high feed-use efficiency can only be achieved when the supply is synchronized with the feed demand of the animals [19]. Under optimal grazing, the forage utilization efficiency is around 80% [20], while under cut-and-carry systems losses are around 30% due to harvesting, ensiling, and feeding processes [21].
To optimize herbage quantity and nutritive value for animal production and to utilise the genetic potentials of the animals, grazing or cutting should be done frequently and in the early “three-leaf stage” [14,22]. This ensures excellent forage quality with high energy and protein qualities and prevents senescence of the plants. Knowledge about current and upcoming growth rates can help farmers to better manage the valuable feed resource of grasslands and to adjust the number of animals per unit area, if needed (stocking density). However, forecasting pasture growth rates is challenging, as they are determined by many interacting environmental and management factors [23]. This, and the seasonally strong fluctuations, have led to great planning uncertainties, which have contributed to the neglect of the efficient use of grasslands.
Pasture growth models are increasingly being used to aid farm management and ensure economic viability of a pasture-based dairy-production system. Models can be used to calculate plant growth rates based on environmental conditions (climate, site characteristics such as soil type, and water and nutrient availability), and management practices. Various process-based models have been developed for simulating seasonal pasture growth, with different complexity and at different hierarchical levels, from the individual plant to the field or landscape level. Complex process-based models include numerous plant–physiological functions, which are very parameter-intensive [24,25,26]. In contrast, simple empirical models use mathematical functions derived from observations and, generally, require only a few input parameters, yet can be used to make general statements about a system when used in the same environment as developed [27]. A compromise in terms of the complexity of the processes depicted are semi-mechanistic growth models, which require few input parameters and, therefore, are often used in decision-support tools [28,29]. In order to optimize forage use efficiency on pasture, model-based forecasts of average daily growth rates and software-based applications are already an integral part of practical pasture management in intensive grazing regions, such as in Ireland [29,30]. In Germany, the grassland model FOPROQ has been developed for simulating pasture growth for swards dominated by perennial ryegrass (Lolium perenne). The model has been parameterised for individual cuts depending on management/cutting regime [31,32].
The aim of the current study was to refine the FOPROQ model to enable pasture-growth simulation throughout the entire growing season rather than for only individual periods. The refined model, GrasProg, was then parameterised for intensively managed ryegrass-dominated grass swards with typical non-limiting N fertilization rates. For this, DM increment was measured weekly over a period of two years (2016/2017) from pasture sites on the three main landscape types of Schleswig-Holstein (Marshland, Geest, and Eastern Hills).
2. Materials and Methods
2.1. Study Location
The federal state of Schleswig-Holstein is located in Northern Germany and is characterized by four main landscape types: (i) a young moraine landscape in Eastern Hills with fertile sandy loam soils, (ii) an old moraine landscape in Geest, (iii) the post-glacial outwash plains of Vorgeest, and (iv) Marshland in the most western part of Schleswig-Holstein, originating from marine sediments. Soils in Eastern Hills and in Marshland are fertile, with sandy loam to silt loam textures, and those in Geest are less fertile sandy soils. Accordingly, soils in Eastern Hills and Marshland have a high plant-available water-holding capacity (PAW), and those in Geest and Vorgeest a low PAW. The latter are, therefore, more likely to experience drought-related growth limitations but can warm up faster in spring due to the coarse pores and the associated higher thermal conductivity. The soil properties of the test sites represent a typical picture of the soil types found in the landscape areas of Schleswig-Holstein (Figure 1; Table 1).
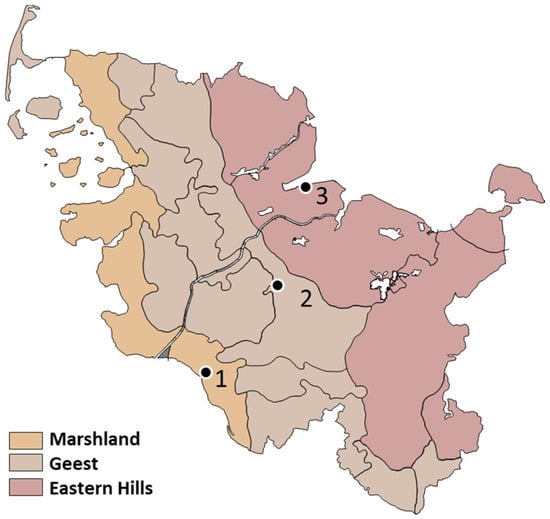
Figure 1.
Study site locations in Schleswig-Holstein, with locations 1 = Marshland, 2 = Geest and 3 = Eastern Hills.

Table 1.
Site Characteristics of the study sites, with soil classification based on the FAO system [33], with PAW (plant-available water) and C:N provided for the top 300 mm.
Schleswig-Holstein has a temperate, maritime climate, with an average annual precipitation of 833 mm and an average temperature of 8.9 °C (1981–2010) and, thus, represents typical climatic pattern relevant for grass growth ranging from Brittany in France to Jütland in Denmark. Climatic weather data were obtained from the German Meteorological Service (Deutscher Wetterdienst) from stations within close approximation to the experimental sites (≤18 km). Those were Freiburg/Elbe for Site 1, Ostenfeld (Rendsburg) for Site 2, and Kiel-Holtenau for Site 3. As the temperate and global radiation between the three stations did not vary significantly, the mean of the three stations is presented (Figure 2). For the rainfall, data for the three stations are presented separately (Figure 3). During the study years (2016 and 2017), spring and autumn were warmer than the long-term average. Based on the corrected grassland temperature sum of 200 °C [34], the onset of growth was between 20 and 24 March 2016, and between 16 and 20 March 2017, well before the long-term (1986–2015) average growth start in the beginning of April for these sites. In 2016, the average total rainfall over the three stations was 786 mm, slightly lower than the long-term average (817 mm), especially during spring and at the end of the year (Figure 3). In 2017 rainfall was above average with 980 mm, mainly due to higher rainfall in autumn. Rainfall was lowest in Eastern Hills, followed by Geest regions (on average over the two years 12% higher), and Marshland (18% higher). In both years precipitation in summer was higher than the long-term average, which, combined with favorable temperatures, led to very good growing conditions in both experimental years.
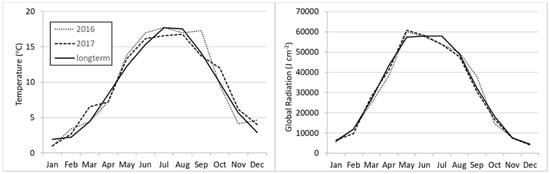
Figure 2.
Average monthly temperatures (left) and global radiation (right) for 2016 and 2017, and the long-term mean (1981–2010) from meteorological stations near the study sites.
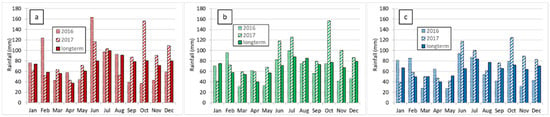
Figure 3.
Monthly rainfall for 2016 and 2017, and the long-term mean (1981–2010) from the three meteorological stations near the study sites (a) Marshland, (b) Geest, and (c) Eastern Hills.
2.2. Experimental Sites
The experiments were conducted on intensively managed perennial ryegrass–white clover dominated pastures (Lolio-Cynosuretum typicum) on commercial farms, which were grazed in the previous years. The average percentage of perennial ryegrass (Lolium perenne), was 71% in late summer. Thus, the sites can be classified as highly productive grassland. Other species present were those of typical intensively managed permanent grassland, including common bluegrass (Poa trivialis), white clover (Trifolium repens), timothy (Phleum pratense), and meadowgrass (Poa pratensis).
Within the pastures, the experimental area was excluded from grazing and arranged in a randomized complete block design with three blocks. In each block, four plots (1.5 m × 5 m) represented the series consecutively sampled after the methodology described by Corrall and Fenlon [35]. In a weekly interval dry-matter yields (DMYt; kg ha−1) of four-week-old swards were determined non-destructively using a rising plate meter (Filips Manual Folding Platemeter, Jenquip Agriworks Ltd., Feilding, New Zealand) with five measurements per plot, and using a formula derived for perennial ryegrass-dominated grassland by Trott, Ingwersen [36]:
where t is the week of measurement, a and b are constants calibrated by Trott, Ingwersen [36] as −1026 and 208, and H is the height of the compressed sward (cm).
The mean daily pasture-growth rate (GGRt) was then calculated as the moving average of four consecutive measurements following Corrall and Fenlon [35]:
Subsequent to height measurement, the plots were cut with a mower to a height of 40 mm and the biomass was removed. This cutting strategy mimicked an intensive rotational grazing system due to the regular sampling with 7–8 cuts per year. Prior to the beginning of the experiment, the sites were fertilized with 300 kg K2O ha−1, 53 kg P2O5 ha−1, and 30 kg S ha−1 to ensure ideal soil-fertility conditions [37,38]. N fertilizer application was divided into eight equal applications throughout the growing season. For each cut mineral N was applied at a rate of 35 kg N ha−1 (CAN; 13.5% nitrate and 13.5% ammonia N), which resulted in an annual application rate of 280 kg N ha−1 year−1, based on the recommended rate for intensively managed pastures, according to the rules of good agricultural practice for grazed pastures in Germany (140 kg N ha−1 year−1), and taking into account a potential N return from excrements of grazing animals [37]. Alternatively, this level of N fertilization (280 kg/ha) is also in line with the recommendations for intensively managed cut-and-carry systems and, thus, representative for the time being.
2.3. Model Description
The following provides a brief description of the GrasProg model and how the model was parameterised based on the above study sites. The model is based on the grassland model developed and parameterised for Swedish conditions [39,40,41], and the FOPROQ model (FOrage PROduction Quality [42]), which models pasture growth for individual growth periods and has been used in Germany to predict the optimum cutting date for silage production, especially in the first cut, such as a “maturity test for grassland” [43]. GrasProg calculates the daily growth rate resulting in Wt (kg DM ha−1 day−1) from the product of the existing biomass of the previous day (Wt−1), the relative growth rate (RSt, kg kg−1 day−1), and an environmental index (GI):
The initial value of Wt−1 (W0) in the model describes the existing biomass at the beginning of each growth period, and depends on yield–physiological factors, such as the photosynthetically active residual leaf area and the tiller density at the beginning of the growth period. The initial value of the relative growth rate (RS) during each growth period reflects the phenological development during the upcoming growth period of the pasture, and is related to the proportion of reproductive tillers and, thus, stem elongation and enhanced radiation use efficiency during the growth period [16]. As such, both RS and W0 are time-specific parameters, reflecting the potential productivity of a grassland sward, which is affected by the management intensity (grazing or cutting frequency) and the phenological development under non-limiting weather constraints.
Due to a declining proportion of generative shoots [44], the relative growth rate is assumed to be highest at the beginning of the growth period and to decrease thereafter. This phenomenon is accounted for via an age index (AGEt), which describes the effect of plant ageing as a function of the leaf-area index (LAI), whereby the AGE index decreases with increasing LAI:
where LAIt (m2 m−2) is calculated from Wt using two constants (b = 4.8, c = 0.008), LAI50 = 3 m2 m−2) is half the assumed maximum LAI, and a = 5.75 is a constant describing the curvature of the function. The beginning of the growth period (AGE = 1) is assumed to be reached when the temperature sum of mean daily temperatures above a base temperature of 0 °C reaches 250 °C.
The environmental index GI describes the influence of climatic conditions on plant growth and is composed of three indices, TI, RI, and WI, accounting for the limitations imposed by radiation (RI), temperature (TI), and soil water content (WI), all scaled from 0 to 1:
The radiation index (RIt) is calculated from the incident global radiation (R; MJ m−2 d−1) using a saturation function, and increasing with increasing radiation until the insolation at light saturation of the canopy (Ropt) is reached:
where cr = 2 is a constant describing the curvature of the radiation-response curve.
Ropt depends on the development of the grassland canopy:
where:
At LAI < 1 m2 m−2 (LAIlow), Ropt is low (Rlow), and at LAI > 2.5 m2 m−2 (LAIhigh) Ropt is high. Values of 22 to 32 MJ m−2 day−1 are used for Rlow and Rhigh, and dr = 3 is a constant.
The temperature index is described by:
with
where T is the average daily temperature, Tmin = 1 the minimum temperature below which no growth occurs, and (Topt = 17) the optimum temperature for maximum growth, Tmax = 42, and the constant ct = 2.
WI is calculated from the ratio of actual (ETa) to potential evapotranspiration (ETp), and a soil water index SWI:
ETp is calculated as a function of the LAI to represent the low evaporative capacity of the grassland canopy:
where ET0, is the reference evaporation rate which is calculated following FAO56 (1999).
where SWt−1 is the soil water content at any time, PAW (mm) is the plant-available water in the effective rooting zone, which is defined by the difference between the soil water content at field capacity (SWFC (mm); −10 kPa matric potential) and permanent wilting point (SWPWP; −1500 kPa).
SW is calculated via a simple soil water model with a single layer:
where P is the precipitation, D is the drainage, and SWt−1 is set to PAW at the beginning of the growth period. If precipitation is higher than the maximum daily storage capacity, any exceeding water is directly accounted for as drainage.
Model input data are meteorological factors, including global radiation (MJ/m2/day), mean daily temperature (°C), precipitation (mm/day), and evaporation (potential evaporation, mm/day), as well as PAW.
2.4. Model Calibration and Statistical Analysis
During the calibration procedure, the parameters W0 and RS were iteratively adjusted in order to minimize the mean squared residuals of measured and simulated biomass, using the R environment (Package nls “nonlinear least squares”; [45]). A mixed linear model was assumed with cut date (week), location, and year as fixed factors and block as a random factor. After a graphical residuals analysis, variance heterogeneity was found for the data. A multiple sample t-test (ANOVA) was performed to test for significant differences in the target variable between factors. Mean comparisons were performed post-hoc with multiple contrast tests. Physiologically reasonable ranges of Wt−1 (10–500 kg DM ha−2) and RS (0.1–0.9 kg kg−1 DM) were used.
The performance of GrasProg was evaluated based on common measures [46], including the coefficient of determination (R2), Nash–Sutcliffe Efficiency (NSE) and root mean square error (RMSE). Since the aim was to parameterize the model for broader use, rather than optimizing for site-specific use, location was considered as a random factor.
3. Results
3.1. Growth Rates and Annual Dry-Matter Production
The daily growth rates of the grassland show the typical pattern, with higher rates during the generative growth in spring, and drop in summer and decreasing growth rates to the end of vegetation period (Figure 4). While individual cuts had different dry-matter yields between the sites, annual yields were similar, with 10.9 t DM ha−1 for Marshland, 11.2 t DM ha−1 for Geest, and 11.6 t DM ha−1 for Eastern Hills.
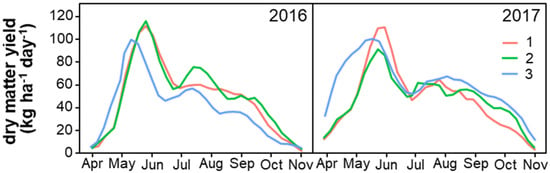
Figure 4.
Daily growth rates for the three main landscape types of Schleswig-Holstein (Marshland, Geest, and Eastern Hills) for two years (2016 and 2017) based on weekly measurements of dry-matter yields using a rising plate meter and calculated as the moving average of four consecutive measurements following Corrall and Fenlon [35].
3.2. GrasProg Calibration
The GrasProg model was calibrated based on the weekly measured biomass at the three sites and the two different years, by consecutively adjusting two parameters, namely, first RS and then W0.
For the relative growth rate throughout the growing period, an exponential function was fitted to the measured pasture growth:
with fitted values of m = 1.34, and n = −0.0558, with a Pseudo R2 of 0.8.
For the biomass at the start of each growth period (W0), a fourth-degree polynomial function as a function of week over the vegetation period was fitted to the measured biomass data (Figure 5):
with fitted values of a = −257, b = 40.3, c = −2.21, d = 0.0508, and e = −0.000413, with an adjusted R2 of 0.86.
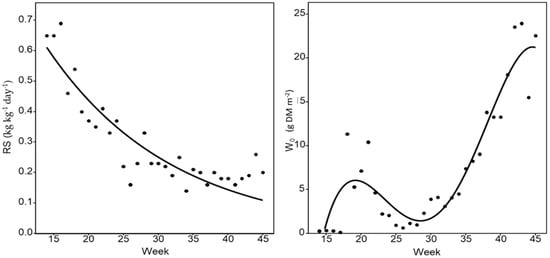
Figure 5.
Measured (dots) and fitted values for the biomass at the start of each growth period (W0; g m−2) and the relative growth rate (RS; kg kg−1 day−1) over the vegetation period, using a fourth-degree polynomial function as a function of the week of the year for W0 and an exponential function for RS.
At the beginning of the vegetation period W0 is close to zero, and the function is characterized by two maximums, one around calendar week 18 and the other one at week 44, close to the end of vegetation.
GrasProg with the fitted model parameter values (below Equations (17) and (18)) shows generally good agreement with the measured DM yields for the different cuts and locations over the vegetation period (Figure 6). In some instances, the model under-estimated the growth rate in the first period (April–May), but, generally, the model performed well with an R2 of 0.65 and RMSE of 49.5 g DM m−2 and an NSE of 0.64.
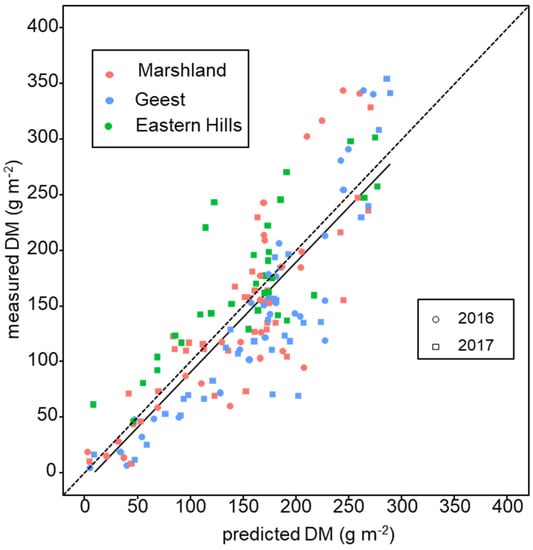
Figure 6.
Measured vs. predicted pasture biomass of different cuts for two years (2016 and 2017) and for the three main landscape types of Schleswig-Holstein (Marshland, Geest, and Eastern Hills) based on weekly measurements of dry-matter yields using a rising plate meter and calculated as the moving average of four consecutive measurements following Corrall and Fenlon [35].
4. Discussion and Conclusions
The measured patterns of biomass growth throughout the vegetation period (March to November) represent the typical seasonal growth in temperate climate regions with a characteristic asymmetric curve. Due to the above-average precipitation during summer of the experimental years, there were only slight drought-related growth deficits after the first growth peak in spring, with only short growth depressions in summer (June–July). The high precipitation also meant that annual yields between the sites were similar, ranging from an average of 10.9 to 11.6 t DM ha−1, as the PAW of the soil had negligible effects. Sufficient precipitation and above-average temperatures in spring and autumn, especially in 2017, led to an extension of the growing season. However, the generative growth of the grass sward in spring is the key factor for the high annual yield levels [47]. Under non-limiting growth conditions such high yields of perennial ryegrass are common, for example, Cashman et al. [48] observed average annual yields of 11.7 t DM ha−1 under similar experimental conditions in Ireland under simulated grazing with 10 cuts with annual N fertilization of 350 kg N ha−1. High inter-annual yield variations, due to precipitation and temperature [49,50], however, need to be accounted for in the planning of feeding strategies.
The decreasing value of RS mimics the number of generative tillers, with high values in spring during intense generative growth, and subsequent lower values during the development of new tillers. The value of W0, a proxy for the tillering density, reaches a minimum in mid-June, reflecting tiller death following defoliation of reproductive tillers in the previous cut [18,51], which results in a low production of new tillers. Following this lack of tillers in midsummer a recovery in tillering of all vegetative mother tillers until August is well documented and, thus, W0 increases. The increase in W0 can be additionally explained by the intensive management with 7–8 cuts per year, which enables high light penetration, and, thereby, promotes tillering [52].
Apart from the environmental factors described before, and included in GrasProg, N fertilization has a major influence on productivity and yield stability in temperate grassland systems [53]. The management of the study grassland sites is characterized by high N supply via mineral and organic fertilizers, with an average annual N supply in the last two years of about 230 kg N ha−1. Additional N input from grazing animals via excreta and urine ranges from 80 to 95% of the ingested N, depending on animal type, production level, and nitrogen (N) concentration of the herbage [54]. Potential N mineralization rates of these sites with narrow C:N are, thus, likely very high. This, with the good supply of basic nutrients (phosphors, potassium, and sulphur) mean that Schleswig-Holstein is a favorable region for intensively managed grassland due to the advantageous climate and site characteristics.
The semi-mechanistic GrasProg model was successful in simulating pasture growth rates at the three contrasting landscapes of Schleswig-Holstein. Model-predicted seasonal patterns also reflected the typical pattern with high growth during the generative growth in spring, and decreasing thereafter. Some discrepancies between simulation and measurement were observed, especially for the first growth period in spring. These disparities may arise from simplifications made in the model, including the temperature function and the use or air rather than soil temperature. But they may also arise from difficulties in accurately measuring herbage growth [55,56]. We conclude that the model has potential for integration into a decision-support tool. Providing predictions of future grass growth based on meteorological forecasts facilitates balancing stocking rate and feed supply for grazing herds and identifying optimum grazing or cutting strategies while ensuring high levels of pasture utilization and yields in intensive grassland production systems.
Author Contributions
Conceptualization, T.P., F.T. and F.F.; methodology, T.P., R.L. and F.F.; validation, R.L., I.V. and F.F.; formal analysis, T.P., C.K., I.V. and F.F.; investigation, T.P., I.V. and F.F.; resources, R.L.; data curation, C.K. and R.L.; writing—original draft preparation, T.P.; writing—review and editing, I.V., F.T. and F.F.; visualization, T.P., C.K. and F.F.; supervision, F.T. and R.L.; funding acquisition, F.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the European Innovation Partnership (EIPagri) within the project “Optimised pasture management-smart grazing” (EU registration number FKZ: 704.06.EIP-06-2015), and by the arismo GmbH within the project “GrasProg (Ertragsmodell Grünlandversicherung)”. The APC was funded by the German Research Foundation (DFG) within the funding programme “Open Access Publizieren”.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available upon reasonable request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Dierschke, H.; Briemle, G. Kulturgrasland–Ökosysteme Mitteleuropas aus Geobotanischer Sicht; Eugen Ulmer: Stuttgart, Germany, 2008. [Google Scholar]
- van den Pol-van Dasselaar, A.; Hennessy, D.; Isselstein, J. Grazing of Dairy Cows in Europe—An In-Depth Analysis Based on the Perception of Grassland Experts. Sustainability 2020, 12, 1098. [Google Scholar] [CrossRef] [Green Version]
- Taube, F.; Gierus, M.; Hermann, A.; Loges, R.; Schonbach, P. Grassland and globalization–challenges for north-west European grass and forage research. Grass Forage Sci. 2014, 69, 2–16. [Google Scholar] [CrossRef]
- Vogeler, C.S.; Hornung, J.; Bandelow, N.C. Farm animal welfare policymaking in the European Parliament—A social identity perspective on voting behaviour. J. Environ. Policy Plan. 2020, 22, 518–530. [Google Scholar] [CrossRef]
- Clay, N.; Garnett, T.; Lorimer, J. Dairy intensification: Drivers, impacts and alternatives. Ambio 2020, 49, 35–48. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schils, R.; Philipsen, B.; Hoekstra, N.; Holshof, G.; Zom, R.; Hoving, I.; van Reenen, K.; Stienezen, M.; Klootwijk, C.; van der Werf, J.; et al. Amazing Grazing: A Public and Private Partnership to Stimulate Grazing Practices in Intensive Dairy Systems. Sustainability 2019, 11, 5868. [Google Scholar] [CrossRef] [Green Version]
- Eurostat. LUCAS the EU’s Land Use and Land Cover Survey. Available online: https://ec.europa.eu/eurostat/statistics-explained/index.php?title=LUCAS_-_Land_use_and_land_cover_survey (accessed on 15 April 2022).
- Destatis. Bodennutzung der Betriebe-Landwirtschaftlich Genutzte Flächen-Fachserie 3 Reihe 3.1.2–2019. 2019. Available online: https://www.destatis.de/DE/Themen/Branchen-Unternehmen/Landwirtschaft-Forstwirtschaft-Fischerei/Publikationen/Bodennutzung/landwirtschaftliche-nutzflaeche-2030312197004.html (accessed on 15 April 2022).
- Smit, H.J.; Metzger, M.J.; Ewert, F. Spatial distribution of grassland productivity and land use in Europe. Agric. Syst. 2008, 98, 208–219. [Google Scholar] [CrossRef]
- Dellar, M.; Topp, C.; Banos, G.; Wall, E. A meta-analysis on the effects of climate change on the yield and quality of European pastures. Agric. Ecosyst. Environ. 2018, 265, 413–420. [Google Scholar] [CrossRef]
- Wilkinson, J.M.; Lee, M.R.F.; Rivero, M.J.; Chamberlain, A.T. Some challenges and opportunities for grazing dairy cows on temperate pastures. Grass Forage Sci. 2019, 75, 1–17. [Google Scholar] [CrossRef]
- White, S.L.; Benson, G.; Washburn, S.; Green, J. Milk Production and Economic Measures in Confinement or Pasture Systems Using Seasonally Calved Holstein and Jersey Cows. J. Dairy Sci. 2002, 85, 95–104. [Google Scholar] [CrossRef]
- Loges, R.; Mues, S.; Kluß, C.; Reinsch, T.; Lorenz, H.; Humphreys, J.; Taube, F. Eco-efficient milk production in northern Germany inspired by the Irish rotational grazing system. In Sustainable Meat and Milk Production from Grasslands, Proceedings of the 27th General Meeting of the European Grassland Federation, Cork, Ireland, 17–21 June 2018; Horan, B., Hennessy, D., O’Donovan, M., O’Donovan, O., Kennedy, E., McCarthy, B., Finn, J.A., O’Brien, B., Eds.; Wageningen Academic Publishers: Wageningen, The Netherlands, 2018. [Google Scholar]
- Reinsch, T.; Loza, C.; Malisch, C.S.; Vogeler, I.; Kluß, C.; Loges, R.; Taube, F. Proceedings of the New Zealand Society of Animal Production toward Specialized or Integrated Systems in Northwest Europe: On-Farm Eco-Efficiency of Dairy Farming in Germany. Front. Sustain. Food Syst. 2021, 5, 167. [Google Scholar]
- Dillon, P. Achieving high dry-matter intake from pasture with grazing dairy cows. Frontis 2007, 1–26. [Google Scholar]
- Taube, F. Growth Characteristics of Contrasting Varieties of Perennial Ryegrass (Lolium perenne L.). J. Agron. Crop Sci. 1990, 165, 159–170. [Google Scholar] [CrossRef]
- Wingler, A.; Hennessy, D. Limitation of grassland productivity by low temperature and seasonality of growth. Front. Plant Sci. 2016, 7, 1130. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jewiss, O.R. Tillering in grasses—Its significance and control. Grass Forage Sci. 1972, 27, 65–82. [Google Scholar] [CrossRef]
- Peyraud, J.; Delagarde, R. Managing variations in dairy cow nutrient supply under grazing. Animal 2013, 7 (Suppl. S1), 57–67. [Google Scholar] [CrossRef] [Green Version]
- Vibart, R.; Vogeler, I.; Dennis, S.; Kaye-Blake, W.; Monaghan, R.; Burggraaf, V.; Beautrais, J.; Mackay, A. A regional assessment of the cost and effectiveness of mitigation measures for reducing nutrient losses to water and greenhouse gas emissions to air from pastoral farms. J. Environ. Manag. 2015, 156, 276–289. [Google Scholar] [CrossRef] [PubMed]
- Köhler, B.; Thurner, S.; Diepolder, M.; Spiekers, H. Effiziente Futterwirtschaft und Eiweißbereitstellung in Futterbaubetrieben. In LfL-Schriftenreihe; Bayerische Landesanstalt für Landwirtschaft (LfL): Freising, Germany, 2014; ISSN 1611-4159. [Google Scholar]
- Fulkerson, W.J.; Donaghy, D.J. Plant-soluble carbohydrate reserves and senescence-Key criteria for developing an effective grazing management system for ryegrass-based pastures: A review. Aust. J. Exp. Agric. 2001, 41, 261. [Google Scholar] [CrossRef]
- Barrett, P.D.; Laidlaw, A.S.; Mayne, C.S. An evaluation of selected perennial ryegrass growth models for development and integration into a pasture management decision support system. J. Agric. Sci. 2004, 142, 327–334. [Google Scholar] [CrossRef]
- Thornley, J.H.M. Grassland Dynamics: An Ecosystem Simulation Model; CAB International: Wallingford, UK, 1998. [Google Scholar]
- Schapendonk, A.; Stol, W.; van Kraalingen, D.; Bouman, B. LINGRA, a sink/source model to simulate grassland productivity in Europe. Eur. J. Agron. 1998, 9, 87–100. [Google Scholar] [CrossRef]
- Duru, M.; Adam, M.; Cruz, P.; Martin, G.; Ansquer, P.; Ducourtieux, C.; Jouany, C.; Theau, J.; Viegas, J. Modelling above-ground herbage mass for a wide range of grassland community types. Ecol. Model. 2009, 220, 209–225. [Google Scholar] [CrossRef]
- Brereton, A.J.; O’Riordan, E. A comparison of grass growth models. In Agrometeorological Modelling: Principles, Data and Applications; AGMET: Dublin, Ireland, 2001; pp. 136–155. [Google Scholar]
- Barrett, P.D.; Laidlaw, A.S.; Mayne, C.S. GrazeGro: A European herbage growth model to predict pasture production in perennial ryegrass swards for decision support. Eur. J. Agron. 2005, 23, 37–56. [Google Scholar] [CrossRef]
- Ruelle, E.; Hennessy, D.; Delaby, L. Development of the Moorepark St Gilles grass growth model (MoSt GG model): A predictive model for grass growth for pasture based systems. Eur. J. Agron. 2018, 99, 80–91. [Google Scholar] [CrossRef]
- Hanrahan, L.; Geoghegan, A.; O’Donovan, M.; Griffith, V.; Ruelle, E.; Wallace, M.; Shalloo, L. PastureBase Ireland: A grassland decision support system and national database. Comput. Electron. Agric. 2017, 136, 193–201. [Google Scholar] [CrossRef]
- Petersen-Fredrich, E.C.; Kornher, A.; Taube, F. Ertragsbildung unterschiedlicher Sortentypen des Deutschen Weidelgrases im Vegetationsablauf in Abhaengigkeit vom Nutyungsregime. 2. Mitteilung: Modellberechnungen. Das Wirtsch. Futter 1989, 35, 289–300. [Google Scholar]
- Herrmann, A.; Kelm, M.; Kornher, A.; Taube, F. Performance of grassland under different cutting regimes as affected by sward composition, nitrogen input, soil conditions and weather—A simulation study. Eur. J. Agron. 2005, 22, 141–158. [Google Scholar] [CrossRef]
- Hartwich, R.; Haase, G.; Richter, A.; Roeschmann, G.; Schmidt, R. Bodenübersichtskarte von Deutschland 1:1.000.000. 1998. Available online: https://www.bgr.bund.de/DE/Themen/Boden/Produkte/Karten/Downloads/BUEK1000.pdf?__blob=publicationFile&v=2 (accessed on 8 May 2022).
- Ernst, P.; Loeper, E.G. Temperaturentwicklung und Vegetationsbeginn auf dem Grünland. Aus der Grünlandlehranstalt und Marschversuchsstation für Niedersachsen. Das Wirtsch. Futter 1976, 22, 5–11. [Google Scholar]
- Corrall, A.J.; Fenlon, J.S. A comparative method for describing the seasonal distribution of production from grasses. J. Agric. Sci. 1978, 91, 61–67. [Google Scholar] [CrossRef]
- Trott, H.; Ingwersen, B.; Wachendorf, M.; Taube, F. Estimation of dry matter yield on permanent grassland by means of height assessment. Pflanzenbauwissenschaften 2002, 6, 78–83. [Google Scholar]
- DLG. Düngung von Wiesen. DLG-Merkblatt 433. 2018. Available online: https://www.dlg.org/de/landwirtschaft/themen/pflanzenbau/pflanzenernaehrung/dlg-merkblatt-433-duengung-von-wiesen-weiden-und-feldfutter?msclkid=50888a50cf8b11ec88df3ba18bba181b (accessed on 7 May 2022).
- Whitehead, D.C. Nutrient Elements in Grassland: Soil-Plant-Animal Relationships; CABI Publishing: Wallingford, UK, 2000. [Google Scholar]
- Torssell, B.W.R.; Kornher, A.; Svensson, A. Optimization of Parameters in a Yield Prediction Model for Temporary Grasslands; Swedish University of Agricultural Sciences: Uppsala, Sweden, 1982. [Google Scholar]
- Kornher, A.; Torssell, B.W.R. Estimation of parameters in a yield prediction model for temporary grasslands using regional experimental data. Swed. J. Agric. Res. 1983, 13, 137–144. [Google Scholar]
- Kornher, A.; Torssell, B.W.R. Simulation of weather x management interactions in temporary grasslands in Sweden. Swed. J. Agric. Res. 1983, 13, 145–155. [Google Scholar]
- Kornher, A.; Torssell, B.W.R. Validation of a yield prediction model for temporary grasslands. Swed. J. Agric. Res. 1983, 13, 125–136. [Google Scholar]
- Herrmann, A.; Kornher, A.; Ernst, P.; Löpmeier, F.-J.; Taube, F. Reifeprüfung Grünland–Einführung des Prognosemodells in Nordrhein-Westfalen. In 46. Jahrestagung vom 29. bis 31. August 2002 in Rostock, Referate und Poster; Im Auftrag der Arbeitsgemeinschaft für Grünland und Futterbau in der Gesellschaft für Pflanzenbauwissenschaften: Rostock, Germany, 2002; pp. 222–225. [Google Scholar]
- Taube, F.; Kornher, A.; Petersen-Fredrich, E.C. Ertragsbildung unterschiedlicher Sortentypen des Deutschen Weidelgrases im Vegetationsablauf in Abhaengigkeit vom Nutyungsregime. 1. Mitteilung: Ergebnisse eines Feldversuches. Das Wirtsch. Futter 1989, 35, 278–288. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2020; Available online: https://www.R-project.org/ (accessed on 11 April 2022).
- Moriasi, D.N.; Arnold, J.G.; van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Parsons, A.J.; Chapman, D.F. The principles of pasture growth and utilization. In Grass: Its Production and Utilization; Hopkins, A., Ed.; Blackwell Science: Oxford, UK, 2000; pp. 31–89. [Google Scholar]
- Cashman, P.A.; McEvoy, M.; Gilliland, T.J.; O’Donovan, M. A comparison between cutting and animal grazing for dry-matter yield, quality and tiller density of perennial ryegrass cultivars. Grass Forage Sci. 2016, 71, 112–122. [Google Scholar] [CrossRef]
- Enriquez-Hidalgo, D.; Gilliland, T.J.; Hennessy, D. Herbage and nitrogen yields, fixation and transfer by white clover to companion grasses in grazed swards under different rates of nitrogen fertilization. Grass Forage Sci. 2016, 71, 559–574. [Google Scholar] [CrossRef]
- Vogeler, I.; Thomas, S.; van der Weerden, T. Effect of irrigation management on pasture yield and nitrogen losses. Agric. Water Manag. 2019, 216, 60–69. [Google Scholar] [CrossRef]
- Korte, C.J. Tillering in ‘Grasslands Nui’ perennial ryegrass swards 2. Seasonal pattern of tillering and age of flowering tillers with two mowing frequencies. N. Z. J. Agric. Res. 1986, 29, 629–638. [Google Scholar] [CrossRef]
- Grant, S.A.; Barthram, G.T.; Torvell, L. Components of regrowth in grazed and cut Lolium perenne swards. Grass Forage Sci. 1981, 36, 155–168. [Google Scholar] [CrossRef]
- Whitehead, D.C. The Role of Nitrogen in Grassland Productivity. A Review of Information from Temperate Regions; Commonwealth Agricultural Bureaux: Farnham Royal, UK, 1970. [Google Scholar]
- Deenen, P.J.A.G.; Middelkoop, N. Effects of cattle dung and urine on nitrogen uptake and yield of perennial ryegrass. Neth. J. Agric. Sci. 1992, 40, 469–482. [Google Scholar] [CrossRef]
- Rueda-Ayala, V.P.; Peña, J.M.; Höglind, M.; Bengochea-Guevara, J.M.; Andújar, D. Comparing UAV-based technologies and RGB-D reconstruction methods for plant height and biomass monitoring on grass ley. Sensors 2019, 19, 535. [Google Scholar] [CrossRef] [Green Version]
- Cosgrove, G.P.; Betteridge, K.; Thomas, V.J.; Corson, D.C. A sampling strategy for estimating dairy pasture quality. In Proceedings of the New Zealand Society of Animal Production; New Zealand Society of Animal Production: Online, 1998; Volume 58, pp. 25–28. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).