Statistical Approach to Assess Chill and Heat Requirements of Olive Tree Based on Flowering Date and Temperatures Data: Towards Selection of Adapted Cultivars to Global Warming
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Site and Plant Material
2.2. Climate and Phenological Records
2.3. Variability Analysis of Flowering Dates
2.4. Temperature Trends
2.5. Delineating Chilling and Forcing Phases Based on PLS Analysis
2.6. Comparison of Chilling Models
2.7. Chill and Heat Computation
2.8. Impacts of Chilling and Forcing Temperatures on Flowering Dates
3. Results
3.1. Temperature Trends and Chill Availability
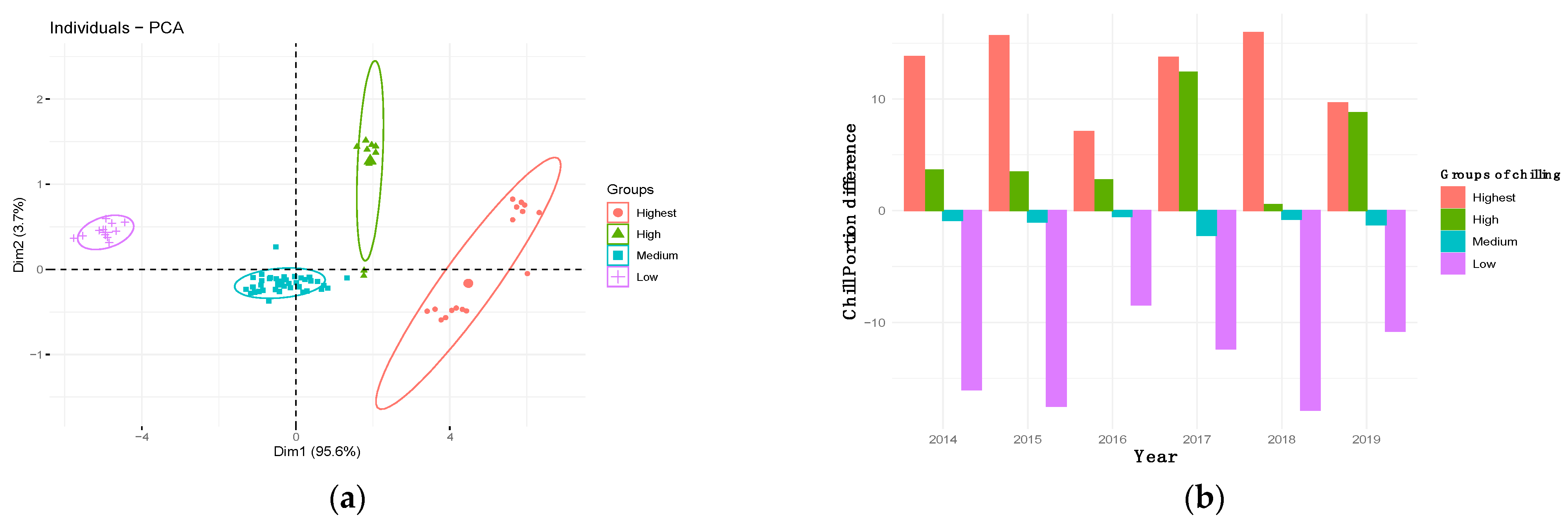
3.2. Flowering Trends, Variability and Cultivar Classification
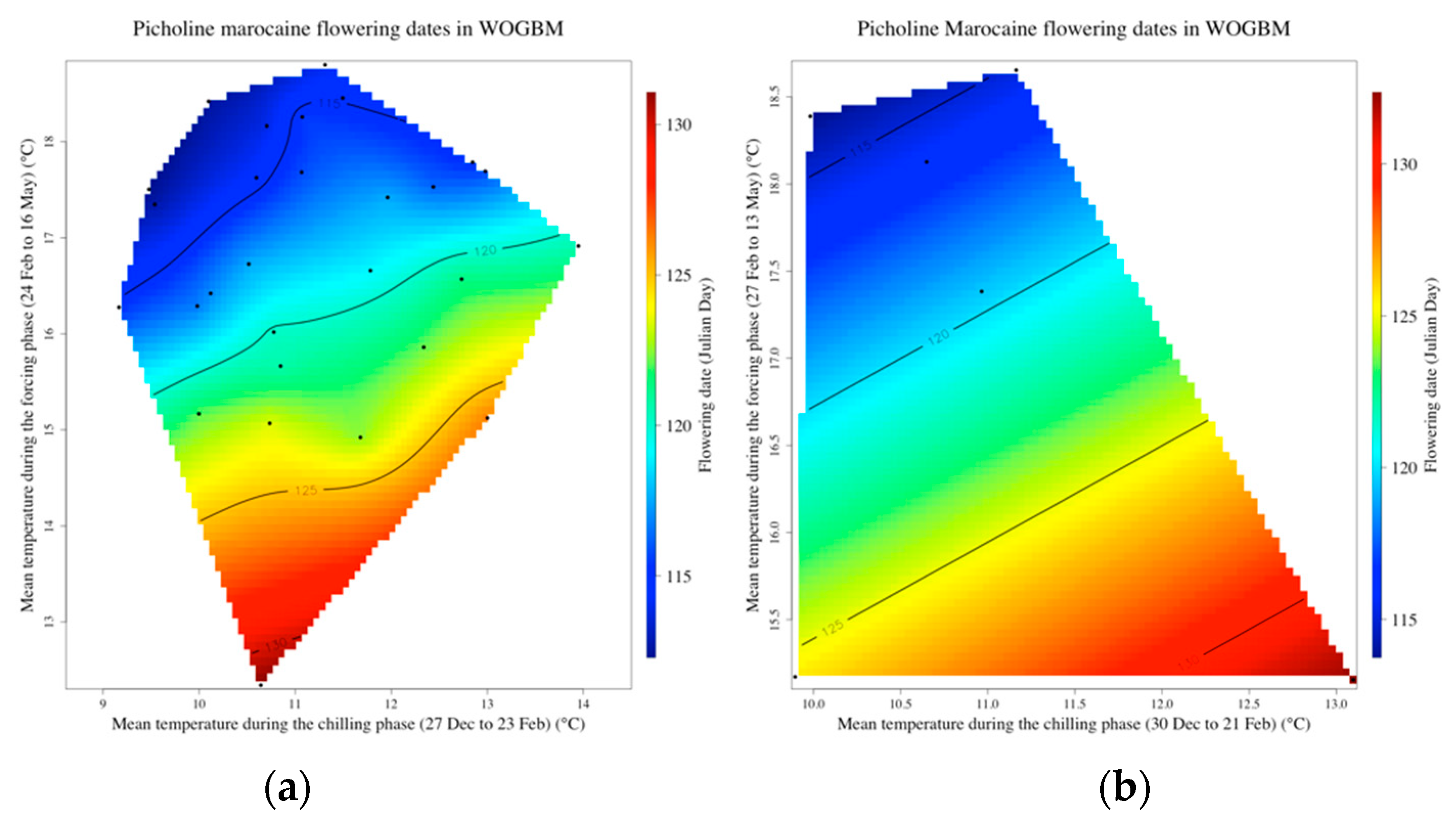
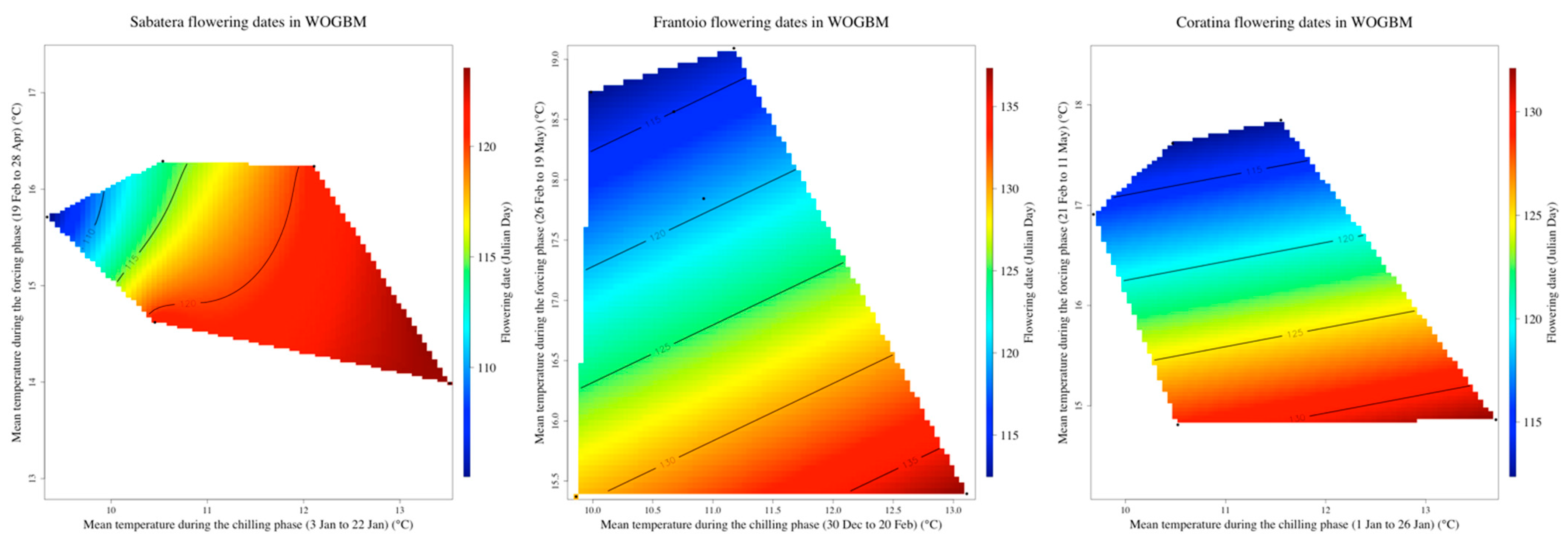
3.3. Delineating the Chilling and the Forcing Periods of ‘Picholine Marocaine’ Cultivar
3.4. PLS Comparison between Long- and Short-Term Flowering Date Records
3.5. Comparison of Chilling Models
3.6. Determination of Chill and Heat Requirements of WOGBM Cultivars
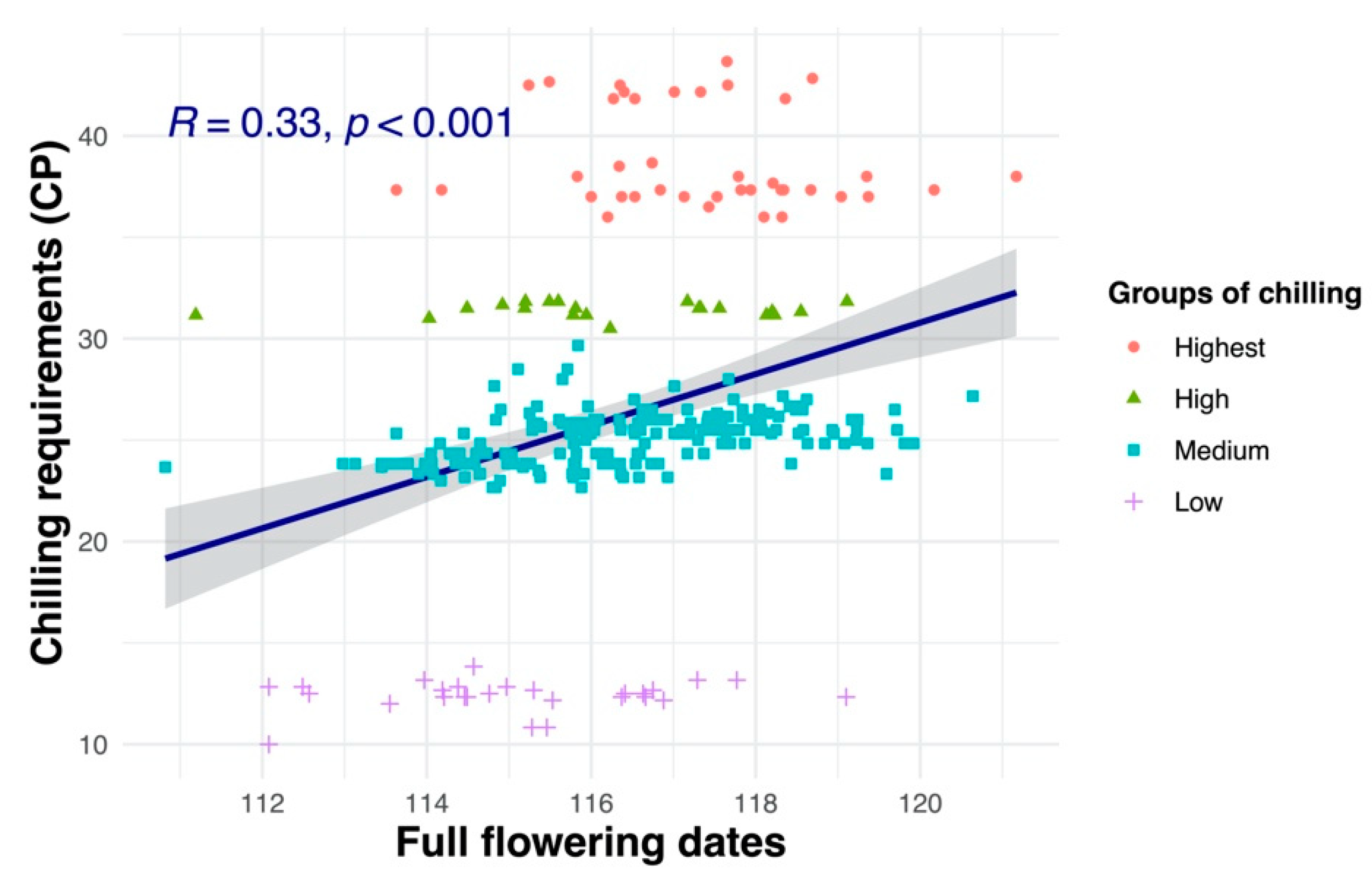
3.7. Relationships between Flowering Dates and Chill and Heat Requirements
4. Discussion
4.1. Inter-Annual Variability of Daily Temperature Is More Important Than a Long-Term Record for the Accurate Delineation of Chill and Heat Accumulation Phases
4.2. Dynamic Model Is the Best Suitable to Accurately Assess CR for Cultivars of the Worldwide Collection of Marrakech
4.3. CR Patterns and Their Possible Significance to Adaptive Traits of Cultivars
4.4. HR Variability and Limits of Its Assessment
4.5. Flowering Date of Olive Tree Is Likely Governed by Cold and Heat Temperatures
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Besnard, G.; Terral, J.-F.; Cornille, A. On the origins and domestication of the olive: A review and perspectives. Ann. Bot. 2017, 121, 587–588. [Google Scholar] [CrossRef] [PubMed]
- Ponti, L.; Gutierrez, A.P.; Ruti, P.M.; Dell’Aquila, A. Fine-scale ecological and economic assessment of climate change on olive in the Mediterranean Basin reveals winners and losers. Proc. Natl. Acad. Sci. USA 2014, 111, 5598–5603. [Google Scholar] [CrossRef]
- Menzel, A.; Sparks, T.H.; Estrella, N.; Koch, E.; Aasa, A.; Ahas, R.; Alm-KÜBler, K.; Bissolli, P.; BraslavskÁ, O.G.; Briede, A.; et al. European phenological response to climate change matches the warming pattern. Glob. Chang. Biol. 2006, 12, 1969–1976. [Google Scholar] [CrossRef]
- El Yaacoubi, A.; Malagi, G.; Oukabli, A.; Hafidi, M.; Legave, J.M. Global warming impact on floral phenology of fruit trees species in Mediterranean region. Sci. Hortic. 2014, 180, 243–253. [Google Scholar] [CrossRef]
- Benlloch-González, M.; Sánchez-Lucas, R.; Benlloch, M.; Ricardo, F.-E. An approach to global warming effects on flowering and fruit set of olive trees growing under field conditions. Sci. Hortic. 2018, 240, 405–410. [Google Scholar] [CrossRef]
- Orlandi, F.; Rojo, J.; Picornell, A.; Oteros, J.; Pérez-Badia, R.; Fornaciari, M. Impact of Climate Change on Olive Crop Production in Italy. Atmosphere 2020, 11, 595. [Google Scholar] [CrossRef]
- Fraga, H.; Pinto, J.G.; Viola, F.; Santos, J.A. Climate change projections for olive yields in the Mediterranean Basin. Int. J. Clim. 2019, 40, 769–781. [Google Scholar] [CrossRef]
- Elloumi, O.; Ghrab, M.; Chatti, A.; Chaari, A.; Ben Mimoun, M. Phenological performance of olive tree in a warm production area of central Tunisia. Sci. Hortic. 2020, 259, 108759. [Google Scholar] [CrossRef]
- Rojo, J.; Orlandi, F.; Ben Dhiab, A.; Lara, B.; Picornell, A.; Oteros, J.; Msallem, M.; Fornaciari, M.; Pérez-Badia, R. Estimation of Chilling and Heat Accumulation Periods Based on the Timing of Olive Pollination. Forests 2020, 11, 835. [Google Scholar] [CrossRef]
- Cannell, M.G.R.; Smith, R.I. Thermal Time, Chill Days and Prediction of Budburst in Picea sitchensis. J. Appl. Ecol. 1983, 20, 951–963. [Google Scholar] [CrossRef]
- Murray, M.J.; Campbell, C. Guava and passionfruit as commercial crops in Florida. In Proceedings of the Annual Meeting of the Florida State Horticulture Society (USA), Tampa, FL, USA, 31 October–2 November 1989. [Google Scholar]
- Pope, K.S.; Da Silva, D.; Brown, P.H.; DeJong, T.M. A biologically based approach to modeling spring phenology in temperate deciduous trees. Agric. For. Meteorol. 2014, 198–199, 15–23. [Google Scholar] [CrossRef]
- Legave, J.M.; Blanke, M.; Christen, D.; Giovannini, D.; Mathieu, V.; Oger, R. A comprehensive overview of the spatial and temporal variability of apple bud dormancy release and blooming phenology in Western Europe. Int. J. Biometeorol. 2013, 57, 317–331. [Google Scholar] [CrossRef] [PubMed]
- Kaufmann, H.; Blanke, M. Substitution of winter chilling by spring forcing for flowering using sweet cherry as model crop. Sci. Hortic. 2019, 244, 75–81. [Google Scholar] [CrossRef]
- Harrington, C.A.; Gould, P.J.; St.Clair, J.B. Modeling the effects of winter environment on dormancy release of Douglas-fir. For. Ecol. Manag. 2010, 259, 798–808. [Google Scholar] [CrossRef]
- Kovaleski, A.P.; Reisch, B.I.; Londo, J.P. Deacclimation kinetics as a quantitative phenotype for delineating the dormancy transition and thermal efficiency for budbreak in Vitis species. AoB Plants 2018, 10, ply066. [Google Scholar] [CrossRef]
- Hackett, W.P.; Hartmann, H.T. The Influence of Temperature on Floral Initiation in the Olive. Physiol. Plant. 1967, 20, 430–436. [Google Scholar] [CrossRef]
- Lavee, S.; Rallo, L.; Rapoport, H.F.; Troncoso, A. The floral biology of the olive: Effect of flower number, type and distribution on fruitset. Sci. Hortic. 1996, 66, 149–158. [Google Scholar] [CrossRef]
- Haberman, A.; Bakhshian, O.; Cerezo-Medina, S.; Paltiel, J.; Adler, C.; Ben-Ari, G.; Mercado, J.A.; Pliego-Alfaro, F.; Lavee, S.; Samach, A. A possible role for flowering locus T-encoding genes in interpreting environmental and internal cues affecting olive (Olea europaea L.) flower induction. Plant. Cell Environ. 2017, 40, 1263–1280. [Google Scholar] [CrossRef] [PubMed]
- Ouksili, A. Contribution à l’étude de la Biologie Florale de L’olivier Olea europea L.: De la Formation des Fleurs à la Période de Pollinisation Effective.In Colloque sur les Recherches Fruitières, Le Catalogue du Système Universitaire de Documentation, France. 1983. Available online: https://agris.fao.org/agris-search/search.do;jsessionid=8CBC22D054E9CF3125AC25A6BF61829E?request_locale=fr&recordID=US201302026354&query=&sourceQuery=&sortField=&sortOrder=&agrovocString=&advQuery=¢erString=&enableField= (accessed on 1 October 2022).
- Malik, N.S.A.; Bradford, J.M. Is Chilling a Prerequisite for Flowering and Fruiting in ‘Arbequina’ Olives? Int. J. Fruit Sci. 2005, 5, 29–39. [Google Scholar] [CrossRef]
- Diez-Palet, I.; Funes, I.; Save, R.; Biel, C.; de Herralde, F.; Miarnau, X.; Vargas, F.; Avila, G.; Carbo, J.; Aranda, X. Blooming under Mediterranean Climate: Estimating Cultivar-Specific Chill and Heat Requirements of Almond and Apple Trees Using a Statistical Approach. Agronomy 2019, 9, 760. [Google Scholar] [CrossRef]
- El Yaacoubi, A.; Oukabli, A.; Legave, J.-M.; Ainane, T.; Mouhajir, A.; Zouhair, R.; Hafidi, M. Response of almond flowering and dormancy to Mediterranean temperature conditions in the context of adaptation to climate variations. Sci. Hortic. 2019, 257, 108687. [Google Scholar] [CrossRef]
- Pertille, R.H.; Citadin, I.; Oliveira, L.d.S.d.; Broch, J.d.C.; Kvitschal, M.V.; Araujo, L. The influence of temperature on the phenology of apple trees grown in mild winter regions of Brazil, based on long-term records. Sci. Hortic. 2022, 305, 111354. [Google Scholar] [CrossRef]
- Luedeling, E.; Kunz, A.; Blanke, M.M. Identification of chilling and heat requirements of cherry trees—A statistical approach. Int. J. Biometeorol. 2013, 57, 679–689. [Google Scholar] [CrossRef] [PubMed]
- Luedeling, E.; Gassner, A. Partial Least Squares Regression for analyzing walnut phenology in California. Agric. For. Meteorol. 2012, 158–159, 43–52. [Google Scholar] [CrossRef]
- Guo, L.; Dai, J.; Ranjitkar, S.; Xu, J.; Luedeling, E. Response of chestnut phenology in China to climate variation and change. Agric. For. Meteorol. 2013, 180, 164–172. [Google Scholar] [CrossRef]
- Haouane, H.; El Bakkali, A.; Moukhli, A.; Tollon, C.; Santoni, S.; Oukabli, A.; El Modafar, C.; Khadari, B. Genetic structure and core collection of the World Olive Germplasm Bank of Marrakech: Towards the optimised management and use of Mediterranean olive genetic resources. Genetica 2011, 139, 1083–1094. [Google Scholar] [CrossRef]
- El Bakkali, A.; Haouane, H.; Moukhli, A.; Costes, E.; Van Damme, P.; Khadari, B. Construction of Core Collections Suitable for Association Mapping to Optimize Use of Mediterranean Olive (Olea europaea L.) Genetic Resources. PLoS ONE 2013, 8, e61265. [Google Scholar] [CrossRef] [PubMed][Green Version]
- El Bakkali, A.; Essalouh, L.; Tollon, C.; Rivallan, R.; Mournet, P.; Moukhli, A.; Zaher, H.; Mekkaoui, A.; Hadidou, A.; Sikaoui, L.; et al. Characterization of Worldwide Olive Germplasm Banks of Marrakech (Morocco) and Cordoba (Spain): Towards management and use of olive germplasm in breeding programs. PLoS ONE 2019, 14, e0223716. [Google Scholar] [CrossRef]
- Sanz-Cortes, F.; Martinez-Calvo, J.; Badenes, M.L.; Bleiholder, H.; Hack, H.; Llacer, G.; Meier, U. Phenological growth stages of olive trees (Olea europaea). Ann. Appl. Biol. 2002, 140, 151–157. [Google Scholar] [CrossRef]
- Luedeling, E.; Fernandez, E. ChillR: Statistical Methods for Phenology Analysis in Temperate Fruit, R Package Vesrsion 0.72.7. 2022. Available online: https://CRAN.R-project.org/package=chillR (accessed on 1 October 2022).
- Linvill, D.E. Calculating Chilling Hours and Chill Units from Daily Maximum and Minimum Temperature Observations. HortScience 1990, 25, 14–16. [Google Scholar] [CrossRef]
- Team, R.C. R: A Language and Environment for Statistical Computing; R 3.6.3; R Foundation for Statistical Computing: Vienna, Austria, 2021. [Google Scholar]
- Peterson, B.G.; Carl, P. PerformanceAnalytics: Econometric Tools for Performance and Risk Analysis, R Package Version 2.0.4. 2020. Available online: https://CRAN.R-project.org/package=PerformanceAnalytics (accessed on 1 October 2022).
- Bates, D.; Mächler, M.; Bolker, B.; Walker, S. Fitting Linear Mixed-Effects Models Using lme4. J. Stat. Softw. 2015, 67, 48. [Google Scholar] [CrossRef]
- Charrad, M.; Ghazzali, N.; Boiteau, V.; Niknafs, A. NbClust: An R Package for Determining the Relevant Number of Clusters in a Data Set. J. Stat. Softw. 2014, 61, 1–36. [Google Scholar] [CrossRef]
- Wickham, H. ggplot2: Elegant Graphics for Data Analysis; Springer: New York, NY, USA, 2016. [Google Scholar]
- Kassambara, A. ggpubr: ‘ggplot2’ Based Publication Ready Plots; R Package Version 0.4.0. 2020. Available online: https://CRAN.R-project.org/package=ggpubr (accessed on 1 October 2022).
- Wold, S. PLS for multivariate linear modeling. Chemom. Methods Mol. Des. 1995, 2, 195–218. [Google Scholar]
- Bennett, J. Temperature and bud rest period: Effect of temperature and exposure on the rest period of deciduous plant leaf buds investigated. Hilgardia 1949, 3, 9–12. [Google Scholar] [CrossRef]
- Weinberger, J.H. Chilling requirements of peach varieties. Am. Soc. Hortic. Sci. 1950, 56, 122–128. [Google Scholar]
- Richardson, E.A.; Seeley, S.D.; Walker, D.R. A model for estimating the completion of rest for ‘Redhaven’ and ‘Elberta’ peach trees. HortScience 1974, 9, 331–332. [Google Scholar] [CrossRef]
- Erez, A.; Fishman, S.; Linsley-Noakes, G.C.; Allan, P. The dynamic model for rest completion in peach buds. Acta Hortic. 1990, 276, 165–174. [Google Scholar] [CrossRef]
- Fishman, S.; Erez, A.; Couvillon, G.A. The temperature dependence of dormancy breaking in plants: Computer simulation of processes studied under controlled temperatures. J. Theor. Biol. 1987, 126, 309–321. [Google Scholar] [CrossRef]
- Anderson, J.L.; Richardson, E.A.; Kesner, C.D. Validation of chill unit and flower bud phenology models for ‘montmorency’ sour cherry. Acta Hortic. 1986, 184, 71–78. [Google Scholar] [CrossRef]
- Luedeling, E.; Guo, L.; Dai, J.; Leslie, C.; Blanke, M.M. Differential responses of trees to temperature variation during the chilling and forcing phases. Agric. For. Meteorol. 2013, 181, 33–42. [Google Scholar] [CrossRef]
- Oliver, M.A.; Webster, R. A tutorial guide to geostatistics: Computing and modelling variograms and kriging. Catena 2014, 113, 56–69. [Google Scholar] [CrossRef]
- Faust, M.; Erez, A.; Rowland, L.J.; Wang, S.Y.; Norman, H.A. Bud Dormancy in Perennial Fruit Trees: Physiological Basis for Dormancy Induction, Maintenance, and Release. HortScience 1997, 32, 623–629. [Google Scholar] [CrossRef]
- Lang, G.A. Dormancy: A new universal terminology. HortScience 1987, 22, 817–820. [Google Scholar] [CrossRef]
- Sanchez-Perez, R.; Del Cueto, J.; Dicenta, F.; Martinez-Gomez, P. Recent advancements to study flowering time in almond and other Prunus species. Front. Plant Sci. 2014, 5, 334. [Google Scholar] [CrossRef]
- Campoy, J.A.; Ruiz, D.; Egea, J. Dormancy in temperate fruit trees in a global warming context: A review. Sci. Hortic. 2011, 130, 357–372. [Google Scholar] [CrossRef]
- Orlandi, F.; Ruga, L.; Romano, B.; Fornaciari, M. Olive flowering as an indicator of local climatic changes. Theor. Appl. Climatol. 2005, 81, 169–176. [Google Scholar] [CrossRef]
- Aguilera, F.; Fornaciari, M.; Ruiz-Valenzuela, L.; Galan, C.; Msallem, M.; Dhiab, A.B.; la Guardia, C.D.; Del Mar Trigo, M.; Bonofiglio, T.; Orlandi, F. Phenological models to predict the main flowering phases of olive (Olea europaea L.) along a latitudinal and longitudinal gradient across the Mediterranean region. Int. J. Biometeorol. 2015, 59, 629–641. [Google Scholar] [CrossRef] [PubMed]
- Luedeling, E.; Zhang, M.; Luedeling, V.; Girvetz, E.H. Sensitivity of winter chill models for fruit and nut trees to climatic changes expected in California’s Central Valley. Agric. Ecosyst. Environ. 2009, 133, 23–31. [Google Scholar] [CrossRef]
- Benmoussa, H.; Ghrab, M.; Ben Mimoun, M.; Luedeling, E. Chilling and heat requirements for local and foreign almond (Prunus dulcis Mill.) cultivars in a warm Mediterranean location based on 30 years of phenology records. Agric. For. Meteorol. 2017, 239, 34–46. [Google Scholar] [CrossRef]
- Guo, L.; Dai, J.; Ranjitkar, S.; Yu, H.; Xu, J.; Luedeling, E. Chilling and heat requirements for flowering in temperate fruit trees. Int. J. Biometeorol. 2014, 58, 1195–1206. [Google Scholar] [CrossRef]
- Campoy, J.A.; Ruiz, D.; Cook, N.; Allderman, L.; Egea, J. Clinal variation of dormancy progression in apricot. S. Afr. J. Bot. 2011, 77, 618–630. [Google Scholar] [CrossRef]
- El Yaacoubi, A.; El Jaouhari, N.; Bourioug, M.; El Youssfi, L.; Cherroud, S.; Bouabid, R.; Chaoui, M.; Abouabdillah, A. Potential vulnerability of Moroccan apple orchard to climate change-induced phenological perturbations: Effects on yields and fruit quality. Int. J. Biometeorol. 2020, 64, 377–387. [Google Scholar] [CrossRef]
- Alburquerque, N.; García-Montiel, F.; Carrillo, A.; Burgos, L. Chilling and heat requirements of sweet cherry cultivars and the relationship between altitude and the probability of satisfying the chill requirements. Environ. Exp. Bot. 2008, 64, 162–170. [Google Scholar] [CrossRef]
- Fadon, E.; Rodrigo, J.; Luedeling, E. Cultivar-specific responses of sweet cherry flowering to rising temperatures during dormancy. Agric. For. Meteorol. 2021, 307, 108486. [Google Scholar] [CrossRef]
- Benmoussa, H.; Luedeling, E.; Ghrab, M.; Ben Yahmed, J.; Ben Mimoun, M. Performance of pistachio (Pistacia vera L.) in warming Mediterranean orchards. Environ. Exp. Bot. 2017, 140, 76–85. [Google Scholar] [CrossRef]
- Guo, L.; Xu, J.C.; Dai, J.H.; Cheng, J.M.; Luedeling, E. Statistical identification of chilling and heat requirements for apricot flower buds in Beijing, China. Sci. Hortic. 2015, 195, 138–144. [Google Scholar] [CrossRef]
- Fernandez, E.; Krefting, P.; Kunz, A.; Do, H.; Fadón, E.; Luedeling, E. Boosting statistical delineation of chill and heat periods in temperate fruit trees through multi-environment observations. Agric. For. Meteorol. 2021, 310, 108652. [Google Scholar] [CrossRef]
- Luedeling, E.; Brown, P.H. A global analysis of the comparability of winter chill models for fruit and nut trees. Int. J. Biometeorol. 2011, 55, 411–421. [Google Scholar] [CrossRef]
- Fernandez, E.; Whitney, C.; Luedeling, E. The importance of chill model selection—A multi-site analysis. Eur. J. Agron. 2020, 119, 126103. [Google Scholar] [CrossRef]
- Darbyshire, R.; Pope, K.; Goodwin, I. An evaluation of the chill overlap model to predict flowering time in apple tree. Sci. Hortic. 2016, 198, 142–149. [Google Scholar] [CrossRef]
- Chuine, I.; Bonhomme, M.; Legave, J.M.; de Cortazar-Atauri, I.G.; Charrier, G.; Lacointe, A.; Ameglio, T. Can phenological models predict tree phenology accurately in the future? The unrevealed hurdle of endodormancy break. Glob. Chang. Biol. 2016, 22, 3444–3460. [Google Scholar] [CrossRef]
- Sahli, A.; Dakhlaoui, H.; Aounallah, M.K.; Hellali, R.; Aïachi Mezghani, M.; Bornaz, S. Estimation of chilling and heat requirement of ‘chemlali’ olive cultivar and its use to predict flowering date. Acta Hortic. 2012, 949, 155–164. [Google Scholar] [CrossRef]
- Gibson, P.G.; Reighard, G.L. Chilling Requirement and Postrest Heat Accumulation in Peach Trees Inoculated with Peach Latent Mosaic Viroid. J. Am. Soc. Hortic. Sci. 2002, 127, 333–336. [Google Scholar] [CrossRef][Green Version]
- Okie, W.R.; Blackburn, B. Increasing Chilling Reduces Heat Requirement for Floral Budbreak in Peach. HortScience 2011, 46, 245–252. [Google Scholar] [CrossRef]
- Ebtedaei, M.; Arzani, K.; Sarikhani, S. Evaluation of chilling requirement and heat accumulation in three European pear cultivars and genotypes. Acta Hortic. 2021, 1315, 69–76. [Google Scholar] [CrossRef]
 , mid
, mid  , late
, late  and extra late
and extra late  flowering cultivars.
flowering cultivars.
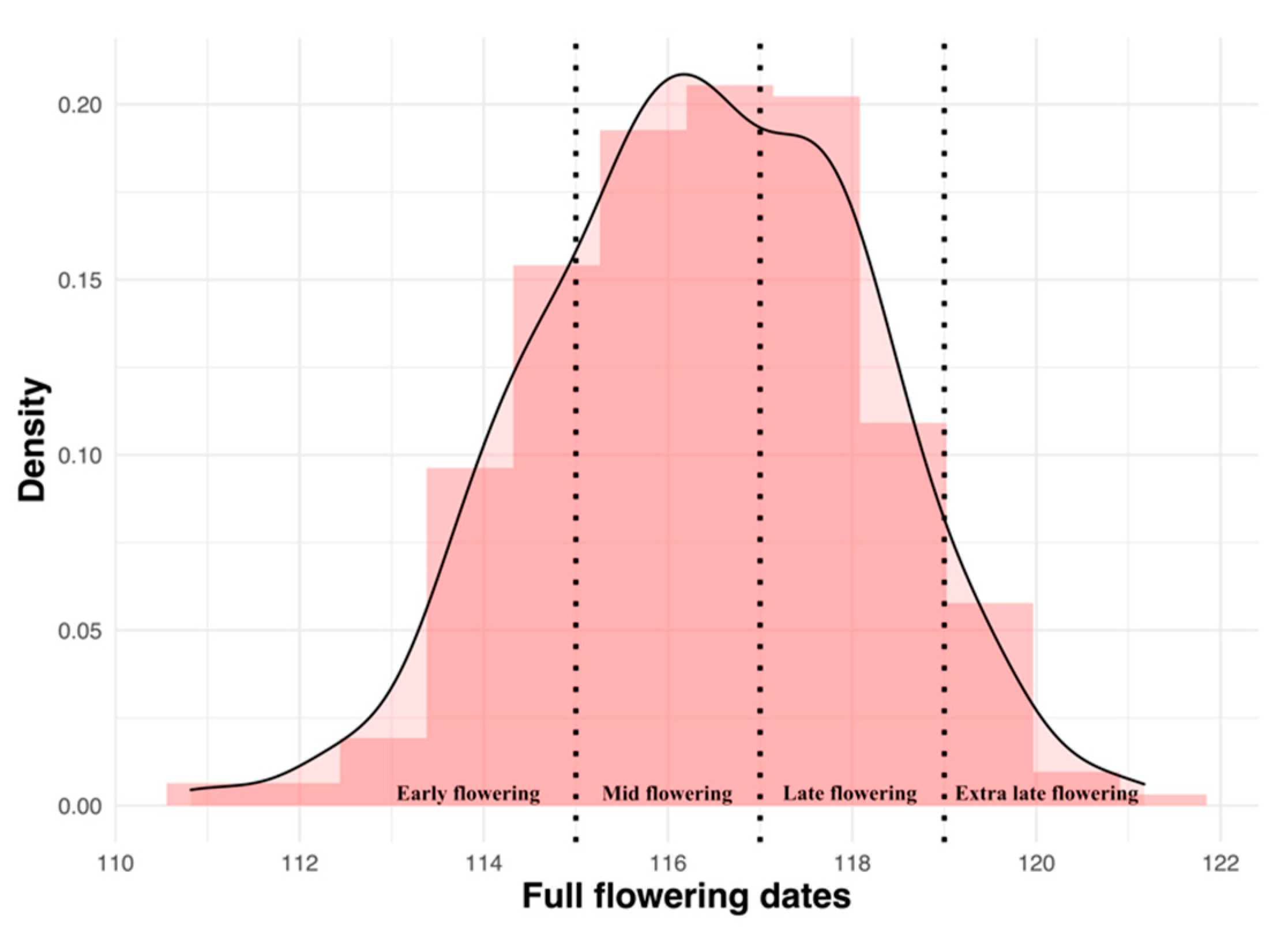
 , mid
, mid  , late
, late  and extra late
and extra late  flowering cultivars.
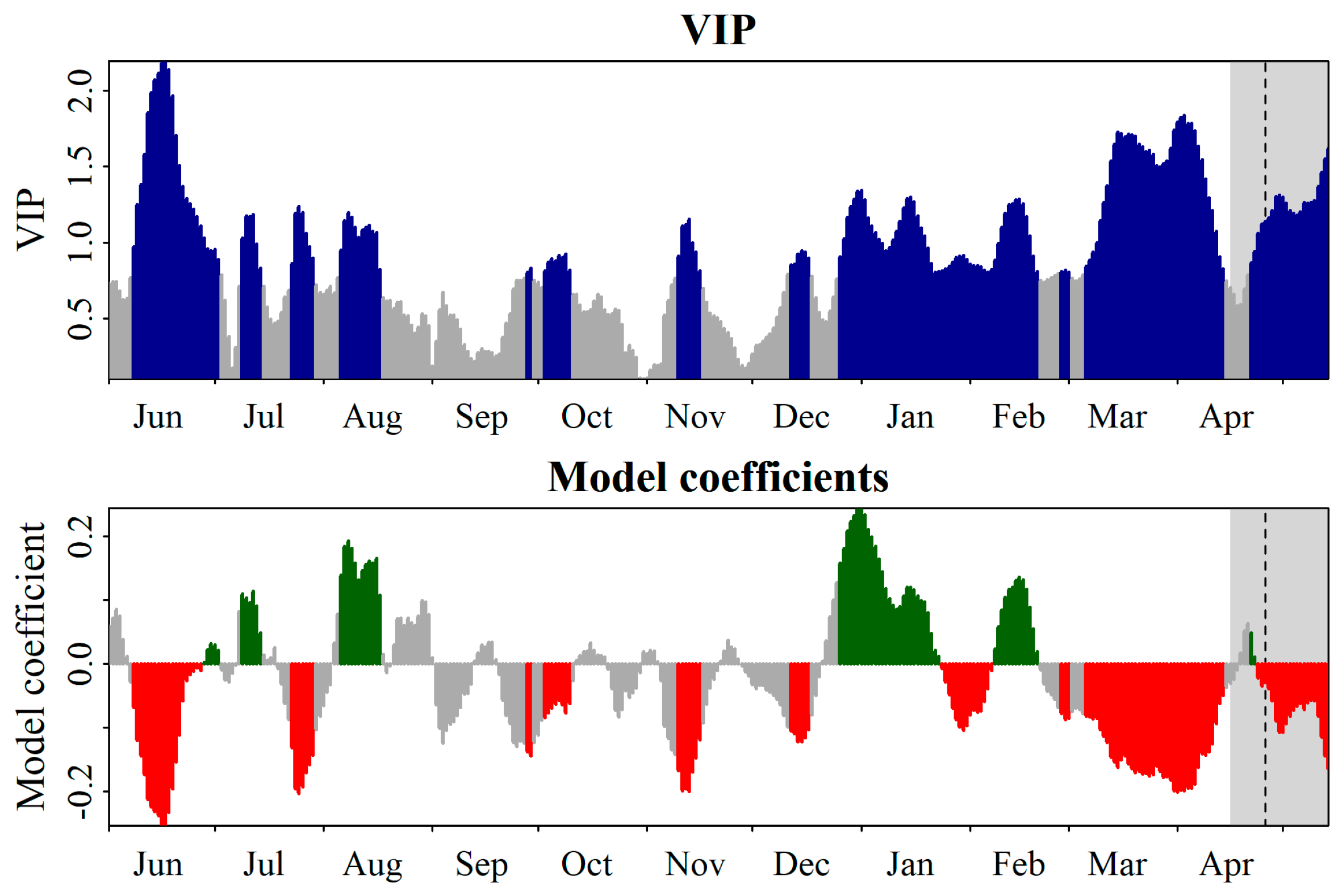
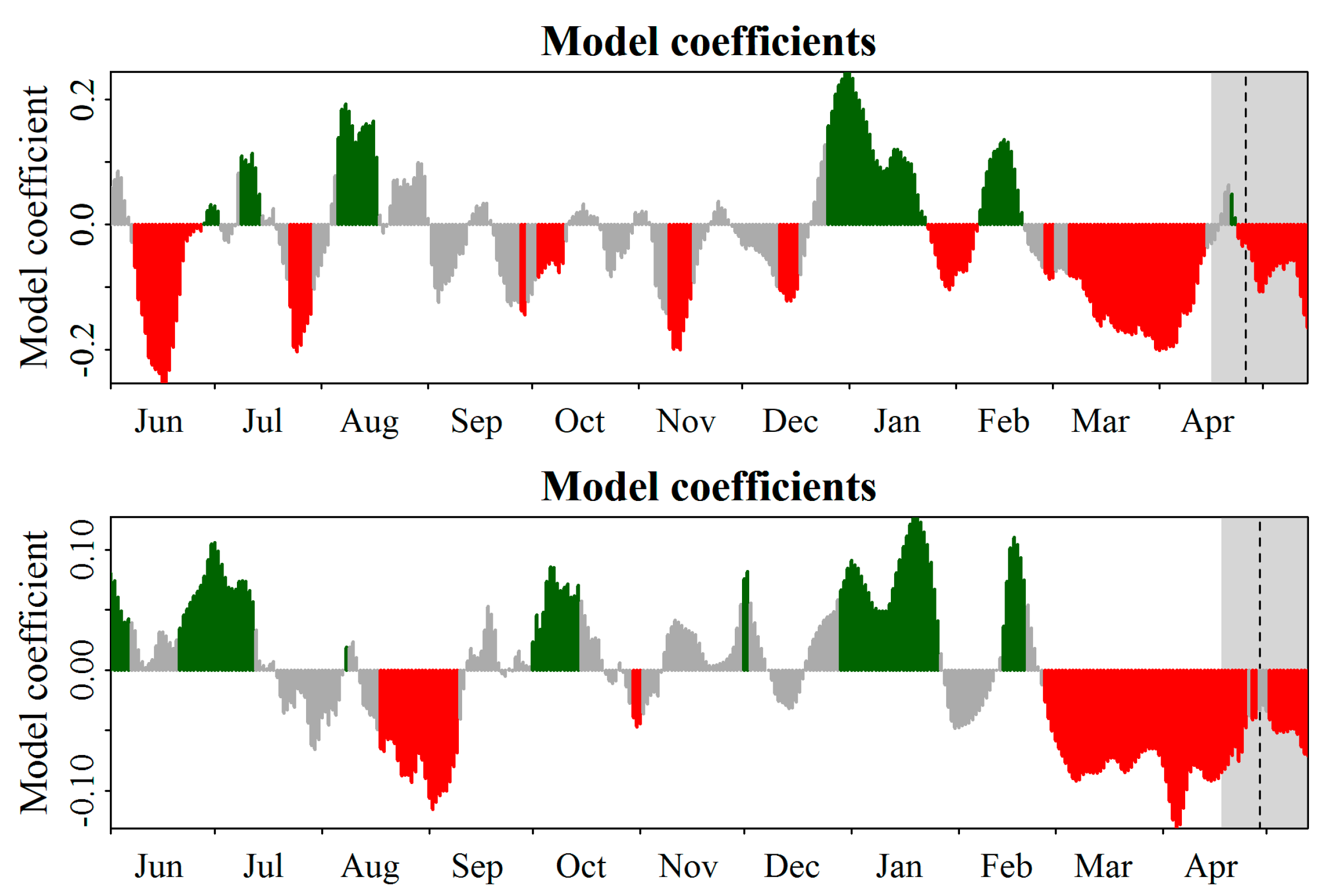
flowering cultivars.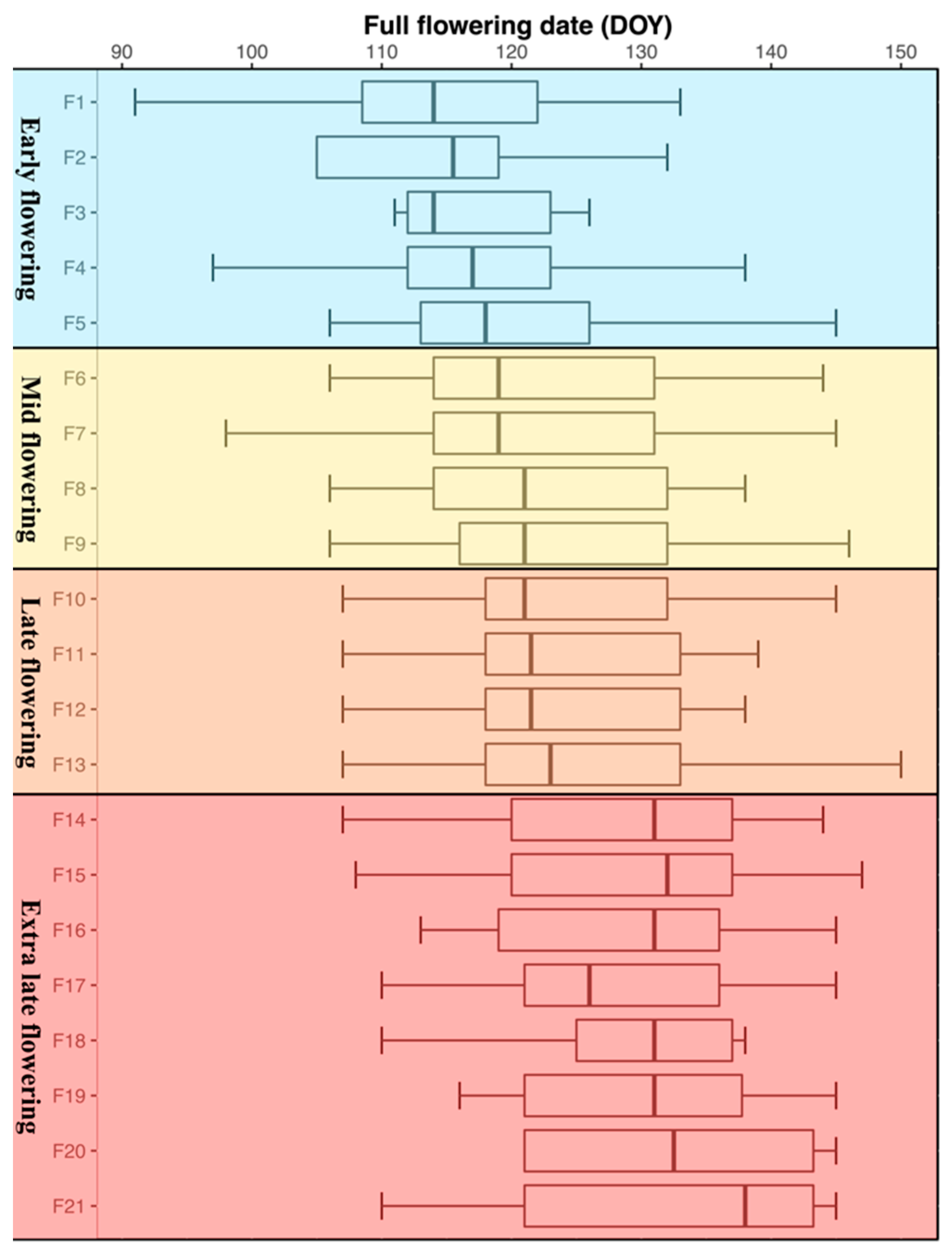
| Mixed Model | Equation | Df | AIC | BIC | X2 | p Value | H2 |
|---|---|---|---|---|---|---|---|
| Model-1 | FFD =|Cultivar | 44,967 | 44,987 | 0.098 | |||
| Model-2 | FFD = Year +|Cultivar | 5 | 31,049 | 31,102 | 13,928 | <0.001 *** | 0.79 |
| Model-3 | FFD = Year +|Cultivar +|Cultivar ² × Year | 1 | 29,639 | 29,699 | 1412 | <0.001 *** | 0.75 |
| Chilling Phase | Forcing Phase | Chilling Hours Model | Utah Model | Dynamic Model | GDH Model | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Time Serie | Start | End | Duration | Start | End | Duration | CH | CV% | CU | CV% | CP | CV% | GDH | CV% |
| 29 years (1986–2019) | 27 December | 21 February | 58 | 24 February | 16 May | 82 | 438 ± 114 | 25.94 | 512 ± 157 | 30.63 | 27.99 ± 6.16 | 22.02 | 21,559 ± 1952 | 9.05 |
| 6 years (2014–2019) | 30 December | 21 February | 53 | 27 February | 13 May | 76 | 459 ± 99 | ____ | 516 ± 150 | ____ | 26.25 ± 5.93 | ____ | 19,684 ± 1348 | ____ |
| Cluster of CR | Representative Cultivar * | Number of Cultivars | Chill Requirements | Heat Requirements | FFD (DOY) | ||
|---|---|---|---|---|---|---|---|
| Mean ± SD | Mean ± SD | Mean ± SD | Min | Max | |||
| Low | Arbequina | 27 | 12.39 ± 0.78 | 20,467.17 ± 2013.37 | 122 ± 3.09 | 115 | 127 |
| Medium | Picholine Marocaine | 198 | 25.04 ± 1.26 | 20,882.92 ± 747.82 | 123 ± 2.23 | 115 | 130 |
| High | Rossello | 21 | 31.42 ± 0.34 | 21,382.66 ± 1224.78 | 124 ± 3.22 | 117 | 130 |
| Highest | Leccino | 39 | 38.85 ± 2.47 | 21,056.52 ± 1026.91 | 125 ± 2.87 | 118 | 132 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abou-Saaid, O.; El Yaacoubi, A.; Moukhli, A.; El Bakkali, A.; Oulbi, S.; Delalande, M.; Farrera, I.; Kelner, J.-J.; Lochon-Menseau, S.; El Modafar, C.; et al. Statistical Approach to Assess Chill and Heat Requirements of Olive Tree Based on Flowering Date and Temperatures Data: Towards Selection of Adapted Cultivars to Global Warming. Agronomy 2022, 12, 2975. https://doi.org/10.3390/agronomy12122975
Abou-Saaid O, El Yaacoubi A, Moukhli A, El Bakkali A, Oulbi S, Delalande M, Farrera I, Kelner J-J, Lochon-Menseau S, El Modafar C, et al. Statistical Approach to Assess Chill and Heat Requirements of Olive Tree Based on Flowering Date and Temperatures Data: Towards Selection of Adapted Cultivars to Global Warming. Agronomy. 2022; 12(12):2975. https://doi.org/10.3390/agronomy12122975
Chicago/Turabian StyleAbou-Saaid, Omar, Adnane El Yaacoubi, Abdelmajid Moukhli, Ahmed El Bakkali, Sara Oulbi, Magalie Delalande, Isabelle Farrera, Jean-Jacques Kelner, Sylvia Lochon-Menseau, Cherkaoui El Modafar, and et al. 2022. "Statistical Approach to Assess Chill and Heat Requirements of Olive Tree Based on Flowering Date and Temperatures Data: Towards Selection of Adapted Cultivars to Global Warming" Agronomy 12, no. 12: 2975. https://doi.org/10.3390/agronomy12122975
APA StyleAbou-Saaid, O., El Yaacoubi, A., Moukhli, A., El Bakkali, A., Oulbi, S., Delalande, M., Farrera, I., Kelner, J.-J., Lochon-Menseau, S., El Modafar, C., Zaher, H., & Khadari, B. (2022). Statistical Approach to Assess Chill and Heat Requirements of Olive Tree Based on Flowering Date and Temperatures Data: Towards Selection of Adapted Cultivars to Global Warming. Agronomy, 12(12), 2975. https://doi.org/10.3390/agronomy12122975








