UAV-Based Hyperspectral and Ensemble Machine Learning for Predicting Yield in Winter Wheat
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Design and Data Collection
2.2. Acquisition and Processing of Hyperspectral Data
2.3. Acquisition of Spectral Indices
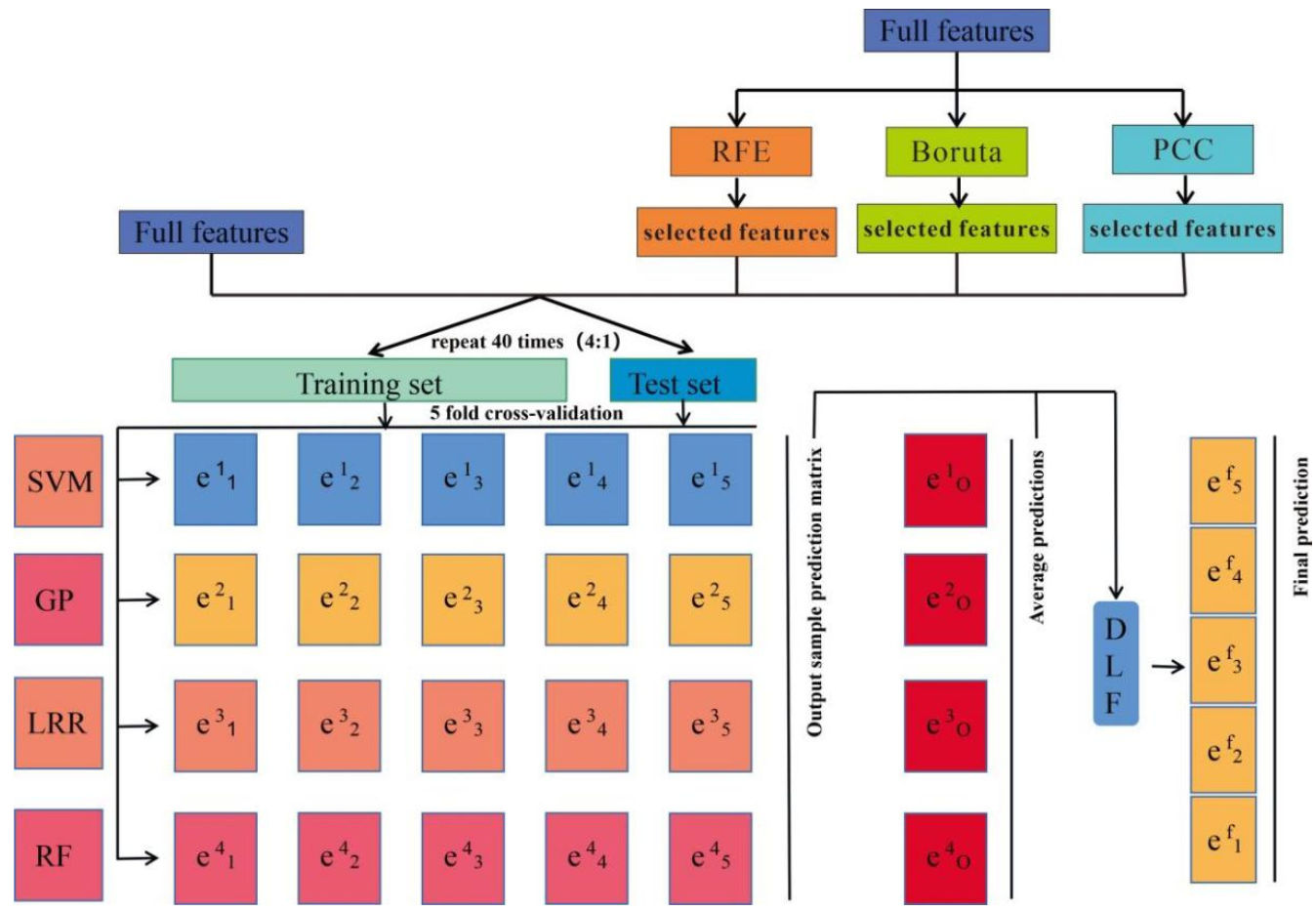
2.4. Feature Selection Methods
2.5. Decision-Level Fusion Model for Ensemble Learning
2.5.1. Regression Methods
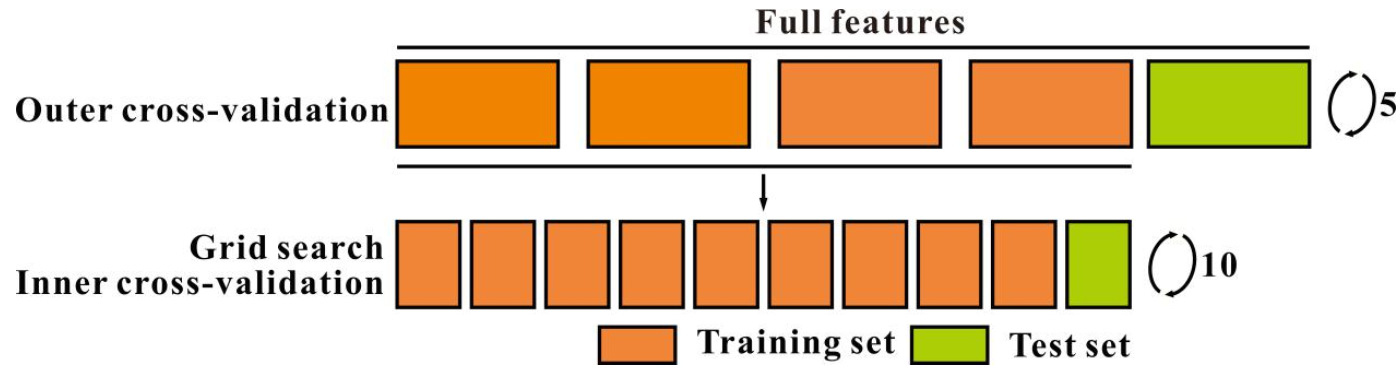
2.5.2. Cross-Validation and Parameter Optimization
2.6. Statistical Analysis
3. Results
3.1. Descriptive Statistics
3.2. Feature Importance Ranking
3.3. Comparison and Performance of Feature Selection Methods and Model Accuracy
3.4. Yield Distribution
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Disclaimer
Appendix A
| Full Form | Spectral Index or Ratio | R2 | |
|---|---|---|---|
| Flowering | Grain Filling | ||
| Curvative index | CI | 0.08 | 0.33 |
| Chlorophyll index red-edge | CIre | 0.21 | 0.40 |
| Datt1 | 0.30 | 0.31 | |
| Datt4 | 0.14 | 0.41 | |
| Datt6 | 0.05 | 0.29 | |
| Double difference index | DDI | 0.24 | 0.26 |
| Double peak index | DPI | 0.14 | 0.30 |
| Gitelson2 | 0.45 | ||
| Green normalized difference vegetation index | GNDVI | 0.40 | |
| Leaf chlorophyll index | LCI | 0.42 | |
| Modified chlorophyll absorption ratio index | MCARI | 0.41 | |
| MCARI3 | 0.43 | ||
| Modified normalized difference | MND[680,800] | 0.45 | |
| Modified normalized difference | MND[705,750] | 0.43 | |
| Modified simple ratio | mSR | 0.32 | |
| Modified simple ratio 2 | mSR2 | 0.41 | |
| MERIS terrestrial chlorophyll index | MTCI | 0.31 | |
| Modified triangular vegetation index 1 | MTVI1 | 0.40 | |
| Modified triangular vegetation index 2 | MTVI2 | 0.47 | |
| Normalized difference 550/531 | ND[531,550] | 0.28 | |
| Normalized difference 682/553 | ND[553,682] | 0.41 | 0.48 |
| Normalized difference chlorophyll | NDchl | 0.23 | 0.36 |
| New double difference index | DDn | 0.45 | 0.39 |
| Normalized difference red-edge | NDRE | 0.36 | |
| Normalized difference vegetation index | NDVI[650,750] | 0.47 | |
| NDVI[550,750] | 0.42 | ||
| NDVI[710,750] | 0.43 | ||
| Normalized pigment chlorophyll index | NPCI | 0.35 | |
| Normalized difference pigment index | NPQI | 0.13 | 0.31 |
| Optimized soil-adjusted vegetation index | OSAVI | 0.31 | 0.48 |
| Plant biochemical index | PBI | 0.20 | 0.37 |
| Plant pigment ratio | PPR | 0.09 | 0.25 |
| Physiological reflectance index | PRI | 0.40 | 0.48 |
| Pigment-specific normalized difference | PSNDb1 | 0.31 | 0.46 |
| PSNDc1 | 0.28 | 0.44 | |
| PSNDc2 | 0.43 | ||
| Plant senescence reflectance index | PSRI | 0.31 | |
| Pigment-pecific simple ratio | PSSRc1 | 0.39 | |
| PSSRc2 | 0.38 | ||
| Photosynthetic vigor ratio | PVR | 0.48 | |
| Plant water index | PWI | 0.28 | |
| Renormalized difference vegetation index | RDVI | 0.44 | |
| RDVI2 | 0.44 | ||
| Reflectance at the inflexion point | Rre | 0.14 | |
| Red-edge stress vegetation index | RVSI | 0.49 | |
| Soil-adjusted vegetation index | SAVI | 0.47 | |
| Structure intensive pigment index | SIPI | 0.35 | |
| Spectral polygon vegetation index | SPVI | 0.40 | |
| Simple ratio | SR[430,680] | 0.34 | |
| SR[440,740] | 0.46 | ||
| SR[550,672] | 0.25 | ||
| SR[550,750] | 0.05 | ||
| Disease-water stress index 4 | DSWI-4 | 0.47 | |
| Simple ratio pigment index | SRPI | 0.34 | |
| Transformed chlorophyll absorption ratio | TCARI | 0.34 | |
| Triangular chlorophyll index | TCI | 0.40 | |
| Triangular vegetation index | TVI | 0.42 | |
| Water band index | WBI | 0.31 | |
| Combined MCARI/MTVI2 | MCARI/MTVI2 | 0.39 | |
| Combined TCARI/OSAVI | TCARI/OSAVI | 0.10 | |
| Ranking | Flowering Features | Grain-Filling Features | ||||
|---|---|---|---|---|---|---|
| RFE | Boruta | PCC | RFE | Boruta | PCC | |
| 1 | RVSI | Gitelson2 | RVSI | DSWI-4 | Gitelson2 | RVSI |
| 2 | RDVI | RVSI | DDn | ND[553,682] | RVSI | ND[553,682] |
| 3 | WBI | NDchl | SPVI | MTVI2 | NDchl | PVR |
| 4 | NDVI[650,750] | ND[553,682] | SIPI | RVSI | ND[553,682] | OSAVI |
| 5 | PRI | OSAVI | MTVI1 | Gitelson2 | OSAVI | PRI |
| 6 | PWI | CIre | RDVI | PVR | CIre | NDVI[650,750] |
| 7 | DSWI-4 | NDVI[710,750] | DSWI-4 | CI | NDVI[710,750] | MTVI2 |
| 8 | SR[440,740] | DPI | TVI | OSAVI | DPI | DSWI-4 |
| 9 | SAVI | MSR2 | RDVI2 | NDchl | MSR2 | SAVI |
| 10 | TCI | MTCI | ND[553,682] | Datt1 | MTCI | SR[440,740] |
| 11 | MTVI1 | DSWI-4 | PRI | SR[450,550] | DSWI-4 | PSNDb1 |
| 12 | OSAVI | MND[705,750] | PVR | PPR | MND[705,750] | MND[680,800] |
| 13 | Datt4 | MTVI2 | MTVI2 | CIre | MTVI2 | Gitelson2 |
| 14 | MSR | PVR | Rre | PRI | PVR | RDVI2 |
| 15 | DDn | NDVI[650,750] | NDVI[650,750] | NPQI | NDVI[650,750] | RDVI |
| 16 | RDVI2 | SAVI | SR[440,740] | SR[450,690] | SAVI | PSNDc1 |
| 17 | MCARI | PRI | PSNDb1 | Rre | PRI | MND[705,750] |
| 18 | ND[553,682] | Datt6 | OSAVI | MSR2 | Datt6 | PSNDc2 |
| 19 | PSNDb1 | SR[440,740] | SAVI | TCARI/OSAVI | SR[440,740] | NDVI[710,750] |
| 20 | SIPI | DDI | WBI | DDI | DDI | MCARI3 |
| 21 | Rre | PSNDb1 | PSNDc1 | MCARI | PSNDb1 | NDVI[550,750] |
| 22 | TVI | LCI | PSNDc2 | PSRI | LCI | LCI |
| 23 | Gitelson2 | MND[680,800] | MND[680,800] | LCI | MND[680,800] | TVI |
| 24 | Datt1 | NDRE | PSSRc1 | Datt4 | NDRE | MSR2 |
| 25 | NDchl | PSSRc1 | DDI | MCARI/MTVI2 | PSSRc1 | Datt4 |
| 26 | TCARI | PSNDc1 | PSSRc2 | MTCI | PSNDc1 | MCARI |
| 27 | MCARI3 | NDVI[550,750] | PSRI | PSNDc2 | NDVI[550,750] | CIre |
| 28 | MCARI/MTVI2 | NPQI | NDVI[550,750] | WBI | NPQI | TCI |
| 29 | PSNDc2 | MCARI3 | MSR2 | DPI | MCARI3 | GNDVI |
| 30 | Datt6 | CI | NDVI[710,750] | PWI | CI | MTVI1 |
| 31 | SR[450,550] | ND[531,550] | MSR | MTVI1 | ND[531,550] | SPVI |
| 32 | ND[531,550] | MCARI | GNDVI | PSNDb1 | MCARI | DDn |
| 33 | PSNDc1 | MCARI/MTVI2 | CIre | MSR | MCARI/MTVI2 | MCARI/MTVI2 |
| 34 | CI | TCARI/OSAVI | PBI | MND[705,750] | TCARI/OSAVI | PSSRc1 |
| 35 | SPVI | PBI | MND[705,750] | TCI | PBI | PSSRc2 |
| 36 | NDRE | PSNDc2 | LCI | MCARI3 | PSNDc2 | PBI |
| 37 | TCARI/OSAVI | PSSRc2 | NDRE | NDVI[650,750] | PSSRc2 | NDRE |
| 38 | PVR | PSRI | NPCI | PSNDc1 | PSRI | NPCI |
| 39 | MTVI2 | Datt1 | SR[430,680] | SR[440,740] | Datt1 | SIPI |
| 40 | PPR | SRPI | SRPI | Datt6 | SRPI | TCARI |
| 41 | DDI | RDVI2 | MCARI | TCARI | RDVI2 | SR[430,680] |
| 42 | NPQI | GNDVI | PWI | SR[430,680] | GNDVI | SRPI |
| 43 | MND[680,800] | RDVI | Datt4 | NDVI[710,750] | RDVI | CI |
| 44 | PSSRc1 | NPCI | ND[531,550] | NDVI[550,750] | NPCI | MSR |
| 45 | PSRI | TVI | MTCI | ND[531,550] | TVI | WBI |
| 46 | PSSRc2 | SR[450,550] | MCARI/MTVI2 | PSSRc2 | SR[450,550] | MTCI |
| 47 | MTCI | SR[430,680] | TCI | SIPI | SR[430,680] | PSRI |
| 48 | SR[450,690] | PPR | Datt1 | NDRE | PPR | DPI |
| 49 | MND[705,750] | DDn | Datt6 | SAVI | DDn | Datt6 |
| 50 | GNDVI | MSR | DPI | NPCI | MSR | ND[531,550] |
| 51 | CIre | TCI | NPQI | PSSRc1 | TCI | PWI |
| 52 | LCI | SR[450,690] | NDchl | RDVI2 | SR[450,690] | DDI |
| 53 | NPCI | PWI | TCARI/OSAVI | SRPI | PWI | PPR |
| 54 | NDVI[550,750] | Datt4 | PPR | SPVI | Datt4 | SR[450,550] |
| 55 | SR[430,680] | SIPI | SR[450,550] | DDn | SIPI | NDchl |
| 56 | DPI | MTVI1 | MCARI3 | GNDVI | MTVI1 | Rre |
| 57 | SRPI | SPVI | SR[450,690] | TVI | SPVI | TCARI/OSAVI |
| 58 | PBI | WBI | Gitelson2 | PBI | WBI | SR[450,690] |
| 59 | MSR2 | TCARI | TCARI | MND[680,800] | TCARI | NPQI |
| 60 | NDVI[710,750] | Rre | CI | RDVI | Rre | Datt1 |
References
- Nausheen, M.; Shirazi, S.A.; Stringer, L.C.; Sohail, M. Using UAV imagery to measure plant and water stress in winter wheat fields of drylands, south Punjab, Pakistan. Pak. J. Agric. Sci. 2021, 58, 1041–1050. [Google Scholar]
- Fei, S.; Hassan, M.; He, Z.; Chen, Z.; Shu, M.; Wang, J.; Li, C.; Xiao, Y. Assessment of Ensemble Learning to Predict Wheat Grain Yield Based on UAV-Multispectral Reflectance. Remote Sens. 2021, 13, 2338. [Google Scholar] [CrossRef]
- Yue, J.; Zhou, C.; Guo, W.; Feng, H.; Xu, K. Estimation of winter-wheat above-ground biomass using the wavelet analysis of unmanned aerial vehicle-based digital images and hyperspectral crop canopy images. Int. J. Remote Sens. 2021, 42, 1602–1622. [Google Scholar] [CrossRef]
- Galan, R.J.; Bernal-Vasquez, A.; Jebsen, C.; Piepho, H.; Thorwarth, P.; Steffan, P.; Gordillo, A.; Miedaner, T. Integration of genotypic, hyperspectral, and phenotypic data to improve biomass yield prediction in hybrid rye. Theor. Appl. Genet. 2020, 133, 3001–3015. [Google Scholar] [CrossRef]
- Yue, J.; Feng, H.; Li, Z.; Zhou, C.; Xu, K. Mapping winter-wheat biomass and grain yield based on a crop model and UAV remote sensing. Int. J. Remote Sens. 2021, 42, 1577–1601. [Google Scholar] [CrossRef]
- Zhou, X.; Kono, Y.; Win, A.; Matsui, T.; Tanaka, T.S.T. Predicting within-field variability in grain yield and protein content of winter wheat using UAV-based multispectral imagery and machine learning approaches. Plant. Prod. Sci. 2020, 24, 137–151. [Google Scholar] [CrossRef]
- Li, B.; Xu, X.; Zhang, L.; Han, J.; Bian, C.; Li, G.; Liu, J.; Jin, L. Above-ground biomass estimation and yield prediction in potato by using UAV-based RGB and hyperspectral imaging. ISPRS J. Photogramm. 2020, 162, 161–172. [Google Scholar] [CrossRef]
- Wheeler, T.; von Braun, J. Climate Change Impacts on Global Food Security. Science 2013, 341, 508–513. [Google Scholar] [CrossRef]
- Ma, B.L.; Dwyer, L.M.; Costa, C.; Cober, E.R.; Morrison, M.J. Early prediction of soybean yield from canopy reflectance measurements. Agron. J. 2001, 93, 1227–1234. [Google Scholar] [CrossRef] [Green Version]
- Elsayed, S.; El-Hendawy, S.; Khadr, M.; Elsherbiny, O.; Al-Suhaibani, N.; Alotaibi, M.; Tahir, M.U.; Darwish, W. Combining Thermal and RGB Imaging Indices with Multivariate and Data-Driven Modeling to Estimate the Growth, Water Status, and Yield of Potato under Different Drip Irrigation Regimes. Remote Sens. 2021, 13, 1679. [Google Scholar] [CrossRef]
- Fernandez-Manso, A.; Fernandez-Manso, O.; Quintano, C. SENTINEL-2A red-edge spectral indices suitability for discriminating burn severity. Int. J. Appl. Earth Obs. 2016, 50, 170–175. [Google Scholar] [CrossRef]
- Jiao, C.; Zheng, G.; Xie, X.; Cui, X.; Shang, G. Prediction of Soil Organic Matter Using Visible-Short Near-Infrared Imaging Spectroscopy. Spectrosc. Spect. Anal. 2020, 40, 3277–3281. [Google Scholar]
- Han, Y.; Liu, H.; Zhang, X.; Yu, Z.; Meng, X.; Kong, F.; Song, S.; Han, J. Prediction Model of Rice Panicles Blast Disease Degree Based on Canopy Hyperspectral Reflectance. Spectrosc. Spect. Anal. 2021, 41, 1220–1226. [Google Scholar]
- Zhang, Y.; Tian, Y.; Sun, W.; Mu, X.; Gao, P.; Zhao, G. Effects of Different Fertilization Conditions on Canopy Spectral Characteristics of Winter Wheat Based on Hyperspectral Technique. Spectrosc. Spect. Anal. 2020, 40, 535–542. [Google Scholar]
- Liu, Y.; Sun, Q.; Feng, H.; Yang, F. Estimation of Above-Ground Biomass of Potato Based on Wavelet Analysis. Spectrosc. Spect. Anal. 2021, 41, 1205–1212. [Google Scholar]
- Galan, R.J.; Bernal-Vasquez, A.; Jebsen, C.; Piepho, H.; Thorwarth, P.; Steffan, P.; Gordillo, A.; Miedaner, T. Early prediction of biomass in hybrid rye based on hyperspectral data surpasses genomic predictability in less-related breeding material. Theor. Appl. Genet. 2021, 134, 1409–1422. [Google Scholar] [CrossRef]
- Guo, W.; Qiao, H.; Zhao, H.; Zhang, J.; Pei, P.; Liu, Z. Cotton Aphid Damage Monitoring Using UAV Hyperspectral Data Based on Derivative of Ratio Spectroscopy. Spectrosc. Spect. Anal. 2021, 41, 1543–1550. [Google Scholar]
- Liu, Y.; Feng, H.; Huang, J.; Yang, F.; Wu, Z.; Sun, Q.; Yang, G. Estimation of Potato Above-Ground Biomass Based on Hyperspectral Characteristic Parameters of UAV and Plant Height. Spectrosc. Spect. Anal. 2021, 41, 903–911. [Google Scholar]
- Wang, L.; Chen, S.; Li, D.; Wang, C.; Jiang, H.; Zheng, Q.; Peng, Z. Estimation of Paddy Rice Nitrogen Content and Accumulation Both at Leaf and Plant Levels from UAV Hyperspectral Imagery. Remote Sens. 2021, 13, 2956. [Google Scholar] [CrossRef]
- Nidamanuri, R.R.; Zbell, B. Use of field reflectance data for crop mapping using airborne hyperspectral image. ISPRS J. Photogramm. Remote Sens. 2011, 66, 683–691. [Google Scholar] [CrossRef]
- Yang, C.; Everitt, J.H.; Fernandez, C.J. Comparison of airborne multispectral and hyperspectral imagery for mapping cotton root rot. Biosyst. Eng. 2010, 107, 131–139. [Google Scholar] [CrossRef]
- Almugren, N.; Alshamlan, H. A Survey on Hybrid Feature Selection Methods in Microarray Gene Expression Data for Cancer Classification. IEEE Access 2019, 7, 78533–78548. [Google Scholar] [CrossRef]
- Jebli, I.; Belouadha, F.; Kabbaj, M.I.; Tilioua, A. Prediction of solar energy guided by Pearson correlation using machine learning. Energy 2021, 224, 124109. [Google Scholar] [CrossRef]
- Miron, B.K.; Witold, R.R. Feature Selection with the Boruta Package. J. Stat. Softw. 2010, 36, 11. [Google Scholar]
- Zhao, J.; Karimzadeh, M.; Masjedi, A.; Wang, T.; Ebert, D.S. FeatureExplorer: Interactive Feature Selection and Exploration of Regression Models for Hyperspectral Images. In Proceedings of the 2019 IEEE Visualization Conference (VIS), Vancouver, BC, Canada, 20–25 October 2019; pp. 161–165. [Google Scholar]
- Feng, L.; Zhang, Z.; Ma, Y.; Du, Q.; Williams, P.; Drewry, J.; Luck, B. Alfalfa Yield Prediction Using UAV-Based Hyperspectral Imagery and Ensemble Learning. Remote Sens. 2020, 12, 2028. [Google Scholar] [CrossRef]
- Pal, M. Ensemble Learning with Decision Tree for Remote Sensing Classification. Pro. World Acad. Sci. Eng. Technol. 2007, 26, 735–737. [Google Scholar]
- Jiang, H.; Tao, C.; Dong, Y.; Xiong, R. Robust low-rank multiple kernel learning with compound regularization. Eur. J. Oper. Res. 2021, 295, 634–647. [Google Scholar] [CrossRef]
- Peterson, K.T.; Sagan, V.; Sidike, P.; Hasenmueller, E.A.; Sloan, J.J.; Knouft, J.H. Machine Learning-Based Ensemble Prediction of Water-Quality Variables Using Feature-Level and Decision-Level Fusion with Proximal Remote Sensing. Photogramm. Eng. Rem. S. 2019, 85, 269–280. [Google Scholar] [CrossRef]
- Liang, L.; Yang, M.; Deng, K.; Zhang, L.; Lin, H.; Liu, Z. A new hyperspectral index for the estimation of nitrogen contents of wheat canopy. Acta Ecol. Sin. 2011, 31, 6594–6605. [Google Scholar]
- Ye, X.; Sakai, K.; He, Y. Development of Citrus Yield Prediction Model Based on Airborne Hyperspectral Imaging. Spectrosc. Spect. Anal. 2010, 30, 1295–1300. [Google Scholar]
- Xu, B.; Wen, G.; Su, Y.; Zhang, Z.; Chen, F.; Sun, Y. Application of multi-level information fusion for wear particle recognition of ferrographic images. Opt. Precis. Eng. 2018, 26, 1551–1560. [Google Scholar]
- Tewary, S.; Mukhopadhyay, S. HER2 Molecular Marker Scoring Using Transfer Learning and Decision Level Fusion. J. Digit. Imaging 2021, 34, 667. [Google Scholar] [CrossRef]
- Teng, S.; Chen, G.; Liu, Z.; Cheng, L.; Sun, X. Multi-Sensor and Decision-Level Fusion-Based Structural Damage Detection Using a One-Dimensional Convolutional Neural Network. Sensors 2021, 21, 3950. [Google Scholar] [CrossRef]
- Zhao, P.; Li, Z.Y.; Wang, C.K. Wood Species Recognition Based on Visible and Near-Infrared Spectral Analysis Using Fuzzy Reasoning and Decision-Level Fusion. J. Spectrosc. 2021, 2021, 1–16. [Google Scholar] [CrossRef]
- Attard, L.; Debono, C.J.; Valentino, G.; Di Castro, M. Vision-Based Tunnel Lining Health Monitoring via Bi-Temporal Image Comparison and Decision-Level Fusion of Change Maps. Sensors 2021, 21, 4040. [Google Scholar] [CrossRef]
- Yu, R.; Luo, Y.; Zhou, Q.; Zhang, X.; Wu, D.; Ren, L. A machine learning algorithm to detect pine wilt disease using UAV-based hyperspectral imagery and LiDAR data at the tree level. Int. J. Appl. Earth Obs. 2021, 101, 102363. [Google Scholar] [CrossRef]
- Ma, H.; Huang, W.; Dong, Y.; Liu, L.; Guo, A. Using UAV-Based Hyperspectral Imagery to Detect Winter Wheat Fusarium Head Blight. Remote Sens. 2021, 13, 3024. [Google Scholar] [CrossRef]
- Ashourloo, D.; Mobasheri, M.R.; Huete, A. Evaluating the Effect of Different Wheat Rust Disease Symptoms on Vegetation Indices Using Hyperspectral Measurements. Remote Sens. 2014, 6, 5107–5123. [Google Scholar] [CrossRef] [Green Version]
- Singh, K.D.; Duddu, H.S.N.; Vail, S.; Parkin, I.; Shirtliffe, S.J. UAV-Based Hyperspectral Imaging Technique to Estimate Canola (Brassica napus L.) Seedpods Maturity. Can. J. Remote Sens. 2021, 47, 33–47. [Google Scholar] [CrossRef]
- Zarco-Tejada, P.J.; Pushnik, J.C.; Dobrowski, S.; Ustin, S.L. Steady-state chlorophyll a fluorescence detection from canopy derivative reflectance and double-peak red-edge effects. Remote Sens. Environ. 2003, 84, 283–294. [Google Scholar] [CrossRef]
- Vergara-Diaz, O.; Zaman-Allah, M.A.; Masuka, B.; Hornero, A.; Zarco-Tejada, P.; Prasanna, B.M.; Cairns, J.E.; Araus, J.L. A Novel Remote Sensing Approach for Prediction of Maize Yield Under Different Conditions of Nitrogen Fertilization. Front. Plant. Sci. 2016, 7, 666. [Google Scholar] [CrossRef] [Green Version]
- Datt, B. A new reflectance index for remote sensing of chlorophyll content in higher plants: Tests using Eucalyptus leaves. J. Plant. Physiol. 1999, 154, 30–36. [Google Scholar] [CrossRef]
- le Maire, G.; Francois, C.; Dufrene, E. Towards universal broad leaf chlorophyll indices using PROSPECT simulated database and hyperspectral reflectance measurements. Remote Sens. Environ. 2004, 89, 1–28. [Google Scholar] [CrossRef]
- Main, R.; Cho, M.A.; Mathieu, R.; O’Kennedy, M.M.; Ramoelo, A.; Koch, S. An investigation into robust spectral indices for leaf chlorophyll estimation. ISPRS J. Photogramm. 2011, 66, 751–761. [Google Scholar] [CrossRef]
- Hunt, E.R., Jr.; Daughtry, C.S.T.; Eitel, J.U.H.; Long, D.S. Remote Sensing Leaf Chlorophyll Content Using a Visible Band Index. Agron. J. 2011, 103, 1090–1099. [Google Scholar] [CrossRef] [Green Version]
- Pu, R.; Gong, P.; Yu, Q. Comparative analysis of EO-1 ALI and Hyperion, and Landsat ETM+ data for mapping forest crown closure and leaf area index. Sensors 2008, 8, 3744–3766. [Google Scholar] [CrossRef] [Green Version]
- Herrmann, I.; Karnieli, A.; Bonfil, D.J.; Cohen, Y.; Alchanatis, V. SWIR-based spectral indices for assessing nitrogen content in potato fields. Int. J. Remote Sens. 2010, 31, 5127–5143. [Google Scholar] [CrossRef]
- Jurgens, C. The modified normalized difference vegetation index (mNDVI)—a new index to determine frost damages in agriculture based on Landsat TM data. Int. J. Remote Sens. 1997, 18, 3583–3594. [Google Scholar] [CrossRef]
- Dash, J.; Curran, P.J. The MERIS terrestrial chlorophyll index. Int. J. Remote Sens. 2004, 25, 5403–5413. [Google Scholar] [CrossRef]
- Haboudane, D.; Miller, J.R.; Pattey, E.; Zarco-Tejada, P.J.; Strachan, I.B. Hyperspectral vegetation indices and novel algorithms for predicting green LAI of crop canopies: Modeling and validation in the context of precision agriculture. Remote Sens. Environ. 2004, 90, 337–352. [Google Scholar] [CrossRef]
- le Maire, G.; Francois, C.; Soudani, K.; Berveiller, D.; Pontailler, J.; Breda, N.; Genet, H.; Davi, H.; Dufrene, E. Calibration and validation of hyperspectral indices for the estimation of broadleaved forest leaf chlorophyll content, leaf mass per area, leaf area index and leaf canopy biomass. Remote Sens. Environ. 2008, 112, 3846–3864. [Google Scholar] [CrossRef]
- Richardson, A.D.; Duigan, S.P.; Berlyn, G.P. An evaluation of noninvasive methods to estimate foliar chlorophyll content. New Phytol. 2002, 153, 185–194. [Google Scholar] [CrossRef] [Green Version]
- Metternicht, G. Vegetation indices derived from high-resolution airborne videography for precision crop management. Int. J. Remote Sens. 2003, 24, 2855–2877. [Google Scholar] [CrossRef]
- Aparicio, N.; Villegas, D.; Royo, C.; Casadesus, J.; Araus, J.L. Effect of sensor view angle on the assessment of agronomic traits by ground level hyper-spectral reflectance measurements in durum wheat under contrasting Mediterranean conditions. Int. J. Remote Sens. 2004, 25, 1131–1152. [Google Scholar] [CrossRef]
- Royo, C.; Aparicio, N.; Villegas, D.; Casadesus, J.; Monneveux, P.; Araus, J.L. Usefulness of spectral reflectance indices as durum wheat yield predictors under contrasting Mediterranean conditions. Int. J. Remote Sens. 2003, 24, 4403–4419. [Google Scholar] [CrossRef]
- Wu, C.; Niu, Z.; Tang, Q.; Huang, W. Estimating chlorophyll content from hyperspectral vegetation indices: Modeling and validation. Agric. For. Meteorol. 2008, 148, 1230–1241. [Google Scholar] [CrossRef]
- Rao, N.R.; Garg, P.K.; Ghosh, S.K.; Dadhwal, V.K. Estimation of leaf total chlorophyll and nitrogen concentrations using hyperspectral satellite imagery. J. Agric. Sci. 2008, 146, 65–75. [Google Scholar]
- Ceccato, P.; Gobron, N.; Flasse, S.; Pinty, B.; Tarantola, S. Designing a spectral index to estimate vegetation water content from remote sensing data: Part 1—Theoretical approach. Remote Sens. Environ. 2002, 82, 188–197. [Google Scholar] [CrossRef]
- Penuelas, J.; Gamon, J.A.; Fredeen, A.L.; Merino, J.; Field, C.B. Reflectance indices associated with physiological changes in nitrogen- and water-limited sunflower leaves. Remote Sens. Environ. 1994, 48, 135–146. [Google Scholar] [CrossRef]
- Blackburn, G.A. Spectral indices for estimating photosynthetic pigment concentrations: A test using senescent tree leaves. Int. J. Remote Sens. 1998, 19, 657–675. [Google Scholar] [CrossRef]
- Sims, D.A.; Gamon, J.A. Relationships between leaf pigment content and spectral reflectance across a wide range of species, leaf structures and developmental stages. Remote Sens. Environ. 2002, 81, 337–354. [Google Scholar] [CrossRef]
- Galvao, L.S.; Formaggio, A.R.; Tisot, D.A. Discrimination of sugarcane varieties in southeastern Brazil with EO-1 hyperion data. Remote Sens. Environ. 2005, 94, 523–534. [Google Scholar] [CrossRef]
- Underwood, E.; Ustin, S.; DiPietro, D. Mapping nonnative plants using hyperspectral imagery. Remote Sens. Environ. 2003, 86, 150–161. [Google Scholar] [CrossRef]
- Clevers, J.; De Jong, S.M.; Epema, G.F.; Van der Meer, F.D.; Bakker, W.H.; Skidmore, A.K.; Scholte, K.H. Derivation of the red edge index using the MERIS standard band setting. Int. J. Remote Sens. 2002, 23, 3169–3184. [Google Scholar] [CrossRef] [Green Version]
- Azadbakht, M.; Ashourloo, D.; Aghighi, H.; Radiom, S.; Alimohammadi, A. Wheat leaf rust detection at canopy scale under different LAI levels using machine learning techniques. Comput. Electron. Agric. 2019, 156, 119–128. [Google Scholar] [CrossRef]
- Wu, J.; Wang, D.; Bauer, M.E. Assessing broadband vegetation indices and QuickBird data in estimating leaf area index of corn and potato canopies. Field Crop. Res. 2007, 102, 33–42. [Google Scholar] [CrossRef]
- Lichtenthaler, H.K. Vegetation stress: An introduction to the stress concept in plants. J. Plant. Physiol. 1996, 148, 4–14. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Merzlyak, M.N. Remote estimation of chlorophyll content in higher plant leaves. Int. J. Remote Sens. 1997, 18, 2691–2697. [Google Scholar] [CrossRef]
- Broge, N.H.; Leblanc, E. Comparing prediction power and stability of broadband and hyperspectral vegetation indices for estimation of green leaf area index and canopy chlorophyll density. Remote Sens. Environ. 2001, 76, 156–172. [Google Scholar] [CrossRef]
- Guyon, I.; Weston, J.; Barnhill, S.; Vapnik, V. Gene selection for cancer classification using support vector machines. Mach. Learn. 2002, 46, 389–422. [Google Scholar] [CrossRef]
- Ramendra, P.; Ravinesh, C.D.; Yan, L.; Tek, M. Weekly soil moisture forecasting with multivariate sequential, ensemble empirical mode decomposition and Boruta-random forest hybridizer algorithm approach. Catena 2019, 177, 149–166. [Google Scholar]
- Gholami, H.; Mohammadifar, A.; Golzari, S.; Kaskaoutis, D.G.; Collins, A.L. Using the Boruta algorithm and deep learning models for mapping land susceptibility to atmospheric dust emissions in Iran. Aeolian Res. 2021, 50, 100682. [Google Scholar] [CrossRef]
- Wang, L.; Zhou, X.; Zhu, X.; Dong, Z.; Guo, W. Estimation of biomass in wheat using random forest regression algorithm and remote sensing data. Crop. J. 2016, 4, 212–219. [Google Scholar] [CrossRef] [Green Version]
- Zhai, Y.; Cui, L.; Zhou, X.; Gao, Y.; Fei, T.; Gao, W. Estimation of nitrogen, phosphorus, and potassium contents in the leaves of different plants using laboratory-based visible and near-infrared reflectance spectroscopy: Comparison of partial least-square regression and support vector machine regression methods. Int. J. Remote Sens. 2013, 34, 2502–2518. [Google Scholar]
- Chlingaryan, A.; Sukkarieh, S.; Whelan, B. Machine learning approaches for crop yield prediction and nitrogen status estimation in precision agriculture: A review. Comput. Electron. Agric. 2018, 151, 61–69. [Google Scholar] [CrossRef]
- Chen, C.C.; Schwender, H.; Keith, J.; Nunkesser, R.; Mengersen, K.; Macrossan, P. Methods for Identifying SNP Interactions: A Review on Variations of Logic Regression, Random Forest and Bayesian Logistic Regression. IEEE ACM Trans. Comput. Bi. 2011, 8, 1580–1591. [Google Scholar] [CrossRef]
- Wang, J.; Shi, T.; Yu, D.; Teng, D.; Ge, X.; Zhang, Z.; Yang, X.; Wang, H.; Wu, G. Ensemble machine-learning-based framework for estimating total nitrogen concentration in water using drone-borne hyperspectral imagery of emergent plants: A case study in an arid oasis, NW China. Environ. Pollut. 2020, 266, 115412. [Google Scholar] [CrossRef]
- Xianxian, G.; Mao, W.; Mingming, J.; Wenqing, W. Estimating mangrove leaf area index based on red-edge vegetation indices: A comparison among UAV, WorldView-2 and Sentinel-2 imagery. Int. J. Appl. Earth Obs. 2021, 103, 102493. [Google Scholar]
- Yu, Z.; Jian-wen, W.; Li-ping, C.; Yuan-yuan, F.U.; Hong-chun, Z.; Hai-kuan, F.; Xin-gang, X.U.; Zhen-hai, L.I. An entirely new approach based on remote sensing data to calculate the nitrogen nutrition index of winter wheat. J. Integr. Agric. 2021, 20, 2535–2551. [Google Scholar]
- Zhu, Y.; Liu, K.; Liu, L.; Myint, S.W.; Wang, S.; Liu, H.; He, Z. Exploring the Potential of WorldView-2 Red-Edge Band-Based Vegetation Indices for Estimation of Mangrove Leaf Area Index with Machine Learning Algorithms. Remote Sens. 2017, 9, 1060. [Google Scholar] [CrossRef] [Green Version]
- Xie, Y.; Wang, C.; Yang, W.; Feng, M.; Qiao, X.; Song, J. Canopy hyperspectral characteristics and yield estimation of winter wheat (Triticum aestivum) under low temperature injury. Sci. Rep. 2020, 10, 109–119. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, G.; Xiang-Nan, L.; Cheng-Qi, C. Research on hyperspectral information parameters of chlorophyll content of rice leaf in Cd-polluted soil environment. Guang Pu Xue Yu Guang Pu Fen Xi 2009, 29, 2713–2716. [Google Scholar]
- Apan, A.; Held, A.; Phinn, S.; Markley, J. Detecting sugarcane ‘orange rust’ disease using EO-1 Hyperion hyperspectral imagery. Int. J. Remote Sens. 2004, 25, 489–498. [Google Scholar] [CrossRef] [Green Version]
- Padalia, H.; Sinha, S.K.; Bhave, V.; Trivedi, N.K.; Kumar, A.S. Estimating canopy LAI and chlorophyll of tropical forest plantation (North India) using Sentinel-2 data. Adv. Space Res. 2020, 65, 458–469. [Google Scholar] [CrossRef]
- Cui, B.; Zhao, Q.; Huang, W.; Song, X.; Ye, H.; Zhou, X. Leaf chlorophyll content retrieval of wheat by simulated RapidEye, Sentinel-2 and EnMAP data. J. Integr. Agric. 2019, 18, 1230–1245. [Google Scholar] [CrossRef]
- Lin, W.; Huang, J.; Hu, X.; Zhao, M. Crop Yield Forecast Based On Modis Temperature-Vegetation Angel Index. J. Infrared Millim. W. 2010, 29, 476–480. [Google Scholar]
- Cao, S.; Liu, X.; Liu, M.; Cao, S.; Yao, S. Estimation of Leaf Area Index by Normalized Composite Vegetation Index Fusing the Spectral Feature of Canopy Water Content. Spectrosc. Spect. Anal. 2011, 31, 478–482. [Google Scholar]
- Kursa, M.B.; Jankowski, A.; Rudnicki, W.R. Boruta—A System for Feature Selection. Fund. Inform. 2010, 101, 271–285. [Google Scholar] [CrossRef]
- Paul, J.; Ambrosio, R.D.; Dupont, P. Kernel methods for heterogeneous feature selection. Neurocomputing 2015, 169, 187–195. [Google Scholar] [CrossRef] [Green Version]
- Salleh, F.H.M.; Arif, S.M.; Zainudin, S.; Firdaus-Raih, M. Reconstructing gene regulatory networks from knock-out data using Gaussian Noise Model and Pearson Correlation Coefficient. Comput. Biol. Chem. 2015, 59, 3–14. [Google Scholar] [CrossRef]
- Jain, D.K.A.; Shetty, N.; Naveen Kumar, L.; Sundaresh, D.C. Assessment of Usefulness of Anthropometric Data for Predicting the Scaphoid and the Screw Length: A New Technique. J. Hand Surg. Asian-Pac. Volume 2017, 22, 435–440. [Google Scholar] [CrossRef]
- Hsu, H.; Hsieh, C.; Lu, M. Hybrid feature selection by combining filters and wrappers. Expert Syst. Appl. 2011, 38, 8144–8150. [Google Scholar] [CrossRef]
- Ge, X.; Ding, J.; Wang, J.; Sun, H.; Zhu, Z. A New Method for Predicting Soil Moisture Based on UAV Hyperspectral Image. Spectrosc. Spect. Anal. 2020, 40, 602–609. [Google Scholar]
- Joris, T.; Jaak, S.; Karl, M.; Yves, M. Two-level preconditioning for Ridge Regression. Numer. Linear Algebr. 2021, 28, 2371. [Google Scholar]
- Yuanyuan, L.; Qianqian, Z.; Won, Y.S. Gaussian process regression-based learning rate optimization in convolutional neural networks for medical images classification. Expert Syst. Appl. 2021, 184, 115357. [Google Scholar]
- Elbeltagi, A.; Azad, N.; Arshad, A.; Mohammed, S.; Mokhtar, A.; Pande, C.; Etedali, H.R.; Bhat, S.A.; Islam, A.R.M.T.; Deng, J. Applications of Gaussian process regression for predicting blue water footprint: Case study in Ad Daqahliyah, Egypt. Agric. Water Manag. 2021, 255, 107052. [Google Scholar] [CrossRef]
- Shafaei, M.; Kisi, O. Predicting river daily flow using wavelet-artificial neural networks based on regression analyses in comparison with artificial neural networks and support vector machine models. Neural Comput. Appl. 2017, 28, 15–28. [Google Scholar] [CrossRef]
- Jurečka, F.; Fischer, M.; Hlavinka, P.; Balek, J.; Semerádová, D.; Bláhová, M.; Anderson, M.C.; Hain, C.; Žalud, Z.; Trnka, M. Potential of water balance and remote sensing-based evapotranspiration models to predict yields of spring barley and winter wheat in the Czech Republic. Agric. Water Manag. 2021, 256, 107064. [Google Scholar] [CrossRef]
- Bhavya, D.N.; Chethan, H.K. Feature and Decision Level Fusion in Children Multimodal Biometrics. Int. J. Recent Technol. Eng. (IJRTE). 2020, 8, 2522–2527. [Google Scholar]
- Fu, H.; Cui, G.; Li, X.; She, W.; Cui, D.; Zhao, L.; Su, X.; Wang, J.; Cao, X.; Liu, J.; et al. Estimation of ramie yield based on UAV (Unmanned Aerial Vehicle) remote sensing images. Acta Agron. Sin. 2020, 46, 1448–1455. [Google Scholar]
- Yuri, S.; Robert, D.; Peter, T. Integrating satellite imagery and environmental data to predict field-level cane and sugar yields in Australia using machine learning. Field Crop. Res. 2021, 260, 107984. [Google Scholar]
- Shen, B.; Liu, Y.; Fu, J. An Integrated Model for Robust Multisensor Data Fusion. Sensors 2014, 14, 19669–19686. [Google Scholar] [CrossRef] [Green Version]
- Verrelst, J.; Muñoz, J.; Alonso, L.; Delegido, J.; Rivera, J.P.; Camps-Valls, G.; Moreno, J. Machine learning regression algorithms for biophysical parameter retrieval: Opportunities for Sentinel-2 and-3. Remote Sens. Environ. 2012, 118, 127–139. [Google Scholar] [CrossRef]
- Garriga, M.; Romero-Bravo, S.; Estrada, F.; Mendez-Espinoza, A.M.; Gonzalez-Martinez, L.; Matus, I.A.; Castillo, D.; Lobos, G.A.; Del Pozo, A. Estimating carbon isotope discrimination and grain yield of bread wheat grown under water-limited and full irrigation conditions by hyperspectral canopy reflectance and multilinear regression analysis. Int. J. Remote Sens. 2021, 42, 2848–2871. [Google Scholar] [CrossRef]
- Zhang, X.; Zhao, J.; Yang, G.; Liu, J.; Cao, J.; Li, C.; Zhao, X.; Gai, J. Establishment of Plot-Yield Prediction Models in Soybean Breeding Programs Using UAV-Based Hyperspectral Remote Sensing. Remote Sens. 2019, 11, 2752. [Google Scholar] [CrossRef] [Green Version]
- Chandel, N.S.; Tiwari, P.S.; Singh, K.P.; Jat, D.; Gaikwad, B.B.; Tripathi, H.; Golhani, K. Yield prediction in wheat (Triticum aestivum L.) using spectral reflectance indices. Curr. Sci. 2019, 116, 272–278. [Google Scholar] [CrossRef]
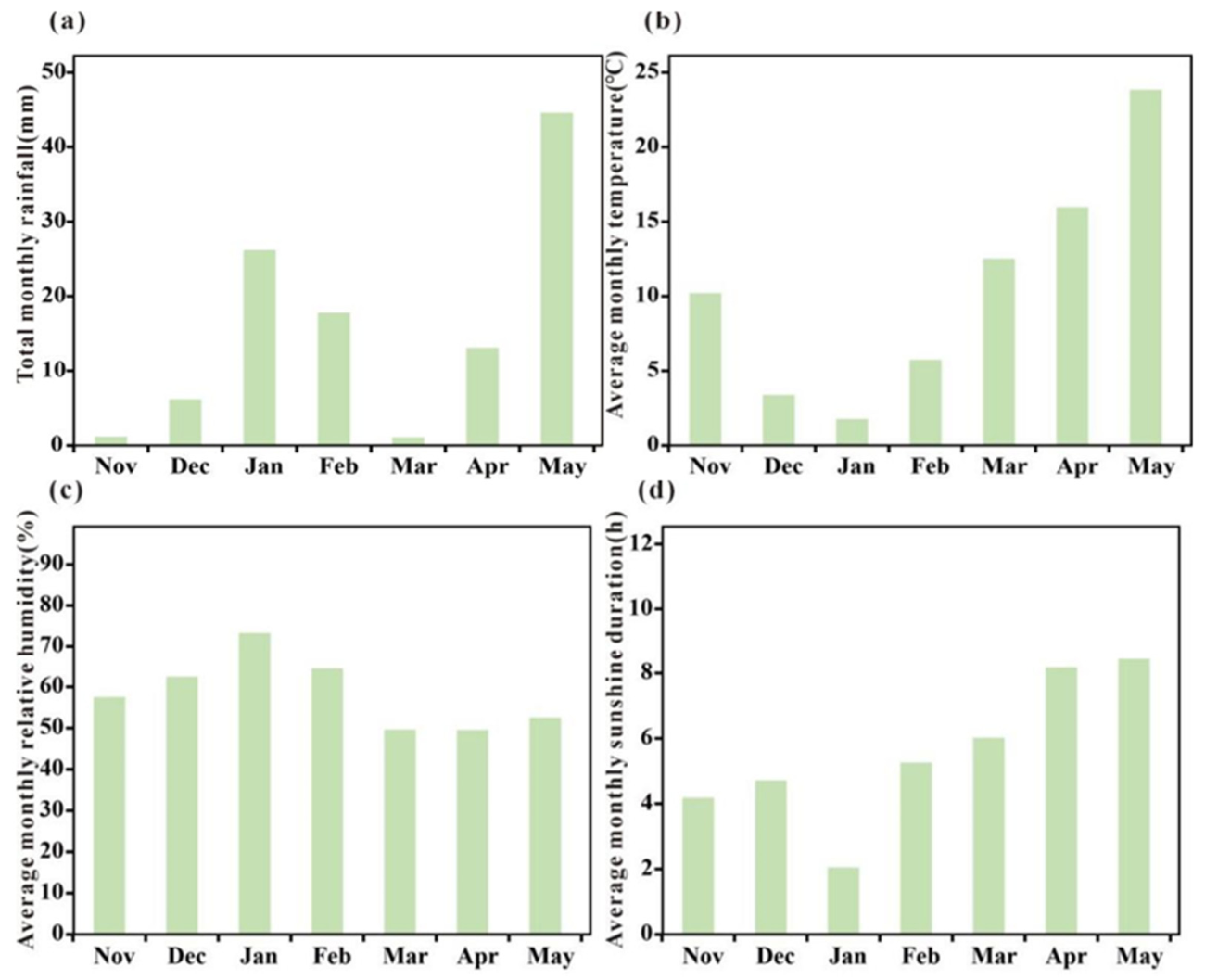
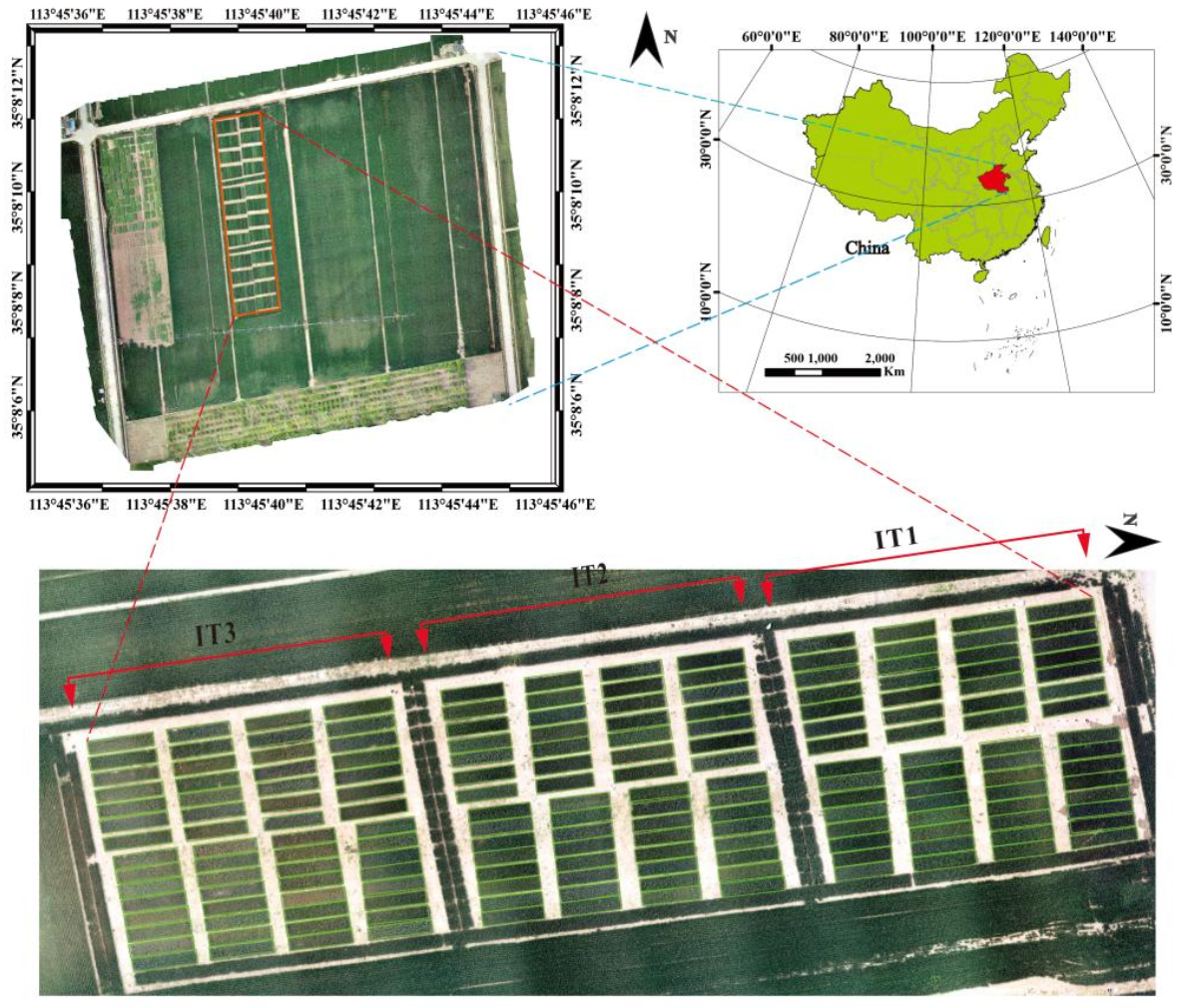


| Growth Itage | High Irrigation (mm) | Moderate Irrigation (mm) | Low Irrigation (mm) |
|---|---|---|---|
| Tillering | 35 | 35 | 35 |
| Overwintering | 35 | 35 | 35 |
| Greening | 35 | 25 | 20 |
| Jointing | 50 | 35 | 20 |
| Heading | 50 | 35 | 20 |
| Grain filling | 35 | 25 | 15 |
| Total | 240 | 190 | 145 |
| Full Form | Spectral Index or Ratio | Formula | Application | Reference |
|---|---|---|---|---|
| Curvative index | CI | . | Chlorophyll | [40] |
| Chlorophyll index red-edge | CIre | Vegetation, chlorophyll | [41] | |
| Datt1 | Vegetation, chlorophyll | [42] | ||
| Datt4 | ||||
| Datt6 | ||||
| Double difference index | DDI | Vegetation | [43] | |
| Double peak index | DPI | Vegetation, chlorophyll | [44] | |
| Gitelson2 | Chlorophyll | |||
| Green normalized difference vegetation index | GNDVI | Vegetation, chlorophyll | [45] | |
| Leaf chlorophyll index | LCI | Vegetation, chlorophyll | [46] | |
| Modified chlorophyll absorption ratio index | MCARI | Vegetation, chlorophyll | [47] | |
| MCARI3 | ||||
| Modified normalized difference | MND[680,800] | Pigments | [48] | |
| Modified normalized difference | MND[705,750] | |||
| Modified simple ratio | mSR | Vegetation | [43] | |
| Modified simple ratio 2 | mSR2 | [44] | ||
| MERIS terrestrial chlorophyll index | MTCI | Vegetation, chlorophyll | [49] | |
| Modified triangular vegetation index 1 | MTVI1 | Vegetation | [50] | |
| Modified triangular vegetation index 2 | MTVI2 | |||
| Normalized difference 550/531 | ND[531,550] | Vegetation, chlorophyll | [44] | |
| Normalized difference 682/553 | ND[553,682] | (R682 − R553)/(R682 + R553) | ||
| Normalized difference chlorophyll | NDchl | (R925 − R710)/(R925 + R710) | [51] | |
| New double difference index | DDn | Chlorophyll | ||
| Normalized difference red-edge | NDRE | Vegetation | [52] | |
| Normalized difference vegetation index | NDVI[650,750] | Vegetation, vitality | [53] | |
| NDVI[550,750] | ||||
| NDVI[710,750] | ||||
| Normalized pigment chlorophyll index | NPCI | Vegetation, chlorophyll | [54] | |
| Normalized difference pigment index | NPQI | (R415 − R435)/(R415 + R435) | Vegetation, chlorophyll | [55] |
| Optimized soil-adjusted vegetation index | OSAVI | Vegetation | [56] | |
| Plant biochemical index | PBI | Vegetation | [57] | |
| Plant pigment ratio | PPR | Vegetation | [58] | |
| Physiological reflectance index | PRI | Vegetation | [59] | |
| Pigment-specific normalized difference | PSNDb1 | Vegetation, chlorophyll | [60] | |
| PSNDc1 | ||||
| PSNDc2 | ||||
| Plant senescence reflectance index | PSRI | Vegetation | [61] | |
| Pigment-specific simple ratio | PSSRc1 | Vegetation, chlorophyll | [62] | |
| PSSRc2 | ||||
| Photosynthetic vigor ratio | PVR | Vegetation | [53] | |
| Plant water index | PWI | Vegetation, water stress | [63] | |
| Renormalized difference vegetation index | RDVI | Vegetation | [64] | |
| RDVI2 | ||||
| Reflectance at the inflexion point | Rre | Vegetation | [51] | |
| Red-edge stress vegetation index | RVSI | . | Vegetation | [65] |
| Soil-adjusted vegetation index | SAVI | Vegetation | [66] | |
| Structure intensive pigment index | SIPI | . | Pigments | [46] |
| Spectral polygon vegetation index | SPVI | Vegetation | [44] | |
| Simple ratio | SR[430,680] | Vegetation | [67] | |
| SR[440,740] | [44] | |||
| SR[550,672] | ||||
| SR[550,750] | ||||
| Disease-water stress index 4 | DSWI-4 | Vegetation, water stress | [68] | |
| Simple ratio pigment index | SRPI | Vegetation, chlorophyll | [69] | |
| Transformed chlorophyll absorption ratio | TCARI | Vegetation, chlorophyll | [45] | |
| Triangular chlorophyll index | TCI | Vegetation, chlorophyll | [45] | |
| Triangular vegetation index | TVI | Vegetation | [69] | |
| Water band index | WBI | Vegetation, water stress | [70] | |
| Combined MCARI/MTVI2 | MCARI/MTVI2 | Vegetation, chlorophyll | [45] | |
| Combined TCARI/OSAVI | TCARI/OSAVI | Vegetation, chlorophyll | [56] |
| Category | N | Mean | SD | Min | Q25 | Q50 | Q75 | Max | CV |
|---|---|---|---|---|---|---|---|---|---|
| All datasets | 180 | 6.55 | 1.59 | 3.13 | 5.27 | 6.65 | 7.71 | 9.71 | 24.33% |
| IT1 dataset | 60 | 7.97 | 1.01 | 5.58 | 7.43 | 7.97 | 8.65 | 9.71 | 12.68% |
| IT2 dataset | 60 | 6.73 | 1.02 | 4.28 | 6.08 | 6.75 | 7.55 | 8.75 | 15.16% |
| IT3 dataset | 60 | 4.94 | 0.96 | 3.13 | 4.31 | 4.89 | 5.55 | 7.54 | 19.50% |
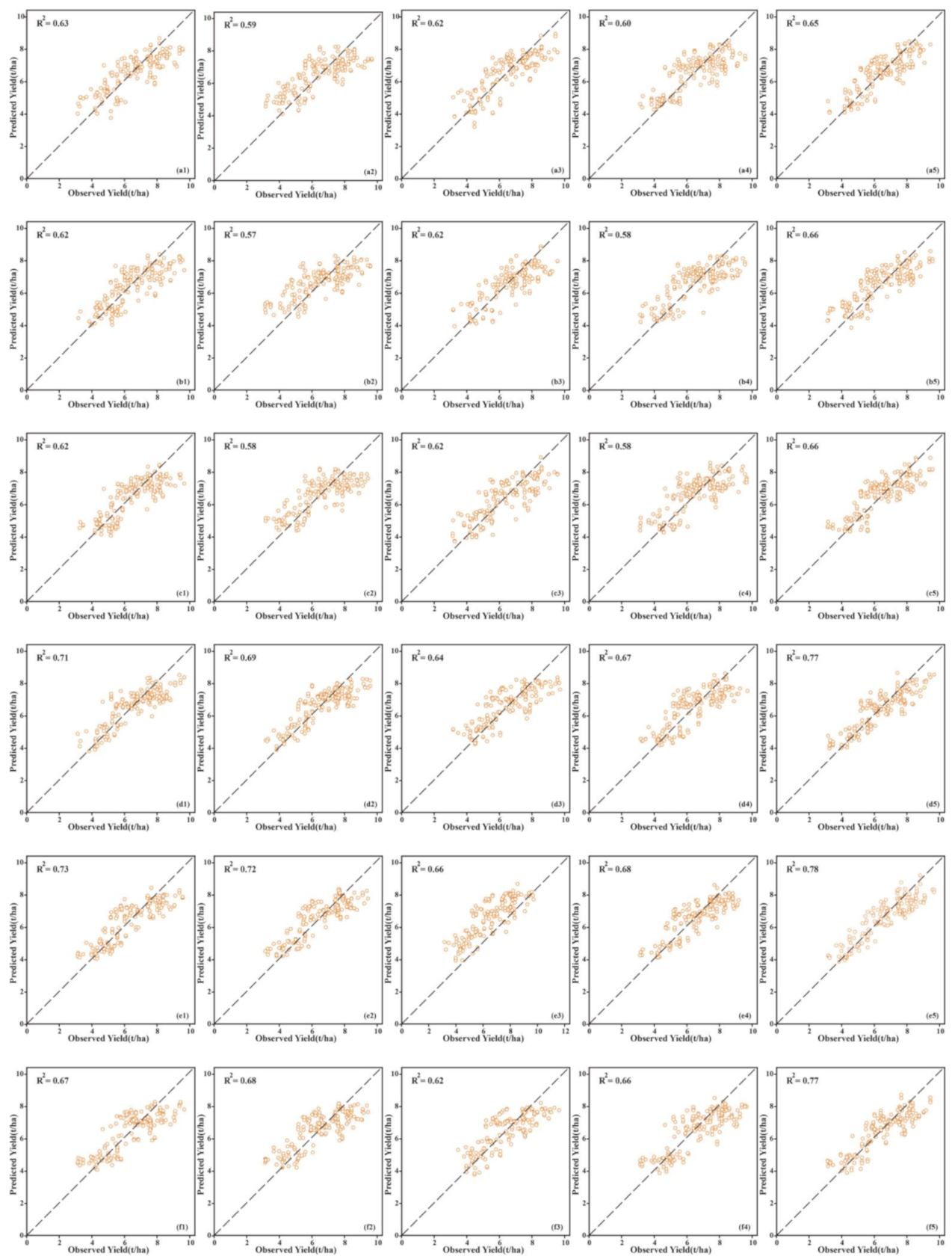
| Feature | Model | Flowering | Grain Filling | ||||||
|---|---|---|---|---|---|---|---|---|---|
| R2 | RMSE(t/ha) | RPIQ | RPD | R2 | RMSE(t/ha) | RPIQ | RPD | ||
| Selected features (RFE) | SVM | 0.63 | 1.03 | 2.40 | 1.60 | 0.71 | 0.90 | 2.64 | 1.83 |
| GP | 0.59 | 1.09 | 2.25 | 1.51 | 0.69 | 0.94 | 2.52 | 1.75 | |
| LRR | 0.62 | 1.03 | 2.38 | 1.59 | 0.64 | 1.00 | 2.36 | 1.64 | |
| RF | 0.60 | 1.05 | 2.35 | 1.57 | 0.67 | 0.94 | 2.51 | 1.74 | |
| DLF | 0.65 | 0.99 | 2.47 | 1.65 | 0.77 | 0.81 | 2.94 | 2.04 | |
| Selected features (Boruta) | SVM | 0.62 | 1.03 | 2.31 | 1.60 | 0.73 | 0.87 | 2.74 | 1.90 |
| GP | 0.57 | 1.11 | 2.12 | 1.48 | 0.72 | 0.89 | 2.65 | 1.84 | |
| LRR | 0.62 | 1.03 | 2.29 | 1.59 | 0.66 | 0.98 | 2.42 | 1.68 | |
| RF | 0.58 | 1.07 | 2.21 | 1.54 | 0.68 | 0.94 | 2.53 | 1.76 | |
| DLF | 0.66 | 0.98 | 2.40 | 1.67 | 0.78 | 0.79 | 2.99 | 2.08 | |
| Selected features (PCC) | SVM | 0.62 | 1.03 | 2.29 | 1.61 | 0.67 | 0.94 | 2.52 | 1.74 |
| GP | 0.58 | 1.11 | 2.12 | 1.49 | 0.68 | 0.96 | 2.49 | 1.71 | |
| LRR | 0.62 | 1.03 | 2.28 | 1.60 | 0.63 | 1.03 | 2.32 | 1.60 | |
| RF | 0.58 | 1.08 | 2.19 | 1.54 | 0.66 | 0.96 | 2.47 | 1.70 | |
| DLF | 0.66 | 0.99 | 2.39 | 1.68 | 0.77 | 0.82 | 2.91 | 2.01 | |
| Full features | SVM | 0.59 | 1.05 | 2.25 | 1.56 | 0.68 | 0.95 | 2.51 | 1.73 |
| GP | 0.56 | 1.10 | 2.14 | 1.48 | 0.67 | 0.97 | 2.45 | 1.69 | |
| LRR | 0.58 | 1.07 | 2.22 | 1.53 | 0.60 | 1.05 | 2.26 | 1.56 | |
| RF | 0.57 | 1.08 | 2.20 | 1.52 | 0.65 | 0.97 | 2.44 | 1.68 | |
| DLF | 0.63 | 1.00 | 2.36 | 1.63 | 0.75 | 0.84 | 2.84 | 1.96 | |
| Feature | t | p-Value |
|---|---|---|
| IT1 VS IT2 | 7.097 | 0.000 |
| IT1 VS IT3 | 16.661 | 0.000 |
| IT2 VS IT3 | 9.348 | 0.000 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Chen, Z.; Cheng, Q.; Duan, F.; Sui, R.; Huang, X.; Xu, H. UAV-Based Hyperspectral and Ensemble Machine Learning for Predicting Yield in Winter Wheat. Agronomy 2022, 12, 202. https://doi.org/10.3390/agronomy12010202
Li Z, Chen Z, Cheng Q, Duan F, Sui R, Huang X, Xu H. UAV-Based Hyperspectral and Ensemble Machine Learning for Predicting Yield in Winter Wheat. Agronomy. 2022; 12(1):202. https://doi.org/10.3390/agronomy12010202
Chicago/Turabian StyleLi, Zongpeng, Zhen Chen, Qian Cheng, Fuyi Duan, Ruixiu Sui, Xiuqiao Huang, and Honggang Xu. 2022. "UAV-Based Hyperspectral and Ensemble Machine Learning for Predicting Yield in Winter Wheat" Agronomy 12, no. 1: 202. https://doi.org/10.3390/agronomy12010202
APA StyleLi, Z., Chen, Z., Cheng, Q., Duan, F., Sui, R., Huang, X., & Xu, H. (2022). UAV-Based Hyperspectral and Ensemble Machine Learning for Predicting Yield in Winter Wheat. Agronomy, 12(1), 202. https://doi.org/10.3390/agronomy12010202






