Deficit Irrigation Strategies on Tree Physiological and Chemical Properties: Treatment Effects, Prediction Based Model Analyses and Inter-Correlations
Abstract
:1. Introduction
2. Materials and Methods
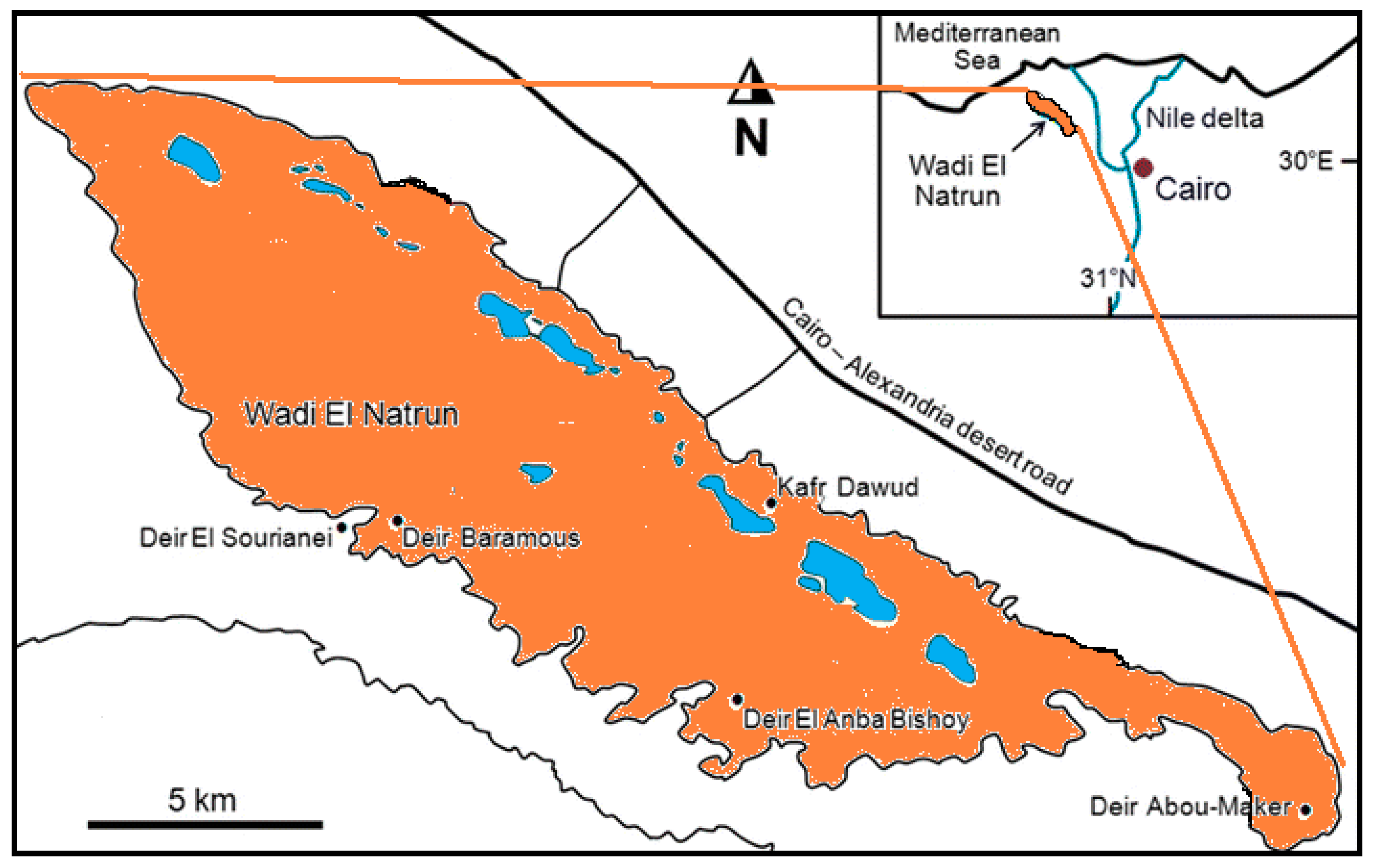
2.1. Plant Material and Experimental Site
2.2. Estimation of Irrigation Requirements for Apricot Tree
2.3. Deficit Irrigation Treatments
2.4. Measures of Tree Physiological Properties
2.4.1. General Measures
2.4.2. Bud Related Measures
2.4.3. Measures for Yield Related Attributes
2.5. Measures of Tree Chemical Properties
2.5.1. The Total Soluble Carbohydrates Content
2.5.2. Total Proline Content in Leaf
2.6. Statistical Analysis
2.6.1. ANOVA
2.6.2. Prediction Based Model Analysis
2.6.3. Correlation and Linear Regression Analyses among Parameters
2.6.4. Principal Component Analysis
3. Results
3.1. The Effect of Treatment Factors on Tree Physiological and Chemical Properties
3.1.1. General Measures for Tree Physiological Properties
3.1.2. Bud Related Measures for Tree Physiological Properties
3.1.3. Yield Related Measures for Tree Physiological Properties
3.1.4. Measures of Tree Chemical Properties
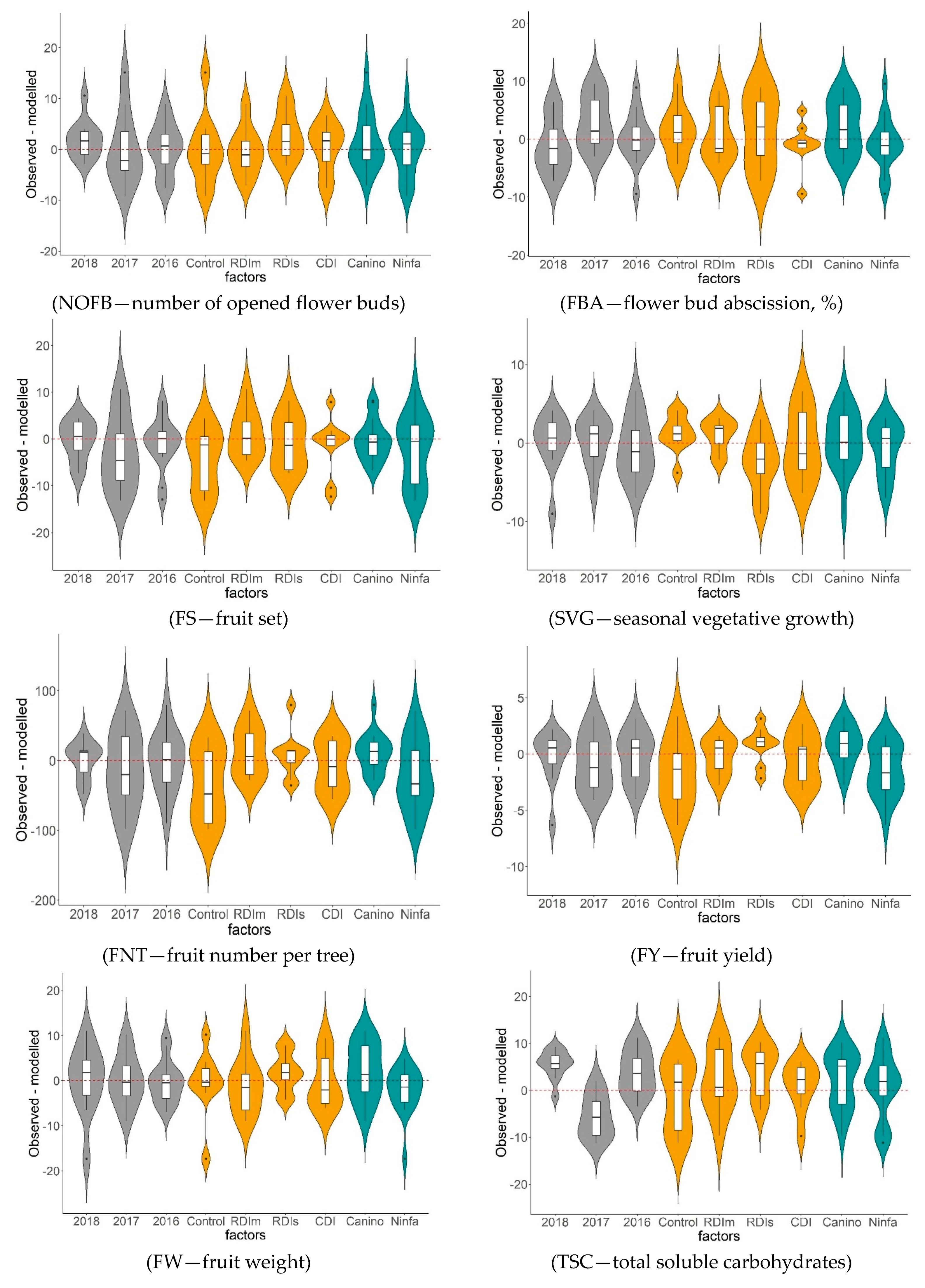
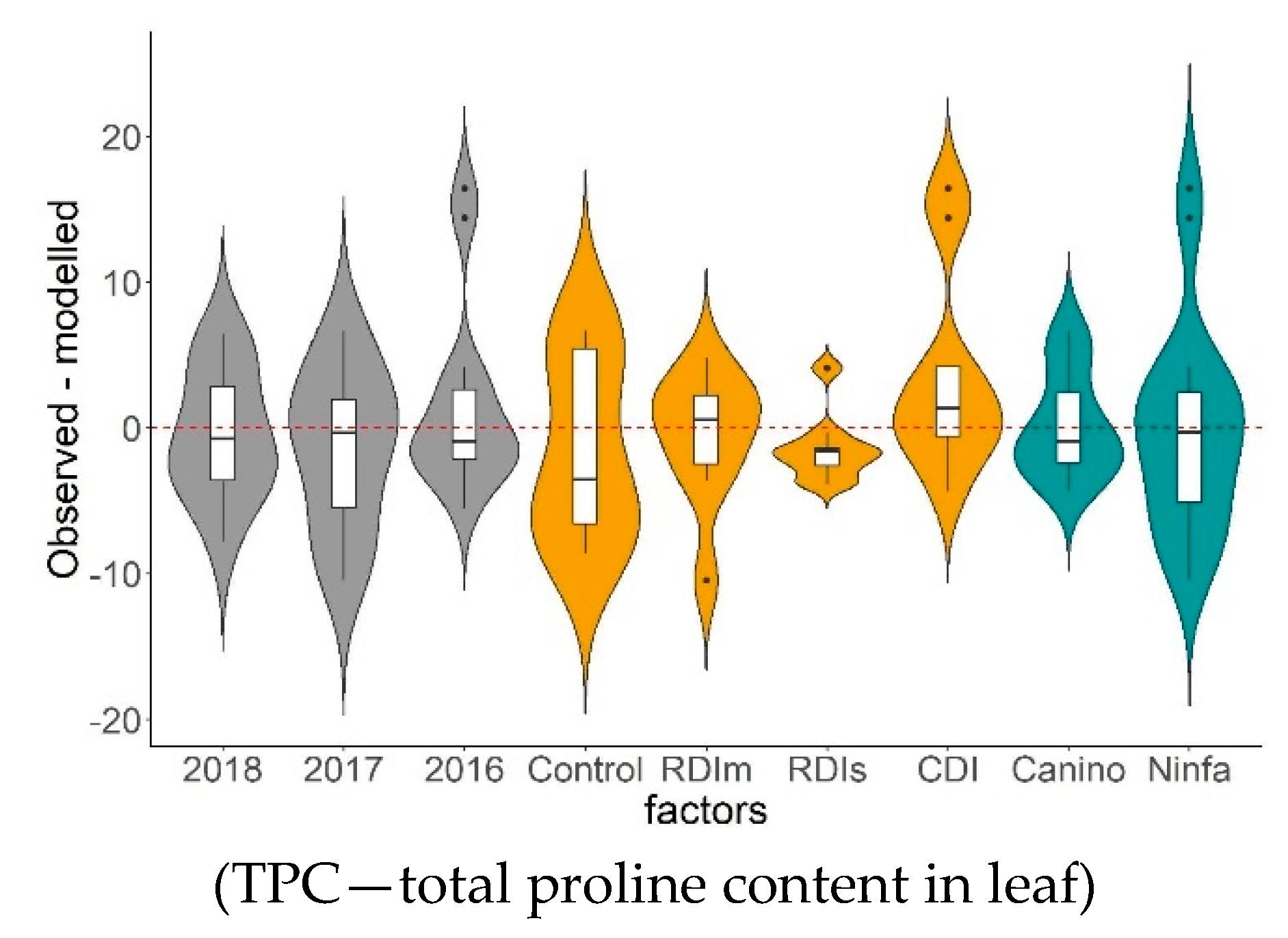
3.2. Prediction Based Model Analysis
3.3. Relationship among Parameters
3.3.1. Pearson Correlation Analyses
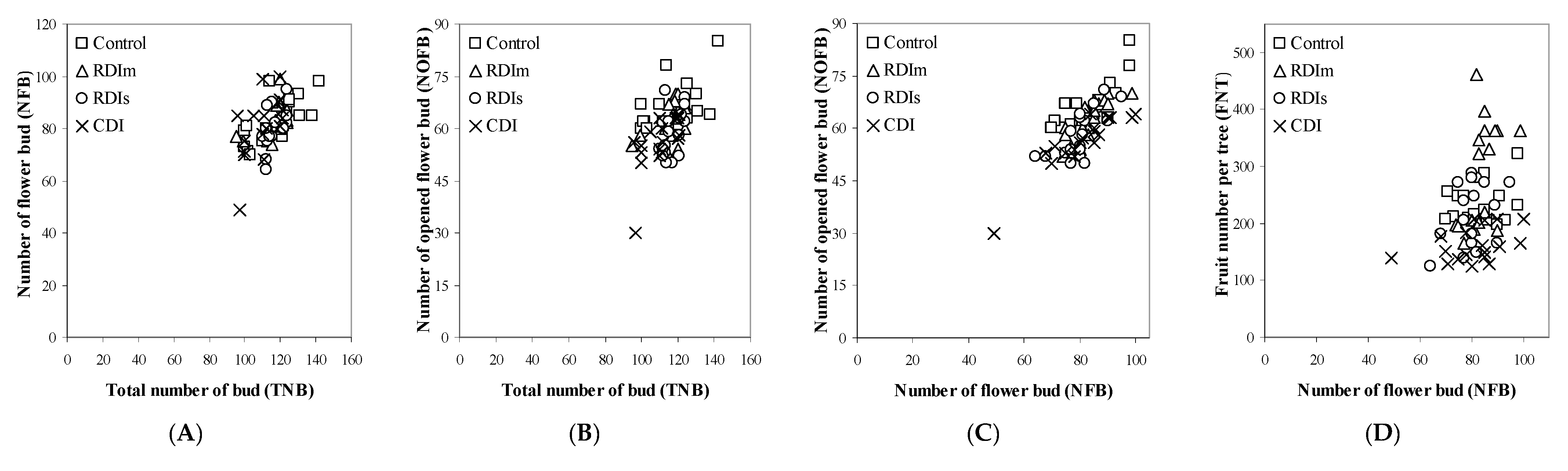
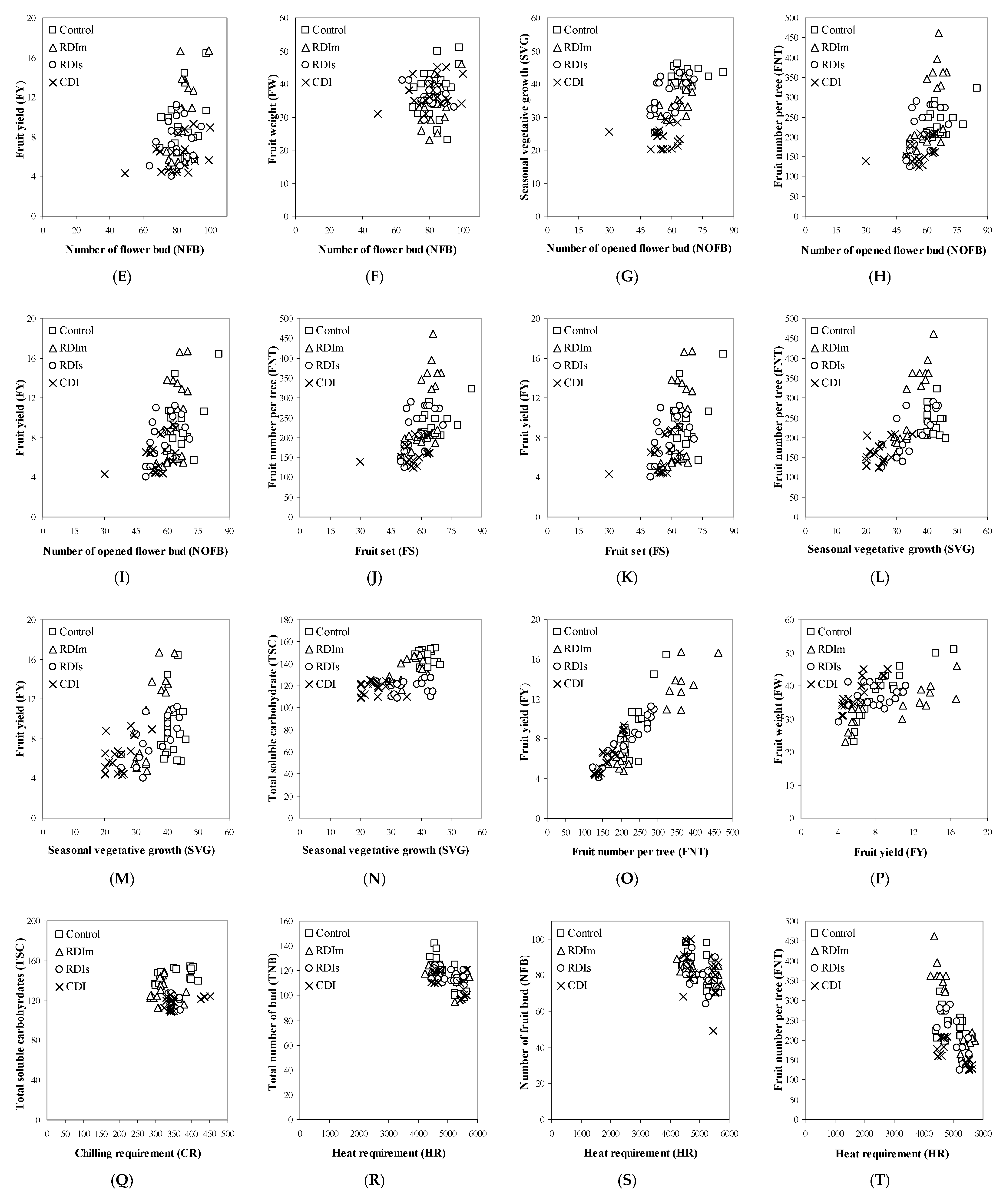
3.3.2. Linear Regression Analyses
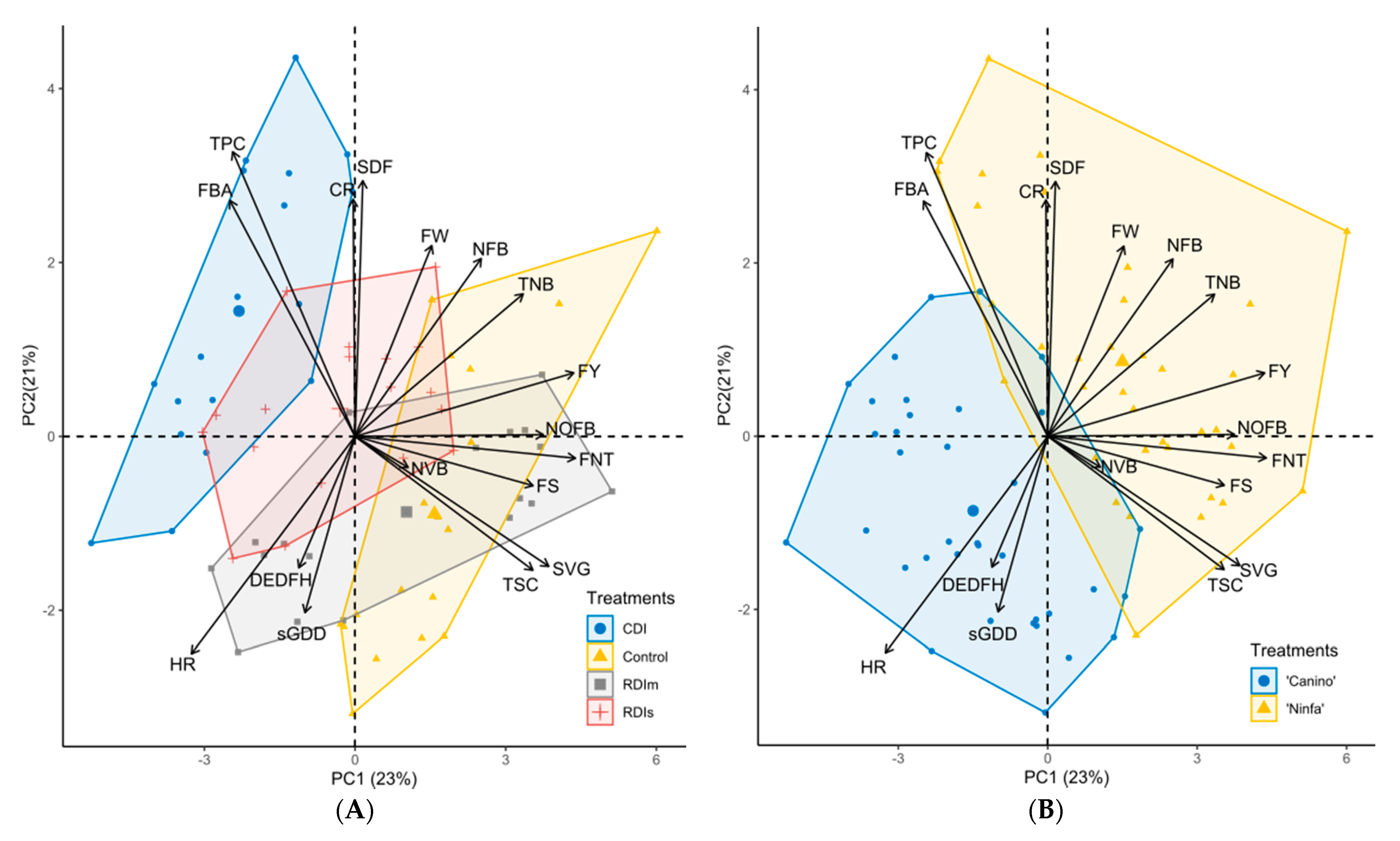
3.3.3. Principal Component Analyses
4. Discussion
5. Conclusions
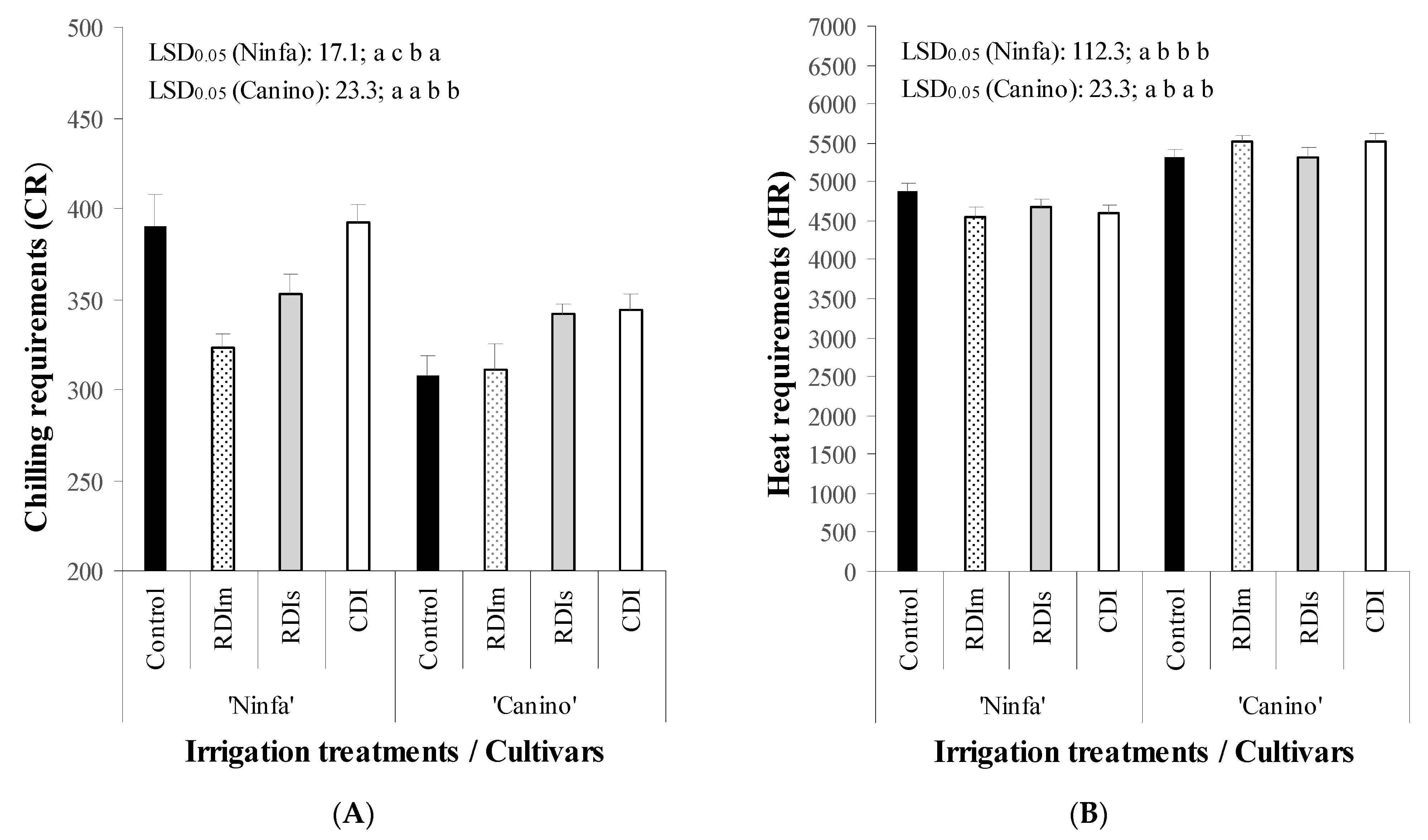
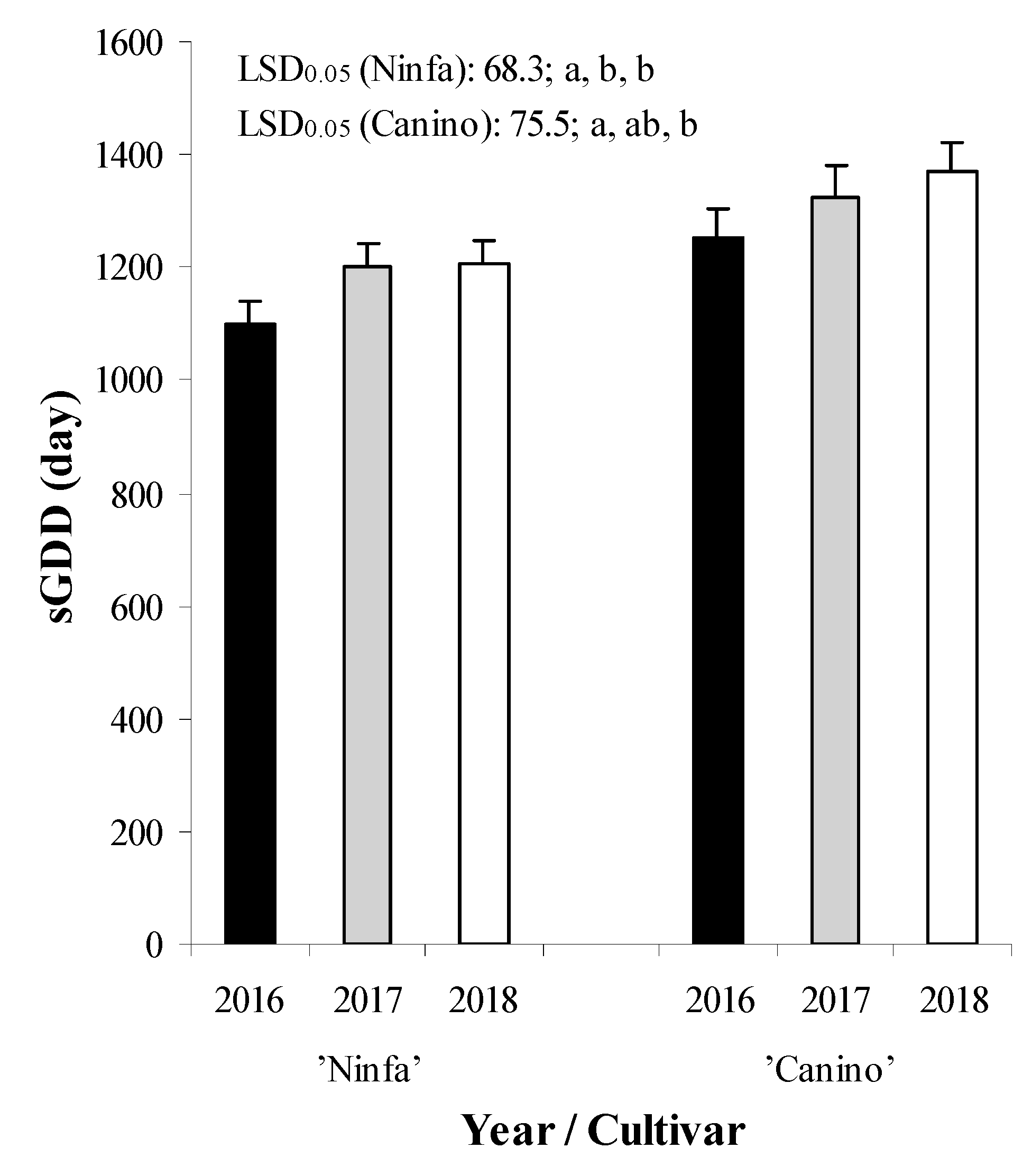
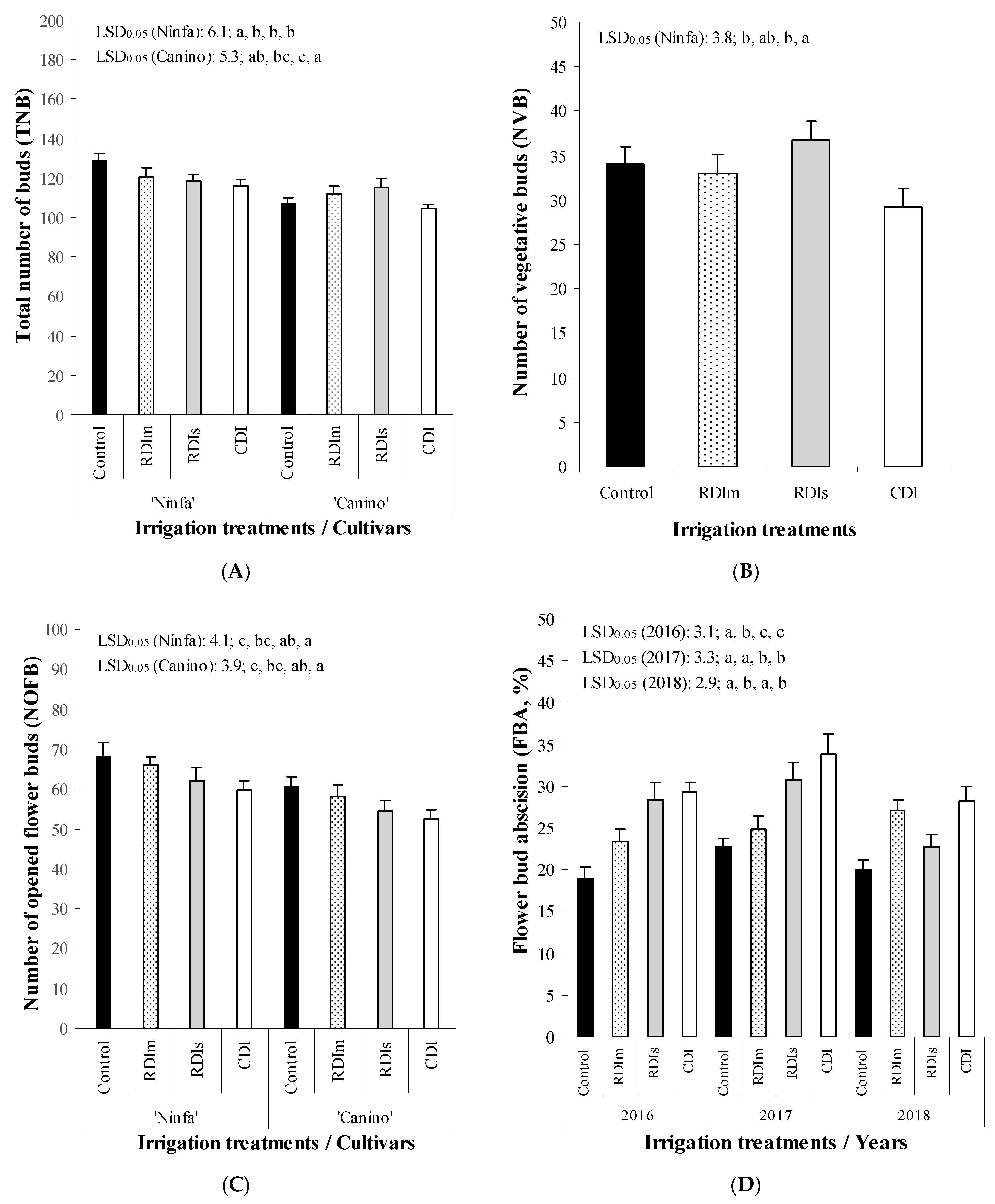
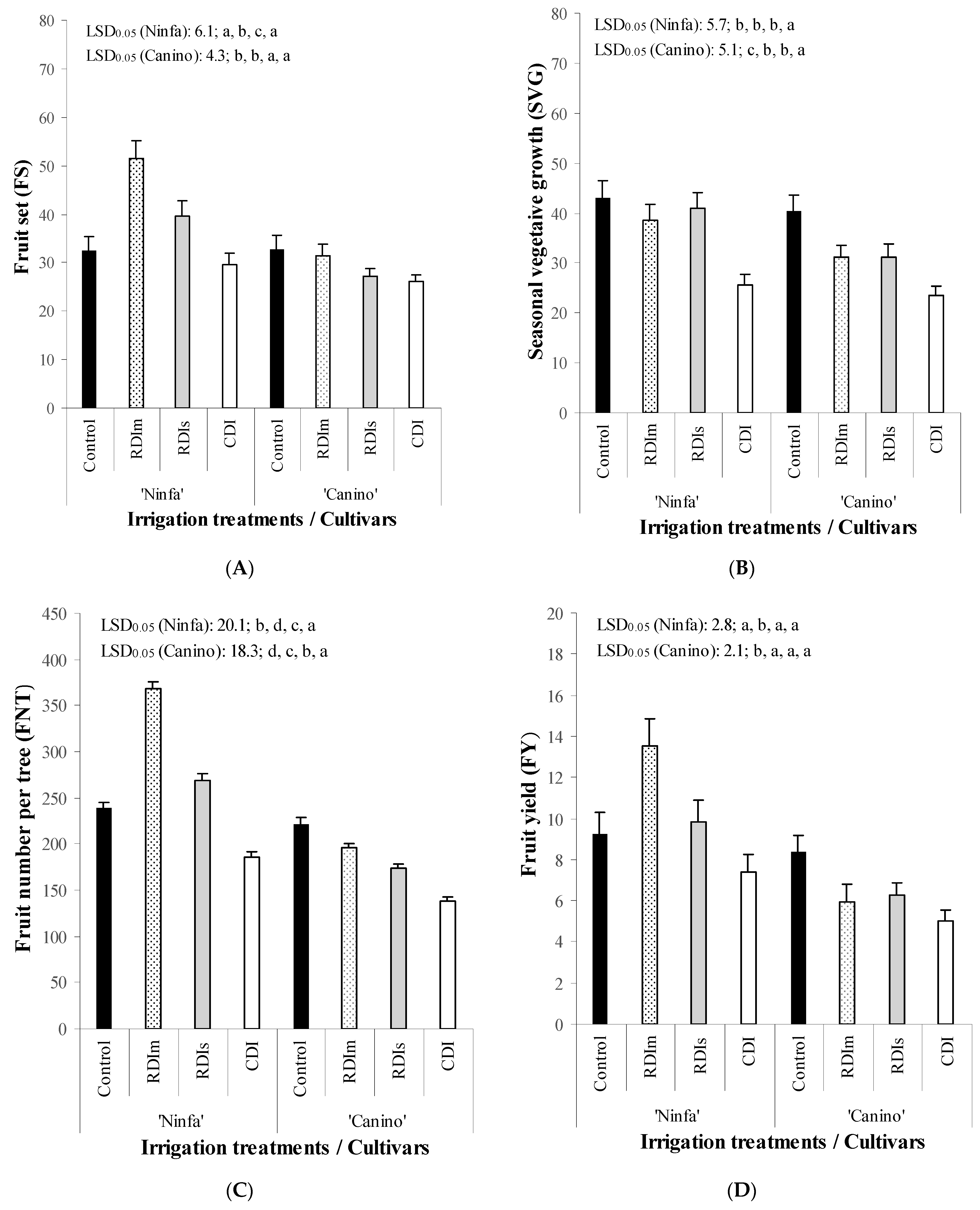
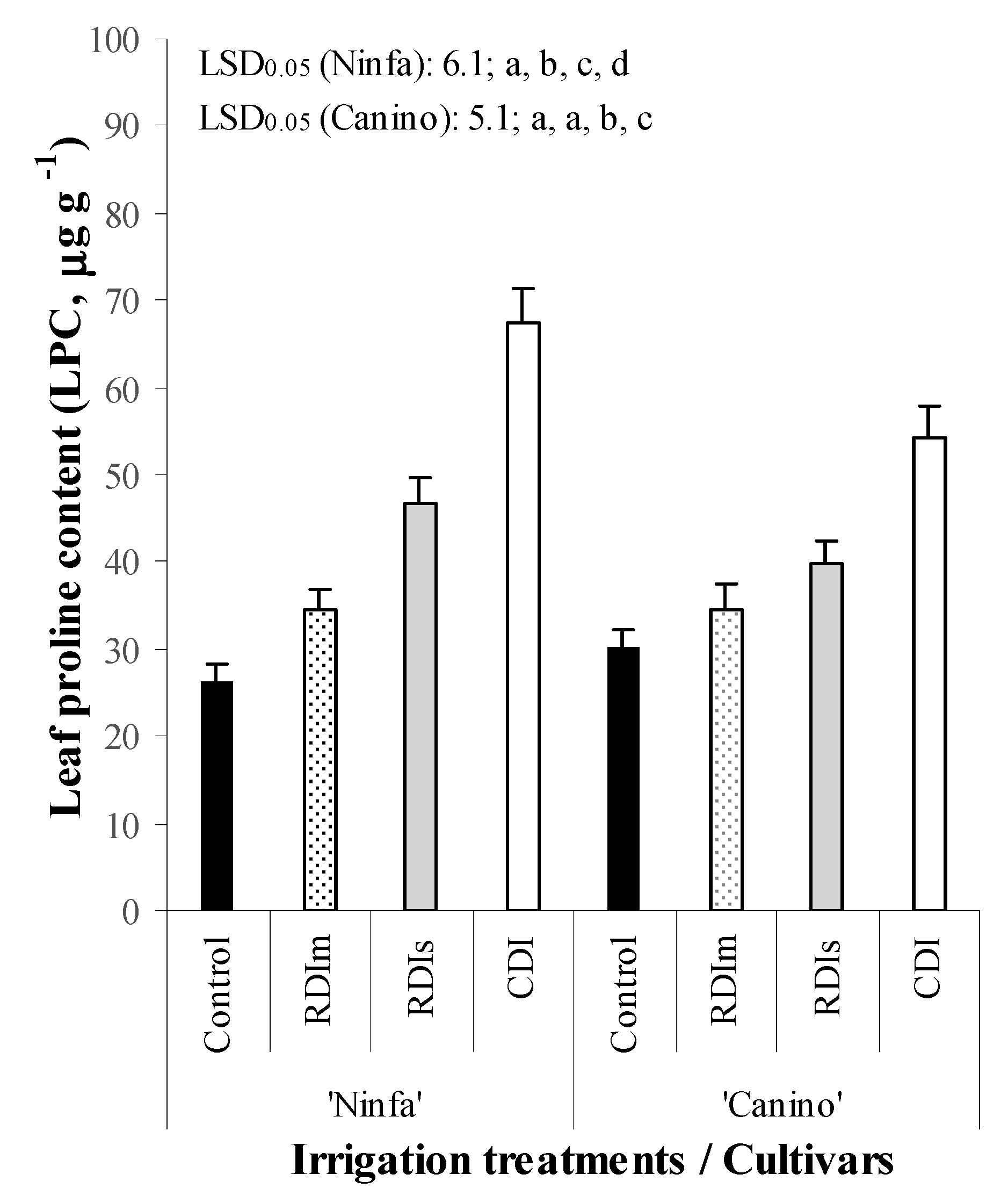
- Results showed that values of CR, HR, TNB, SDF, NOFB, FS, SVG, FNT, FY, TSC, and TPC values were affected significantly by both DI treatments and cultivars. Values of FBA were significantly affected by years and DI treatments, while sGDD by years and cultivars. Values of DEDFH, NFB, and FW were significantly influenced only by cultivars, while NVB only by DI treatments.
- Prediction based GLMs analysis demonstrated that GLMs can be predictors for the measured parameters in the DI treatments for the two cultivars and for the three years. The best goodness-of-fit of the predicted GLMs was reached for the measures of HR, NOFB, FS, SVG, FNT, TSC, and TPC.
- In all the four DI treatments, 22 pair-variables correlated significantly in Pearson correlation analyses, which were further confirmed by linear regression analysis.
- PCA explained 82% of the total variance and PC1, PC2, and PC3 explained 23, 21, and 15% of the total variance and correlated with the HR, TNB, FS, FNT, and FY; FBA, SVG, TSC, and TPC; and NFB, NVB, and NOFB, respectively, indicating strong relationships among tree physiological and chemical properties.
- Treatment effect, prediction model based analyses and inter-correlation analyses together showed that the RDIm treatment and cv. ‘Ninfa’ provided the most acceptable values for most measured properties compared to the fully irrigated control treatment.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Roussos, P.A.; Sefferou, V.; Denaxa, N.K.; Tsantili, E.; Stathis, V. Apricot (Prunus armeniaca L.) fruit quality attributes and phyto-chemicals under different crop load. Sci. Hortic. 2011, 129, 472–478. [Google Scholar] [CrossRef]
- Torrecillas, A.; Corell, M.; Galindo, A.; Pérez-López, D.; Memmi, H.; Rodríguez, P. Agronomical effects of deficit irrigation in apricot, peach, and plum trees. In Water Scarcity and Sustainable Agriculture in Semiarid Environment: Tools, Strategies, and Challenges for Woody Crops; Elsevier Inc.: Amsterdam, The Netherlands, 2018; pp. 87–109. [Google Scholar] [CrossRef]
- Omar, M.E.D.M.; Moussa, A.M.A. Water management in Egypt for facing the future challenges. J. Adv. Res. 2016, 7, 403–412. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Geerts, S.; Raes, D. Deficit irrigation as an on-farm strategy to maximize crop water productivity in dry areas. Agric. Water Manag. 2009, 96, 1275–1284. [Google Scholar] [CrossRef] [Green Version]
- Thakur, A.; Singh, Z. Deficit irrigation in nectarine: Fruit quality, return bloom and incidence of double fruits. Eur. J. Hortic. Sci. 2013, 78, 67–75. [Google Scholar]
- Rahmati, M.; Davarynejad, G.H.; Génard, M.; Bannayan, M.; Azizi, M.; Vercambre, G. Peach water relations, gas exchange, growth and shoot mortality under water deficit in semi-arid weather conditions. PLoS ONE 2015, 10, e0120246. [Google Scholar] [CrossRef] [Green Version]
- Soliman, M.A.M.; Ennab, H.A.; Mikhael, G.B. Effect of periodic deficit irrigation at different fruit growth stages on yield and fruit quality of “Anna” apple trees. J. Plant Prod. 2018, 9, 13–19. [Google Scholar] [CrossRef] [Green Version]
- Vallverdu, X.; Girona, J. Sensory quality and consumer acceptance of ‘Tardibelle’ peach are improved by deficit irrigation applied during stage II of fruit development. HortScience 2012, 47, 656–659. [Google Scholar] [CrossRef] [Green Version]
- Sotiropoulos, T.; Kalfountzos, D.; Aleksiou, I.; Kotsopoulos, S. Response of a clingstone peach cultivar to regulated deficit irrigation. Sci. Agric. 2010, 67, 164–169. [Google Scholar] [CrossRef] [Green Version]
- Ye, S.; Han, J.; Liu, T. Determination of optimum irrigation strategies and effect of drip irrigation system on growth and water use efficiency of pear jujube in Loess Hilly region of northern Shaanxi. PLoS ONE 2019, 14, e0221925. [Google Scholar] [CrossRef]
- Intrigliolo, D.S.; Castel, J.R. Effects of regulated deficit irrigation on growth and yield of young Japanese plum trees. J. Hortic. Sci. Biotechnol. 2005, 80, 177–182. [Google Scholar] [CrossRef]
- Moñino, M.J.; Blanco-Cipollone, F.; Vivas, A.; Bodelón, O.G.; Prieto, M.H. Evaluation of different deficit irrigation strategies in the late-maturing Japanese plum cultivar ‘Angeleno’. Agric. Water Manag. 2020, 234, 106–111. [Google Scholar] [CrossRef]
- Torrecillas, A.; Galego, R.; Pérez-Pastor, A.; Ruiz-Sánchez, M.C. Gas exchange and water relations of young apricot plants under drought conditions. J. Agric. Sci. 1999, 132, 445–452. [Google Scholar] [CrossRef] [Green Version]
- Alburquerque, N.; Burgos, L.; Egea, J. Apricot flower bud development and abscission related to chilling, irrigation and type of shoots. Sci. Hortic. 2003, 98, 265–276. [Google Scholar] [CrossRef]
- Pérez-Pastor, A.; Domingo, R.; Torrecillas, A.; Ruiz-Sánchez, M.C. Response of apricot trees to deficit irrigation strategies. Irrig. Sci. 2009, 27, 231–242. [Google Scholar] [CrossRef]
- Laajimi, N.O.; Abbas, F.; Rezgui, S.; Zekri, M.; Hellali, R. Effect of deficit irrigation on apricot (Prunus armeniaca L.) cv.‘Amor El Euch’ trees grown in the Mediterranean region of Tunisia. Fruit Veg. Cereal Sci. Biotechnol. 2009, 3, 16–21. [Google Scholar]
- Bozkurt, S.; Ödemiş, B.; Durgaç, C. Effects of deficit irrigation treatments on yield and plant growth of young apricot trees. N. Zeal. J. Crop Hortic. Sci. 2015, 43, 73–84. [Google Scholar] [CrossRef]
- Pérez-Sarmiento, F.; Mirás-Avalos, J.M.; Alcobendas, R.; Alarcón, J.J.; Mounzer, O.; Nicolás, E. Effects of regulated deficit irrigation on physiology, yield and fruit quality in apricot trees under mediterranean conditions. Span. J. Agric. Res. 2016, 14, 28. [Google Scholar] [CrossRef] [Green Version]
- Bartolini, S.; Piccolo, E.L.; Remorini, D. Different summer and autumn water deficit affect the floral differentiation and flower bud growth in apricot (Prunus armeniaca L.). Agronomy 2020, 10, 914. [Google Scholar] [CrossRef]
- Wei, J.; Liu, G.; Liu, D.; Chen, Y. Influence of irrigation during the growth stage on yield and quality in mango (Mangifera indica L). PLoS ONE 2017, 12, e0174498. [Google Scholar] [CrossRef]
- Ballester, C.; Castel, J.; Intrigliolo, D.S.; Castel, J.R. Response of Navel Lane Late citrus trees to regulated deficit irrigation: Yield components and fruit composition. Irrig. Sci. 2013, 31, 333–341. [Google Scholar] [CrossRef]
- Nagaz, K.; El Mokh, F.; Ben Hassen, N.; Masmoudi, M.M.; Ben Mechlia, N.; Baba, S.M.O. Impact of deficit irrigation on yield and fruit quality of orange trees (Citrus sinensis, L. Osbeck, cv. Meski Maltaise) in Southern Tunisia. Irrig. Drain. 2020, 69 (Suppl. S1), 186–193. [Google Scholar] [CrossRef] [Green Version]
- Ruiz-Sánchez, M.C.; Torrecillas, A.; Pérez-Pastor, A.; Domingo, R. Regulated deficit irrigation in apricot trees. Acta Hortic. 2000, 537, 759–766. [Google Scholar] [CrossRef]
- Kaya, S.; Evren, S.; Dasci, E.; Adiguzel, M.C.; Yilmaz, H. Effects of different irrigation regimes on vegetative growth, fruit yield and quality of drip-irrigated apricot trees. Afr. J. Biotechnol. 2010, 9, 5902–5907. [Google Scholar]
- Abrisqueta, J.M.; Ruiz, A.; Franco, J.A. Water balance of apricot trees (Prunus armeniaca L) under drip irrigation. Agric. Water Manag. 2001, 50, 211–227. [Google Scholar] [CrossRef]
- Razavi, F.; Hajilou, J.; Tabatabaei, S.J.; Dadpour, M.R. Comparison of chilling and heat requirement in some peach and apricot cultivars. Res. Plant Biol. 2011, 1, 40–47. [Google Scholar]
- Weinberger, J. Chilling requirements of peach varieties. Proc. Am. Soc. Hortic. Sci. 1950, 56, 122–128. [Google Scholar]
- Ruiz, D.; Campoy, J.A.; Egea, J. Chilling and heat requirements of apricot cultivars for flowering. Environ. Exp. Bot. 2007, 61, 254–263. [Google Scholar] [CrossRef]
- Mohamed, S.A.; Eid, T.A.; Water, S. Irrigation regimes for apricot trees under different rates of soil moisture depletion. Egypt J. Hortic. 2013, 40, 205–225. [Google Scholar] [CrossRef]
- Ranganna, S. Handbook of Analysis and Quality Control for Fruit and Vegetable Products, 2nd ed.; McGraw-Hill Inc.: Noida, India, 2007; p. 1152. [Google Scholar]
- Bates, L.S.; Waldren, R.P.; Teare, I.D. Rapid determination of free proline for water-stress studies. Plant Soil 1973, 39, 205–207. [Google Scholar] [CrossRef]
- Field, A.; Miles, J.; Field, Z. Discovering Statistics Using R; Sage Publications Ltd.: Thousand Oaks, CA, USA, 2012; p. 992. [Google Scholar]
- Brownlee, J. Machine Learning Mastery with R; e-Book. 2016, p. 224. Available online: https://machinelearningmastery.com/machine-learning-with-r/ (accessed on 3 October 2016).
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 2nd ed.; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2009; p. 763. [Google Scholar]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2020; Available online: https://www.R-project.org/ (accessed on 10 May 2020).
- Kuhn, M. Caret: Classification and regression training. R package version 6.0-86. 2020. Available online: https://CRAN.R-project.org/package=caret (accessed on 3 March 2020).
- Wickham, H. Ggplot2: Elegant Graphics for Data Analysis; Springer: New York, NY, USA, 2016; Available online: https://ggplot2.tidyverse.org (accessed on 7 June 2016).
- Basto, M.; Pereira, J.M. An SPSS R-menu for ordinal factor analysis. J. Stat. Softw. 2012, 46, 1–29. [Google Scholar] [CrossRef] [Green Version]
- Revelle, W. Psych: Procedures for Personality and Psychological Research; Northwestern University: Evanston, IL, USA, 2015; Available online: http://CRAN.R-project.org/package=psych (accessed on 12 June 2015).
- Lê, S.; Josse, J.; Husson, F. FactoMineR: An R package for multivariate analysis. J. Stat. Softw. 2008, 25, 30294. Available online: https://www.jstatsoft.org/article/view/v025i01 (accessed on 25 October 2008). [CrossRef] [Green Version]
- Kassambara, A.; Mundt, A. Factoextra: Extract and Visualize the Results of Multivariate Data Analyses. R package version 1.0.6. 2019. Available online: https://CRAN.R-project.org/package=factoextra (accessed on 1 June 2019).
- Nasrabadi, M.; Ramezanian, A.; Eshghi, S.; Sarkhosh, A. Chilling and heat requirement of pomegranate (Punica granatum L.) trees grown under sustained deficit irrigation. Sci. Hortic. 2020, 263, 109–117. [Google Scholar] [CrossRef]
- Luedeling, E.; Zhang, M.; Girvetz, E.H. Climatic changes lead to declining winter chill for fruit and nut trees in California during 1950–2099. PLoS ONE 2009, 16, e61664. [Google Scholar] [CrossRef] [PubMed]
- Salama, A.M.; Ezzat, A.; El-Ramady, H.; Alam-Eldein, S.M.; Okba, S.; Elmenofy, H.M.; Hassan, I.F.; Illés, A.; Holb, I.J. Temperate fruit trees under climate change: Challenges for dormancy and chilling requirements in warm winter regions. Horticulturae 2021, 7, 86. [Google Scholar] [CrossRef]
- Valentini, N.; Me, G.; Spanna, F.; Lovisetto, M. Chilling and heat requirement in apricot and peach varieties. Acta Hortic. 2004, 636, 199–203. [Google Scholar] [CrossRef]
- Viti, R.; Andreini, L.; Ruiz, D.; Egea, J.; Bartolini, S.; Iacona, C.; Campoy, J.A. Effect of climatic conditions on the overcoming of dormancy in apricot flower buds in two Mediterranean areas: Murcia (Spain) and Tuscany (Italy). Sci. Hortic. 2010, 124, 217–224. [Google Scholar] [CrossRef]
- Demirtas, C.; Erturk, U.; Yazgan, S.; Candogan, B.N.; Soylu, A. Effects of different irrigation levels on the vegetative growth, flower bud formation and fruit quality of sweet cherry in western part of Turkey. J. Food Agric. Environ. 2008, 6, 168–172. [Google Scholar]
- Blanco, V.; Blaya-Ros, P.J.; Torres-Sánchez, R.; Domingo, R. Influence of regulated deficit irrigation and. Plants 2020, 9, 94. [Google Scholar] [CrossRef] [Green Version]
- Mitchell, P.D.; Chalmers, D.J.; Jerie, P.H.; Burge, G. The use of initial withholding of irrigation and tree spacing to enhance the effect of regulated deficit irrigation on pear trees. J. Am. Soc. Hortic. Sci. 1986, 111, 858–861. [Google Scholar]
- Torrecillas, A.; Ruiz-Sanchez, M.C.; Domingo, R.; Hernández-Borroto, J. Regulated deficit irrigation on Fino lemon trees. Acta Hortic. 1993, 335, 205–212. [Google Scholar] [CrossRef]
- Nuñez-Elisea, R.; Davenport, T. Flowering of mango trees in containers as influenced by seasonal temperature and water stress. Sci. Hortic. 1994, 58, 57–66. [Google Scholar] [CrossRef]
- Ginestar, C.; Castel, J.R. Response of young ‘Clementine’ in citrus trees to water stress during different phenological periods. J. Hortic. Sci. 1996, 71, 551–559. [Google Scholar] [CrossRef]
- González-Altozano, P.; Castel, J.R. Regulated deficit irrigation in ‘Clementina de Nules’ citrus trees. I. Yield and fruit quality effects. J. Hortic. Sci. Biotechnol. 1999, 74, 706–713. [Google Scholar] [CrossRef]
- Ruiz-Sánchez, M.C.; Egea, J.; Galego, R.; Torrecillas, A. Floral biology of ‘Búlida’ apricot trees subjected to postharvest drought stress. Ann. Appl. Biol. 1999, 135, 523–528. [Google Scholar] [CrossRef]
- Arzani, K.; Wood, D.; Lawes, G.S. Influence of first season application of paclobutrazol, root-pruning and regulated deficit irrigation on second season flowering and fruiting of mature ‘Sundrop’ apricot trees. Acta Hortic. 2000, 516, 75–82. [Google Scholar] [CrossRef]
- Marsal, J.; Mata, M.; Arbonés, A.; Rufat, J.; Girona, J. Regulated deficit irrigation and rectification scheduling in young pear trees: An evaluation based on vegetative and productive response. Eur. J. Agron. 2002, 17, 111–122. [Google Scholar] [CrossRef]
- Cuevas, J.; Romero, I.M.; Fernández, M.D.; Hueso, J.J. Deficit irrigation schedules to promote early flowering in ’Algerie’ loquat. Acta Hortic. 2007, 750, 281–286. [Google Scholar] [CrossRef] [Green Version]
- Perez-Perez, J.G.; Romero, P.; Navarro, J.M.; Botıa, P. Response of sweet orange cv ‘Lane late’ to deficit irrigation in two rootstocks. I: Water relations, leaf gas exchange and vegetative growth. Irrig. Sci. 2008, 26, 415–425. [Google Scholar] [CrossRef]
- Perez-Perez, J.G.; Romero, P.; Navarro, J.M.; Botıa, P. Response of sweet orange cv ‘Lane late’ to deficit-irrigation strategy in two rootstocks. II: Flowering, fruit growth, yield and fruit quality. Irrig. Sci. 2008, 26, 519–529. [Google Scholar] [CrossRef]
- Girona, J.; Mata, M.; Arbones, A.; Alegre, S.; Rufat, J.; Marsal, J. Peach tree response to single and combined regulated deficit irrigation regimes under shallow soils. J. Am. Soc. Hortic. Sci. 2003, 128, 432–440. [Google Scholar] [CrossRef] [Green Version]
- Selahvarzi, Y.; Zamani, Z.; Fatahi, R.; Talaei, A.R. Effect of deficit irrigation on flowering and fruit properties of pomegranate (Punica granatum cv. Shahvar). Agric. Water Manag. 2017, 192, 189–197. [Google Scholar] [CrossRef]
- Egea, J.; Burgos, L. Fructification problems in continental apricot cultivars growing under Mediterranean climate. Ovule development at anthesis in two climatic areas. J. Hortic. Sci. Biotechnol. 1998, 73, 107–110. [Google Scholar] [CrossRef]
- Torrecillas, A.; Domingo, R.; Galego, R.; Ruiz-Sánchez, M.C. Apricot tree response to withholding irrigation at different phenological periods. Sci. Hortic. 2000, 85, 201–215. [Google Scholar] [CrossRef]
- Marsal, J.; López, G.; Girona, J. Recent advances in regulated deficit irrigation (RDI) in woody perennials and future perspectives. Acta Hortic. 2008, 792, 429–439. [Google Scholar] [CrossRef]
- Pérez-Pastor, A.; Ruiz-Sánchez, M.C.; Domingo, R. Effects of timing and intensity of deficit irrigation on vegetative and fruit growth of apricot trees. Agric. Water Manag. 2014, 134, 110–118. [Google Scholar] [CrossRef]
- Domingo, R.; Ruiz-Sánchez, M.C.; Sánchez-Blanco, M.J.; Torecillas, A. Water relations, growth and yield of Fino lemon trees under regulated deficit irrigation. Irrig. Sci. 1996, 16, 115–123. [Google Scholar] [CrossRef]
- González-Altozano, P.; Castel, J.R. Regulated deficit irrigation in ‘Clementina de Nules’ citrus trees. II: Vegetative growth. J. Hortic. Sci. Biotechnol. 2000, 75, 388–392. [Google Scholar] [CrossRef]
- Mitchell, P.D.; Chalmers, D.J. The effects of reduced water supply on peach tree growth and yields. J. Am. Soc. Hortic. Sci. 1982, 107, 853–856. [Google Scholar]
- Mitchell, P.D.; Jerie, P.H.; Chalmers, D.J. Effects of regulated water deficits on pear tree growth, flowering, fruit growth and yield. J. Am. Soc. Hortic. Sci. 1984, 109, 604–606. [Google Scholar]
- Hipps, N.A.; Pages, L.; Huguet, J.G.; Serra, V. Influence of controlled water supply on shoot and root development of young peach trees. Tree Physiol. 1995, 15, 95–103. [Google Scholar] [CrossRef] [PubMed]
- Girona, J.; Gelly, M.; Mata, M.; Arbones, A.; Rufat, J.; Marsal, J. Peach tree response to single and combined deficit irrigation regimes in deep soils. Agric. Water Manag. 2005, 72, 97–108. [Google Scholar] [CrossRef]
- Fernandez, E.; Luedeling, E.; Behrend, D.; Van De Vliet, S.; Kunz, A.; Fadón, E. Mild water stress makes apple buds more likely to flower and more responsive to artificial forcing impacts of an unusually warm and dry summer in Germany. Agronomy 2020, 10, 274. [Google Scholar] [CrossRef] [Green Version]
- Candogan, B.N.; Yazgan, S. The effects of different irrigation levels on vegetative growth of young dwarf cherry trees in a sub-humid climate. Pak. J. Bot. 2010, 42, 3399–3408. [Google Scholar]
- Nieto, E.; Prieto, M.H.; Fortes, R.; Gonzalez, V.; Campillo, C. Response of a long-lived cherry cultivar to contrasting irrigation strategies in the Jerte Valley, Extremadura, Spain. Acta Hortic. 2017, 1161, 197–204. [Google Scholar] [CrossRef]
- Blanco, V.; Torres-Sánchez, R.; Blaya-Ros, P.J.; Pérez-Pastor, A.; Domingo, R. Vegetative and reproductive response of ‘Prime Giant’ sweet cherry trees to regulated deficit irrigation. Sci. Hortic. 2019, 249, 478–489. [Google Scholar] [CrossRef]
- Aganchich, B.; Tahi, H.; Wahbi, S.; Elmodaffar, C.; Serraj, R. Growth, water relations and antioxidant defense mechanisms of olive (Olea europaea L.) subjected to Partial Root Drying (PRD) and Regulated Deficit Irrigation (RDI). Plant Biosyst. 2007, 141, 252–264. [Google Scholar] [CrossRef]
- Johnson, R.S.; Handley, D.F. Using water stress to control vegetative growth and productivity of temperate fruit trees. HortScience 2000, 35, 1048–1050. [Google Scholar] [CrossRef] [Green Version]
- Ruiz-Sánchez, M.C.; Domingo, R.; Castel, J.R. Deficit irrigation in fruit trees and vines in Spain. Spanish J. Agric. Res. 2010, 8, S5–S20. [Google Scholar] [CrossRef] [Green Version]
- Cohen, A.; Goell, A. Fruit growth and dry matter accumulation in grapefruit during periods of water withholding and after reirrigation. Funct. Plant Biol. 1988, 15, 633–639. [Google Scholar] [CrossRef]
- González-Altozano, P.; Castel, J.R. Effects of regulated deficit irrigation on ‘Clementina de Nules’ citrus trees growth, yield and fruit quality. Acta Hortic. 2000, 537, 749–758. [Google Scholar] [CrossRef]
- Caspari, H.W.; Behboudian, M.H.; Chalmers, D.J. Water use, growth, and fruit yield of Hosui’ Asian pears under deficit irrigation. J. Am. Soc. Hortic. Sci. 1994, 119, 383–388. [Google Scholar] [CrossRef]
- Ebel, R.C.; Proebsting, E.L.; Evans, R.G. Deficit irrigation to control vegetative growth in apple and monitoring fruit growth to schedule irrigation. HortScience 1995, 30, 1229–1232. [Google Scholar] [CrossRef] [Green Version]
- González-Altozano, P.; Castel, J.R. Regulated deficit irrigation in “Clementina de Nules” citrus tree, 1: Yield and fruit quality effects during four years. Span. J. Agric. Res. 2003, 1, 81–92. [Google Scholar] [CrossRef] [Green Version]
- Girona, J.; Marsal, J.; Mata, M.; Arbones, A.; De Jong, T. A comparison of the combined effect of water stress and crop load on fruit growth during different phenological stages in young peach trees. J. Hortic. Sci. Biotechnol. 2004, 79, 308–315. [Google Scholar] [CrossRef]
- Goldhamer, D.A.; Shackel, K. Irrigation cuto and drought irrigation strategy effects on almond. In Proceedings of the 18th Almond Research Conference, Fresno, CA, USA, 11–13 December 1990; pp. 30–35. [Google Scholar]
- Pérez-Sarmiento, F.; Alcobendas, R.; Mounzer, O.; Alarcón, J.; Nicolás, E. Effects of regulated deficit irrigation on physiology and fruit quality in apricot trees. Span. J. Agric. Res. 2010, 8 (Suppl. S2), S86–S94. [Google Scholar] [CrossRef] [Green Version]
- Wong, B.L.; Baggett, K.L.; Rye, A.H. Cold-season patterns of reserve and soluble carbohydrates in sugar maple and ice-damaged trees of two age classes following drought. Botany 2009, 87, 293–305. [Google Scholar] [CrossRef]
- Romero, P.; Botia, P.; Garcia, F. Effects of regulated deficit irrigation under subsurface drip irrigation conditions on vegetative development and yield of mature almond trees. Plant Soil 2004, 260, 169–181. [Google Scholar] [CrossRef]
- Anjum, S.; Wang, L.; Farooq, M.; Khan, I.; Xue, L. Methyl jasmonate-induced alteration in lipid peroxidation, antioxidative defence system and yield in soybean under drought. J. Agron. Crop Sci. 2011, 197, 296–301. [Google Scholar] [CrossRef]
- Trifilò, P.; Casolo, V.; Raimondo, F.; Petrussa, E.; Boscutti, F.; Lo Gullo, M.A. Effects of prolonged drought on stem non-structural carbohydrates content and post-drought hydraulic recovery in Laurus nobilis L.: The possible link between car-bon starvation and hydraulic failure. Plant Physiol. Biochem. 2017, 120, 232–241. [Google Scholar] [CrossRef]
- Maguire, A.J.; Kobe, R.K. Drought and shade deplete nonstructural carbohydrate reserves in seedlings of five temperate tree species. Ecol. Evol. 2015, 5, 5711–5721. [Google Scholar] [CrossRef]
- Wong, B.; Baggett, K.; Rye, A. Seasonal patterns of reserve and soluble carbohydrates in mature sugar maple (Acer saccharum). Can. J. Bot. 2003, 81, 780–788. [Google Scholar] [CrossRef] [Green Version]
- Faghih, S.; Zamani, Z.; Fatahi, R.; Omidi, M. Influence of kaolin application on most important fruit and leaf characteristics of two apple cultivars under sustained deficit irrigation. Biol. Res. 2011, 54, 1–15. [Google Scholar] [CrossRef]
- Hong, Z.; Lakkineni., K.; Zhang, Z.; Verma, D.P.S. Removal of feedback inhibition ofD1-pyrroline-5-carboxylate synthetase results in increased proline accumulation and protection of plants fromosmotic stress. Plant Physiol. 2000, 122, 1129–1136. [Google Scholar] [CrossRef] [Green Version]
- Deuschle, K.; Funck, D.; Hellmann, H.; Daschner, K.; Binder, S.; Frommer, W.B. A nuclear gene encoding mitochondrial D1-pyrroline-5-carboxylate dehydrogenase and its potential role in protection from proline toxicity. Plant J. 2001, 27, 345–356. [Google Scholar] [CrossRef]
- Ahmed, C.B.; Rouina, B.B.; Sensoy, S.; Boukhris, M.; Abdallah, F.B. Changes in gas exchange, proline accumulation and antioxidative enzyme activities in three olive cultivars under contrasting water availability regimes. Environ. Exp. Bot. 2009, 67, 345–352. [Google Scholar] [CrossRef]
- Zandalinas, S.I.; Rivero, R.M.; Martínez, V.; Gómez-Cadenas, A.; Arbona, V. Tolerance of citrus plants to the combination of high temperatures and drought is associated to the increase in transpiration modulated by a reduction in abscisic acid levels. BMC Plant Biol. 2016, 16, 105. [Google Scholar] [CrossRef] [Green Version]
- Hussain, S.; Khalid, M.F.; Saqib, M.; Ahmad, S.; Zafar, W.; Rao, M.J.; Morillon, R.; Anjum, M.A. Drought tolerance in citrus rootstocks is associated with better antioxidant defense mechanism. Acta Physiol. Plant. 2018, 40, 135. [Google Scholar] [CrossRef]
- Sun, X.; Yan, H.; Kang, X.; Ma, F. Growth, gas exchange, and water-use efficiency response of two young apple cultivars to drought stress in two scion-one rootstock grafting system. Photosynthetica 2013, 51, 404–410. [Google Scholar] [CrossRef]
- Šircelj, H.; Tausz, M.; Grill, D.; Batič, F. Detecting different levels of drought stress in apple trees (Malus domestica Borkh.) with selected biochemical and physiological parameters. Sci. Hortic. 2007, 113, 362–369. [Google Scholar] [CrossRef]
- Wang, S.; Liang, D.; Li, C.; Hao, Y.; Ma, F.; Shu, H. Influence of drought stress on the cellular ultrastructure and antioxidant system in leaves of drought tolerant and drought-sensitive apple rootstocks. Plant Physiol. Biochem. 2012, 51, 81–89. [Google Scholar] [CrossRef] [PubMed]



| Soil Chemical and Physical Properties | Soil Depth (cm) | |
|---|---|---|
| 0–30 | 30–60 | |
| pH | 7.6 | 7.5 |
| Organic carbon % | 0.58 | 0.27 |
| Organic matter % | 1.21 | 0.44 |
| Total nitrogen ‰ | 0.26 | 0.22 |
| K+ Meq L−1 | 1.45 | 1.32 |
| Na+ Meq L−1 | 28.50 | 11.23 |
| Ca++ Meq L−1 | 17.56 | 16.58 |
| Texture | sandy loam | sandy loam |
| Clay (<0.002 mm) % | 7 | 5 |
| Silt (0.002–0.05 mm) % | 6 | 6 |
| Sand (>0.05) % | 87 | 89 |
| Control | RDIm | RDIs | CDI | |
|---|---|---|---|---|
| January | 150 | 75 | 37.5 | 75 |
| February | 950 | 475 | 237.5 | 475 |
| March | 1900 | 950 | 475 | 950 |
| April | 1900 | 1425 | 1187 | 950 |
| May | 1900 | 1900 | 1900 | 950 |
| June | 1900 | 1900 | 1900 | 950 |
| July | 1900 | 1900 | 1900 | 950 |
| August | 1900 | 950 | 475 | 950 |
| September | 1900 | 950 | 475 | 950 |
| October | 690 | 345 | 172.5 | 345 |
| November | 640 | 320 | 160 | 320 |
| December | 230 | 115 | 57.5 | 115 |
| Overall (L tree−1) | 15,960 | 11,305 | 8977 | 7980 |
| Overall (m3 ha−1) | 9975.00 | 7065.63 | 5610.63 | 4987.50 |
| Source of Variance | df | CR | HR | DEDFH | sGDD | ||||
|---|---|---|---|---|---|---|---|---|---|
| MS | P > F | MS | P > F | MS | P > F | MS | P > F | ||
| Year (Y) | 2 | 1181.1 | 0.0765 | 3552.7 | 0.1462 | 2129.7 | 0.0537 | 31,120 | 0.0484 |
| Irrigation (I) | 3 | 80,491 | 0.0432 | 8390.2 | 0.0499 | 219.6 | 0.0654 | 11,512 | 0.1651 |
| Cultivar (C) | 1 | 882.6 | 0.0322 | 4415.5 | 0.0293 | 997.6 | 0.0411 | 51,306 | 0.0359 |
| Y × I | 3 | 5234.5 | 0.2567 | 4586.8 | 0.1792 | 218.8 | 0.1876 | 5494.9 | 0.0981 |
| Y × C | 2 | 2351.3 | 0.1015 | 3625.3 | 0.0987 | 80.53 | 0.1176 | 4580.3 | 0.1812 |
| I × C | 3 | 4325.1 | 0.1768 | 4136.1 | 0.2618 | 90.6 | 0.1265 | 5762.1 | 0.2801 |
| Y × I × C | 6 | 22,567 | 0.3154 | 7271.4 | 0.4259 | 387.4 | 0.2654 | 3365.7 | 0.4108 |
| Error | 174 | 12,317 | 2654.3 | 1076.2 | 3824.1 | ||||
| Total | 191 | ||||||||
| Source of Variance | df | TNB | NFB | NVB | SDF | NOFB | FBA | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MS | P > F | MS | P > F | MS | P > F | MS | P > F | MS | P > F | MS | P > F | ||
| Year (Y) | 2 | 61.1 | 0.7579 | 255.1 | 0.3991 | 43.1 | 0.4321 | 205.1 | 0.0319 | 176.7 | 0.0412 | 176.1 | 0.0451 |
| Irrigation (I) | 3 | 2346.5 | 0.0019 | 326.4 | 0.1060 | 819.2 | 0.0496 | 221.4 | 0.0398 | 829.2 | <0.001 | 2975.8 | 0.0087 |
| Cultivar (C) | 1 | 4680.8 | <0.001 | 4429.1 | <0.001 | 69.3 | 0.3105 | 847.3 | 0.0061 | 2437.8 | <0.001 | 29.49 | 0.2831 |
| Y × I | 3 | 1848.7 | 0.2583 | 106.2 | 0.0761 | 410.6 | 0.1704 | 135.4 | 0.0987 | 86.2 | 0.0539 | 286.1 | 0.0965 |
| Y × C | 2 | 1297.3 | 0.1262 | 419.4 | 0.1193 | 13.9 | 0.6582 | 31.2 | 0.1653 | 103.5 | 0.0917 | 80.4 | 0.4618 |
| I × C | 3 | 448.3 | 0.0712 | 237.1 | 0.5886 | 575.9 | 0.1031 | 148.7 | 0.0509 | 106.2 | 0.0791 | 255.9 | 0.3439 |
| Y × I × C | 6 | 2467.8 | 0.3509 | 411.2 | 0.0510 | 358.3 | 0.0871 | 245.7 | 0.2012 | 82.5 | 0.0696 | 189.2 | 0.1349 |
| Error | 174 | 44.67 | 142.5 | 36.8 | 61.4 | 29.4 | 36.4 | ||||||
| Total | 191 | ||||||||||||
| Cultivar/Irrigation Treatment | Year | |||||||
|---|---|---|---|---|---|---|---|---|
| 2016 | 2017 | 2018 | Overall | |||||
| ‘Ninfa’ | ||||||||
| Control | 75.6 | b | 76.0 | b | 68.0 | a | 73.2 | ab |
| RDIm | 71.3 | a | 69.3 | a | 71.0 | ab | 70.5 | a |
| RDIs | 76.0 | bc | 70.7 | a | 73.0 | b | 73.2 | ab |
| CDI | 77.7 | bc | 78.0 | b | 72.6 | b | 76.1 | b |
| LSD0.05 | 4.2 | 4.5 | 3.9 | 4.2 | ||||
| ‘Canino’ | ||||||||
| Control | 76.0 | ab | 66.6 | a | 68.0 | ns | 70.2 | ns |
| RDIm | 74.3 | a | 66.0 | a | 68.6 | ns | 69.7 | ns |
| RDIs | 79.0 | b | 67.0 | ab | 69.7 | ns | 71.9 | ns |
| CDI | 77.3 | ab | 70.7 | b | 69.3 | ns | 72.4 | ns |
| LSD0.05 | 4.1 | 3.7 | - | 3.9 | ||||
| Overall cultivar | ||||||||
| ‘Ninfa’ | 75.2 | ns | 73.5 | b | 71.2 | ns | 73.3 | ns |
| ‘Canino’ | 76.7 | ns | 67.9 | a | 68.9 | ns | 71.1 | ns |
| LSD0.05 | - | 4.3 | - | - | ||||
| Overall irrigation | ||||||||
| Control | 75.8 | ab | 71.3 | ab | 68.0 | ns | 71.7 | ab |
| RDIm | 72.8 | a | 67.7 | a | 69.8 | ns | 70.1 | a |
| RDIs | 77.5 | b | 68.8 | a | 71.3 | ns | 72.6 | ab |
| CDI | 77.6 | b | 74.3 | b | 71.0 | ns | 74.3 | b |
| LSD0.05 | 4.1 | 4.2 | - | 4.1 | ||||
| Source of Variance | df | FS | SVG | FNT | FY | FW | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| MS | P > F | MS | P > F | MS | P > F | MS | P > F | MS | P > F | ||
| Year (Y) | 2 | 405.5 | 0.2412 | 71.5 | 0.1822 | 598.6 | 0.2412 | 29.1 | 0.3482 | 11.6 | 0.6691 |
| Irrigation (I) | 3 | 4209.3 | 0.0341 | 9706.4 | 0.0214 | 6288.9 | 0.0328 | 374.5 | 0.0432 | 57.2 | 0.2987 |
| Cultivar (C) | 1 | 4753.9 | 0.0197 | 1859.1 | 0.0351 | 2991.9 | 0.0287 | 804.5 | 0.0069 | 155.1 | 0.0497 |
| Y × I | 3 | 229.1 | 0.1836 | 234.3 | 0.1838 | 687.9 | 0.2871 | 169.3 | 0.2576 | 78.2 | 0.5251 |
| Y × C | 2 | 52.6 | 0.3182 | 28.1 | 0.2387 | 973.2 | 0.2371 | 115.6 | 0.1754 | 83.4 | 0.3281 |
| I × C | 3 | 348.9 | 0.1214 | 1141.4 | 0.0986 | 1325.1 | 0.1672 | 56.9 | 0.0629 | 100.8 | 0.1827 |
| Y × I × C | 6 | 128.1 | 0.3839 | 234.2 | 0.2891 | 216.1 | 0.3952 | 181.5 | 0.2980 | 23.1 | 0.6421 |
| Error | 174 | 81.4 | 87.7 | 65.7 | 42.6 | 5.2 | |||||
| Total | 191 | ||||||||||
| Source of Variance | df | TSC | TPC | ||
|---|---|---|---|---|---|
| MS | P > F | MS | P > F | ||
| Year (Y) | 2 | 341.6 | <0.001 | 11.71 | 0.5319 |
| Irrigation (I) | 3 | 976.5 | <0.001 | 1202.6 | <0.001 |
| Cultivar (C) | 1 | 364.5 | 0.0014 | 100.2 | 0.0312 |
| Y × I | 3 | 134.5 | 0.0529 | 4586.8 | 0.1792 |
| Y × C | 2 | 81.7 | 0.1019 | 3625.3 | 0.0987 |
| I × C | 3 | 75.3 | 0.1492 | 4136.1 | 0.2618 |
| Y × I × C | 6 | 173.4 | 0.1158 | 7271.4 | 0.4259 |
| Error | 174 | 18.89 | 17.86 | ||
| Total | 191 | ||||
| Cultivar/Irrigation Treatment | Year | |||||||
|---|---|---|---|---|---|---|---|---|
| 2016 | 2017 | 2018 | Overall | |||||
| ‘Ninfa’ | ||||||||
| Control | 151.0 | c | 140.8 | b | 153.0 | c | 148.3 | c |
| RDIm | 143.3 | b | 134.1 | b | 146.3 | b | 141.2 | b |
| RDIs | 123.6 | a | 113.4 | a | 125.6 | a | 120.8 | a |
| CDI | 122.9 | a | 111.9 | a | 124.1 | a | 119.6 | a |
| LSD0.05 | 6.6 | 6.2 | 6.4 | 6.4 | ||||
| ‘Canino’ | ||||||||
| Control | 144.9 | b | 135.9 | b | 148.2 | b | 143.0 | b |
| RDIm | 123.4 | a | 113.6 | a | 125.8 | a | 120.9 | a |
| RDIs | 121.5 | a | 110.3 | a | 122.5 | a | 118.1 | a |
| CDI | 119.0 | a | 109.4 | a | 121.7 | a | 116.7 | a |
| LSD0.05 | 6.2 | 5.9 | 6.2 | 6.1 | ||||
| Overall cultivar | ||||||||
| ‘Ninfa’ | 135.2 | b | 125.0 | b | 137.3 | b | 132.5 | b |
| ‘Canino’ | 127.2 | a | 117.3 | a | 129.6 | a | 124.7 | a |
| LSD0.05 | 6.4 | 6.1 | 6.3 | 6.3 | ||||
| Overall irrigation | ||||||||
| Control | 147.9 | c | 138.3 | c | 150.6 | c | 145.6 | c |
| RDIm | 133.4 | b | 123.8 | b | 136.1 | b | 131.1 | b |
| RDIs | 122.6 | a | 111.8 | a | 124.1 | a | 119.5 | a |
| CDI | 120.9 | a | 110.7 | a | 122.9 | a | 118.2 | a |
| LSD0.05 | 7.4 | 7.2 | 7.8 | 7.5 | ||||
| A: Total | CR | HR | DEDFH | sGDD | TNB | NFB | NVB | SDF | NOFB | FBA | FS | SVG | FNT | FY | FW | TSC |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| HR | −0.44 | |||||||||||||||
| DEDFH | −0.15 | 0.27 | ||||||||||||||
| sGDD | −0.22 | 0.26 | 0.29 | |||||||||||||
| TNB | 0.32 | −0.64 | −0.23 | −0.18 | ||||||||||||
| NFB | 0.11 | −0.61 | −0.27 | −0.17 | 0.76 | |||||||||||
| NVB | 0.35 | −0.25 | −0.03 | −0.07 | 0.62 | −0.04 | ||||||||||
| SDF | 0.31 | −0.24 | −0.13 | −0.46 | 0.14 | 0.08 | 0.12 | |||||||||
| NOFB | −0.06 | −0.56 | −0.14 | −0.08 | 0.65 | 0.76 | 0.14 | −0.02 | ||||||||
| FBA | 0.23 | 0.11 | −0.12 | −0.07 | −0.11 | −0.04 | 0.23 | 0.10 | −0.61 | |||||||
| FS | −0.24 | −0.58 | −0.27 | −0.20 | 0.31 | 0.21 | 0.22 | 0.01 | 0.44 | −0.41 | ||||||
| SVG | −0.05 | −0.39 | −0.09 | −0.25 | 0.49 | 0.37 | 0.32 | −0.08 | 0.73 | −0.66 | 0.53 | |||||
| FNT | −0.22 | −0.66 | −0.26 | −0.25 | 0.49 | 0.65 | 0.23 | −0.03 | 0.65 | −0.43 | 0.95 | 0.67 | ||||
| FY | −0.16 | −0.71 | −0.33 | −0.27 | 0.56 | 0.64 | 0.21 | 0.11 | 0.68 | −0.38 | 0.85 | 0.62 | 0.93 | |||
| FW | 0.12 | −0.36 | −0.25 | −0.10 | 0.29 | 0.61 | 0.04 | 0.41 | 0.26 | 0.01 | 0.04 | 0.07 | 0.13 | 0.68 | ||
| TSC | −0.62 | −0.24 | 0.01 | −0.09 | 0.43 | 0.32 | 0.27 | −0.05 | 0.71 | 0.53 | 0.40 | 0.65 | 0.51 | 0.53 | 0.18 | |
| TPC | 0.61 | −0.12 | −0.01 | −0.11 | −0.28 | −0.09 | −0.32 | 0.38 | −0.48 | 0.61 | −0.28 | −0.72 | −0.39 | −0.31 | 0.15 | −0.65 |
| B: Cont. | CR | HR | DEDFH | sGDD | TNB | NFB | NVB | SDF | NOFB | FBA | FS | SVG | FNT | FY | FW | TSC |
| HR | −0.90 | |||||||||||||||
| DEDFH | −0.26 | 0.44 | ||||||||||||||
| sGDD | −0.19 | 0.15 | 0.56 | |||||||||||||
| TNB | 0.72 | −0.93 | −0.53 | −0.07 | ||||||||||||
| NFB | 0.51 | −0.78 | −0.54 | −0.06 | 0.95 | |||||||||||
| NVB | 0.88 | −0.98 | −0.43 | −0.07 | 0.91 | −0.72 | ||||||||||
| SDF | 0.34 | −0.39 | −0.63 | −0.53 | 0.24 | 0.03 | 0.47 | |||||||||
| NOFB | 0.26 | −0.59 | −0.39 | 0.04 | 0.84 | 0.92 | 0.59 | −0.01 | ||||||||
| FBA | 0.69 | −0.77 | −0.56 | −0.13 | 0.86 | 0.06 | 0.70 | 0.02 | −0.63 | |||||||
| FS | −0.05 | −0.09 | −0.02 | −0.35 | 0.18 | −0.37 | 0.08 | 0.72 | −0.18 | −0.57 | ||||||
| SVG | 0.84 | −0.65 | −0.42 | −0.16 | 0.49 | 0.31 | 0.64 | 0.35 | 0.61 | −0.67 | 0.24 | |||||
| FNT | 0.19 | −0.63 | −0.47 | −0.34 | 0.58 | 0.62 | 0.56 | 0.59 | 0.70 | −0.17 | 0.66 | 0.61 | ||||
| FY | −0.01 | −0.61 | −0.85 | −0.52 | 0.45 | 0.61 | 0.32 | 0.62 | 0.61 | −0.28 | 0.61 | 0.64 | 0.78 | |||
| FW | −0.14 | −0.10 | −0.92 | −0.51 | 0.26 | 0.61 | 0.10 | 0.53 | 0.33 | 0.27 | 0.09 | 0.06 | 0.47 | 0.92 | ||
| TSC | −0.63 | −0.32 | 0.25 | −0.34 | 0.29 | 0.20 | 0.35 | 0.06 | 0.29 | 0.53 | 0.39 | 0.61 | 0.47 | −0.03 | 0.36 | |
| TPC | 0.51 | 0.81 | 0.01 | 0.09 | −0.62 | −0.41 | −0.78 | 0.16 | −0.19 | 0.59 | 0.07 | −0.74 | −0.08 | 0.22 | 0.38 | −0.52 |
| C: RDIm | CR | HR | DEDFH | sGDD | TNB | NFB | NVB | SDF | NOFB | FBA | FS | SVG | FNT | FY | FW | TSC |
| HR | −0.23 | |||||||||||||||
| DEDFH | −0.42 | 0.11 | ||||||||||||||
| sGDD | −0.17 | 0.50 | 0.10 | |||||||||||||
| TNB | 0.36 | −0.71 | −0.13 | −0.40 | ||||||||||||
| NFB | 0.26 | −0.84 | −0.16 | −0.14 | 0.76 | |||||||||||
| NVB | 0.66 | −0.06 | −0.01 | −0.44 | 0.61 | −0.06 | ||||||||||
| SDF | 0.71 | −0.02 | −0.41 | −0.32 | 0.62 | 0.09 | 0.63 | |||||||||
| NOFB | −0.09 | −0.68 | −0.21 | −0.40 | 0.95 | 0.87 | 0.39 | 0.35 | ||||||||
| FBA | 0.63 | 0.35 | −0.11 | −0.58 | 0.61 | −0.03 | 0.69 | 0.56 | −0.61 | |||||||
| FS | 0.01 | −0.65 | −0.11 | −0.60 | 0.64 | −0.67 | 0.32 | 0.15 | 0.68 | −0.62 | ||||||
| SVG | −0.06 | −0.61 | −0.15 | −0.49 | 0.68 | 0.65 | 0.24 | 0.20 | 0.81 | −0.53 | 0.65 | |||||
| FNT | 0.03 | −0.97 | −0.06 | −0.59 | 0.76 | 0.73 | 0.27 | 0.17 | 0.90 | −0.55 | 0.99 | 0.76 | ||||
| FY | 0.08 | −0.99 | −0.08 | −0.55 | 0.61 | 0.84 | 0.22 | 0.18 | 0.94 | −0.46 | 0.96 | 0.62 | 0.88 | |||
| FW | 0.19 | −0.70 | −0.25 | −0.28 | 0.62 | 0.97 | 0.08 | 0.19 | 0.68 | 0.12 | 0.66 | 0.58 | 0.61 | 0.89 | ||
| TSC | −0.64 | −0.54 | 0.03 | −0.54 | 0.67 | 0.68 | 0.26 | 0.42 | 0.69 | 0.51 | 0.61 | 0.72 | 0.71 | 0.69 | 0.62 | |
| TPC | 0.56 | −0.07 | 0.56 | −0.26 | −0.37 | −0.09 | −0.46 | 0.74 | −0.19 | 0.25 | −0.01 | −0.21 | −0.03 | −0.03 | −0.01 | −0.14 |
| D: RDIs | CR | HR | DEDFH | sGDD | TNB | NFB | NVB | SDF | NOFB | FBA | FS | SVG | FNT | FY | FW | TSC |
| HR | −0.78 | |||||||||||||||
| DEDFH | −0.66 | 0.13 | ||||||||||||||
| sGDD | −0.40 | −0.04 | 0.74 | |||||||||||||
| TNB | 0.22 | −0.63 | −0.02 | −0.25 | ||||||||||||
| NFB | 0.38 | −0.61 | −0.07 | −0.33 | 0.82 | |||||||||||
| NVB | 0.41 | 0.23 | −0.09 | −0.30 | 0.41 | −0.66 | ||||||||||
| SDF | 0.05 | −0.15 | −0.11 | −0.34 | 0.43 | −0.07 | 0.49 | |||||||||
| NOFB | 0.42 | −0.67 | −0.19 | 0.18 | 0.80 | 0.71 | 0.42 | 0.13 | ||||||||
| FBA | −0.17 | 0.69 | −0.35 | −0.63 | 0.25 | 0.06 | 0.32 | 0.25 | −0.66 | |||||||
| FS | −0.26 | −0.64 | −0.46 | −0.24 | 0.53 | −0.29 | 0.01 | 0.49 | 0.64 | −0.58 | ||||||
| SVG | 0.70 | −0.69 | −0.31 | −0.26 | 0.73 | 0.75 | 0.46 | 0.27 | 0.87 | −0.42 | 0.64 | |||||
| FNT | 0.77 | −0.85 | −0.42 | −0.26 | 0.67 | 0.61 | 0.18 | 0.42 | 0.76 | −0.53 | 0.97 | 0.74 | ||||
| FY | 0.73 | −0.88 | −0.33 | −0.15 | 0.63 | 0.61 | −0.08 | 0.44 | 0.77 | −0.65 | 0.98 | 0.70 | 0.89 | |||
| FW | −0.19 | −0.22 | −0.32 | −0.67 | 0.22 | 0.64 | 0.62 | 0.31 | 0.07 | 0.78 | 0.25 | −0.14 | 0.09 | 0.63 | ||
| TSC | −0.65 | −0.34 | 0.36 | −0.35 | 0.01 | 0.41 | 0.65 | 0.62 | 0.24 | 0.54 | 0.42 | 0.67 | 0.28 | 0.41 | 0.61 | |
| TPC | 0.54 | −0.70 | 0.49 | −0.33 | −0.46 | −0.51 | −0.39 | 0.14 | −0.66 | 0.37 | −0.68 | −0.67 | −0.62 | −0.69 | 0.10 | −0.13 |
| E: CDI | CR | HR | DEDFH | sGDD | TNB | NFB | NVB | SDF | NOFB | FBA | FS | SVG | FNT | FY | FW | TSC |
| HR | −0.59 | |||||||||||||||
| DEDFH | −0.51 | 0.52 | ||||||||||||||
| sGDD | −0.47 | 0.34 | 0.55 | |||||||||||||
| TNB | 0.37 | −0.74 | −0.01 | −0.19 | ||||||||||||
| NFB | −0.11 | −0.61 | −0.18 | −0.34 | 0.73 | |||||||||||
| NVB | 0.62 | −0.08 | −0.27 | −0.22 | 0.23 | −0.49 | ||||||||||
| SDF | 0.33 | −0.54 | −0.61 | −0.69 | 0.23 | 0.52 | 0.45 | |||||||||
| NOFB | 0.07 | −0.62 | −0.01 | −0.34 | 0.89 | 0.93 | 0.19 | 0.43 | ||||||||
| FBA | −0.49 | 0.11 | −0.40 | −0.17 | 0.57 | 0.01 | 0.74 | 0.13 | −0.61 | |||||||
| FS | −0.47 | −0.63 | −0.38 | −0.22 | 0.12 | −0.11 | 0.31 | 0.04 | −0.15 | −0.22 | ||||||
| SVG | 0.03 | −0.48 | −0.13 | −0.44 | 0.50 | 0.59 | 0.21 | 0.63 | 0.64 | −0.19 | 0.04 | |||||
| FNT | 0.31 | −0.93 | −0.34 | −0.21 | 0.68 | 0.69 | −0.12 | 0.53 | 0.65 | 0.06 | 0.62 | 0.66 | ||||
| FY | 0.15 | −0.85 | −0.18 | −0.08 | 0.67 | 0.71 | 0.15 | 0.44 | 0.66 | −0.07 | 0.61 | 0.70 | 0.88 | |||
| FW | −0.14 | −0.61 | −0.16 | −0.17 | 0.57 | 0.62 | 0.17 | 0.21 | 0.59 | 0.07 | 0.44 | 0.72 | 0.64 | 0.83 | ||
| TSC | −0.64 | −0.24 | 0.29 | −0.27 | 0.65 | 0.13 | 0.68 | −0.01 | 0.46 | 0.59 | 0.19 | 0.61 | 0.07 | 0.04 | 0.31 | |
| TPC | 0.57 | −0.63 | 0.65 | −0.62 | 0.62 | −0.48 | −0.11 | 0.72 | −0.52 | 0.19 | −0.52 | −0.47 | −0.69 | −0.61 | 0.36 | −0.32 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ezzat, A.; Salama, A.-M.; Szabó, S.; Yaseen, A.A.; Molnár, B.; Holb, I.J. Deficit Irrigation Strategies on Tree Physiological and Chemical Properties: Treatment Effects, Prediction Based Model Analyses and Inter-Correlations. Agronomy 2021, 11, 1361. https://doi.org/10.3390/agronomy11071361
Ezzat A, Salama A-M, Szabó S, Yaseen AA, Molnár B, Holb IJ. Deficit Irrigation Strategies on Tree Physiological and Chemical Properties: Treatment Effects, Prediction Based Model Analyses and Inter-Correlations. Agronomy. 2021; 11(7):1361. https://doi.org/10.3390/agronomy11071361
Chicago/Turabian StyleEzzat, Ahmed, Abdel-Moety Salama, Szilárd Szabó, Arshad Abdulkhalq Yaseen, Bianka Molnár, and Imre J. Holb. 2021. "Deficit Irrigation Strategies on Tree Physiological and Chemical Properties: Treatment Effects, Prediction Based Model Analyses and Inter-Correlations" Agronomy 11, no. 7: 1361. https://doi.org/10.3390/agronomy11071361
APA StyleEzzat, A., Salama, A.-M., Szabó, S., Yaseen, A. A., Molnár, B., & Holb, I. J. (2021). Deficit Irrigation Strategies on Tree Physiological and Chemical Properties: Treatment Effects, Prediction Based Model Analyses and Inter-Correlations. Agronomy, 11(7), 1361. https://doi.org/10.3390/agronomy11071361








