Wheat Yield Forecasting for the Tisza River Catchment Using Landsat 8 NDVI and SAVI Time Series and Reported Crop Statistics
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Site
2.2. Reported Crop
2.3. Landsat 8 NDVI and SAVI
2.4. Data Processing and Yield Forecast
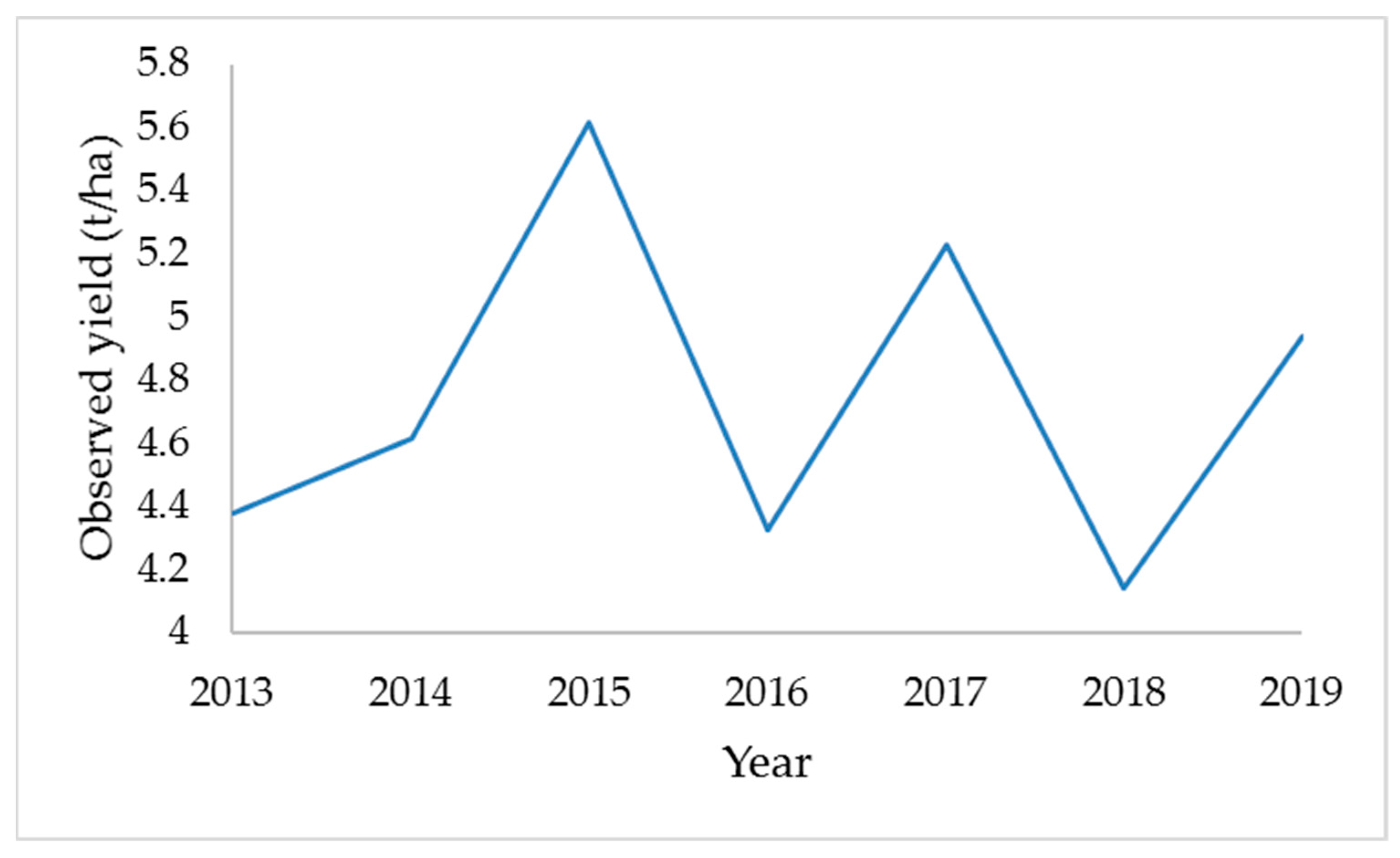
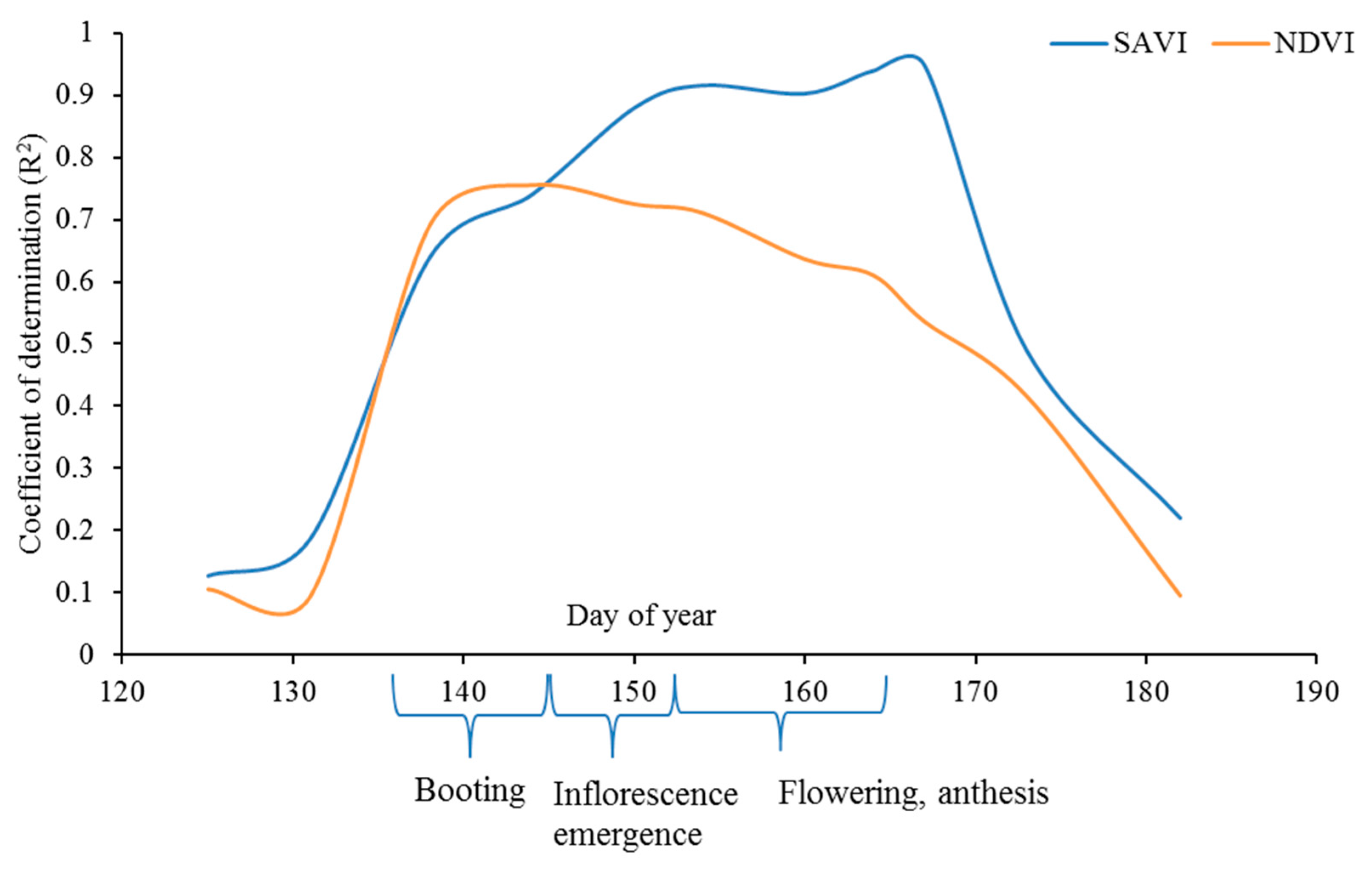
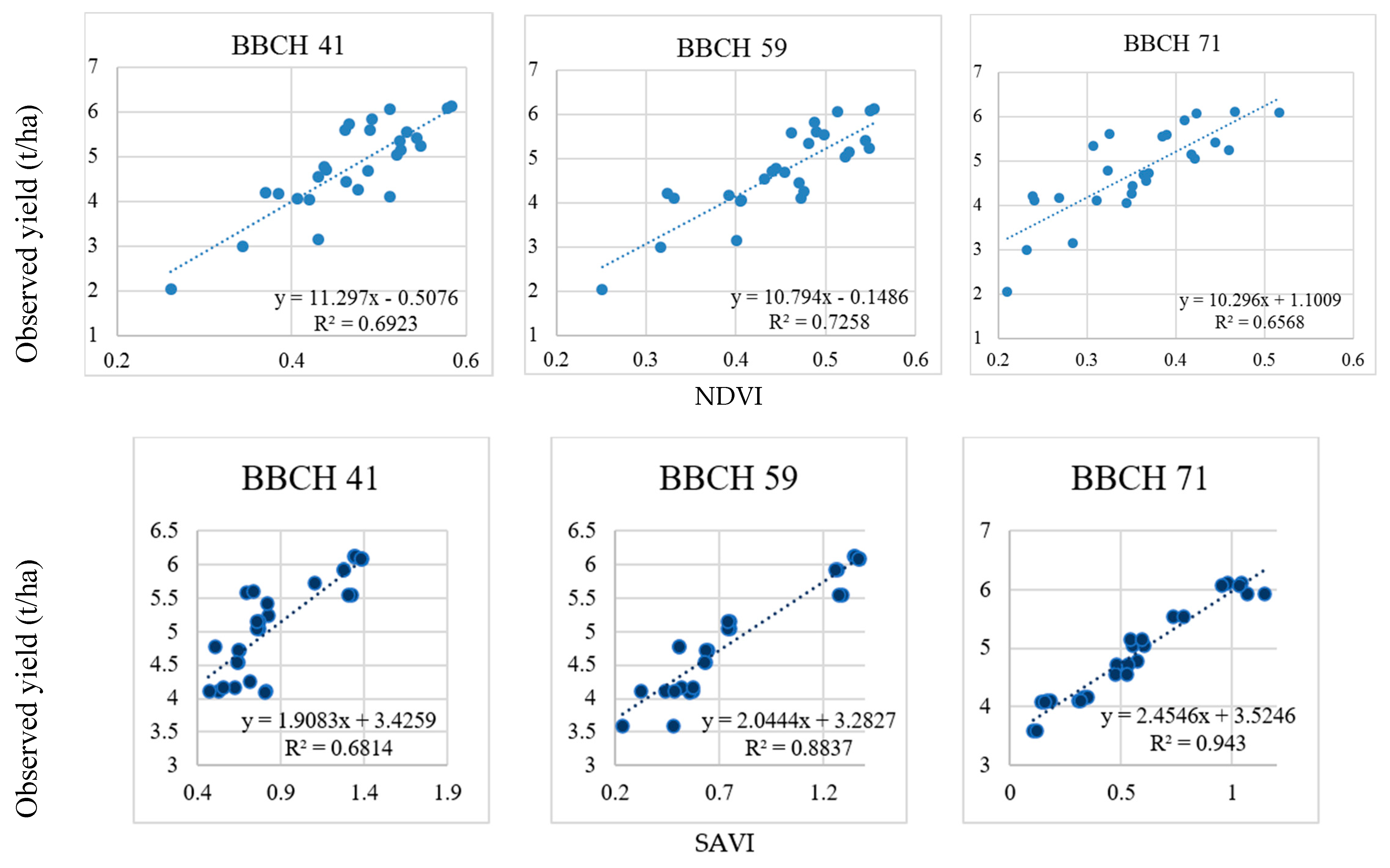
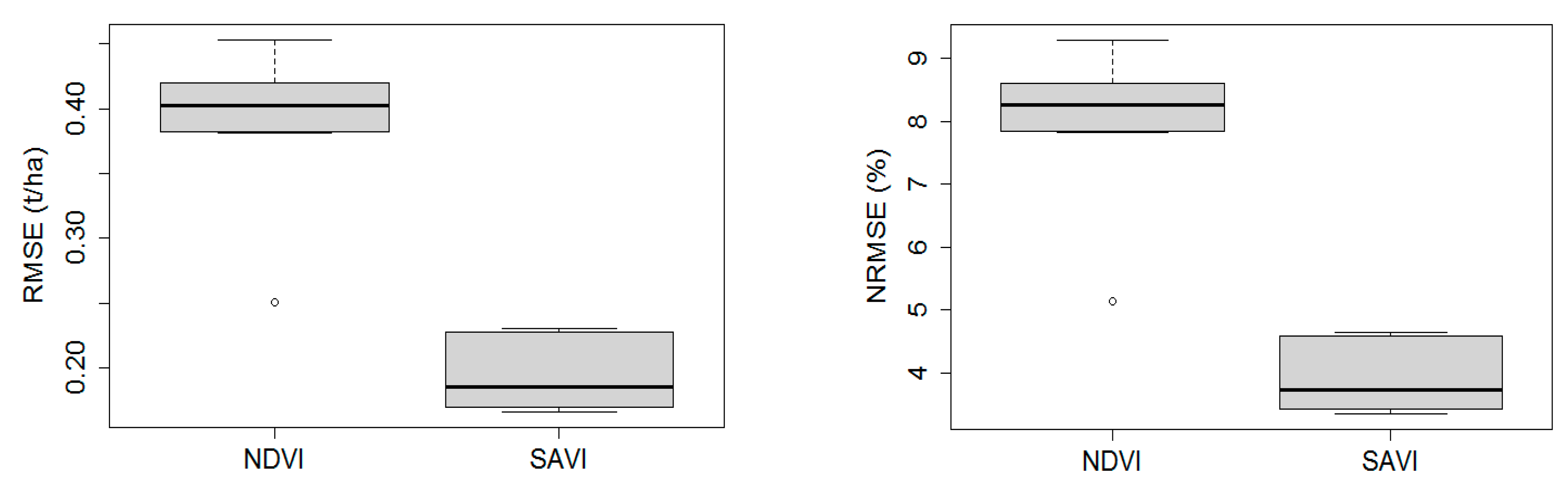
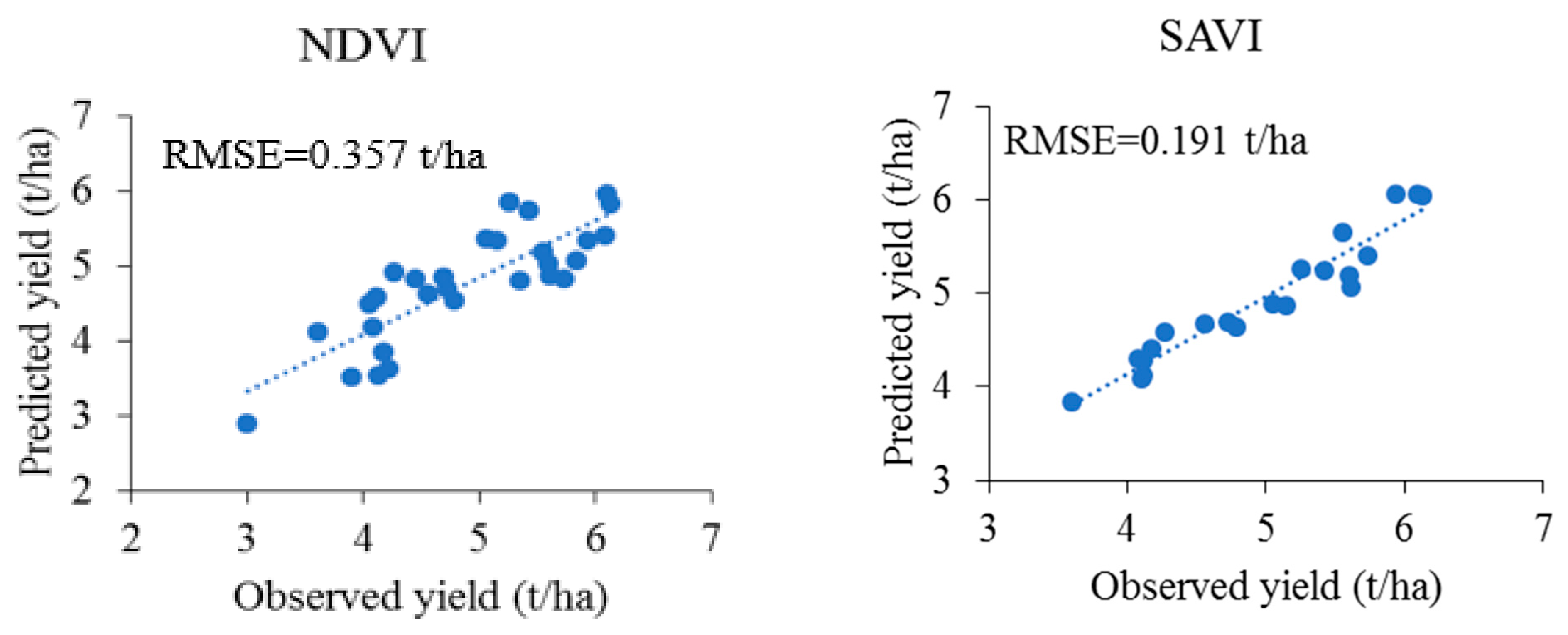
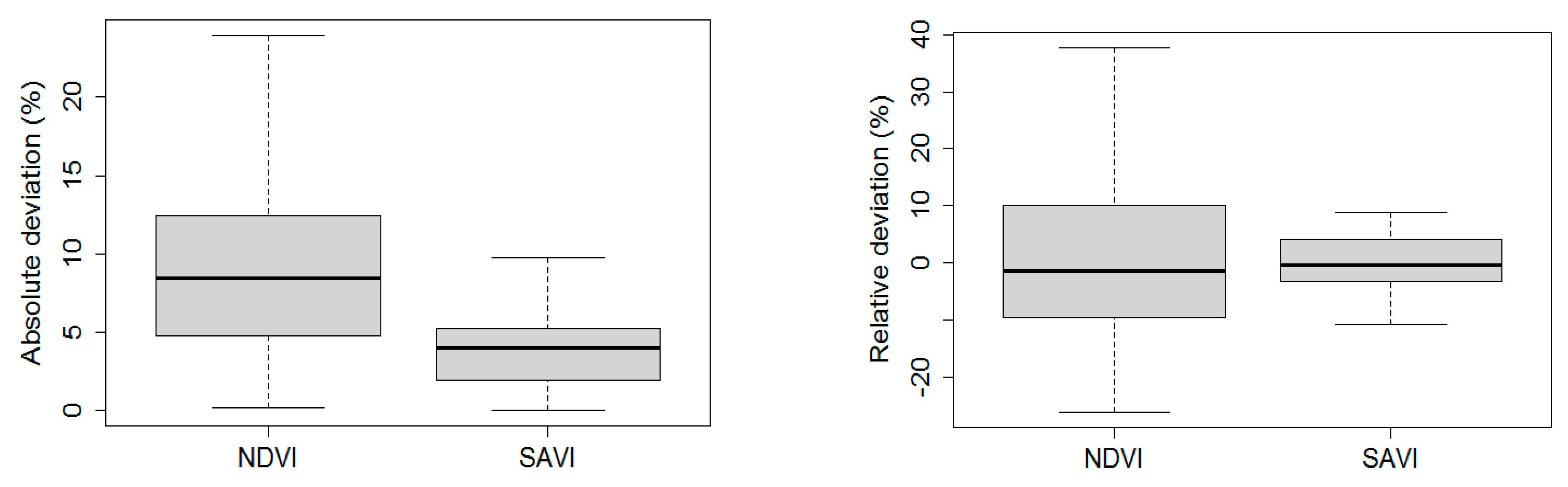
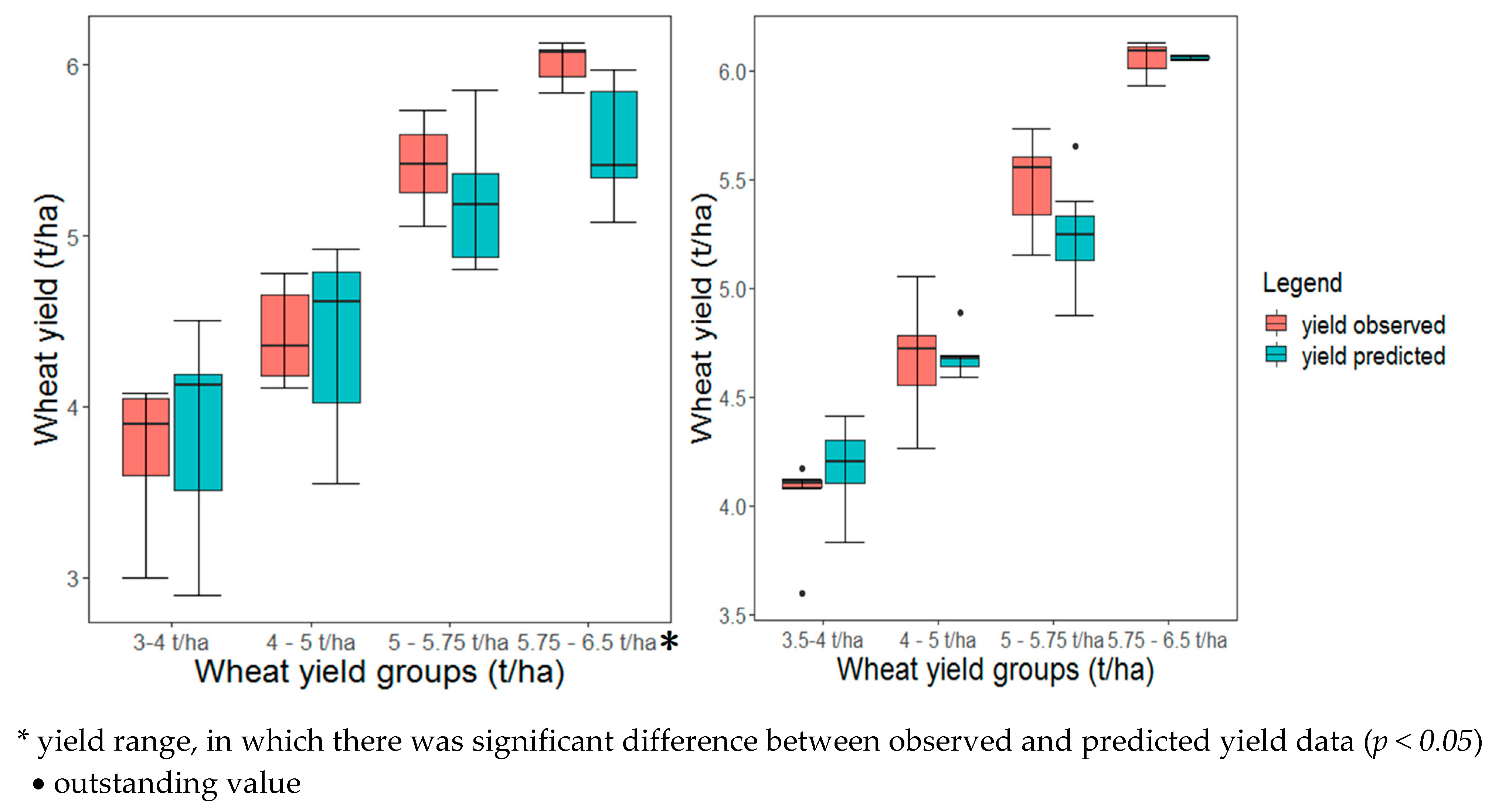
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rembold, F.; Atzberger, C.; Rojas, O.; Savin, I. Using low resolution satellite imagey for yield prediction and yield anomaly detection. Remote Sens. 2013, 11, 1704–1733. [Google Scholar] [CrossRef]
- Atzberger, C. Advances in remote sensing of agriculture: Context description, existing operational monitoring systems and major information needs. Remote Sens. 2013, 5, 949–981. [Google Scholar] [CrossRef]
- Jacobs, C.; Berglund, M.; Kurnik, B.; Dworak, T.; Marras, S.; Mereu, V.; Michetti, M. Climate change adaptation in the agriculture sector in Europe. EEA Rep. 2019, 4, 112. [Google Scholar] [CrossRef]
- Tucker, C. Red and photographic infrared linear combinations for monitoring vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar] [CrossRef]
- Tucker, C.J.; Holben, B.N.; Elgin, J.H., Jr.; McMutrey, J.E., III. Relationship of spectral data to grain yield variation. Photogramm. Eng. Remote Sens. 1980, 46, 657–666. [Google Scholar]
- Tucker, C.J.; Holben, B.N.; Elgin, J.H., Jr.; McMurtrey, J.E., III. Remote sensing of total dry-matter accumulation in winter wheat. Remote Sens. Environ. 1981, 11, 171–189. [Google Scholar] [CrossRef]
- Huete, A.R. A Soil-Adjusted Vegetation Index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- Gilabert, M.A.; Gonzílez-Piqueras, J.; Garcıa-Haro, F.J.; Meliá, J. A generalized soil adjusted vegetation index. Remote Sens. Environ. 2002, 82, 303–310. [Google Scholar] [CrossRef]
- Rhyma, P.; Norizah, K.; Hamdan, O.; Faridah-Hanum, I.; Zulfa, A. Integration of normalised differentvegetation index and Soil-Adjusted Vegetation Index for mangrove vegetation delineation. Remote Sens. Appl. 2020, 17, 100280. [Google Scholar] [CrossRef]
- Ferencz, C.; Bognár, P.; Lichtenberge, J.; Hamar, D.; Tarcsai, G.; Timár, G.; Molnár, G.; Pásztor, S.; Steinbach, P.; Székely, B.; et al. Crop yield estimation by satellite remote sensing. Int. J. Remote Sens. 2004, 25, 4113–4149. [Google Scholar] [CrossRef]
- Reynolds, C.A.; Yitayew, M.; Slack, D.C.; Hatchinson, C.F.; Huete, A.; Petersen, M.S. Estimating crop yields and production by integrating the FAO Crop Specific Water data and ground-based ancillary data. Int. J. Remote Sens. 2000, 21, 3487–3508. [Google Scholar] [CrossRef]
- Patel, N.K.; Patnaik, C.; Dutta, S.; Shekh, A.M.; Dane, A.J. Study of crop growth parameters using Airborne Imaging Spectrometer data. Int. J. Remote Sens. 2001, 22, 2401–2411. [Google Scholar] [CrossRef]
- Richter, K.; Atzberger, C.; Vuolo, F.; D’Urso, G. Evaluation of sentinel-2 spectral sampling for radiative transfer model based LAI estimation of wheat, sugar beet, and maize. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2011, 4, 458–464. [Google Scholar] [CrossRef]
- Vuolo, F.; Neugebauer, N.; Falanga, S.; Atzberger, C.; D’Urso, G. Estimation of Leaf Area Index using DEIMOS-1 data: Calibration and transferability of a semi-empirical relationship between two agricultural areas. Remote Sens. 2013, 5, 1274–1291. [Google Scholar] [CrossRef]
- Pena-Barragan, J.M.; Ngugi, M.K.; Plant, R.E.; Six, J. Object-based crop identification using multiple vegetation indices, textuaral features and crop phenology. Remote Sens. Environ. 2011, 115, 1301–1316. [Google Scholar] [CrossRef]
- Dempewolf, J.; Adusei, B.; Becker-Rehef, I.; Hansen, M.; Potapov, P.; Khan, A.; Barker, B. Wheat Yield Forecasting for Punjab Province from Vegetation Index Time Series and Historic Crop Statistics. Remote Sens. 2014, 6, 9653–9675. [Google Scholar] [CrossRef]
- Fu, Y.; Yang, G.; Wang, J.; Song, X.; Feng, H. Winter wheat biomass estimation based on spectral indices, band depth analysis and partial least sqaures regression using hyperspectral measurements. Comput. Electron. Agric. 2014, 100, 51–59. [Google Scholar] [CrossRef]
- Xie, Q.; Huang, W.; Dash, J.; Song, X.; Huang, L.; Zaho, J.; Wang, R. Evaluating the potential of vegetation indices for winter wheat LAI estimation under different fertilization and Water conditions. Adv. Space Res. 2015, 56, 2365–2373. [Google Scholar] [CrossRef]
- Tamás, J.; Nagy, A.; Fehér, J. Agricultural biomass monitoring on watersheds based on remote sensed data. Water Sci. Technol. 2015, 72, 2212–2220. [Google Scholar] [CrossRef]
- Prasad, P.V.V.; Djanaguiraman, M.; Perumal, R.; Ciampitti, I.A. Impact of high temperature stress on floret fertility and individual grain weight of grain sorghum: Sensitive stages and thresholds for temperature and duration. Front. Plant Sci. 2015, 6, 820. [Google Scholar] [CrossRef]
- Tucker, C.J.; Vanpraet, C.L.; Sharman, M.J.; Van Ittersum, G. Satellite remote sensing of total herbaceous biomass production in the Senegalese Sahel: 1980–1984. Remote Sens. Environ. 1985, 17, 233–249. [Google Scholar] [CrossRef]
- Malingreau, J.P. Global vegetation dynamics: Satellite observations over Asia. Remote Sens. Environ. 1986, 7, 1121–1146. [Google Scholar] [CrossRef]
- Nagy, A.; Tamás, J. Non-invasive water stress assessment methods in orchards. Commun. Soil Sci. Plant Anal. 2013, 44, 366–376. [Google Scholar] [CrossRef]
- Nagy, A.; Fehér, J.; Tamás, J. Wheat and maize yield forecasting for the Tisza river catchment using MODIS NDVI time series and reported crop statistics. Comput. Electron. Agric. 2018, 151, 41–49. [Google Scholar] [CrossRef]
- Kismányoky, T. Versenyképes búzatermesztés. In Mezőgazda Kiadó; Budapest: Magyarország, 2013; p. 288. ISBN 9789632866925. [Google Scholar]
- Juhász, C.; Gálya, B.; Kovács, E.; Nagy, A.; Tamás, J.; Huzsvai, L. Seasonal predictability of weather and crop yield in regions of Central European continental climate. Comput. Electron. Agric. 2020, 0168-1699, 173. [Google Scholar] [CrossRef]
- Biro, S.; Apáti, F.; Szőllősi, L.; Szűcs, I. The economic context of irrigation development. (in Hungarian). In Water Use and Irrigation Development in Hungarian Agriculture (in Hungarian); Biro, S., Kapronczai, I., Szűcs, I., Váradi, L., Eds.; Agricultural Research Institute: Budapest, Hungary, 2011; pp. 45–74. [Google Scholar]
- Gobron, N.; Verstraete, M.M. Fraction of Absorbed Photosynthetically Active Radiation (FAPAR) Global Terrestrial Observing System NRC; Food and Agriculture Organization of the United Nations (FAO): Rome, Italy, 2009; p. 14. [Google Scholar]
- Woodcock, C.E.; Allen, R.; Anderson, M.; Belward, A.; Bindschadler, R.; Cohen, W.; Gao, F.; Goward, S.N.; Helder, D.; Helmer, E.; et al. Free access to Landsat imagery. Science 2008, 320, 1011. [Google Scholar] [CrossRef]
- Lobell, D.B. The use of satellite data for cop yield gap analysis. Field Crops Res. 2013, 143, 56–64. [Google Scholar] [CrossRef]
- Liu, L.; Wang, J.; Bao, Y.; Huang, W.; Ma, Z.; Zhao, C. Predicting winter wheat condition, grain yield and protein content using multi-temporal EnviSat-ASAR and Landsat TM satellite images. Int. J. Remote Sens. 2006, 27, 737–753. [Google Scholar] [CrossRef]
- Lyle, G.; Lewis, M.; Ostendorf, B. Testing the Temporal Ability of Landsat Imagery and Precision Agriculture Technology to Provide High Resolution Historical Estimates of Wheat Yield at the Farm Scale. Remote Sens. 2013, 5, 1549–1567. [Google Scholar] [CrossRef]
- Potgieter, A.B.; Power, B.; Mclean, J.; Davis, P.; Rodriguez, D. Spatial Estimation of Wheat Yields from Landsat’s Visible, near Infrared and Thermal Reflectance Bands. Int. J. Remote Sens. Appl. 2014, 4, 134–143. [Google Scholar] [CrossRef]
- Panek, E.; Gozdowski, D.; Stepien, M.; Samborski, S.; Rucinski, D.; Buszke, B. Within-Field Relationships between Satellite-Derived Vegetation Indices, Grain Yield and Spike Number of Winter Wheat and Triticale. Agronomy 2020, 10, 1842. [Google Scholar] [CrossRef]
- Mokhtari, A.; Noory, H.; Vazifedoust, M. Improving crop yield estimation by assimilating LAI and inputting satellite-based surface incoming solar radiation into SWAP model. Agric. Forest Meteorol. 2018, 250–251, 159–170. [Google Scholar] [CrossRef]
- Darvishzadeh, R.; Skidmore, A.; Schlerf, M.; Atzberger, C.; Corsi, F.; Cho, M. LAI and chlorophyll estimation for a heterogeneous grass-land using hyperspectral measurements. ISPRS J. Photogramm. Remote Sens. 2008, 63, 409–426. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models, Part I–A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Delécolle, R.; Maas, S.J.; Guérif, M.; Baret, F. Remote sensing and crop production models: Present trends. ISPRS J. Photogramm. 1992, 47, 145–161. [Google Scholar] [CrossRef]
- Boken, V.K.; Shaykewich, C.F. Improving an operational wheat yield model using phenological phase-based normalized difference vegetation index. Int. J. Remote Sens. 2002, 23, 4155–4168. [Google Scholar] [CrossRef]
- Basnyat, P.; McConkey, B.; Lafond, G.P.; Moulin, A.; Pelcat, Y. Optimal time for remote sensing to relate to crop grain yield on the Canadian prairies. Can. J. Plant Sci. 2004, 84, 97–103. [Google Scholar]
- Becker-Reshef, I.; Vermote, E.; Lindeman, M.; Justice, C. A generalized regressionbased model for forecasting winter wheat yields in Kansas and Ukraine using MODIS data. Remote Sens. Environ. 2010, 114, 1312–1323. [Google Scholar] [CrossRef]
- Marti, J.; Bort, J.; Slafer, G.A.; Araus, J.L. Can wheat yield be assessed by early measurements of Normalized Difference Vegetation Index? Ann. Appl. Biol. 2007, 150, 253–257. [Google Scholar] [CrossRef]
- Labus, M.P.; Nielsen, G.A.; Lawrence, R.L.; Engel, R.; Long, D.S. Wheat yield estimates using multi-temporal NDVI satellite imagery. Int. J. Remote Sens. 2002, 23, 4169–4180. [Google Scholar] [CrossRef]
- Mkhabela, M.K.; Bullock, P.; Raj, S.; Wang, S.; Yang, Y. Crop yield forecasting on the Canadian Prairies using MODIS NDVI data. Agric. Forest Meteorol. 2011, 151, 385–393. [Google Scholar] [CrossRef]
- Bai, T.; Zhang, N.; Mercatoris, B.; Chen, Y. Jujube yield prediction method combining Landsat 8 Vegetation Index and the phenological length. Comput. Electron. Agric. 2019, 162, 1011–1027. [Google Scholar] [CrossRef]
- Yousfi, S.; Kellas, N.; Saidi, L.; Benlakehal, Z.; Chaou, L.; Siad, D.; Herda, F.; Karrou, M.; Vergara, O.; Gracia, A. Comparative performance of remote sensing methods in assessing wheat performance under Mediterranean conditions. Agric. Water Mangement 2016, 164, 137–147. [Google Scholar] [CrossRef]
- Rudorff, B.F.T.; Batista, G.T. Wheat yield estimation at the farm level using TM Landsat and agrometeorological data. Int. J. Remote Sens. 1991, 12, 2477–2484. [Google Scholar] [CrossRef]
- Sellers, P.J. Canopy reflectance, photosynthesis and transpiration. Int. J. Remote Sens. 1985, 6, 1335–1372. [Google Scholar] [CrossRef]
- Goswami, S.; Gamon, J.; Vargas, S.; Tweedie, C. Relationships of NDVI, Biomass, and Leaf Area Index (LAI) for six key plant species in Barrow, Alaska. PeerJ PrePrints 2015, 3, e913v1. [Google Scholar] [CrossRef]
- Muller, S.J.; Sithole, P.; Singels, A.; Van Niekerk, A. Assessing the fidelity of Landsat-based fAPAR models in two diverse sugarcane growing regions. Comput. Electron. Agric. 2020, 170, 105248. [Google Scholar] [CrossRef]
- Liaqat, U.M.; Cheema, M.J.M.; Huang, W.; Mahmood, T.; Zaman, M.; Khan, M.M. Evaluation of MODIS and Landsat multiband vegetation indices used for wheat yield estimation in irrigated. Comput. Electron. Agric. 2017, 138, 39–47. [Google Scholar] [CrossRef]
- Uno, Y.; Prasher, S.O.; Lacroix, R.; Goel, P.K.; Karimi, Y.; Viau, A.; Patel, R.M. Artificial neural networks to predict corn yield from compact airborne spectrographic imager data. Comput. Electron. Agr. 2005, 47, 149–161. [Google Scholar] [CrossRef]
- Ferrio, J.P.; Villegas, D.; Zarco, J.; Aparicio, N.; Araus, J.L.; Royo, C. Assessment of durum wheat yield using visible and near-infrared reflectance spectra of canopies. Field Crop. Res. 2005, 94, 126–148. [Google Scholar] [CrossRef]
- Ye, X.; Sakai, K.; Manago, M.; Asada, S.; Sasao, A. Prediction of citrus yield from airborne hyperspectral imagery. Precis. Agric. 2007, 8, 111–125. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nagy, A.; Szabó, A.; Adeniyi, O.D.; Tamás, J. Wheat Yield Forecasting for the Tisza River Catchment Using Landsat 8 NDVI and SAVI Time Series and Reported Crop Statistics. Agronomy 2021, 11, 652. https://doi.org/10.3390/agronomy11040652
Nagy A, Szabó A, Adeniyi OD, Tamás J. Wheat Yield Forecasting for the Tisza River Catchment Using Landsat 8 NDVI and SAVI Time Series and Reported Crop Statistics. Agronomy. 2021; 11(4):652. https://doi.org/10.3390/agronomy11040652
Chicago/Turabian StyleNagy, Attila, Andrea Szabó, Odunayo David Adeniyi, and János Tamás. 2021. "Wheat Yield Forecasting for the Tisza River Catchment Using Landsat 8 NDVI and SAVI Time Series and Reported Crop Statistics" Agronomy 11, no. 4: 652. https://doi.org/10.3390/agronomy11040652
APA StyleNagy, A., Szabó, A., Adeniyi, O. D., & Tamás, J. (2021). Wheat Yield Forecasting for the Tisza River Catchment Using Landsat 8 NDVI and SAVI Time Series and Reported Crop Statistics. Agronomy, 11(4), 652. https://doi.org/10.3390/agronomy11040652






