1. Introduction
Water is a key natural resource for the economic, social and political development of any region or country. Increasing agriculture, industrial and urban water demand, under the context of climate change, is causing freshwater availability to be a global and complex challenge [
1]. The world population will increase from 6 billion in 2000 to 9 billion in 2050 [
2]. Thus, water requirements for food production will increase to meet the future world population demand. A 70%increase in food requirements is expected during the next thirty years [
3]. Irrigated crops produce 40% of the world food with only 18% of cultivated land [
4], with irrigation playing a crucial role in food security. On the other hand, it can have a significant impact on the sustainability of water resources, because it represents 67% of the freshwater world extractions and 87% of the consumptive use of water [
5].
In Europe, 42% of the water resources are used in irrigation, 23% in industry, 18% in urban demand and 18% in energy production [
6]. However, there are large differences between regions. For instance, 74% of Europe’s irrigation area is concentrated in countries of the South [
7] and all of the Mediterranean region.
Around a third of the irrigation in the world uses groundwater resources [
8]. In countries with an arid and semi-arid climate, groundwater is widely used for irrigation. Groundwater sources represent 45% of cultivated land in the United States, 58% in Iran and 67% in Algeria [
9]. This fact frequently leads to the overexploitation of resources. Moreover, the initial low energy of water means that the energy consumed for groundwater abstraction can reach up to 70% [
10] of the total energy demanded in the irrigation process, with a high carbon footprint associated with it [
11].
Different strategies have been implemented to reduce the energy consumption and, therefore, the carbon footprint in the process of groundwater abstraction. Some of these measures are the implementation of energy audits to improve the energy efficiency of the pumping systems [
10,
12,
13] and the use of a variable frequency drive (VFD) to optimize the energy consumed per cubic meter abstracted [
8].
The carbon footprint linked to the energy consumption required for groundwater abstraction and the pressurization of the irrigation systems can be largely reduced through the use of renewable energy, with solar pumping systems playing a key role [
14,
15]. In solar pumping systems, it is necessary to install a VFD to activate and control the motor depending on the irradiance value, so that both, photovoltaic generator and pumping system operates under optimal conditions. Although there are recent studies that conclude that the inclusion of a VFD can lead to energy savings in pumping systems of groundwater abstraction [
8], many others conclude that the inclusion of a VFD can decrease the global efficiency of pumping systems, mainly when operating in low frequency values [
16,
17].
Solar pumping systems are exposed to sudden changes in the motor excitation due to the high variability in power generation. Additionally, these systems suffer sudden stops due to cloud cover, long periods working with low frequency values, among many other events. These operation conditions certainly affect the operation and capabilities of these systems. The useful life of the system is shortened, and energy efficiency can be reduced. These types of systems demand real-time monitoring to detect, in a preventive manner, the potential problems of operation [
18]. The main parameters to monitor in groundwater pumping systems are discharge, absorbed power, pressure and the dynamic water table level. Monitoring the pattern of these variables over time allows technicians to detect possible performance problems. However, these parameters are highly variable, which requires the expert analysis of these parameters by a well-trained technician to predict potential breakdowns before they happen and propose adequate actions. Some tools generate alarms in case some indicators [
19], such as energy indicators (kWh·m
−3), are out of a range. Several publications [
20] for pump maintenance engineers and technicians describe classical approaches for the performance analysis of pumping systems, based on the predictive maintenance of pumps using condition monitoring [
18], which relies on classical measures of the performance of these systems.
However, there are not automatic solutions that, based on the hydraulic and energy system modelling, predict the malfunctioning of the system and determine the component of the system (motor, pump or piping) that is generating the problem.
The objective of this work is to develop a decision support system (DSS) called AS-Solar to evaluate, in real-time, the operation of groundwater abstraction pumping systems. The DSS model integrates a hydraulic and energy model with a monitoring system that permits the early anomaly detection of failures and detect the component that can cause the problem. The proposed DSS was calibrated and validated in a solar pumping system located in a semi-arid area of the southeast of Spain.
2. Materials and Methods
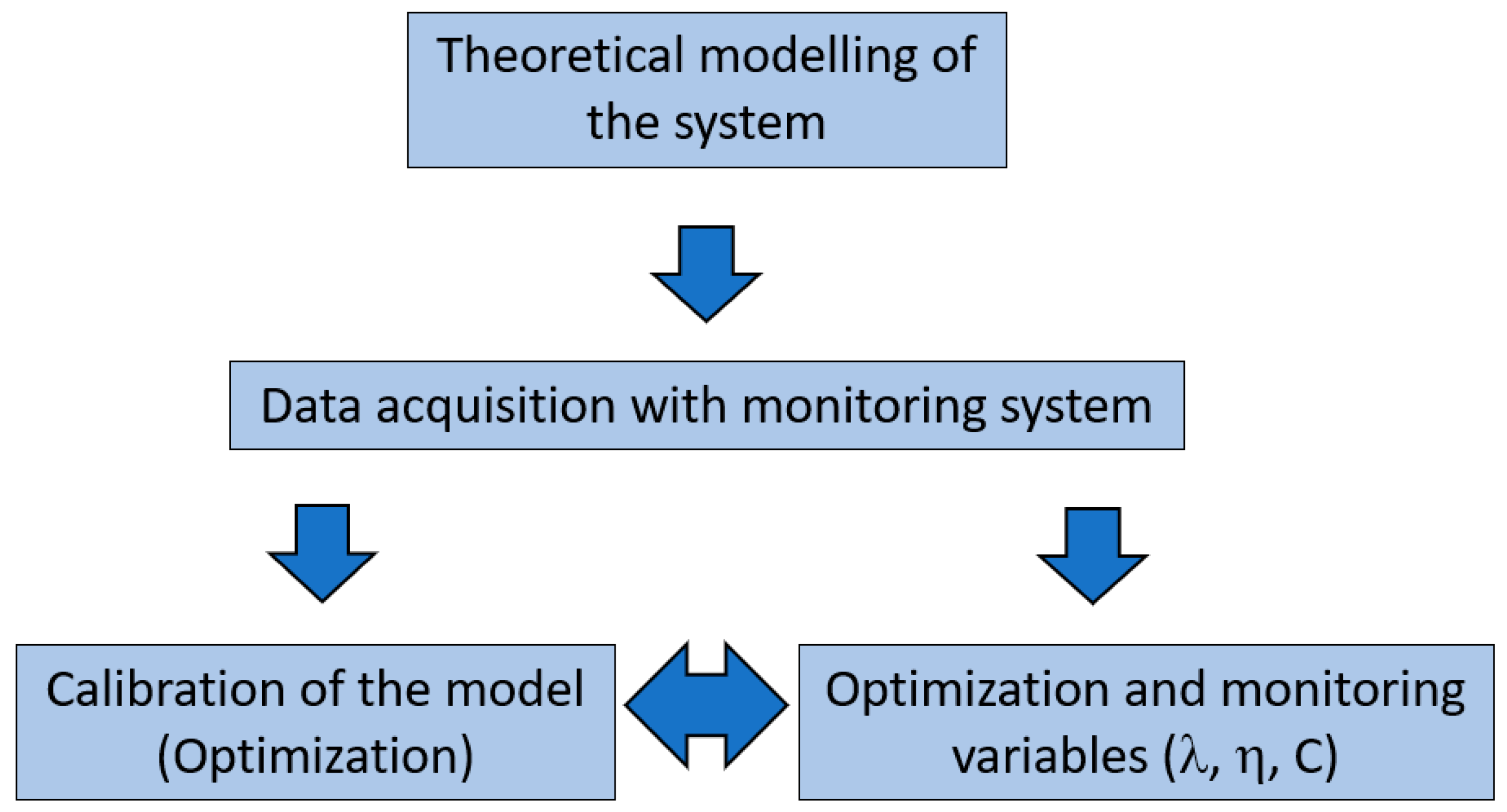
To develop a decision support system model that permits the predictive maintenance of pumping systems for groundwater abstraction, the following three steps were followed: (1) generate and integrate accurate simulation models for each of the pumping system components, (2) design a system for the accurate monitoring of the parameters that define the system performance (hydraulic and electrical parameters) and (3) calibrate and validate the hydraulic and energy model using an optimization process using monitoring data.
Once calibrated for the monitored systems, the monitoring systems fed the model information. A comparison was established between the data measured by the monitoring system and the simulated data derived from the model. In the case of a mismatch between both sets of information, an alarm was generated. Additionally, after every working day, a new optimization process was performed to obtain a new set of calibrated variables. The tendency of this calibrated variables over time was also used to determine possible problems in the system. Depending on the variable that changes, the problem would be electrical, hydraulic or related to the pump.
2.1. Hydraulic and Energy Modelling
The hydraulic and energy model included in the DSS AS-Solar was based on the hydraulic and energy simulation of each of the components of the pumping systems for water abstraction from aquifers. It has the possibility of incorporating a VFD, which is required in the case of solar pumping systems, or optional in the conventional energy supply for an energy consumption decrease [
8].
The main sources of failures in pumping systems for groundwater abstraction are [
20,
21]: (1) the impeller wearing out, mainly when the water includes solid elements such as silts, (2) the deterioration of the electric motor, due to insulation failure in overheating processes, low voltage supply or frequent work at low frequencies of the VFD and (3) failures in the hydraulic system, mainly due to the deterioration of the pumping pipe, with an increase in roughness values or even perforation of the pipe.
To develop the hydraulic and energy model able to predict any anomaly in the functioning of the pumping system, affinity laws were implemented to simulate, on one hand, the performance of the VFD, and on the other hand, the impeller wear out, assuming a similar effect to impeller cutting. The hydraulic performance of the pumping pipe was simulated using the Hazen–Williams equation. This permits the decrease in diameter to be simulated due to deposits in the pipe wall that cause an increase in the roughness value [
22,
23]. The electrical component was simulated considering a component of the efficiency that multiplies the pump efficiency and the motor efficiency so that it includes the rest of the components that affect the electrical efficiency.
The characteristic curves of the centrifugal pump can be defined with the Equations (1) and (2).
where
H is the manometric height of the pump;
a,
b and
c are the coefficients that define the characteristic curve
Q-
H;
e and
f are coefficients that define the curve
Q-efficiency;
Q is the discharge; and
ηp is the pump efficiency.
The impeller wear out was simulated using the affinity laws, as described in Equations (3) and (4).
where λ is the diameter of the impeller cut divided by the diameter of the original impeller (λ = Dr/Do).
The variation of the rotational speed in the pump to feed the motor with a frequency less than the nominal (50 Hz in Spain) was simulated using the affinity laws, as described the Equations (5) and (6).
where
α is the relationship between the supplied frequency to the motor and nominal frequency of the electrical grid (50 Hz in Spain).
The hydraulic model of the pumping pipe considers the discharge (Q, in m
3·h
−1), the pipe diameter (D, in m), the pipe length (L, in m) and the Hazen–Williams coefficient (C), using Equation (7) for the determination of the head loss (Δh, in m).
To take into account the possible failures and underperformance of the electrical components of the pumping system (cables, motor or VFD), an efficiency component (
ηelectric) in the equation of the absorbed power (Equation (8)) was considered.
where
NT is the absorbed power (kW)’ γ is the specific weight of water (KN·m
−3); Q is the pump discharge (m
3·s
−1); H is the piezometric height of the pump (m);
ηp is the pump efficiency;
ηm is the motor efficiency, which is considered a constant value in this work and
ηelectric is a variable that considers the efficiency of the rest of the system’s electric components.
In addition, energy losses in the different lines of cables were simulated. The lines from the VFD output to the borehole inlet and from the borehole inlet to the motor were considered (Equation (9)). They were considered as resistive lines, as depicted by Equation (9).
where
LOPOW is the power losses in the cables (kW), I
max is the circulating current (A), N is the number of cables, L
c is the length of the cable (m) and R is the resistance according to the temperature reached (Ω).
2.2. The Case Study
To analyze, calibrate and validate the proposed method, a commercial farm located in the southeast of Spain was used. The irrigated area was approximately 90 ha, where almond trees in a 7 × 7 m
2 spacing were established. The irrigation system in the plot was subsurface drip irrigation energized using a photovoltaic (PV) system. The irrigation system consisted of 20 subunits with a highly irregular shape and topography with elevation differences of up to 60 m. Thus, the energy demand of the irrigation system was highly variable depending on the activated irrigation subunit. A full description of the irrigation system can be found in [
24].
The photovoltaic generator was composed by 152 polycrystalline silicon modules (
Table 1) Astronergy, model ASM6610P 265 (Astronergy/Chint Solar, Frankfurt, Germany), with eight lines and 19 modules per line. The total installed power was 40 kWp. The nominal power of the variable frequency drive was 30 kW. The generator was oriented south with a slope of 8.5°. A full description of the photovoltaic system can be found in [
25].
The variable frequency drive (VFD) installed was the 3G3RX-A4220-E1F (Omron Europe B.V., Hoofddorp, Netherlands), with an output nominal current of 57 A and an overvoltage protection of 800 V. The VFD efficiency, according to the manufacturer, is 89.7% at 25% of the maximum power and 95% at maximum power.
Groundwater was the source of water, using a borehole with a high variability in the dynamic water table level. The static water table level was 130 m with the values of the dynamic water table level reaching 192 m during the period with maximum requirements.
The pumping pipe was a helical welded steel with a length of 215 m and a nominal diameter of 90 mm. The submersible pump installed was a DBM, model DX6-30 29-6 (DIBOMUR S.L., Murcia, Spain), with a nominal power of 26 kW. The pump was located at a depth of 215 m.
Table 2 shows the main hydraulic characteristics of the pump. The motor presented a nominal power of 30 kW with a rotational speed of 2880 rpm and a nominal voltage and current of 400 V and 59.9 A, respectively.
In the system, the following two different lines of cables fed the three-phase motor: (1) a line from the VFD up to the borehole inlet, which involves a buried aluminum cable XZ1 0.6/1kV with a section of 150 mm2 and a length of 470 m, and (2) a line from the borehole inlet up to the submersible motor, which involves a copper cable RVK 0.6/1kV with a section of 25 mm2 and a length of 225 m.
2.3. Monitoring System
The equipment used for system monitoring was programmed to record the parameters with a time interval of 10 min. Power generated in direct current (DC) was measured using an electrical network analyzer PEL 103 (Chauvin Arnoux, Paris, France) and power (in kW) and frequency (in Hz) at the VFD output were measured with an AR5 electrical network analyzer (CIRCUTOR, Barcelona, Spain) as both analyzers have an accuracy better than 1.5%; dynamic water table level was measured with a microtube and an air compressor, discharge was measured (in L·min
−1) with a Woltman flowmeter WST-SB (Arad Group, Dalia, Israel) and calibrated using a General Electric PT878 ultrasound flowmeter (General Electric Company, Boston, MA, USA), and pressure was measured (in kPa) with a pressure transducer WIKA model A-10 bar (Instruments WIKA, S.A.U, Barcelona, Spain). Data were acquired over 9 months (December 2017–August 2018). This monitoring period describes the performance of the system in periods of low-, medium- and high-water demand of the crop (almond trees in this case study) and also includes different values of the water table level. Thus, the data set considers all the conditions of the system performance, which make it ideal for system modelling under different conditions. After the replacement of the whole pumping system in 2016, intensive testing was performed utilizing the methodology of energy audits [
10,
12] and the proper performance of the system was verified.
Figure 1 shows the illustration of the complete monitoring system.
2.4. Model Calibration and Determination of Robust Monitoring Variables
Once the theoretical model of the system was formulated and implemented, a calibration of the model was performed using the acquired massive data with the monitoring system. To calibrate the theoretical hydraulic and energy model, an optimization process based on Downhill Simplex Method [
26] was implemented (
Figure 2). The optimization variables were (1) the coefficient “λ”, which simulates the wear out of the pump impellers; (2) the coefficient “C” of Hazen–Williams, which simulates the increase in the roughness and decrease in the diameter of the pumping pipe; and (3) the coefficient “
ηelectric”, which determines electrical problems in a VFD, cables and motor. The objective function was to minimize the root mean squared error (RMSE) between measured and simulated power and discharge.
2.5. Statistical Analysis of the Results
To analyze the goodness of fit of the model, a statistical analysis was performed based on the calculation of the RMSE, the relative error (RE) and the coefficient of determination (R2) using programed functions in MATLAB® R2018b. Moreover, the adjustment to the normal of the residuals and homoscedasticity were evaluated.
3. Results and Discussion
3.1. Optimizing Variables
The results obtained with the optimization process for the pumping system working under non-fault or anomalies were λ = 0.9998, C = 66.5 and ηelectric = 0.8333.
With these results, it can be concluded that the impellers of the pump were in perfect condition (values very close to 1). This is logical because the pump was installed a few months before the start of this work.
Studies in Iran assume optimal motor-pump working conditions in solar pumping systems up to 10 years [
27], which is questionable, as it depends on the type of motor insulation, motor, cooling, the variation of the frequency and the VFD control algorithm, among many other factors. Thus, it is essential to monitor this variable to detect pump wear out and to be able to make the right decisions regarding their maintenance.
The obtained Hazen–Williams coefficient “C” was 66.5, which compared with the theoretical value (C = 100) shows a high increase in the roughness of the pipe. It is due to local losses and silt deposits, which decrease the effective diameter. Thus, the demand curve of the system increases, and the discharge is much lower than the theoretical one.
The electrical component (ηelectric) results in a value far below the expected one in a system replaced a short time ago. This is due to the different assumptions considered in the development of the energy model such as (1) the motor efficiency is considered to be constant, (2) inaccuracies in the determination of energy losses in the cables and (3) considering the efficiency values for the VFD supplied by the manufacturer.
Motor efficiency, in the case study, was considered to have a value of 84%, which was supplied by the manufacturer. Motor efficiency depends on the motor load and working conditions, established by the IEC 60034-2-1 standard. These conditions can be very different from those found in a pumping system energized using photovoltaic generators, where the motor is fed with low frequencies and low voltage, among other factors.
The assumptions considered in energy losses’ simulation in cables are the section of the cables is considered invariable, there is no wear on the cables’ insulation, the cable works on maximum cable temperature, among many other factors.
Concerning the efficiency of the VFD, it is usually much lower than that determined by the manufacturer under standard testing conditions (
Figure 3), primarily due to increases in the VFD temperature. In
Figure 3, it can be observed that all the efficiency values are much lower than those determined by the manufacturer. This difference is higher for the low and medium power (low and medium frequencies), having less difference at maximum power (frequency of 50 Hz and voltage of 400 V).
3.2. Calibration of the AS-Solar Model
With the values obtained from the optimization process, the goodness of fit of the model was carried out by comparing the simulated and measured absorbed power (
Figure 4).
The statistic indicators of the goodness of fit of the simulated vs. measured power can be observed in
Table 3.
A good adjustment of the AS-Solar model can be observed regarding the simulation of absorbed power, for the whole range of powers. The model slightly overestimates for high values of absorbed power, with a clear heteroscedasticity of the errors (
Figure 5). This may be because the efficiency of the motor is variable depending on the load, while in this model, it was considered constant. However, these detected problems have a low effect on the final model.
However, when evaluating the fitting of the simulated discharge to the measured discharge, a lower accuracy than the adjustment of power was found (
Figure 6). The goodness of fit of the discharge is shown in
Table 4. An RE of approximately 8% can be observed. According to the metrological control standards UNE-EN 1,4268: “Irrigation techniques. Water meters”, the error assumable in flowmeters within the limits of the nominal flow rate must be at ±2% (4% relative error) or ±5% for values out of the nominal flow rate.
Figure 7 shows a histogram of the model errors regarding the discharge simulation. The error in the % of the residuals is above the value of 2%, but generally within the range of 5%.
These data indicate that most of the errors fit the typical error of the volumetric meter acting as a flowmeter. Additionally, it should be considered that the measured flow rate can often be very far from the nominal flow rate of the flowmeter, which means the average error is high, mainly for the cases of low flow rates, as shown in
Figure 7.
With the obtained optimization variables, the model permits the efficiency of the pump to be determined for different rotational speeds (
Figure 8). These values are much lower than those supplied by the manufacturer at 50 Hz, but the slope of the curve is smaller. Of course, it includes the efficiency of the VFD and the rest of the electrical components of the system.
4. Conclusions
In this work, we present a novel method that combines the hydraulic and energy simulation models of the pumping systems, monitoring systems and optimization procedures to generate a DSS this is able to discriminate the source of failure in complex groundwater abstraction systems. In groundwater abstraction systems, the motor and pump are not accessible, unless the whole system is extracted. Thus, inferring the performance of these components through basic monitoring data contributes to performance and integrated predictive maintenance. Additionally, with the development of a DSS, this work contributes to the performance of the predictive maintenance of pumping systems controlled by a VFD, such as the systems utilized in solar pumping systems, which greatly increase the complexity of the hydraulic and energy models. Additionally, in these types of systems, the necessity of generating these predictive maintenance systems is of higher importance due to the pump and motor, which are working under highly variable conditions of frequency and voltage, wearing out more.
A robust and efficient DSS for the predictive maintenance of pumping systems, named AS-Solar, was developed. It increases the utility of the monitoring system by supplying the capability of determining the component of the pumping system that is functioning with anomalies: the pump, electrical components or pumping pipe. Therefore, it helps in the decision-making process when repairing and maintaining the system.
The optimizing variables obtained with the generated model have allowed a goodness of fit of the calibrated model for the absorbed electric power and for the discharge with relative errors (REs) of 2.89 and 7.93%, respectively. Therefore, this means the AS-Solar model can, with good accuracy, obtain the highly predictive capacity of the system.
The groundwater abstraction system is complex to maintain because the motor and the pump are not accessible, which emphasizes the usefulness of the developed model. Additionally, the developed model was applied to a solar pumping system, in which the high variability in energy conditions make the implementation of predictive maintenance models even more difficult. Although AS-Solar has been applied to this complex case study to validate its usefulness, it can be applied to any other type of pumping system.
The main weakness of the model appears in the simulation of the performance of the electrical components: motor, cables and a VFD. A better simulation of the performance of these components could lead to an improvement of the model. However, the inclusion of the optimization parameter “ηelectric” solved this weakness.