Translation of Irrigation, Drainage, and Electrical Conductivity Data in a Soilless Culture System into Plant Growth Information for the Development of an Online Indicator Related to Plant Nutritional Aspects
Abstract
1. Introduction
2. Materials and Methods
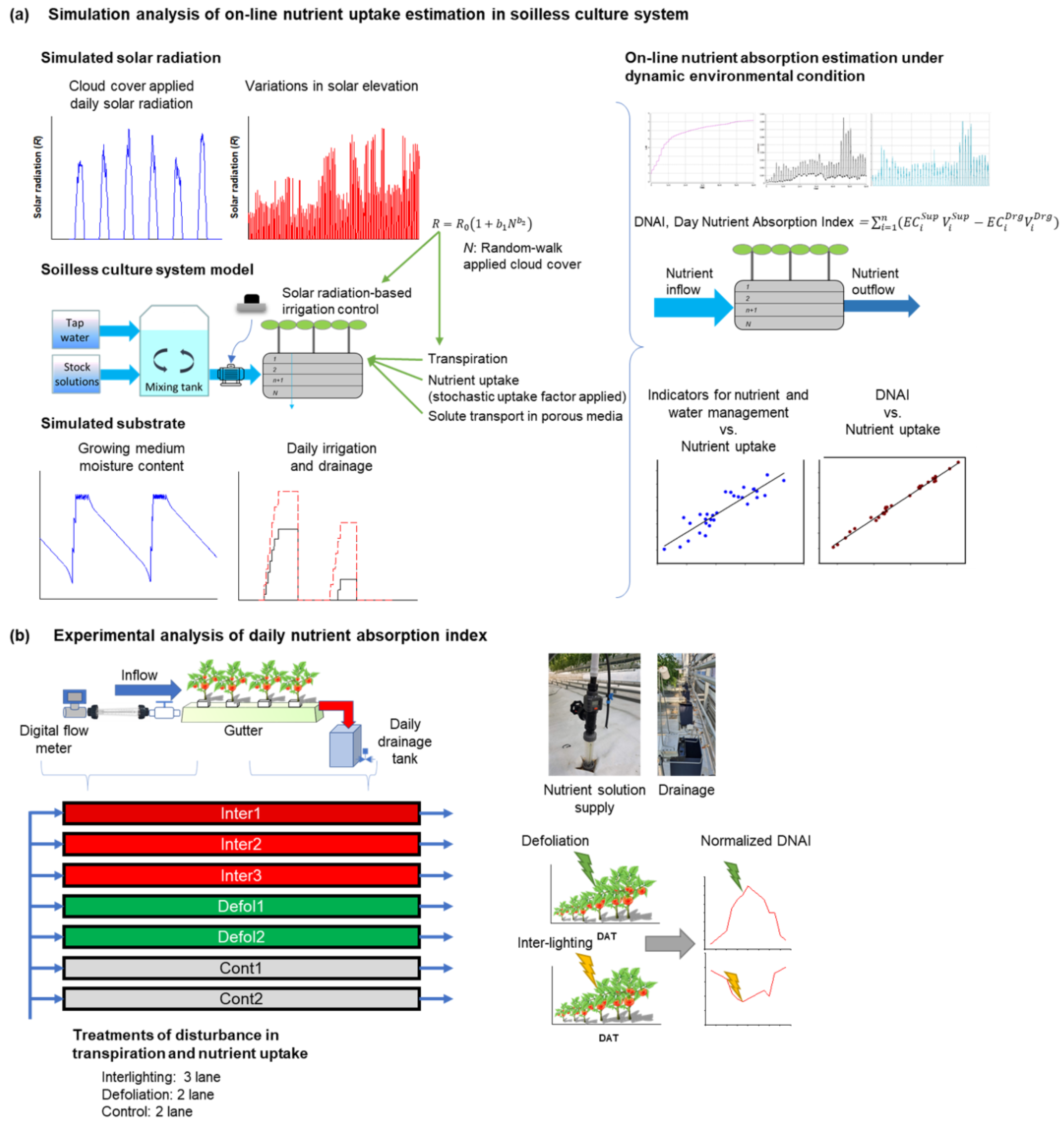
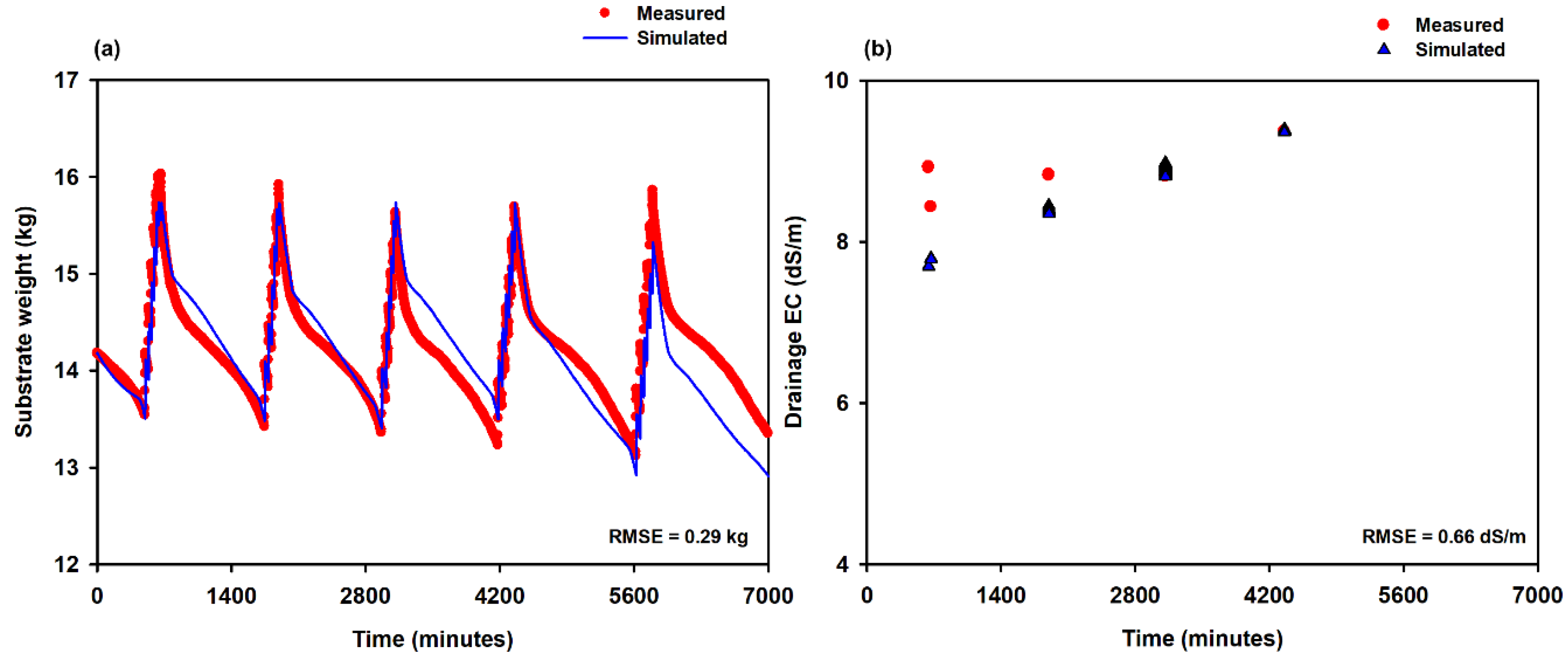
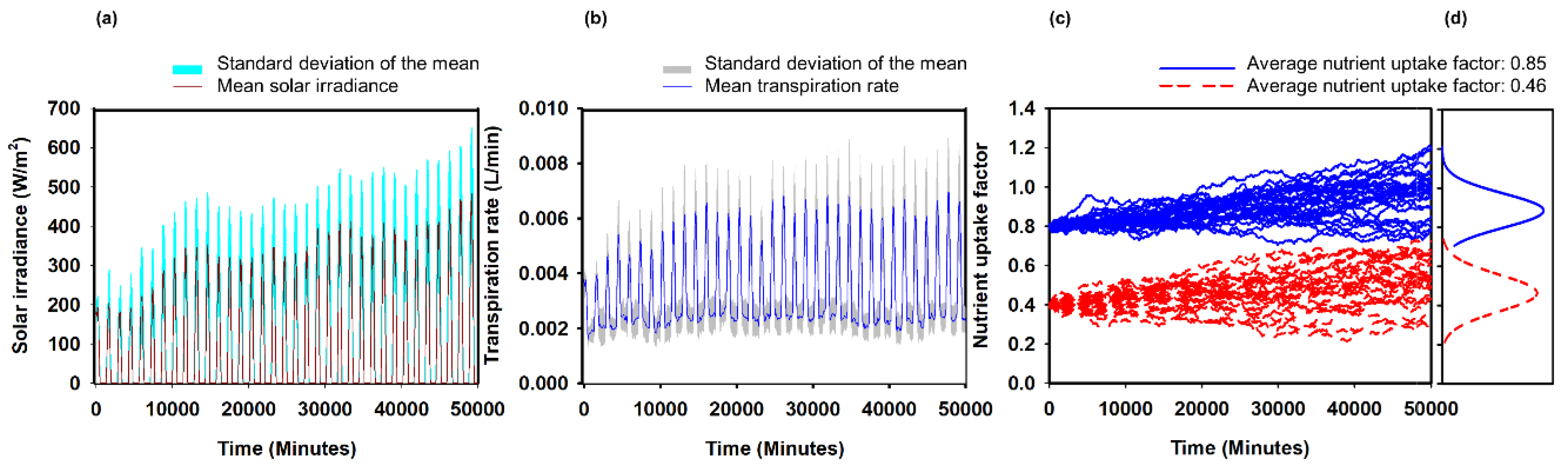
2.1. Simulation Analysis on Nutrient Uptake Estimation
2.2. Experimental Demonstration of DNAI
2.3. Treatments for Disturbance Application on Nutrient Uptake and Transpiration
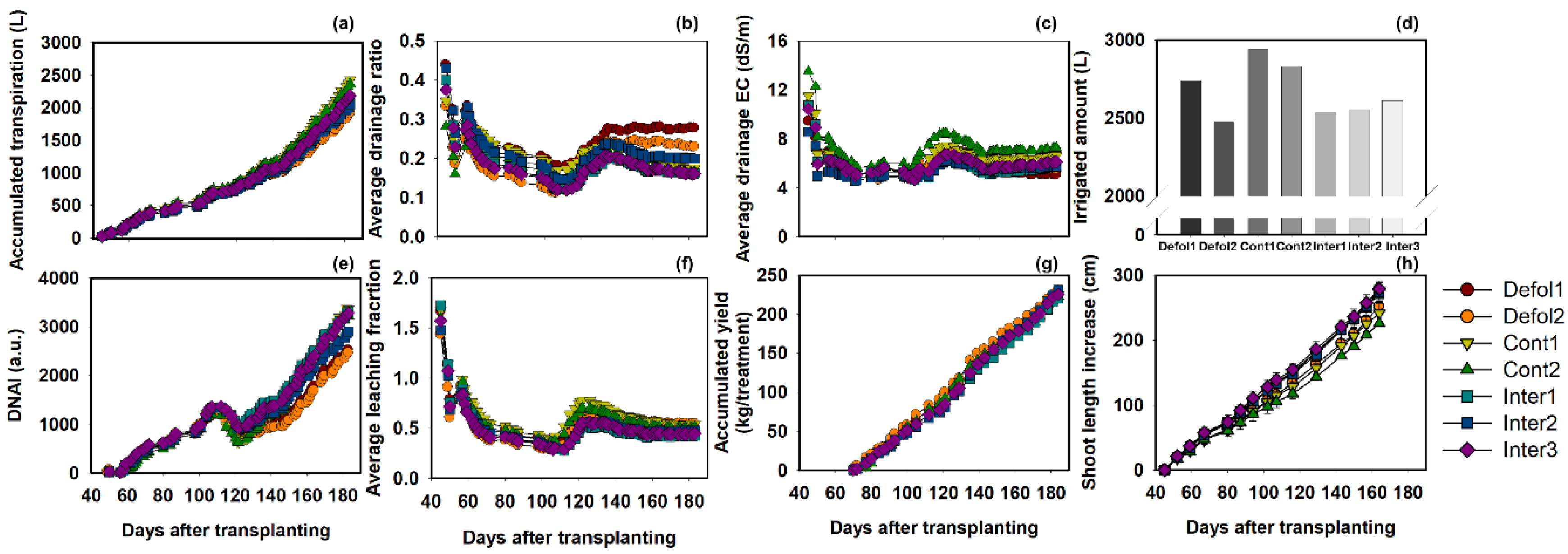
3. Results
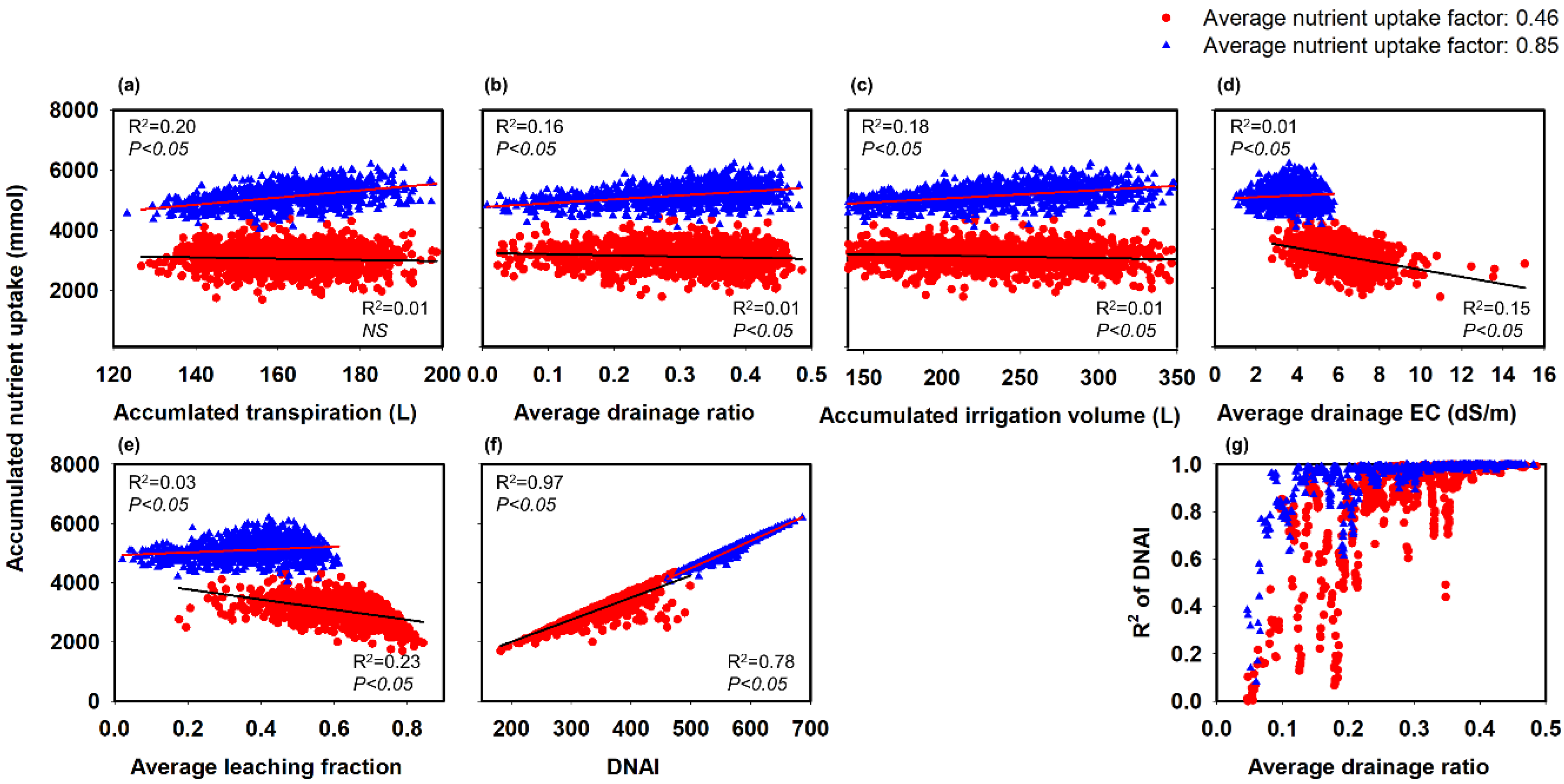
3.1. Simulation Analysis of DNAI
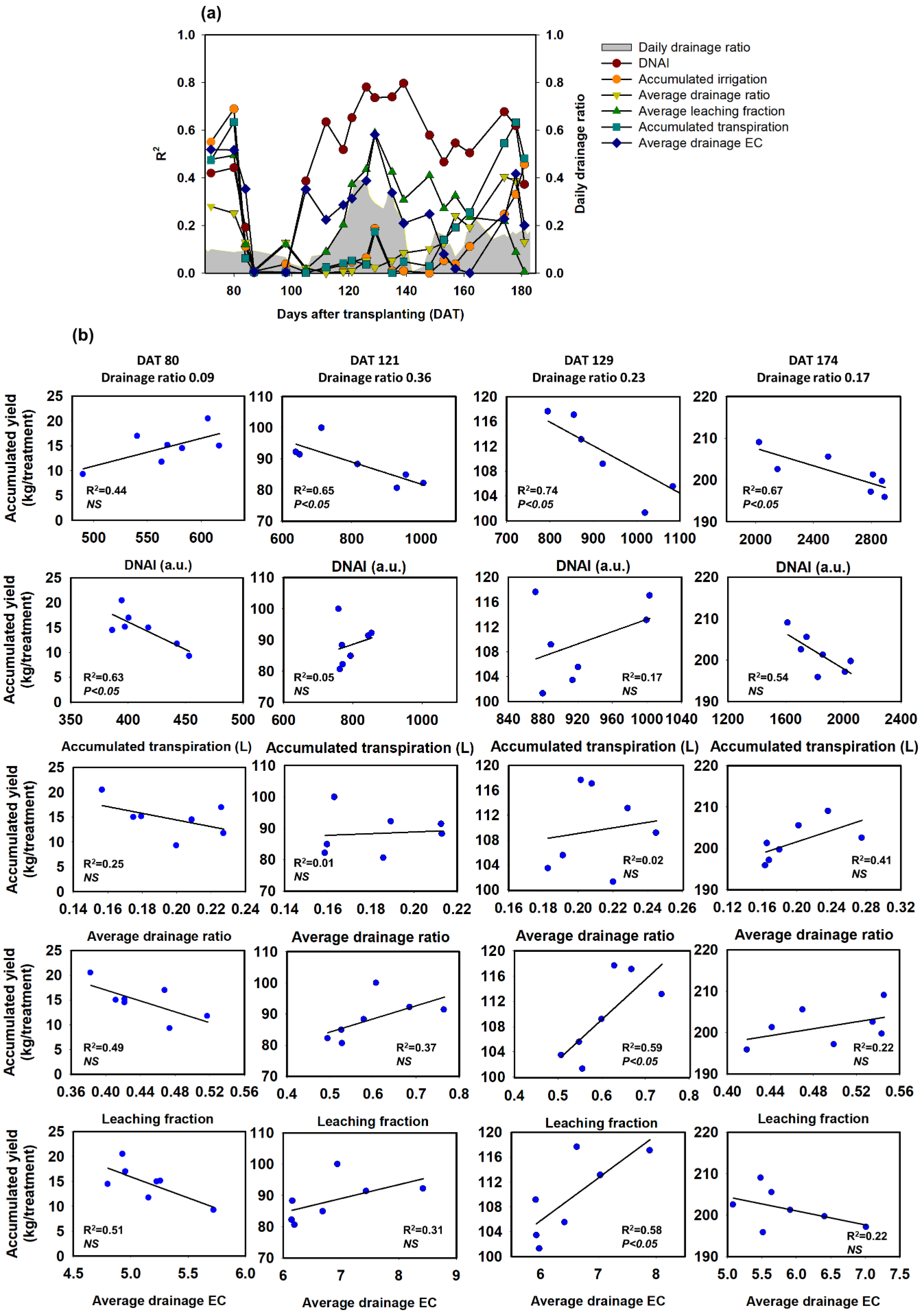
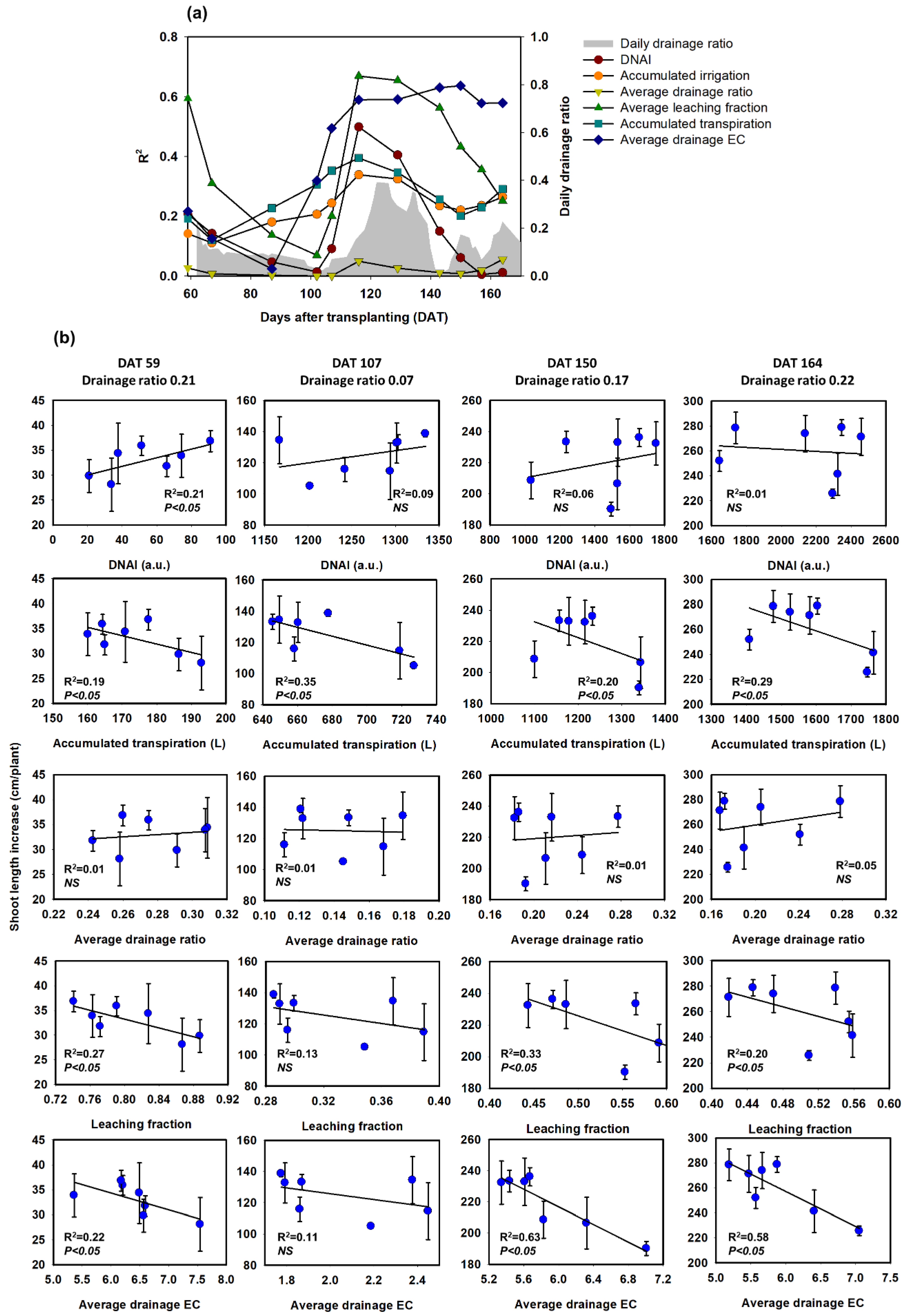
3.2. Correlation between DNAI and Plant Growth in the Cultivation Experiment
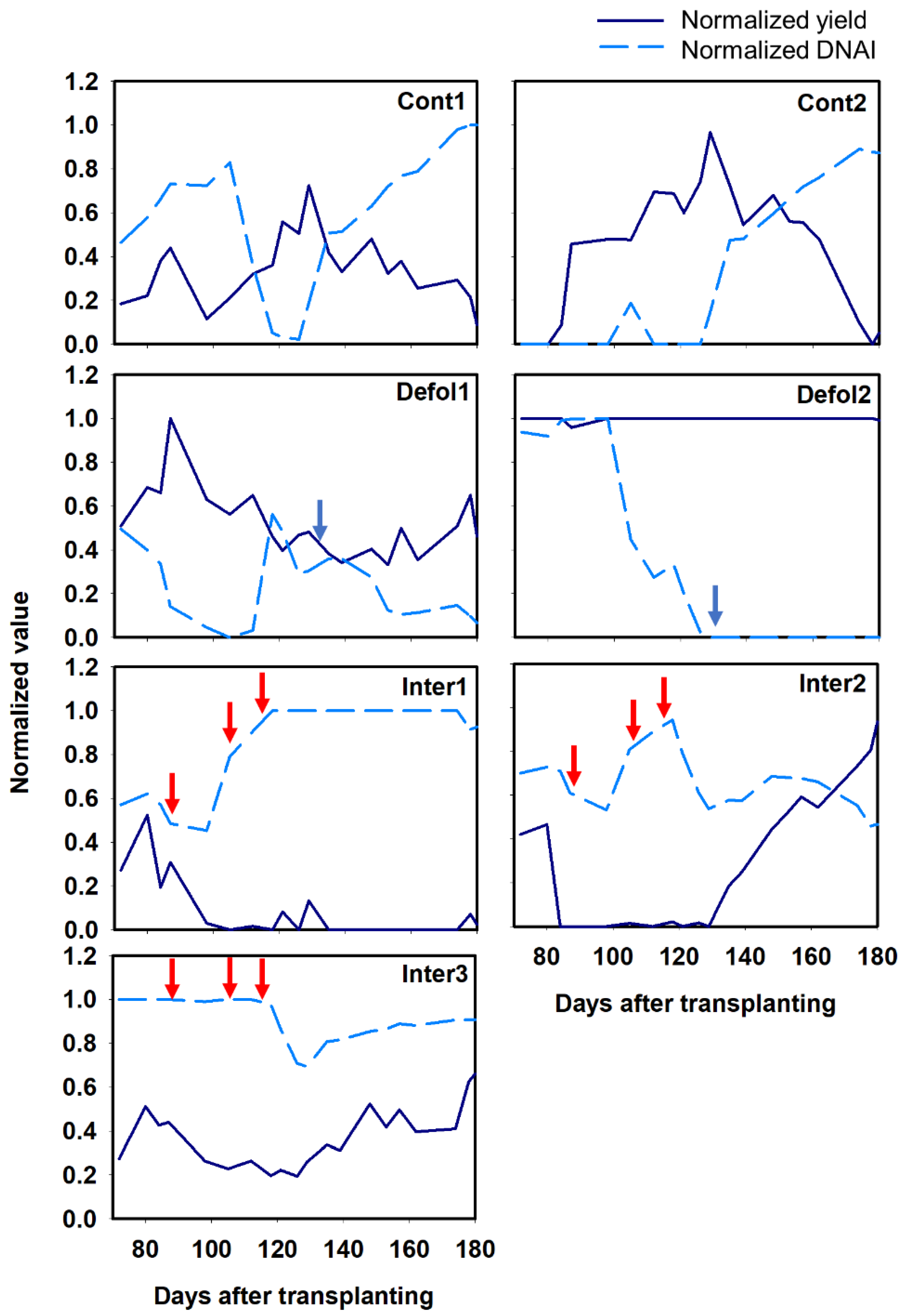
3.3. Normalized Tomato Yield and DNAI in the Cultivation Experiment
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Walter, A.; Finger, R.; Huber, R.; Buchmann, N. Opinion: Smart farming is key to developing sustainable agriculture. Proc. Natl. Acad. Sci. USA 2017, 114, 6148–6150. [Google Scholar] [CrossRef] [PubMed]
- Wolfert, S.; Ge, L.; Verdouw, C.; Bogaardt, M. Big data in smart farming—A review. Agric. Syst. 2017, 153, 69–80. [Google Scholar] [CrossRef]
- Weersink, A.; Fraser, E.; Pannell, D.; Duncan, E.; Rotz, S. Opportunities and challenges for big data in agricultural and environmental analysis. Annu. Rev. Resour. Econ. 2018, 10, 19–37. [Google Scholar] [CrossRef]
- Kang, S.; van Iersel, M.W.; Kim, J. Plant root growth affects FDR soil moisture sensor calibration. Sci. Hortic. 2019, 252, 208–211. [Google Scholar] [CrossRef]
- Liu, Z.; Xu, Q. An automatic irrigation control system for soilless culture of lettuce. Water 2018, 10, 1692. [Google Scholar] [CrossRef]
- Montesano, F.F.; van Iersel, M.W.; Boari, F.; Cantore, V.; D’Amato, G.; Parente, A. Sensor-based irrigation management of soilless basil using a new smart irrigation system: Effects of set-point on plant physiological responses and crop performance. Agric. Water Manag. 2018, 203, 20–29. [Google Scholar] [CrossRef]
- Jahromi, N.B.; Fulcher, A.; Walker, F.; Altland, J. Photosynthesis, growth, and water use of Hydrangea paniculata ‘Silver Dollar’ using a physiological-based or a substrate physical properties-based irrigation schedule and a biochar substrate amendment. Irrig. Sci. 2020. [Google Scholar] [CrossRef]
- Opazo, I.; Toro, G.; Salvatierra, A.; Pastenes, C.; Pimentel, P. Rootstocks modulate the physiology and growth responses to water deficit and long-term recovery in grafted stone fruit trees. Agric. Water Manag. 2020, 228, 105897. [Google Scholar] [CrossRef]
- Shin, J.H.; Son, J.E. Application of a modified irrigation method using compensated radiation integral, substrate moisture content, and electrical conductivity for soilless cultures of paprika. Sci. Hortic. 2016, 198, 170–175. [Google Scholar] [CrossRef]
- Zhang, D.; Du, Q.; Zhang, Z.; Jiao, X.; Song, X.; Li, J. Vapour pressure deficit control in relation to water transport and water productivity in greenhouse tomato production during summer. Sci. Rep. 2017, 7, 43461. [Google Scholar] [CrossRef]
- Tardieu, F.; Cabrera-Bosquet, L.; Pridmore, T.; Bennett, M. Plant phenomics, from sensors to knowledge. Curr. Biol. 2017, 27, R770–R783. [Google Scholar] [CrossRef] [PubMed]
- Lee, A.; Grodan, B.V. Steering the root zone environment. Pract. Hydroponics Greenh. 2010, 110, 47. [Google Scholar]
- de Koning, A.N.M.; Tsafaras, I. Real-time comparison of measured and simulated crop transpiration in greenhouse process control. Acta Hortic. 2017, 1170, 301–308. [Google Scholar] [CrossRef]
- Lee, J.W.; Son, J.E. Nondestructive and continuous fresh weight measurements of bell peppers grown in soilless culture systems. Agronomy 2019, 9, 652. [Google Scholar] [CrossRef]
- Wang, H.; Sánchez-Molina, J.A.; Li, M.; Berenguel, M.; Yang, X.T.; Bienvenido, J.F. Leaf area index estimation for a greenhouse transpiration model using external climate conditions based on genetics algorithms, back-propagation neural networks and nonlinear autoregressive exogenous models. Agric. Water Manag. 2017, 183, 107–115. [Google Scholar] [CrossRef]
- García-Tejera, O.; López-Bernal, Á.; Testi, L.; Villalobos, F.J. A soil-plant-atmosphere continuum (SPAC) model for simulating tree transpiration with a soil multi-compartment solution. Plant Soil 2017, 412, 215–233. [Google Scholar] [CrossRef]
- Pieruschka, R.; Huber, G.; Berry, J.A. Control of transpiration by radiation. Proc. Natl. Acad. Sci. USA 2010, 107, 13372. [Google Scholar] [CrossRef] [PubMed]
- Xiang, K.; Li, Y.; Horton, R.; Feng, H. Similarity and difference of potential evapotranspiration and reference crop evapotranspiration—A review. Agric. Water Manag. 2020, 232, 106043. [Google Scholar] [CrossRef]
- Ågren, G.I. Stoichiometry and nutrition of plant growth in natural communities. Annu. Rev. Ecol. Evol. Syst. 2008, 39, 153–170. [Google Scholar] [CrossRef]
- Huett, D.O. Prospects for manipulating the vegetative-reproductive balance in horticultural crops through nitrogen nutrition: A review. Aust. J. Agric. Res. 1996, 47, 47–66. [Google Scholar] [CrossRef]
- Rivas-Ubach, A.; Sardans, J.; Perez-Trujillo, M.; Estiarte, M.; Penuelas, J. Strong relationship between elemental stoichiometry and metabolome in plants. Proc. Natl. Acad. Sci. USA 2012, 109, 4181–4186. [Google Scholar] [CrossRef] [PubMed]
- Shin, J.H.; Park, J.S.; Son, J.E. Estimating the actual transpiration rate with compensated levels of accumulated radiation for the efficient irrigation of soilless cultures of paprika plants. Agric. Water Manag. 2014, 135, 9–18. [Google Scholar] [CrossRef]
- Van Noordwijk, M. Synchronisation of supply and demand is necessary to increase efficiency of nutrient use in soilless horticulture. In Proceedings of the Plant Nutrition—Physiology and Applications: Proceedings of the Eleventh International Plant Nutrition Colloquium, Wageningen, The Netherlands, 30 July–4 August 1989; van Beusichem, M.L., Ed.; Springer: Dordrecht, The Netherlands, 1990; pp. 525–531. [Google Scholar]
- Nordstrom, D.K. 5.02—Modeling Low-Temperature Geochemical Processes. In Treatise on Geochemistry; Holland, H.D., Turekian, K.K., Eds.; Pergamon: Oxford, UK, 2007; pp. 1–38. [Google Scholar]
- Ta, T.H.; Shin, J.H.; Noh, E.H.; Son, J.E. Transpiration, growth, and water use efficiency of paprika plants (Capsicum annuum L.) as affected by irrigation frequency. Hortic. Environ. Biotechnol. 2012, 53, 129–134. [Google Scholar] [CrossRef]
- Ko, M.T.; Ahn, T.I.; Shin, J.H.; Son, J.E. Effects of renewal pattern of recycled nutrient solution on the ion balance in nutrient solutions and root media and the growth and ion uptake of paprika (Capsicum annuum L.) in closed soilless cultures. Korean J. Hortic. Sci. Technol. 2014, 32, 463–472. [Google Scholar] [CrossRef]
- Rincón, L.; Pérez, A.; Abadia, A.; Pellicer, C. Yield, water use and nutrient uptake of a tomato crop grown on coconut coir dust. Acta Hortic. 2005, 73–79. [Google Scholar] [CrossRef]
- Holtslag, A.A.M.; Van Ulden, A.P. A simple scheme for daytime estimates of the surface fluxes from routine weather data. J. Clim. Appl. Meteorol. 1983, 22, 517–529. [Google Scholar] [CrossRef]
- Kasten, F.; Czeplak, G. Solar and terrestrial radiation dependent on the amount and type of cloud. Sol. Energy 1980, 24, 177–189. [Google Scholar] [CrossRef]
- Ahn, T.I.; Son, J.E. Theoretical and experimental analysis of nutrient variations in electrical conductivity-based closed-loop soilless culture systems by nutrient replenishment method. Agronomy 2019, 9, 649. [Google Scholar] [CrossRef]
- Silberbush, M.; Ben-Asher, J.; Ephrath, J.E. A model for nutrient and water flow and their uptake by plants grown in a soilless culture. Plant Soil 2005, 271, 309–319. [Google Scholar] [CrossRef]
- Snape, J.B.; Dunn, I.J.; Ingham, J.; Prenosil, J.E. Dynamics of Environmental Bioprocesses: Modelling and Simulation; VCH: New York, NY, USA, 1995. [Google Scholar]
- Bailey, B.J.; Montero, J.I.; Biel, C.; Wilkinson, D.J.; Anton, A.; Jolliet, O. Transpiration of Ficus benjamina: Comparison of measurements with predictions of the Penman-Monteith model and a simplified version. Agric. For. Meteorol. 1993, 65, 229–243. [Google Scholar] [CrossRef]
- Choi, Y.B.; Shin, J.H. Development of a transpiration model for precise irrigation control in tomato cultivation. Sci. Hortic. 2020, 267, 109358. [Google Scholar] [CrossRef]
- Carmassi, G.; Incrocci, L.; Incrocci, G.; Pardossi, A. Non-destructive estimation of leaf area in tomato (Solanum lycopersicum L.) and gerbera (Gerbera jamesonii H. Bolus). Agric. Mediterr. 2007, 137, 172–176. [Google Scholar]
- Savvas, D.; Adamidis, K. Automated management of nutrient solutions based on target electrical conductivity, pH, and nutrient concentration ratios. J. Plant Nutr. 1999, 22, 1415–1432. [Google Scholar] [CrossRef]
- Kim, W.S.; Lieth, J.H. Simulation of year-round plant growth and nutrient uptake in Rosa hybrida over flowering cycles. Hortic. Environ. Biotechnol. 2012, 53, 193–203. [Google Scholar] [CrossRef]
- Islam, A.F.M.S.; Haque, M.M.; Tabassum, R.; Islam, M.d.M. Effect of defoliation on growth and yield response in two tomato (Solanum lycopersicum Mill.) varieties. J. Agron. 2016, 15, 68–75. [Google Scholar] [CrossRef][Green Version]
- Eavis, B.W.; Taylor, H.M. Transpiration of soybeans as related to leaf area, root length, and soil water content. Agron. J. 1979, 71, 441–445. [Google Scholar] [CrossRef]
- Tewolde, F.T.; Lu, N.; Shiina, K.; Maruo, T.; Takagaki, M.; Kozai, T.; Yamori, W. Nighttime supplemental LED inter-lighting improves growth and yield of single-truss tomatoes by enhancing photosynthesis in both winter and summer. Front. Plant Sci. 2016, 7. [Google Scholar] [CrossRef]
- Murage, E.N.; Watashiro, N.; Masuda, M. Leaf chlorosis and carbon metabolism of eggplant in response to continuous light and carbon dioxide. Sci. Hortic. 1996, 67, 27–37. [Google Scholar] [CrossRef]
- Stanghellini, C. Transpiration of greenhouse crops: An Aid to Climate Management. Ph.D. Thesis, Wageningen University of Agriculture, Wageningen, The Netherlands, 1987. [Google Scholar]
- Silberbush, M.; Ben-Asher, J. Simulation study of nutrient uptake by plants from soilless cultures as affected by salinity buildup and transpiration. Plant Soil 2001, 233, 59–69. [Google Scholar] [CrossRef]
- Jones, J.W.; Dayan, E.; Allen, L.H.; van Keulen, H.; Challa, H. A dynamic tomato growth and yield model (TOMGRO). Trans. ASABE 1991, 34, 0663–0672. [Google Scholar] [CrossRef]
- Barradas, V.L.; Nicolás, E.; Torrecillas, A.; Alarcón, J.J. Transpiration and canopy conductance in young apricot (Prunus armenica L.) trees subjected to different PAR levels and water stress. Agric. Water Manag. 2005, 77, 323–333. [Google Scholar] [CrossRef]
- Tanguilig, V.C.; Yambao, E.B.; O’toole, J.C.; De Datta, S.K. Water stress effects on leaf elongation, leaf water potential, transpiration, and nutrient uptake of rice, maize, and soybean. Plant Soil 1987, 103, 155–168. [Google Scholar] [CrossRef]
- Ku, C.S.M.; Hershey, D.R. Leachate electrical-conductivity and growth of potted poinsettia with leaching fractions of 0 to 0.4. J. Am. Soc. Hortic. Sci. 1991, 116, 802–806. [Google Scholar] [CrossRef]
- Schon, M.K.; Compton, M.P. Comparison of cucumbers grown in rockwool or perlite at two leaching fractions. HortTechnology 1997, 7, 30–33. [Google Scholar] [CrossRef]
- Amtmann, A.; Leigh, R. Ion homeostasis. In Abiotic Stress Adaptation in Plants; Pareek, A., Sopory, S.K., Bohnert, H.J., Eds.; Springer: Dordrecht, The Netherlands, 2009; pp. 245–262. [Google Scholar]
- Ågren, G.I.; Martin, W.J.Å.; Billberger, M.F.K. Nutrient limitation on terrestrial plant growth – modeling the interaction between nitrogen and phosphorus. New Phytol. 2012, 194, 953–960. [Google Scholar] [CrossRef] [PubMed]
- Yan, W.; Du, M.; Zhao, W.; Li, F.; Wang, X.; Eneji, A.E.; Yang, F.; Huang, J.; Meng, L.; Qi, H.; et al. Relationships between plant architecture traits and cotton yield within the plant height range of 80–120 cm desired for mechanical harvesting in the yellow river valley of china. Agronomy 2019, 9, 587. [Google Scholar] [CrossRef]
- De Kreij, C.; Van den Berg, T.h.J.M. Nutrient uptake, production and quality of Rosa hybrida in rockwool as affected by electrical conductivity of the nutrient solution. In Plant Nutrition—Physiology and Applications; van Beusichem, M.L., Ed.; Springer: Dordrecht, The Netherlands, 1990; pp. 519–523. [Google Scholar]
- Montesano, F.F.; van Iersel, M.W. Calcium can prevent toxic effects of Na+ on tomato leaf photosynthesis but does not restore growth. J. Am. Soc. Hortic. Sci. 2007, 132, 310–318. [Google Scholar] [CrossRef]
- Velez-Ramirez, A.I.; van Ieperen, W.; Vreugdenhil, D.; Millenaar, F.F. Plants under continuous light. Trends Plant Sci. 2011, 16, 310–318. [Google Scholar] [CrossRef]
| Symbol | Description | Value | Reference |
|---|---|---|---|
| Leaf area index | 7.4 | Measured in this study | |
| Transpiration empirical parameter | 1.52 × 10−7 | Calibrated in this study | |
| Transpiration empirical parameter | 1.71 × 10−4 | Calibrated in this study | |
| Extinction coefficient | 0.84 | [34] | |
| Maximum absorption rate | 0.009 | [37] | |
| Maximum absorption rate | 0.003 | ||
| Maximum absorption rate | 0.012 | ||
| Maximum absorption rate | 0.002 | ||
| Michaelis-Menten constant | 3.185 | ||
| Michaelis-Menten constant | 0.617 | ||
| Michaelis-Menten constant | 0.252 | ||
| Michaelis-Menten constant | 4.432 | ||
| Michaelis-Menten constant | 0.358 | ||
| Minimal concentration for uptake | 0.002 | ||
| Minimal concentration for uptake | 0.002 | ||
| Minimal concentration for uptake | 0.002 | ||
| Minimal concentration for uptake | 0.002 | ||
| Minimal concentration for uptake | 0.002 | ||
| Root surface area | 0.8 | Calibrated in this study |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahn, T.I.; Yang, J.-S.; Park, S.H.; Moon, H.W.; Lee, J.Y. Translation of Irrigation, Drainage, and Electrical Conductivity Data in a Soilless Culture System into Plant Growth Information for the Development of an Online Indicator Related to Plant Nutritional Aspects. Agronomy 2020, 10, 1306. https://doi.org/10.3390/agronomy10091306
Ahn TI, Yang J-S, Park SH, Moon HW, Lee JY. Translation of Irrigation, Drainage, and Electrical Conductivity Data in a Soilless Culture System into Plant Growth Information for the Development of an Online Indicator Related to Plant Nutritional Aspects. Agronomy. 2020; 10(9):1306. https://doi.org/10.3390/agronomy10091306
Chicago/Turabian StyleAhn, Tae In, Jung-Seok Yang, Soo Hyun Park, Heon Woo Moon, and Ju Young Lee. 2020. "Translation of Irrigation, Drainage, and Electrical Conductivity Data in a Soilless Culture System into Plant Growth Information for the Development of an Online Indicator Related to Plant Nutritional Aspects" Agronomy 10, no. 9: 1306. https://doi.org/10.3390/agronomy10091306
APA StyleAhn, T. I., Yang, J.-S., Park, S. H., Moon, H. W., & Lee, J. Y. (2020). Translation of Irrigation, Drainage, and Electrical Conductivity Data in a Soilless Culture System into Plant Growth Information for the Development of an Online Indicator Related to Plant Nutritional Aspects. Agronomy, 10(9), 1306. https://doi.org/10.3390/agronomy10091306





