Genome-wide Association Study and Genomic Prediction for Fusarium graminearum Resistance Traits in Nordic Oat (Avena sativa L.)
Abstract
1. Introduction
2. Materials and Methods
2.1. Plant Germplasm and Genotype Data
2.2. Phenotypic Data
2.3. Experimental Analysis
2.4. Association Analysis
2.5. Genomic Prediction
2.6. Prediction Model Validation
3. Results
3.1. Phenotypic Records
3.2. Genotypes and Population Structure
3.3. Heritability Estimates and Correlations Between Traits
3.4. Genome-wide Association Study
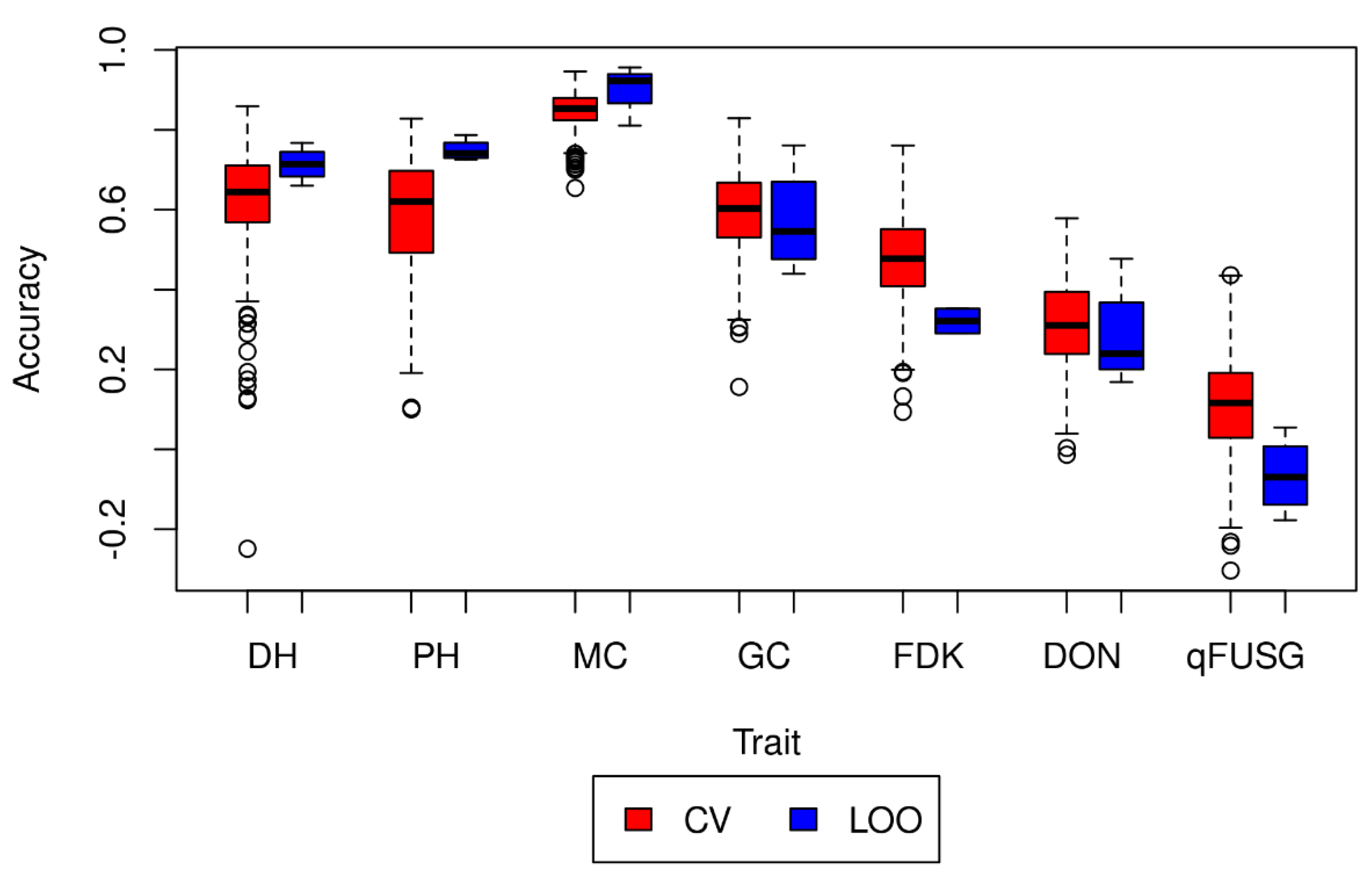
3.5. Prediction Model Validation
4. Discussion
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Agency for Rural Affairs (former Finnish food authority). Viljat lajikkeittain 2018. 2018. Available online: https://www.vyr.fi/document/1/735/3d6172b/tilast_cfa52da_VYR_viljat_ja_oljykasvit_lajikkeittain_2018.pdf (accessed on 23 October 2019).
- Marshall, A.; Cowan, S.; Edwards, S.; Griffiths, I.; Howarth, C.; Langdon, T.; White, E. Crops that feed the world 9. Oats-A cereal crop for human and livestock feed with industrial applications. Food Secur. 2013, 5, 13–33. [Google Scholar] [CrossRef]
- Hietaniemi, V.; Kontturi, M.; Rämö, S.; Eurola, M.; Kangas, A.; Niskanen, M.; Saastamoinen, M. Contents of trichothecenes in oats during official variety, organic cultivation and nitrogen fertilization trials in Finland. Agric. Food Sci. 2004, 13, 54–67. [Google Scholar] [CrossRef]
- Hietaniemi, V.; Rämö, S.; Yli-Mattila, T.; Jestoi, M.; Peltonen, S.; Kartio, M.; Sieviläinen, E.; Koivisto, T.; Parikka, P. Updated survey of Fusarium species and toxins in Finnish cereal grains. Food Addit. Contam. Part 2016, 33, 831–848. [Google Scholar] [CrossRef] [PubMed]
- Elen, O.; Liu, W.; Langseth, W.; Skinnes, H.; Gullord, M.; Sundheim, L. Deoxynivalenol content of cereal grain from naturally infected and artificially inoculated plants in field trials in Norway. Acta Agric. Scand. Sect. B-Soil Plant Sci. 2003, 53, 183–189. [Google Scholar] [CrossRef]
- Langseth, W.; Elen, O. Differences between barley, oats and wheat in the occurrence of deoxynivalenol and other trichothecenes in Norwegian grain. J. Phytopathol. 1996, 144, 113–118. [Google Scholar] [CrossRef]
- Langseth, W.; Høie, R.; Gullord, M. The influence of cultivars, location and climate on deoxynivalenol contamination in Norwegian oats 1985–1990. Acta Agric. Scand. Sect. B-Soil Plant Sci. 1995, 45, 63–67. [Google Scholar] [CrossRef]
- Bjørnstad, Å.; He, X.; Tekle, S.; Klos, K.; Huang, Y.; Tinker, N.A.; Dong, Y.; Skinnes, H. Genetic variation and associations involving Fusarium head blight and deoxynivalenol accumulation in cultivated oat (Avena sativa L.). Plant Breed. 2017, 136, 620–636. [Google Scholar] [CrossRef]
- Gagkaeva, T.; Gavrilova, O.; Yli-Mattila, T.; Loskutov, I. Sources of resistance to Fusarium head blight in VIR oat collection. Euphytica 2013, 191, 355–364. [Google Scholar] [CrossRef]
- Lindblad, M.; Börjesson, T.; Hietaniemi, V.; Elen, O. Statistical analysis of agronomical factors and weather conditions influencing deoxynivalenol levels in oats in Scandinavia. Food Addit. Contam. Part 2012, 29, 1566–1571. [Google Scholar] [CrossRef]
- Nielsen, L.; Jensen, J.; Nielsen, G.; Jensen, J.; Spliid, N.; Thomsen, I.; Justesen, A.; Collinge, D.; Jørgensen, L. Fusarium head blight of cereals in Denmark: Species complex and related mycotoxins. Phytopathology 2011, 101, 960–969. [Google Scholar] [CrossRef]
- Schollenberger, M.; Müller, H.-M.; Rüfle, M.; Suchy, S.; Plank, S.; Drochner, W. Natural occurrence of 16 Fusarium toxins in grains and feedstuffs of plant origin from Germany. Mycopathologia 2006, 161, 43–52. [Google Scholar] [CrossRef] [PubMed]
- Müller, H.; Reimann, J.; Schumacher, U.; Schwadorf, K. Natural occurrence of Fusarium toxins in oats harvested during five years in an area of southwest Germany. Food Addit. Contam. 2001, 15, 801–806. [Google Scholar] [CrossRef] [PubMed]
- Edwards, S.G. Fusarium mycotoxin content of UK organic and conventional oats. Food Addit. Contam. Part 2009, 26, 1063–1069. [Google Scholar] [CrossRef] [PubMed]
- Scudamore, K.; Baillie, H.; Patel, S.; Edwards, S. Occurrence and fate of Fusarium mycotoxins during commercial processing of oats in the UK. Food Addit. Contam. 2007, 24, 1374–1385. [Google Scholar] [CrossRef]
- Yan, W.; Pageau, D.; Martin, R.; Cummiskey, A.; Blackwell, B. Is deoxynivalenol contamination a serious problem for oat in Eastern Canada? Crop Sci. 2016, 57, 88–98. [Google Scholar] [CrossRef]
- Tekauz, A.; Fetch, J.; Rossnagel, B.; Savard, M. Progress in assessing the impact of Fusarium head blight on oat in Western Canada and screening of Avena germplasm for resistance. Cereal Res. Commun. 2008, 36, 49–56. [Google Scholar] [CrossRef]
- Tekauz, A.; Mccallum, B.; Ames, N.; Fetch, J. Fusarium head blight of oat-Current status in Western Canada. Can. J. Plant Pathol. 2004, 473–479. [Google Scholar] [CrossRef]
- Jones, R.; Mirocha, C. Quality parameters in small grains from Minnesota affected by Fusarium head blight. Plant Dis. 1999, 83, 506–511. [Google Scholar] [CrossRef]
- Rotter, B.; Thompson, B.; Lessard, M. Effects of deoxynivalenol-contaminated diet on performance and blood parameters in growing swine. Can J. Anim. Sci. 1995, 75, 297–302. [Google Scholar] [CrossRef]
- Čonková, E.; Laciaková, A.; Kováč, G.; Seidel, H. Fusarial toxins and their role in animal diseases. Vet J. 2003, 165, 214–220. [Google Scholar] [CrossRef]
- Bjørnstad, Å.; Skinnes, H. Resistance to Fusarium infection in oats (Avena sativa L.). Cereal Res. Commun. 2008, 36, 57–62. [Google Scholar] [CrossRef]
- Tekle, S.; Skinnes, H.; Bjørnstad, Å. The germination problem of oat seed lots affected by Fusarium head blight. Eur. J. Plant Pathol. 2013, 135, 147–158. [Google Scholar] [CrossRef]
- Commission European. Commission regulation (EC) No. 1881/2006 setting maximum levels of certain contaminants in foodstuffs. Offcial J. Eur. Union. 2006, L 364, 5–24. [Google Scholar]
- Hofgaard, I.; Aamot, H.; Torp, T.; Jestoi, M.; Lattanzio, V.; Klemsdal, S.; Waalwijk, C.; der Lee, V.T.; Brodal, G. Associations between Fusarium species and mycotoxins in oats and spring wheat from farmers’ fields in Norway over a six-Year period. World Mycotoxin. J. 2016, 9, 365–378. [Google Scholar] [CrossRef]
- Fredlund, E.; Gidlund, A.; Olsen, M.; Börjesson, T.; Spliid, N.; Simonsson, M. Method evaluation of Fusarium DNA extraction from mycelia and wheat for down-Stream real-time PCR quantification and correlation to mycotoxin levels. J. Microbiol. Meth. 2008, 73, 33–40. [Google Scholar] [CrossRef] [PubMed]
- Waalwijk, C.; Kastelein, P.; de Vries, I.; Kerényi, Z.; van der Lee, T.; Hesselink, T.; Köhl, J.; Kema, G. Major changes in Fusarium spp. in wheat in the Netherlands. Eur. J. Plant Pathol. 2003, 109, 743–754. [Google Scholar] [CrossRef]
- Finnish Cereal Committee; Yhteenveto viljan hometoksiiniseurannasta ja tuloksista viime vuosilta sekä tarpeet seurannan kehittämiselle ja hyödyntämiselle. 2015. Available online: https://www.vyr.fi/document/1/63/6ef8d20/viljan_3a17dc4_Turvallisuusraportti_web.pdf (accessed on 23 October 2019).
- Yan, W.; Fregeau-Reid, J.; Rioux, S.; Pageau, D.; Xue, A.; Martin, R.; Fedak, G.; de Haan, B.; Lajeunesse, J.; Savard, M. Response of oat genotypes to Fusarium head blight in Eastern Canada. Crop Sci. 2010, 50, 134–142. [Google Scholar] [CrossRef]
- Lacey, J.; Teman, G.; Mirocha, C. Effects of infection time and moisture on development of ear blight and deoxynivalenol production by Fusarium spp. in wheat. Ann. Appl. Biol. 1999, 134, 277–283. [Google Scholar] [CrossRef]
- Brennan, J.; Egan, D.; Cooke, B.; Doohan, F. Effect of temperature on head blight of wheat caused by Fusarium culmorum and F. graminearum. Plant Pathol. 2005, 54, 156–160. [Google Scholar] [CrossRef]
- Doohan, F.M.; Brennan, J.; Cooke, B.M. Influence of climatic factors on Fusarium species pathogenic to cereals. Eur. J. Plant Pathol. 2003, 109, 755–768. [Google Scholar] [CrossRef]
- Tekle, S.; Dill-Macky, R.; Skinnes, H.; Tronsmo, A.; Bjørnstad, Å. Infection process of Fusarium graminearum in oats (Avena sativa L.). Eur. J. Plant Pathol. 2012, 132, 431–442. [Google Scholar] [CrossRef]
- Parry, D.; Jenkinson, P.; McLeod, L. Fusarium ear blight (scab) in small grain cereals—a review. Plant Pathol. 1995, 44, 207–238. [Google Scholar] [CrossRef]
- Hjelkrem, A.-G.; Torp, T.; Brodal, G.; Aamot, H.; Strand, E.; Nordskog, B.; Dill-Macky, R.; Edwards, S.G.; Hofgaard, I. DON content in oat grains in Norway related to weather conditions at different growth stages. Eur. J. Plant Pathol. 2017, 148, 577–594. [Google Scholar] [CrossRef]
- Schroeder, H.; Christensen, J. Factors affecting resistance of wheat to scab caused by Gibberella zeae. Phytopathology 1963, 53, 831–838. [Google Scholar]
- Tekle, S.; Lillemo, M.; Skinnes, H.; Reitan, L.; Buraas, T.; Bjørnstad, Å. Screening of oat accessions for Fusarium head blight resistance using spawn-Inoculated field experiments. Crop Sci. 2018, 58, 143–151. [Google Scholar] [CrossRef]
- Mesterházy, A. Types and components of resistance to Fusarium head blight of wheat. Plant Breed. 1995, 114, 377–386. [Google Scholar] [CrossRef]
- Miller, J.; Young, J.; Sampson, D. Deoxynivalenol and Fusarium head blight resistance in spring cereals. J. Phytopathol. 1985, 113, 359–367. [Google Scholar] [CrossRef]
- Campbell, H.; Choo, T.; Vigier, B.; Underhill, L. Mycotoxins in barley and oat samples from Eastern Canada. Can. Plant Sci. 2000, 80, 977–980. [Google Scholar] [CrossRef]
- Langevin, F.; Eudes, F.; Comeau, A. Effect of trichothecenes produced by Fusarium graminearum during Fusarium head blight development in six cereal species. Eur. J. Plant Pathol. 2004, 110, 735–746. [Google Scholar] [CrossRef]
- Misonoo, G. Eological and physiological studies on the blooming of oat flowers. J. Fac. Agric. 1936, 37, 211–337. [Google Scholar]
- Percival, J. The Wheat Plant; Duckworth & Co: London, UK, 1921; p. 124. Available online: https://archive.org/details/wheatplantperciv00percrich/page/ (accessed on 23 October 2019).
- Loskutov, I.; Blinova, E.; Gavrilova, O.; Gagkaeva, Y.T. The valuable characteristics of oats genotypes and resistance to Fusarium disease. Vavilov J. Genet. Breed. 2016, 20, 286–294. [Google Scholar] [CrossRef][Green Version]
- Gagkaeva, T.; Gavrilova, O.; Yli-Mattila, T.; Loskutov, I. Evaluation of oat germplasm for resistance to Fusarium head blight. Plant Breed. Seed Sci. 2011, 64, 15–22. [Google Scholar] [CrossRef]
- Gagkaeva, T.Y.; Gavrilova, O.P.; Orina, A.S.; Blinova, E.V.; Loskutov, I.G. Response of wild Avena species to fungal infection of grain. Crop J. 2017, 5, 499–508. [Google Scholar] [CrossRef]
- Rainio, A. Punahome Fusarium roseum link gibberella saubinetii (Mont,) Sacc, ja sen aiheuttamat myrkytykset kaurassa. Valt. Maatal. Julk. 1932, 50. (In Finnish) [Google Scholar]
- He, X.; Skinnes, H.; Oliver, R.E.; Jackson, E.W.; Bjørnstad, Å. Linkage mapping and identification of QTL affecting deoxynivalenol (DON) content (Fusarium resistance) in oats (Avena sativa L.). Theor. Appl. Genet. 2013, 126, 2655–2670. [Google Scholar] [CrossRef]
- Langseth, W.; Stabbetorp, H. The effect of lodging and time of harvest on deoxynivalenol contamination in barley and oats. J. Phytopathol. 1996, 144, 241–245. [Google Scholar] [CrossRef]
- Gavrilova, O.; Gagkaeva, T.; Burkin, A.; Kononenko, G.; Loskutov, I. Susceptibility of Oat Germplasm to Fusarium Infection and Mycotoxin Accumulation in Grains. In Proceedings of the 8th International Oat Conference, Minneapolis, USA, 27 June–2 July 2008; pp. 7–16. [Google Scholar]
- Parikka, P.; Hietaniemi, V.; Rämö, S.; Jalli, H. Fusarium infection and mycotoxin contents of oats under different tillage treatments. J. Plant Pathol. 2008, 90 (Suppl. 3). [Google Scholar]
- Buerstmayr, H.; Ban, T.; Anderson, J. QTL mapping and marker-assisted selection for Fusarium head blight resistance in wheat: A review. Plant Breed. 2009, 128, 1–26. [Google Scholar] [CrossRef]
- Emrich, K.; Wilde, F.; Miedaner, T.; Piepho, H. REML approach for adjusting the Fusarium head blight rating to a phenological date in inoculated selection experiments of wheat. Theor. Appl. Genet. 2008, 117, 65–73. [Google Scholar] [CrossRef]
- Lu, Q.; Lillemo, M.; Skinnes, H.; He, X.; Shi, J.; Ji, F.; Dong, Y.; Bjørnstad, Å. Anther extrusion and plant height are associated with Type I resistance to Fusarium head blight in bread wheat line ‘Shanghai-3/Catbird. ’ Theor. Appl. Genet. 2013, 126, 317–334. [Google Scholar] [CrossRef]
- Skinnes, H.; Semagn, K.; Tarkegne, Y.; Marøy, A.; Bjørnstad, Å. The inheritance of anther extrusion in hexaploid wheat and its relationship to Fusarium head blight resistance and deoxynivalenol content. Plant Breed. 2010, 129, 149–155. [Google Scholar] [CrossRef]
- Strange, R.N.; Smith, H. A fungal growth stimulant in anthers which predisposes wheat to attack by Fusarium graminearum. Physiol. Plant Pathol. 1971, 1, 141–150. [Google Scholar] [CrossRef]
- Bjørnstad, Å.; Tekle, S.; Lillemo, M.; Buraas, T.; Reitan, L. Breeding resistant cultivars to reduce mycotoxin risks in oats. In Proceedings of the 10th International Oat Conference, St. Petersburg, Russia, 11–15 July 2016. [Google Scholar]
- Stråbø, S. Genetic Variation of Anther Extrusion in Oat and Its Relationship to Fusarium. Master’s Thesis, Norwegian University of Life Sciences, January 2015. [Google Scholar]
- Buerstmayr, H.; Legzdina, L.; Steiner, B.; Lemmens, M. Variation for resistance to Fusarium head blight in spring barley. Euphytica 2004, 137, 279–290. [Google Scholar] [CrossRef]
- Mesterházy, A.; Lehoczki-Krsjak, S.; Varga, M.; Szabó-Hevér, Á.; Tóth, B.; Lemmens, M. Breeding for FHB resistance via Fusarium damaged kernels and deoxynivalenol accumulation as well as inoculation methods in winter wheat. Agric. Sci. 2015, 06, 970–1002. [Google Scholar] [CrossRef]
- Hautsalo, J.; Jalli, M.; Manninen, O.; Veteläinen, M. Evaluation of resistance to Fusarium graminearum in oats. Euphytica 2018, 214, 139. [Google Scholar] [CrossRef]
- Mirocha, C.J.; Kolaczkowski, E.; Xie, W.; Yu, H.; Jelen, H. Analysis of deoxynivalenol and its derivatives (batch and single kernel) using gas chromatography/mass spectrometry. J. Agric. Food Chem. 1998, 46, 1414–1418. [Google Scholar] [CrossRef]
- Kokkonen, M.K.; Jestoi, M.N. A Multi-Compound LC-MS/MS method for the screening of mycotoxins in grains. Food Anal. Methods 2009, 2, 128–140. [Google Scholar] [CrossRef]
- Mesterházy, Á.; Bartók, T.; Mirocha, C.; Komoróczy, R. Nature of wheat resistance to Fusarium head blight and the role of deoxynivalenol for breeding. Plant Breed. 1999, 118, 97–110. [Google Scholar] [CrossRef]
- Saiki, R.; Gelfand, D.; Stoffel, S.; Scharf, S.; Higuchi, R.; Horn, G.; Mullis, K.; Erlich, H. Primer-Directed enzymatic amplification of DNA with a thermostable DNA polymerase. Science 1988, 239, 487–491. [Google Scholar] [CrossRef]
- Niessen, L. PCR-Based diagnosis and quantification of mycotoxin producing fungi. Int. J. Food Microbiol. 2007, 119, 38–46. [Google Scholar] [CrossRef]
- Yli-Mattila, T.; Paavanen-Huhtala, S.; Jestoi, M.; Parikka, P.; Hietaniemi, V.; Gagkaeva, T.; Sarlin, T.; Haikara, A.; Laaksonen, S.; Rizzo, A. Real-time PCR detection and quantification of Fusarium poae, F. graminearum, F. sporotrichioides and F. langsethiae in cereal grains in Finland and Russia. Arch. Phytopathol. Plant Prot. 2008, 41, 243–260. [Google Scholar] [CrossRef]
- Fredlund, E.; Gidlund, A.; Pettersson, H.; Olsen, M.; Börjesson, T. Real-Time PCR detection of Fusarium species in Swedish oats and correlation to T-2 and HT-2 toxin content. World Mycotoxin J. 2010, 3, 77–88. [Google Scholar] [CrossRef]
- Zhu, C.; Gore, M.; Buckler, E.S.; Yu, J. Status and prospects of association mapping in plants. Plant Genome J. 2008, 1, 5–20. [Google Scholar] [CrossRef]
- Thornsberry, J.M.; Goodman, M.M.; Doebley, J.; Kresovich, S.; Nielsen, D.; Edward, B.S. Dwarf8 polymorphisms associate with variation in flowering time. Nat. Genet. 2001, 28, 286–289. [Google Scholar] [CrossRef] [PubMed]
- Risch, N.; Merikangas, K. The future of genetic studies of complex human diseases. Science 1996, 273, 1516–1517. [Google Scholar] [CrossRef] [PubMed]
- Astle, W.; Balding, D.J. Population structure and cryptic relatedness in genetic association studies. Stat. Sci. 2009, 24, 451–471. [Google Scholar] [CrossRef]
- Matthies, I.E.; van Hintum, T.; Weise, S.; Röder, M.S. Population structure revealed by different marker types (SSR or DArT) has an impact on the results of genome-wide association mapping in European barley cultivars. Mol. Breed. 2012, 30, 951–966. [Google Scholar] [CrossRef]
- Price, A.L.; Zaitlen, N.A.; Reich, D.; Patterson, N. New approaches to population stratification in genome-Wide association studies. Nat. Rev. Genet. 2010, 11, 459–463. [Google Scholar] [CrossRef]
- Crossa, J.; Pérez-Rodríguez, P.; Cuevas, J.; Montesinos-López, O.; Jarquín, D.; de los Campos, G.; Burgueño, J.; González-Camacho, J.M.; Pérez-Elizalde, S.; Beyene, Y.; et al. Genomic selection in plant breeding: Methods, models, and perspectives. Trends Plant Sci. 2017, 22, 961–975. [Google Scholar] [CrossRef]
- Meuwissen, T.; Hayes, B.; Goddard, M. Prediction of total genetic value using genome-wide dense marker maps. Genetics 2001, 157, 1819–1829. [Google Scholar]
- Heslot, N.; Yang, H.-P.; Sorrells, M.E.; Jannink, J.-L. Genomic selection in plant breeding: A comparison of models. Crop Sci. 2012, 52, 146–160. [Google Scholar] [CrossRef]
- Juliana, P.; Singh, R.P.; Singh, P.K.; Crossa, J.; Huerta-Espino, J.; Lan, C.; Bhavani, S.; Rutkoski, J.E.; Poland, J.A.; Bergstrom, G.C.; et al. Genomic and pedigree-based prediction for leaf, stem, and stripe rust resistance in wheat. Theor. Appl. Genet. 2017, 130, 1415–1430. [Google Scholar] [CrossRef] [PubMed]
- Rajhathy, T.; Thomas, H. Cytogenetics of Oats (Avena L.); Miscellaneous Publications of the Genetics Society of Canada 2; Wilkes, A., Ed.; The Genetics Society of Canada: Ottawa, Canada, 1976; p. 67. [Google Scholar]
- Jellen, E.; Beard, J. Geographical distribution of a chromosome 7C and 17 intergenomic translocation in cultivated oat. Crop Sci. 2000, 400, 256–263. [Google Scholar] [CrossRef]
- Chaffin, A.S.; Huang, Y.-F.; Smith, S.; Bekele, W.A.; Babiker, E.; Gnanesh, B.N.; Foresman, B.J.; Blanchard, S.G.; Jay, J.J.; Reid, R.W.; et al. A consensus map in cultivated hexaploid oat reveals conserved grass synteny with substantial subgenome rearrangement. Plant Genome 2016, 9, 2. [Google Scholar] [CrossRef]
- Oliver, R.E.; Tinker, N.A.; Lazo, G.R.; Chao, S.; Jellen, E.N.; Carson, M.L.; Rines, H.W.; Obert, D.E.; Lutz, J.D.; Shackelford, I.; et al. SNP discovery and chromosome anchoring provide the first physically-anchored hexaploid oat map and reveal synteny with model species. PLoS ONE 2013, 8, 3. [Google Scholar] [CrossRef]
- Newell, M.A.; Asoro, F.G.; Scott, M.P.; White, P.J.; Beavis, W.D.; Jannink, J.-L. Genome-wide association study for oat (Avena sativa L.) beta-glucan concentration using germplasm of worldwide origin. Theor. Appl. Genet. 2012, 125, 1687–1696. [Google Scholar] [CrossRef]
- Asoro, F.G.; Newell, M.A.; Scott, P.M.; Beavis, W.D.; Jannink, J.-L. Genome-wide association study for beta-glucan concentration in elite North American oat. Crop Sci. 2013, 53, 542–553. [Google Scholar] [CrossRef]
- Klos, K.; Yimer, B.A.; Babiker, E.M.; Beattie, A.D.; Bonman, M.J.; Carson, M.L.; Chong, J.; Harrison, S.A.; Ibrahim, A.M.; Kolb, F.L.; et al. Genome-wide association mapping of crown rust resistance in oat elite germplasm. Plant Genome 2017, 10, 2. [Google Scholar] [CrossRef]
- Tumino, G.; Voorrips, R.E.; Morcia, C.; Ghizzoni, R.; Germeier, C.U.; Paulo, M.-J.; Terzi, V.; Smulders, M.J. Genome-wide association analysis for lodging tolerance and plant height in a diverse European hexaploid oat collection. Euphytica 2017, 213, 163. [Google Scholar] [CrossRef]
- Tumino, G.; Voorrips, R.E.; Rizza, F.; Badeck, F.W.; Morcia, C.; Ghizzoni, R.; Germeier, C.U.; Paulo, M.-J.; Terzi, V.; Smulders, M.J. Population structure and genome-wide association analysis for frost tolerance in oat using continuous SNP array signal intensity ratios. Theor. Appl. Genet. 2016, 129, 1711–1724. [Google Scholar] [CrossRef]
- Liu, S.; Hall, M.D.; Griffey, C.A.; McKendry, A.L. Meta-analysis of QTL associated with Fusarium head blight resistance in wheat. Crop Sci. 2009, 49, 1955–1968. [Google Scholar] [CrossRef]
- Huang, Y.; Haas, M.; Heinen, S.; Steffenson, B.J.; Smith, K.P.; Muehlbauer, G.J. QTL mapping of Fusarium head blight and correlated agromorphological traits in an elite barley cultivar Rasmusson. Front Plant Sci. 2018, 9, 1260. [Google Scholar] [CrossRef] [PubMed]
- Massman, J.; Cooper, B.; Horsley, R.; Neate, S.; Dill-Macky, R.; Chao, S.; Dong, Y.; Schwarz, P.; Muehlbauer, G.; Smith, K. Genome-wide association mapping of Fusarium head blight resistance in contemporary barley breeding germplasm. Mol. Breed. 2011, 27, 439–454. [Google Scholar] [CrossRef]
- Li, T.; Zhang, H.; Huang, Y.; Su, Z.; Deng, Y.; Liu, H.; Mai, C.; Yu, G.; Li, H.; Yu, L.; et al. Effects of the Fhb1 gene on Fusarium head blight resistance and agronomic traits of winter wheat. Crop J. 2019. [Google Scholar] [CrossRef]
- Su, Z.; Bernardo, A.; Tian, B.; Chen, H.; Wang, S.; Ma, H.; Cai, S.; Liu, D.; Zhang, D.; Li, T.; et al. A deletion mutation in TaHRC confers Fhb1 resistance to Fusarium head blight in wheat. Nat. Genet. 2019, 51, 1099–1105. [Google Scholar] [CrossRef] [PubMed]
- Rawat, N.; Pumphrey, M.O.; Liu, S.; Zhang, X.; Tiwari, V.K.; Ando, K.; Trick, H.N.; Bockus, W.W.; Akhunov, E.; Anderson, J.A.; et al. Wheat Fhb1 encodes a chimeric lectin with agglutinin domains and a pore-forming toxin-like domain conferring resistance to Fusarium head blight. Nat. Genet. 2016, 48, 1576–1580. [Google Scholar] [CrossRef]
- Arruda, M.P.; Brown, P.J.; Lipka, A.E.; Krill, A.M.; Thurber, C.; Kolb, F.L. Genomic selection for predicting head blight resistance in a wheat breeding program. Plant Genome 2015, 8, 3. [Google Scholar] [CrossRef]
- Jiang, Y.; Schulthess, A.; Rodemann, B.; Ling, J.; Plieske, J.; Kollers, S.; Ebmeyer, E.; Korzun, V.; Argillier, O.; Stiewe, G.; et al. Validating the prediction accuracies of marker-assisted and genomic selection of Fusarium head blight resistance in wheat using an independent sample. Theor. Appl. Genet. 2017, 130, 471–482. [Google Scholar] [CrossRef]
- Rutkoski, J.; Benson, J.; Jia, Y.; Brown-Guedira, G.; Jannink, J.-L.; Sorrells, M. Evaluation of genomic prediction methods for Fusarium head blight resistance in wheat. Plant Genome J. 2012, 5, 51–61. [Google Scholar] [CrossRef]
- Mirdita, V.; Liu, G.; Zhao, Y.; Miedaner, T.; Longin, F.C.; Gowda, M.; Mette, M.; Reif, J.C. Genetic architecture is more complex for resistance to Septoria tritici blotch than to Fusarium head blight in Central European winter wheat. BMC Genom. 2015, 16, 430. [Google Scholar] [CrossRef][Green Version]
- Haikka, H.; Knürr, T.; Manninen, O.; Pietilä, L.; Isolahti, M.; Teperi, E.; Mäntysaari, E.; Stranden, I. Genomic prediction of grain yield in commercial Finnish oat (Avena sativa L.) and barley (Hordeum vulgare L.) breeding programs. Plant Breed 2020. [Google Scholar] [CrossRef]
- Asoro, F.G.; Newell, M.A.; Beavis, W.D.; Scott, P.M.; Jannink, J.-L. Accuracy and training population design for genomic selection on quantitative traits in elite North American oats. Plant Genome J. 2011, 4, 132–144. [Google Scholar] [CrossRef]
- Endelman, J.B. Ridge regression and other kernels for genomic selection with R package rrBLUP. Plant Genome J. 2011, 4, 250–255. [Google Scholar] [CrossRef]
- Hill, W.G.; Weir, B.S. Variances and covariances of squared linkage disequilibria in finite populations. Theor. Popul. Biol. 1988, 33, 54–78. [Google Scholar] [CrossRef]
- R core team. R: A Language and Environment for Statistical Computing. 2017. Available online: https://www.R-project.org (accessed on 19 December 2019).
- Fabio Marroni’s Blog Post. Available online: https://fabiomarroni.wordpress.com/2011/08/09/estimate-decay-of-linkage-disequilibrium-with-distance/ (accessed on 21 December 2019).
- Williams, E.R.; Matheson, A.C.; Harwood, C.E. Experimental Design and Analysis for Tree Improvement, 2nd ed; CSIRO Publishing: Collingwood, Australia, 2002; pp. 132–135. [Google Scholar]
- Zadoks, J.; Chang, T.; Konzak, C. A decimal code for the growth stages of cereals. Weed Res. 1974, 14, 415–421. [Google Scholar] [CrossRef]
- Parikka, P.; Hietaniemi, V.; Rämö, S.; Jalli, H. The effect of cultivation practices on Fusarium langsethiae infections of oats and barley. In Proceedings of the COST SUSVAR Fusarium Workshop: Fusarium Diseases in Cereals—Potential Impact from Sustainable Cropping Systems; Velence, Hungary, 1–2 June 2007, Vogelgsang, S., Jalli, M., Kovács, G., Vida, G., Eds.;
- Nelson, P.; Toussoun, T.; Marasas, W. Fusarium Species, an Illustrated Manual for Identification; Pennsylvania State University Press: University Park, PA, USA, 1983. [Google Scholar]
- Divon, H.; Razzaghian, J.; Udnes-Aamot, H.; Klemsdal, S. Fusarium langsethiae (Torp and Nirenberg), investigation of alternative infection routes in oats. Eur. J. Plant Pathol. 2012, 132, 147–161. [Google Scholar] [CrossRef]
- IBM. SPSS Statistics for Windows, Version 25.0; IBM Corp: Armonk, NY, USA, 2017. [Google Scholar]
- Piepho, H.-P.; Möhring, J. Computing heritability and selection response from unbalanced plant breeding trials. Genetics 2007, 177, 1881–1888. [Google Scholar] [CrossRef]
- Schmidt, P.; Hartung, J.; Bennewitz, J.; Piepho, H.-P. Heritability in plant breeding on a genotype-difference basis. Genetics 2019, 212, 991–1008. [Google Scholar] [CrossRef]
- Lipka, A.E.; Tian, F.; Wang, Q.; Peiffer, J.; Li, M.; Bradbury, P.J.; Gore, M.A.; Buckler, E.S.; Zhang, Z. GAPIT: Genome association and prediction integrated tool. Bioinformatics 2012, 28, 2397–2399. [Google Scholar] [CrossRef]
- Zhang, Z.; Todhunter, R.; Buckler, E.; Vleck, V.L. Technical note: Use of marker-based relationships with multiple-trait derivative-free restricted maximal likelihood. J. Anim. Sci. 2007, 85, 881–885. [Google Scholar] [CrossRef]
- Isidro-Sánchez, J.; Akdemir, D.; Montilla-Bascón, G. Genome-wide association analysis using R. In Oat Methods and Protocols; Methods in Molecular Biology 1536; Gasparis, S., Ed.; Springer Nature: New York, USA, 2017; pp. 189–208. [Google Scholar]
- Bates, D.; Mächler, M.; Bolker, B.M.; Walker, S.C. Fitting linear mixed-effects models using lme4. J. Stat. Softw. 2015, 67, 1–48. [Google Scholar] [CrossRef]
- VanRaden, P.M. Efficient methods to compute genomic predictions. J. Dairy Sci. 2008, 91, 4414–4423. [Google Scholar] [CrossRef] [PubMed]
- User Manual for GAPIT. Available online: http://www.zzlab.net/GAPIT/gapit_help_document.pdf (accessed on 23 October 2019).
- Benjamini, Y.; Hochberg, Y. Controlling the false discovery rate: A practical and powerful approach to multiple testing. J. R. Stat. Soc. Ser. B Methodol. 1995, 57, 289–300. [Google Scholar] [CrossRef]
- Jensen, J.; Mäntysaari, E.A.; Madsen, P.; Thompson, R. Residual maximum likelihood estimation od (co) variance components in multivariate mixed linear models using average information. J. Indian Soc. Agr. Stat. 1997, 49, 215–236. [Google Scholar]
- Madsen, P.; Su, G.; Labouriau, R.; Christensen, O.F. Users Guide to DMU-A Package for Analyzing Multivariate Mixed Models; University of Aarhus, Tjele, Denmark, 2013. Available online: http://dmu.agrsci.dk (accessed on 19 December 2019).
- MiX99 Development Team. MiX99: A Software Package for Solving Large Mixed Model Equations; VIII/2015; Natural Resources Institute Finland (Luke): Jokioinen, Finland, 2015; Available online: http://www.luke.fi/mix99 (accessed on 19 December 2019).
- Hautsalo, J.; Jauhiainen, L.; Hannukkala, A.; Manninen, O.; Veteläinen, M.; Pietilä, L.; Peltoniemi, K.; Jalli, M. Resistance to DON accumulation in oats based on analyses of multiple field and greenhouse studies. under review.
- Klos, K.; Huang, Y.-F.; Bekele, W.A.; Obert, D.E.; Babiker, E.; Beattie, A.D.; Bjørnstad, Å.; Bonman, M.J.; Carson, M.L.; Chao, S.; et al. Population genomics related to adaptation in elite oat germplasm. Plant Genome 2016, 9, 1–12. [Google Scholar]
- Hoffstetter, A.; Cabrera, A.; Huang, M.; Sneller, C. Optimizing training population data and validation of genomic selection for economic traits in soft winter wheat. G3 Genes Genomes Genet. 2016, 6, 2919–2928. [Google Scholar] [CrossRef]
- Zwart, R.S.; Muylle, H.; Bockstaele, E.; Roldán-Ruiz, I. Evaluation of genetic diversity of Fusarium head blight resistance in European winter wheat. Theor. Appl. Genet. 2008, 117, 813–828. [Google Scholar] [CrossRef]
- Herter, C.; Ebmeyer, E.; Kollers, S.; Korzun, V.; Würschum, T.; Miedaner, T. Accuracy of within- and among-Family genomic prediction for Fusarium head blight and Septoria tritici blotch in winter wheat. Theor. Appl. Genet. 2019, 132, 1121–1135. [Google Scholar] [CrossRef]
- Liu, W.; Elen, O.N.; Sundheim, L.; Langseth, W.; Skinnes, H. Comparison of visual head blight ratings, seed infection levels, and deoxynivalenol production for assessment of resistance in cereals inoculated with Fusarium culmorum. Eur. J. Plant Pathol. 1997, 103, 589–595. [Google Scholar] [CrossRef]
- Schulthess, A.W.; Zhao, Y.; Longin, F.C.; Reif, J.C. Advantages and limitations of multiple-trait genomic prediction for Fusarium head blight severity in hybrid wheat (Triticum aestivum L.). Theor. Appl. Genet. 2018, 131, 685–701. [Google Scholar] [CrossRef]
- Fernandes, S.B.; Dias, K.O.; Ferreira, D.F.; Brown, P.J. Efficiency of multi-trait, indirect, and trait-assisted genomic selection for improvement of biomass sorghum. Theor. Appl. Genet. 2018, 131, 747–755. [Google Scholar] [CrossRef] [PubMed]
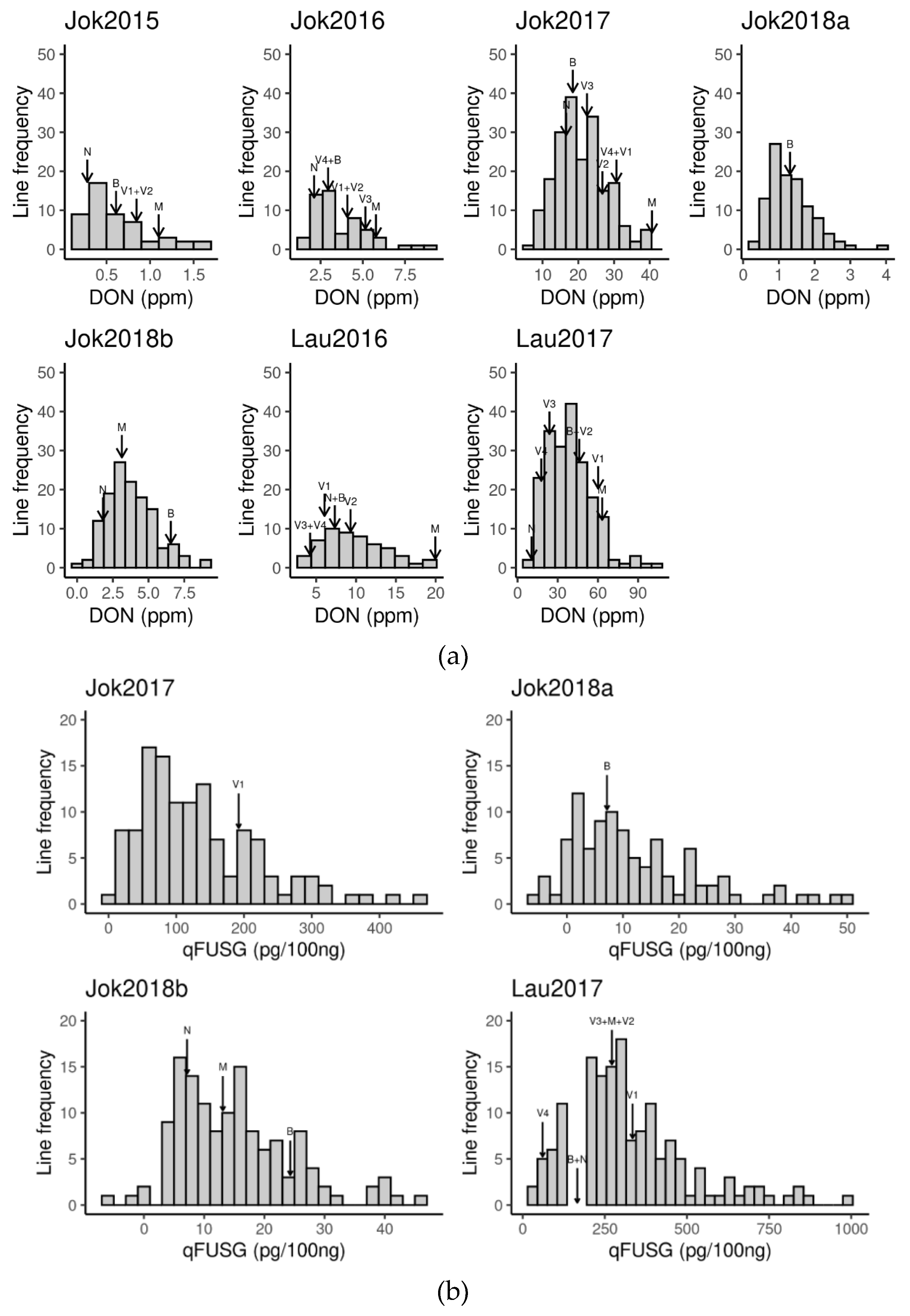
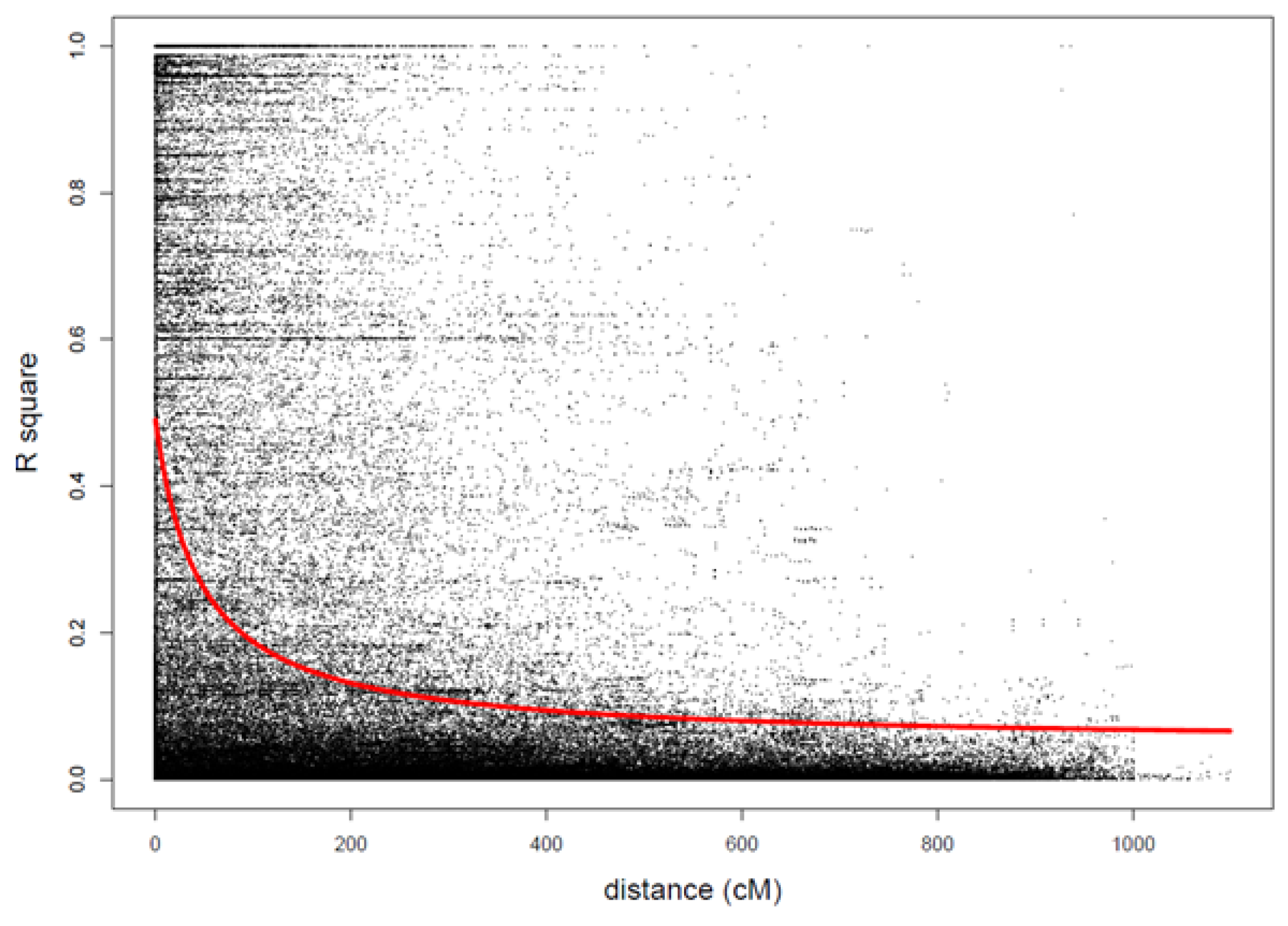
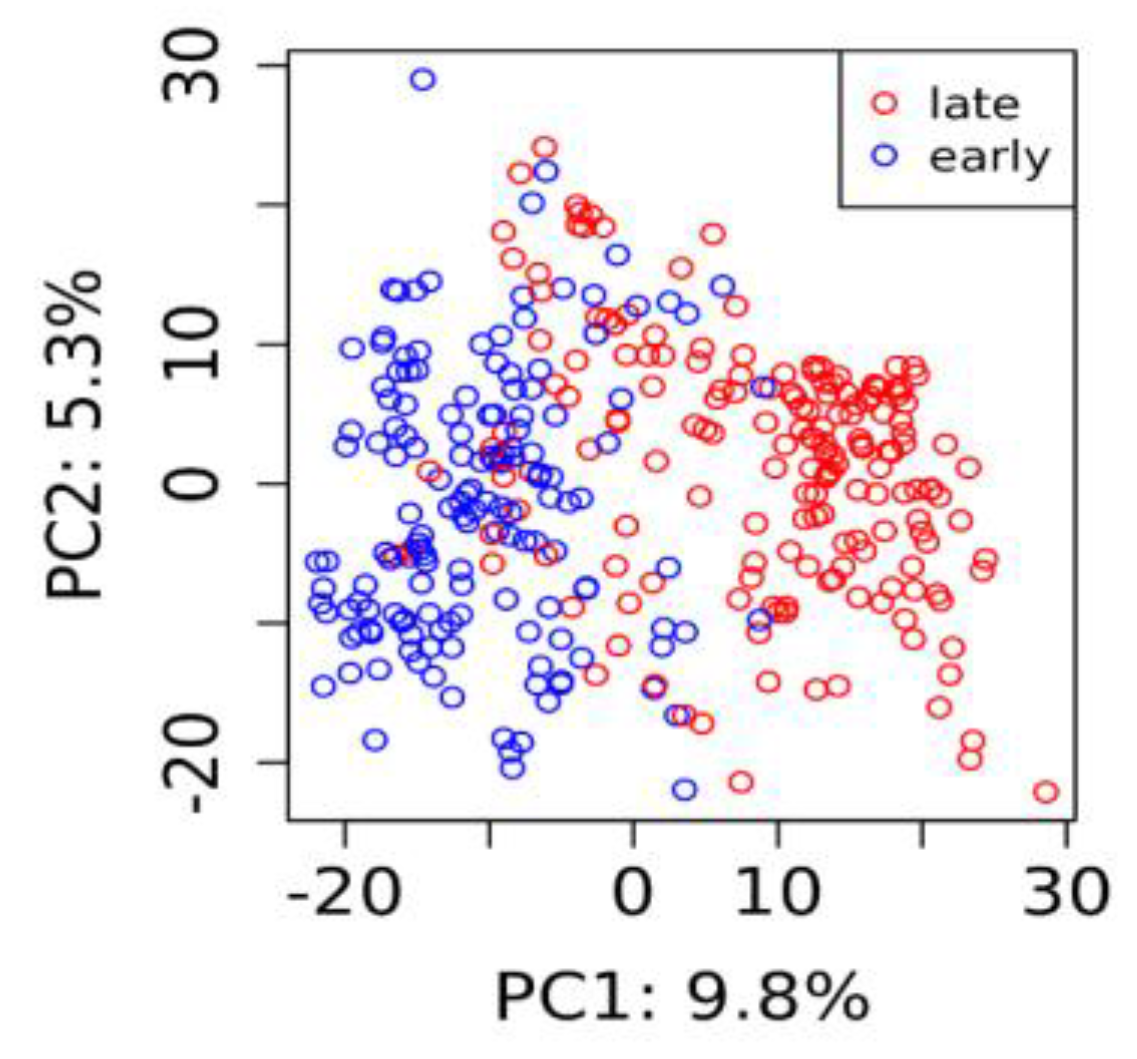
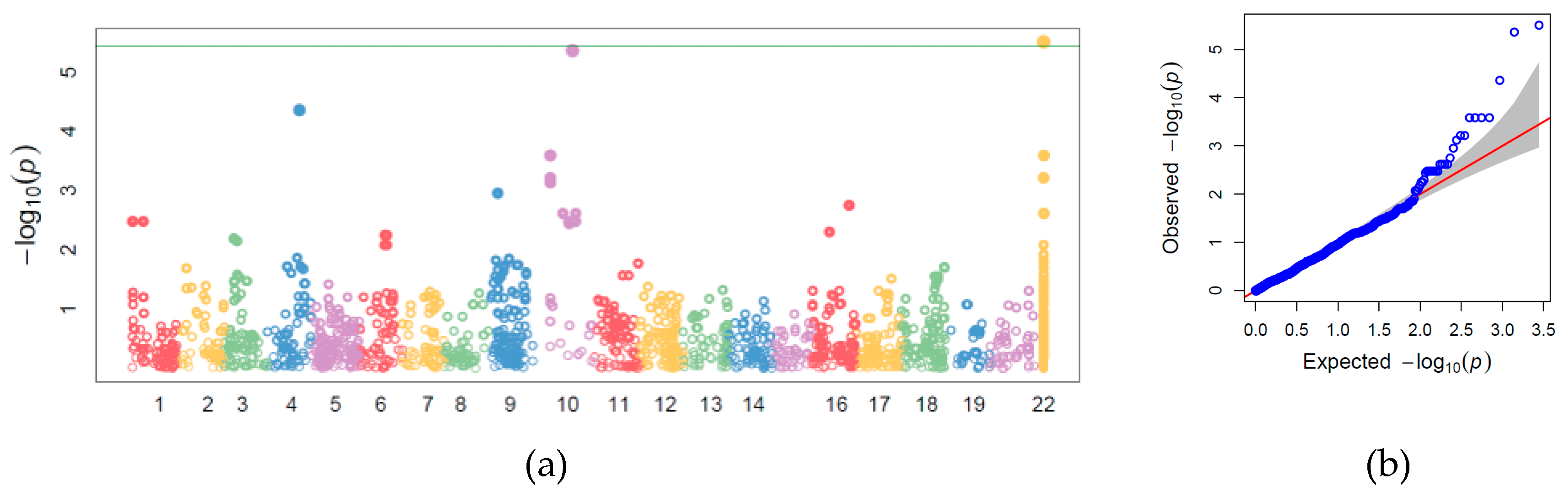
| Trait | N Obs | N Lines | N Trials | Mean | SD | Min | Max | h2 |
|---|---|---|---|---|---|---|---|---|
| DH | 506 | 210 | 4 | 57.9 | 2.64 | 51 | 68 | 0.90 |
| PH | 506 | 210 | 4 | 99.7 | 7.50 | 69 | 146 | 0.89 |
| MC | 307 | 210 | 3 | 3.21 | 0.96 | 1 | 5 | 0.91 |
| GC | 335 | 209 | 4 | 67.5 | 14.0 | 26 | 97 | 0.60 |
| FIK | 254 | 209 | 2 | 43.9 | 17.6 | 12.7 | 91.2 | 0.45 |
| DON 1 | 797 | 327 | 7 | 2.05 | 1.44 | -2.18 | 4.66 | 0.48 |
| qFUSG 1 | 555 | 315 | 4 | 4.34 | 1.24 | 1.55 | 6.90 | 0.19 |
| Trait_Trial | n | Mean | SD | CV% | LSD (α = 0.05) | h2 |
|---|---|---|---|---|---|---|
| DON_Jok2015 | 51 | 0.6 | 0.4 | 63,2 | 0.7 | 0.41 |
| DON_Jok2016 | 55 | 3.6 | 1.7 | 52.7 | 3.0 | 0.56 |
| DON_Jok2017 | 200 | 20.1 | 6.9 | 33.8 | 11.2 | 0.55 |
| DON_Jok2018a | 106 | 1.3 | 0.6 | 50.1 | 1.1 | 0.31 |
| DON_Jok2018b | 132 | 3.8 | 1.6 | 55.2 | 3.3 | 0.49 |
| DON_Lau2016 | 54 | 9.8 | 3.9 | 32.6 | 5.2 | 0.63 |
| DON_Lau2017 | 199 | 38.8 | 16.9 | 36.0 | 22.8 | 0.71 |
| qFUSG_Jok2017 | 125 | 133.8 | 89.9 | 95.3 | 211.2 | 0.40 |
| qFUSG_Jok2018a | 91 | 12.0 | 11.9 | 58.6 | 21.1 | 0.54 |
| qFUSG_Jok2018b | 129 | 15.1 | 9.6 | 61.6 | 17.8 | 0.45 |
| qFUSG_Lau2017 | 198 | 289.8 | 174.4 | 47.1 | 281.6 | 0.59 |
| FIK_Lau2016 | 73 | 72.5 | 10.4 | 17.4 | 20.6 | 0.51 |
| FIK_Lau2017 | 200 | 36.0 | 8.8 | 27.9 | 16.3 | 0.46 |
| GC_Jok2015 | 62 | 89.9 | 4.8 | 4.9 | 7.1 | 0.60 |
| GC_Jok2017 | 29 | 68.9 | 11.0 | 9.8 | 10.8 | 0.71 |
| GC_Lau2016 | 73 | 70.4 | 9.6 | 9.8 | 11.4 | 0.72 |
| GC_Lau2017 | 200 | 60.5 | 9.6 | 12.8 | 12.5 | 0.68 |
| Variance Estimates | Correlations | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Trait | ADD (SE) | RES (SE) | h2 | DH | PH | MC | GC | FIK | DON1 | qFUSG 1 |
| DH | 1.78 (0.31) | 1.11 (0.09) | 0.62 | 0.33 | 0.61 | −0.03 | 0.01 | −0.06 | −0.09 | |
| PH | 30.4 (4.64) | 13.2 (1.04) | 0.70 | 0.50 (0.31, 0.68) | 0.28 | −0.03 | −0.19 | −0.15 | −0.20 | |
| MC | 0.32 (0.06) | 0.13 (0.01) | 0.71 | 0.75 (0.63, 0.87) | 0.37 (0.17, 0.58) | −0.16 | NA | 0.06 | 0.04 | |
| GC | 21.3 (5.91) | 47.9 (4.41) | 0.31 | −0.10 (−0.43, 0.23) | −0.12 (−0.43, 0.18) | −0.44 (−0.73, −0.15) | −0.58 | −0.44 | −0.28 | |
| FIK | 25.1 (8.57) | 53.3 (6.29) | 0.32 | 0.05 (−0.39, 0.29) | −0.26 (−0.55, 0.03) | NA | −0.88 (−1, −0.66) | 0.50 | 0.33 | |
| DON 1 | 0.04 (0.01) | 0.16 (0.01) | 0.21 | 0.06 (−0.25, 0.36) | −0.12 (−0.41, 0.16) | 0.15 (−0.15, 0.44) | −0.63 (−0.90, −0.36) | 0.57 (0.23, 0.90) | 0.38 | |
| qFUSG 1 | 0.03 (0.01) | 0.29 (0.02) | 0.08 | −0.03 (−0.50, 0.45) | −0.45 (−0.84, −0.07) | 0.11 (−0.32, 0.53) | −0.45 (−0.90, 0.01) | 0.66 (0.28, 1) | 0.60 (0.28, 0.93) | |
| Trait | Naive | Q | K | QK |
|---|---|---|---|---|
| DH | 553 | 253 | 0 | 0 |
| PH | 332 | 303 | 0 | 0 |
| MC | 1970 | 349 | 3 | 0 |
| QC | 1121 | 3 | 0 | 0 |
| FIK | 884 | 0 | 0 | 0 |
| DON 1 | 310 | 0 | 0 | 0 |
| DON17 | 956 | 0 | 0 | 0 |
| DON18 | 0 | 0 | 0 | 0 |
| qFUSG 1 | 0 | 0 | 0 | 0 |
| qFUSG17 | 132 | 0 | 0 | 0 |
| qFUSG18 | 534 | 29 | 0 | 0 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Haikka, H.; Manninen, O.; Hautsalo, J.; Pietilä, L.; Jalli, M.; Veteläinen, M. Genome-wide Association Study and Genomic Prediction for Fusarium graminearum Resistance Traits in Nordic Oat (Avena sativa L.). Agronomy 2020, 10, 174. https://doi.org/10.3390/agronomy10020174
Haikka H, Manninen O, Hautsalo J, Pietilä L, Jalli M, Veteläinen M. Genome-wide Association Study and Genomic Prediction for Fusarium graminearum Resistance Traits in Nordic Oat (Avena sativa L.). Agronomy. 2020; 10(2):174. https://doi.org/10.3390/agronomy10020174
Chicago/Turabian StyleHaikka, Hanna, Outi Manninen, Juho Hautsalo, Leena Pietilä, Marja Jalli, and Merja Veteläinen. 2020. "Genome-wide Association Study and Genomic Prediction for Fusarium graminearum Resistance Traits in Nordic Oat (Avena sativa L.)" Agronomy 10, no. 2: 174. https://doi.org/10.3390/agronomy10020174
APA StyleHaikka, H., Manninen, O., Hautsalo, J., Pietilä, L., Jalli, M., & Veteläinen, M. (2020). Genome-wide Association Study and Genomic Prediction for Fusarium graminearum Resistance Traits in Nordic Oat (Avena sativa L.). Agronomy, 10(2), 174. https://doi.org/10.3390/agronomy10020174





