Geostatistical Analysis of Soil C/N Deficiency and Its Effect on Agricultural Land Management of Major Crops in Eastern Croatia
Abstract
1. Introduction
2. Materials and Methods
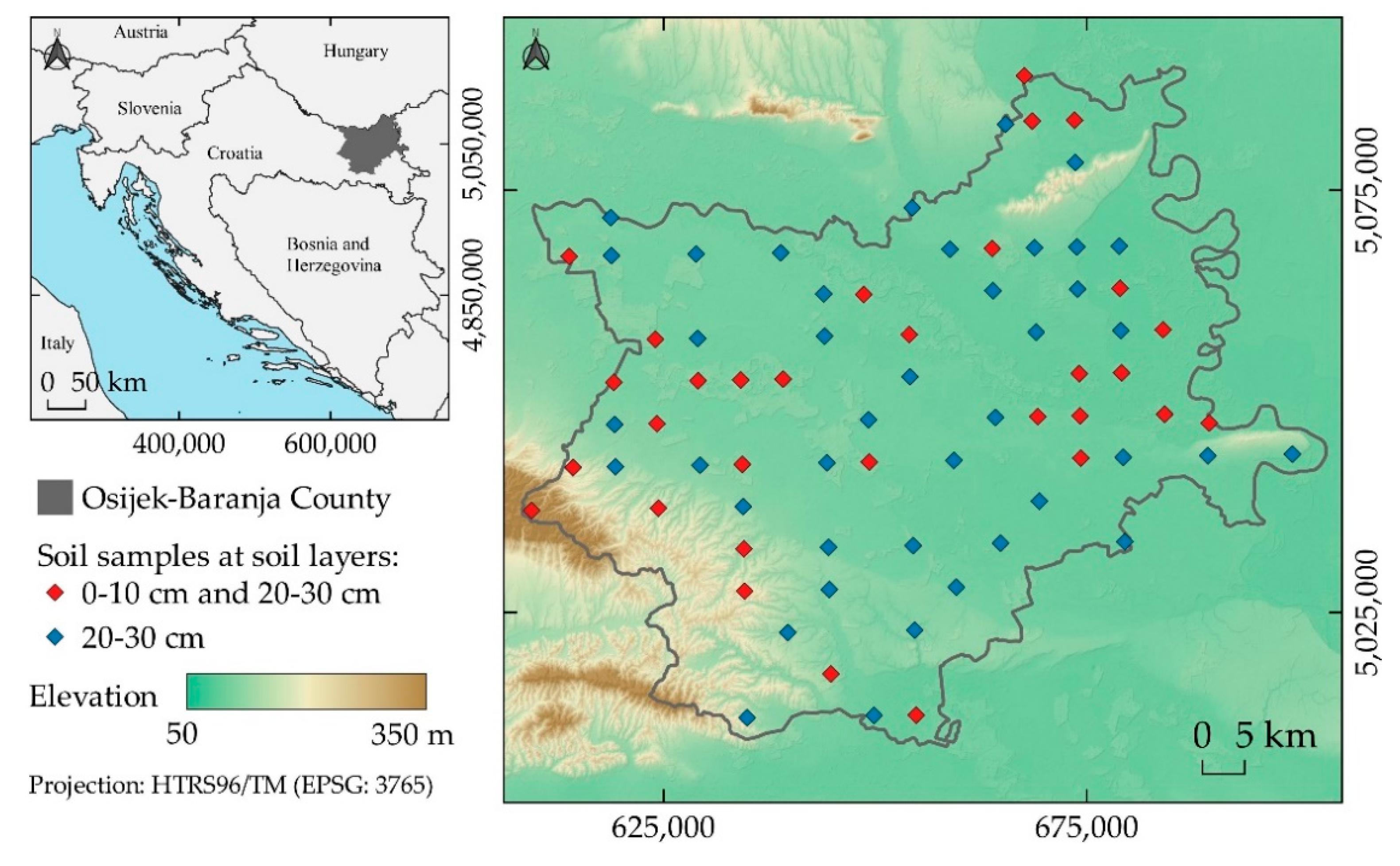
2.1. Study Area and Data Acquisition
2.2. Geostatistical Analysis
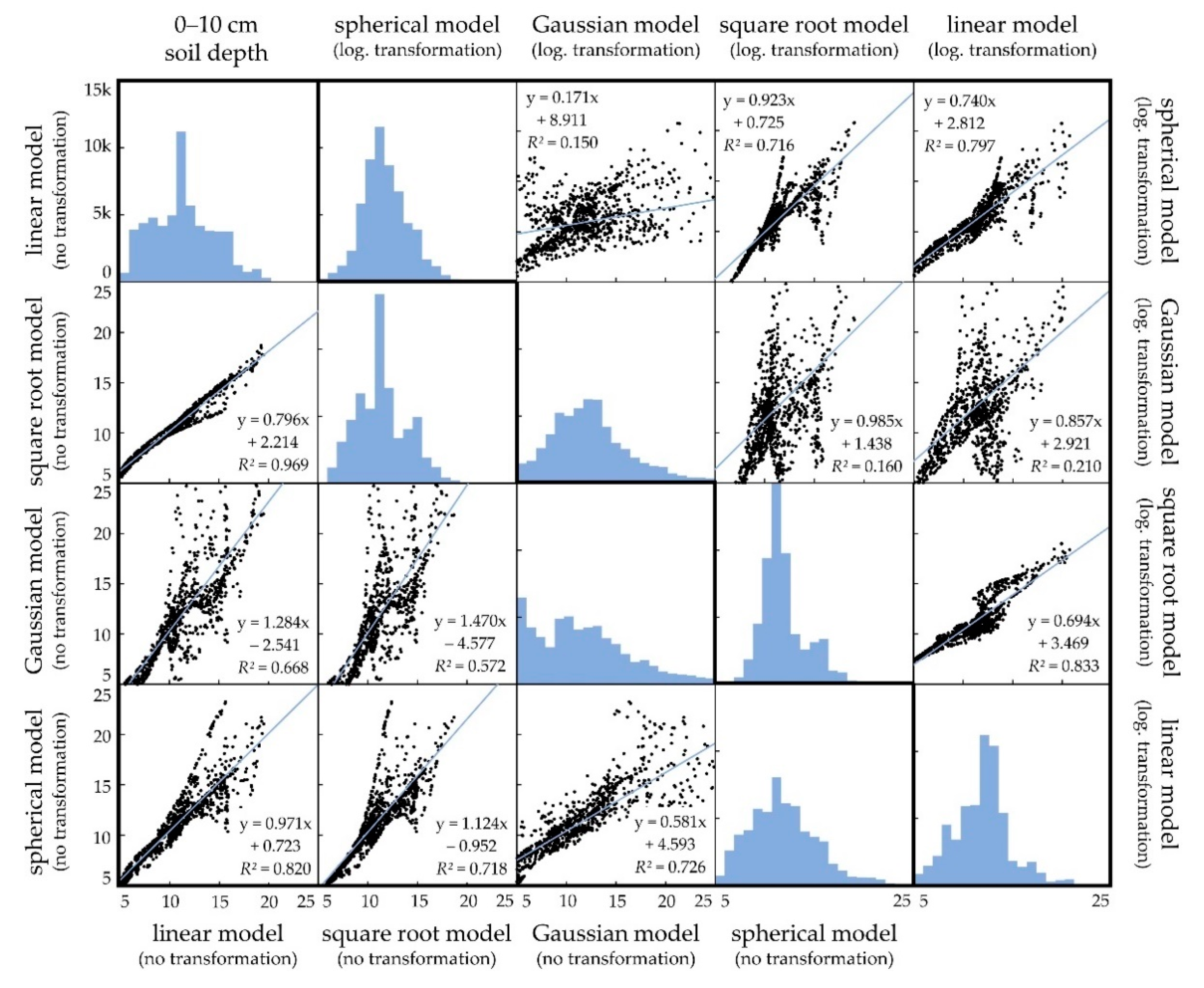
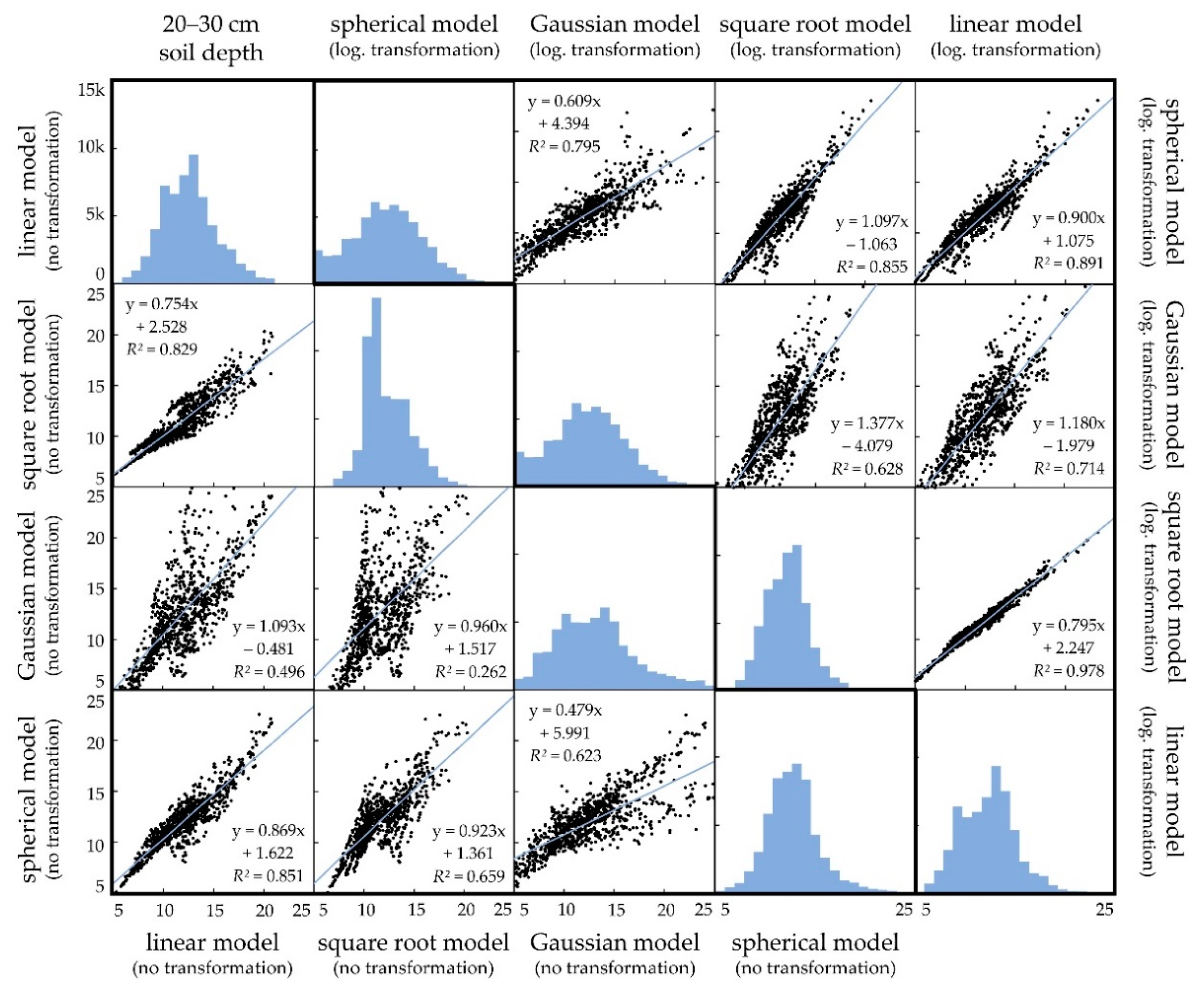
2.3. Accuracy Assessment of Interpolated Results
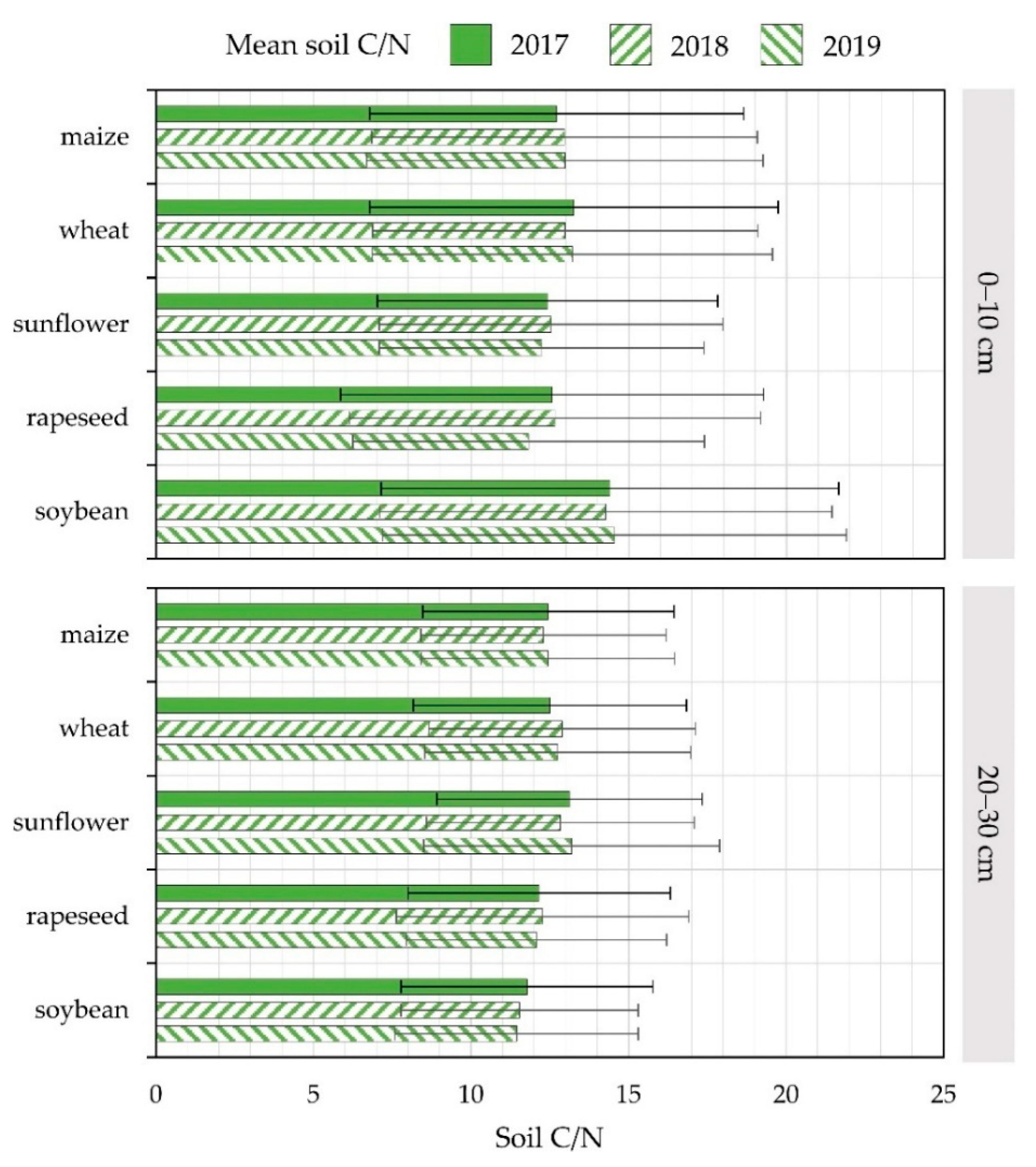
2.4. Soil Carbon-to-Nitrogen Ratio (C/N) Deficiency Evaluation for Five Major Crops during 2017–2019
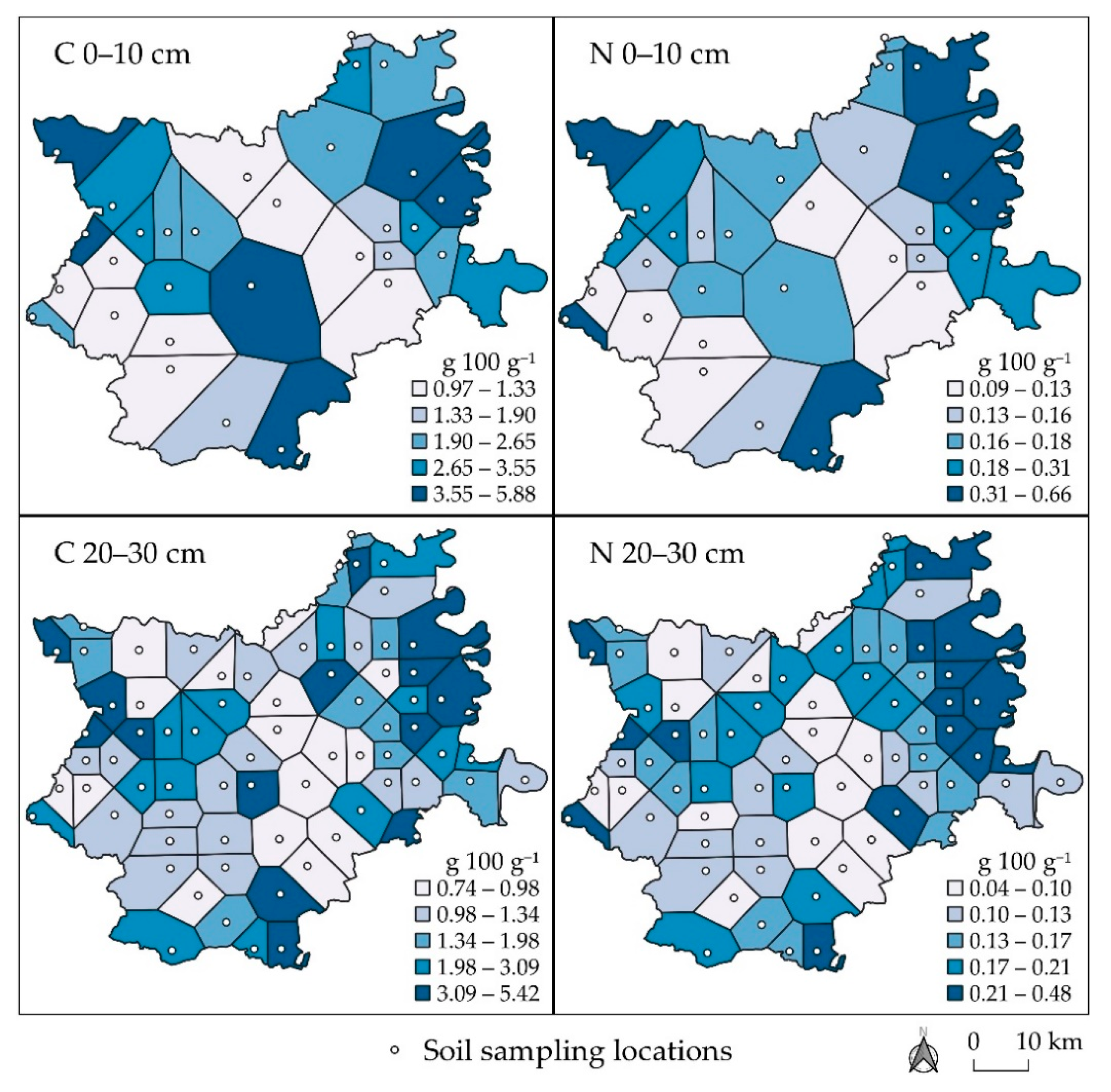
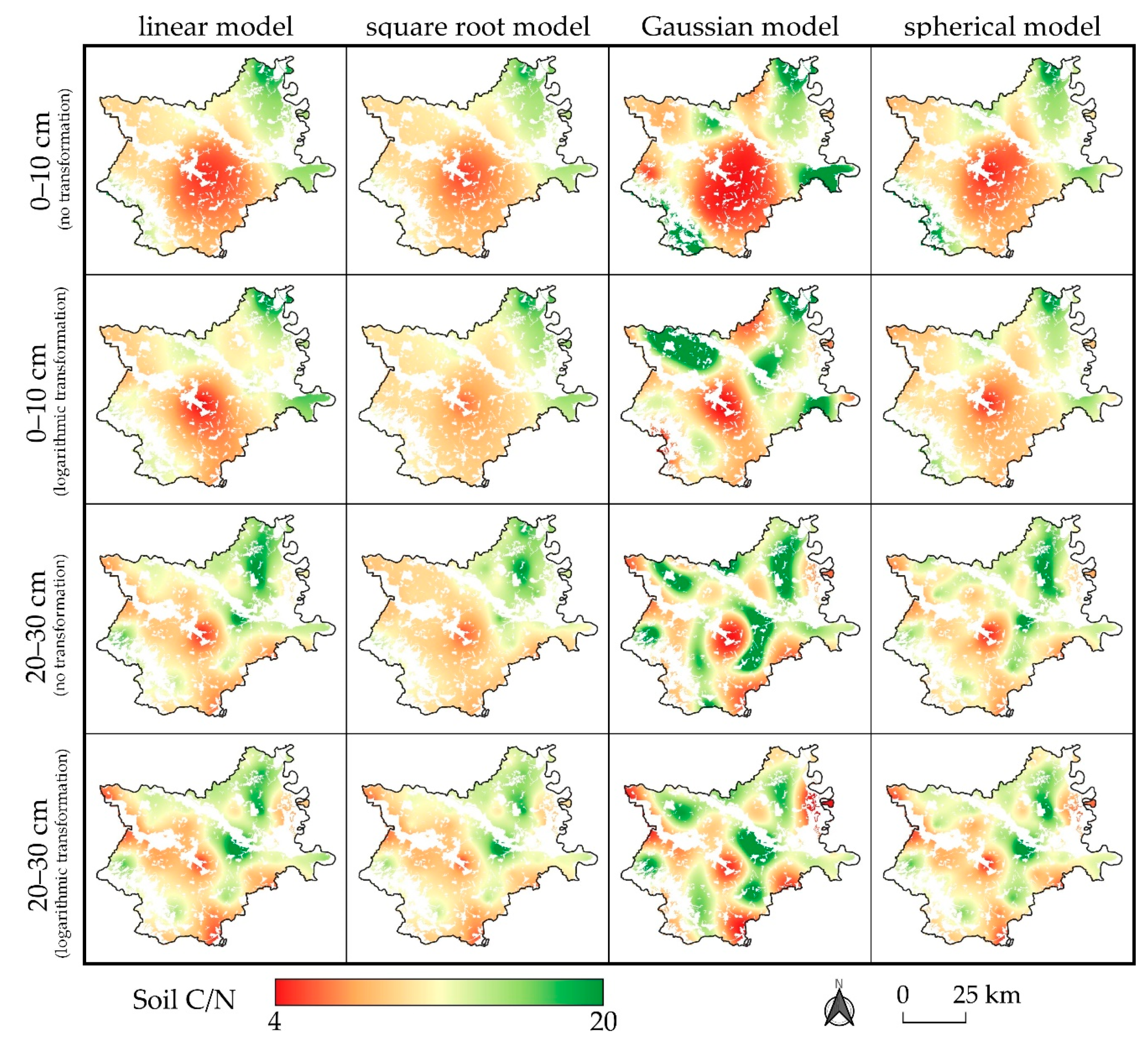
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Scotti, R.; Bonanomi, G.; Scelza, R.; Zoina, A.; Rao, M.A. Organic amendments as sustainable tool to recovery fertility in intensive agricultural systems. J. Soil Sci. Plant Nut. 2015, 15, 333–352. [Google Scholar] [CrossRef]
- Peter, P.C. Soil Organic Matter/Carbon Dynamics in Contrasting Tillage and Land Management Systems: A Case for Smallholder Farmers with Degraded and Marginal Soils. Commun. Soil Sci. Plant Anal. 2017, 48, 2013–2031. [Google Scholar] [CrossRef]
- Puttaso, P.; Namanusart, W.; Thumanu, K.; Kamolmanit, B.; Brauman, A.; Lawongsa, P. Assessing the Effect of Rubber (Hevea brasiliensis (Willd. ex A. Juss.) Muell. Arg.) Leaf Chemical Composition on Some Soil Properties of Differently Aged Rubber Tree Plantations. Agronomy 2020, 10, 1871. [Google Scholar] [CrossRef]
- Truong, T.H.H.; Marschner, P. Presence of wheat straw in soil influences nutrient availability and leaching in soil mulched with high or low C/N organic materials. Arch. Agron. Soil Sci. 2020, 1–12. [Google Scholar] [CrossRef]
- Zhang, Z.C.; Hou, G.; Liu, M.; Wei, T.X.; Sun, J. Degradation induces changes in the soil C: N: P stoichiometry of alpine steppe on the Tibetan Plateau. J. Mt. Sci. 2019, 16, 2348–2360. [Google Scholar] [CrossRef]
- Dlamini, P.; Chivenge, P.; Manson, A.; Chaplot, V. Land degradation impact on soil organic carbon and nitrogen stocks of sub-tropical humid grasslands in South Africa. Geoderma 2014, 235, 372–381. [Google Scholar] [CrossRef]
- Aher, G.; Cihacek, L.J.; Cooper, K. An evaluation of C and N on fresh and aged crop residue from mixed long-term no-till cropping systems. J. Plant. Nutr. 2017, 40, 177–186. [Google Scholar] [CrossRef]
- Bogunovic, I.; Viduka, A.; Magdic, I.; Telak, L.J.; Francos, M.; Pereira, P. Agricultural and Forest Land-Use Impact on Soil Properties in Zagreb Periurban Area (Croatia). Agronomy 2020, 10, 1331. [Google Scholar] [CrossRef]
- Meseldžija, M.; Rajković, M.; Dudić, M.; Vranešević, M.; Bezdan, A.; Jurišić, A.; Ljevnaić-Mašić, B. Economic Feasibility of Chemical Weed Control in Soybean Production in Serbia. Agronomy 2020, 10, 291. [Google Scholar] [CrossRef]
- Dekemati, I.; Simon, B.; Bogunovic, I.; Kisic, I.; Kassai, K.; Kende, Z.; Birkás, M. Long Term Effects of Ploughing and Conservation Tillage Methods on Earthworm Abundance and Crumb Ratio. Agronomy 2020, 10, 1552. [Google Scholar] [CrossRef]
- McAllister, C.H.; Beatty, P.H.; Good, A.G. Engineering nitrogen use efficient crop plants: The current status. Plant. Biotechnol. J. 2012, 10, 1011–1025. [Google Scholar] [CrossRef] [PubMed]
- Leifeld, J. How sustainable is organic farming? Agric. Ecosyst. Environ. 2012, 150, 121–122. [Google Scholar] [CrossRef]
- Boone, L.; Roldán-Ruiz, I.; Muylle, H.; Dewulf, J. Environmental sustainability of conventional and organic farming: Accounting for ecosystem services in life cycle assessment. Sci. Total Environ. 2019, 695, 133841. [Google Scholar] [CrossRef] [PubMed]
- Eurostat, Organic Crop Area by Agricultural Production Methods and Crops (from 2012 Onwards). Available online: https://appsso.eurostat.ec.europa.eu/nui/submitViewTableAction.do (accessed on 28 November 2020).
- Nabiollahi, K.; Golmohamadi, F.; Taghizadeh-Mehrjardi, R.; Kerry, R.; Davari, M. Assessing the effects of slope gradient and land use change on soil quality degradation through digital mapping of soil quality indices and soil loss rate. Geoderma 2018, 318, 16–28. [Google Scholar] [CrossRef]
- Fu, W.; Zhao, K.; Tunney, H.; Zhang, C. Using GIS and geostatistics to optimize soil phosphorus and magnesium sampling in temperate grassland. Soil. Sci. 2013, 178, 240–247. [Google Scholar] [CrossRef]
- Gašparović, I.; Gašparović, M. Determining Optimal Solar Power Plant Locations Based on Remote Sensing and GIS Methods: A Case Study from Croatia. Remote Sens. 2019, 11, 1481. [Google Scholar] [CrossRef]
- Zhang, Z.; Yu, D.; Wang, X.; Pan, Y.; Zhang, G.; Shi, X. Influence of the Selection of Interpolation Method on Revealing Soil Organic Carbon Variability in the Red Soil Region, China. Sustainability 2018, 10, 2290. [Google Scholar] [CrossRef]
- Oliver, M.A.; Webster, R. Basic Steps in Geostatistics: The Variogram and Kriging; SpringerBriefs in Agriculture; Springer International Publishing: Cham, Switzerland, 2015. [Google Scholar]
- Oliver, M.A.; Bishop, T.F.A.; Marchant, B.P. Precision Agriculture for Sustainability and Environmental Protection; Routledge: Abingdon, UK, 2013. [Google Scholar]
- Benslama, A.; Khanchoul, K.; Benbrahim, F.; Boubehziz, S.; Chikhi, F.; Navarro-Pedreño, J. Monitoring the Variations of Soil Salinity in a Palm Grove in Southern Algeria. Sustainability 2020, 12, 6117. [Google Scholar] [CrossRef]
- Dai, F.; Zhou, Q.; Lv, Z.; Wang, X.; Liu, G. Spatial prediction of soil organic matter content integrating artificial neural network and ordinary kriging in Tibetan Plateau. Ecol. Indic. 2014, 45, 184–194. [Google Scholar] [CrossRef]
- Chabala, L.M.; Mulolwa, A.; Lungu, O. Application of ordinary kriging in mapping soil organic carbon in Zambia. Pedosphere 2017, 27, 338–343. [Google Scholar] [CrossRef]
- Song, J.J.; Kwon, S.; Lee, G. Incorporation of parameter uncertainty into spatial interpolation using Bayesian trans-Gaussian kriging. Adv. Atmos. Sci. 2015, 32, 413–423. [Google Scholar] [CrossRef]
- Radočaj, D.; Jurišić, M.; Gašparović, M.; Plaščak, I. Optimal Soybean (Glycine max L.) Land Suitability Using GIS-Based Multicriteria Analysis and Sentinel-2 Multitemporal Images. Remote Sens. 2020, 12, 1463. [Google Scholar] [CrossRef]
- Jurišić, M.; Plaščak, I.; Antonić, O.; Radočaj, D. Suitability Calculation for Red Spicy Pepper Cultivation (Capsicum annum L.) Using Hybrid GIS-Based Multicriteria Analysis. Agronomy 2020, 10, 3. [Google Scholar] [CrossRef]
- Radočaj, D.; Jurišić, M.; Zebec, V.; Plaščak, I. Delineation of Soil Texture Suitability Zones for Soybean Cultivation: A Case Study in Continental Croatia. Agronomy 2020, 10, 823. [Google Scholar] [CrossRef]
- Zhao, J.; Zhan, X.; Jiang, Y.; Xu, J. Variations in climatic suitability and planting regionalization for potato in northern China under climate change. PLoS ONE 2018, 13, e0203538. [Google Scholar] [CrossRef] [PubMed]
- Bogunovic, I.; Trevisani, S.; Seput, M.; Juzbasic, D.; Durdevic, B. Short-range and regional spatial variability of soil chemical properties in an agro-ecosystem in eastern Croatia. Catena 2017, 154, 50–62. [Google Scholar] [CrossRef]
- Croatian Bureau of Statistics, Statistical Yearbook of the Republic of Croatia. 2018. Available online: https://www.dzs.hr/Hrv_Eng/ljetopis/2018/sljh2018.pdf (accessed on 28 November 2020).
- Croatian Meteorological and Hydrological Service, Monthly Values and Extremes, Osijek. Available online: https://meteo.hr/klima_e.php?section=klima_podaci¶m=k1&Grad=osijek (accessed on 8 December 2020).
- Liu, N.; Li, Y.; Cong, P.; Wang, J.; Guo, W.; Pang, H.; Zhang, L. Depth of straw incorporation significantly alters crop yield, soil organic carbon and total nitrogen in the North China Plain. Soil Tillage Res. 2021, 205, 104772. [Google Scholar] [CrossRef]
- Metwally, M.S.; Shaddad, S.M.; Liu, M.; Yao, R.-J.; Abdo, A.I.; Li, P.; Jiao, J.; Chen, X. Soil Properties Spatial Variability and Delineation of Site-Specific Management Zones Based on Soil Fertility Using Fuzzy Clustering in a Hilly Field in Jianyang, Sichuan, China. Sustainability 2019, 11, 7084. [Google Scholar] [CrossRef]
- Gan, Y.T.; Liang, B.C.; Liu, L.P.; Wang, X.Y.; McDonald, C.L. C: N ratios and carbon distribution profile across rooting zones in oilseed and pulse crops. Crop. Pasture Sci. 2011, 62, 496–503. [Google Scholar] [CrossRef]
- Rosner, K.; Bodner, G.; Hage-Ahmed, K.; Steinkellner, S. Long-term Soil Tillage and Cover Cropping Affected Arbuscular Mycorrhizal Fungi, Nutrient Concentrations, and Yield in Sunflower. Agron. J. 2018, 110, 2664–2672. [Google Scholar] [CrossRef]
- Liu, Z.; Chen, X.; Jing, Y.; Li, Q.; Zhang, J.; Huang, Q. Effects of biochar amendment on rapeseed and sweet potato yields and water stable aggregate in upland red soil. Catena 2014, 123, 45–51. [Google Scholar] [CrossRef]
- Ruffo, M.L.; Bullock, D.G.; Bollero, G.A. Soybean yield as affected by biomass and nitrogen uptake of cereal rye in winter cover crop rotations. Agron. J. 2004, 96, 800–805. [Google Scholar] [CrossRef]
- Mendes, M.P.; Ribeiro, L. Nitrate probability mapping in the northern aquifer alluvial system of the river Tagus (Portugal) using Disjunctive Kriging. Sci. Total Environ. 2010, 408, 1021–1034. [Google Scholar] [CrossRef] [PubMed]
- Isaaks, E.H.; Srivastava, R.M. An Introduction to Applied Geostatistics; Oxford University Press: New York, NY, USA, 1989. [Google Scholar]
- Panday, D.; Maharjan, B.; Chalise, D.; Shrestha, R.K.; Twanabasu, B. Digital soil mapping in the Bara district of Nepal using kriging tool in ArcGIS. PLoS ONE 2018, 13, e0206350. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, M.; Sun, J.; Wei, T. Degradation leads to dramatic decrease in topsoil but not subsoil root biomass in an alpine meadow on the Tibetan Plateau, China. J. Arid Land 2020, 1–13. [Google Scholar] [CrossRef]
- United States Department of Agriculture, Soil Survey Laboratory Information Manual. Available online: https://www.nrcs.usda.gov/Internet/FSE_DOCUMENTS/nrcs142p2_052226.pdf (accessed on 8 December 2020).
- Thomsen, I.K.; Petersen, B.M.; Bruun, S.; Jensen, L.S.; Christensen, B.T. Estimating soil C loss potentials from the C to N ratio. Soil Biol. Biochem. 2008, 40, 849–852. [Google Scholar] [CrossRef]
- Marchetti, A.; Piccini, C.; Francaviglia, R.; Mabit, L. Spatial distribution of soil organic matter using geostatistics: A key indicator to assess soil degradation status in central Italy. Pedosphere 2012, 22, 230–242. [Google Scholar] [CrossRef]
- Sun, X.L.; Yang, Q.; Wang, H.L.; Wu, Y.J. Can regression determination, nugget-to-sill ratio and sampling spacing determine relative performance of regression kriging over ordinary kriging? Catena 2019, 181, 104092. [Google Scholar] [CrossRef]
- Varouchakis, E.A.; Hristopulos, D.T.; Karatzas, G.P. Improving kriging of groundwater level data using nonlinear normalizing transformations—A field application. Hydrol. Sci. J. 2012, 57, 1404–1419. [Google Scholar] [CrossRef]
- Schloeder, C.A.; Zimmerman, N.E.; Jacobs, M.J. Comparison of methods for interpolating soil properties using limited data. Soil Sci. Soc. Am. J. 2001, 65, 470–479. [Google Scholar] [CrossRef]
- Ding, J.; Yu, D. Monitoring and evaluating spatial variability of soil salinity in dry and wet seasons in the Werigan–Kuqa Oasis, China, using remote sensing and electromagnetic induction instruments. Geoderma 2014, 235, 316–322. [Google Scholar] [CrossRef]
- Fashi, F.H.; Sharifi, F.; Kamali, K. Modelling infiltration and geostatistical analysis of spatial variability of sorptivity and transmissivity in a flood spreading area. Span. J. Agric. Res. 2014, 12, 277–288. [Google Scholar] [CrossRef]
- Jenkinson, D.S.; Poulton, P.R.; Bryant, C. The turnover of organic carbon in subsoils. Part 1. Natural and bomb radiocarbon in soil profiles from the Rothamsted long-term field experiments. Eur. J. Soil Sci. 2008, 59, 391–399. [Google Scholar] [CrossRef]
- Rumpel, C.; Kögel-Knabner, I. Deep soil organic matter—A key but poorly understood component of terrestrial C cycle. Plant Soil 2011, 338, 143–158. [Google Scholar] [CrossRef]
- Tesfahunegn, G.B.; Tamene, L.; Vlek, P.L. Catchment-scale spatial variability of soil properties and implications on site-specific soil management in northern Ethiopia. Soil Tillage Res. 2011, 117, 124–139. [Google Scholar] [CrossRef]
- Yang, L.; Wang, L.; Huang, J.; Mansaray, L.R.; Mijiti, R. Monitoring policy-driven crop area adjustments in northeast China using Landsat-8 imagery. Int. J. Appl. Earth Obs. Geoinf. 2019, 82, 101892. [Google Scholar] [CrossRef]
- Singha, C.; Swain, K.C.; Swain, S.K. Best Crop Rotation Selection with GIS-AHP Technique Using Soil Nutrient Variability. Agriculture 2020, 10, 213. [Google Scholar] [CrossRef]
- Radočaj, D.; Obhođaš, J.; Jurišić, M.; Gašparović, M. Global Open Data Remote Sensing Satellite Missions for Land Monitoring and Conservation: A Review. Land 2020, 9, 402. [Google Scholar] [CrossRef]
- Gašparović, M.; Zrinjski, M.; Barković, Đ.; Radočaj, D. An automatic method for weed mapping in oat fields based on UAV imagery. Comput. Electron. Agric. 2020, 173, 105385. [Google Scholar] [CrossRef]
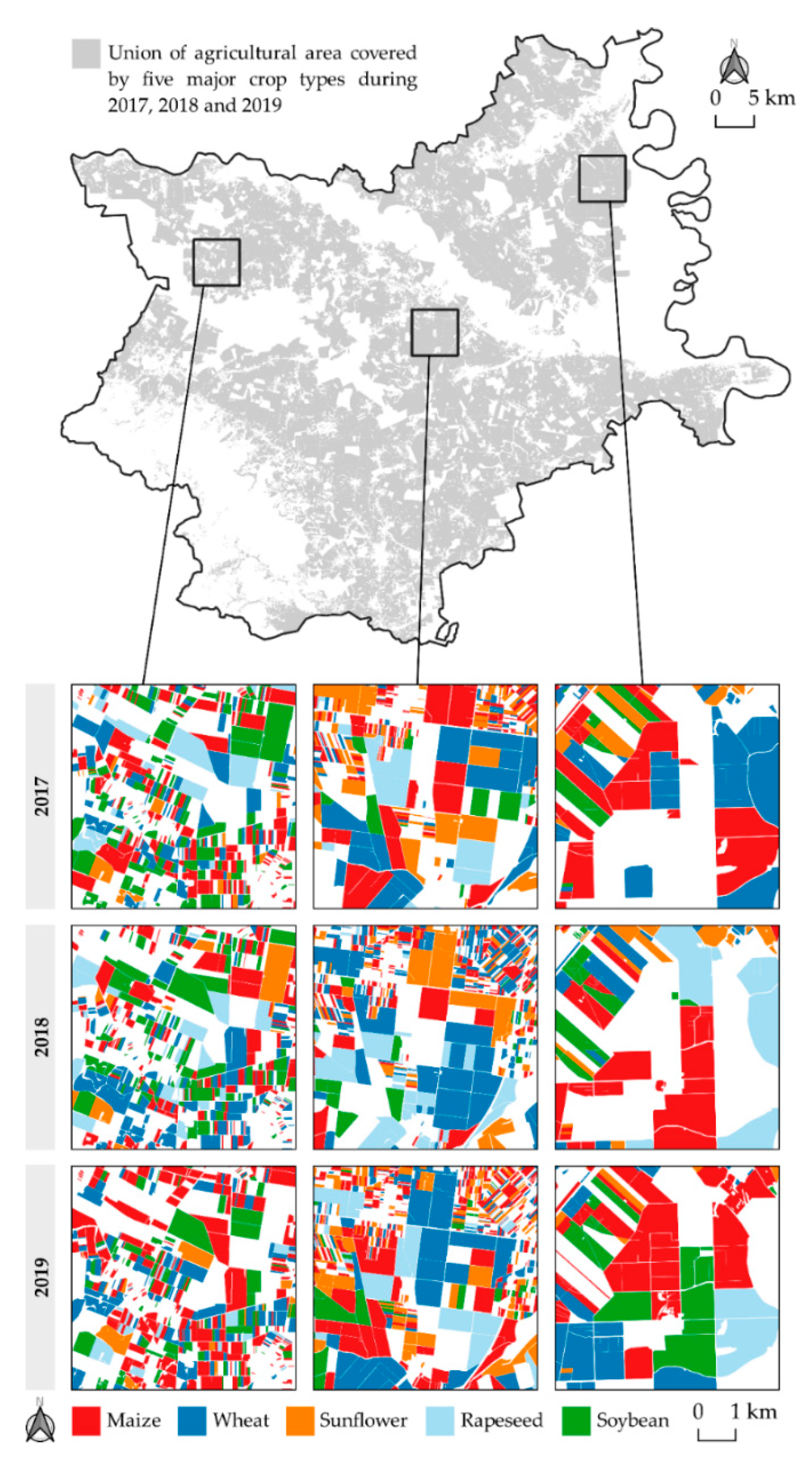
| Crop | 2017 | 2018 | 2019 | |||
|---|---|---|---|---|---|---|
| Area Cultivated (ha) | Part of Total Agricultural Area (%) | Area Cultivated (ha) | Part of Total Agricultural Area (%) | Area Cultivated (ha) | Part of Total Agricultural Area (%) | |
| Maize | 42,368 | 20.19 | 40,232 | 19.19 | 56,549 | 27.17 |
| Wheat | 32,941 | 15.70 | 40,486 | 19.31 | 42,048 | 20.20 |
| Sunflower | 22,347 | 10.65 | 23,818 | 11.36 | 20,179 | 9.69 |
| Rapeseed | 20,981 | 10.00 | 21,039 | 10.03 | 14,137 | 6.79 |
| Soybean | 16,642 | 7.93 | 15,117 | 7.21 | 13,199 | 6.34 |
| Total | 135,279 | 64.46 | 140,692 | 67.09 | 146,112 | 70.19 |
| Values | C 0–10 cm | N 0–10 cm | C 20–30 cm | N 20–30 cm | |
|---|---|---|---|---|---|
| Mean (g 100 g−1) | 2.58 | 0.24 | 1.98 | 0.16 | |
| Minimum (g 100 g−1) | 0.97 | 0.09 | 0.74 | 0.04 | |
| Maximum (g 100 g−1) | 5.88 | 0.66 | 5.42 | 0.48 | |
| CV | 0.48 | 0.52 | 0.59 | 0.53 | |
| Skewness | 0.95 | 1.50 | 1.34 | 1.87 | |
| Kurtosis | 0.53 | 1.82 | 1.26 | 3.61 | |
| Shapiro–Wilk | W | 0.81 | 0.47 | 0.85 | 0.42 |
| p | 0.029 | >0.001 | >0.001 | >0.001 | |
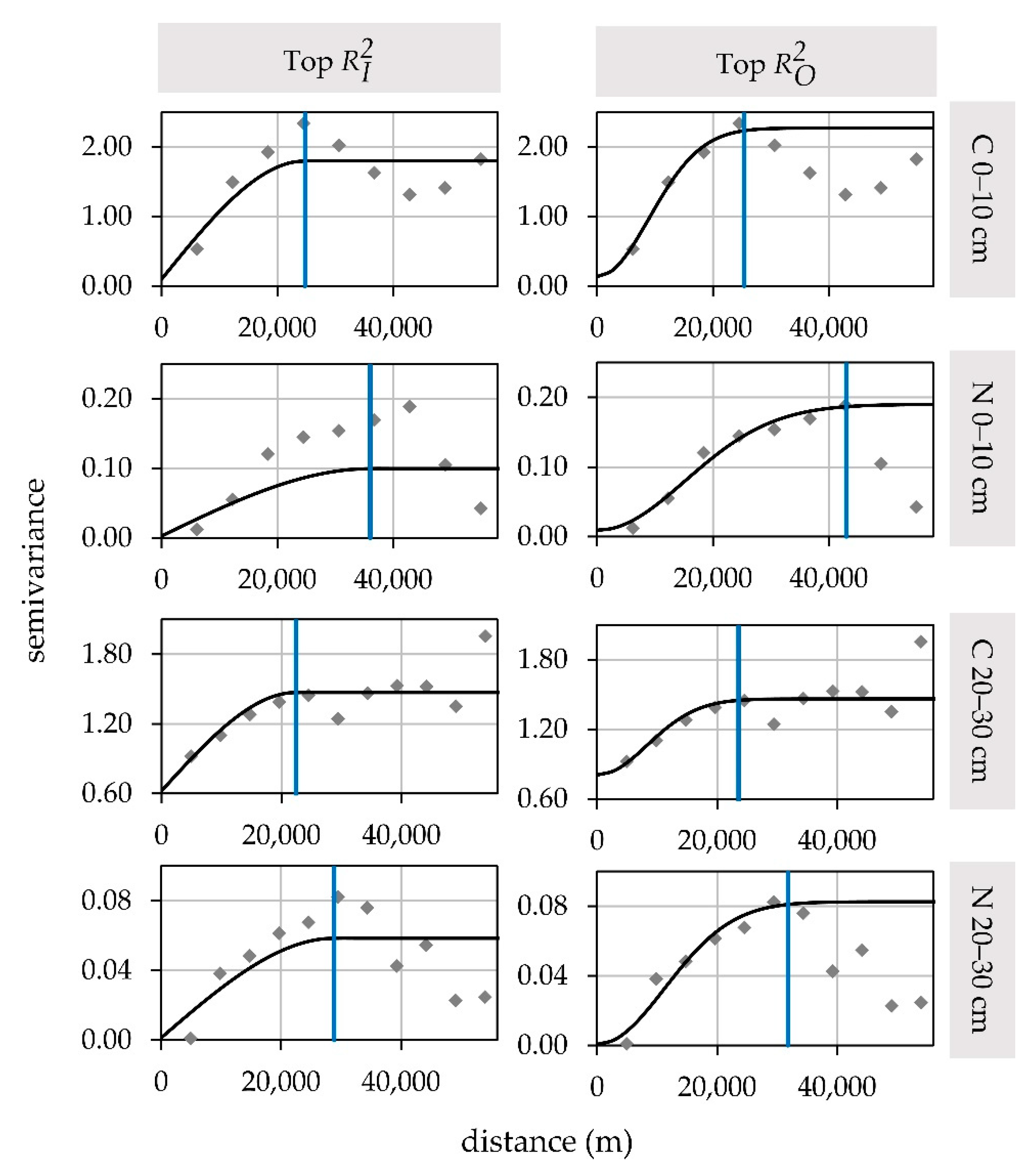
| Soil Element | Model | Transformation Method | n | s | Spatial Dependence | r (m) | ||
|---|---|---|---|---|---|---|---|---|
| C | linear | none | 0.359 | 2.367 | 0.848 | 25348 | 95.7 | 53.5 |
| logarithmic | 0.064 | 0.345 | 0.814 | 93.6 | 58.8 | |||
| square root | none | 0.298 | 2.159 | 0.862 | 37471 | 96.0 | 42.8 | |
| logarithmic | 0.025 | 0.342 | 0.927 | 96.8 | 55.1 | |||
| Gaussian | none | 0.136 | 2.270 | 0.940 | 25348 | 97.1 | 58.7 | |
| logarithmic | 0.041 | 0.330 | 0.876 | 95.0 | 59.5 | |||
| spherical | none | 0.098 | 1.798 | 0.945 | 24768 | 99.2 | 54.3 | |
| logarithmic | 0.022 | 0.280 | 0.921 | 98.5 | 59.1 | |||
| N | linear | none | 0.037 | 0.188 | 0.803 | 42981 | 95.8 | 42.9 |
| logarithmic | 0.147 | 0.672 | 0.781 | 80.5 | 65.5 | |||
| square root | none | 0.035 | 0.135 | 0.741 | 55089 | 97.4 | 38.0 | |
| logarithmic | 0.158 | 0.514 | 0.693 | 81.1 | 63.0 | |||
| Gaussian | none | 0.009 | 0.190 | 0.953 | 42981 | 93.8 | 49.5 | |
| logarithmic | 0.071 | 0.649 | 0.891 | 88.1 | 66.3 | |||
| spherical | none | 0.003 | 0.100 | 0.970 | 36049 | 99.7 | 50.9 | |
| logarithmic | 0.087 | 0.417 | 0.791 | 92.2 | 63.3 |
| Soil Element | Model | Transformation Method | n | s | Spatial Dependence | r (m) | ||
|---|---|---|---|---|---|---|---|---|
| C | linear | none | 0.705 | 1.536 | 0.541 | 21,194 | 72.0 | 57.5 |
| logarithmic | 0.220 | 0.297 | 0.259 | 54.5 | 56.2 | |||
| square root | none | 0.319 | 1.458 | 0.781 | 20,017 | 89.0 | 57.0 | |
| logarithmic | 0.196 | 0.286 | 0.315 | 64.5 | 58.7 | |||
| Gaussian | none | 0.806 | 1.461 | 0.448 | 23,549 | 68.5 | 44.4 | |
| logarithmic | 0.243 | 0.285 | 0.147 | 55.5 | 67.3 | |||
| spherical | none | 0.623 | 1.471 | 0.576 | 22,390 | 81.4 | 43.1 | |
| logarithmic | 0.218 | 0.320 | 0.319 | 68.5 | 64.7 | |||
| N | linear | none | 0.004 | 0.086 | 0.953 | 25,904 | 95.6 | 40.7 |
| logarithmic | 0.014 | 0.489 | 0.971 | 93.0 | 74.6 | |||
| square root | none | 0.002 | 0.077 | 0.974 | 41,211 | 95.5 | 38.6 | |
| logarithmic | 0.003 | 0.445 | 0.993 | 89.0 | 79.3 | |||
| Gaussian | none | 0.001 | 0.083 | 0.988 | 31,791 | 68.9 | 61.5 | |
| logarithmic | 0.001 | 0.444 | 0.998 | 99.3 | 80.1 | |||
| spherical | none | 0.001 | 0.059 | 0.983 | 28,849 | 97.9 | 47.8 | |
| logarithmic | 0.006 | 0.356 | 0.981 | 96.2 | 78.7 |
| Soil Depth | Model | Transformation Method | Mean | Min | Max | CV |
|---|---|---|---|---|---|---|
| 0–10 cm | linear | none | 10.80 | 4.69 | 20.26 | 0.31 |
| logarithmic | 11.28 | 3.76 | 20.85 | 0.26 | ||
| square root | none | 10.81 | 4.93 | 19.28 | 0.25 | |
| logarithmic | 11.28 | 5.82 | 19.86 | 0.20 | ||
| Gaussian | none | 11.45 | 3.92 | 31.70 | 0.48 | |
| logarithmic | 12.77 | 3.88 | 37.35 | 0.46 | ||
| spherical | none | 11.25 | 4.16 | 23.91 | 0.32 | |
| logarithmic | 11.17 | 4.24 | 21.77 | 0.22 | ||
| 20–30 cm | linear | none | 12.05 | 4.47 | 22.20 | 0.24 |
| logarithmic | 11.70 | 4.44 | 26.76 | 0.25 | ||
| square root | none | 12.04 | 5.53 | 22.57 | 0.14 | |
| logarithmic | 11.54 | 4.68 | 25.74 | 0.21 | ||
| Gaussian | none | 12.88 | 3.97 | 31.94 | 0.39 | |
| logarithmic | 11.86 | 3.15 | 31.02 | 0.36 | ||
| spherical | none | 12.10 | 4.17 | 26.15 | 0.23 | |
| logarithmic | 11.62 | 3.65 | 28.60 | 0.25 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jurišić, M.; Radočaj, D.; Krčmar, S.; Plaščak, I.; Gašparović, M. Geostatistical Analysis of Soil C/N Deficiency and Its Effect on Agricultural Land Management of Major Crops in Eastern Croatia. Agronomy 2020, 10, 1996. https://doi.org/10.3390/agronomy10121996
Jurišić M, Radočaj D, Krčmar S, Plaščak I, Gašparović M. Geostatistical Analysis of Soil C/N Deficiency and Its Effect on Agricultural Land Management of Major Crops in Eastern Croatia. Agronomy. 2020; 10(12):1996. https://doi.org/10.3390/agronomy10121996
Chicago/Turabian StyleJurišić, Mladen, Dorijan Radočaj, Stjepan Krčmar, Ivan Plaščak, and Mateo Gašparović. 2020. "Geostatistical Analysis of Soil C/N Deficiency and Its Effect on Agricultural Land Management of Major Crops in Eastern Croatia" Agronomy 10, no. 12: 1996. https://doi.org/10.3390/agronomy10121996
APA StyleJurišić, M., Radočaj, D., Krčmar, S., Plaščak, I., & Gašparović, M. (2020). Geostatistical Analysis of Soil C/N Deficiency and Its Effect on Agricultural Land Management of Major Crops in Eastern Croatia. Agronomy, 10(12), 1996. https://doi.org/10.3390/agronomy10121996









