Near Real-Time Biophysical Rice (Oryza sativa L.) Yield Estimation to Support Crop Insurance Implementation in India
Abstract
1. Introduction
2. Materials and Methods
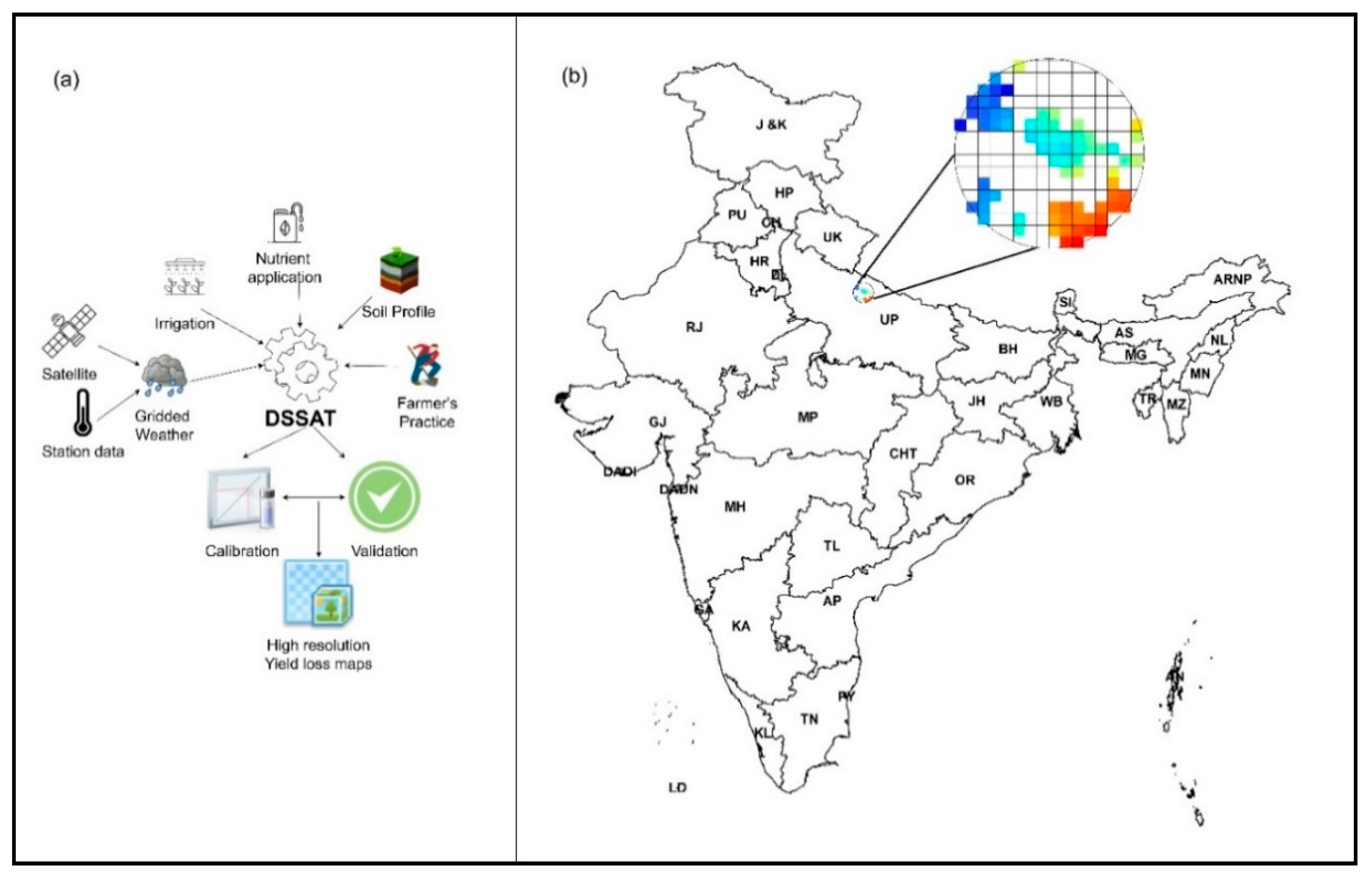
2.1. Crop Model
2.2. Model Input Data
2.3. Observed Yields
2.4. Data Quality Filtering
2.5. Rice Crop Masking
2.6. Daily Weather
2.7. Soil
2.8. Irrigation
2.9. Fertilizer
2.10. Planting Practices
2.11. Crop Variety and Genetic Coefficients
2.12. Model Calibration and Performance Evaluation
3. Results
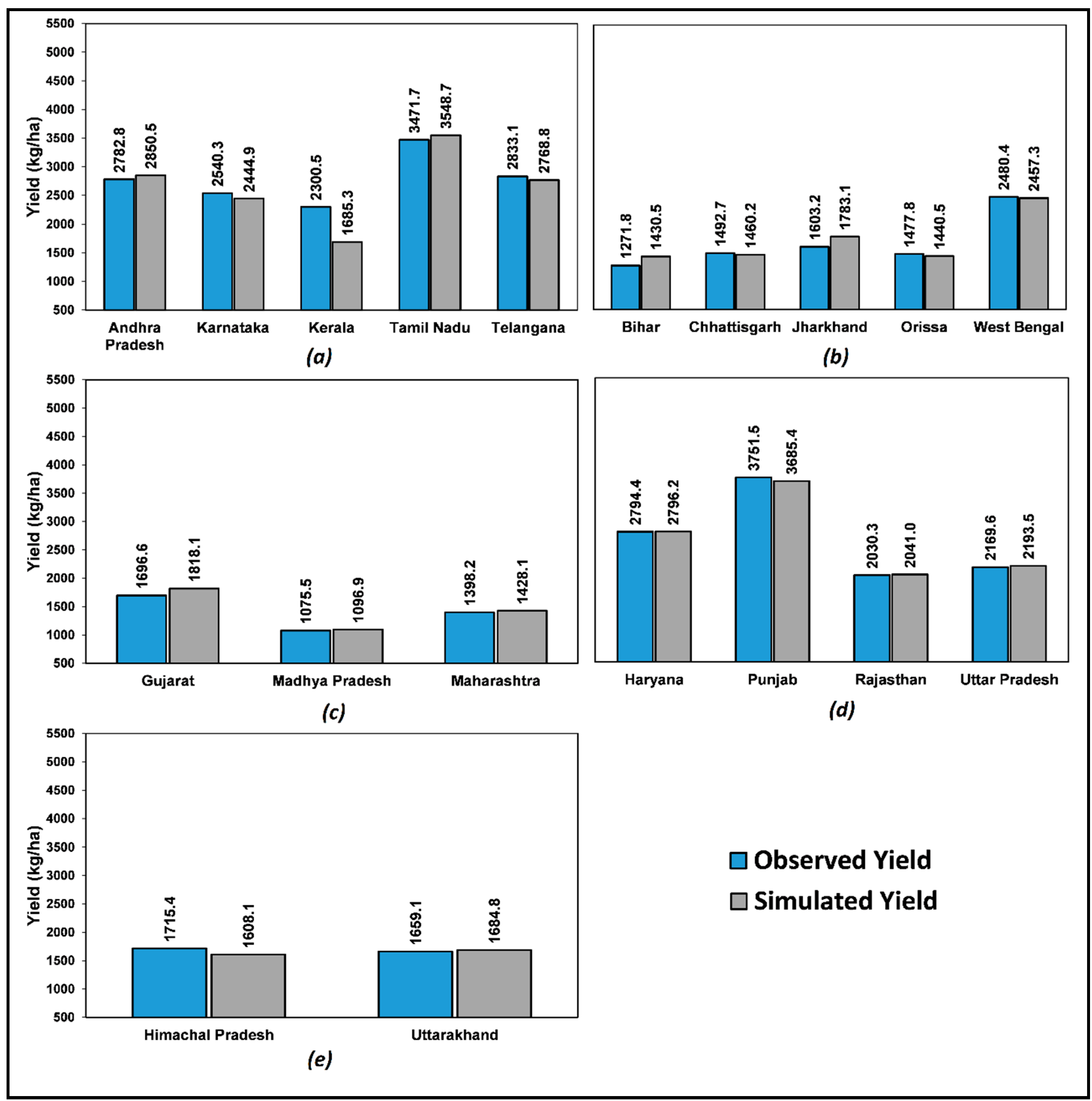
3.1. Model Calibration
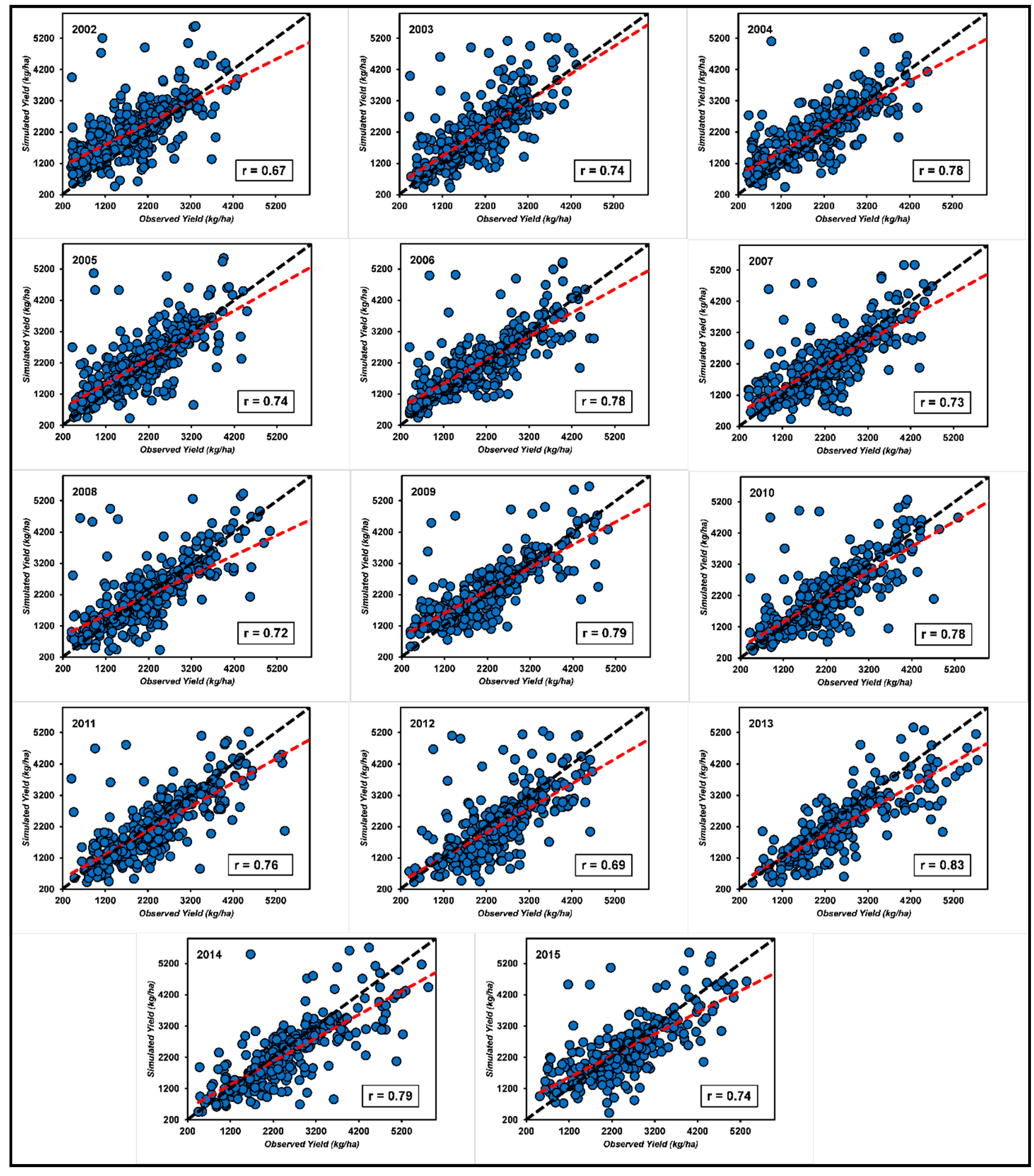
3.2. Long-Term Model Performance Assessment
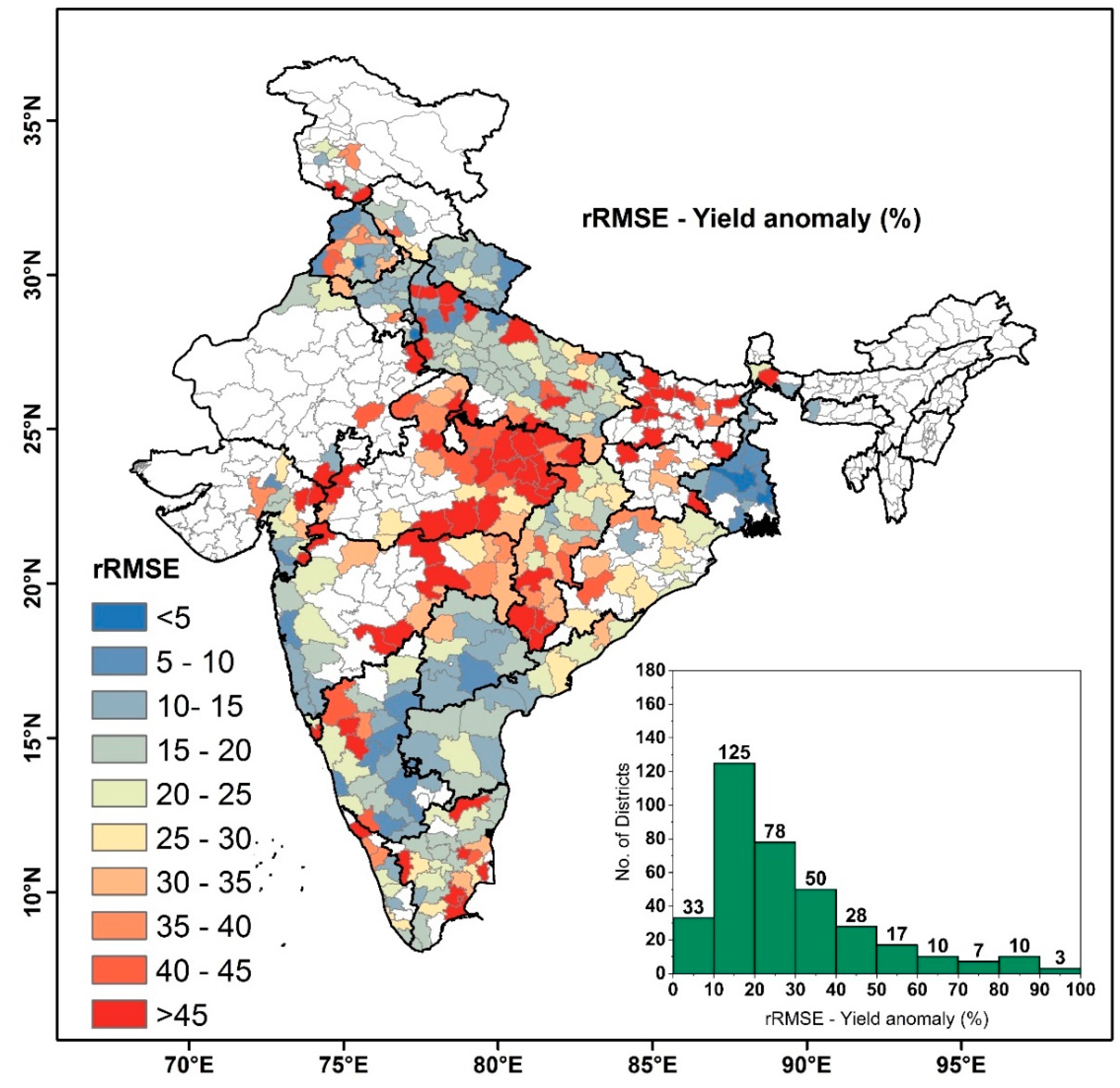
3.3. rRMSE of Yield Anomalies
3.4. Index of Agreement (d) of Yield Anomalies
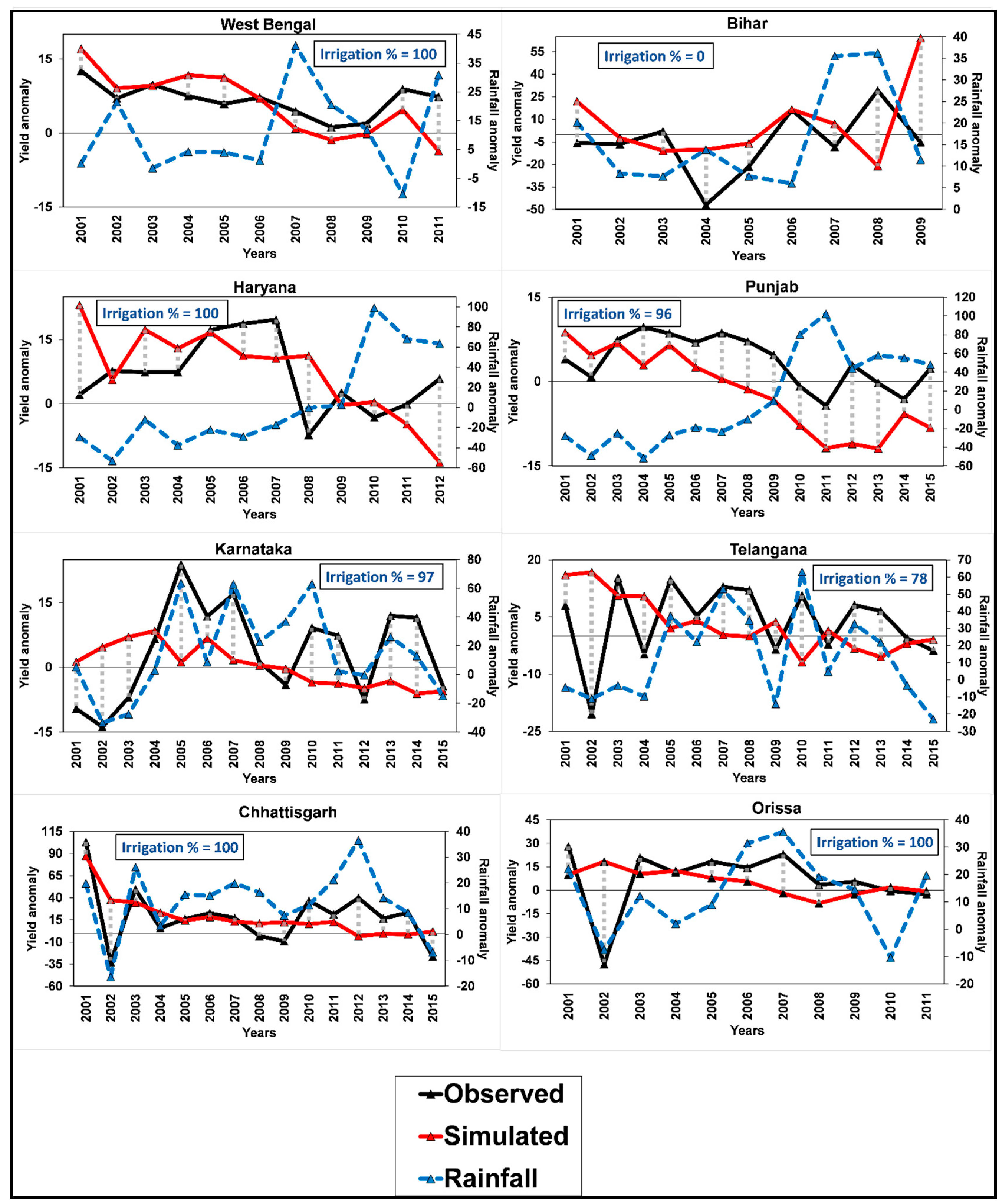
3.5. Effect of Rainfall on Yield Anomalies
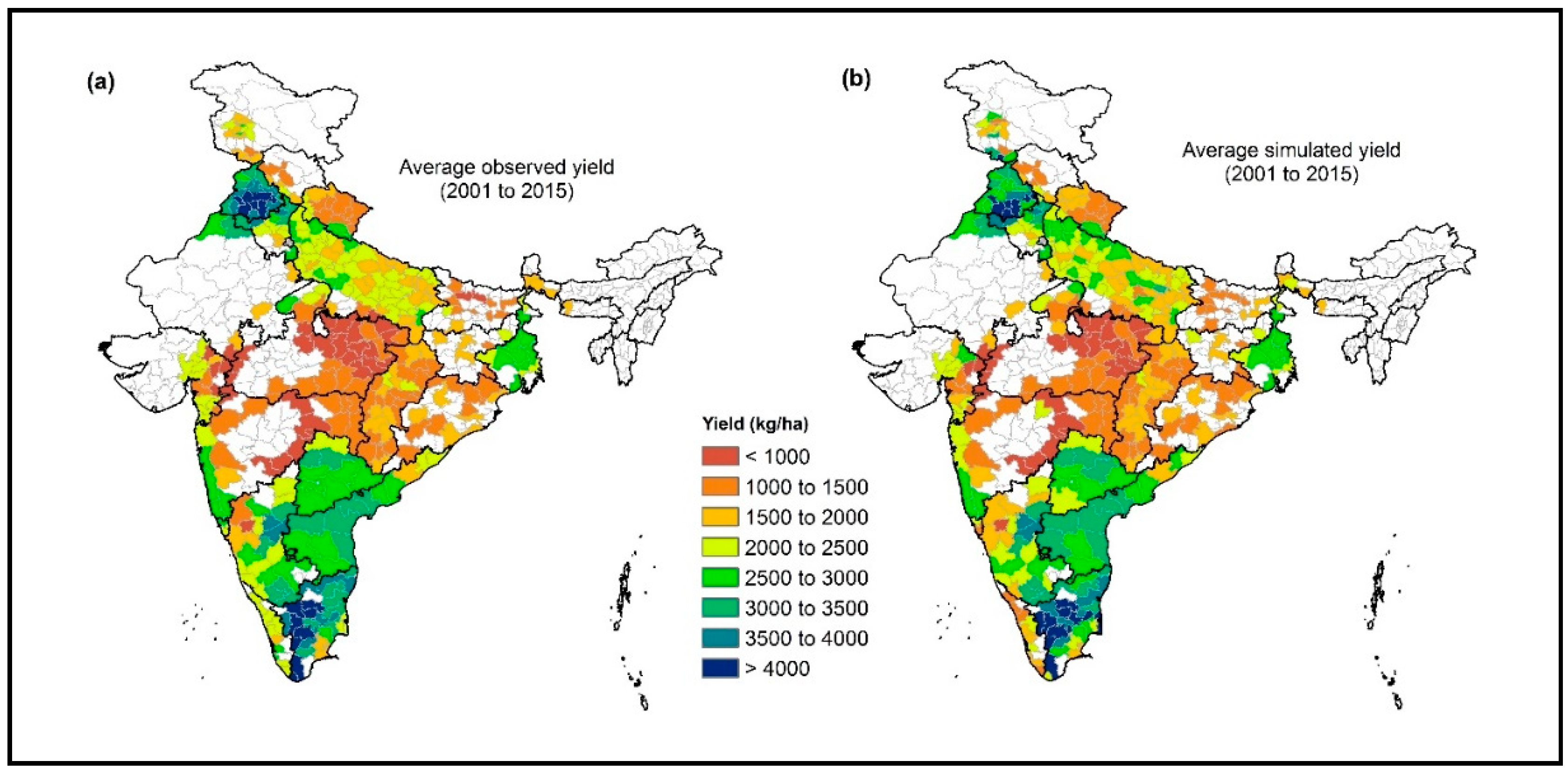
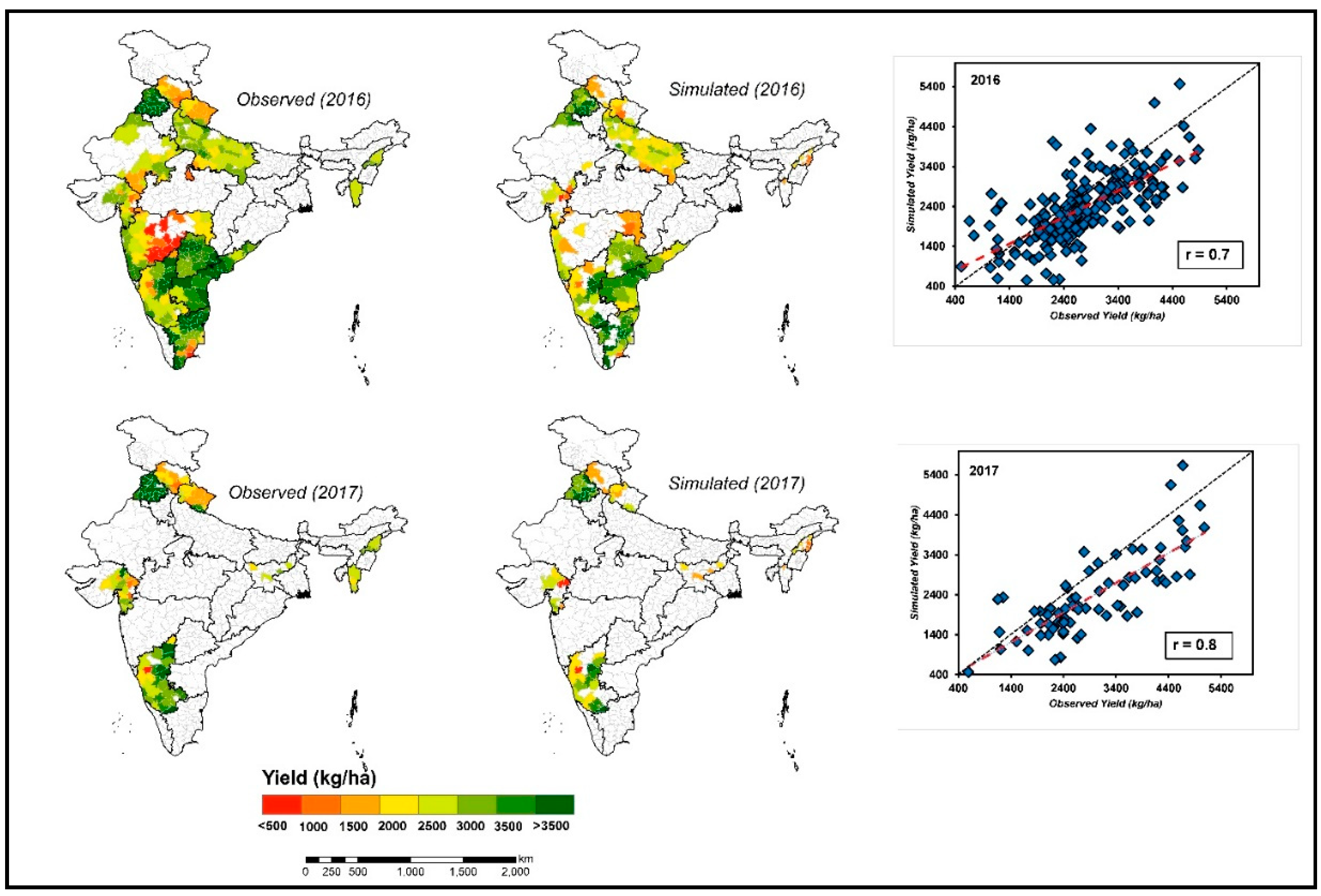
3.6. Model Validation
3.7. Spatial Distribution Performance Evaluation
4. Discussion
4.1. Data Quality
4.2. Model Accuracy
4.3. Time Series Trend Analysis
4.4. Model Applicability for Crop Insurance
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gulati, A.; Terway, P.; Hussain, S. Crop Insurance in India: Key Issues and Way Forward; Working Paper 352; Econstor: Kiel, Germany, 2018. [Google Scholar]
- Rai, R. Pradhan Mantri Fasal Bima Yojana: An Assessment of India’s Crop Insurance Scheme; Centre for Science and Environment: New Delhi, India, 2019; p. 16. [Google Scholar]
- GRiSP. A CGIAR Program on Rice-Based Production Systems; Global Rice Science Partnership (GRiSP): Cotonou, Benin, 2011. [Google Scholar]
- Pradhan Mantri Fasal Bima Yojana (PMFBY). Revised Guidelines; Ministry of Agriculture & Farmers Welfare, Government of India: New Delhi, India, 2017.
- Geethalakshmi, V.; Lakshmanan, A.; Rajalakshmi, D.; Jagannathan, R.; Sridhar, G.; Ramaraj, A.P.; Bhuvaneswari, K.; Gurusamy, L.; Anbhazhagan, R. Climate change impact assessment and adaptation strategies to sustain rice production in Cauvery basin of Tamil Nadu. Curr. Sci. 2011, 101, 6. [Google Scholar]
- Lal, M.; Singh, K.K.; Rathore, L.S.; Srinivasan, G.; Saseendran, S.A. Vulnerability of rice and wheat yields in NW India to future changes in climate. Agric. For. Meteorol. 1998, 89, 101–114. [Google Scholar] [CrossRef]
- Mishra, A.; Singh, R.; Raghuwanshi, N.S.; Chatterjee, C.; Froebrich, J. Spatial variability of climate change impacts on yield of rice and wheat in the Indian Ganga Basin. Sci. Total Environ. 2013, 468–469, S132–S138. [Google Scholar] [CrossRef]
- Priya, S.; Shibasaki, R. National spatial crop yield simulation using GIS-based crop production model. Ecol. Model. 2001, 136, 113–129. [Google Scholar] [CrossRef]
- Sudharsan, D.; Adinarayana, J.; Reddy, D.R.; Sreenivas, G.; Ninomiya, S.; Hirafuji, M.; Kiura, T.; Tanaka, K.; Desai, U.B.; Merchant, S.N. Evaluation of weather-based rice yield models in India. Int. J. Biometeorol. 2013, 57, 107–123. [Google Scholar] [CrossRef]
- Asseng, S.; Martre, P.; Maiorano, A.; Rötter, R.P.; O’Leary, G.J.; Fitzgerald, G.J.; Girousse, C.; Motzo, R.; Giunta, F.; Babar, M.A.; et al. Climate change impact and adaptation for wheat protein. Glob. Chang. Biol. 2019, 25, 155–173. [Google Scholar] [CrossRef]
- Basso, B.; Ritchie, J.T.; Pierce, F.J.; Braga, R.P.; Jones, J.W. Spatial validation of crop models for precision agriculture. Agric. Syst. 2001, 68, 97–112. [Google Scholar] [CrossRef]
- Folberth, C.; Elliott, J.; Müller, C.; Balkovič, J.; Chryssanthacopoulos, J.; Izaurralde, R.C.; Jones, C.D.; Khabarov, N.; Liu, W.; Reddy, A.; et al. Parameterization-induced uncertainties and impacts of crop management harmonization in a global gridded crop model ensemble. PLoS ONE 2019, 14, e0221862. [Google Scholar] [CrossRef]
- Irmak, A.; Jones, J.W.; Batchelor, W.D.; Paz, J.O. Estimating Spatially Variable Soil Properties for Application of Crop Models in Precision Farming. Trans. ASAE 2001, 44. [Google Scholar] [CrossRef]
- Liu, J.; Williams, J.R.; Zehnder, A.J.B.; Yang, H. GEPIC – modelling wheat yield and crop water productivity with high resolution on a global scale. Agric. Syst. 2007, 94, 478–493. [Google Scholar] [CrossRef]
- Rosenzweig, C.; Elliott, J.; Deryng, D.; Ruane, A.C.; Müller, C.; Arneth, A.; Boote, K.J.; Folberth, C.; Glotter, M.; Khabarov, N. Assessing agricultural risks of climate change in the 21st century in a global gridded crop model intercomparison. Proc. Natl. Acad. Sci. USA 2014, 111, 3268–3273. [Google Scholar] [CrossRef]
- Awad, M. Toward Precision in Crop Yield Estimation Using Remote Sensing and Optimization Techniques. Agriculture 2019, 9, 54. [Google Scholar] [CrossRef]
- Shiu, Y.-S.; Chuang, Y.-C. Yield Estimation of Paddy Rice Based on Satellite Imagery: Comparison of Global and Local Regression Models. Remote Sens. 2019, 11, 111. [Google Scholar] [CrossRef]
- Jin, X.; Kumar, L.; Li, Z.; Feng, H.; Xu, X.; Yang, G.; Wang, J. A review of data assimilation of remote sensing and crop models. Eur. J. Agron. 2018, 92, 141–152. [Google Scholar] [CrossRef]
- Son, N.T.; Chen, C.F.; Chen, C.R.; Chang, L.Y.; Chiang, S.H. Rice Yield Estimation Through Assimilating Satellite Data Into A Crop Simumlation Model. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 8, 993–996. [Google Scholar] [CrossRef]
- Wang, D.; Wang, J.; Liang, S. Retrieving crop leaf area index by assimilation of MODIS data into a crop growth model. Sci. China Earth Sci. 2010, 53, 721–730. [Google Scholar] [CrossRef]
- Kamilaris, A.; Kartakoullis, A.; Prenafeta-Boldú, F.X. A review on the practice of big data analysis in agriculture. Comput. Electron. Agric. 2017, 143, 23–37. [Google Scholar] [CrossRef]
- Aggarwal, P.K.; Shirsath, P.; Arumugam, P.; Goroshi, S.; Nagpal, M.; Vyas, S. Monitoring weather deviations and crop conditions for agriculture insurance in India. Csalp South. Asia Q. Newsl. 2018, 1, 11. [Google Scholar]
- Hoogenboom, G.; Porter, C.H.; Shelia, V.; Boote, K.J.; Singh, U.; White, J.W.; Hunt, L.A.; Ogoshi, R.; Lizaso, J.I.; Koo, J. Decision Support System for Agrotechnology Transfer (DSSAT) Version 4.7; DSSAT Foundation: Gainesville, FL, USA, 2017. [Google Scholar]
- Jones, J.W.; Hoogenboom, G.; Porter, C.H.; Boote, K.J.; Batchelor, W.D.; Hunt, L.A.; Wilkens, P.W.; Singh, U.; Gijsman, A.J.; Ritchie, J.T. The DSSAT cropping system model. Eur. J. Agron. 2003, 18, 235–265. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2018. [Google Scholar]
- ESRI. ArcMap 10.7.1; ESRI Inc.: Redlands, CA, USA, 2018. [Google Scholar]
- DES. Directorate of Economics and Statistics, Ministry of Agriculture and Farmers Welfare, Government of India. 2015. Available online: https://aps.dac.gov.in/APY/Index.htm (accessed on 7 October 2019).
- Sudduth, K.A.; Drummond, S.T. Yield Editor: Software for Removing Errors from Crop Yield Maps. Agron. J. 2007, 99, 1471–1482. [Google Scholar] [CrossRef]
- Vega, A.; Córdoba, M.; Castro-Franco, M.; Balzarini, M. Protocol for automating error removal from yield maps. Precis. Agric. 2019, 20, 1030–1044. [Google Scholar] [CrossRef]
- Gumma, M.K. Mapping rice areas of South Asia using MODIS multitemporal data. J. Appl. Remote Sens. 2011, 5, 053547. [Google Scholar] [CrossRef]
- The World Bank Group. Agricultural Land (% of Land Area); Food and Agriculture Organization: Rome, Italy, 2019. [Google Scholar]
- Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Shukla, S.; Husak, G.; Rowland, J.; Harrison, L.; Hoell, A. The climate hazards infrared precipitation with stations—A new environmental record for monitoring extremes. Sci. Data 2015, 2, 150066. [Google Scholar] [CrossRef]
- Srivastava, A.K.; Rajeevan, M.; Kshirsagar, S.R. Development of a high resolution daily gridded temperature data set (1969–2005) for the Indian region. Atmos. Sci. Lett. 2009. [Google Scholar] [CrossRef]
- Mahmood, R.; Hubbard, K.G. Effect of time of temperature observation and estimation of daily solar radiation for the Northern Great Plains, USA. Agron. J. 2002, 94, 723–733. [Google Scholar] [CrossRef]
- Hengl, T.; de Jesus, J.M.; Heuvelink, G.B.; Gonzalez, M.R.; Kilibarda, M.; Blagotić, A.; Shangguan, W.; Wright, M.N.; Geng, X.; Bauer-Marschallinger, B. SoilGrids250m: Global gridded soil information based on machine learning. PLoS ONE 2017, 12, e0169748. [Google Scholar] [CrossRef]
- Hengl, T.; de Jesus, J.M.; MacMillan, R.A.; Batjes, N.H.; Heuvelink, G.B.; Ribeiro, E.; Samuel-Rosa, A.; Kempen, B.; Leenaars, J.G.; Walsh, M.G. SoilGrids1km—Global soil information based on automated mapping. PLoS ONE 2014, 9, e105992. [Google Scholar] [CrossRef]
- International Research Institute for Climate and Society (IRI); Michigan State University (MSU); HarvestChoice/International Food Policy Research Institute (IFPRI). Global High.-Resolution Soil Profile Database for Crop Modeling Applications; International Research Institute for Climate and Society (IRI): New York, NY, USA; Michigan State University: East Lansing, MI, USA; International Food Policy Research Institute (IFPRI): Washington, DC, USA, 2015. [Google Scholar]
- Shangguan, W.; Hengl, T.; de Jesus, J.M.; Yuan, H.; Dai, Y. Mapping the global depth to bedrock for land surface modeling. J. Adv. Model. Earth Syst. 2017, 9, 65–88. [Google Scholar] [CrossRef]
- Han, E.; Ines, A.; Koo, J. Global High-Resolution Soil Profile Database for Crop. Modeling Applications; Working Paper; HarvestChoice/International Food Policy Research Institute: Washington, DC, USA, 2015. [Google Scholar]
- Potter, P.; Ramankutty, N.; Bennett, E.M.; Donner, S.D. Global Fertilizer and Manure, Version 1: Nitrogen Fertilizer Application; NASA Socioeconomic Data and Applications Center (SEDAC): Palisades, NY, USA, 2011. [Google Scholar]
- Lu, G.Y.; Wong, D.W. An adaptive inverse-distance weighting spatial interpolation technique. Comput. Geosci. 2008, 34, 1044–1055. [Google Scholar] [CrossRef]
- Jain, S.; Sastri, A.; Manikandan, N.; Chaudhary, J.L.; Kumar, B. Assessment of yield and yield attributes gap under irrigated and rainfed condition in rice crop for different agroclimatic zones of Chhattisgarh using DSSAT Simulation model. IJCS 2018, 6, 23–28. [Google Scholar]
- Satapathy, S.S.; Swain, D.K.; Herath, S. Field experiments and simulation to evaluate rice cultivar adaptation to elevated carbon dioxide and temperature in sub-tropical India. Eur. J. Agron. 2014, 54, 21–33. [Google Scholar] [CrossRef]
- Singh, K.K.; Baxla, A.K.; Chattopadhyay, N.; Balasubramanian, R.; Singh, P.K.; Rana, M.; Gohain, G.B.; Vishnoi, L.; Singh, P. Crop Yield forecasting under FASAL. In Forecasting Agricultural Output Using SPACE Agrometeorology and Land Based Observations; Indian Meteorological Department: Pune, India, 2017; p. 162. [Google Scholar]
- Lu, J.; Carbone, G.J.; Gao, P. Detrending crop yield data for spatial visualization of drought impacts in the United States, 1895–2014. Agric. For. Meteorol. 2017, 237–238, 196–208. [Google Scholar] [CrossRef]
- Ye, T.; Nie, J.; Wang, J.; Shi, P.; Wang, Z. Performance of detrending models of crop yield risk assessment: Evaluation on real and hypothetical yield data. Stoch. Environ. Res. Risk Assess. 2015, 29, 109–117. [Google Scholar] [CrossRef]
- Parkes, B.; Higginbottom, T.P.; Hufkens, K.; Ceballos, F.; Kramer, B.; Foster, T. Weather dataset choice introduces uncertainty to estimates of crop yield responses to climate variability and change. Environ. Res. Lett. 2019, 14, 124089. [Google Scholar] [CrossRef]
- Gupta, V.; Jain, M.K.; Singh, P.K.; Singh, V. An assessment of global satellite-based precipitation datasets in capturing precipitation extremes: A comparison with observed precipitation dataset in India. Int. J. Climatol. 2019. [Google Scholar] [CrossRef]
- Grassini, P.; van Bussel, L.G.J.; Van Wart, J.; Wolf, J.; Claessens, L.; Yang, H.; Boogaard, H.; de Groot, H.; van Ittersum, M.K.; Cassman, K.G. How good is good enough? Data requirements for reliable crop yield simulations and yield-gap analysis. Field Crop. Res. 2015, 177, 49–63. [Google Scholar] [CrossRef]
- Heuvelink, G.B. Error Propagation in Environmental Modelling with GIS; CRC Press: Boca Raton, FL, USA, 1998; ISBN 0-7484-0744-8. [Google Scholar]
- Roy, A.D.; Shah, T. Socio-ecology of groundwater irrigation in India. In Intensive Use of Groundwater: Challenges and Opportunities; Swets & Zeitlinger B.V.: Lisse, The Netherlands, 2002; pp. 307–335. [Google Scholar]
- TNAU. Tamil Nadu Cropping Season. In Expert System for Paddy; Tamil Nadu Agricultural University: Coimbatore, India, 2009. [Google Scholar]
- Xiao, X.; Boles, S.; Frolking, S.; Li, C.; Babu, J.Y.; Salas, W.; Moore, B., III. Mapping paddy rice agriculture in South and Southeast Asia using multi-temporal MODIS images. Remote Sens. Environ. 2006, 100, 95–113. [Google Scholar] [CrossRef]
- Handral, A.R.; Singh, A.; Singh, D.R.; Suresh, A.; Jha, G.K. Scenario of changing dynamics in production and productivity of major cereals in India. Indian J. Agric. Sci. 2017, 87, 1371–1376. [Google Scholar]
- Naresh Kumar, M.; Murthy, C.S.; Sesha Sai, M.V.R.; Roy, P.S. Spatiotemporal analysis of meteorological drought variability in the Indian region using standardized precipitation index. Meteorol. Appl. 2012, 19, 256–264. [Google Scholar] [CrossRef]
- Cardoen, D.; Joshi, P.; Diels, L.; Sarma, P.M.; Pant, D. Agriculture biomass in India: Part 2. Post-harvest losses, cost and environmental impacts. Resour. Conserv. Recycl. 2015, 101, 143–153. [Google Scholar] [CrossRef]
- Elabed, G.; Bellemare, M.F.; Carter, M.R.; Guirkinger, C. Managing basis risk with multiscale index insurance. Agric. Econ. 2013, 44, 419–431. [Google Scholar] [CrossRef]
- Kumar, A.; Nath, S.; Balpande, R.; Kumar, P.; Mishra, A.; Kumar, V. Decision support system for agro technology (DSSAT) modeling for estimation of rice production and validation. J. Pharmacogn. Phytochem. 2019, 8, 3883–3886. [Google Scholar]
- Chandrasekhar, S.; Sahoo, S. Short-Term Migration in Rural India: The Impact of Nature and Extent of Participation in Agriculture; Indira Gandhi Institute of Development Research: Mumbai, India, 2018. [Google Scholar]
| Input Category | Detailed Inputs |
|---|---|
| Weather (Daily) |
|
| Soil |
|
| Farmer’s practices |
|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arumugam, P.; Chemura, A.; Schauberger, B.; Gornott, C. Near Real-Time Biophysical Rice (Oryza sativa L.) Yield Estimation to Support Crop Insurance Implementation in India. Agronomy 2020, 10, 1674. https://doi.org/10.3390/agronomy10111674
Arumugam P, Chemura A, Schauberger B, Gornott C. Near Real-Time Biophysical Rice (Oryza sativa L.) Yield Estimation to Support Crop Insurance Implementation in India. Agronomy. 2020; 10(11):1674. https://doi.org/10.3390/agronomy10111674
Chicago/Turabian StyleArumugam, Ponraj, Abel Chemura, Bernhard Schauberger, and Christoph Gornott. 2020. "Near Real-Time Biophysical Rice (Oryza sativa L.) Yield Estimation to Support Crop Insurance Implementation in India" Agronomy 10, no. 11: 1674. https://doi.org/10.3390/agronomy10111674
APA StyleArumugam, P., Chemura, A., Schauberger, B., & Gornott, C. (2020). Near Real-Time Biophysical Rice (Oryza sativa L.) Yield Estimation to Support Crop Insurance Implementation in India. Agronomy, 10(11), 1674. https://doi.org/10.3390/agronomy10111674






