Vegetable Crop Biomass Estimation Using Hyperspectral and RGB 3D UAV Data
Abstract
1. Introduction
2. Methods
2.1. Field Experiment
2.2. Biomass Sampling
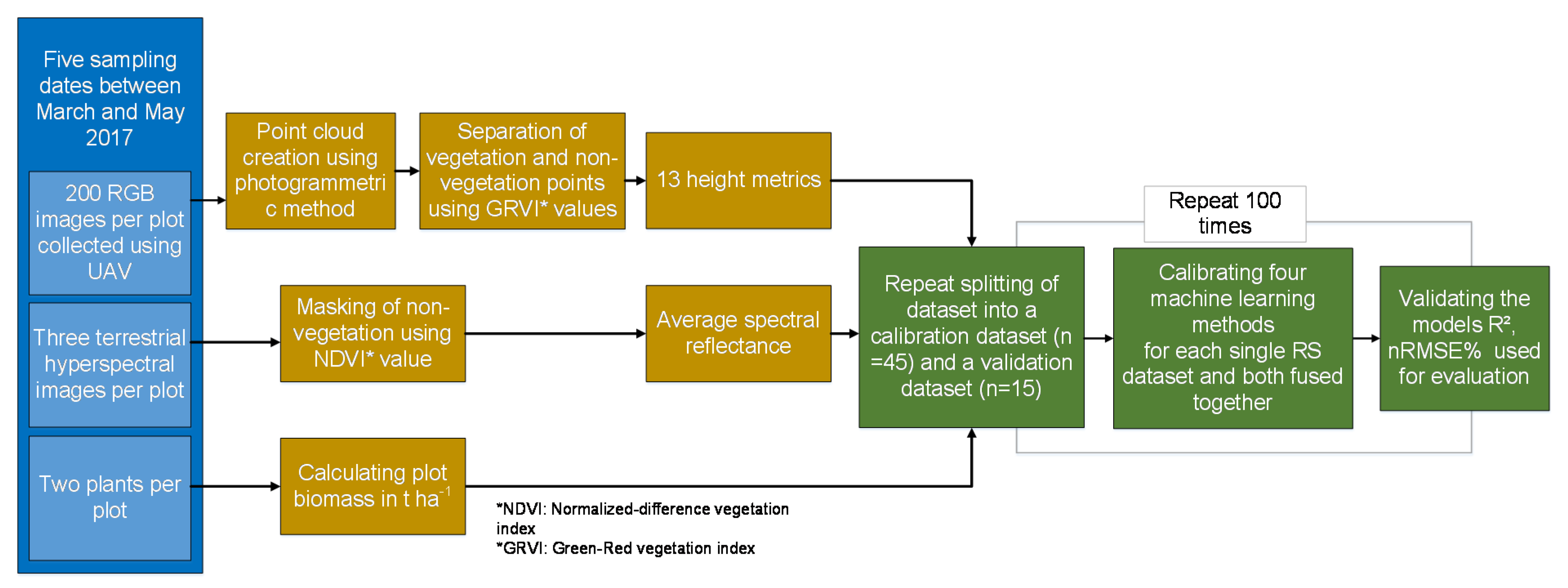
2.3. D UAV Point Cloud Data
2.4. Sampling of Spectral Data
2.5. Statistical Analysis
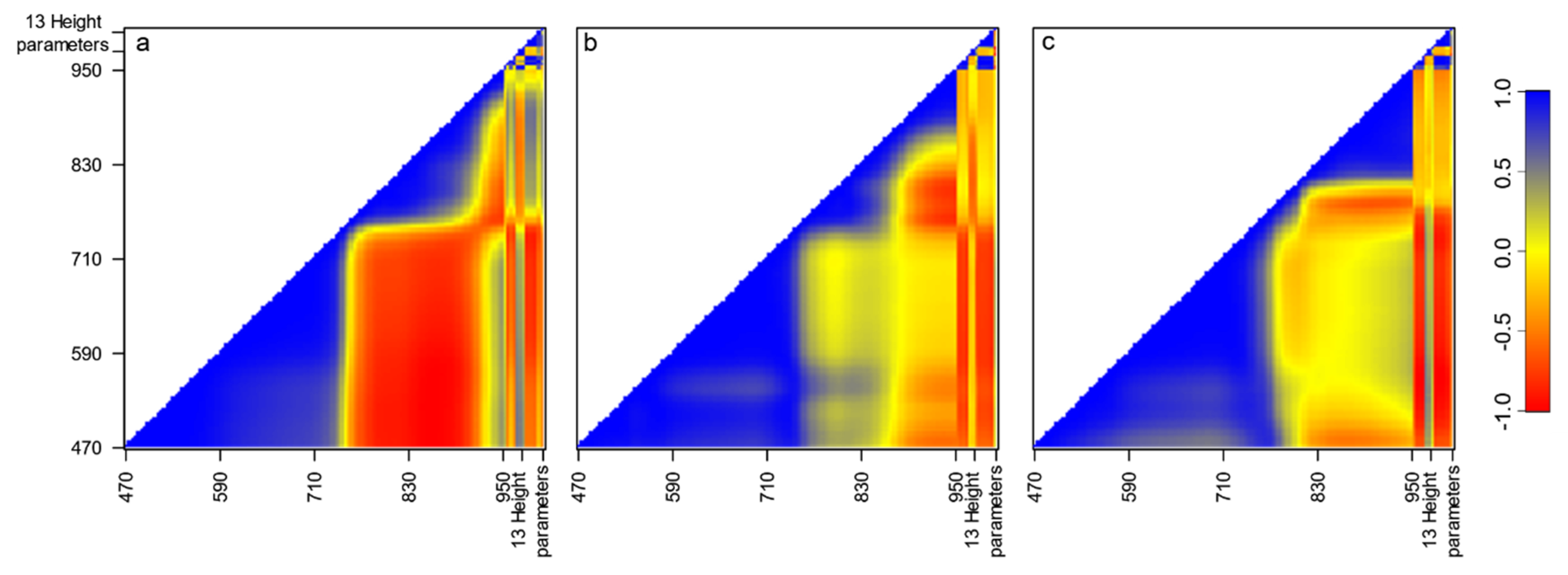
3. Results
4. Discussion
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Rockström, J.; Steffen, W.; Noone, K.; Persson, Å.; Chapin, F.S., III; Lambin, E.F.; Lenton, T.M.; Scheffer, M.; Folke, C.; Schellnhuber, H.J.; et al. A safe operating space for humanity. Nature 2009, 461, 472–475. [Google Scholar] [CrossRef] [PubMed]
- UN. World Population Prospects: The 2017 Revision, Key Findings and Advance Tables; Working Paper No. ESA/P/WP/248; UN: New York, NY, USA, 2017. [Google Scholar]
- Tilman, D.; Balzer, C.; Hill, J.; Befort, B.L. Global food demand and the sustainable intensification of agriculture. Proc. Natl. Acad. Sci. USA 2011, 108, 20260–20264. [Google Scholar] [CrossRef]
- Pettorelli, N.; Vik, J.O.; Mysterud, A.; Gaillard, J.-M.; Tucker, C.J.; Stenseth, N.C. Using the satellite-derived NDVI to assess ecological responses to environmental change. Trends Ecol. Evol. 2005, 20, 503–510. [Google Scholar] [CrossRef] [PubMed]
- Tucker, C.J. Red and photographic infrared linear combinations for monitoring vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar] [CrossRef]
- Atzberger, C. Advances in Remote Sensing of agriculture: Context description, existing operational monitoring systems and major information needs. Remote Sens. 2013, 5, 949–981. [Google Scholar] [CrossRef]
- Duncan, J.M.A.; Dash, J.; Atkinson, P.M. The potential of satellite-observed crop phenology to enhance yield gap assessments in smallholder landscapes. Front. Environ. Sci. 2015, 3, 132. [Google Scholar] [CrossRef]
- Hannerz, F.; Lotsch, A. Assessment of remotely sensed and statistical inventories of African agricultural fields. Int. J. Remote Sens. 2008, 29, 3787–3804. [Google Scholar] [CrossRef]
- Mondal, S.; Jeganathan, C.; Sinha, N.K.; Rajan, H.; Roy, T.; Kumar, P. Extracting seasonal cropping patterns using multi-temporal vegetation indices from IRS LISS-III data in Muzaffarpur District of Bihar, India. Egypt. J. Remote Sens. Space Sci. 2014, 17, 123–134. [Google Scholar] [CrossRef]
- Thompson, R.B.; Voogt, W.; Incrocci, L.; Fink, M.; de Neve, S. Strategies for optimal fertiliser management of vegetable crops in Europe. Acta Hortic. 2018, 1192, 129–140. [Google Scholar] [CrossRef]
- Padilla, F.M.; Gallardo, M.; Peña-Fleitas, M.T.; de Souza, R.; Thompson, R.B. Proximal optical sensors for nitrogen management of vegetable crops: A review. Sensors (Basel) 2018, 18, 2083. [Google Scholar] [CrossRef]
- Trout, T.J.; Johnson, L.F.; Gartung, J. Remote Sensing of Canopy Cover in Horticultural Crops. HortScience 2008, 43, 333–337. [Google Scholar] [CrossRef]
- Zude-Sasse, M.; Fountas, S.; Gemtos, T.A.; Abu-Khalaf, N. Applications of precision agriculture in horticultural crops. Eur. J. Hortic. Sci. 2016, 81, 78–90. [Google Scholar] [CrossRef]
- Nidamanuri, R.R.; Zbell, B. Transferring spectral libraries of canopy reflectance for crop classification using hyperspectral Remote Sensing data. Biosyst. Eng. 2011, 110, 231–246. [Google Scholar] [CrossRef]
- Moeckel, T.; Dayananda, S.; Nidamanuri, R.R.; Nautiyal, S.; Hanumaiah, N.; Buerkert, A.; Wachendorf, M. Estimation of vegetable crop parameter by multi-temporal UAV-borne images. Remote Sens. 2018, 10, 805. [Google Scholar] [CrossRef]
- Panigrahy, S.; Sharma, S.A. Mapping of crop rotation using multidate Indian Remote Sensing satellite digital data. ISPRS J. Photogramm. Remote Sens. 1997, 52, 85–91. [Google Scholar] [CrossRef]
- Hoffmeister, D.; Bolten, A.; Curdt, C.; Waldhoff, G.; Bareth, G. (Eds.) High-Resolution Crop Surface Models (CSM) and Crop Volume Models (CVM) on Field Level by Terrestrial Laser Scanning; International Society for Optics and Photonics: Bellingham, WA, USA, 2010. [Google Scholar]
- Schirrmann, M.; Hamdorf, A.; Giebel, A.; Gleiniger, F.; Pflanz, M.; Dammer, K.-H. Regression Kriging for Improving Crop Height Models Fusing Ultra-Sonic Sensing with UAV Imagery. Remote Sens. 2017, 9, 665. [Google Scholar] [CrossRef]
- Zhang, C.; Kovacs, J.M. The application of small unmanned aerial systems for precision agriculture: A review. Precis. Agric. 2012, 13, 693–712. [Google Scholar] [CrossRef]
- Maimaitijiang, M.; Ghulam, A.; Sidike, P.; Hartling, S.; Maimaitiyiming, M.; Peterson, K.; Shavers, E.; Fishman, J.; Peterson, J.; Kadam, S.; et al. Unmanned Aerial System (UAS)-based phenotyping of soybean using multi-sensor data fusion and extreme learning machine. ISPRS J. Photogram. Remote Sens. 2017, 134, 43–58. [Google Scholar] [CrossRef]
- Aasen, H.; Bolten, A. Multi-temporal high-resolution imaging spectroscopy with hyperspectral 2D imagers—From theory to application. Remote Sens. Environ. 2018, 205, 374–389. [Google Scholar] [CrossRef]
- Pohl, C.; van Genderen, J.L. Review article multisensor image fusion in Remote Sensing: Concepts, methods and applications. Int. J. Remote Sens. 1998, 19, 823–854. [Google Scholar] [CrossRef]
- Rischbeck, P.; Elsayed, S.; Mistele, B.; Barmeier, G.; Heil, K.; Schmidhalter, U. Data fusion of spectral, thermal and canopy height parameters for improved yield prediction of drought stressed spring barley. Eur. J. Agron. 2016, 78, 44–59. [Google Scholar] [CrossRef]
- Gao, S.; Niu, Z.; Huang, N.; Hou, X. Estimating the Leaf Area Index, height and biomass of maize using HJ-1 and RADARSAT-2. Int. J. Appl. Earth Obs. Geoinf. 2013, 24, 1–8. [Google Scholar] [CrossRef]
- Yue, J.; Feng, H.; Yang, G.; Li, Z. A comparison of regression techniques for estimation of above-ground winter wheat biomass using near-surface spectroscopy. Remote Sens. 2018, 10, 66. [Google Scholar] [CrossRef]
- Wu, C.; Shen, H.; Shen, A.; Deng, J.; Gan, M.; Zhu, J.; Xu, H.; Wang, K. Comparison of machine-learning methods for above-ground biomass estimation based on Landsat imagery. J. Appl. Remote Sens. 2016, 10, 35010. [Google Scholar] [CrossRef]
- Wold, S.; Sjöström, M.; Eriksson, L. Partial least squares projections to latent structures (PLS) in chemistry. In Encyclopedia of Computational Chemistry; Ragu Schleyer, P., von Allinger, N.L., Clark, T., Gasteiger, J., Kollman, P.A., Schaefer, H.F., Schreiner, P.R., Eds.; Wiley-Interscience: Hoboken, NJ, USA, 2008; p. 523. ISBN 0470845015. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Prasad, J.V.N.S.; Rao, C.S.; Srinivas, K.; Jyothi, C.N.; Venkateswarlu, B.; Ramachandrappa, B.K.; Dhanapal, G.N.; Ravichandra, K.; Mishra, P.K. Effect of ten years of reduced tillage and recycling of organic matter on crop yields, soil organic carbon and its fractions in Alfisols of semi arid tropics of southern India. Soil Tillage Res. 2016, 156, 131–139. [Google Scholar] [CrossRef]
- Harwin, S.; Lucieer, A.; Osborn, J. The impact of the calibration method on the accuracy of point clouds derived using unmanned aerial vehicle multi-view stereopsis. Remote Sens. 2015, 7, 11933–11953. [Google Scholar] [CrossRef]
- Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vision 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Snavely, N.; Seitz, S.M.; Szeliski, R. Modeling the world from internet photo collections. Int. J. Comput. Vision 2008, 80, 189–210. [Google Scholar] [CrossRef]
- Mesas-Carrascosa, F.-J.; Torres-Sánchez, J.; Clavero-Rumbao, I.; García-Ferrer, A.; Peña, J.-M.; Borra-Serrano, I.; López-Granados, F. Assessing optimal flight parameters for generating accurate multispectral orthomosaicks by uav to support site-specific crop management. Remote Sens. 2015, 7, 12793–12814. [Google Scholar] [CrossRef]
- Westoby, M.J.; Brasington, J.; Glasser, N.F.; Hambrey, M.J.; Reynolds, J.M. ‘Structure-from-Motion’ photogrammetry: A low-cost, effective tool for geoscience applications. Geomorphology 2012, 179, 300–314. [Google Scholar] [CrossRef]
- Silva, C.A.; Hudak, A.T.; Klauberg, C.; Vierling, L.A.; Gonzalez-Benecke, C.; de Carvalho, S.P.C.; Rodriguez, L.C.E.; Cardil, A. Combined effect of pulse density and grid cell size on predicting and mapping aboveground carbon in fast-growing Eucalyptus forest plantation using airborne LiDAR data. Carbon Balance Manag. 2017, 12, 13. [Google Scholar] [CrossRef] [PubMed]
- Næsset, E.; Økland, T. Estimating tree height and tree crown properties using airborne scanning laser in a boreal nature reserve. Remote Sens. Environ. 2002, 79, 105–115. [Google Scholar] [CrossRef]
- Roussel, J.-R.; Auty, D. lidR: Airborne LiDAR data manipulation and visualization for forestry applications. R Package Version 2018, 1, 1. Available online: https://CRAN.R-project.org/package=lidR (accessed on 10 October 2020).
- R Core Team. R: A Language and Environment for Statistical Computing; R Core Team: Vienna, Austria, 2018; Available online: https://www.R-project.org/ (accessed on 10 October 2020).
- Cao, F.; Yang, Z.; Ren, J.; Jiang, M.; Ling, W.-K. Does Normalization Methods Play a Role for Hyperspectral Image Classification? arXiv 2017, arXiv:1710.02939. [Google Scholar]
- Mosin, V.; Aguilar, R.; Platonov, A.; Vasiliev, A.; Kedrov, A.; Ivanov, A. Remote Sensing and machine learning for tree detection and classification in forestry applications. In Proceedings of the Image and Signal Processing for Remote Sensing XXV, Strasbourg, France, 9–12 September 2019; Bruzzone, L., Bovolo, F., Benediktsson, J.A., Eds.; SPIE: Bellingham, WA, USA, 2019; p. 14, ISBN 9781510630130. [Google Scholar]
- Rouse, J.W., Jr.; Haas, R.H.; Schell, J.A.; Deering, D.W. Monitoring vegetation systems in the Great Plains with ERTS. NASA Spec. Publ. 1974, 351, 309. [Google Scholar]
- Holloway, J.; Mengersen, K. Statistical machine learning methods and Remote Sensing for sustainable development goals: A Review. Remote Sens. 2018, 10, 1365. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Karatzoglou, A.; Meyer, D.; Hornik, K. Support vector machines in R. J. Stat. Softw. 2006, 15, 1–28. [Google Scholar] [CrossRef]
- Probst, P.; Boulesteix, A.-L. To Tune or Not to Tune the Number of Trees in Random Forest. J. Mach. Learn. Res. 2018, 18, 1–18. [Google Scholar]
- Caruana, R.; Niculescu-Mizil, A. An empirical comparison of supervised learning algorithms using different performance metrics. In Proceedings of the 23rd International Conference on Machine Learning, Pittsburgh, WA, USA, 25–29 June 2006; pp. 161–168. [Google Scholar]
- Madec, S.; Baret, F.; de Solan, B.; Thomas, S.; Dutartre, D.; Jezequel, S.; Hemmerlé, M.; Colombeau, G.; Comar, A. High-throughput phenotyping of plant height: Comparing unmanned aerial vehicles and ground LiDAR estimates. Front. Plant Sci. 2017, 8, 2002. [Google Scholar] [CrossRef]
- Li, W.; Niu, Z.; Chen, H.; Li, D.; Wu, M.; Zhao, W. Remote estimation of canopy height and aboveground biomass of maize using high-resolution stereo images from a low-cost unmanned aerial vehicle system. Ecol. Indic. 2016, 67, 637–648. [Google Scholar] [CrossRef]
- Bendig, J.; Yu, K.; Aasen, H.; Bolten, A.; Bennertz, S.; Broscheit, J.; Gnyp, M.L.; Bareth, G. Combining UAV-based plant height from crop surface models, visible, and near infrared vegetation indices for biomass monitoring in barley. Int. J. Appl. Earth Observ. Geoinf. 2015, 39, 79–87. [Google Scholar] [CrossRef]
- Nasi, R.; Viljanen, N.; Kaivosoja, J.; Alhonoja, K.; Hakala, T.; Markelin, L.; Honkavaara, E. Estimating biomass and nitrogen amount of barley and grass using UAV and aircraft based spectral and photogrammetric 3D features. Remote Sens. 2018, 10, 1082. [Google Scholar] [CrossRef]
- Powell, S.L.; Cohen, W.B.; Healey, S.P.; Kennedy, R.E.; Moisen, G.G.; Pierce, K.B.; Ohmann, J.L. Quantification of live aboveground forest biomass dynamics with Landsat time-series and field inventory data: A comparison of empirical modeling approaches. Remote Sens. Environ. 2010, 114, 1053–1068. [Google Scholar] [CrossRef]
- Belgiu, M.; Drăguţ, L. Random forest in Remote Sensing: A review of applications and future directions. ISPRS J. Photogram. Remote Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]
- Flach, P. Machine learning. The Art and Science of Algorithms that Make Sense of Data; Cambridge University Press: Cambridge, UK, 2012; ISBN 9781107422223. [Google Scholar]
- Malambo, L.; Popescu, S.C.; Murray, S.C.; Putman, E.; Pugh, N.A.; Horne, D.W.; Richardson, G.; Sheridan, R.; Rooney, W.L.; Avant, R.; et al. Multitemporal field-based plant height estimation using 3D point clouds generated from small unmanned aerial systems high-resolution imagery. Int. J. Appl. Earth Observ. Geoinf. 2018, 64, 31–42. [Google Scholar] [CrossRef]
- Schulz, V.S.; Munz, S.; Stolzenburg, K.; Hartung, J.; Weisenburger, S.; Graeff-Hönninger, S. Impact of Different Shading Levels on Growth, Yield and Quality of Potato (Solanum tuberosum L.). Agronomy 2019, 9, 330. [Google Scholar] [CrossRef]
- Çakir, R. Effect of water stress at different development stages on vegetative and reproductive growth of corn. Field Crops Res. 2004, 89, 1–16. [Google Scholar] [CrossRef]
- Kaur, S.; Aulakh, J.; Jhala, A.J. Growth and seed production of glyphosate-resistant giant ragweed (Ambrosia trifida L.) in response to water stress. cjps 2016, 96, 828–836. [Google Scholar] [CrossRef]
- Paradiso, R.; Arena, C.; de Micco, V.; Giordano, M.; Aronne, G.; de Pascale, S. Changes in Leaf Anatomical Traits Enhanced Photosynthetic Activity of Soybean Grown in Hydroponics with Plant Growth-Promoting Microorganisms. Front. Plant Sci. 2017, 8, 674. [Google Scholar] [CrossRef]
- Viña, A.; Gitelson, A.A.; Rundquist, D.C.; Keydan, G.; Leavitt, B.; Schepers, J. Monitoring Maize (L.) Phenology with Remote Sensing. Agron. J. 2004, 96, 1139. [Google Scholar] [CrossRef]
- Kurunç, A.; Ünlükara, A. Growth, yield, and water use of okra (Abelmoschus esculentus ) and eggplant (Solanum melongena ) as influenced by rooting volume. New Zeal. J. Crop Hort. Sci. 2009, 37, 201–210. [Google Scholar] [CrossRef]
- Rasooli Sharabian, V.; Noguchi, N.; Ishi, K. Optimal vegetation indices for winter wheat growth status based on multi-spectral reflectance. Environ. Control. Biol. 2013, 51, 105–112. [Google Scholar] [CrossRef]
- Knipling, E.B. Physical and physiological basis for the reflectance of visible and near-infrared radiation from vegetation. Remote Sens. Environ. 1970, 1, 155–159. [Google Scholar] [CrossRef]
- Viña, A.; Gitelson, A.A.; Nguy-Robertson, A.L.; Peng, Y. Comparison of different vegetation indices for the remote assessment of green leaf area index of crops. Remote Sens. Environ. 2011, 115, 3468–3478. [Google Scholar] [CrossRef]
- Wang, C.; Nie, S.; Xi, X.; Luo, S.; Sun, X. Estimating the biomass of maize with hyperspectral and LiDAR data. Remote Sens. 2017, 9, 11. [Google Scholar] [CrossRef]
- Prošek, J.; Šímová, P. UAV for mapping shrubland vegetation: Does fusion of spectral and vertical information derived from a single sensor increase the classification accuracy? Int. J. Appl. Earth Observ. Geoinf. 2019, 75, 151–162. [Google Scholar] [CrossRef]
- Tilly, N.; Hoffmeister, D.; Cao, Q.; Huang, S.; Lenz-Wiedemann, V.; Miao, Y.; Bareth, G. Multitemporal crop surface models: Accurate plant height measurement and biomass estimation with terrestrial laser scanning in paddy rice. J. Appl. Remote Sens. 2014, 8, 083671. [Google Scholar] [CrossRef]




| p-Values | |||
|---|---|---|---|
| Sampling Date (SD) | N Fertilizer (NF) | SD × NF | |
| Eggplant | *** | 0.805 | 0.670 |
| Tomato | *** | 0.177 | 0.575 |
| Cabbage | *** | 0.594 | 0.972 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Astor, T.; Dayananda, S.; Nautiyal, S.; Wachendorf, M. Vegetable Crop Biomass Estimation Using Hyperspectral and RGB 3D UAV Data. Agronomy 2020, 10, 1600. https://doi.org/10.3390/agronomy10101600
Astor T, Dayananda S, Nautiyal S, Wachendorf M. Vegetable Crop Biomass Estimation Using Hyperspectral and RGB 3D UAV Data. Agronomy. 2020; 10(10):1600. https://doi.org/10.3390/agronomy10101600
Chicago/Turabian StyleAstor, Thomas, Supriya Dayananda, Sunil Nautiyal, and Michael Wachendorf. 2020. "Vegetable Crop Biomass Estimation Using Hyperspectral and RGB 3D UAV Data" Agronomy 10, no. 10: 1600. https://doi.org/10.3390/agronomy10101600
APA StyleAstor, T., Dayananda, S., Nautiyal, S., & Wachendorf, M. (2020). Vegetable Crop Biomass Estimation Using Hyperspectral and RGB 3D UAV Data. Agronomy, 10(10), 1600. https://doi.org/10.3390/agronomy10101600






