The Semiflexible Polymer Translocation into Laterally Unbounded Region between Two Parallel Flat Membranes
Abstract
:1. Introduction
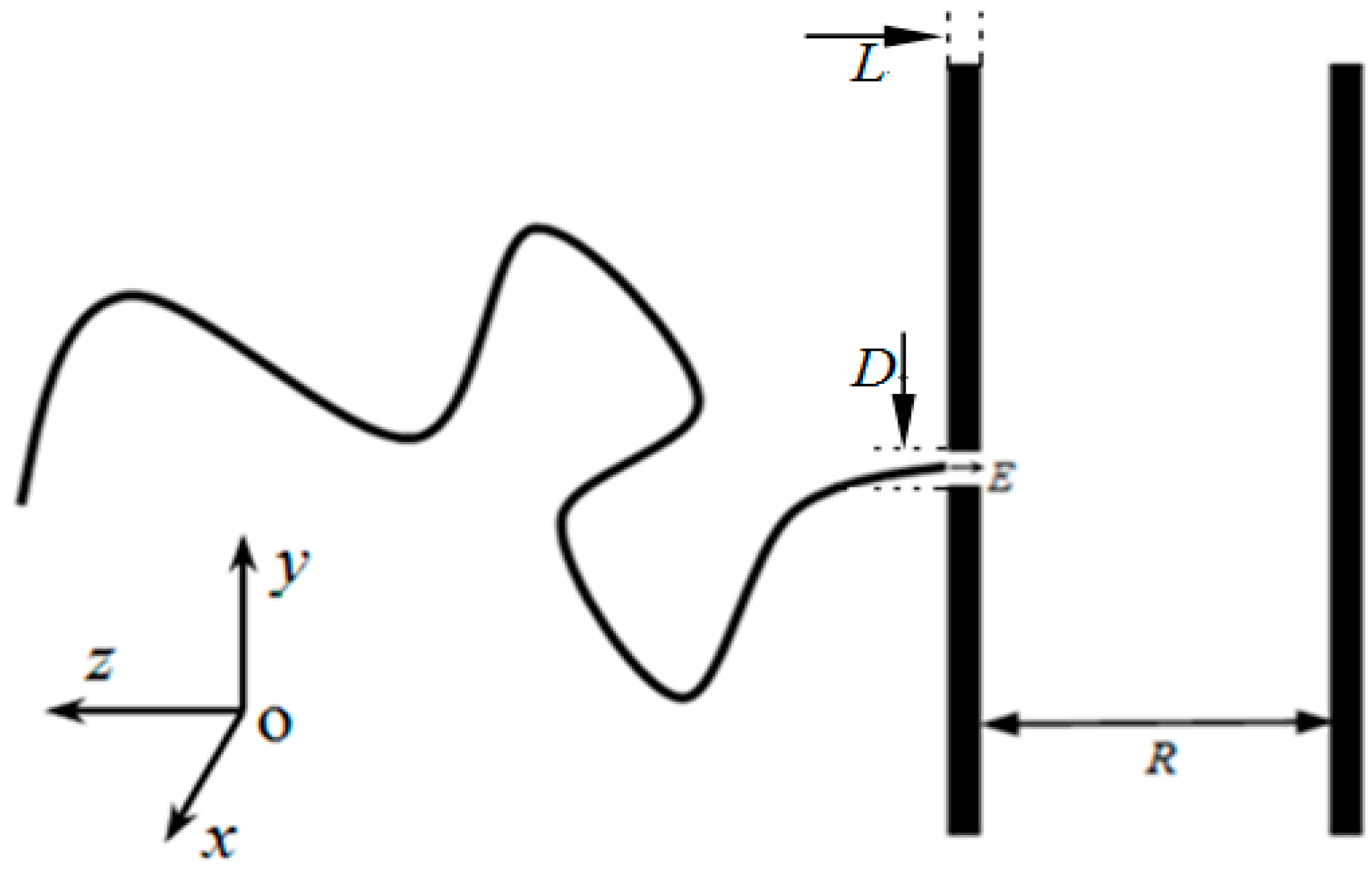
2. Model and Methods
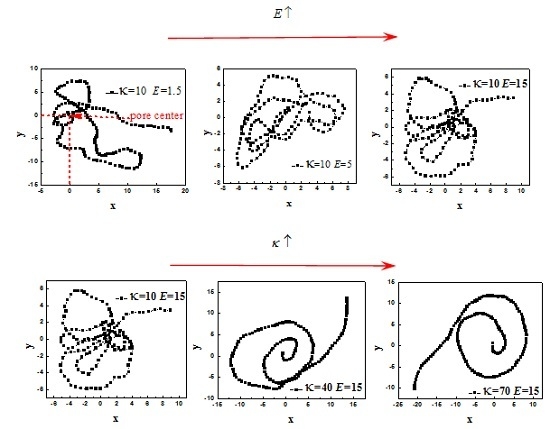
3. Results and Discussion
3.1. Effect of R on the Average Translocation Time
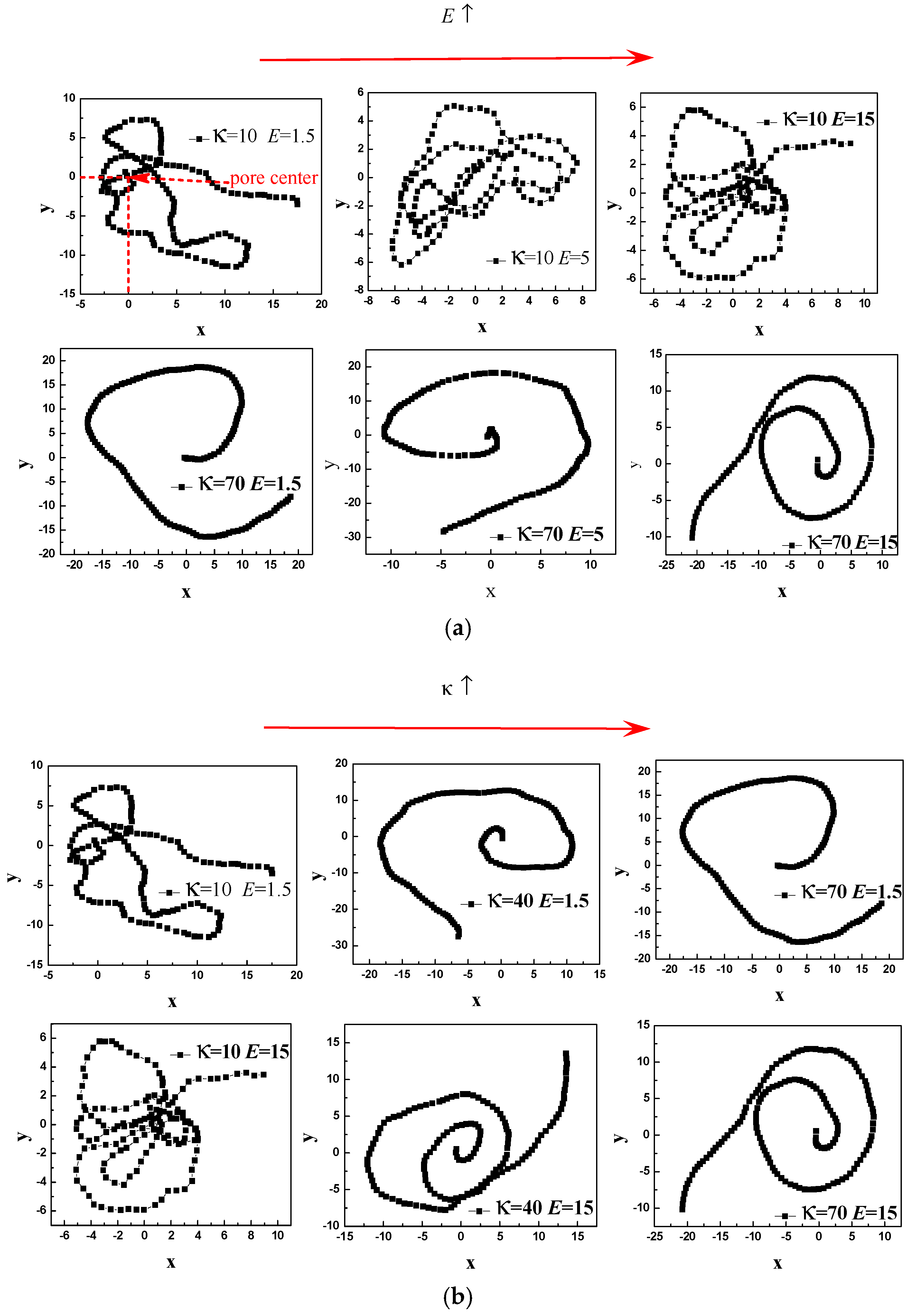
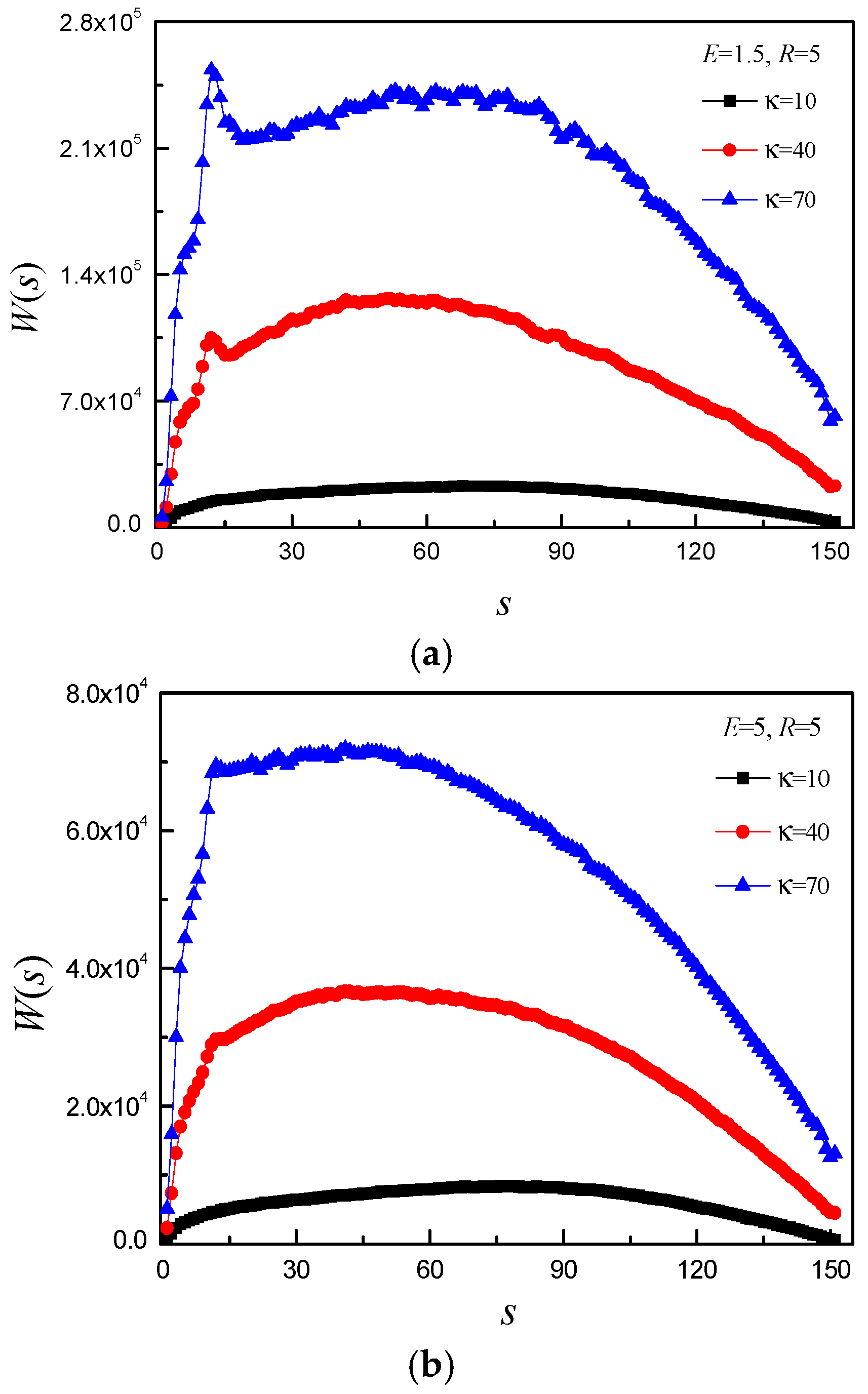
3.2. Effect of E and b on Average Translocation Time
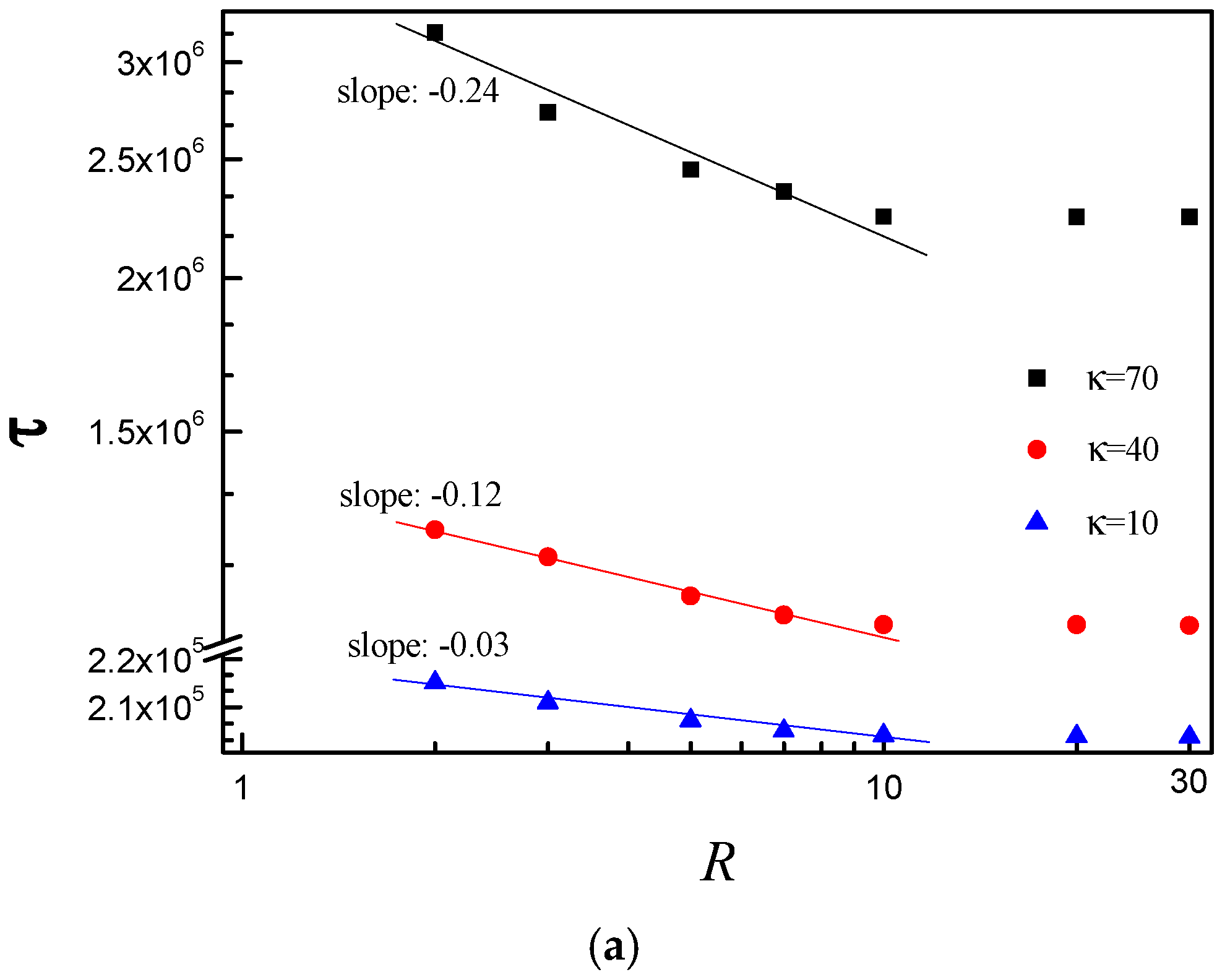
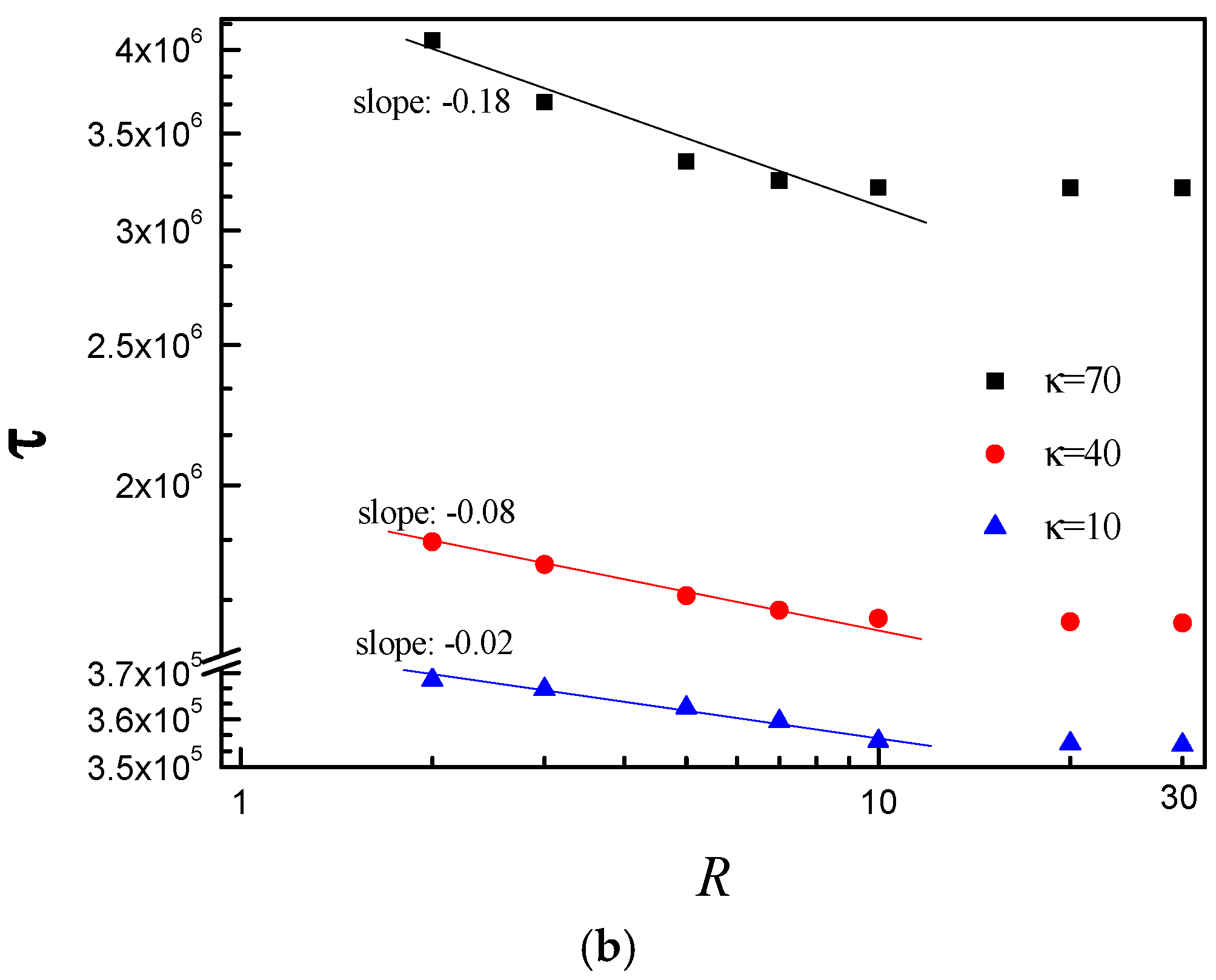
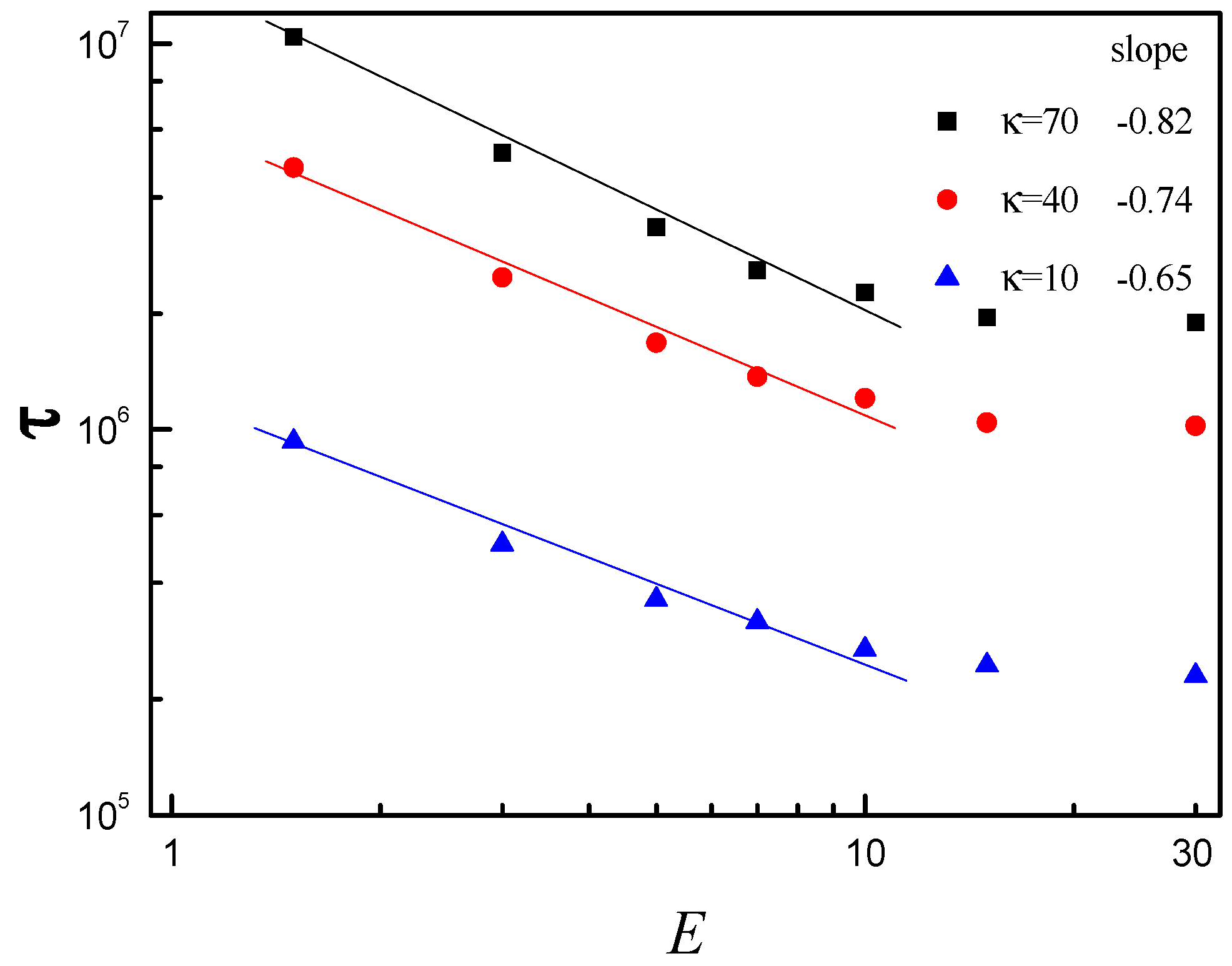
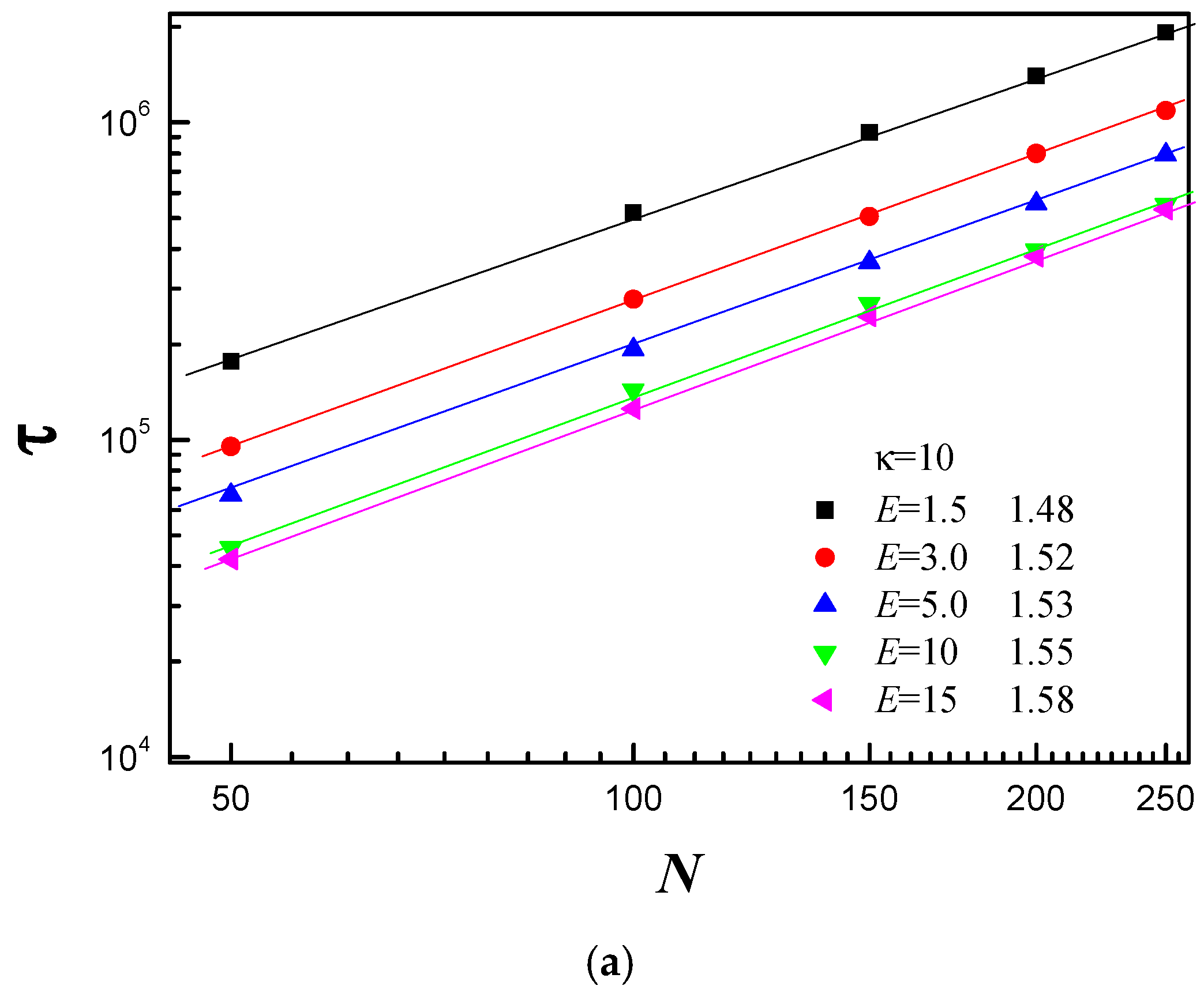
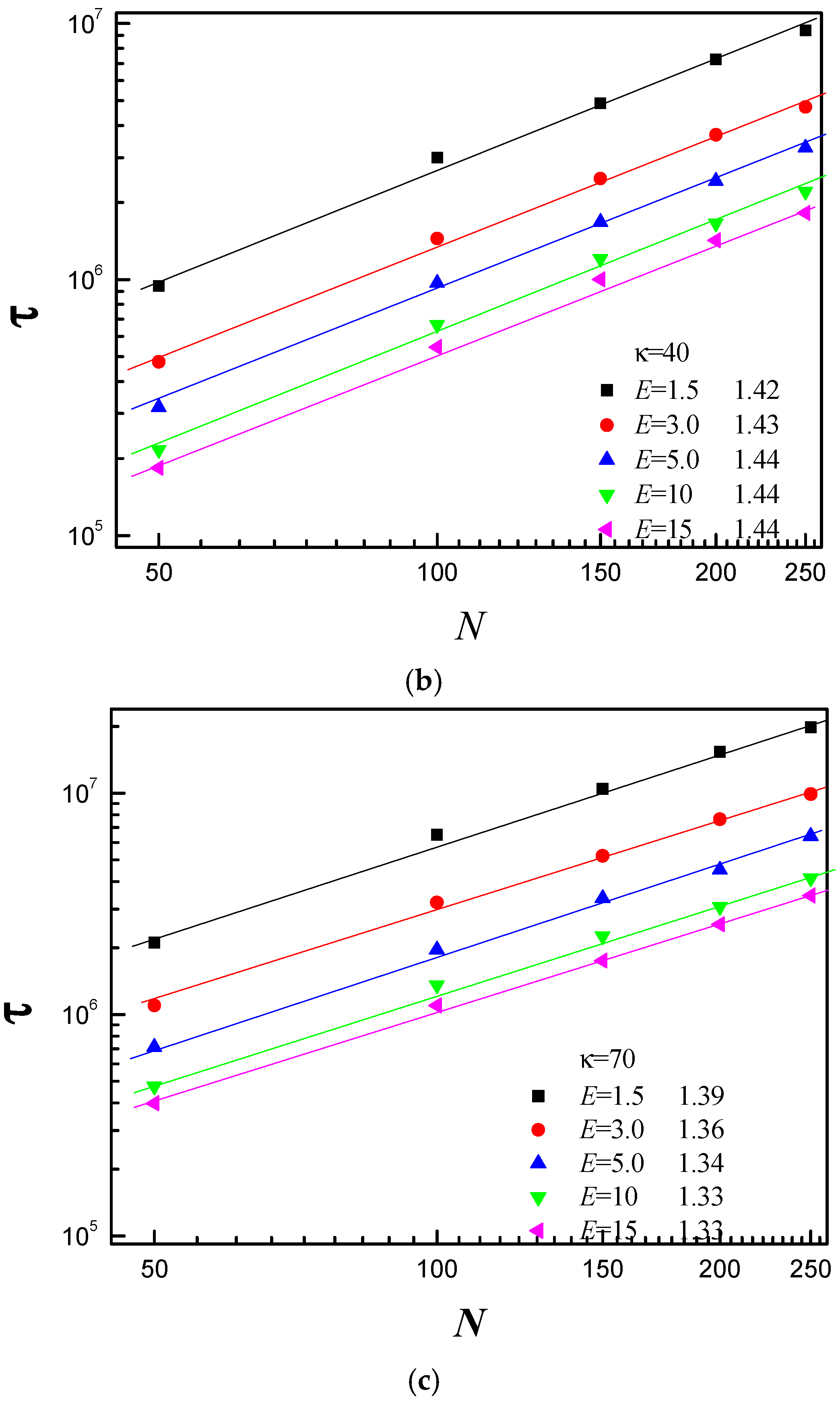
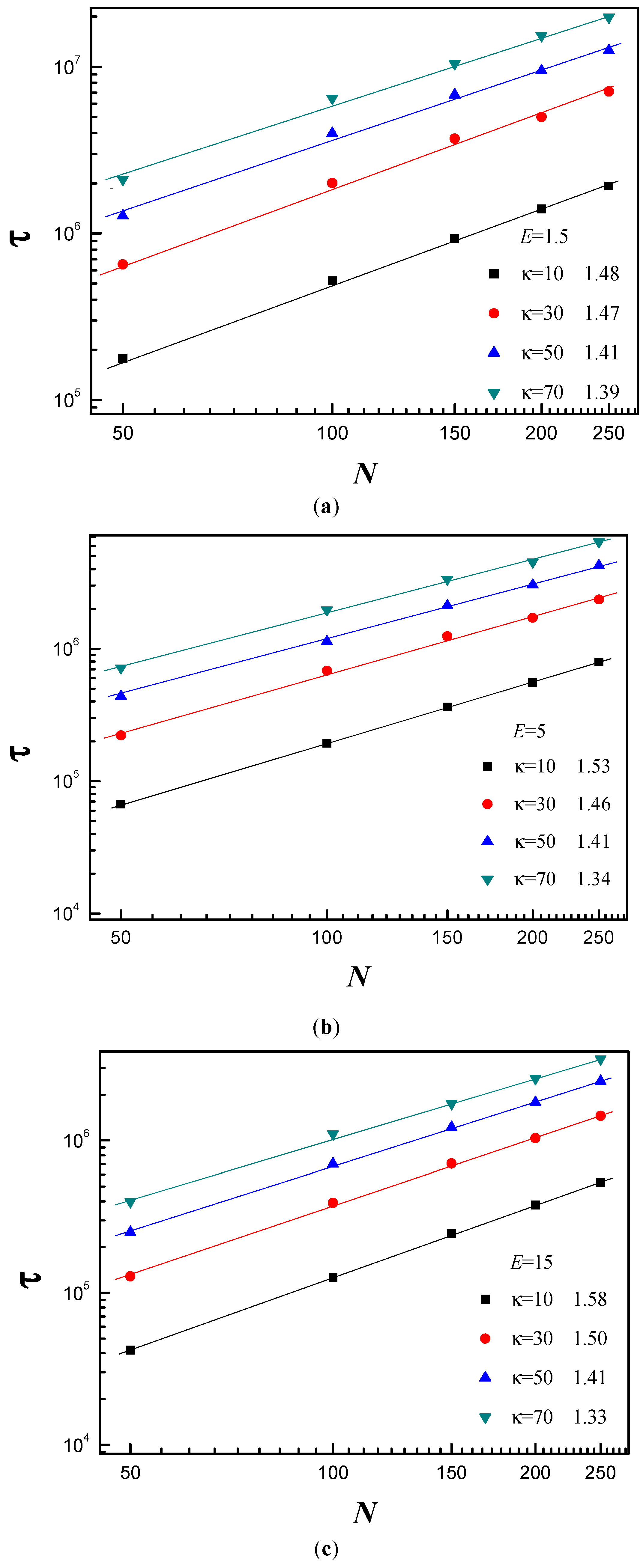
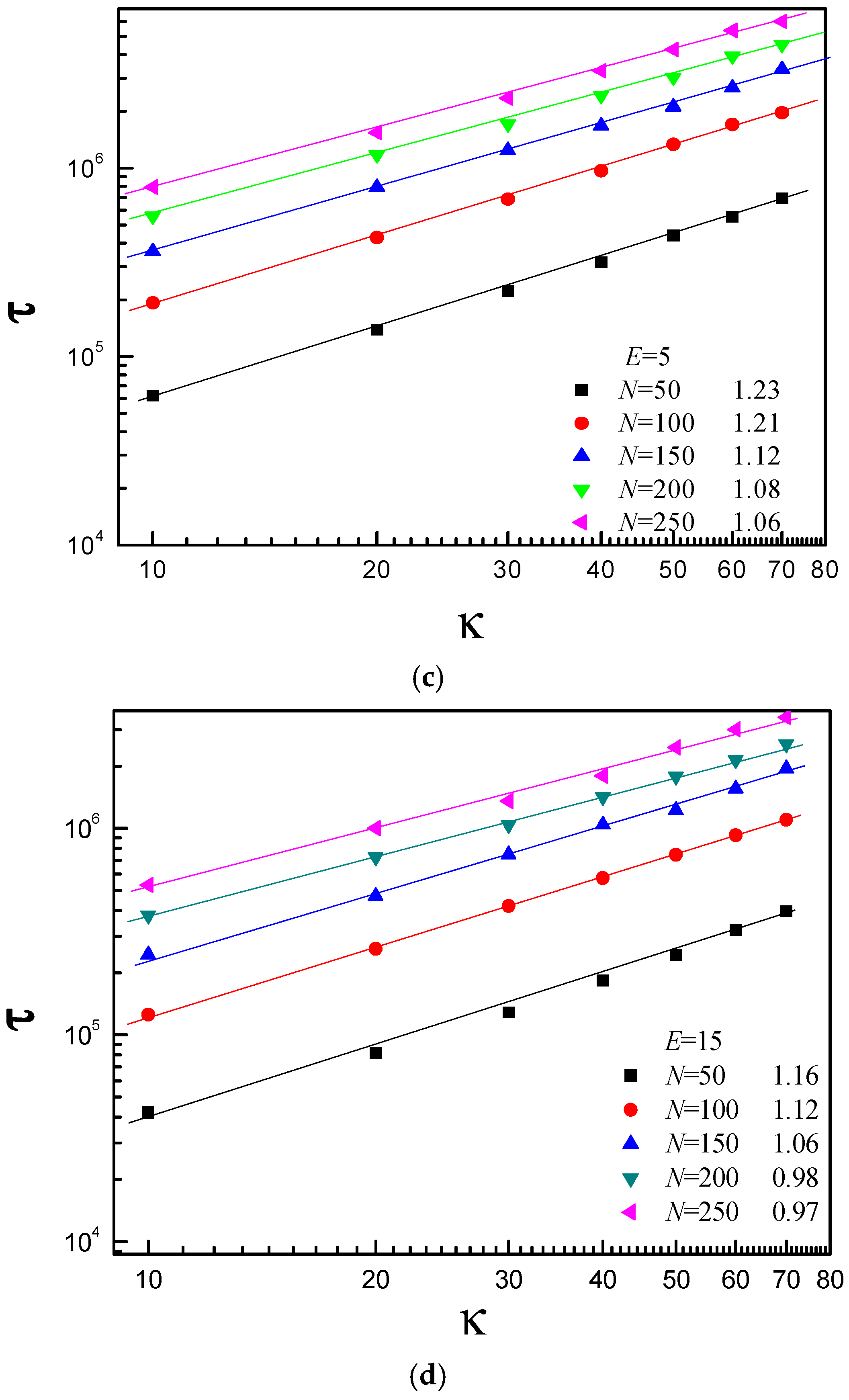
3.3. Scaling Behavior of Average Translocation Time
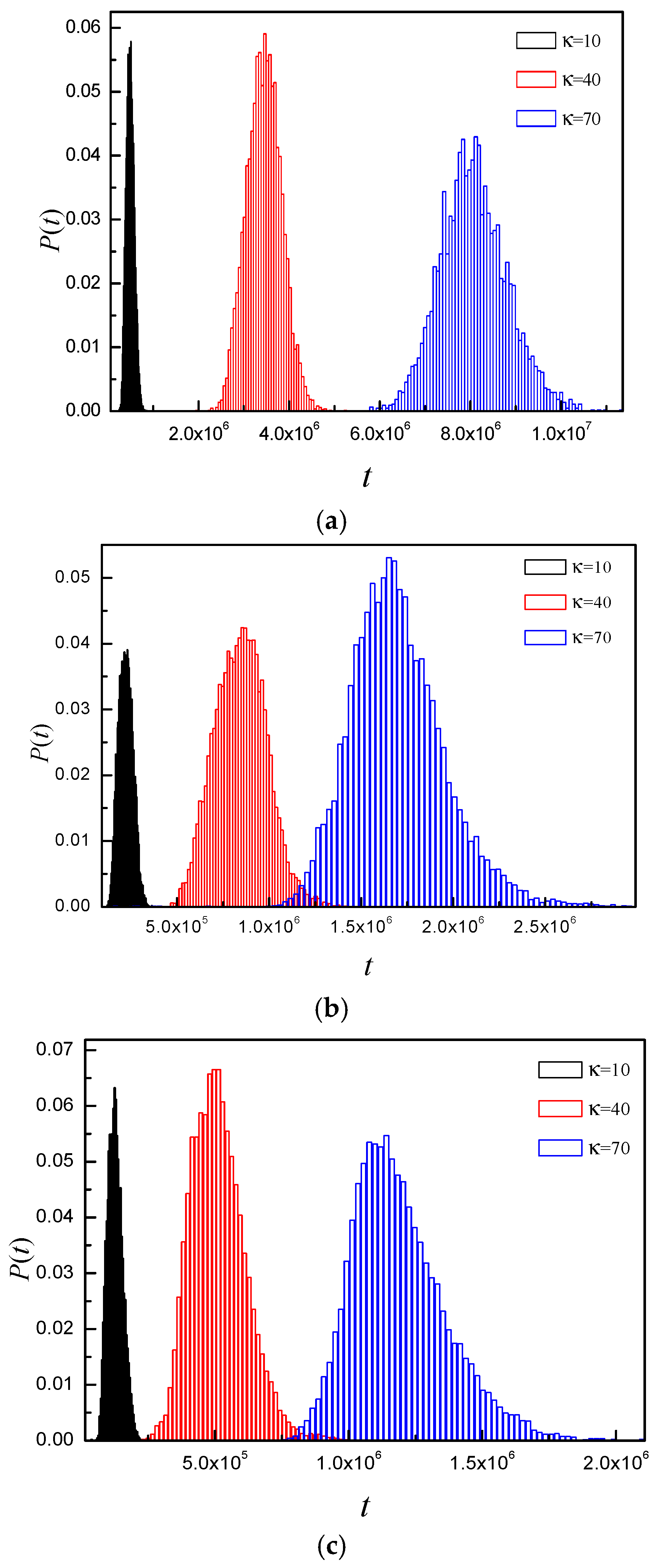
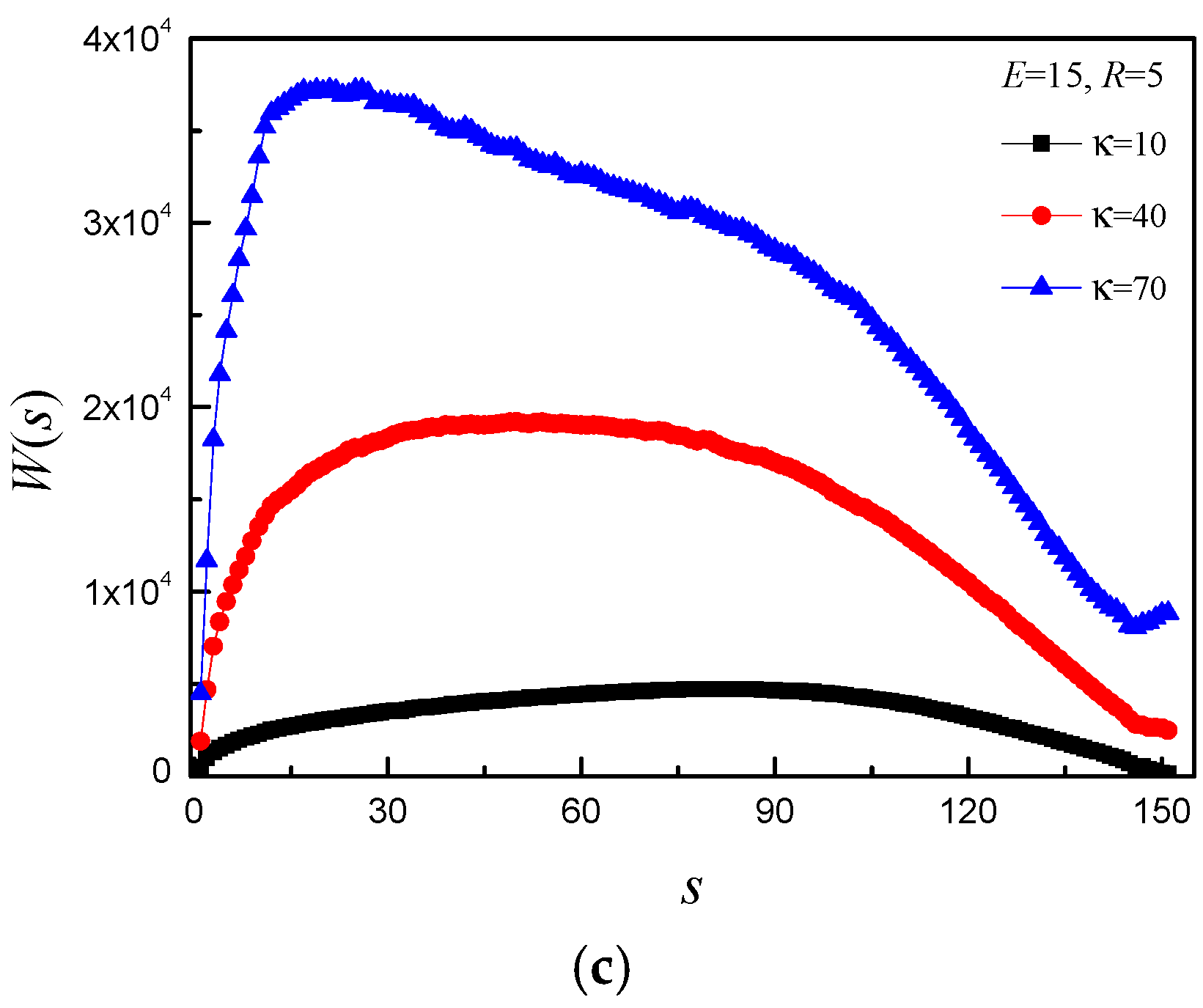
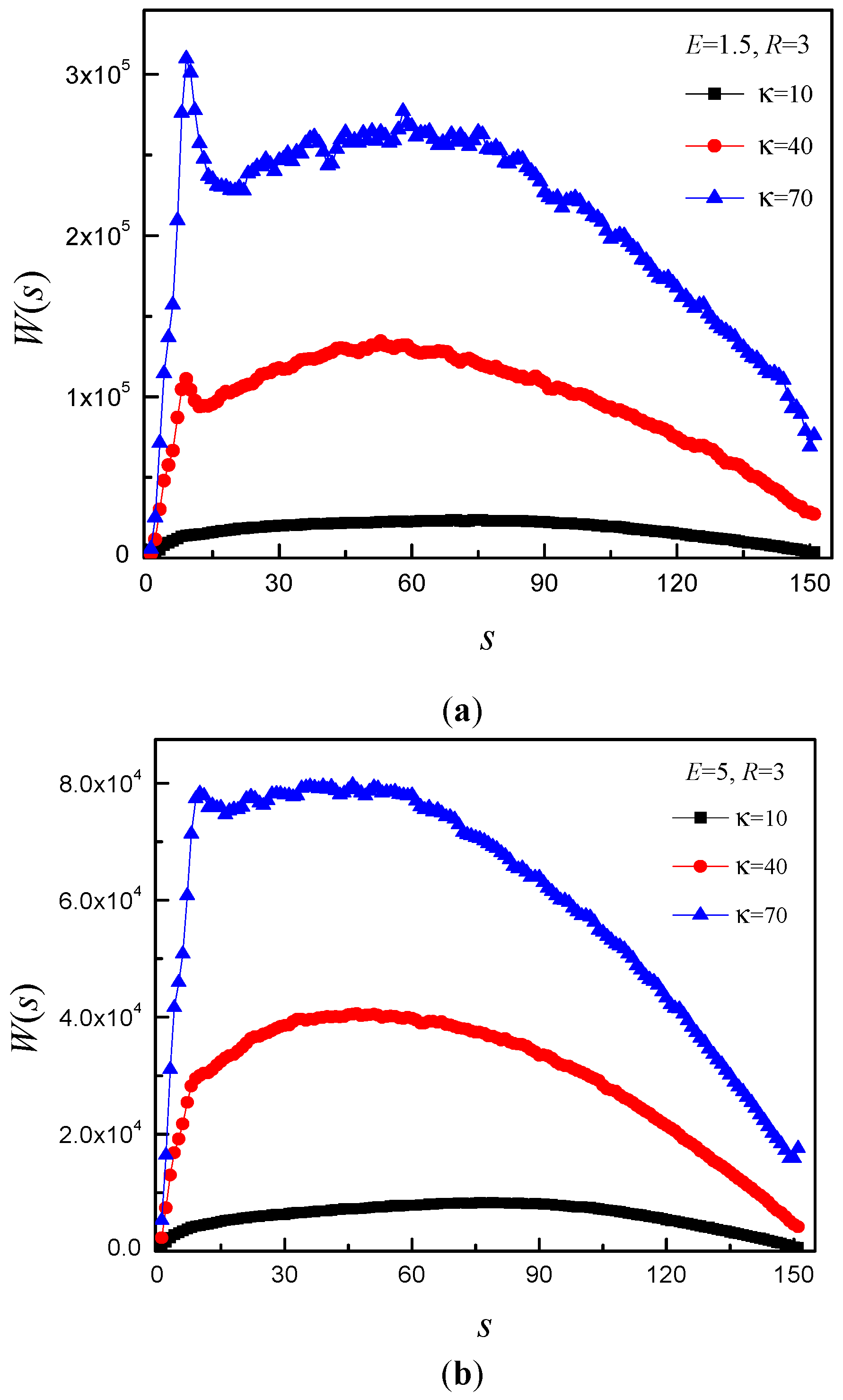
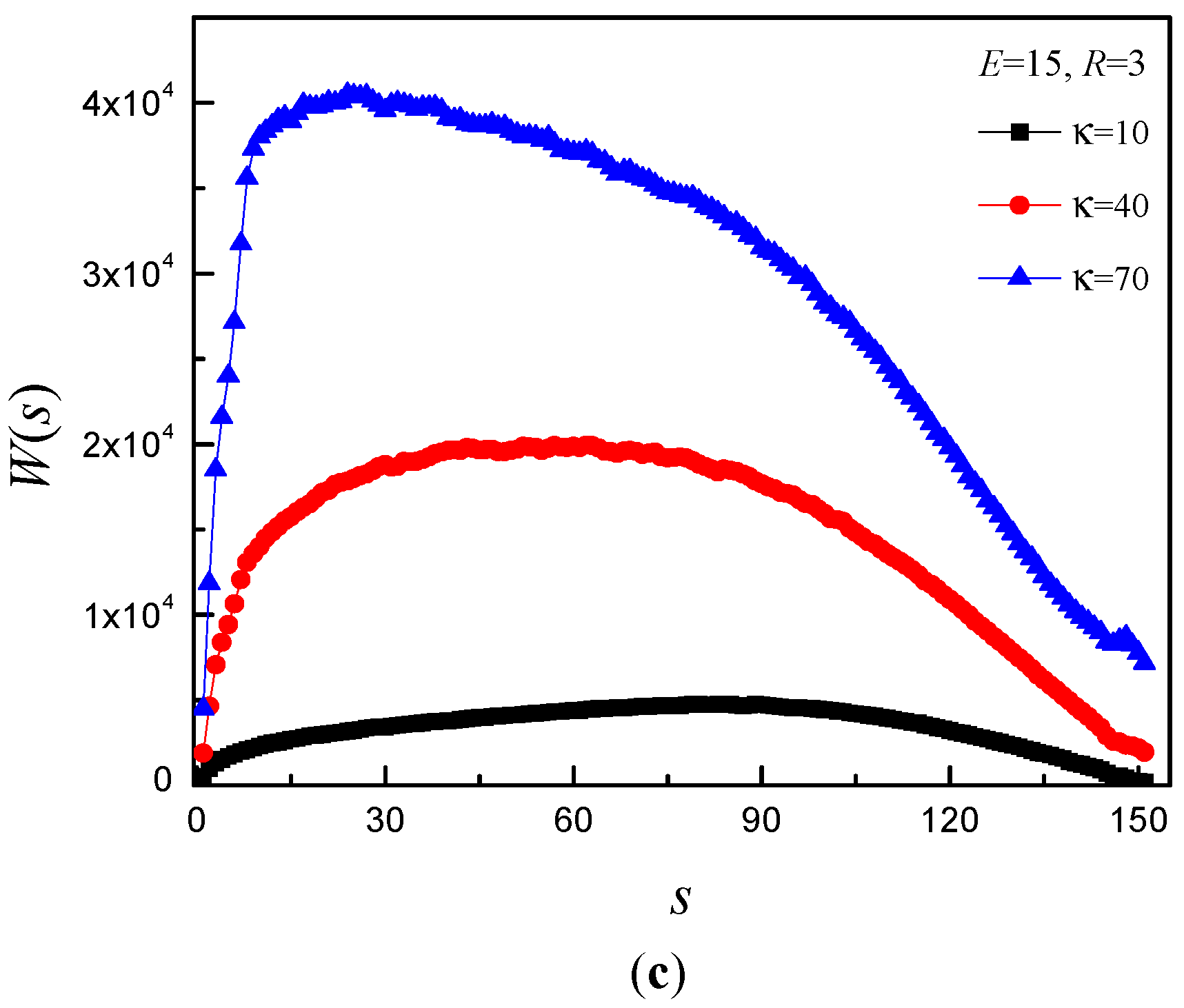
3.4. Time Distribution
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Alberts, B.; Bray, D.; Lewis, J.; Raff, M.; Watson, J.D. Molecular Biology of the Cell; Garland: New York, NY, USA, 1994; p. 1361. [Google Scholar]
- Kasianowicz, J.J.; Brandin, E.; Branton, D.; Deamer, D.W. Characterization of individual polynucleotide molecules using a membrane channel. Proc. Natl. Acad. Sci. USA 1996, 93, 13770–13773. [Google Scholar] [CrossRef] [PubMed]
- Carson, S.; Wanunu, M. Challenges in DNA motion control and sequence readout using nanopore devices. Nanotechnology 2015, 26, 074004. [Google Scholar] [CrossRef] [PubMed]
- Steinbock, L.J.; Radenovic, A. The emergence of nanopores in next-generation sequencing. Nanotechnology 2015, 26, 074003. [Google Scholar] [CrossRef] [PubMed]
- Wanunu, M. Nanopores: A journey towards DNA sequencing. Phys. Life Rev. 2012, 9, 125–158. [Google Scholar] [CrossRef] [PubMed]
- Venkatesan, B.M.; Bashir, R. Nanopore sensors for nucleic acid analysis. Nat. Nanotechnol. 2011, 6, 615–624. [Google Scholar] [CrossRef] [PubMed]
- Stefureac, R.; Waldner, L.; Howard, P.; Lee, J.S. Nanopore analysis of a small 86-residue protein. Small 2008, 4, 59–63. [Google Scholar] [CrossRef] [PubMed]
- Striemer, C.C.; Gaborski, T.R.; McGrath, J.L.; Fauchet, P.M. Charge- and size-based separation of macromolecules using ultrathin silicon membranes. Nature 2007, 445, 749–753. [Google Scholar] [CrossRef] [PubMed]
- Yang, P.; Gai, S.; Lin, J. Cheminform abstract: Functionalized mesoporous silica materials for controlled drug delivery. Chem. Soc. Rev. 2012, 41, 3679–3698. [Google Scholar] [CrossRef] [PubMed]
- Muthukumar, M. Polymer Translocation; CRC Press: Boca Raton, FL, USA, 2011; p. 372. [Google Scholar]
- Milchev, A. Single-polymer dynamics under constraints: Scaling theory and computer experiment. J. Phys. Condens. Matter 2011, 23, 1409–1413. [Google Scholar] [CrossRef] [PubMed]
- Panja, D.; Barkema, G.T.; Kolomeisky, A.B. Through the eye of the needle: Recent advances in understanding biopolymer translocation. J. Phys. Condens. Matter 2013, 25, 4977–4984. [Google Scholar] [CrossRef] [PubMed]
- Palyulin, V.V.; Ala-Nissila, T.; Metzler, R. Polymer translocation: The first two decades and the recent diversification. Soft Matter 2014, 10, 9016–9037. [Google Scholar] [CrossRef] [PubMed]
- Polson, J.M. Polymer translocation into and out of an ellipsoidal cavity. J. Chem. Phys. 2015, 142, 174903. [Google Scholar] [CrossRef] [PubMed]
- Muthukumar, M. Polymer escape through a nanopore. J. Chem. Phys. 2003, 118, 5174–5184. [Google Scholar] [CrossRef]
- Kong, C.Y.; Muthukumar, M. Polymer translocation through a nanopore. II. Excluded volume effect. J. Chem. Phys. 2004, 120, 3460–3466. [Google Scholar] [CrossRef] [PubMed]
- Ali, I.; Marenduzzo, D.; Yeomans, J. Dynamics of polymer packaging. J. Chem. Phys. 2004, 121, 8635–8641. [Google Scholar] [CrossRef] [PubMed]
- Ali, I.; Marenduzzo, D.; Micheletti, C.; Yeomans, J. A coarse grained model for DNA and polymer packaging: Statics and dynamics. J. Theor. Med. 2005, 6, 115–117. [Google Scholar] [CrossRef]
- Cacciuto, A.; Luijten, E. Confinement-driven translocation of a flexible polymer. Phys. Rev. Lett. 2006, 96, 238104. [Google Scholar] [CrossRef] [PubMed]
- Ali, I.; Marenduzzo, D.; Yeomans, J. Polymer packaging and ejection in viral capsids: Shape matters. Phys. Rev. Lett. 2006, 96, 208102. [Google Scholar] [CrossRef] [PubMed]
- Forrey, C.; Muthukumar, M. Langevin dynamics simulation of genome packing in bacteriophage. Biophys. J. 2006, 91, 25–41. [Google Scholar] [CrossRef] [PubMed]
- Ali, I.; Marenduzzo, D.; Yeomans, J.M. Ejection dynamics of polymeric chains from viral capsids: Effect of solvent quality. Biophys. J. 2008, 94, 4159–4164. [Google Scholar] [CrossRef] [PubMed]
- Sakaue, T.; Yoshinaga, N. Dynamics of polymer decompression: Expansion, unfolding, and ejection. Phys. Rev. Lett. 2009, 102, 148302. [Google Scholar] [CrossRef] [PubMed]
- Matsuyama, A.; Yano, M.; Matsuda, A. Packaging-ejection phase transitions of a polymer chain: Theory and Monte Carlo simulation. J. Chem. Phys. 2009, 131, 3282–3285. [Google Scholar] [CrossRef]
- Ali, I.; Marenduzzo, D. Influence of ions on genome packaging and ejection: A molecular dynamics study. J. Chem. Phys. 2011, 135, 10122–10127. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.; Neimark, A.V. Adsorption-driven translocation of polymer chain into nanopore. J. Chem. Phys. 2012, 136, 121–125. [Google Scholar] [CrossRef] [PubMed]
- Rasmussen, C.J.; Vishnyakov, A.; Neimark, A.V. Translocation dynamics of freely jointed Lennard-Jones chains into adsorbing pores. J. Chem. Phys. 2012, 137, 144903. [Google Scholar] [CrossRef] [PubMed]
- Ghosal, S. Capstan friction model for DNA ejection from bacteriophages. Phys. Rev. Lett. 2012, 109, 6380–6383. [Google Scholar] [CrossRef] [PubMed]
- Zhang, K.H.; Luo, K.F. Dynamics of polymer translocation into a circular nanocontainer through a nanopore. J. Chem. Phys. 2012, 136, 185103. [Google Scholar] [CrossRef] [PubMed]
- Al Lawati, A.; Ali, I.; Al Barwani, M. Effect of temperature and capsid tail on the packing and ejection of viral DNA. PLoS ONE 2013, 8, e52958. [Google Scholar] [CrossRef] [PubMed]
- Zhang, K.H.; Luo, K.F. Dynamics of polymer translocation into an anisotropic confinement. Soft Matter. 2013, 9, 2069–2075. [Google Scholar] [CrossRef]
- Polson, J.M.; Hassanabad, M.F.; McCaffrey, A. Simulation study of the polymer translocation free energy barrier. J. Chem. Phys. 2013, 138, 244–251. [Google Scholar] [CrossRef] [PubMed]
- Polson, J.M.; McCaffrey, A.C. Polymer translocation dynamics in the quasi-static limit. J. Chem. Phys. 2013, 138, 3869–3876. [Google Scholar] [CrossRef] [PubMed]
- Mahalik, J.; Hildebrandt, B.; Muthukumar, M. Langevin dynamics simulation of DNA ejection from a phage. J. Biol. Phys. 2013, 39, 229–245. [Google Scholar] [CrossRef] [PubMed]
- Linna, R.P.; Moisio, J.E.; Suhonen, P.M.; Kaski, K. Dynamics of polymer ejection from capsid. Phys. Rev. E. 2014, 89, 052702. [Google Scholar] [CrossRef] [PubMed]
- Zhang, K.H.; Luo, K.F. Polymer translocation into a confined space: Influence of the chain stiffness and the shape of the confinement. J. Chem. Phys. 2014, 140, 094902. [Google Scholar] [CrossRef] [PubMed]
- Cao, Q.; Bachmann, M. Dynamics and limitations of spontaneous polyelectrolyte intrusion into a charged nanocavity. Phys. Rev. E 2014, 90, 060601. [Google Scholar] [CrossRef] [PubMed]
- Luo, K.; Metzler, R.; Ala-Nissila, T.; Ying, S.-C. Polymer translocation out of confined environments. Phys. Rev. E 2009, 80, 021907. [Google Scholar] [CrossRef] [PubMed]
- Luo, K.; Metzler, R. Polymer translocation into a fluidic channel through a nanopore. Phys. Rev. E 2010, 82, 021922. [Google Scholar] [CrossRef] [PubMed]
- Luo, K.; Metzler, R. The chain sucker: Translocation dynamics of a polymer chain into a long narrow channel driven by longitudinal flow. J. Chem. Phys. 2011, 134, 135102. [Google Scholar] [CrossRef] [PubMed]
- Sheng, J.; Luo, K. Ejection dynamics of a ring polymer out of a nanochannel. Soft Matter 2012, 8, 367. [Google Scholar] [CrossRef]
- Kindt, J.; Tzlil, S.; Ben-Shaul, A.; Gelbart, W.M. DNA packaging and ejection forces in bacteriophage. Proc. Natl. Acad. Sci. USA 2001, 98, 13671–13674. [Google Scholar] [CrossRef] [PubMed]
- Rubinstein, M.; Colby, R.H. Polymer Physics; Oxford University Press: New York, NY, USA, 2003; p. 440. [Google Scholar]
- Grosberg, A.Y.; Khokhlov, A.R. Statistical Physics of Macromolecules; AIP Press: New York, NY, USA, 1994. [Google Scholar]
- De Gennes, P.G. Scaling Concepts in Polymer Physics; Cornell University Press: Ithaca, NY, USA, 1979. [Google Scholar]
- Baumgärtner, A.; Binder, K. Monte Carlo studies on the freely jointed polymer chain with excluded volume interaction. J. Chem. Phys. 1979, 71, 2541–2545. [Google Scholar] [CrossRef]
- Cifra, P. Channel confinement of flexible and semiflexible macromolecules. J. Chem. Phys. 2009, 131, 224903. [Google Scholar] [CrossRef] [PubMed]
- Yang, Z.Y.; Zhang, D.; Zhang, L.X.; Chen, C.H.; Rehaman, A.U.; Liang, H.J. Local coil–helix transition of semiflexible polymers confined in spheres. Soft Matter 2011, 7, 6836–6843. [Google Scholar] [CrossRef]
- Suhonen, P.M.; Kaski, K.; Linna, R.P. Criteria for minimal model of driven polymer translocation. Phys. Rev. E 2014, 90, 042702. [Google Scholar] [CrossRef] [PubMed]

© 2016 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Z.-Y.; Chai, A.-H.; Yang, Y.-F.; Li, X.-M.; Li, P.; Dai, R.-Y. The Semiflexible Polymer Translocation into Laterally Unbounded Region between Two Parallel Flat Membranes. Polymers 2016, 8, 332. https://doi.org/10.3390/polym8090332
Yang Z-Y, Chai A-H, Yang Y-F, Li X-M, Li P, Dai R-Y. The Semiflexible Polymer Translocation into Laterally Unbounded Region between Two Parallel Flat Membranes. Polymers. 2016; 8(9):332. https://doi.org/10.3390/polym8090332
Chicago/Turabian StyleYang, Zhi-Yong, Ai-Hua Chai, Yong-Fu Yang, Xiao-Mao Li, Ping Li, and Run-Ying Dai. 2016. "The Semiflexible Polymer Translocation into Laterally Unbounded Region between Two Parallel Flat Membranes" Polymers 8, no. 9: 332. https://doi.org/10.3390/polym8090332
APA StyleYang, Z.-Y., Chai, A.-H., Yang, Y.-F., Li, X.-M., Li, P., & Dai, R.-Y. (2016). The Semiflexible Polymer Translocation into Laterally Unbounded Region between Two Parallel Flat Membranes. Polymers, 8(9), 332. https://doi.org/10.3390/polym8090332