Conformation and Rheological Properties of Calf-Thymus DNA in Solution
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials and Solution Preparation
2.2. Purity and Thermal Stability
2.3. Rheological Measurements
3. Results and Discussion
3.1. Conformation


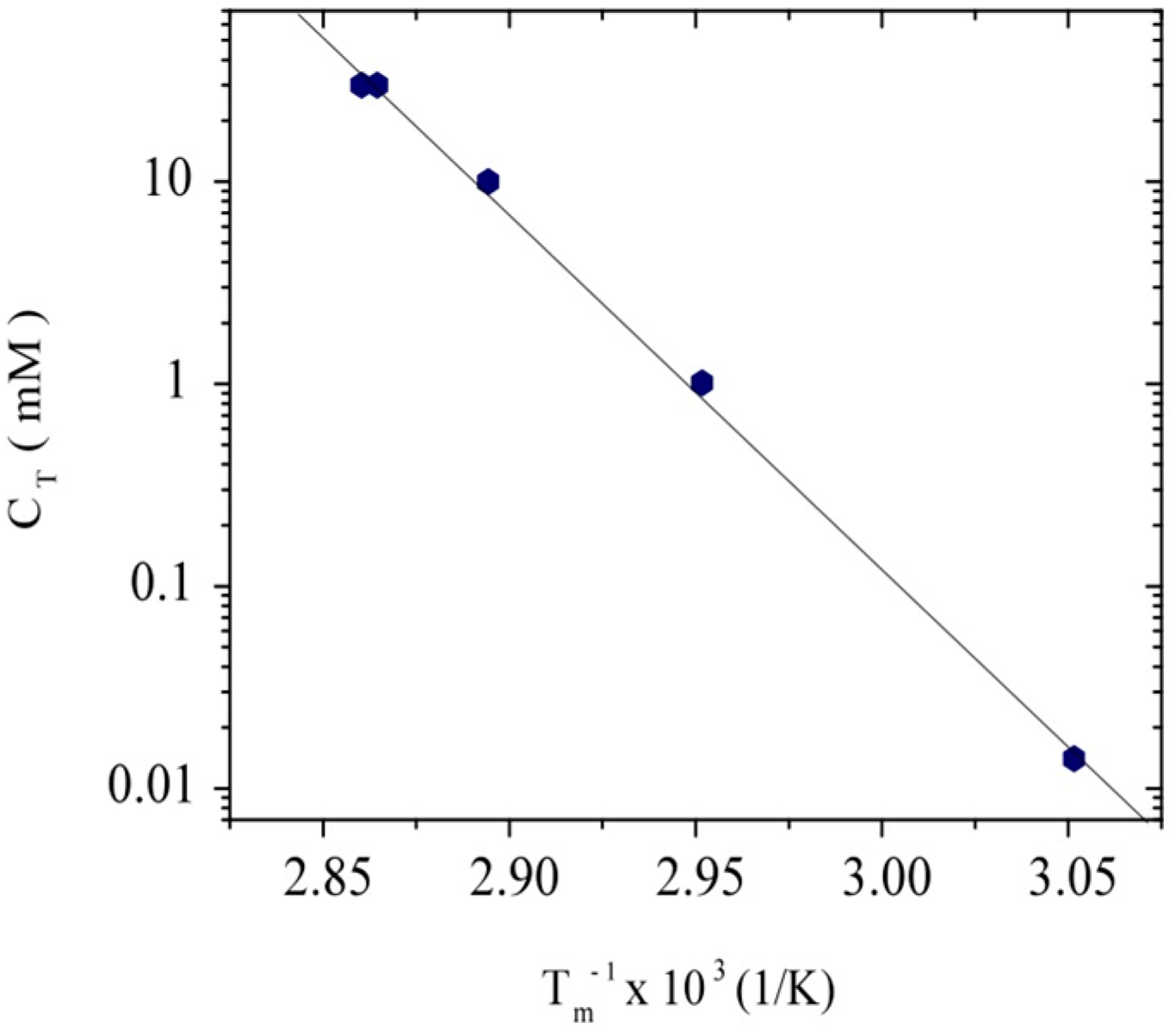
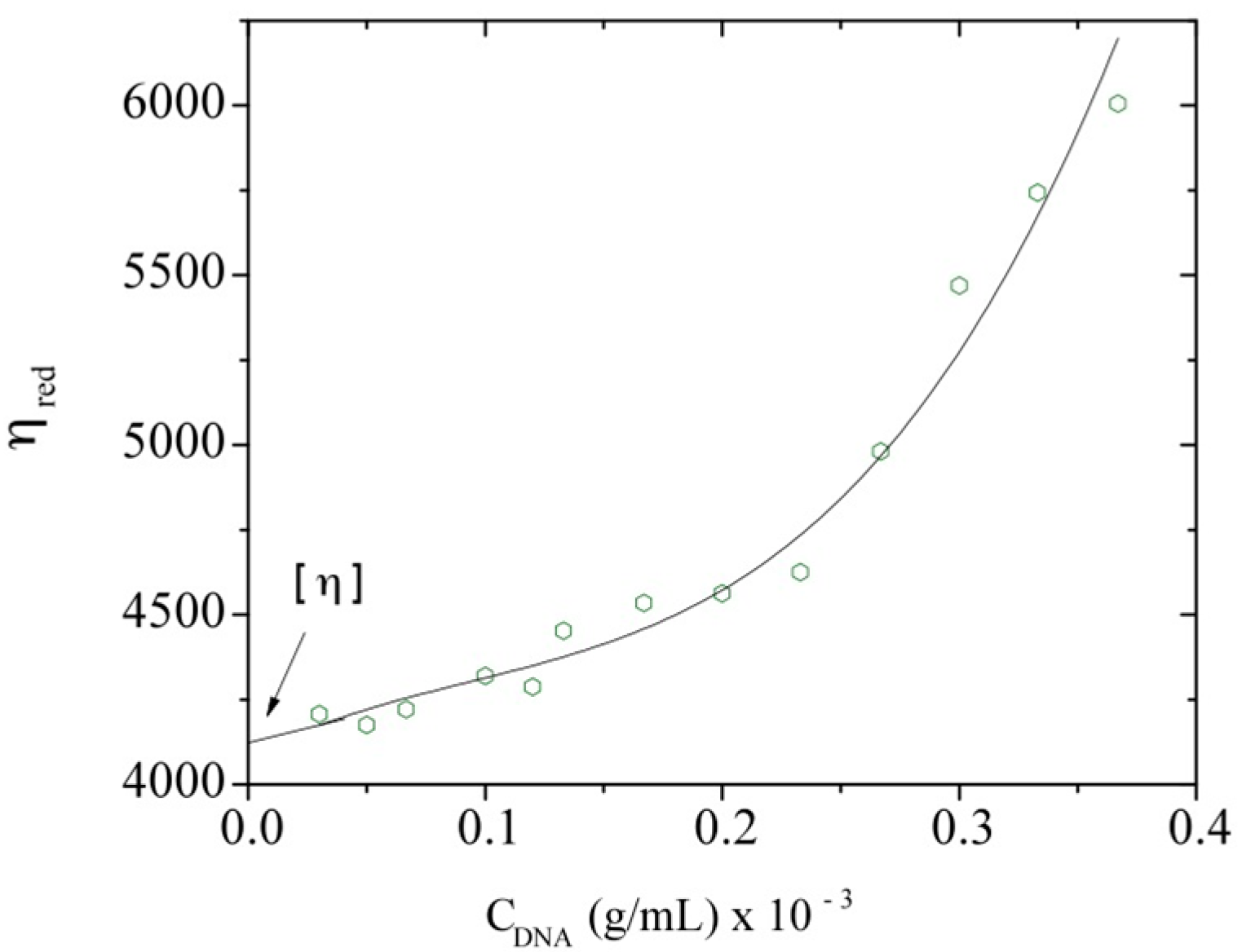
3.2. Intrinsic Viscosity and Molecular Weight
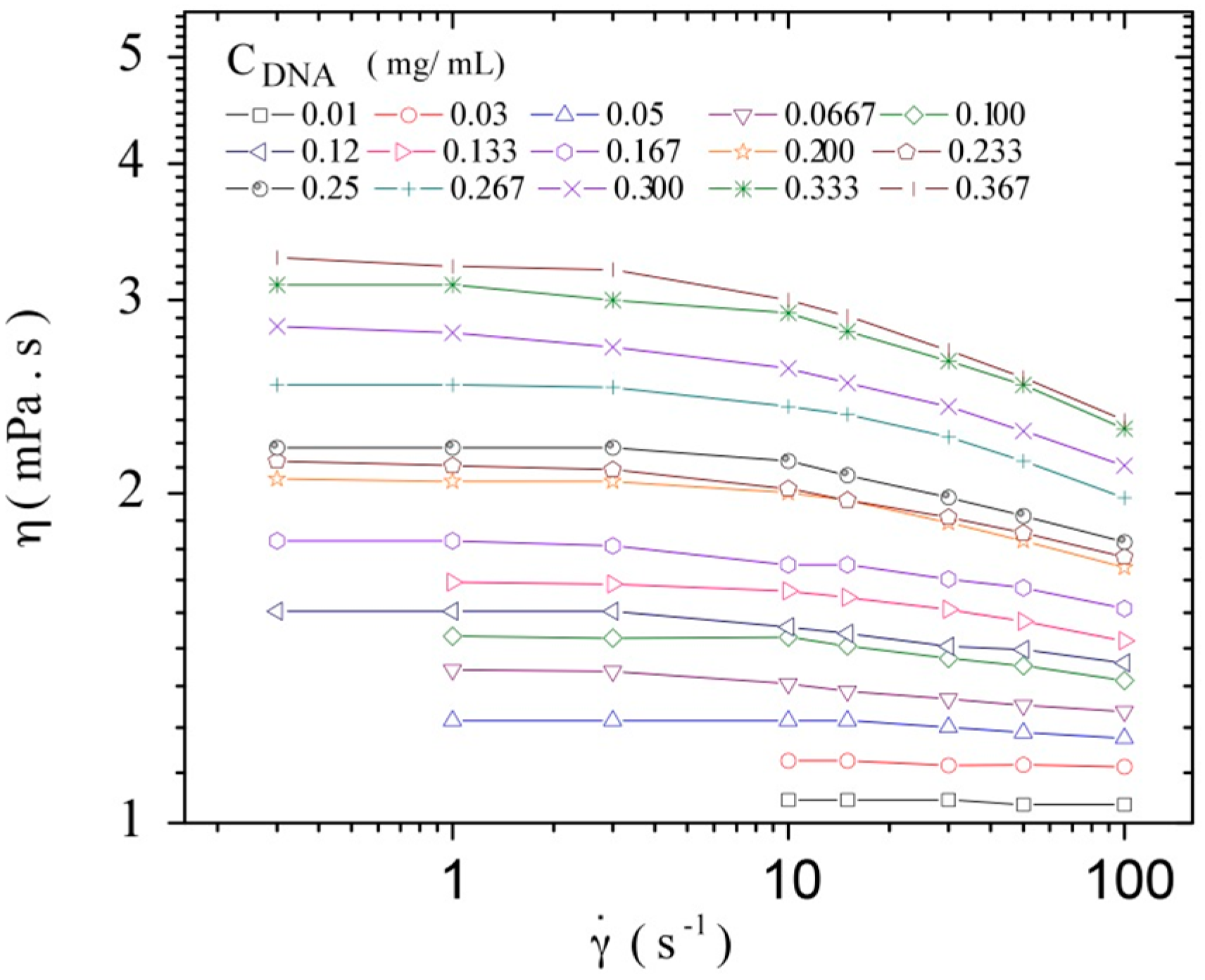
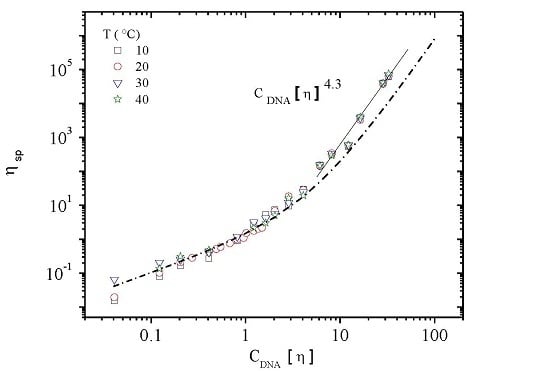
3.3. Rheological Properties of Calf-Thymus DNA
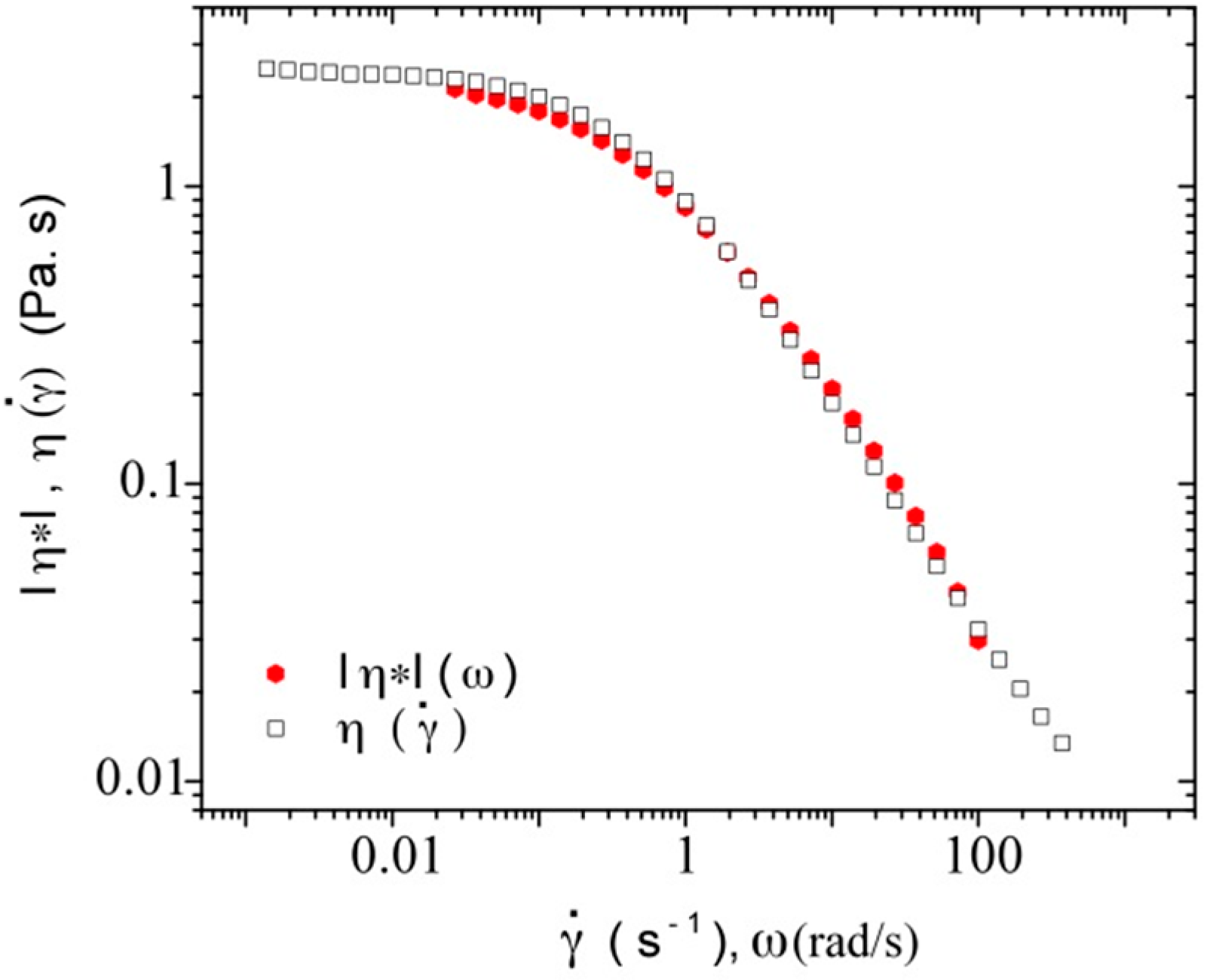
3.3.1. Steady Shear Viscometry
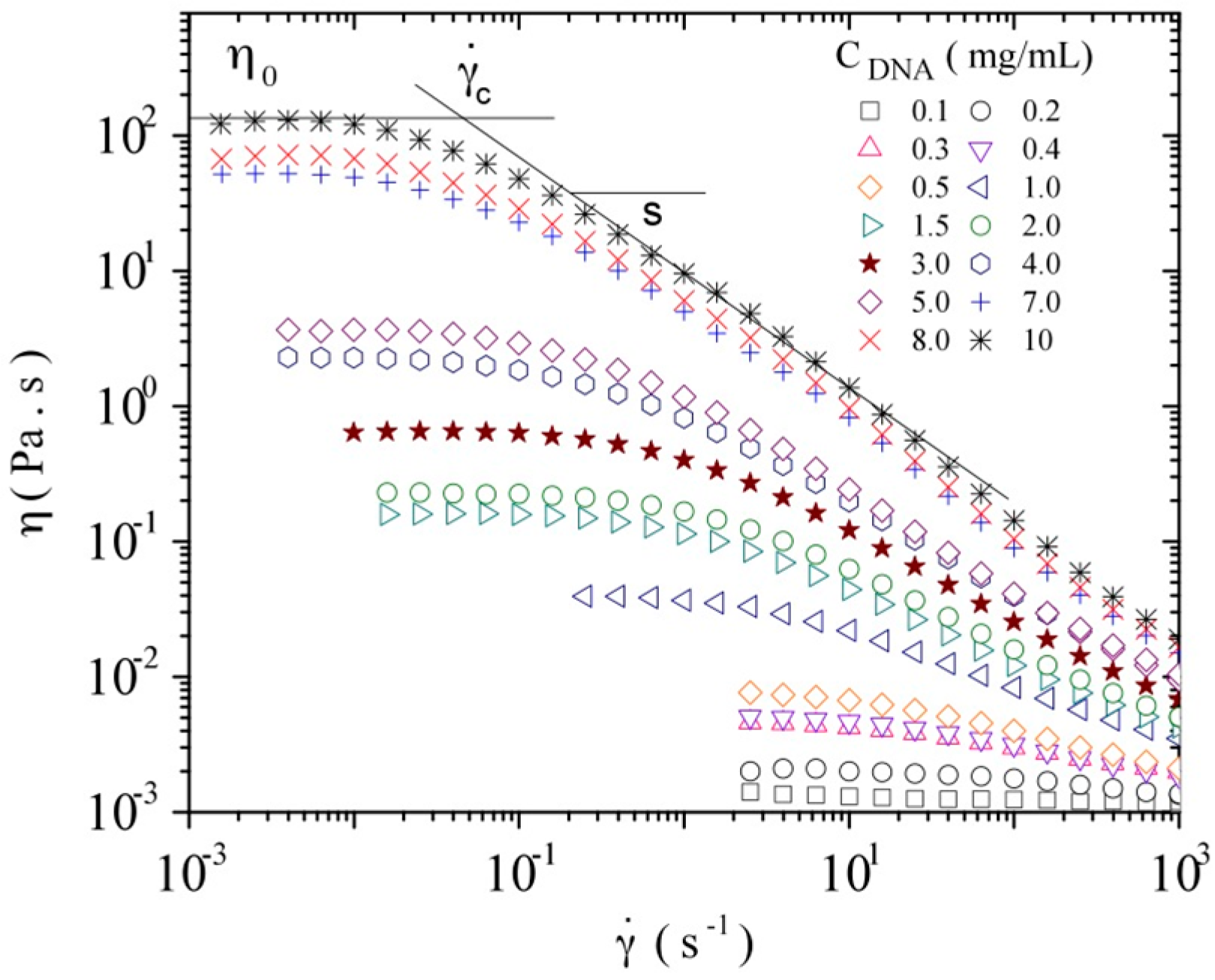
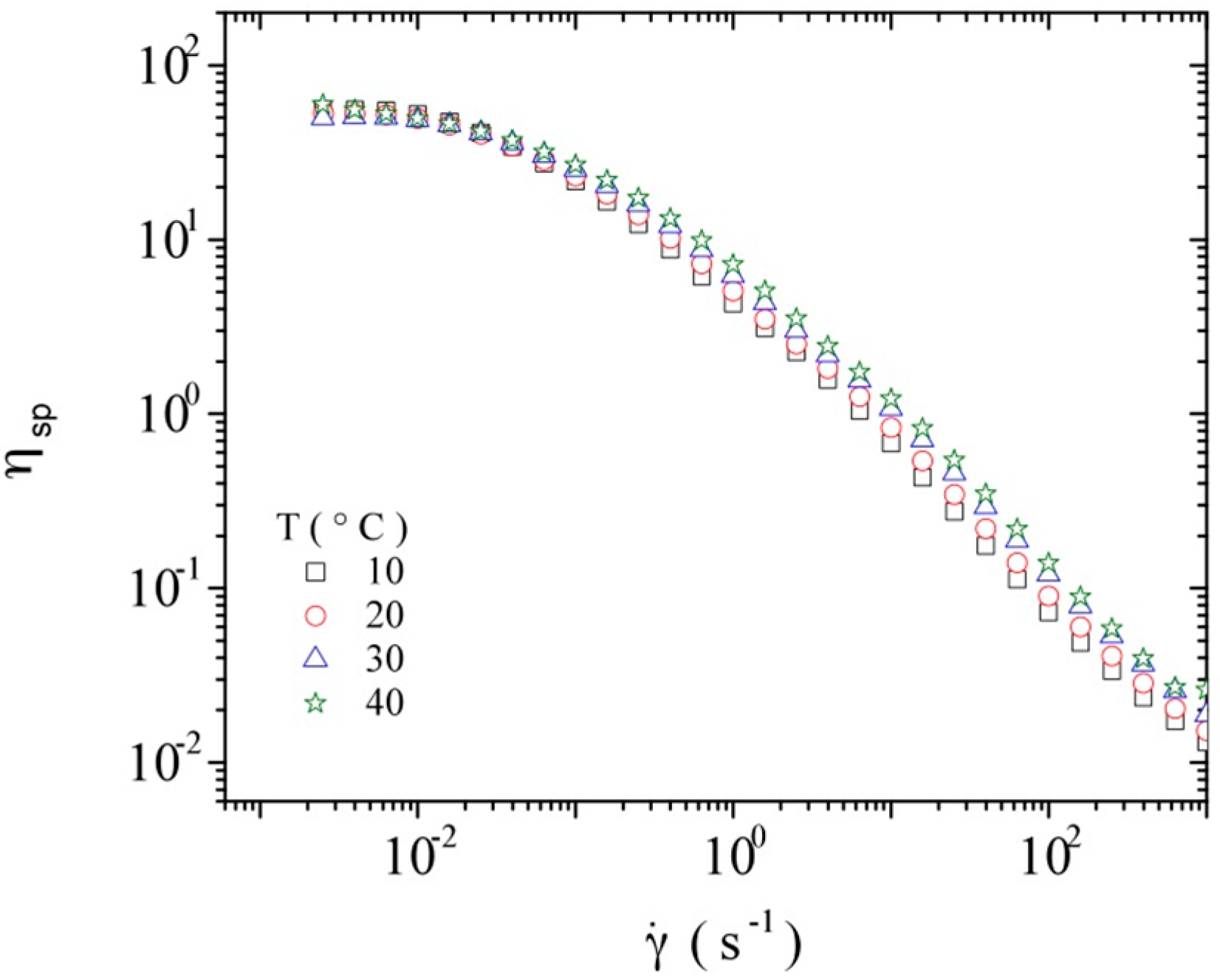
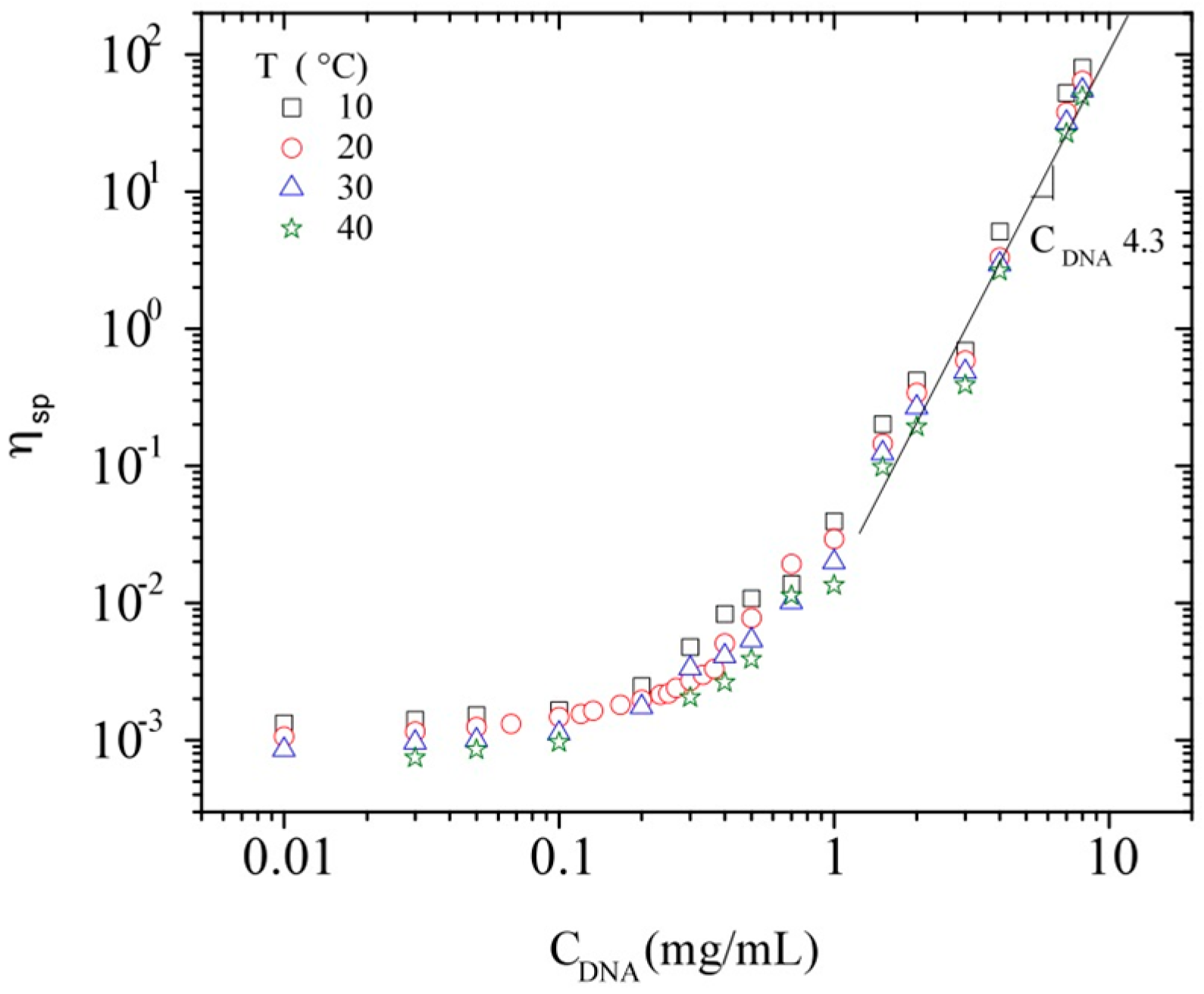

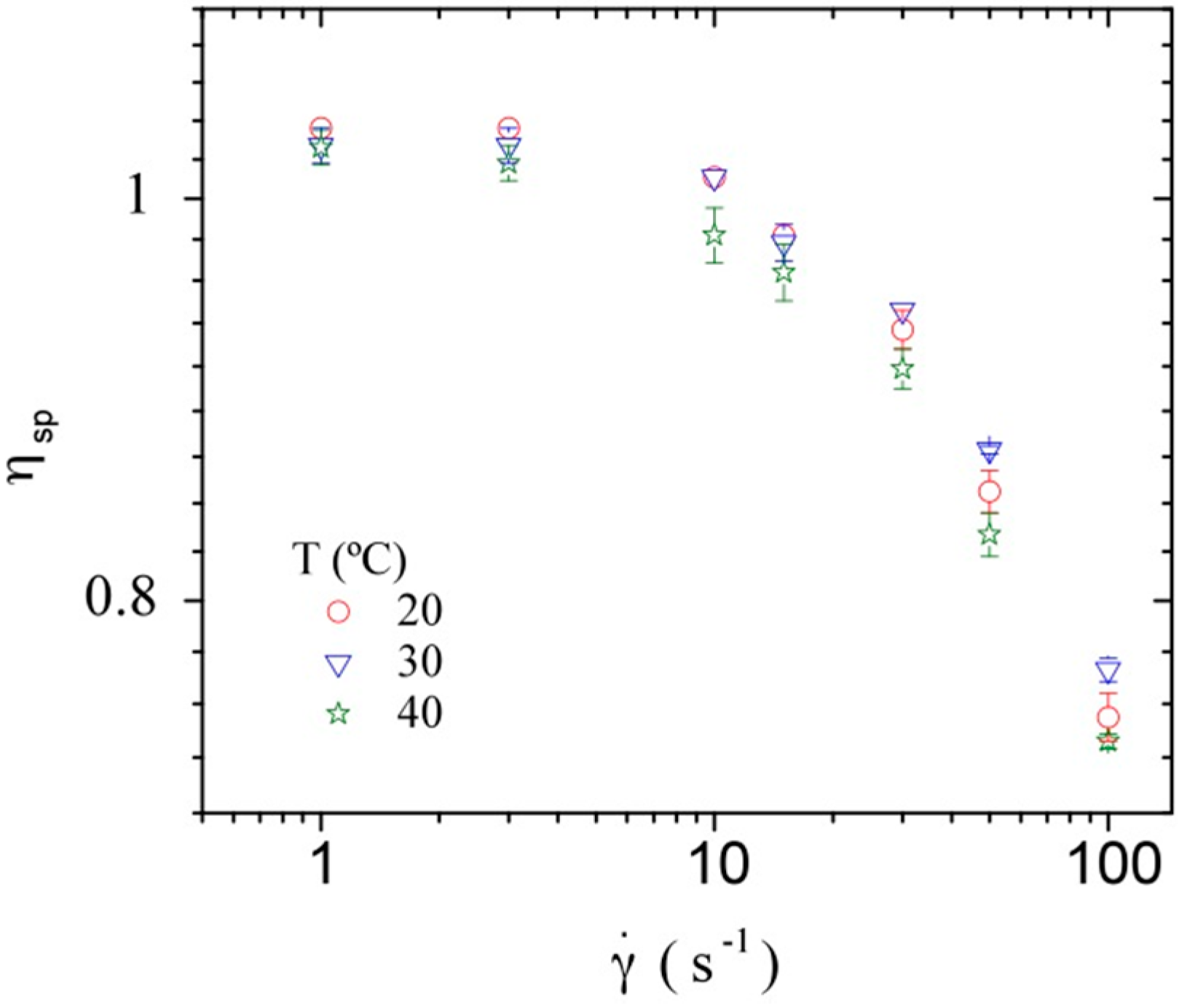
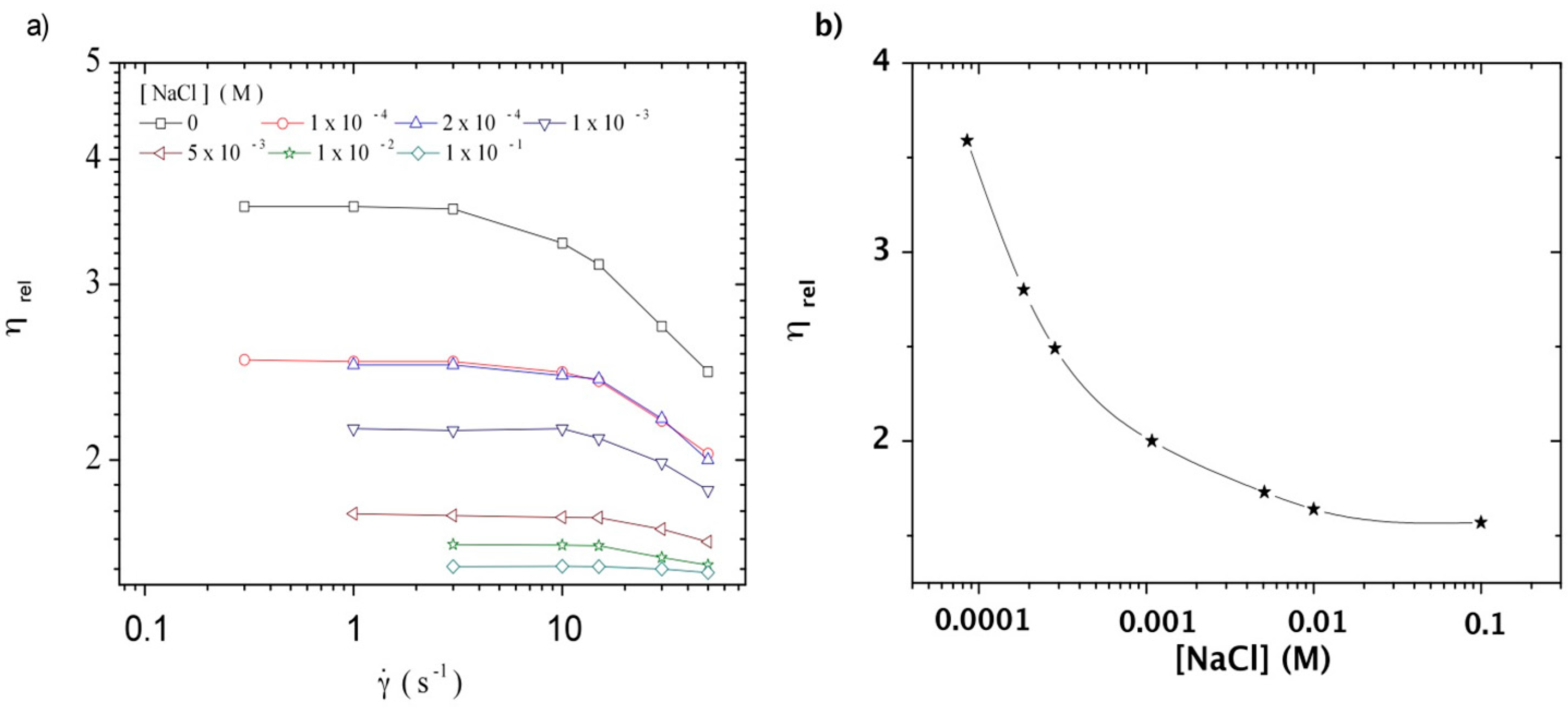
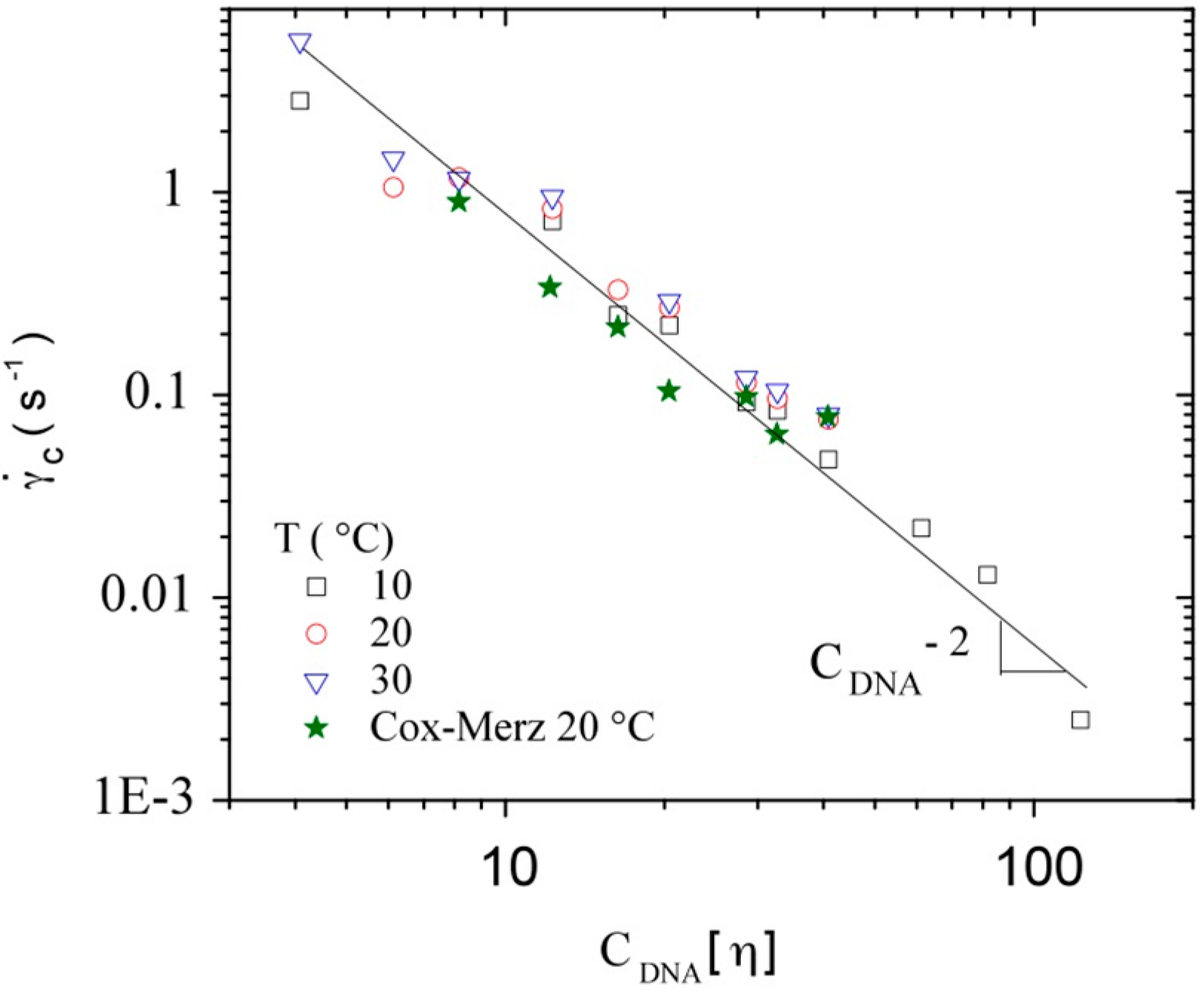
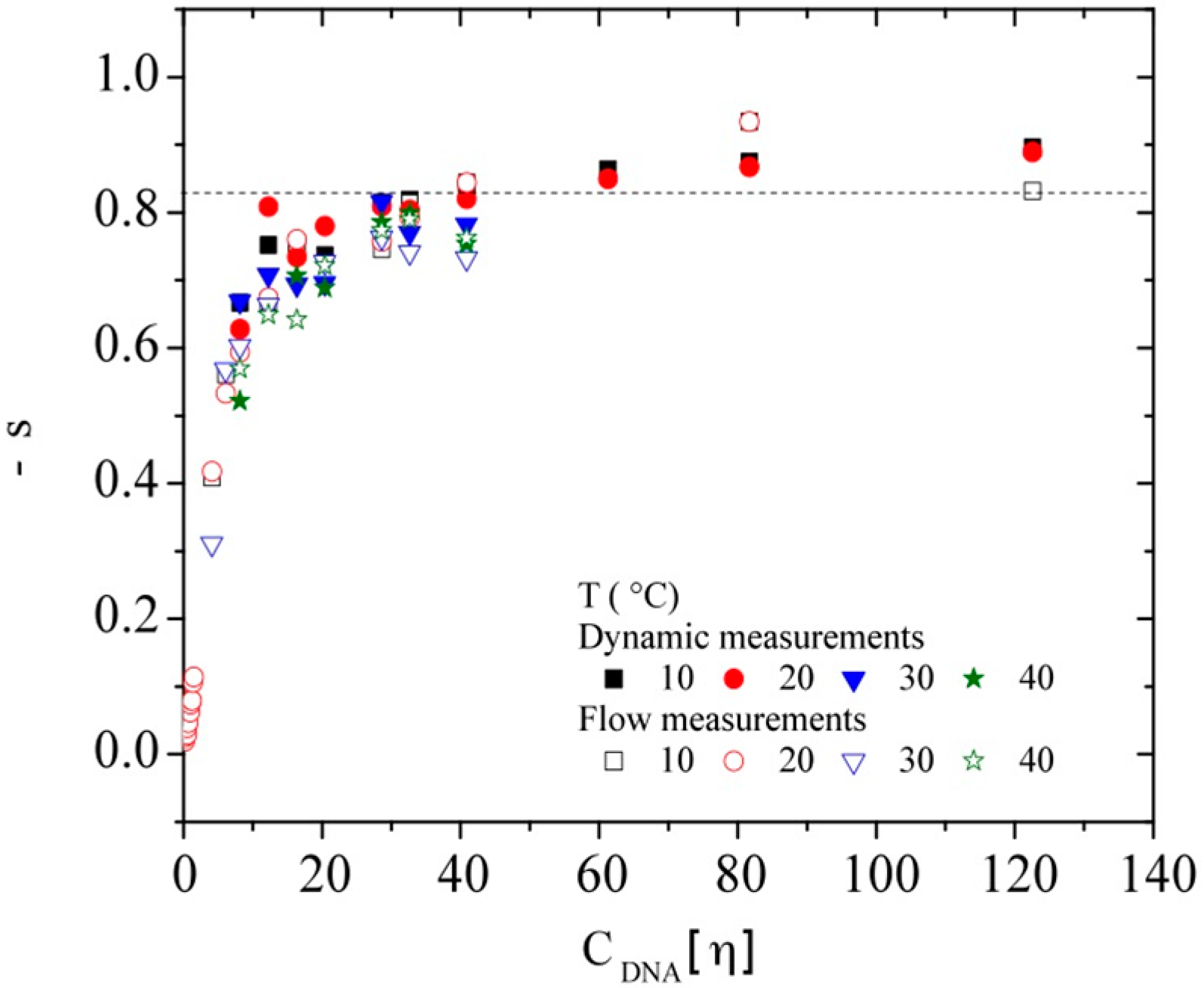
3.3.2. Dynamic Rheometry
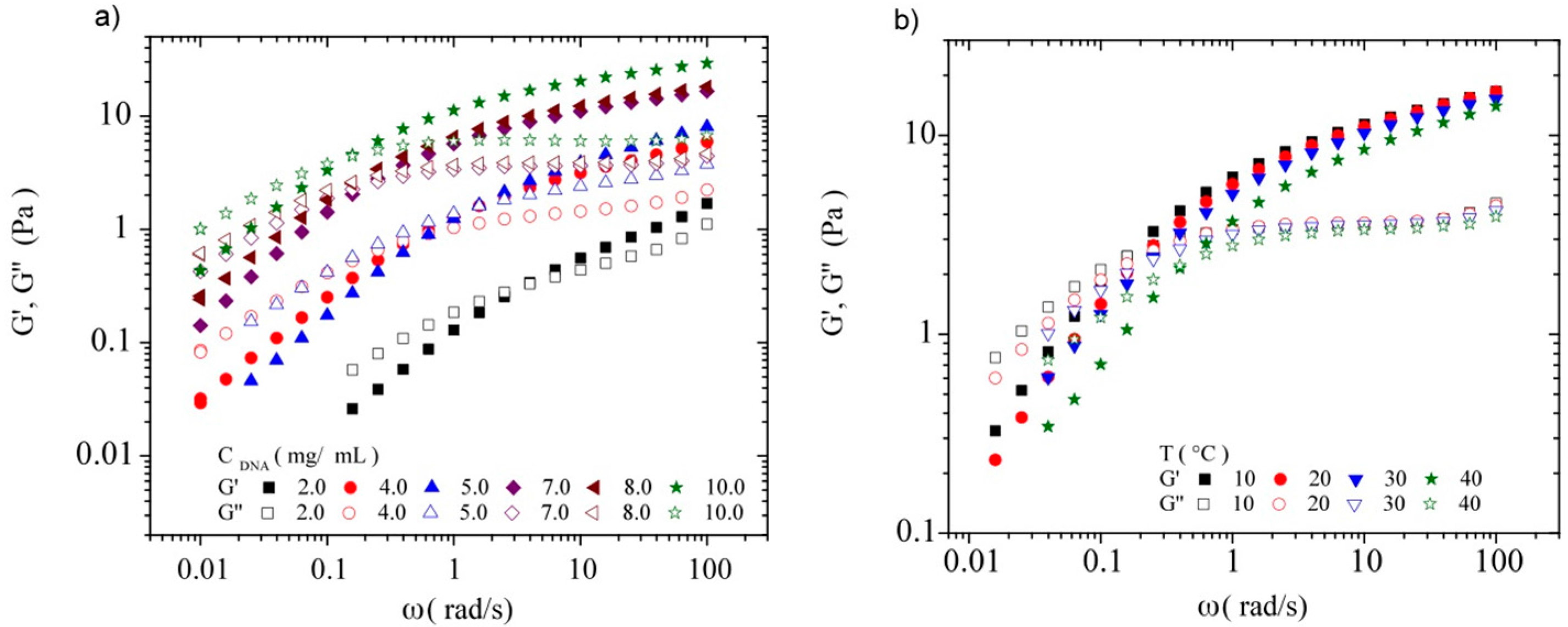
3.3.3. Rheological Behavior Analysis

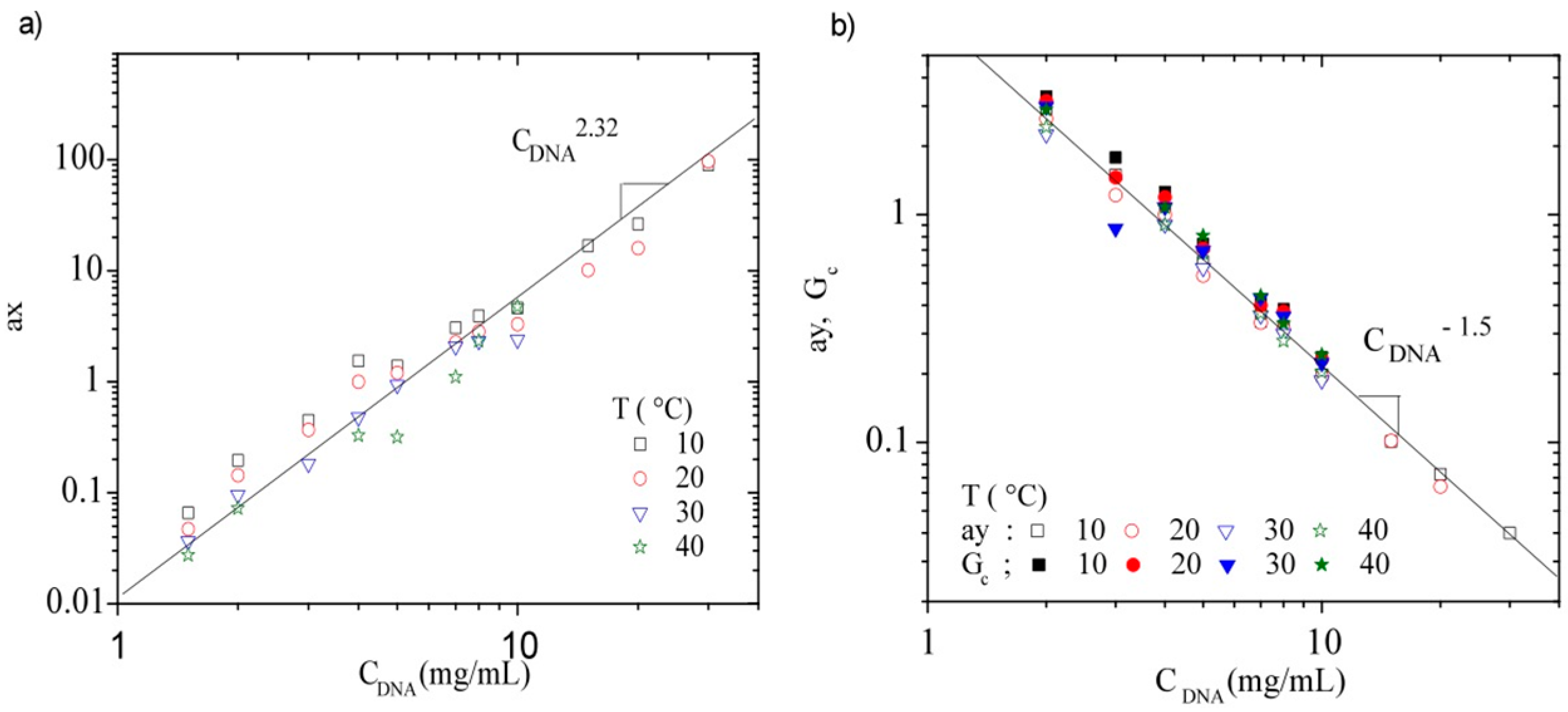
4. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| DNA: | Deoxyribonucleic Acid |
| Mw: | weight–average molecular weight |
| MW: | molecular weight |
| TE: | Tris–HCl-EDTA buffer |
References
- Anderson, C.F.; Record, M.T. Polyelectrolyte theories and their applications to DNA. Annu. Rev. Phys. Chem. 1982, 33, 191–222. [Google Scholar] [CrossRef]
- Bloomfield, V.A. Hydrodynamic properties of DNA. J. Macromol. Sci. Polym. Rev. 1968, 3, 255–316. [Google Scholar] [CrossRef]
- Păun, G.; Rozenberg, G.; Salomaa, A. DNA: Its Structure and Processing in DNA Computing; Springer-Verlag: Berlin, Germany, 1998; pp. 10–22. [Google Scholar]
- Lavery, R.; Sklenar, H.; Zakrzewska, K.; Pullman, B. The flexibility of the nucleic acids: (II) The calculation of internal energy and applications to mononucleotide repeat DNA. J. Biomol. Struct. Dyn. 1986, 5, 989–1014. [Google Scholar] [CrossRef] [PubMed]
- Frank-Kamenetskii, M.D. Biophysics of the DNA molecule. Phys. Rep. 1997, 288, 13–60. [Google Scholar] [CrossRef]
- Gerstein, M.B.; Bruce, C.; Rozowsky, J.S.; Zheng, D.; Du, J.; Korbel, J.O.; Emanuelsson, O.; Zhang, Z.D.; Weissman, S.; Snyder, M. What is a gene, post-ENCODE? History and updated definition. Genome Res. 2007, 17, 669–681. [Google Scholar] [CrossRef] [PubMed]
- Wood, R.D.; Mitchell, M.; Sgouros, J.; Lindahl, T. Human DNA repair genes. Science 2001, 291, 1284–1289. [Google Scholar] [CrossRef] [PubMed]
- Watson, J.D.; Crick, F.H.C. The structure of DNA. Cold Spring Harb. Symp. Quant. Biol. 1953, 18, 123–131. [Google Scholar] [CrossRef] [PubMed]
- Klein, A.; Bonhoeffer, F. DNA replication. Annu. Rev. Biochem. 1972, 41, 301–332. [Google Scholar] [CrossRef] [PubMed]
- Jacob, F.; Brenner, S.; Cuzin, F. On the regulation of DNA replication in bacteria. Cold Spring Harb. Symp. Quant. Biol. 1963, 28, 329–348. [Google Scholar] [CrossRef]
- Rosenberg, A.H.; Studier, F.W. Intrinsic viscosity of native and single stranded T7 DNA and its relationship to sedimentation coefficient. Biopolymers 1969, 7, 765–774. [Google Scholar] [CrossRef] [PubMed]
- Schildkraut, C.; Lifson, S. Dependence of the melting temperature of DNA on salt concentration. Biopolymers 1965, 3, 195–208. [Google Scholar] [CrossRef] [PubMed]
- Vedenov, A.A.; Dykhne, A.M.; Frank-Kamanestskii, M.D. The helix-coil transition in DNA. Sov. Phys. Usp. 1972, 14, 715–736. [Google Scholar] [CrossRef]
- Manning, G.S. The molecular theory of polyelectrolyte solutions with applications to the electrostatic properties of polynucleotides. Q. Rev. Biophys. 1978, 2, 179–246. [Google Scholar] [CrossRef]
- DeVoe, H.; Tinoco, I., Jr. The stability of helical polynucleotides: Base contributions. J. Mol. Biol. 1962, 4, 500–517. [Google Scholar] [CrossRef]
- Fixman, M.; Freire, J.J. Theory of DNA melting curves. Biopolymers 1977, 16, 2693–2704. [Google Scholar] [CrossRef] [PubMed]
- Nelson, D.L.; Cox, M.M. Lehninger Principles of Biochemistry, 5th ed.; W.H. Freeman and Company: New York, NY, USA, 2008; p. 292. [Google Scholar]
- Owen, R.J.; Hill, L.R.; Lapage, S.P. Determination of DNA base compositions from melting profiles in dilute buffers. Biopolymers 1969, 7, 503–516. [Google Scholar] [CrossRef] [PubMed]
- Bloomfield, V.A. DNA condensation by multivalent cations. Biopolymers 1997, 44, 269–282. [Google Scholar] [CrossRef]
- Tan, Z.-J.; Chen, S.-J. Nucleic acid helix stability: Effects of salt concentration, cation valence and size, and chain length. Biophys. J. 2006, 90, 1175–1190. [Google Scholar] [CrossRef] [PubMed]
- Odijk, T. On the ionic-strength dependence of the intrinsic viscosity of DNA. Biopolymers 1979, 18, 3111–3113. [Google Scholar] [CrossRef] [PubMed]
- Manning, G.S. The persistence length of DNA is reached from the persistence length of its null isomer through an internal electrostatic stretching force. Biophys. J. 2006, 91, 3607–3616. [Google Scholar] [CrossRef] [PubMed]
- Odijk, T.; Houwaart, A.C. On the theory of the excluded-volume effect of a polyelectrolyte in a 1–1 electrolyte solution. J. Polym. Sci. Polym. Phys. 1978, 16, 627–639. [Google Scholar] [CrossRef]
- Harrington, R.E. Opticohydrodynamic properties of high-molecular-weight DNA. III. The effects of NaCl concentration. Biopolymers 1978, 17, 919–936. [Google Scholar] [CrossRef]
- Maret, G.; Weill, G. Magnetic birefringence study of the electrostatic and intrinsic persistence length of DNA. Biopolymers 1983, 22, 2727–2744. [Google Scholar] [CrossRef] [PubMed]
- Odijk, T. Possible scaling relations for semidilute polyelectrolyte Solutions. Macromolecules 1979, 12, 688–693. [Google Scholar] [CrossRef]
- Reed, W.F. Light-scattering results on polyelectrolyte conformations, diffusion, and interparticle and correlations. In Macro-Ion Characterization, From Dilute Solutions to Complex Fluids; Kenneth, S.S., Ed.; American Chemical Society: Washington, DC, USA, 1994. [Google Scholar]
- Mason, T.G.; Dhople, A.; Wirtz, D. Linear viscoelastic moduli of concentrated DNA Solutions. Macromolecules 1998, 31, 3600–3603. [Google Scholar] [CrossRef]
- Raspaud, E.; Lairez, D.; Adam, M. On the number of blobs per entanglement in semidilute and good solvent solution: Melt influence. Macromolecules 1995, 28, 927–933. [Google Scholar] [CrossRef]
- Milas, M.; Rinaudo, M.; Knipper, M.; Schuppiser, J.L. Flow and viscoelastic properties of xanthan gum solutions. Macromolecules 1990, 23, 2506–2511. [Google Scholar] [CrossRef]
- Fouissac, E.; Milas, M.; Rinaudo, M. Shear-Rate, Concentration, Molecular Weight, and Temperature Viscosity Dependences of Hyaluronate, a Wormlike Polyelectrolyte. Macromolecules. 1993, 26, 6945–6951. [Google Scholar] [CrossRef]
- Musti, R.; Sikorav, J.-L.; Lairez, D.; Jannink, G.; Adam, M. Viscoelastic properties of entangled DNA solutions. C. R. Acad. Sci. Série II b 1995, 320, 599–605. [Google Scholar]
- Sun, M.; Pejanović, S.; Mijović, J. Dynamics of deoxyribonucleic acid solutions as studied by dielectric relaxation spectroscopy and dynamic mechanical spectroscopy. Macromolecules 2005, 38, 9854–9864. [Google Scholar] [CrossRef]
- Anselmi, C.; DeSantis, P.; Scipioni, A. Nanoscale mechanical and dynamical properties of DNA single molecules. Biophys. Chem. 2005, 113, 209–221. [Google Scholar] [CrossRef] [PubMed]
- Taulier, N.; Chalikian, T.V. Compressibility of protein transitions. Biochim. Biophys. Acta 2002, 1595, 48–70. [Google Scholar] [CrossRef]
- Wang, N. Mechanical interactions among cytoskeletal filaments. Hypertension 1998, 32, 162–165. [Google Scholar] [CrossRef] [PubMed]
- Chan, E.Y.; Goncalves, N.M.; Haeusler, R.A.; Hatch, A.J.; Larson, J.W.; Maletta, A.M.; Yantz, G.R.; Carstea, E.D.; Fuchs, M.; Wong, G.C.; et al. DNA mapping using microfluidic stretching and single-molecule detection of fluorescent site-specific tags. Genome Res. 2004, 14, 1137–1146. [Google Scholar] [CrossRef] [PubMed]
- Bader, J.S.; Hammond, R.W.; Henck, S.A.; Demm, M.W.; McDermott, G.A.; Bustillo, J.M.; Simpson, J.W.; Mulhern, G.T.; Rothberg, J.M. DNA transport by a micromachined Brownian ratchet device. Proc. Natl. Acad. Sci. USA 1999, 96, 13165–13169. [Google Scholar] [CrossRef] [PubMed]
- Aktins, E.D.; Taylor, M.A. Elongational flow studies on DNA in aqueous solution and stress-induced scission of the double helix. Biopolymers 1992, 32, 911–923. [Google Scholar]
- Juarez, G.; Arratia, P.E. Extensional rheology of DNA suspensions in microfluidic devices. Soft Matter 2011, 7, 9444–9452. [Google Scholar] [CrossRef]
- Graessley, W.M. Polymer chain dimensions and the dependence of viscoelastic properties on concentration, molecular weight and solvent power. Polymer 1980, 21, 258–262. [Google Scholar] [CrossRef]
- Colby, R.H.; Rubinstein, M.; Daoud, M. Hydrodynamics of polymer solutions via two-parameter scaling. J. Phys. II France 1994, 4, 1299–1310. [Google Scholar] [CrossRef]
- Colby, R.H.; Fetters, L.J.; Funk, W.G.; Graessley, W.W. Effects of concentration and thermodynamic interaction on the viscoelastic properties of polymer solutions. Macromolecules 1991, 24, 3873–3882. [Google Scholar] [CrossRef]
- Wilfinger, W.W.; Mackey, K.; Chomczynski, P. Effect of pH and ionic strength on the spectrophotometric assessment of nucleic acid purity. Biotechniques 1997, 22, 478–481. [Google Scholar]
- Alatorre-Meda, M.; Taboada, P.; Hartl, F.; Wagner, T.; Freis, M.; Rodríguez, J.R. The influence of chitosan valence on the complexation and transfection of DNA: The weaker the DNA–chitosan binding the higher the transfection efficiency. Colloids Surf. B Biointerfaces 2011, 82, 54–62. [Google Scholar] [CrossRef] [PubMed]
- Pouton, C.W.; Lucas, P.; Thomas, B.J.; Uduehi, A.N.; Milroy, D.A.; Moss, S.H. Polycation–DNA complexes for gene delivery: A comparison of the biopharmaceutical properties of cationic polypeptides and cationic lipids. J. Control. Release 1998, 53, 289–299. [Google Scholar] [CrossRef]
- Frank-Kamenetskii, M.D. DNA chemistry. How the double helix breathes. Nature 1987, 328, 17–18. [Google Scholar] [CrossRef] [PubMed]
- Record, M.T., Jr. Effects of Na+ and Mg++ Ions on the helix-coil transition of DNA. Biopolymers 1975, 14, 2137–2158. [Google Scholar] [CrossRef]
- Tsortos, A.; Papadakis, G.; Gizeli, E. The intrinsic viscosity of linear DNA. Biopolymers 2011, 95, 824–832. [Google Scholar] [CrossRef] [PubMed]
- Porsch, B.; Laga, R.; Horský, J.; Koňák, Č.; Ulbrich, K. Molecular weight and polydispersity of calf-thymus DNA: Static light-scattering and size-exclusion chromatography with dual detection. Biomacromolecules 2009, 10, 3148–3150. [Google Scholar] [CrossRef] [PubMed]
- Tanigawa, M.; Suzuzuto, M.; Fukudome, K.; Yamaoka, K. Changes in molecular weights and molecular weight distributions of differently stranded nucleic acids after sonication: Gel permeation chromatography/low angle laser light scattering evaluation and computer simulation. Macromolecules 1996, 29, 7418–7425. [Google Scholar] [CrossRef]
- Sundaresan, N.; Suresh, C.H.; Thomas, T.; Thomas, T.J.; Pillai, C.K.S. Liquid crystalline phase behavior of high molecular weight DNA: A comparative study of the influence of metal ions of different size, charge and binding mode. Biomacromolecules 2008, 9, 1860–1869. [Google Scholar] [CrossRef] [PubMed]
- Milas, M.; Rinaudo, M.; Tinland, B. The viscosity dependence on concentration, molecular weight and shear rate of xanthan solutions. Polym. Bull. 1985, 14, 157–164. [Google Scholar] [CrossRef]
- Barnes, H.A.; Hutton, J.F.; Walters, K. An Introduction to Rheology; Elsevier Science: Amsterdam, Netherlands & London, UK & New York, NY, USA & Tokyo, Japan, 1989; p. 128. [Google Scholar]
- Ferry, J.D. Viscoelastic Properties of Polymers, 3rd ed.; John Wiley & Sons: New York, NY, USA, 1980. [Google Scholar]
- Kwei, T.K.; Nakazawa, M.; Matsuoka, S.; Cowman, M.K.; Okamoto, Y. Concentration dependence of solution viscosities of rigid rod polymers. Macromolecules 2000, 33, 235–236. [Google Scholar] [CrossRef]
- Rinaudo, M. Relation between the Molecular Structure of Some Polysaccharides and Original Properties in Sol and Gel States. Food Hydrocoll. 2001, 15, 433–440. [Google Scholar] [CrossRef]
- Kapoor, V.P.; Milas, M.; Taravel, F.R.; Rinaudo, M. Rheological properties of a seed galactomannan from Cassia siamea lamk. Food Hydrocoll. 1996, 10, 167–172. [Google Scholar] [CrossRef]
- Frisman, E.V.; Vorobiev, V.I.; Shchagina, L.V.; Yanovskaya, N.K. Flow birefringence in solutions of deoxyribonucleic acids DNA-I the optical anisotropy of native and aggregated denatured DNA. Vysokomol. Soedin 1962, 4, 762–768. [Google Scholar]
- Berriaud, N.; Milas, M.; Rinaudo, M. Rheological study on mixtures of different molecular weight hyaluronates. Int. J. Biol. Macromol. 1994, 16, 137–142. [Google Scholar] [CrossRef]
- Milas, M.; Rinaudo, M.; Roure, I.; Al-Assaf, S.; Phillips, G.O.; Williams, P.A. Comparative rheological behavior of hyaluronan from bacterial and animal sources with cross-linked hyaluronan (hylan) in aqueous solution. Biopolymers 2001, 59, 191–204. [Google Scholar] [CrossRef]
- Colby, R.H. Structure and linear viscoelasticity of flexible polymer solutions: comparison of polyelectrolyte and neutral polymer Solutions. Rheol. Acta 2010, 49, 425–442. [Google Scholar] [CrossRef]
- Graessley, W.W. The Entanglement Concept in Polymer Rheology; Springer: Berlin, Germany, 1974; pp. 1–179. [Google Scholar]
- Yılmaz, M.T.; Karaman, S.; Cankurt, H.; Kayacier, A.; Sagdic, O. Steady and dynamic oscillatory shear rheological properties of ketchup–processed cheese mixtures: Effect of temperature and concentration. J. Food Eng. 2011, 103, 197–210. [Google Scholar] [CrossRef]
© 2016 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bravo-Anaya, L.M.; Rinaudo, M.; Martínez, F.A.S. Conformation and Rheological Properties of Calf-Thymus DNA in Solution. Polymers 2016, 8, 51. https://doi.org/10.3390/polym8020051
Bravo-Anaya LM, Rinaudo M, Martínez FAS. Conformation and Rheological Properties of Calf-Thymus DNA in Solution. Polymers. 2016; 8(2):51. https://doi.org/10.3390/polym8020051
Chicago/Turabian StyleBravo-Anaya, Lourdes Mónica, Marguerite Rinaudo, and Félix Armando Soltero Martínez. 2016. "Conformation and Rheological Properties of Calf-Thymus DNA in Solution" Polymers 8, no. 2: 51. https://doi.org/10.3390/polym8020051
APA StyleBravo-Anaya, L. M., Rinaudo, M., & Martínez, F. A. S. (2016). Conformation and Rheological Properties of Calf-Thymus DNA in Solution. Polymers, 8(2), 51. https://doi.org/10.3390/polym8020051