Hydrodynamic Interactions and Entanglements of Polymer Solutions in Many-Body Dissipative Particle Dynamics
Abstract
:1. Introduction
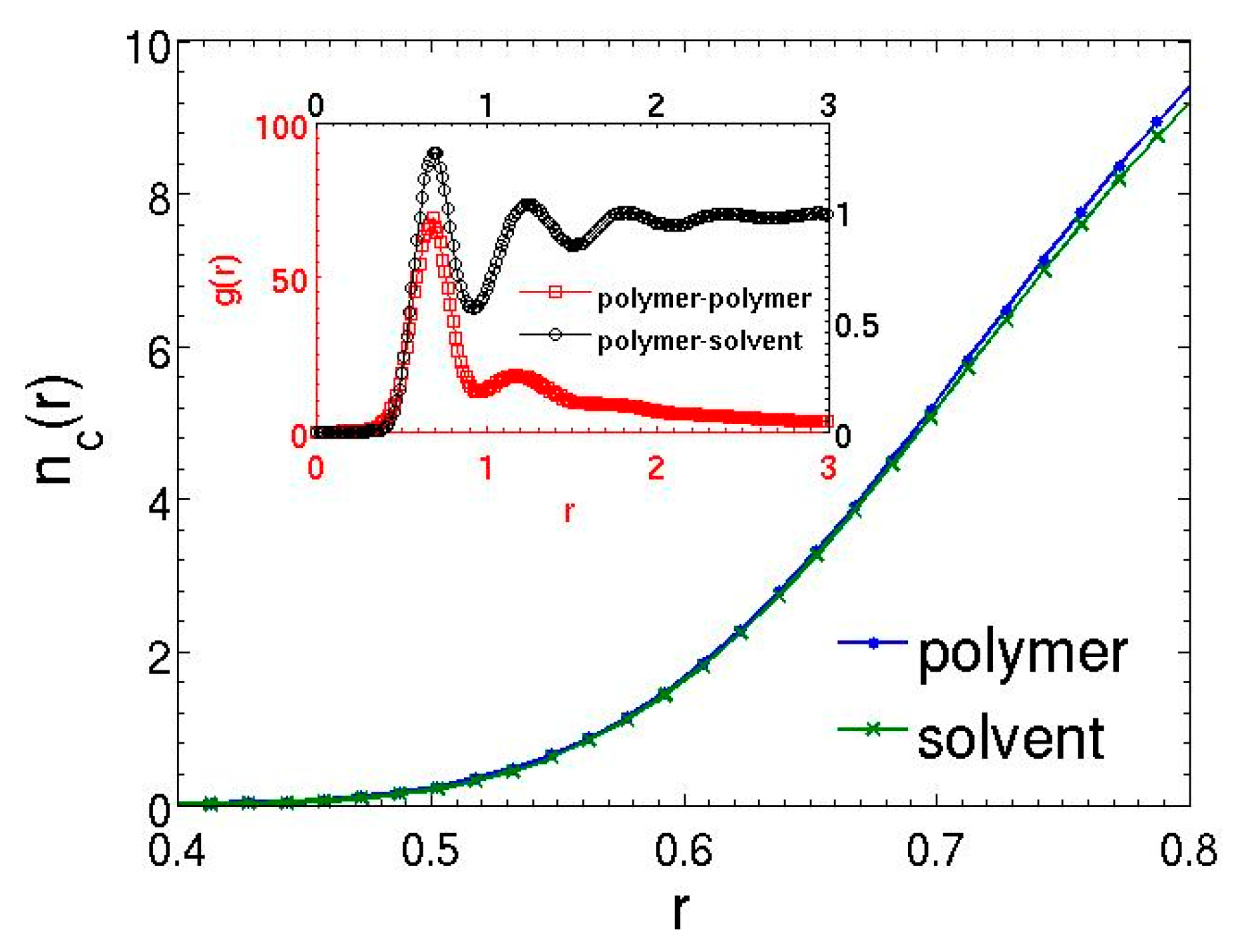
2. Methods
3. Results and Discussion
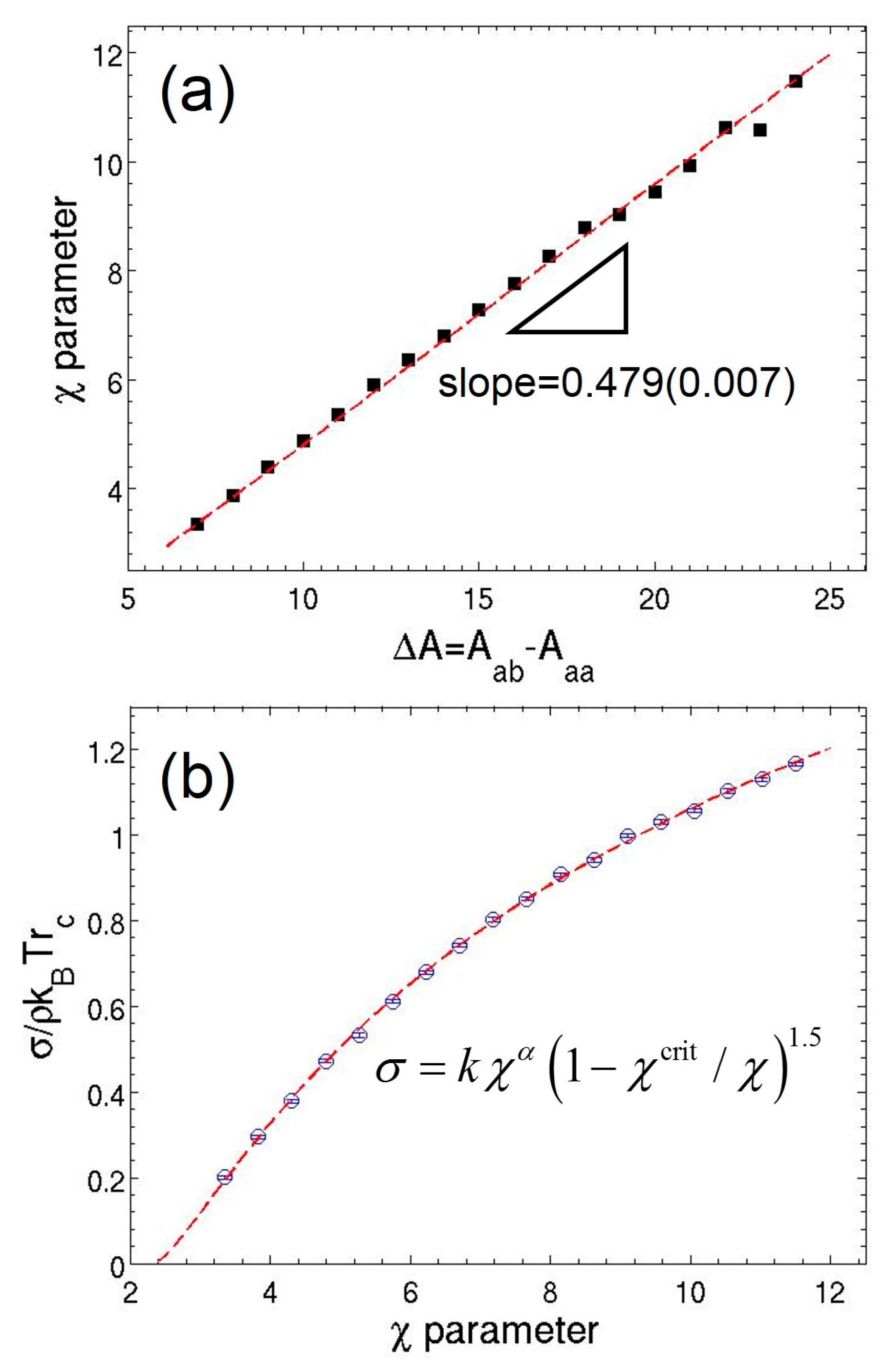
3.1. Parameterization of MDPD Parameters
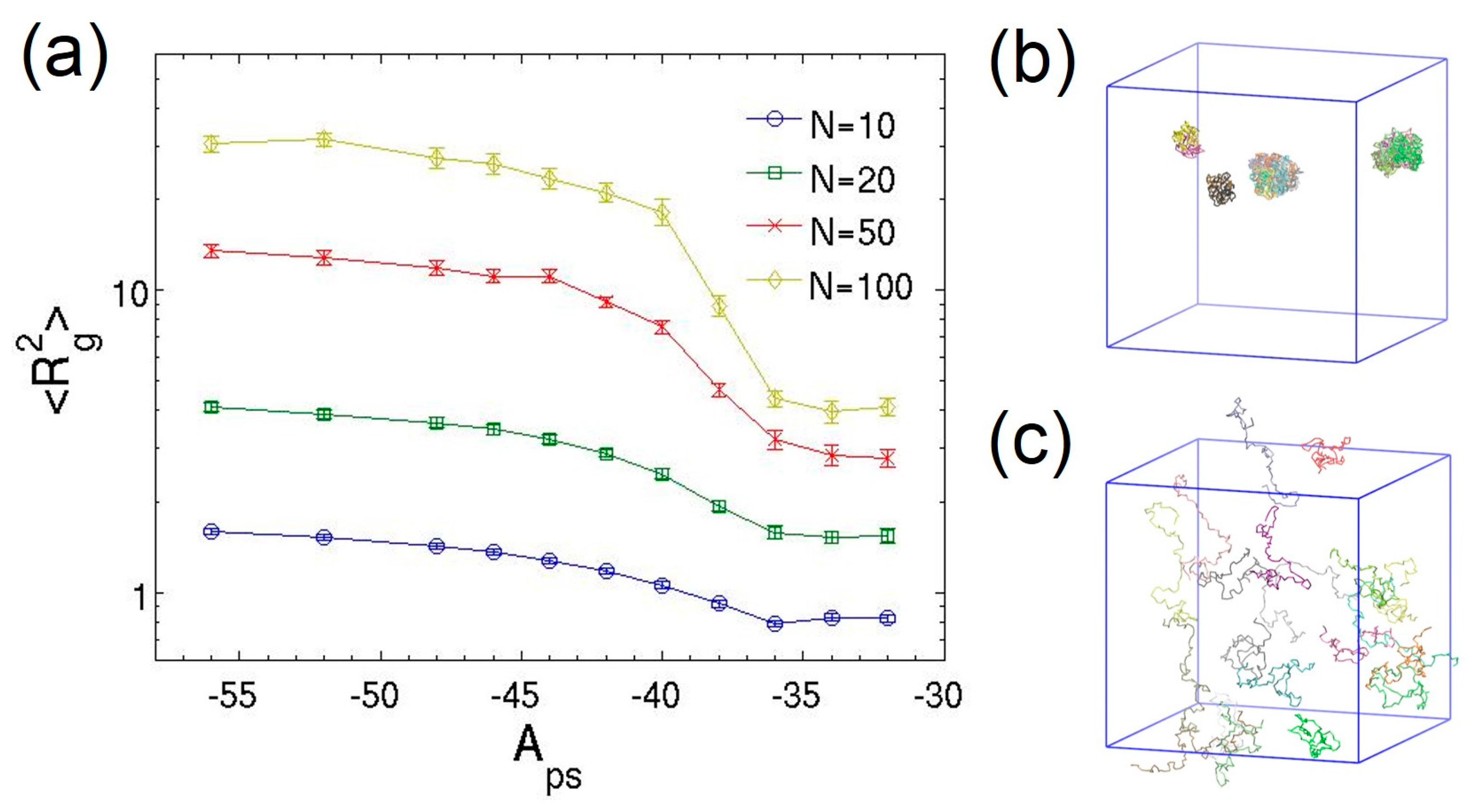
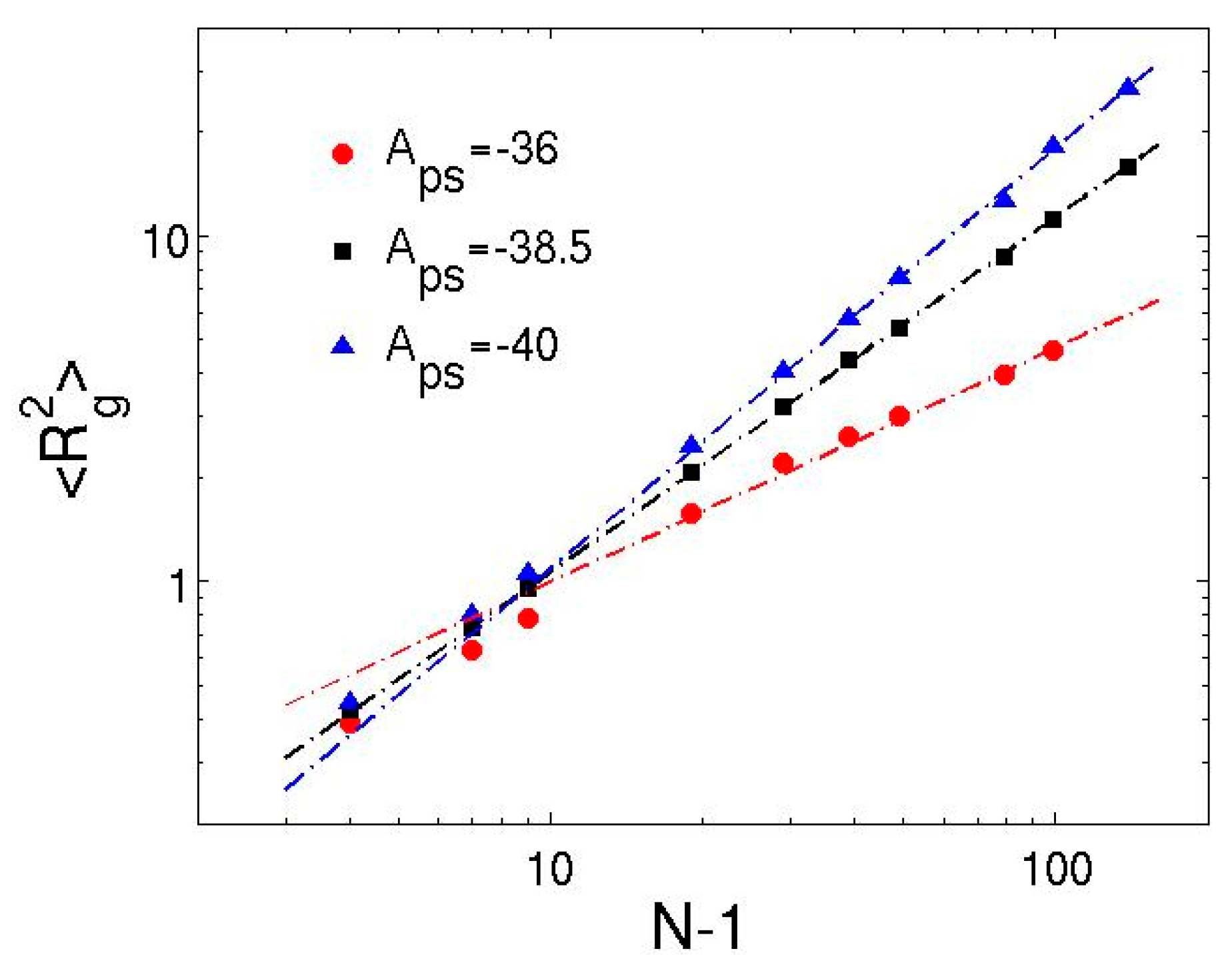
3.2. Dilute Polymer Solutions for Different Solvent Quality
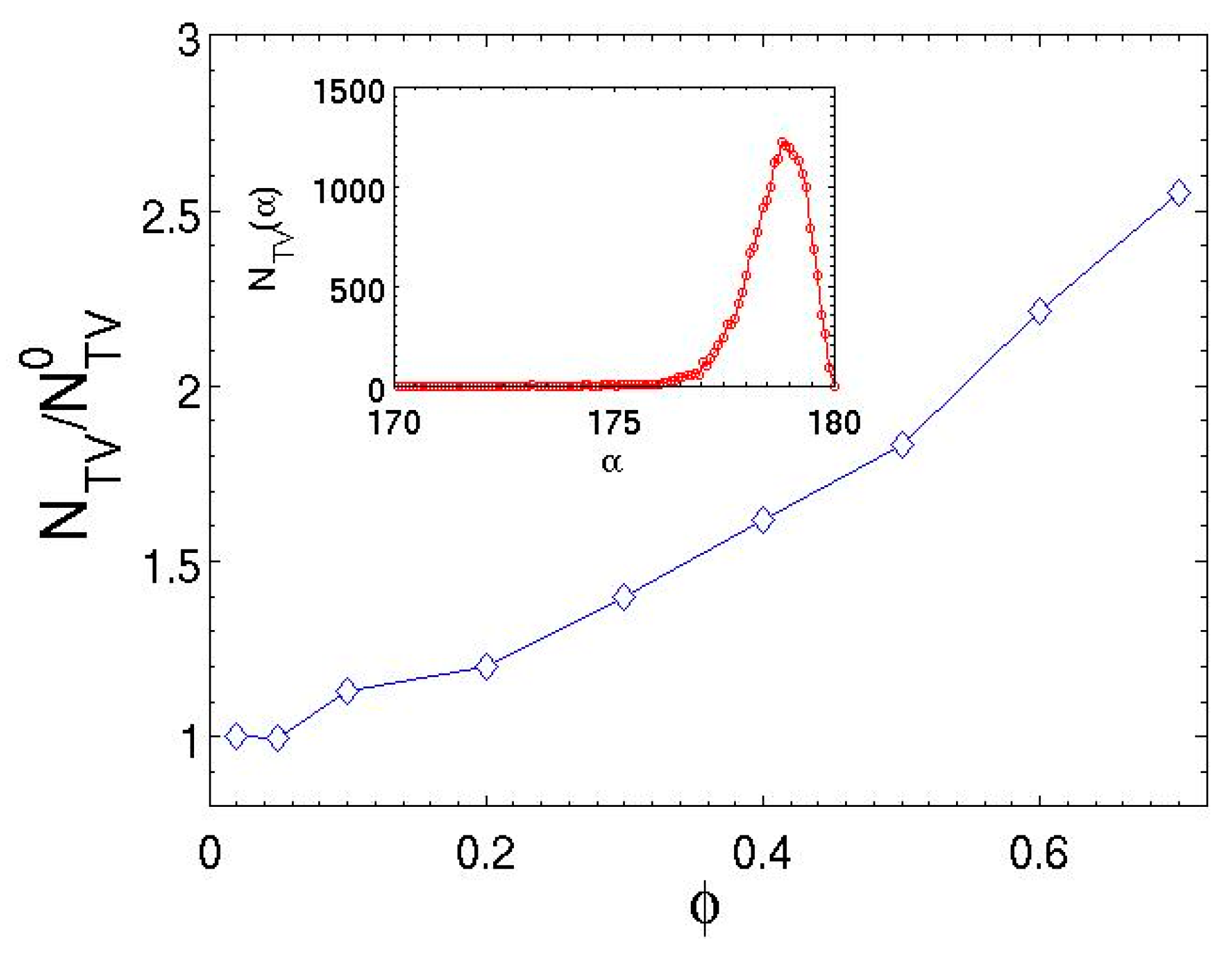
3.3. Semidilute Solutions and Entanglements
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Hench, L.L.; West, J.K. The sol-gel process. Chem. Rev. 1990, 90, 33–72. [Google Scholar] [CrossRef]
- Brinker, C.J.; Lu, Y.; Sellinger, A.; Fan, H. Evaporation-induced self-assembly: Nanostructures made easy. Adv. Mater. 1999, 11, 579–585. [Google Scholar] [CrossRef]
- Eslamian, M. Spray-on thin film PV solar cells: Advances, potentials and challenges. Coatings 2014, 4, 60–84. [Google Scholar] [CrossRef]
- Derby, B. Inkjet printing of functional and structural materials: Fluid property requirements, feature stability, and resolution. Annu. Rev. Mater. Res. 2010, 40, 395–414. [Google Scholar] [CrossRef]
- Faustini, M.; Boissière, C.; Nicole, L.; Grosso, D. From chemical solutions to inorganic nanostructured materials: A journey into evaporation-driven processes. Chem. Mater. 2014, 26, 709–723. [Google Scholar] [CrossRef]
- Han, W.; Lin, Z. Learning from “coffee rings”: Ordered structures enabled by controlled evaporative self-assembly. Angew. Chem. Int. Ed. 2012, 51, 1534–1546. [Google Scholar] [CrossRef] [PubMed]
- Rabani, E.; Reichman, D.R.; Geissler, P.L.; Brus, L.E. Drying-mediated self-assembly of nanoparticles. Nature 2003, 426, 271–274. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Douglas, J.F.; Jones, R.L. Influence of film casting method on block copolymer ordering in thin films. Soft Matter 2012, 8, 4980–4987. [Google Scholar] [CrossRef]
- Strawhecker, K.E.; Kumar, S.K.; Douglas, J.F.; Karim, A. The critical role of solvent evaporation on the roughness of spin-cast polymer films. Macromolecules 2001, 34, 4669–4672. [Google Scholar] [CrossRef]
- De Gennes, P.-G. Solvent evaporation of spin cast films: Crust effects. Eur. Phys. J. E 2001, 7, 31–34. [Google Scholar] [CrossRef]
- Jouault, N.; Zhao, D.; Kumar, S.K. Role of casting solvent on nanoparticle dispersion in polymer nanocomposites. Macromolecules 2014, 47, 5246–5255. [Google Scholar] [CrossRef]
- Español, P. Hydrodynamics from dissipative particle dynamics. Phys. Rev. E 1995, 52, 1734–1742. [Google Scholar] [CrossRef]
- Pivkin, I.V.; Caswell, B.; Karniadakisa, G.E. Dissipative particle dynamics. In Reviews in Computational Chemistry; John Wiley & Sons, Inc.: New York, NY, USA, 2010. [Google Scholar]
- Hoogerbrugge, P.J.; Koelman, J.M.V.A. Simulating microscopic hydrodynamic phenomena with dissipative particle dynamics. Europhys. Lett. 1992, 19, 155–160. [Google Scholar] [CrossRef]
- Groot, R.D.; Warren, P.B. Dissipative particle dynamics: Bridging the gap between atomistic and mesoscopic simulation. J. Chem. Phys. 1997, 107, 4423–4435. [Google Scholar] [CrossRef]
- Groot, R.D.; Madden, T.J. Dynamic simulation of diblock copolymer microphase separation. J. Chem. Phys. 1998, 108, 8713–8724. [Google Scholar] [CrossRef]
- Groot, R.D.; Madden, T.J.; Tildesley, D.J. On the role of hydrodynamic interactions in block copolymer microphase separation. J. Chem. Phys. 1999, 110, 9739. [Google Scholar] [CrossRef]
- Symeonidis, V.; Karniadakis, G.E.; Caswell, B. Dissipative particle dynamics simulations of polymer chains: Scaling laws and shearing response compared to DNA experiments. Phys. Rev. Lett. 2005, 95. [Google Scholar] [CrossRef]
- Li, Z.; Drazer, G. Hydrodynamic interactions in dissipative particle dynamics. Phys. Fluids 2008, 20, 103601. [Google Scholar] [CrossRef]
- Schlijper, A.G.; Hoogerbrugge, P.J.; Manke, C.W. Computer simulation of dilute polymer solutions with the dissipative particle dynamics method. J. Rheol. 1995, 39, 567–579. [Google Scholar] [CrossRef]
- Spenley, N.A. Scaling laws for polymers in dissipative particle dynamics. Europhys. Lett. 2000, 49, 534–540. [Google Scholar] [CrossRef]
- Kong, Y.; Manke, C.W.; Madden, W.G.; Schlijper, A.G. Effect of solvent quality on the conformation and relaxation of polymers via dissipative particle dynamics. J. Chem. Phys. 1997, 107, 592–602. [Google Scholar] [CrossRef]
- Jiang, W.; Huang, J.; Wang, Y.; Laradji, M. Hydrodynamic interaction in polymer solutions simulated with dissipative particle dynamics. J. Chem. Phys. 2007, 126, 044901. [Google Scholar] [CrossRef] [PubMed]
- Zhao, T.; Wang, X.; Jiang, L.; Larson, R.G. Dissipative particle dynamics simulation of dilute polymer solutions—Inertial effects and hydrodynamic interactions. J. Rheol. 2014, 58, 1039–1058. [Google Scholar] [CrossRef]
- Malfreyt, P.; Tildesley, D.J. Dissipative particle dynamics simulations of grafted polymer chains between two walls. Langmuir 2000, 16, 4732–4740. [Google Scholar] [CrossRef]
- Raos, G.; Moreno, M.; Elli, S. Computational experiments on filled rubber viscoelasticity: What is the role of particle-particle interactions? Macromolecules 2006, 39, 6744–6751. [Google Scholar] [CrossRef]
- Yong, X.; Kuksenok, O.; Matyjaszewski, K.; Balazs, A.C. Harnessing interfacially-active nanorods to regenerate severed polymer gels. Nano Lett. 2013, 13, 6269–6274. [Google Scholar] [CrossRef] [PubMed]
- Yong, X. Modeling the assembly of polymer-grafted nanoparticles at oil-water interfaces. Langmuir 2015, 31, 11458–11469. [Google Scholar] [CrossRef] [PubMed]
- Yong, X.; Simakova, A.; Averick, S.; Gutierrez, J.; Kuksenok, O.; Balazs, A.C.; Matyjaszewski, K. Stackable, covalently fused gels: Repair and composite formation. Macromolecules 2015, 48, 1169–1178. [Google Scholar] [CrossRef]
- Pagonabarraga, I.; Frenkel, D. Dissipative particle dynamics for interacting systems. J. Chem. Phys. 2001, 115, 5015–5026. [Google Scholar] [CrossRef]
- Trofimov, S.Y.; Nies, E.L.F.; Michels, M.A.J. Constant-pressure simulations with dissipative particle dynamics. J. Chem. Phys. 2005, 123, 144102. [Google Scholar] [CrossRef] [PubMed]
- Warren, P.B. Vapor-liquid coexistence in many-body dissipative particle dynamics. Phys. Rev. E 2003, 68, 066702. [Google Scholar] [CrossRef] [PubMed]
- Tiwari, A.; Abraham, J. Dissipative-particle-dynamics model for two-phase flows. Phys. Rev. E 2006, 74, 056701. [Google Scholar] [CrossRef] [PubMed]
- Arienti, M.; Pan, W.; Li, X.; Karniadakis, G. Many-body dissipative particle dynamics simulation of liquid/vapor and liquid/solid interactions. J. Chem. Phys. 2011, 134, 204114. [Google Scholar] [CrossRef] [PubMed]
- Yong, X.; Qin, S.; Singler, T.J. Nanoparticle-mediated evaporation at liquid–vapor interfaces. Extreme Mech. Lett. 2016, 7, 90–103. [Google Scholar] [CrossRef]
- Ghoufi, A.; Malfreyt, P. Mesoscale modeling of the water liquid-vapor interface: A surface tension calculation. Phys. Rev. E 2011, 83, 051601. [Google Scholar] [CrossRef] [PubMed]
- Ghoufi, A.; Malfreyt, P. Coarse grained simulations of the electrolytes at the water-air interface from many body dissipative particle dynamics. J. Chem. Theory Comput. 2012, 8, 787–791. [Google Scholar] [CrossRef] [PubMed]
- Ghoufi, A.; Emile, J.; Malfreyt, P. Recent advances in many body dissipative particles dynamics simulations of liquid-vapor interfaces. Eur. Phys. J. E 2013, 36, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.; Zhuang, L.; Li, X.; Dong, J.; Lu, J. A Many-body dissipative particle dynamics study of forced water-oil displacement in capillary. Langmuir 2012, 28, 1330–1336. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Chen, S. Numerical study on droplet sliding across micropillars. Langmuir 2015, 31, 4673–4677. [Google Scholar] [CrossRef] [PubMed]
- Jamali, S.; Boromand, A.; Khani, S.; Wagner, J.; Yamanoi, M.; Maia, J. Generalized mapping of multi-body dissipative particle dynamics onto fluid compressibility and the Flory-Huggins Theory. J. Chem. Phys. 2015, 142, 164902. [Google Scholar] [CrossRef] [PubMed]
- Trofimov, S.Y.; Nies, E.L.F.; Michels, M.A.J. Thermodynamic consistency in dissipative particle dynamics simulations of strongly nonideal liquids and liquid mixtures. J. Chem. Phys. 2002, 117, 9383–9394. [Google Scholar] [CrossRef]
- Zhu, Y.-L.; Liu, H.; Lu, Z.-Y. A highly coarse-grained model to simulate entangled polymer melts. J. Chem. Phys. 2012, 136, 144903. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.C.; Liu, H.; Huang, X.R.; Sun, C.C. Evaporation- and surface-induced morphology of symmetric diblock copolymer thin films: A multibody dissipative particle dynamics study. Mol. Simul. 2011, 37, 875–883. [Google Scholar] [CrossRef]
- Tiwari, A.; Reddy, H.; Mukhopadhyay, S.; Abraham, J. Simulations of liquid nanocylinder breakup with dissipative particle dynamics. Phys. Rev. E 2008, 78, 1–11. [Google Scholar] [CrossRef]
- Stroberg, W.; Keten, S.; Liu, W.K. Hydrodynamics of capillary imbibition under nanoconfinement. Langmuir 2012, 28, 14488–14495. [Google Scholar] [CrossRef] [PubMed]
- Cupelli, C.; Henrich, B.; Glatzel, T.; Zengerle, R.; Moseler, M.; Santer, M. Dynamic capillary wetting studied with dissipative particle dynamics. New J. Phys. 2008, 10, 1–4. [Google Scholar] [CrossRef]
- Li, Z.; Hu, G.-H.; Wang, Z.-L.; Ma, Y.-B.; Zhou, Z.-W. Three dimensional flow structures in a moving droplet on substrate: A dissipative particle dynamics study. Phys. Fluids 2013, 25, 072103. [Google Scholar] [CrossRef]
- Chen, C.; Gao, C.; Zhuang, L.; Li, X.; Wu, P.; Dong, J.; Lu, J. A many-body dissipative particle dynamics study of spontaneous capillary imbibition and drainage. Langmuir 2010, 26, 9533–9538. [Google Scholar] [CrossRef] [PubMed]
- Español, P.; Warren, P. Statistical mechanics of dissipative particle dynamics. Europhys. Lett. 1995, 30, 191–196. [Google Scholar] [CrossRef]
- Sirk, T.W.; Slizoberg, Y.R.; Brennan, J.K.; Lisal, M.; Andzelm, J.W. An enhanced entangled polymer model for dissipative particle dynamics. J. Chem. Phys. 2012, 136, 134903. [Google Scholar] [CrossRef] [PubMed]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Warren, P.B. No-go theorem in many-body dissipative particle dynamics. Phys. Rev. E 2013, 87, 045303. [Google Scholar] [CrossRef] [PubMed]
- Binder, K. Monte Carlo and Molecular Dynamics Simulations in Polymer Science; Oxford University Press: New York, NY, USA, 1995. [Google Scholar]
- Hossain, D.; Tschopp, M.A.; Ward, D.K.; Bouvard, J.L.; Wang, P.; Horstemeyer, M.F. Molecular dynamics simulations of deformation mechanisms of amorphous polyethylene. Polymer 2010, 51, 6071–6083. [Google Scholar] [CrossRef]
- Groot, R.D.; Rabone, K.L. Mesoscopic simulation of cell membrane damage, morphology change and rupture by nonionic surfactants. Biophys. J. 2001, 81, 725–736. [Google Scholar] [CrossRef]
- Flory, P.J. Principles of Polymer Chemistry, 1st ed.; Cornell University Press: Ithaca, NY, USA, 1953. [Google Scholar]
- Maiti, A.; McGrother, S. Bead–bead interaction parameters in dissipative particle dynamics: Relation to bead-size, solubility parameter, and surface tension. J. Chem. Phys. 2004, 120, 1594. [Google Scholar] [CrossRef] [PubMed]
- Travis, K.P.; Bankhead, M.; Good, K.; Owens, S.L. New parametrization method for dissipative particle dynamics. J. Chem. Phys. 2007, 127, 014109. [Google Scholar] [CrossRef] [PubMed]
- Liyana-Arachchi, T.P.; Jamadagni, S.N.; Eike, D.; Koenig, P.H.; Siepmann, J.I. Liquid-liquid equilibria for soft-repulsive particles: Improved equation of state and methodology for representing molecules of different sizes and chemistry in dissipative particle dynamics. J. Chem. Phys. 2015, 142, 044902. [Google Scholar] [CrossRef] [PubMed]
- Irving, J.H.; Kirkwood, J.G. The statistical mechanical theory of transport processes. IV. The equations of hydrodynamics. J. Chem. Phys. 1950, 18, 817. [Google Scholar] [CrossRef]
- De Gennes, P.G. Collapse of a polymer chain in poor solvents. J. Phys. Lett. 1975, 36, 55–57. [Google Scholar] [CrossRef]
- De Gennes, P.G. Collapse of a flexible polymer chain II. J. Phys. Lett. 1978, 39, 299–301. [Google Scholar] [CrossRef]
- Zimm, B.H. Dynamics of polymer molecules in dilute solution: Viscoelasticity, flow birefringence and dielectric loss. J. Chem. Phys. 1956, 24, 269–278. [Google Scholar] [CrossRef]
- Rouse, P.E. A theory of the linear viscoelastic properties of dilute solutions of coiling polymers. J. Chem. Phys. 1953, 21, 1272–1280. [Google Scholar] [CrossRef]
- Pierotti, R.A. A scaled particle theory of aqueous and nonaqueous solutions. Chem. Rev. 1976, 76, 717–726. [Google Scholar] [CrossRef]
- Simmons, D.S.; Sanchez, I.C. Scaled particle theory for the coil–globule transition of an isolated polymer chain. Macromolecules 2013, 46, 4691–4697. [Google Scholar] [CrossRef]
- Pan, G.; Manke, C.W. Developments toward simulation of entangled polymer melts by dissipative particle dynamics (DPD). Int. J. Mod. Phys. B 2003, 17, 231–235. [Google Scholar] [CrossRef]
- Kaznessis, Y.N.; Hill, D.A.; Maginn, E.J. A molecular dynamics study of macromolecules in good solvents: Comparison with dielectric spectroscopy experiments. J. Chem. Phys. 1998, 109, 5078–5088. [Google Scholar] [CrossRef]
- Kumar, S.; Larson, R.G. Brownian dynamics simulations of flexible polymers with spring–spring repulsions. J. Chem. Phys. 2001, 114, 6937–6941. [Google Scholar] [CrossRef]
- Padding, J.T.; Briels, W.J. Uncrossability constraints in mesoscopic polymer melt simulations: Non-rouse behavior of C120H242. J. Chem. Phys. 2001, 115, 2846–2859. [Google Scholar] [CrossRef]
- Hoda, N.; Larson, R.G. Brownian dynamics simulations of single polymer chains with and without self-entanglements in theta and good solvents under imposed flow fields. J. Rheol. 2010, 54, 1061–1081. [Google Scholar] [CrossRef]
- Nikunen, P.; Vattulainen, I.; Karttunen, M. Reptational dynamics in dissipative particle dynamics simulations of polymer melts. Phys. Rev. E 2007, 75, 036713. [Google Scholar] [CrossRef] [PubMed]
- Sliozberg, Y.R.; Sirk, T.W.; Brennan, J.K.; Andzelm, J.W. Bead-spring models of entangled polymer melts: Comparison of hard-core and soft-core potentials. J. Polym. Sci. Part B 2012, 50, 1694–1698. [Google Scholar] [CrossRef]
- Goujon, F.; Malfreyt, P.; Tildesley, D.J. Mesoscopic simulation of entanglements using dissipative particle dynamics: Application to polymer brushes. J. Chem. Phys. 2008, 129, 034902. [Google Scholar] [CrossRef] [PubMed]
- Holleran, S.P.; Larson, R.G. Using spring repulsions to model entanglement interactions in brownian dynamics simulations of bead-spring chains. Rheol. Acta 2008, 47, 3–17. [Google Scholar] [CrossRef]
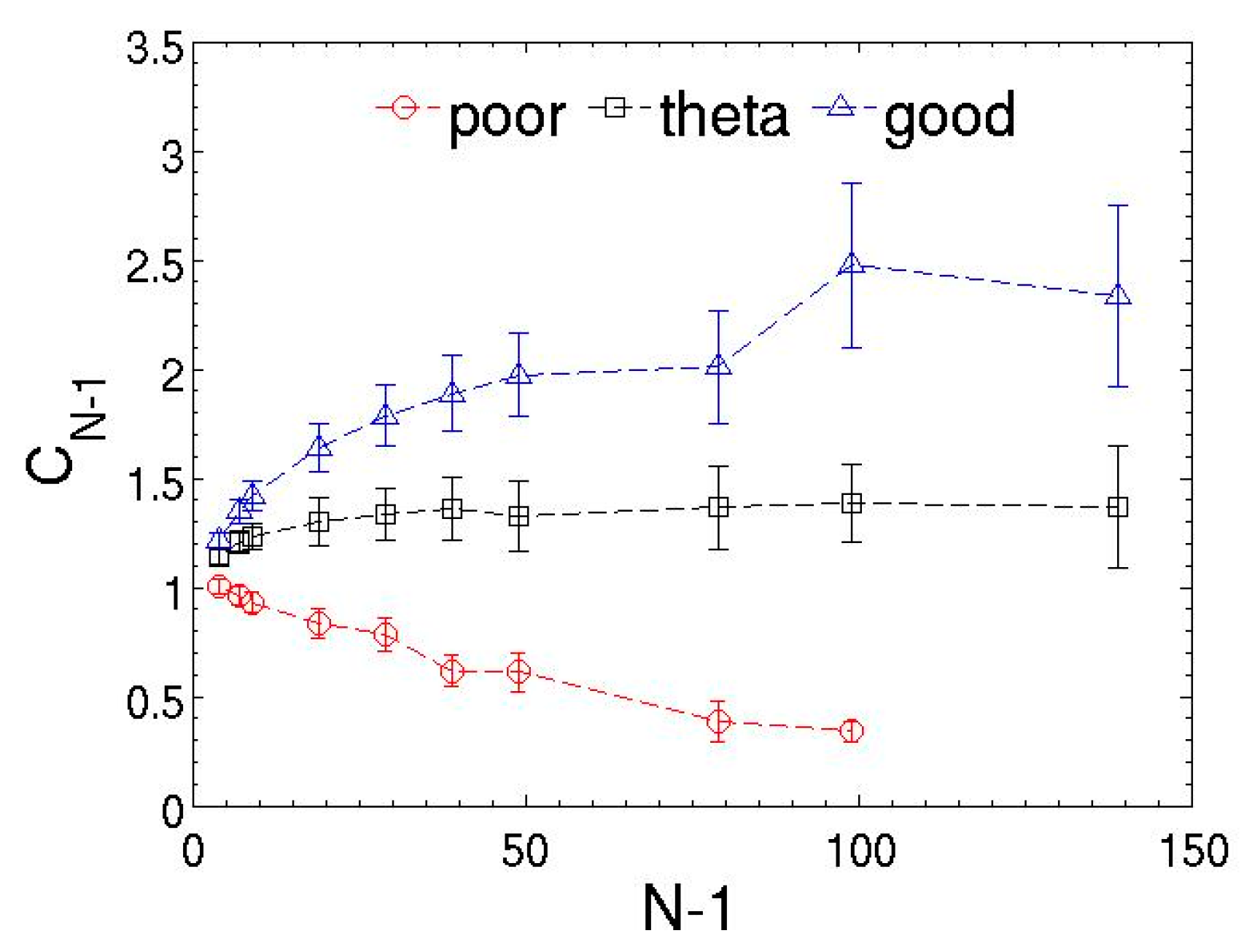
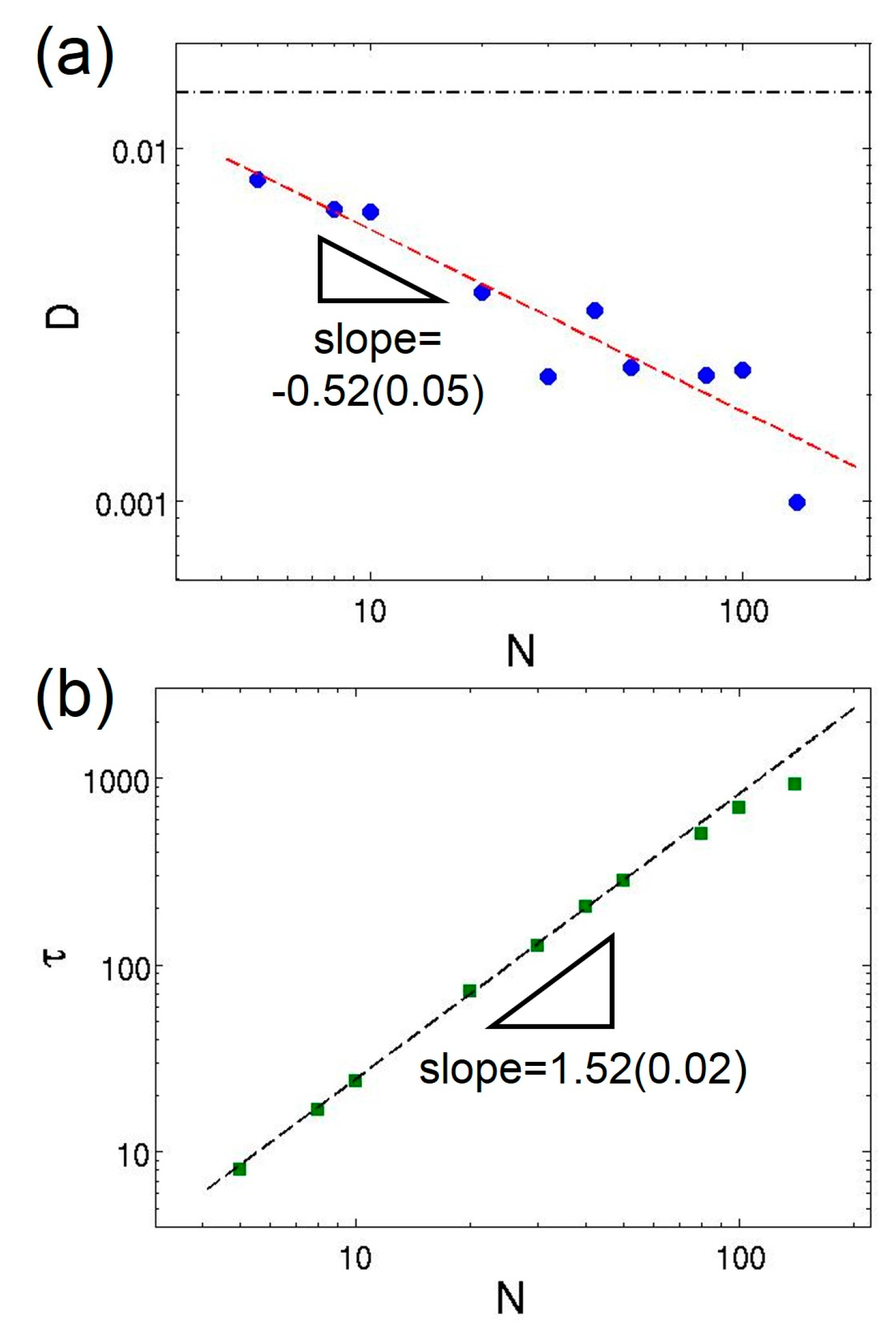
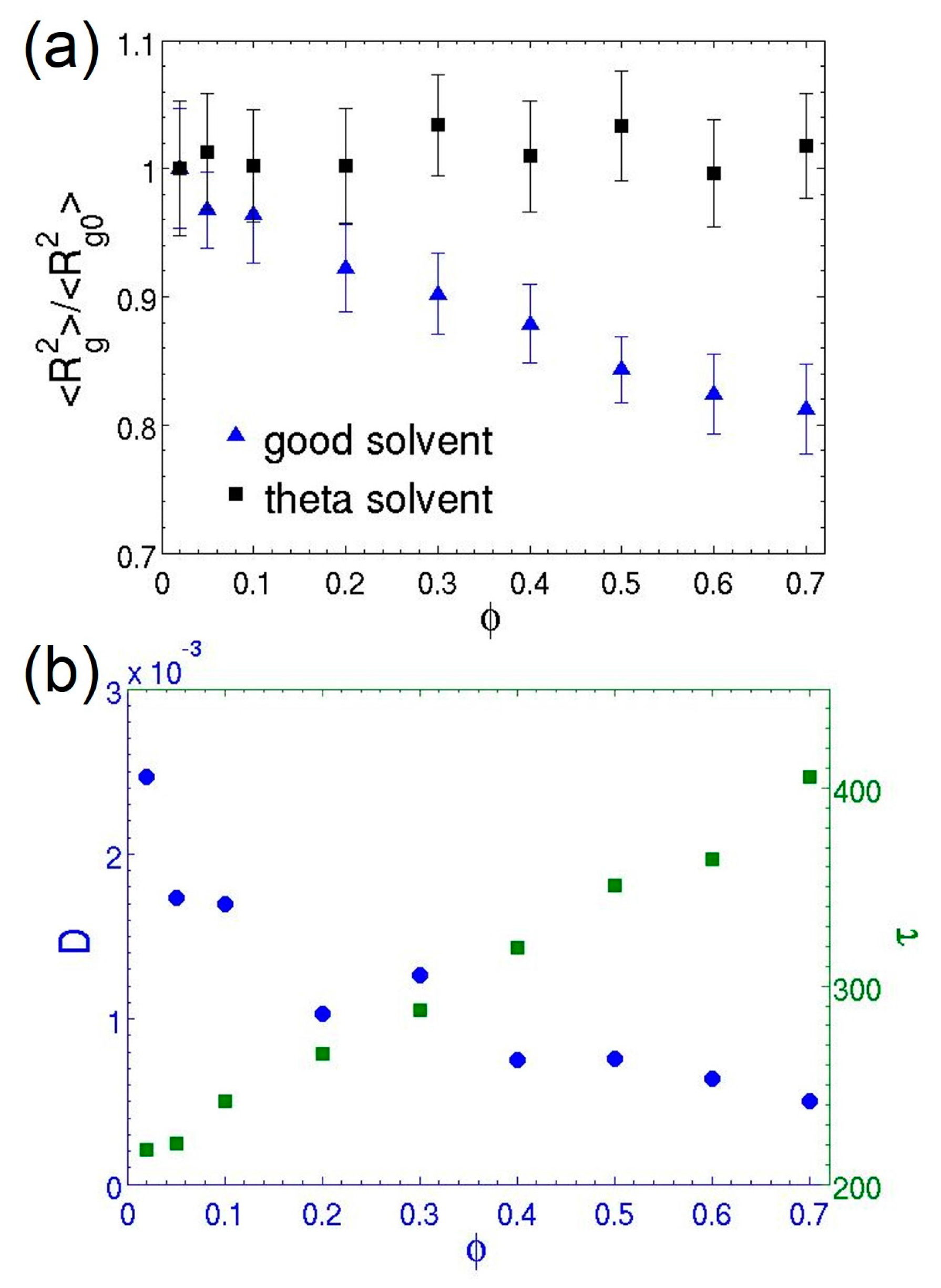
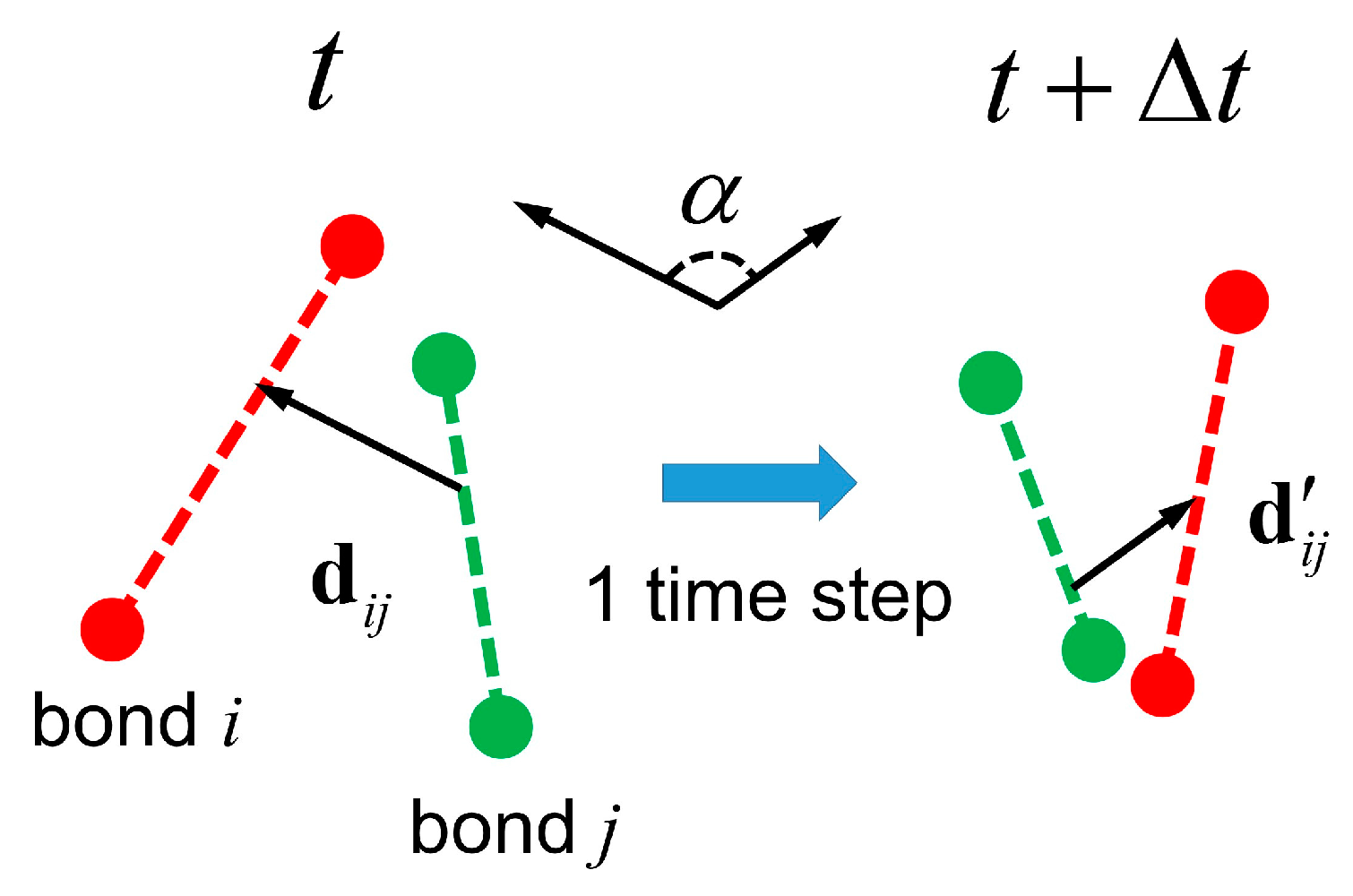
| 5 | 0.43 | 2.22 | 5.23 | 1.14 |
| 8 | 0.74 | 4.12 | 5.57 | 1.21 |
| 10 | 0.95 | 5.41 | 5.68 | 1.23 |
| 20 | 2.06 | 12.06 | 5.85 | 1.30 |
| 30 | 3.20 | 18.89 | 5.90 | 1.34 |
| 40 | 4.36 | 25.87 | 5.94 | 1.36 |
| 50 | 5.39 | 31.71 | 5.89 | 1.32 |
| 80 | 8.74 | 52.64 | 6.03 | 1.37 |
| 100 | 11.21 | 66.91 | 5.97 | 1.38 |
| 140 | 15.82 | 92.87 | 5.8 | 1.37 |
| φ | 0.02 | 0.05 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 |
|---|---|---|---|---|---|---|---|---|---|
| 169.7 | 168.7 | 191.3 | 203.6 | 237.4 | 274.3 | 310.9 | 376.0 | 432.8 |
© 2016 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yong, X. Hydrodynamic Interactions and Entanglements of Polymer Solutions in Many-Body Dissipative Particle Dynamics. Polymers 2016, 8, 426. https://doi.org/10.3390/polym8120426
Yong X. Hydrodynamic Interactions and Entanglements of Polymer Solutions in Many-Body Dissipative Particle Dynamics. Polymers. 2016; 8(12):426. https://doi.org/10.3390/polym8120426
Chicago/Turabian StyleYong, Xin. 2016. "Hydrodynamic Interactions and Entanglements of Polymer Solutions in Many-Body Dissipative Particle Dynamics" Polymers 8, no. 12: 426. https://doi.org/10.3390/polym8120426
APA StyleYong, X. (2016). Hydrodynamic Interactions and Entanglements of Polymer Solutions in Many-Body Dissipative Particle Dynamics. Polymers, 8(12), 426. https://doi.org/10.3390/polym8120426





