Dynamics of DNA Squeezed Inside a Nanochannel via a Sliding Gasket
Abstract
:1. Introduction
2. DNA Simulation Approaches
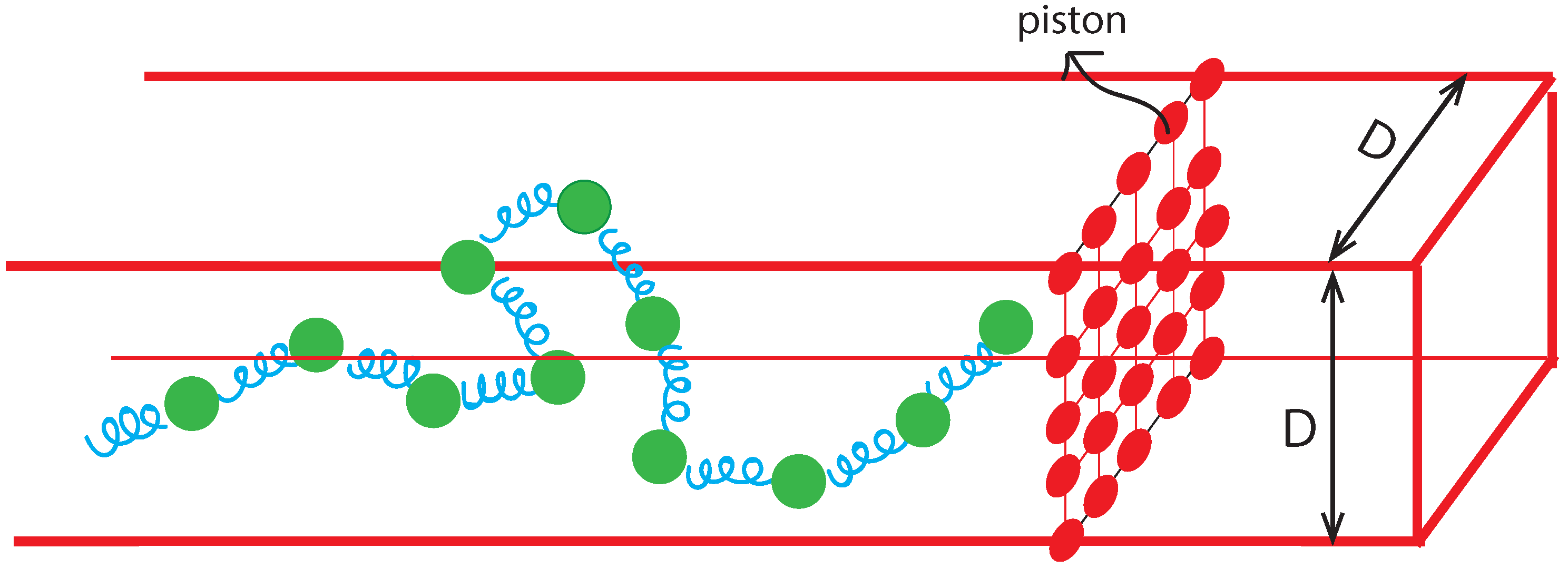
2.1. Bead-Spring Model and BD Simulation
2.2. The Nonlinear Partial Differential Equation (NPDE) Approach
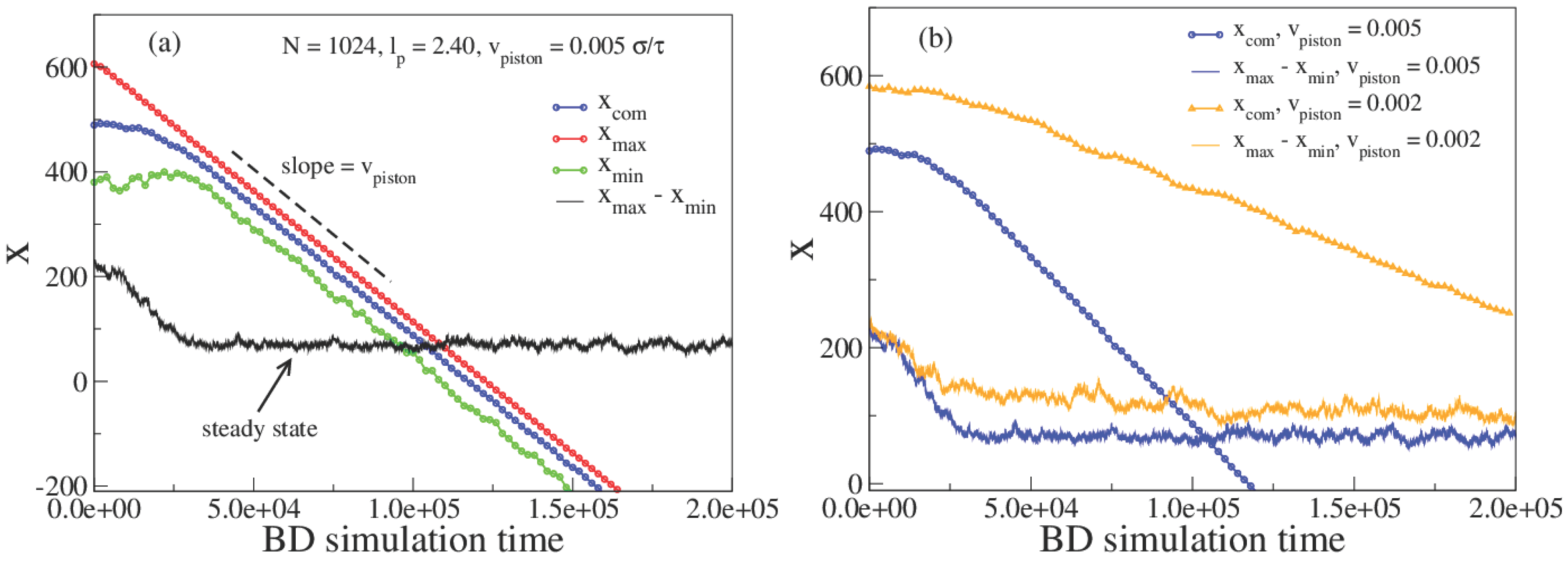
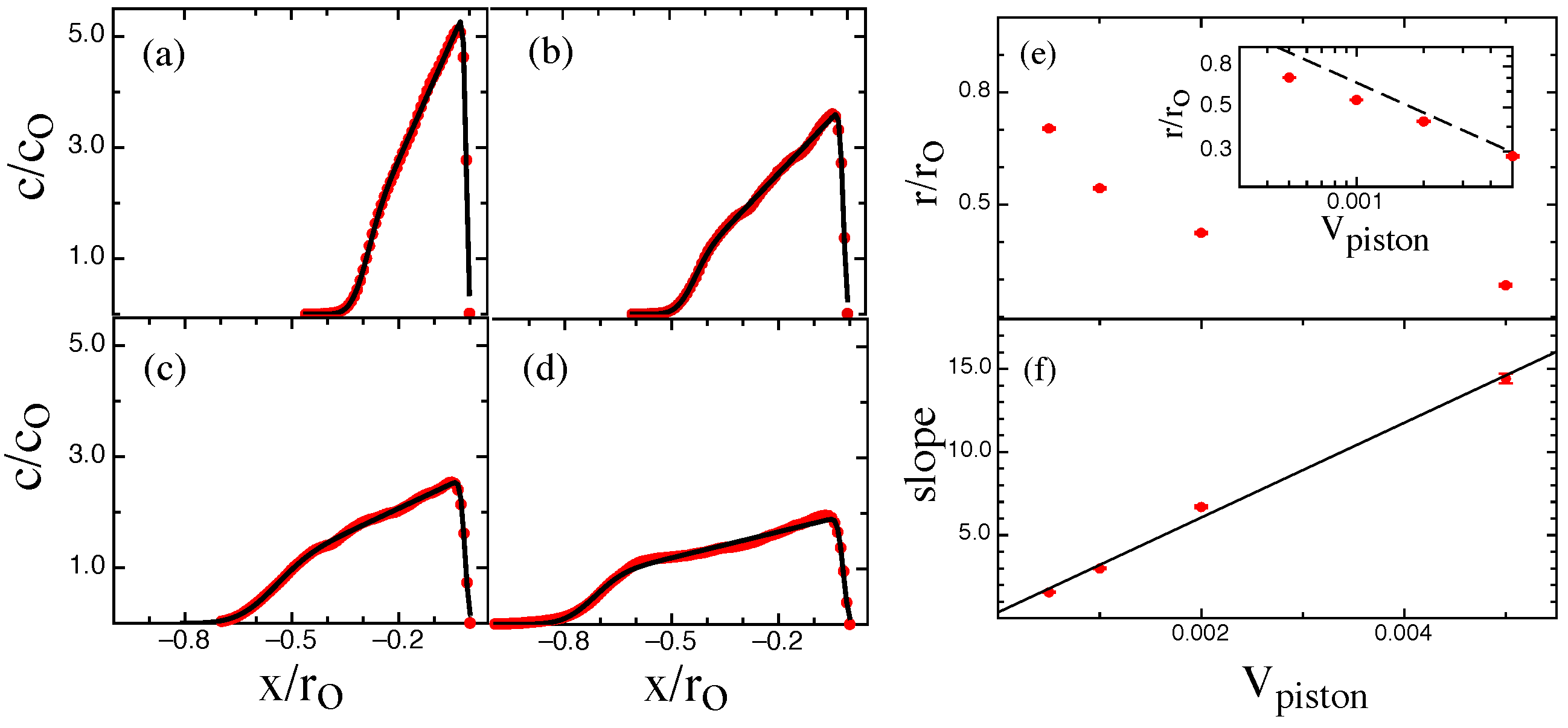
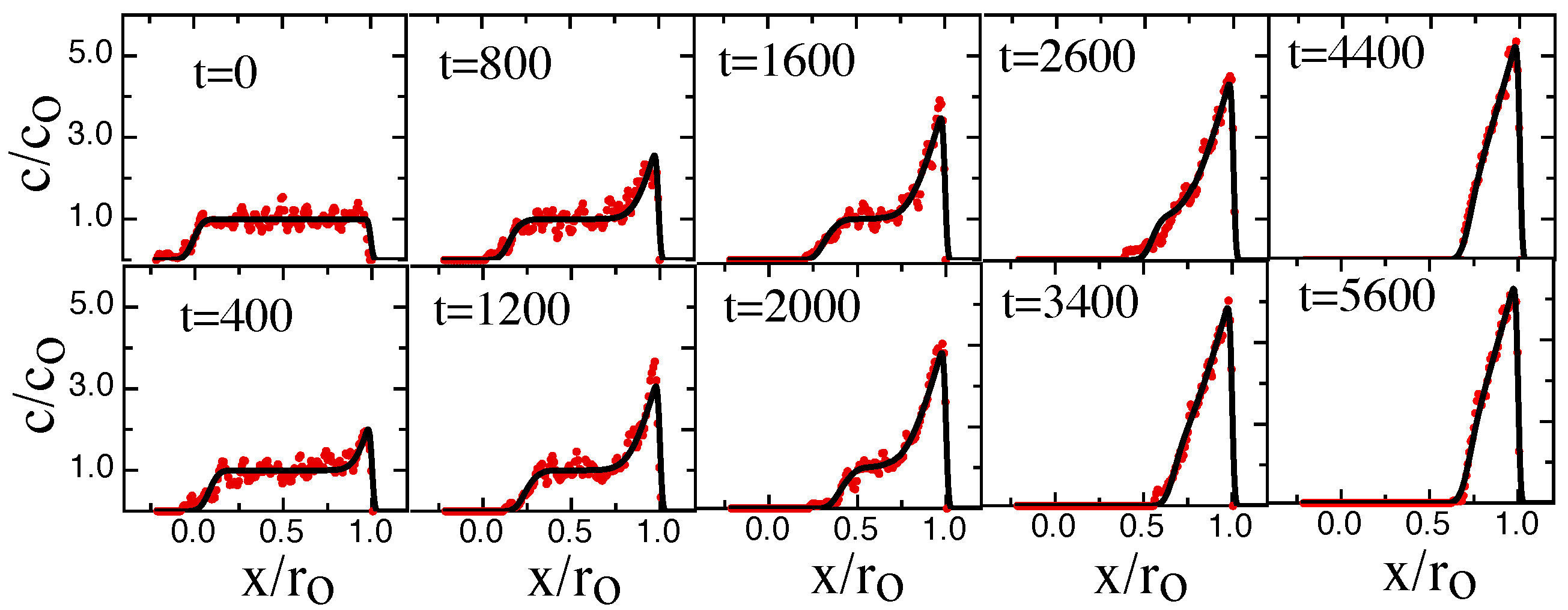
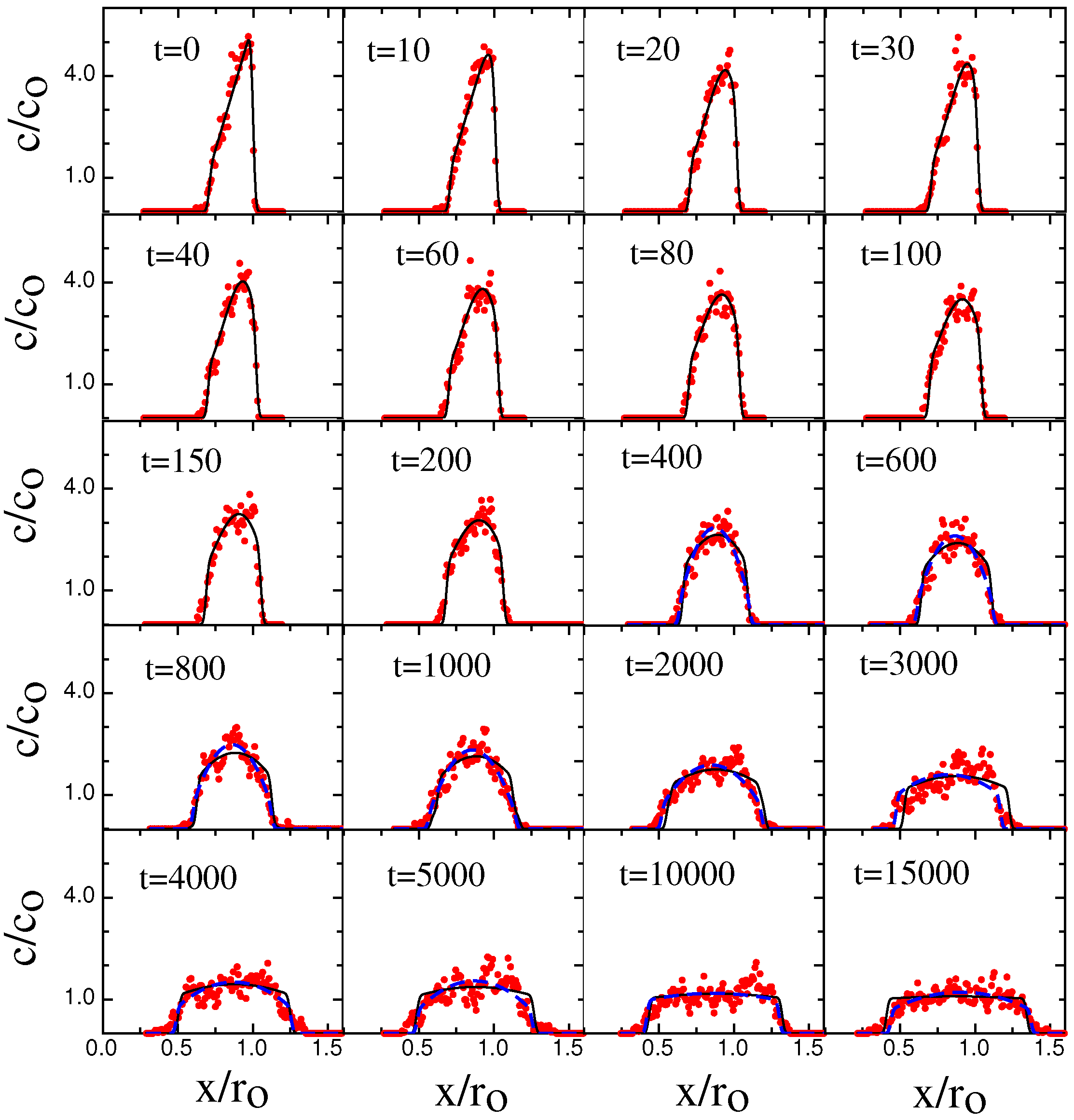
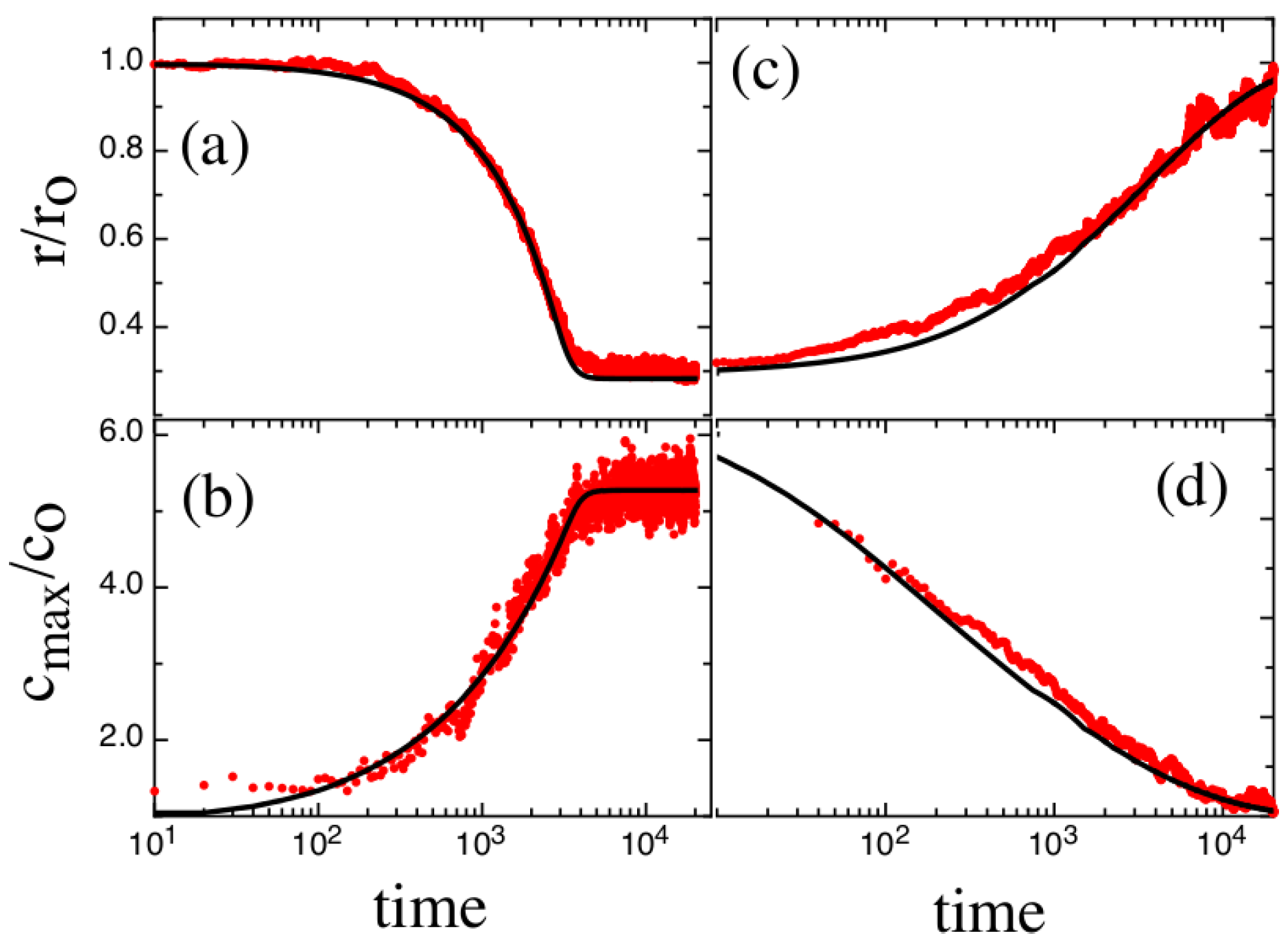
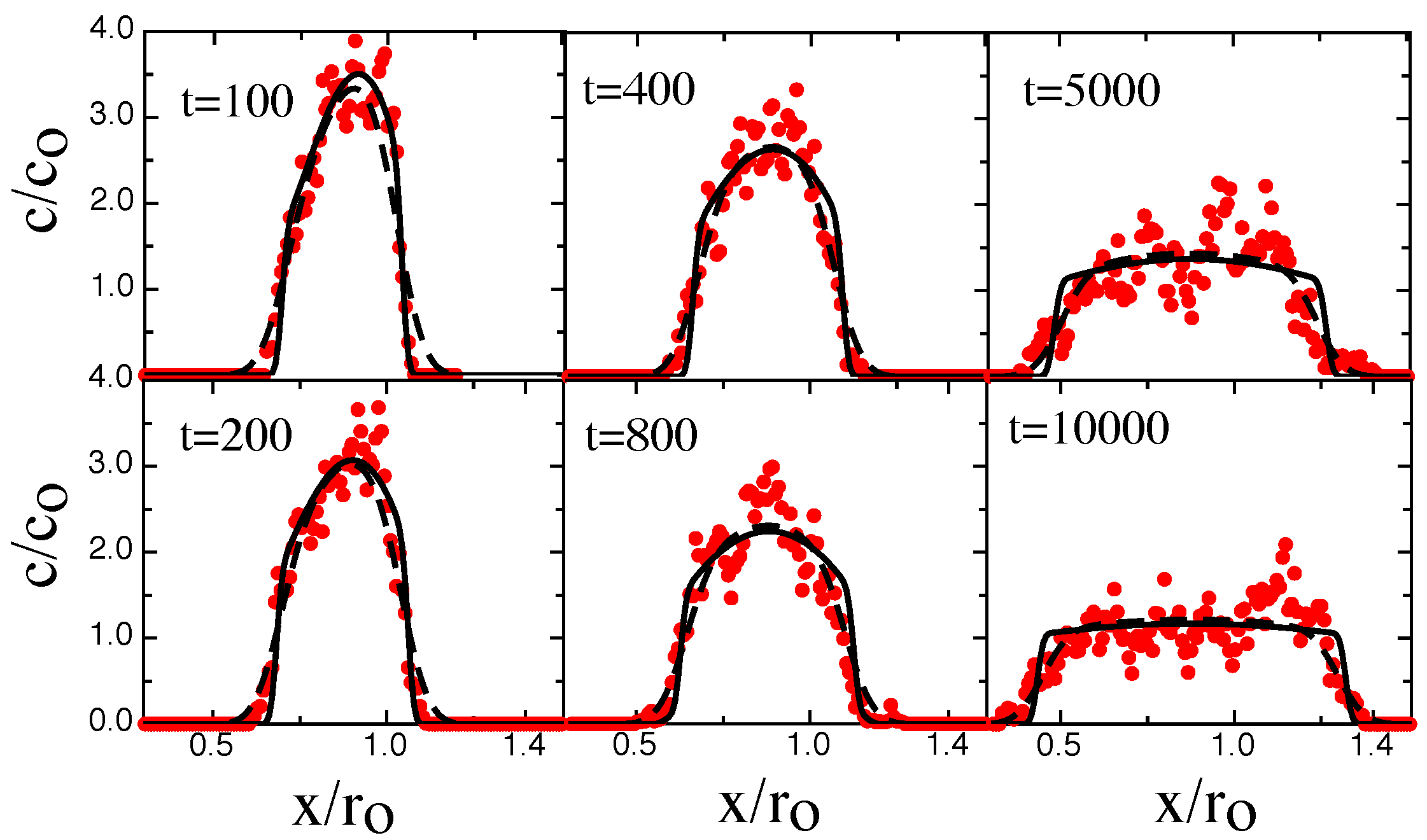
3. Results
4. Summary and Outlook
Acknowledgments
Author Contributions
Conflicts of Interest
References and Note
- Reisner, W.; Pedersen, J.N.; Austin, R.H. DNA confinement in nanochannels: Physics and biological applications. Rep. Prog. Phys. 2012, 75, 106601. [Google Scholar] [CrossRef] [PubMed]
- De Gennes, P.G. Scaling Concepts in Polymer Physics; Cornell University Press: Ithaca, NY, USA, 1979. [Google Scholar]
- Rubinstein, M.; Colby, R.H. Polymer Physics; Oxford University Press: New York, NY, USA, 2003. [Google Scholar]
- Daoud, M.; de Gennes, P.G. Statistics of macromolecular solution trapped in small pores. J. Phys. 1977, 38, 85. [Google Scholar] [CrossRef]
- Brochard, F.; de Gennes, P.G. Dynamics of confined polymer chains. J. Chem. Phys. 1977, 67, 52. [Google Scholar] [CrossRef]
- Jun, S.; Thirumalai, D.; Ha, B.Y. Compression and Stretching of a Self-Avoiding Chain in Cylindrical Nanopores. Phys. Rev. Lett. 2008, 101, 138101. [Google Scholar] [CrossRef] [PubMed]
- Odijk, T. The statistics and dynamics of confined or entangled stiff polymers. Macromolecules 1983, 16, 1340–1344. [Google Scholar] [CrossRef]
- Tree, D.R.; Wang, Y.; Dorfman, K.D. Extension of DNA in a Nanochannel as a Rod-to-Coil Transition. Phys. Rev. Lett. 2013, 110, 208103. [Google Scholar] [CrossRef] [PubMed]
- Dai, L.; Tree, D.R.; van der Maarel, J.R.C.; Dorfman, K.D.; Doyle, P.S. Revisiting Blob Theory for DNA Diffusivity in Slitlike Confinement. Phys. Rev. Lett. 2013, 110, 168105. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Tree, D.R.; Dorfman, K.D. Simulation of DNA Extension in Nanochannels. Macromolecules 2011, 44, 6594–6604. [Google Scholar] [CrossRef] [PubMed]
- Khorshid, A.; Zimny, P.; Tétreault-La Roche, D.; Massarelli, G.; Sakaue, T.; Reisner, W.W. Dynamic Compression of Single Nanochannel Confined DNA via a Nanodozer Assay. Phys. Rev. Lett. 2004, 113, 268104. [Google Scholar] [CrossRef] [PubMed]
- Khorshid, A.; Amin, S.; Zhang, Z.; Sakaue, T.; Reisner, W.W. Nonequilibrium Dynamics of Nanochannel Confined DNA. Macromolecules 2016, 49, 1933–1940. [Google Scholar] [CrossRef]
- Kim, Y.; Kim, K.S.; Kounovsky, K.L.; Chang, R.; Jung, G.Y.; de Pablo, J.J.; Jo, K.; Schwartz, D.C. Nanochannel confinement: DNA stretch approaching full contour length. Lab Chip 2011, 11, 1721–1729. [Google Scholar] [CrossRef] [PubMed]
- Teague, B.; Waterman, M.S.; Goldstein, S.; Potamousis, K.; Zhou, S.; Reslewic, S.; Sarkar, D.; Valouev, A.; Churas, C.; Kidd, J.M.; et al. High-resolution human genome structure by single-molecule analysis. Proc. Natl. Acad. Sci. USA 2010, 107, 10848–10853. [Google Scholar] [CrossRef] [PubMed]
- Tegenfeldt, J.O.; Prinz, C.; Cao, H.; Chou, S.; Reisner, W.; Riehn, R.; Wang, Y.M.; Cox, E.C.; Sturm, J.C. The dynamics of genomic-length DNA molecules in 100-nm channels. Proc. Natl. Acad. Sci. USA 2004, 101, 10979–10983. [Google Scholar] [CrossRef] [PubMed]
- Bonthuis, D.J.; Meyer, C.; Stein, D.; Dekker, C. Conformation and Dynamics of DNA Confined in Slitlike Nanofluidic Channels. Phys. Rev. Lett. 2008, 101, 108303. [Google Scholar] [CrossRef] [PubMed]
- Su, T.; Das, S.K.; Xiao, M.; Purohit, P.K. Transition between Two Regimes Describing Internal Fluctuation of DNA in a Nanochannel. PLoS ONE 2011, 6, e16890. [Google Scholar] [CrossRef] [PubMed]
- Reisner, W.; Morton, K.J.; Riehn, R.; Wang, Y.M.; Yu, Z.; Rosen, M.; Sturm, J.C.; Chou, S.Y.; Frey, E.; Austin, R.H. Statics and Dynamics of Single DNA Molecules Confined in Nanochannels. Phys. Rev. Lett. 2005, 94, 196101. [Google Scholar] [CrossRef] [PubMed]
- Reisner, W.; Larsen, N.B.; Silahtaroglu, A.; Kristensen, A.; Tommerup, N.; Tegenfeldt, J.O.; Flyvbjerg, H. Single-molecule denaturation mapping of DNA in nanofluidic channels. Proc. Natl. Acad. Sci. USA 2010, 107, 13294–13299. [Google Scholar] [CrossRef] [PubMed]
- Ostergaard, P.F.; Matteucci, M.; Reisner, W.; Taboryski, R. DNA barcoding via counterstaining with AT/GC sensitive ligands in injection-molded all-polymer nanochannel devices. Analyst 2013, 138, 1249–1255. [Google Scholar] [CrossRef] [PubMed]
- Presson, F.; Utko, P.; Reisner, W.; Larsen, N.B.; Kistensen, A. Confinement Spectroscopy: Probing Single DNA Molecules with Tapered Nanochannels. Nano Lett. 2009, 9, 1382–1385. [Google Scholar] [CrossRef] [PubMed]
- Huang, A.; Bhattacharya, A. DNA confined in a two-dimensional strip geometry. Europhys. Lett. 2014, 106, 18004. [Google Scholar] [CrossRef]
- Huang, A.; Bhattacharya, A.; Binder, K. Conformations, transverse fluctuations, and crossover dynamics of a semi-flexible chain in two dimensions. J. Chem. Phys. 2014, 140, 214902. [Google Scholar] [CrossRef] [PubMed]
- Huang, A.; Hsu, H.-P.; Bhattacharya, A.; Binder, K. Semiflexible macromolecules in quasi-one-dimensional confinement: Discrete versus continuous bond angles. J. Chem. Phys. 2015, 143, 243102. [Google Scholar] [CrossRef] [PubMed]
- Reccius, C.H.; Mannion, J.T.; Cross, J.D.; Craighead, H.G. Compression and Free Expansion of Single DNA Molecules in Nanochannels. Phys. Rev. Lett. 2005, 95, 268101. [Google Scholar] [CrossRef] [PubMed]
- Pelletier, J.; Halvorsen, K.; Ha, B.-Y.; Paparcone, R.; Sandler, S.J.; Woldring, C.L.; Wong, W.P.; Jun, S. Physical manipulation of the Escherichia coli chromosome reveals its soft nature. Proc. Natl. Acad. Sci. USA 2012, 14, E2649. [Google Scholar] [CrossRef] [PubMed]
- Schaefer, D.W.; Joanny, J.F.; Pincus, P. Dynamics of Semiflexible Polymers in Solution. Macromolecules 1980, 13, 1280–1289. [Google Scholar] [CrossRef]
- Amin, S.; Khorshid, A.; Zeng, L.; Zimny, P.; Reisner, W. To Knot or Not, That is the Question! A Nanofluidic Knot Factory Based on Compression of Single DNA in Nanochannels. (under review for Phys. Rev. Lett, 2016).
- Grest, G.S.; Kremer, K. Molecular dynamics simulation for polymers in the presence of a heat bath. Phys. Rev. A 1986, 33, 3628(R). [Google Scholar] [CrossRef]
- Huang, A.; Adhikari, R.; Bhattacharya, A.; Binder, K. Universal monomer dynamics of a two-dimensional semi-flexible chain. Europhys. Lett. 2014, 105, 18002. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Statistical Physics, Part 1, 3rd ed.; Pergamon Press: Waltham, MA, USA, 1980. [Google Scholar]
- Van Gunsteren, W.F.; Berendsen, H.J.C. Algorithms for brownian dynamics. Mol. Phys. 1982, 3, 637. [Google Scholar] [CrossRef]
- We have found from previous BD simulation studies of semi-flexible chains using exactly the same model and parameters that the average bond length remains unaffected by the chain stiffness within statistical error bars [23].

© 2016 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, A.; Reisner, W.; Bhattacharya, A. Dynamics of DNA Squeezed Inside a Nanochannel via a Sliding Gasket. Polymers 2016, 8, 352. https://doi.org/10.3390/polym8100352
Huang A, Reisner W, Bhattacharya A. Dynamics of DNA Squeezed Inside a Nanochannel via a Sliding Gasket. Polymers. 2016; 8(10):352. https://doi.org/10.3390/polym8100352
Chicago/Turabian StyleHuang, Aiqun, Walter Reisner, and Aniket Bhattacharya. 2016. "Dynamics of DNA Squeezed Inside a Nanochannel via a Sliding Gasket" Polymers 8, no. 10: 352. https://doi.org/10.3390/polym8100352
APA StyleHuang, A., Reisner, W., & Bhattacharya, A. (2016). Dynamics of DNA Squeezed Inside a Nanochannel via a Sliding Gasket. Polymers, 8(10), 352. https://doi.org/10.3390/polym8100352





