Abstract
We consider four criteria of acceptability for single-chain mean-field entangled polymer models: consistency with a multi-chain level of description, consistency with nonequilibrium thermodynamics, consistency with the stress-optic rule, and self-consistency between Green–Kubo predictions and linear viscoelastic predictions for infinitesimally driven systems. Each of these topics has been considered independently elsewhere. However, we are aware of no molecular entanglement model that satisfies all four criteria simultaneously. Here we show that an idea from Ronca and Allegra, generalized to arbitrary flows, can be implemented in a slip-link model to create a model that does satisfy all four criteria. Aside from the direct benefits of agreement, the result modifies the relation between the initial relaxation modulus and the entanglement molecular weight . If this implementation is correct, current estimates for would require modification that brings their values more in line with estimates based on topological analysis of molecular dynamics simulations.
1. Introduction
Since the single-chain mean-field nonlinear rheology model of Doi and Edwards [1,2,3,4,5], there has been considerable progress in describing the dynamics of entangled polymers. With a small number of adjustable parameters it is now possible to describe many experiments simultaneously [6,7,8,9,10,11,12,13]. Other work has recently suggested that one of these parameters—the entanglement density—might be accessible from atomistic simulations [14,15,16,17,18,19,20,21,22,23,24,25,26]. As a result, the goal of ab initio polymer rheology predictions now seems close.
There remain a few important obstacles to this goal, such as determination of the fundamental time scales, related to friction coefficients. However, in this paper we focus on the determination of the entanglement density. There are several issues that need to be resolved for this, which might be usefully separated into two categories. The first set of issues involves extraction of the entanglement density from atomistic simulations using topological analysis. For example, the literature contains discussions of annealing versus geometrical methods [24,27,28]. Also, the results are necessarily statistical quantities, and one therefore needs a coarse-grained model onto which these statistics are mapped: a target. Candidate targets contain some set of assumptions, in particular which quantities are allowed to fluctuate, such as entanglement number, entanglement spacing, monomer density, or entanglement positions. Since chains are finite-sized objects, it seems obvious that the more fluctuations included in the model, the better [29]. At least, this is the position that we take here.
The second category of issues involves relating the entanglement density parameters in the model to the observed rheology, typically the plateau of the storage modulus, . We are primarily concerned with these issues here. Determining how fluctuations affect the predicted plateau modulus has plagued entanglement theories from early on [30,31,32,33,34]. The Doi–Edwards model contains very few fluctuations, yet the question of a factor of 4/5 in the plateau modulus persisted for many years, presumably related to monomer density fluctuations along a fixed, constant-length primitive path [7,35]. As one adds primitive-path-length fluctuations (usually called “contour-length fluctuations” or CLF), entanglement spacing fluctuations, etc., the prefactor changes more [10]. These fluctuations can be handled in a natural way using slip-link models and nonequilibrium thermodynamics.
This manuscript focuses on entanglement spatial fluctuations (ESFs) in single-chain models. Unlike in multi-chain simulations or models, inclusion of these effects does not appear to be so natural or rigorous. Moreover, the effect is clearly important in relating the entanglement density to the plateau modulus, since the primitive chain network simulations of Masubuchi and co-workers estimate the entanglement density to be twice that found in most single-chain models, when comparing with experiment [36]. A similar difference is seen when using topological analysis to estimate entanglement density from a more fundamental basis [37].
There exist attempts to put ESFs in single-chain models, which involves virtual springs that attach entanglements to an affinely deforming background. However, other issues that at first seem unrelated come into play. For example, we know that we do not wish to include the contribution to stress from these virtual springs, or the model would almost certainly violate the well-established empirical relation between the stress tensor and the refractive index tensor: the stress-optic rule (SOR) [38]. However, one can then run into difficulties satisfying linear response theory [39], which states that relaxation of spontaneous stress fluctuations should be identical to relaxation from small external perturbations [40]. Even more disturbing, one can violate the second law of thermodynamics [41]. A simple virtual-work argument requires that the change of free energy of the virtual springs upon sample deformation should contribute to the stress [42,43,44,45]. More sophisticated nonequilibrium thermodynamics formalisms, such as GENERIC [46,47,48,49,50], give the same results. Yet each virtual spring represents a confinement potential due to interaction of the probe chain with at least one other chain. Hence, even though the stress tensor is derived from the free energy in a thermodynamically consistent way, for a single-chain model this leads to overcounting of the confinement potentials. (According to the principle of virtual work, the scalar product of the stress exerted on the system and the strain equals the change in free energy of the system. For a single-chain model, the latter is calculated as , where is the number density of chains and is the ensemble average of the change in the chain free energy.) If we do not include virtual springs, we have no ESFs and an incorrect relation between the plateau modulus and the entanglement molecular weight (and therefore the entanglement density) results. Hence, one seems to go in a circle where resolution of one violation leads to another problem.
We seek here simultaneous resolution of these issues. We show that dynamics proposed for nodes in cross-linked rubber by Ronca and Allegra [51], which we call RA dynamics, can resolve them and allows one to include entanglement spatial fluctuations in single-chain models without creating any fundamental violations. We consider then these four criteria for single-chain entanglement models:
- Consistency with multi-chain models. The single-chain model should predict the same magnitude for the elastic modulus as multi-chain models and therefore estimate the same entanglement density when comparing with rheological data. Cross-linked network calculations have already established the importance of node fluctuations for this agreement [30,31,32,33,34]. In the present paper, we verify only qualitatively whether the effect of ESFs on the plateau modulus in single-chain mean-field models is consistent with that observed in multi-chain models. Specifically, the plateau modulus should decrease when the size of ESFs increases.
- Consistency with nonequilibrium thermodynamics. Equilibrium thermodynamics and statistical mechanics can be applied in a straightforward way to cross-linked systems [52]. Similarly one can apply nonequilibrium thermodynamics to entangled melts, using either GENERIC or a simple virtual-work argument to derive the stress tensor. For cross-linked systems we simply require that the entropy of the universe not decrease when reversibly deforming a network.
- Consistency with the stress-optic rule (for moderate deformations). It is well established experimentally [38] that polymer melts show a linear relationship between the stress tensor and the refractive index tensor when the chains are Gaussian [53,54]. The dependence of the refractive index tensor on chain conformations has a straightforward derivation [55], so we assume that it is correct. The refractive index tensor should be compared to the stress tensor from criterion 2.
- Consistency between Green–Kubo predictions and the relaxation modulus predicted for infinitesimal deformations. Linear response theory requires that the relaxation of stress from small external perturbations should be the same as relaxation from small fluctuations that arise at equilibrium [56]. Both expressions require as input an expression for the stress tensor, and this expression should come from criterion 2.
Since discussions of these topics individually exist in the literature already, we attempt to keep mathematics to a minimum. We begin by summarizing, in Section 2, where each of several existing single-chain models for entangled polymer melts fails for at least one of these criteria. Section 3 gives a little history and an explanation of the RA dynamics [51]. We point out that equilibrium models by Heinrich et al. [57], Rubinstein and Panyukov [58,59], and Everaers [60] for cross-linked entangled networks have already incorporated the ideas from Ronca and Allegra. The RA dynamics in these network models are based on a decomposition of node fluctuations in the principal strain directions. A more general formulation is necessary for entangled melts, because entanglements have different lifetimes, hence different deformation histories and different principal directions. We present such a formulation, which we call the generalized RA dynamics. Finally, using these dynamics, we propose a single-strand unentangled network model (Section 4) and a single-chain slip-link model (Section 5) that both satisfy the four criteria.
A similar issue was recently considered by Everaers [37], vis-a-vis the entanglement molecular weight that arises from topological analysis and is predicted by models for the plateau modulus. That work focuses on the different ways to estimate the entanglement molecular weight from topological analysis, but does point out the importance of ESFs and the front factor in the plateau modulus. Like we do, Everaers concludes that the estimate of the entanglement molecular weight from the multi-chain simulations is probably more accurate. On the other hand, he uses expressions for the topological analysis that ignore fluctuations in the degree of entanglement, entanglement spacing, and monomer density as well as the observed primitive-path persistence length, which is larger than the average entanglement spacing. Unfortunately, these effects are all observed in atomistic simulations [16,17,18] and give corrections of similar magnitude as ESFs [61].
As an aside, we mention a similar, but unrelated question about microscopic motion in cross-linked gels. Nonaffine motion of beads embedded in such materials was observed experimentally by Basu et al. [62]. However, the mean squared displacement relative to affine motion was two orders of magnitude larger than what would be expected based on spatial fluctuations of cross-links. The authors showed that the observed nonaffinity was more likely due to inhomogeneities in the distribution of cross-linker during synthesis of the networks.
2. Existing Entangled Melt Models and the Four Criteria
We consider several network-like liquid models and their conformance to the four criteria. The network is formed either through entanglements, or associating groups on the chain. We consider only models that are valid for both linear and nonlinear flows. Although our focus is on single-chain models, we also mention a few multi-chain simulations for entangled polymers.
2.1. Doi–Edwards Model and Öttinger’s Generalization
The famous Doi–Edwards model [1,2,3,4,5] exists on a very crude level of description: the second moment of the orientation of a single entangled strand in the melt. It assumes affine motion for the strand, constant entanglement spacing, and constant primitive-path length. The orientation vector is attached to a tube segment, and the primitive path undergoes simple one-dimensional diffusion inside. The plateau modulus is proportional to the entangled strand density with a prefactor of 4/5. This prefactor is assumed to arise from monomer density fluctuations along the primitive path, not from ESFs, so the plateau modulus is consistent with nonfluctuating entanglement positions. However, the model is consistent with the stress-optic rule, thermodynamics and the Green–Kubo relation. These conclusions are summarized in Table 1.

Table 1.
Several models/simulations and their agreement with the four criteria, which are numbered the same as in Section 1: ESFs = entanglement spatial fluctuations, NETD = nonequilibrium thermodynamics, SOR = stress-optic rule, OC = overcounting, GKR = Green–Kubo relation, NA = not applicable. The last three entries are cross-linked network models. The others are entangled melt models/simulations.
| Model ↓ | Criterion → | 1: ESFs | 2: NETD | 3: SOR/OC | 4: GKR |
|---|---|---|---|---|---|
| Doi–Edwards model [1,2,3,4,5] | ✕ | ✓ | ✓ | ✓ | |
| Öttinger model [63] | ✓ | ✓ | ? | ✓ | |
| Associating polymer model I [41] | ✕ | ✓ | ✕ | ✓ | |
| Associating polymer model II [41] | ✓ | ✕ | ✓ | ✓ | |
| Slip-link model [10,64] | ✕ | ✓ | ✓ | ✓ | |
| Slip-spring simulation (2005) [65] | ✓ | ✕ | ✓ | ✕ | |
| Slip-spring simulation (2007) [39] | ✓ | ✕ | ✓ | ✓ | |
| PCN simulation [66] | ✓ | ✕ | ✓ | ✓ | |
| Heinrich–Straube–Helmis model [57] | ✓ | ✓ | ✓ | NA | |
| Rubinstein–Panyukov model [58,59] | ✓ | ✓ | ✓ | NA | |
| Everaers model [60] | ✓ | ✓ | ✓ | NA | |
There is an interesting generalization by Öttinger [63] to include anisotropic tube cross section. On one hand, his work relaxes the typical independent alignment assumption of the Doi–Edwards model in a thermodynamically rigorous way. More interesting for our discussion is his introduction of anisotropy in the tube cross section, motivated by Ianniruberto and Marrucci [67], who used virtual springs. These virtual springs imply possible fluctuations in entanglement positions. This second generalization by Öttinger required addition of another dynamic variable , whose conformation distribution describes the shape of the tube cross section. (We add primes to the variables and parameters from Öttinger [63] to avoid confusion with other quantities used here.) Its dynamics were, like the tube orientation vector , deterministic except for creation and destruction at the tube ends. Thermodynamic considerations permitted two adjustable parameters and , the first influencing deformation of directly by flow and the second compression of by coupling with the stretching of the primitive-path length. Thermodynamics also required two additional contributions to the stress tensor, and a modification of the prefactor in the classical Doi–Edwards stress.
The tube cross-section variable has dynamics
where denotes the length of and κ is defined as the transpose of the velocity gradient tensor, . The stress tensor has three additive contributions; see Equations (19–21) of [63]. The first one is proportional to the average tube-orientation dyad , similar to the Doi–Edwards stress, but with a prefactor . The second contribution is due to nonuniformity of the monomer density, related to avoidance of the independent alignment assumption. This contribution is independent of the tube cross-section dynamics and therefore not relevant to our discussion. Moreover, since it vanishes at equilibrium, the second contribution does not affect the modulus front factor and thus does not improve the consistency with multi-chain models. We refer to the literature for a discussion on preserving thermodynamic admissibility with and without the independent alignment assumption [68,69,70]. The third contribution is proportional to with a prefactor . For comparison below, we point out that the dyad of has dynamics
as obtained from Equation (1) using the chain rule. Presumably, should have isotropic initial distribution, but might be coupled with the tube-segment orientation vector through a nonzero .
The concept of finite tube cross section implies the presence of ESFs, which suggests putting a check mark in the first column of Table 1 for this model. A step-strain calculation shows that the modulus front factor is ; see Section 2.5 of [63]. The same result can be derived straightforwardly from the Green–Kubo relation, hence the check mark in the last column. Assuming that entanglements are binary interactions, which are analogous to tetrafunctional cross-links, consistency with multi-chain network models [30,31,32,33,34] then suggests that , so that the front factor becomes . A second relation between and may be obtained from consistency with the stress-optic rule. However, it is not obvious to us how to derive the birefringence tensor for this model. Therefore we put a question mark in the second column. Thus Öttinger’s reptation model satisfies at least three of the four criteria.
There is another model by Wagner and coworkers [71,72] that also considers changing tube cross sections. This model includes an added dynamics for stretch of the primitive path due to a decrease in the tube cross section (through a dynamic variable f, which represents the ratio of the “tube diameter” at equilibrium and in flow). One justification for the specific form of this dynamical equation comes from an argument by Marrucci and Ianniruberto [73] regarding pressure from the tube on the chain. In these formulations the tube cross section is treated as a hard boundary instead of as harmonic springs. Although, to the best of our knowledge, GENERIC compliance has not been checked for this model, there does not appear to be any problem. A thorough check requires conversion of Wagner’s integral equation to a differential form, which is given in Appendix A. Since there are no explicit fluctuations here, and since the plateau modulus and relaxation function of the model are just phenomenological, we do not place the model in our table. We do not consider further any similar models [74].
2.2. Associating Polymers
An associating polymer (AP) contains associative groups (often called stickers) along its backbone [75,76]. In solution, the stickers aggregate to form micelles, and a polymer network cross-linked by these micellar junctions is constructed above a certain polymer concentration. The binding energy between stickers is typically on the order of the thermal energy , so that stickers can dissociate from the junctions due to thermal agitation. On the other hand, detached free stickers recapture other (or the same) junctions nearby. Thus the members of the junctions are frequently replaced, or the junction itself created or annihilated. Therefore solutions of APs are physically cross-linked networks, and are often called reversible or transient networks. The association/dissociation kinetics of stickers are similar to the constraint dynamics (creation and destruction of entanglements away from the chain ends) in entangled polymers. (The main difference is that the constraint dynamics in entangled polymers are related to sliding dynamics of the ends of surrounding chains, whereas association and disassociation events in APs may involve stickers located anywhere along the surrounding chains.) Therefore it is appropriate to discuss a few AP models briefly.
A transient network model developed by Tanaka and Edwards (TE) was the first systematic theory for rheological properties of unentangled AP networks [77,78,79,80]. This theory is based on the classical models for entangled polymer solutions and melts that assume the entanglement points as temporal junction points that can break and regenerate [81,82,83,84,85,86]. The TE theory is a single-chain model for polymers carrying stickers only on both ends (called telechelic polymers), and chains are modeled by dumbbells.
Several modifications of the TE model have been proposed so far: inclusion of free chains [87], imperfect relaxation of dangling chains and shear-induced enhancement of the association rate [88,89], and competing effects between the nonlinear stretching of active chains and a stretch-induced dissociation rate [90]. All of these are single-chain, dumbbell, affine network models like the TE model. A stochastic model [91] belonging to this category was also proposed. (Cifre et al. [91] studied the effects of nonaffine motion of junctions by assuming that the junctions have finite friction coefficient. For example, the steady-state viscosity decreases with decreasing friction of the junctions [91]. However, the mobile junctions are not connected with the background network by virtual springs, as often assumed in the study of junction fluctuations [41,65,92]. A lack of virtual springs enhances the deviation of mobile junctions from affine motion.)
Recently Indei and Takimoto [93] proposed a single-chain, affine network model for unentangled APs having multiple stickers, based on an idea of Jongschaap et al. [94]. Indei et al. [41] also studied the effects of junction fluctuations on the viscoelasticity of multisticker AP networks by relaxing the affine-motion assumption. Fluctuations were implemented by introducing virtual springs that connect associated stickers (which are supposed to be incorporated into junctions) with a background that deforms affinely. Two situations were studied, i.e., whether or not to include the direct contribution from the virtual springs into the total stress. If included (model I), the plateau modulus is not affected by the fluctuations, which is inconsistent with the multi-chain prediction. A softening occurs, but only in the lower frequency regime where the associative Rouse-like behavior [95] is observed. Also the stress-optic rule is not obeyed because the virtual springs do not contribute to the optical properties but do contribute to the stress [96]. It should be mentioned that the SOR is not as well established for AP networks as it is for polymer melts and cross-linked networks. (For telechelic ionomers (-lithium sulfonato polystyrene), the SOR is confirmed in a wide range of shear rates including the shear-thickening regime [97]. On the other hand, for telechelic poly(ethylene oxide) (HEUR), the SOR is obeyed only well inside the linear regime [98]. The authors attribute this observation to the formation of flowerlike micelles. Due to the interference by a corona of looped chains, active chains connecting neighboring micelle cores may be stretched even at rest, thereby shifting the onset of SOR violation to smaller strain.) Nevertheless, the problem of overcounting the virtual-spring contributions to the stress exists for all these systems.
On the other hand, if the virtual-spring contribution is not included (model II), the fluctuations decrease the plateau modulus consistently with the multi-chain result, but the second law of thermodynamics is violated [41]. The stress-optic rule is satisfied because of the absence of the virtual-spring contribution. In both cases, the Green–Kubo prediction at equilibrium can be shown analytically to be consistent with the relaxation modulus after an infinitesimal deformation. Thus, neither of these two models satisfies all four criteria. Ronca–Allegra dynamics resolve this inconsistency issue in the same way as shown for the single-chain slip-link model in Section 5 and the single-strand unentangled network model in Section 4. For the AP model with Ronca–Allegra dynamics, consistency between the Green–Kubo prediction and the modulus under infinitesimal deformations can be proven analytically.
2.3. Slip-Link Model
Hua and Schieber [99,100,101] introduced a single-chain stochastic tube/slip-link model in 1998 that modeled the chain as a one-dimensional Rouse chain in a tube, but the entanglements were discrete, like slip-links. This model was superseded by a more natural level of description without Rouse chains or tubes [64]. In the newer model, the entanglements were explicitly slip-links and the number of Kuhn steps between entanglements was treated as a stochastic variable. Many fluctuations arise naturally in the model, such as spacing between entanglements, primitive-path length, monomer density along the primitive path, and fluctuations in the number of entanglements. Most of these statistics were later found to be in agreement with topological analysis of atomistic simulations, except at the smallest length scales [17,18]. In particular, Tzoumanekas and Theodorou [18] found that entanglements appear to have a short-range repulsive interaction that is not accounted for in the model.
Thermodynamics play a large role in restricting the dynamics of the model, and compliance with GENERIC was demonstrated [102]. Entanglements are imposed by a chemical potential bath that allows the number of entanglements on the chain to fluctuate. Together with the free energy of the chain, this formulation allows analytic expressions for equilibrium chain conformations [21,103].
Initially, the number of Kuhn steps in an entangled strand was treated as a continuous variable [9,104], but this formulation was supplanted by a more rigorous formulation that treats this number as a discrete variable, and in which dynamics are modeled by a discrete hopping process [10,11,12,13]. In particular, while the discretization in itself is a minor approximation, it allows a mathematically rigorous implementation of entanglement creation and destruction at the chain ends by sliding dynamics. Constraint dynamics (creation and destruction of the entanglements everywhere along the chain) are determined self-consistently with sliding dynamics. This self-consistency is not required by thermodynamics, but it does not cause any violation either, and is accepted on physical grounds. Thermodynamics does restrict the rates of creation and destruction of entanglements insofar that they are related by detailed balance.
Although the model is thermodynamically consistent, it does not include fluctuation of the entanglement positions. As a result, its relation between the plateau modulus and the entanglement molecular weight is similar to that of Doi and Edwards. However, since it contains more fluctuations, it has a somewhat smaller front factor. ESFs were incorporated in a more recent version of the slip-link model by Schieber and Horio [92]. However, they showed analytically that the plateau modulus was the same as for the original slip-link model, with affine motion of entanglements. Recall that this was also found for AP networks. In Section 5, we show that the plateau modulus does decrease with the strength of ESFs when these fluctuations become anisotropic under deformation according to the generalized RA dynamics.
2.4. Slip-Spring Simulation
Likhtman [65] introduced a slip-spring simulation in 2005, which consists of a three-dimensional Rouse chain, anchored to an affinely deforming elastic background through slip-links and virtual springs. The simulation includes fluctuations of the entanglements through the virtual springs. Although the resulting dynamics are similar to the slip-link model in the limit of stiff virtual springs, there are several differences. The simulation requires an ensemble of chains, since it is not rigorously single-chain. The number of slip-springs is fixed for a given simulation ensemble. Destruction of an entanglement at a chain end due to Rouse motion requires creation of a new entanglement at a randomly chosen chain end elsewhere in the ensemble. The creation rate is completely determined by this algorithm, whereas in the slip-link model it is derived from the destruction rate through detailed balance. Upon slip-spring creation at a chain end, another chain is chosen randomly and a slip-spring is added somewhere along its primitive path. These two slip-springs are then permanently paired such that death of one by Rouse motion results in death of the other. This is in contrast to the slip-link model, which shows disentanglement under flow. Such disentanglement is crucial for agreement with shear flow data [13].
Also different from the slip-link model, the number of Kuhn steps between adjacent entanglements is not treated as the stochastic variable, but this information is instead carried by the beads and springs of the Rouse chain, whose dynamics are given by Brownian dynamics. Although the virtual springs modify the chain dynamics, they do not contribute directly to the stress. A virtual-work argument suggests that the model has thermodynamic issues [41]. However, the underlying mathematical model is not completely specified, and therefore compliance with GENERIC has not been checked. Some challenges that need to be overcome to enable a GENERIC check are (1) choosing convenient variables to describe the chain conformations and the topology of the pseudo multi-chain system, and (2) deriving an evolution equation for the probability density of these variables.
Similar issues were later confirmed in a paper by Ramírez et al. [39], where the relaxation modulus found from a linear step-strain deformation did not agree with that found from Green–Kubo simulations. The authors did find that the discrepancy could be eliminated by considering cross correlations between the stress from virtual springs and that from the real chains in the Green–Kubo calculations [40]. Such a repair does not address the problem of violation of the principle of virtual work and the second law of thermodynamics, however. Therefore, we add an “X” under nonequilibrium thermodynamics (NETD) for the 2005 version of the model, although we suspect that in nonlinear flow it could be repaired by the generalized RA dynamics, introduced below. Even though compliance has not been rigorously checked, we also add an “X” under NETD for the 2007 version of the model, which is strongly suggested by the principle of virtual work.
2.5. PCN Simulation
In 2001, Masubuchi and coworkers introduced the primitive chain network (PCN) simulation [66]. Although this is a multi-chain model, it is applied to nonlinear flows and we consider it worthwhile to add a few comments here. The model exists on a level of description similar to the single-chain slip-link model of Schieber and coworkers, since it treats the number of Kuhn steps as a stochastic variable, instead of using Rouse chains. The chains are entangled through rigid slip-links, but they do fluctuate in space by a force balance and Brownian forces in the network. The number of entanglements is neither determined by a grand-canonical approach as in the single-chain slip-link model, nor held fixed in an ensemble as in Likhtman’s model [65]. Instead, creation and destruction of entanglements are determined by an algorithm involving the numbers of Kuhn steps in dangling chain ends. Because of the multi-chain level of description, the authors also found it necessary to include “osmotic pressure” forces between slip-links to avoid network collapse. These forces might be similar to the repulsive forces observed by Tzoumanekas and Theodorou [18] mentioned above.
Interestingly, this model indeed predicts a relationship between the plateau modulus and the entanglement molecular weight that is similar to multi-chain cross-linked models [36]. In fact, this difference from the Doi–Edwards model raised some concern among the authors. However, we argue here that their result is more in line with theory [30,31,32,33,34] than that of the single-chain models above.
On the other hand, the model has several critical thermodynamic issues. Rather than using chemical potential differences between neighboring strands to drive Kuhn-step dynamics, they use tensions. These same tensions also drive entanglement position dynamics. Hence there does not appear to be a single consistent chain free energy in the model. Secondly, the osmotic pressure forces preventing network collapse do not contribute to the stress, although they are argued to be small. Perhaps more problematic, these forces do not exist on the same level of description as the simulation formulation. Instead, the simulation box is discretized on a coarser level to estimate the local entanglement density. Such a formulation cannot be examined in the limit of vanishing discretization, and sensitivity to this conveniently chosen length scale is unknown. Ideally, the repulsive forces between entanglements should be formulated on the same level of description as all other dynamics. Finally, the underlying mathematical model is not fully specified, and compliance with thermodynamics has not been examined rigorously.
Very recently there have appeared newer multi-chain simulations [105,106] that fix many of the thermodynamic issues [107] associated with dynamics in the code by Masubuchi et al. Therefore, these are a considerable improvement over the earlier PCN simulations. Both groups use the idea of Schieber [103] to treat the number of entanglements as a stochastic variable, which is controlled by a chemical potential bath as in a grand-canonical ensemble. However, they have also added springs between the chains, which raises issues about three of the criteria above. First, since the model is already multi-chain, these springs add additional fluctuation and relaxation to the plateau modulus. Therefore, one might expect a possible “overcompensation” between entanglement molecular weight and the plateau modulus. Second, if the virtual springs contribute to the stress predictions, then one would expect violation of the stress-optic rule. Third, if these springs do not contribute to the stress, then one expects violation of the principle of virtual work. Chappa et al. [105] do not specify their stress tensor expression, whereas Uneyama and Masubuchi [106] consider both forms of stress, with and without the virtual springs.
3. Proposed Virtual-Spring Dynamics of Ronca and Allegra
Consideration of entanglements begins historically with cross-linked rubber [52]. The so-called “phantom network models” treat strands that can pass through one another, but whose ends are cross-linked to other chains. James and Guth [108,109,110] considered a multi-strand network model with Gaussian strands, and made two different assumptions for cross-link dynamics when (to prevent the network from collapsing) strand ends at the sample surface were fixed to an affinely deforming boundary. The first assumption is that the cross-links initially move to their equilibrium position by free energy minimization (or, equivalently, force balance) and are then themselves deformed affinely. The second assumption was that these cross-links were free to fluctuate before and after deformation, and only the boundary nodes were deformed affinely. They showed that these two assumptions give the same stress predictions, and that the fluctuations in the second case are isotropic and their magnitude is independent of deformation. Duiser and Staverman [30,34], and later Graessley [31,32], showed that the fluctuations of the cross-links give a modulus of the phantom network that is proportional to its cycle rank. It is important to note that one could also assume that the cross-links are deformed affinely from their initial fluctuating positions instead of their average positions, but that this would give a modulus higher than the cycle rank. For cross-links of functionality 4, this would give a modulus twice as large as the fully fluctuating cross-links. Freezing the nodes at an instantaneous configuration followed by affine deformation decouples all the strands, which makes the multi-strand system equivalent to an ensemble of single-strand models; hence the larger modulus predicted for many single-strand models.
One seldom knows the cycle rank of a real network, but one can still make relative strain-dependent predictions of stress with the phantom network model, and it was established that the phantom network model does not give predictions in agreement with experiments [52]. Also shown experimentally was the fact that stress in the network is linearly proportional to temperature at fixed strain. Thermodynamics implies then that entropy dominates the contribution to stress, so the suspects in the discrepancy were isolated to network conformations. One group, including Paul Flory [33] as well as Ronca and Allegra [51], thought that the culprit might be modification of the fluctuations in the cross-links during deformation from excluded volume forces, whereas another, including Sam Edwards [111], thought that the culprit was the restriction of strand conformations from the topological constraints imposed by surrounding strands. Individuals from both groups called these conformational restrictions “entanglements”. While the view of Edwards has prevailed to the present, there were still some interesting works by the other group that might have relevance for models that incorporate the topological view of entanglements.
To modify node fluctuations, Ronca and Allegra [51] took a single-strand description of a cross-linked Gaussian network. (To be precise, they started with a multi-strand system, but they chose the principal directions of the deformation as their coordinate axes. Since there is no correlation between the principal components of node fluctuations, their model is equivalent to an ensemble of single-strand models. The same is true for the more recent, similar formulations of Heinrich et al. [57], Rubinstein and Panyukov [58,59], and Everaers [60].) Each node is attached via a virtual spring to an anchor stuck in an affinely deforming background; see Figure 1. Ronca and Allegra considered the nodes to be cross-links, but we might also think of them as entanglements, as in Figure 2. These sketches are special cases of the general networks considered by James and Guth [108,109,110], where the anchors are those points on the surface of the sample. As James and Guth proved, the nodes also move affinely on average. (This is no longer true with RA dynamics; cf. Equation (71) in Appendix B.3, which gives the mean strand end-to-end vector for a single-strand model after a step strain.) It is straightforward to show that thermodynamics requires that the virtual springs contribute to the stress of the system. Otherwise, deformation would lead to a decrease in the entropy of the universe [41], which is not good. On the other hand, if we include the virtual-spring contributions to stress, we overcount the contribution of the potential and violate the stress-optic rule. To avoid these problems, we require that the free energy of the virtual springs does not change during the deformation. Ronca and Allegra showed that this can be (uniquely) accomplished by a special anisotropic deformation of the harmonic potential. If represents the positions in space of all the nodes, and represents the positions of all the anchors, we write the (Helmholtz) free energy of all the virtual springs
where is Boltzmann’s constant, T is the temperature, is the Kuhn length, and is the shape tensor of the virtual-spring potential. Due to its tensorial nature, may couple the fluctuations in different directions, but it cannot be a function of the node and anchor positions.
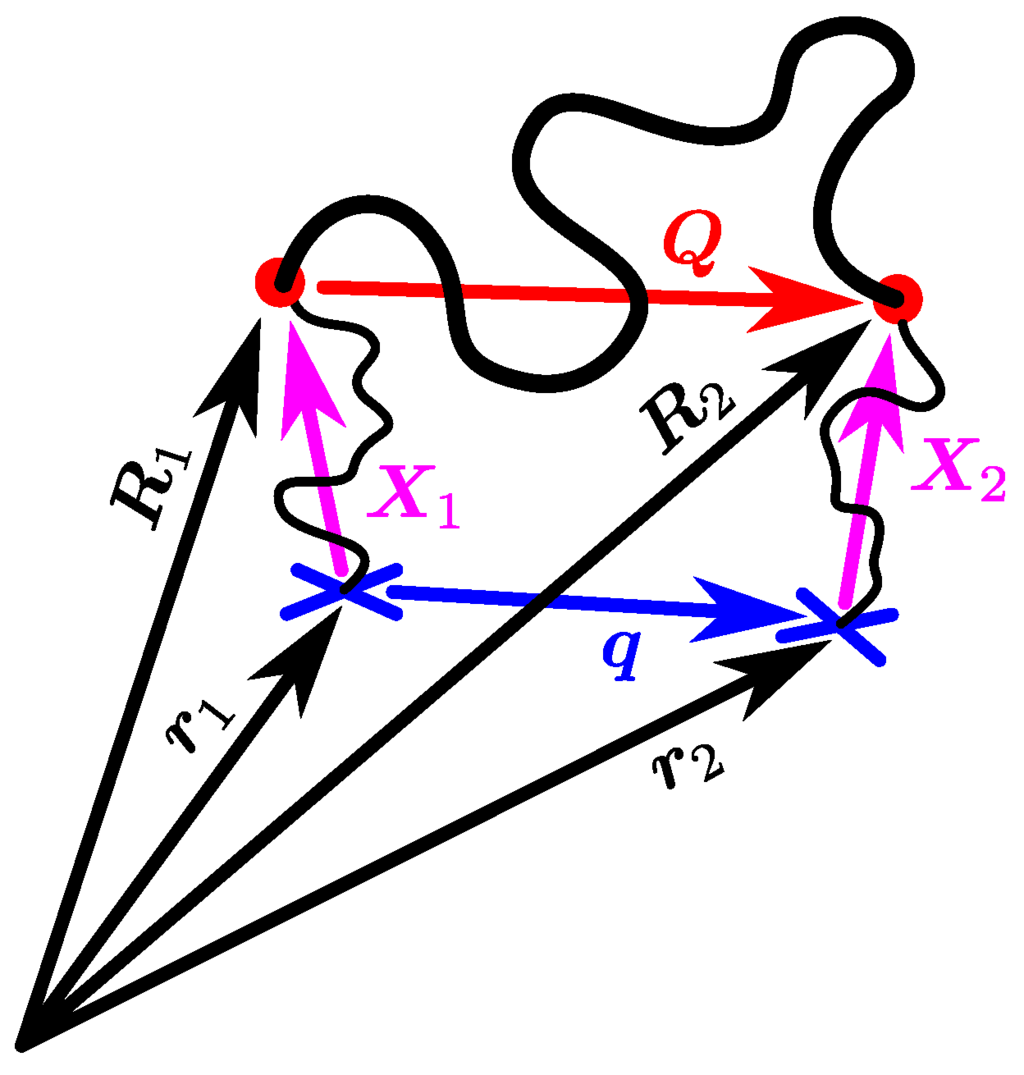
Figure 1.
Sketch of single-strand network model on detailed level of description. The strand (thick black line) is attached to cross-links (red dots) connected to affinely moving anchors (blue crosses) by virtual springs (thin black lines). Position vectors and connector vectors are indicated by black and colored arrows, respectively.
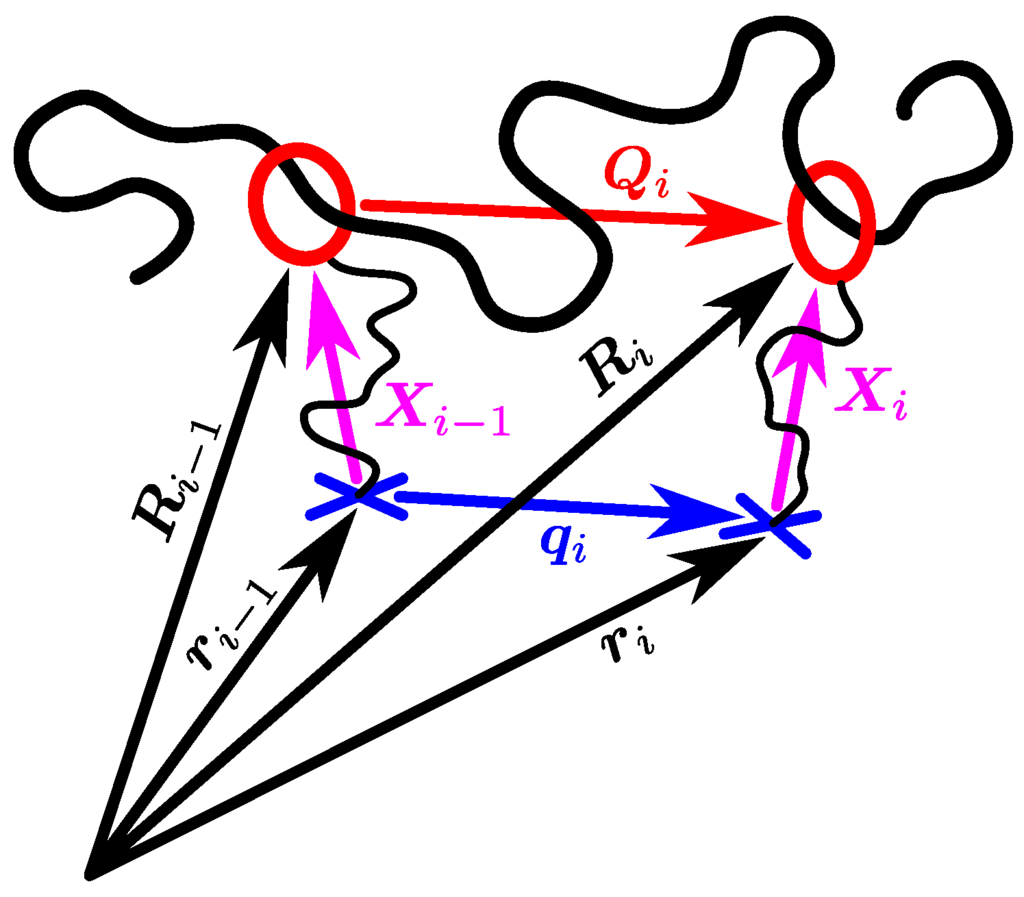
Figure 2.
Sketch of proposed slip-link model on detailed level of description. The chain (thick black line) passes through slip-links (red circles) connected to affinely moving anchors (blue crosses) by virtual springs (thin black lines). Position vectors and connector vectors are indicated by black and colored arrows, respectively.
We now consider a deformation given by the velocity gradient transpose , where the dagger indicates transpose. Thus, the anchors have motions and the nodes have motions . Since the cross-links are always at equilibrium, we use t here as a parametric label for the deformation, and means the initial zero-stress state.
Thermodynamics demands that for an isomolar, isothermal deformation, the rate of work to perform the deformation is equal to the rate of change of the system’s free energy. Since the rate of work is the scalar product of the stress tensor and the velocity gradient, if changes with t, then there should be a contribution to the stress from the virtual springs. Taking the derivative with respect to t of each side of Equation (3) allowing to change, we obtain
where as shown in Figure 1. If were held constant, then the free energy of the virtual springs would change during the deformation, and they would need to contribute to the stress to avoid thermodynamics problems. However, if we give lower-convected evolution,
then the virtual springs do not contribute to the stress. Note that has upper-convected dynamics, i.e., , which can be proven by taking the derivative of with respect to t. These are the generalized RA dynamics.
The evolution requires an “initial” condition. For an initially isotropic system, it seems necessary to assume that , which introduces a new parameter n. We recently proposed a way to estimate this parameter from topological analysis of atomistic simulations [61].
If the nodes are entanglements in a polymer melt, an additional modification is required. Since the entanglements are created and destroyed by the sliding dynamics of the chains, we must assign a tensor to each entanglement i upon creation at time , and it needs an initial condition upon creation. To retain the proper isotropic equilibrium state, this initial condition should be . Now the parameter t becomes the independent variable time. The stress tensor can be derived rigorously by applying a step strain, , integrating over the infinitesimal free-energy increment from to , taking the ensemble average, and finally using the principle of virtual work. (This leads to , where is the number density of chains. All stochastic terms in average to zero, which is why we only considered the affine part of the node displacements in the derivation of Equation (4). If the nodes are entanglements, contains additional deterministic terms, which are independent of κ and therefore vanish identically when the integration is carried out [112].) The free energy change due to deformation of each virtual spring then cancels with that due to the deformation of its potential, analogous to the example given here for a cross-linked network. The same holds true for associating polymer networks.
We finish this section with a few comments about the implied physics and previous work. The generalized RA dynamics suggest that deformation gives anisotropy to the network node fluctuations. For example, in uniaxial elongation the nodes would have greater fluctuations in the direction of stretch, and smaller fluctuation in the perpendicular directions. In tube language, this looks like shrinking of the tube diameter. Or, more generally, it allows anisotropic tube cross-section. In fact, the dynamics of are equivalent to those of the dyad in Öttinger’s single-segment reptation model, Equation (2), in the special case that and [63]. Note that this implies that should not be interpreted as the tube radius, but rather as the “inverse” of the tube radius. More importantly, however, setting leaves the stress-tensor predictions unchanged from Doi and Edwards. Thus it seems that there is no one-to-one correspondence between the tube cross-section dynamics in Öttinger’s reptation model and the generalized RA dynamics. This is not necessarily a cause for concern, given the difference in level of description between the models considered here (in which the entanglements are discrete objects whose actual positions are tracked) and the reptation model (where these discrete objects are replaced by a continuous tube). We will draw somewhat more definitive conclusions from a comparison with the coarse-grained single-strand network model in Section 4.2.
On a more detailed level, Ianniruberto and Marrucci [67] considered a Rouse chain trapped in a tube segment with anisotropic tube cross section, described by virtual springs along the primitive path. They concluded that, when the virtual springs are included in the stress, there is no violation of the stress-optic rule. Their calculation relies heavily on a slight modification of a Green’s function that was first derived by Doi and Edwards for a Gaussian chain in a harmonic confinement potential. Ianniruberto and Marrucci considered a straight, single tube segment in the z direction, with elliptical harmonic potential in the x and y directions. Unfortunately, both the Doi–Edwards expression and the Ianniruberto–Marrucci expression for the Green’s function are not exact, since they do not satisfy the continuity condition and the boundary condition. We have recently derived the exact Green’s function [96] for the problem and showed that the SOR is violated if the virtual springs are included in the stress. Since the work of Ianniruberto and Marrucci is not a complete model, we do not place it in Table 1.
Heinrich et al. [57], Rubinstein and Panyukov [58,59], and Everaers [60] implemented Ronca and Allegra’s idea of anisotropic node fluctuations in cross-linked network models. Some of these include entanglements between network strands, but entanglements involving dangling ends are not explicitly modeled. Therefore all nodes are permanent, and as a result the principal directions of their fluctuations all correspond to those of the macroscopic deformation. When the coordinate system is aligned with the principal directions, the virtual-spring tensors become diagonal and the system becomes equivalent to an ensemble of single-strand models. The generalized RA dynamics, introduced in Equation (5), can also be implemented in models for networks with entangled dangling ends [113] or melts. We did not consider the cross-linked network models of references [57,58,59,60] above because we are primarily interested in liquids. Because nonlinear deformations were considered, we still add them to Table 1 and put check marks in all but the last column, which is not applicable for purely elastic models.
4. Examples: Single-Strand Mean-Field Unentangled Network Models
Before introducing slip-link models that satisfy all four criteria, it is worthwhile to look at two illustrative examples. We first consider a single-strand mean-field model for a cross-linked network. Similar to the multi-strand phantom network model of James and Guth [108,109,110], entanglements are neglected. Fluctuations of the cross-link positions are described by virtual springs with generalized RA dynamics [51]. The first model is formulated on a detailed level of description, which resolves the cross-link positions. The second model is obtained from the first by integrating out these positions. It is shown that all four criteria are satisfied on both levels of description.
4.1. Detailed Single-Strand Unentangled Network Model
We choose the variables
where and are the end-to-end vectors of the strand and the virtual springs, as shown in Figure 1, and is the shape tensor of the potentials describing the cross-link fluctuations (or the compliance tensor of the virtual springs).
Gaussian statistics are assumed for the strand as well as the virtual springs. The free energy is then
where N is the number of Kuhn steps in the strand. The last term normalizes the equilibrium probability density, which is given by the Maxwell–Boltzmann relation . The choice to include a normalization constant in the free energy or as a prefactor in the expression for is arbitrary. However, the term is not constant—see Equation (5)—and therefore needs to be included in the free energy.
In the mobile slip-link model, discussed in Section 5, the anisotropy of ESFs in flow is the result of two competing processes. As long as an entanglement exists, its fluctuations become more and more anisotropic due to the generalized RA dynamics, Equation (5). When the entanglement is destroyed, this anisotropy is lost. Since newly created entanglements start out with isotropic ESFs, the process of destruction and creation counteracts the generalized RA dynamics and, when the flow stops, restores the isotropic equilibrium state. A similar relaxation occurs in the associating polymer model with anisotropic confinement potentials, where detachment of a sticker removes the anisotropy built up by the generalized RA dynamics, and newly attached stickers have isotropic spatial fluctuations. On the other hand, the equilibrium state of a cross-linked network changes with deformation. The amount of anisotropy retained after flow depends on the relative numbers of finite-lifetime entanglements versus permanent entanglements and cross-links. A finite-lifetime entanglement involves one or more dangling ends, whereas a permanent entanglement involves only network strands. We consider an unentangled network model here, which means that all of the anisotropy persists. Thus each confinement potential has the same shape tensor .
This model and the coarse-grained version of it, which is presented in the next section, are special cases of slip-link models, whose thermodynamic consistency is proven elsewhere [114]. Therefore we only need to verify three of the four criteria here: consistency of the stress tensor with the stress-optic rule, consistency of the plateau modulus from the Green–Kubo relation with the relaxation modulus after an infinitesimal deformation, and consistency with multi-strand network models.
4.1.1. Stress Tensor and Stress-Optic Rule
The stress tensor is obtained from the principle of virtual work, as explained in Section 3, or from restrictions imposed by the GENERIC structure of nonequilibrium thermodynamics [114]. The result is
with the number density of strands. In the virtual-work derivation, the isotropic contribution follows from the normalization term in the free energy, when taking the derivative using Jacobi’s rule, , together with Equation (5). Other than this, due to the generalized RA dynamics, deformation of the virtual springs causes no change in the free energy and hence no contribution to the stress tensor. The form of Equation (8) is consistent with the stress-optic rule [55].
4.1.2. Green–Kubo Relation and Infinitesimal Deformations
The single-strand contribution to the stress tensor is
According to the Green–Kubo relation, the relaxation modulus is given by the autocorrelation of the stress at equilibrium. The initial relaxation modulus is
Note that we have to specify whether the system is in the isotropic equilibrium state or some anisotropic equilibrium state because we are dealing with a solid. The subscript “iso, eq” here indicates that the system is in isotropic equilibrium. The right-hand side of Equation (10) is identical to the initial relaxation modulus of the single-strand unentangled network model without RA dynamics, which is known to be inconsistent with that of the multi-strand phantom network model.
The cross-link fluctuations are expected to be of the same order of magnitude as spatial fluctuations of the Kuhn steps in the strand, which we coarse-grained out from the outset. By including virtual springs on this level of description, we keep track of the cross-link positions but, inconsistently, not of the inner Kuhn-step positions. A self-consistent approach is possible either on a more-detailed level of description, where all the Kuhn-step positions are resolved, or a less-detailed one, where the cross-link positions are coarse-grained out like the inner Kuhn-step positions. The second option is more relevant for our purpose, because node fluctuations are expected to relax on a time scale that is usually not accessible in mechanical rheology. The plateau modulus of our model, which is relevant for comparison with experimental data, is reached after relaxation of the cross-link fluctuations and is lower than the initial modulus calculated in Equation (10).
The Green–Kubo result does agree with the relaxation modulus after an infinitesimal step strain γ. This can be seen by substituting in Equation (8), where the superscript 0 refers to the system in the isotropic equilibrium state at , before the step. The stress tensor after the step is then
to first order in the strain, and hence the modulus is
in agreement with the Green–Kubo result, Equation (10).
We have now established that three of the four criteria are satisfied. The remaining one is consistency with multi-strand network models. This means that the plateau modulus, which is reached after the virtual springs have relaxed, should be lower than that of a network with affinely moving cross-links. Instead of checking this here, we proceed by coarse-graining out the cross-link fluctuations and verifying that the resulting less-detailed model satisfies all four criteria. Since the plateau modulus of this coarse-grained model corresponds to the plateau modulus of the detailed model after equilibration of the cross-link fluctuations, the remaining criterion is then also satisfied for the detailed model.
4.2. Coarse-Grained Single-Strand Unentangled Network Model
We integrate the equilibrium probability density over all possible conformations of the virtual springs, as explained in Appendix B.2. The level of description of the resulting coarse-grained model is expressed in the set of variables
The free energy in terms of these variables is
where . Note that can be mapped onto the fully equivalent set by means of Equation (58) from Appendix B.1. The stress tensor and the modulus are more concisely expressed in terms of , as shown below.
4.2.1. Stress Tensor and Stress-Optic Rule
The time derivative of the free energy is calculated in Equation (68) in Appendix B.2. According to the principle of virtual work, the stress tensor is then
The single-strand contribution to the stress tensor,
corresponds (on the detailed level of description) to the average of for fixed and , assuming that the cross-link positions are at equilibrium. This proves that Equation (15) is the appropriate stress tensor expression for our coarse-grained level of description and that it satisfies the stress-optic rule.
4.2.2. Green–Kubo Relation and Infinitesimal Deformations
The term between the parentheses in Equation (15) is related to fluctuations of the cross-links around their mean positions. In an undeformed network, these fluctuations are isotropic. The Green–Kubo relation for an isotropic network at equilibrium yields the plateau modulus
To prove that this result is consistent with the relaxation modulus under infinitesimal deformation, we perturb the system by a step strain γ from the isotropic equilibrium state at . After the step, the anchor connector is and the shape tensor of the confinement potentials is . Substituting these results in Equation (15) and using , we find
The relaxation modulus after the step is therefore
as predicted by the Green–Kubo relation, Equation (17).
4.2.3. Consistency with the Multi-Strand Front Factor
Consistency with the modulus front factor from multi-strand network models [30,31,32,33,34], where ϕ is the functionality of the network, suggests that the ratio of “virtual Kuhn steps” to real Kuhn steps is
For , we find . Hence the stiffness of the virtual springs, mapping a tetrafunctional phantom network onto a single-strand model, is about five times the strand stiffness.
To summarize, all four criteria are satisfied by our single-strand unentangled network model with anisotropic cross-link fluctuations, when the actual positions of the crosslinks are included as dynamic variables as well as when they are coarse-grained out. The RA dynamics play a key role in this. They lead to a cancellation of virtual-spring contributions to the stress tensor. These contributions should not be naively omitted, because that would violate thermodynamics [41]. The cancellation prevents such violations. The resulting stress tensor expression agrees with the stress-optic rule and, through the Green–Kubo relation, predicts a modulus lower than that of a network with fixed or isotropically fluctuating cross-links. Finally, the modulus after a step strain is consistent with the Green–Kubo relation.
We end this section by drawing a comparison between our coarse-grained single-strand unentangled network model and Öttinger’s single-segment reptation model [63]. A straightforward derivation shows that our tensor evolves according to
which is very similar to Equation (2) for the dyad of Öttinger’s tube cross-section variable. The equivalence suggests two things. First, as already pointed out in Section 3, should be interpreted as the “inverse” of the tube radius, rather than the tube radius. Second, must be positive. Recall that the reptation model has modulus front factor . This means that we would need a negative to agree with multi-chain models (). A negative makes increase with stretch of the primitive path. In the language of reptation models: the diameter of the tube shrinks when its length is stretched.
5. Proposed Slip-Link Models
We propose two slip-link models whose slip-links are allowed to fluctuate in an anisotropic harmonic potential. The potential changes with imposed deformation according to the generalized RA dynamics. As before, the numbers of Kuhn steps are treated stochastically instead of using Rouse-like beads. In the detailed model, we track the positions of the slip-links. In the coarse-grained version, assuming that the slip-link spatial fluctuations are sufficiently rapid compared with overall chain dynamics, we integrate out these fast degrees of freedom. The first model is computationally more expensive, but provides a check for the algorithm of the second model. These models are generalizations of the single-strand network models discussed in Section 4, for which details of the derivations are given in Appendix B. Since all derivations for the slip-link models are analogous, we omit the details here.
5.1. Detailed Mobile Slip-Link Model
In the detailed model, our level of description is the number of strands Z, the number of Kuhn steps in each strand, the connector vector between two slip-links, the vector pointing from the center of the confinement potential (the anchor) to the slip-link, and a dimensionless tensor describing the strength and shape of the confinement potential:
Figure 2 illustrates the notation for the vectors used. The tensors are new compared with earlier work [92]. The free energy on this level of description is given by
where is the free energy of a strand, usually assumed to be Gaussian. Note that it is possible to write the free energy either in terms of the set of connector vectors , or , or the set of position vectors . Which set is used is a matter of convenience. The tensors are assumed to obey Equation (5) with the initial condition at creation .
We discuss compliance with the four criteria briefly and without going into details of the derivations. The single-strand unentangled network model presented in Section 4.1 satisfies the four criteria in an analogous but mathematically simpler way. For the sake of clarity, we show more details there and focus on results here. It is shown elsewhere that the mobile slip-link model is GENERIC [114], so we need only consider three criteria here.
The stress tensor can be derived from the principle of virtual work or from GENERIC. In both cases we find
where is the number density of chains. It can be seen that this agrees with the stress-optic rule [55] by inserting the derivative of the Gaussian strand free energy, .
The relaxation modulus can be calculated by inserting the single-chain contribution to the stress tensor, , into the Green–Kubo relation. Using the Gaussian strand free energy, we find the initial modulus
This is equal to the plateau modulus for the fixed slip-link model [10] because the stress tensors of both models are the same.
The relaxation modulus after a step strain is found to be
consistent with the prediction of the Green–Kubo relation, Equation (25). Since both results are equal to the plateau modulus for the fixed slip-link model [10], and also equal to the plateau modulus for the mobile slip-link model without RA dynamics [92], it seems that we have no consistency with multi-chain models. However, the modulus given by Equation (26) is not the rubbery plateau modulus because it contains (indirectly) some stress from ESFs, which relax on a time scale that is not accessible by mechanical rheology experiments. It is not some higher modulus either, since it neglects dynamics on the level of single Kuhn steps, whose time scale is comparable to that of ESFs; see also the discussion after Equation (10).
Our next step is to coarse-grain out the ESFs from this mobile slip-link model. The plateau modulus of the resulting less-detailed model then corresponds more closely to the experimentally accessible plateau modulus. If its value decreased with increasing ESFs, that would be consistent with multi-chain models.
5.2. Coarse-Grained Mobile Slip-Link Model
Since our model does not resolve dynamics on the time scale of single Kuhn-step motion, it is natural to coarse-grain out the ESFs (which are on the time scale of single Kuhn-step motion). In other words, we integrate the probability density over all possible while holding fixed. Based on the assumed separation of time scales between ESFs and strand conformations, the slip-links may be considered to be equilibrated around their mean positions, set by the fixed variables. This allows us to perform the integrations analytically. Our new level of description is then
where are the mean values of the strand end-to-end vectors for fixed anchor positions (given by Equation (30) below), Kuhn-step numbers, and virtual-spring potentials. The new free energy is then
with the variance matrix
Equation (28) is derived in Appendix C. The logarithmic term on the right-hand side contains the determinant of , which involves the anisotropic tensors . This may seem strange, since the determinant of would suffice to normalize the equilibrium probability density. We come back to this point below.
Sliding dynamics and constraint dynamics of the chains should now be governed by the new free energy, but are otherwise unchanged. The anchors are assumed to move affinely. We can pass between anchor connector vectors and mean strand end-to-end vectors by
and from this it is possible to derive the dynamics of the mean strand end-to-end vectors.
Now we are in a position to verify whether all our criteria are met for the coarse-grained mobile slip-link model with generalized RA dynamics. We point out that, also for this model, a GENERIC check is performed elsewhere [114], so we are concerned with only three of the four criteria here. The generalized RA dynamics are again of crucial importance to achieve full consistency. Similar to the previous subsection, we omit derivations here, and refer to the coarse-grained single-strand unentangled network model in Section 4.2 as an example that displays the general issues.
Thermodynamics gives the stress tensor expression
It can be shown that the terms between parentheses are equivalent to the average (in the detailed model) of for fixed . Therefore Equation (31) is the appropriate coarse-grained stress tensor and satisfies the stress-optic rule. The terms in Equation (31) are related to fluctuations of the entanglements around their mean positions. Now it becomes clear why the logarithmic term in the free energy, Equation (28), has to be of the form rather than . In the latter case, the stress tensor is and the stress-optic rule is violated. For an associating polymer model with generalized RA dynamics, one obtains a stress tensor expression analogous to Equation (31), with Z corresponding to the number of bound stickers per chain and to the numbers of Kuhn steps between neighboring bound stickers.
With the single-chain contribution to the stress tensor,
the Green–Kubo relation gives the plateau modulus
The matrix on the right-hand side is the scalar part of the variance matrix when all virtual springs are isotropic. The derivation of is similar to that given in reference [92] for the mobile slip-link model with isotropic ESFs, although the result is different.
Applying an infinitesimal step strain, starting from equilibrium at , we find that the modulus directly after the step is
The right-hand side of Equation (34) is identical to the Green–Kubo prediction, Equation (33). This self-consistency, like the agreement with the stress-optic rule, is obtained only if the logarithmic term in the free energy has the form given in Equation (28).
Finally, decreases with increasing ESFs, which is consistent with multi-chain results. From Equations (25) and (33), or Equations (26) and (34), follows the front factor
Thus our mobile slip-link model satisfies all four criteria on both the detailed and the coarse-grained level of description. A quantitative comparison between this model and multi-chain simulations, using primitive-path analysis, is presented in a separate paper [61].
6. Conclusions
We have introduced four consistency criteria for single-chain mean-field entangled polymer melt models and proposed a slip-link model that (to our knowledge, for the first time) satisfies all these criteria. The free energy of the model is given in Equation (28), which is equivalent to
where the set of stochastic variables is
Here are the anchor connector vectors, see Figure 2, and
The evolution of the probability density is given by the differential Chapman–Kolmogorov equation,
where is the substantial derivative of the scalar density p [48]. The transition probabilities are
where , , , and are the transition probabilities for destruction (d) and creation (c) of entanglements by sliding dynamics (SD) and constraint dynamics (CD), which are given in Equations (6,10–13,16,17) of Andreev et al. [13]. Shuffling of Kuhn steps through entanglements is given by from Equation (7) of Khaliullin and Schieber [10], where has to be replaced by , as pointed out in the text following Equation (6) of reference [13].
The generalized RA dynamics play a central role in satisfying the four criteria. The slip-link model with generalized RA dynamics is consistent with nonequilibrium thermodynamics [114]. The stress tensor
which is required for thermodynamic consistency, leads to compliance with the other three criteria as well.
Acknowledgements
We are grateful to the Army Research Office (grants W911NF-08-2-0058, W911NF-09-1-0378 and W911NF-11-2-0018) for financial support.
Appendix
A. Differential Formulation of the Molecular Stress Function Model
Wagner and coworkers [71,72] have given several versions of the “molecular stress function model”. The model is in integral form, and involves two dynamic variables: a function f that represents the inverse of the dimensionless “tube diameter”, and a unit vector for the tube orientation. The variations in model formulation involve modifications to the evolution equation for f. The model also involves a phenomenological memory function that is found from a fit to linear viscoelasticity. We give here a differential form of the model. This form is necessary for checking compliance with the nonequilibrium thermodynamic formalism GENERIC [47,48,49,50], or for finite element calculations in complex flow fields using conformation fields [115,116].
In order to make the model differential, we use a probability density p with an added dynamic variable j, which is an integer indicating the mode. The number of modes m is determined by a fit to the relaxation function . The Markovian evolution equation for the conditional probability density (probability that the tube segment has conformation in the neighborhood of with mode j at time t given that it had conformation with mode at time ) is
where we have used the shorthand , and depends on the particular formulation in the model. The jump transition probability is given by
The equilibrium probability density is given by
The probability density evolution Equation (42) has solution
where is the solution to the differential equation
with “initial condition” . When the stress tensor is found by the average
the formulation is mathematically equivalent to the molecular stress function model. Therefore Equations (42–44) are a Markovian representation of Wagner’s integral model, suitable for study by GENERIC.
B. Details of the Single-Strand Mean-Field Unentangled Network Models
B.1. Derivation of the Mean Strand Conformation
The goal here is to derive the mean cross-link positions and their relation to the anchor positions . From this information, we then calculate the mean strand end-to-end vector and its relation to the anchor connector . This is useful for the coarse-grained model derived in the next section, in which part of the stress tensor turns out to be proportional to .
We choose as our set of variables the position vectors of the cross-links and anchors (see Figure 1) and the compliance tensor of the virtual springs ,
The superscript + indicates that, on this level of description, the center-of-mass position of the strand is known. We assume Gaussian statistics for the end-to-end vector of the strand,
as well as the virtual springs,
The free energy of the system is the sum of these strand and virtual-spring contributions plus an additional term that normalizes the equilibrium probability density. The latter can be derived by writing the free energy in the form
where includes the normalization term. Between Equations (49,50) and Equation (51), we match up the terms quadratic in to find the inverse variance matrix,
and the terms linear in to find the mean cross-link positions,
Equations (52) and (53) are used below to find the mean strand end-to-end vector and its relation to the anchor connector.
Merely for completeness, we note that the terms depending only on add up to
where
and the last term in Equation (54) provides the normalization.
Since the variance matrix is symmetric,
we obtain from Equation (53)
and from the inverse of Equation (53), using Equation (52),
Another way to derive Equation (58) is by taking the derivatives of the free energy with respect to and using the fact that these derivatives are zero when . See for example Read et al. [117] and the supplementary material of Steenbakkers and Schieber [112]. Combining Equations (57) and (58) yields
Equation (59) also follows from multiplication of with , given by Equation (52), and subtraction of the resulting two expressions. Those expressions can be solved for and , but we need only the difference of these tensors here.
B.2. Coarse-Graining
For common rheological predictions, it is not necessary to track the center of mass of the strand and it is therefore more convenient to replace the absolute positions of the cross-links and anchors by their relative positions. If we choose the variables Ω as in Equation (6), the free energy is given by Equation (7).
We now coarse-grain our unentangled network model by integrating the equilibrium probability density over all possible . To facilitate this, we first write the free energy in a canonical Gaussian form for these variables. The same approach was taken by Schieber and Horio [92] and Steenbakkers and Schieber [112] for the mobile slip-link model. Details can be found in Section S III of the supplementary material of the latter paper.
If we choose
as our variables for the strand conformation, the free energy can be written in the form
with as in Equation (13). The fact that the variance matrix of the virtual-spring free energy is follows from the terms in Equations (7) and (61) that are quadratic in . Matching up the terms linear in , we find
The terms that depend only on give
with
where we have made use of Equation (59). It can be shown that
and hence
By integrating the equilibrium probability density over all possible , we obtain
as the free energy of the coarse-grained model.
B.3. Change of Free Energy and Mean Path Under Infinitesimal Deformation
We merely present a few expressions that are used in Section 4.2. The time derivative of the free energy is
In the last step, Equations (59) and (64) were used. By the principle of virtual work, this result leads to the stress tensor Equation (15).
C. Coarse-Graining of the Detailed Mobile Slip-Link Model
We integrate the equilibrium probability density of the slip-link model from Section 5.1 over all possible , keeping the other variables,
fixed. This is a straightforward generalization of our coarse-graining of the single-strand unentangled network model in Appendix B.2. The derivation is equivalent to that for the slip-link model with isotropic ESFs, which has been presented in detail ([112] [supplementary material, section S III]). Here only one step is repeated, which is not obvious for our slip-link model with generalized RA dynamics. Equation numbers preceded by an “S” refer to equations from the supplementary material of reference [112].
In the case of anisotropic ESFs, the coarse-grained free energy is
with
The second term on the right-hand side of Equation (73) is not determined by the coarse-graining, but by the requirement that the stress-optic rule be obeyed, as explained in Section 5.2. Equation (74) has the same form as Equation (S26), but the inverse of the matrix is now
instead of Equation (S15). Differences are due to the anisotropy of the ESFs and the absence of virtual springs at the chain ends in the current model.
Minimization of the free energy of the detailed model with respect to the entanglement positions, for fixed , leads to the mean strand end-to-end vectors given by Equation (30). Here we write this as
with
The evolution equation for the inverse of this matrix is
due to the generalized RA dynamics, Equation (5). In the same way, the time derivative of can be calculated from Equation (75). Substitution in Equation (74) yields, after some algebra,
In previous work ([112] [supplementary material]), we confirmed that . Since σ and ξ have the same time evolution, we can generalize this to
Substituting this in Equation (73) and making use of Equation (30), we obtain Equation (28) for .
References
- Doi, M.; Edwards, S.F. Dynamics of concentrated polymer systems. Part 1. Brownian motion in the equilibrium state. J. Chem. Soc. Faraday Trans. 2 1978, 74, 1789–1801. [Google Scholar] [CrossRef]
- Doi, M.; Edwards, S.F. Dynamics of concentrated polymer systems. Part 2. Molecular motion under flow. J. Chem. Soc. Faraday Trans. 2 1978, 74, 1802–1817. [Google Scholar] [CrossRef]
- Doi, M.; Edwards, S.F. Dynamics of concentrated polymer systems. Part 3. The constitutive equation. J. Chem. Soc. Faraday Trans. 2 1978, 74, 1818–1832. [Google Scholar] [CrossRef]
- Doi, M.; Edwards, S.F. Dynamics of concentrated polymer systems. Part 4. Rheological properties. J. Chem. Soc. Faraday Trans. 2 1979, 75, 38–54. [Google Scholar] [CrossRef]
- Doi, M.; Edwards, S.F. The Theory of Polymer Dynamics. Volume 73, In International Series of Monographs on Physics; Clarendon Press: Oxford, NY, USA, 1986. [Google Scholar]
- Milner, S.T.; McLeish, T.C.B. Parameter-free theory for stress relaxation in star polymer melts. Macromolecules 1997, 30, 2159–2166. [Google Scholar] [CrossRef]
- Likhtman, A.E.; McLeish, T.C.B. Quantitative theory for linear dynamics of linear entangled polymers. Macromolecules 2002, 35, 6332–6343. [Google Scholar] [CrossRef]
- Graham, R.S.; Likhtman, A.E.; McLeish, T.C.B.; Milner, S.T. Microscopic theory of linear, entangled polymer chains under rapid deformation including chain stretch and convective constraint release. J. Rheol. 2003, 47, 1171–1200. [Google Scholar] [CrossRef]
- Schieber, J.D.; Nair, D.; Kitkrailard, T. Comprehensive comparisons with nonlinear flow data of a consistently unconstrained Brownian slip-link model. J. Rheol. 2007, 51, 1111–1141. [Google Scholar] [CrossRef]
- Khaliullin, R.N.; Schieber, J.D. Self-consistent modeling of constraint release in a single-chain mean-field slip-link model. Macromolecules 2009, 42, 7504–7517. [Google Scholar] [CrossRef]
- Khaliullin, R.N.; Schieber, J.D. Application of the slip-link model to bidisperse systems. Macromolecules 2010, 43, 6202–6212. [Google Scholar] [CrossRef]
- Pilyugina, E.; Andreev, M.; Schieber, J.D. Dielectric relaxation as an independent examination of relaxation mechanisms in entangled polymers using the discrete slip-link model. Macromolecules 2012, 45, 5728–5743. [Google Scholar] [CrossRef]
- Andreev, M.; Khaliullin, R.N.; Steenbakkers, R.J.A.; Schieber, J.D. Approximations of the discrete slip-link model and their effect on nonlinear rheology predictions. J. Rheol. 2013, 57, 535–557. [Google Scholar] [CrossRef]
- Everaers, R.; Sukumaran, S.K.; Grest, G.S.; Svaneborg, C.; Sivasubramanian, A.; Kremer, K. Rheology and microscopic topology of entangled polymeric liquids. Science 2004, 303, 823–826. [Google Scholar] [CrossRef] [PubMed]
- Svaneborg, C.; Grest, G.G.; Everaers, R. Strain-dependent localization, microscopic deformations, and macroscopic normal tensions in model polymer networks. Phys. Rev. Lett. 2004, 93, 257801:1–257801:4. [Google Scholar] [CrossRef] [PubMed]
- Kröger, M. Shortest multiple disconnected path for the analysis of entanglements in two- and three-dimensional polymeric systems. Comput. Phys. Commun. 2005, 168, 209–232. [Google Scholar] [CrossRef]
- Foteinopoulou, K.; Karayiannis, N.C.; Mavrantzas, V.G.; Kröger, M. Primitive path identification and entanglement statistics in polymer melts: Results from direct topological analysis on atomistic polyethylene models. Macromolecules 2006, 39, 4207–4216. [Google Scholar] [CrossRef]
- Tzoumanekas, C.; Theodorou, D.N. Topological analysis of linear polymer melts: A statistical approach. Macromolecules 2006, 39, 4592–4604. [Google Scholar] [CrossRef]
- Kamio, K.; Moorthi, K.; Theodorou, D.N. Coarse grained end bridging Monte Carlo simulations of poly(ethylene terephthalate) melt. Macromolecules 2007, 40, 710–722. [Google Scholar] [CrossRef]
- Spyriouni, T.; Tzoumanekas, C.; Theodorou, D.; Müller-Plathe, F.; Milano, G. Coarse-grained and reverse-mapped united-atom simulations of long-chain atactic polystyrene melts: Structure, thermodynamic properties, chain conformation, and entanglements. Macromolecules 2007, 40, 3876–3885. [Google Scholar] [CrossRef]
- Khaliullin, R.N.; Schieber, J.D. Analytic expressions for the statistics of the primitive-path length in entangled polymers. Phys. Rev. Lett. 2008, 100, 188302:1–188302:4. [Google Scholar] [CrossRef] [PubMed]
- Foteinopoulou, K.; Karayiannis, N.C.; Laso, M.; Kröger, M.; Mansfield, M.L. Universal scaling, entanglements, and knots of model chain molecules. Phys. Rev. Lett. 2008, 101, 265702:1–265702:4. [Google Scholar] [CrossRef] [PubMed]
- Harmandaris, V.A.; Kremer, K. Dynamics of polystyrene melts through hierarchical multiscale simulations. Macromolecules 2009, 42, 791–802. [Google Scholar] [CrossRef]
- Hoy, R.S.; Foteinopoulou, K.; Kröger, M. Topological analysis of polymeric melts: Chain-length effects and fast-converging estimators for entanglement length. Phys. Rev. E 2009, 80, 031803:1–031803:13. [Google Scholar] [CrossRef] [PubMed]
- Toepperwein, G.N.; Karayiannis, N.C.; Riggleman, R.A.; Kröger, M.; de Pablo, J.J. Influence of nanorod inclusions on structure and primitive path network of polymer nanocomposites at equilibrium and under deformation. Macromolecules 2011, 44, 1034–1045. [Google Scholar] [CrossRef]
- Li, Y.; Kröger, M.; Liu, W.K. Primitive chain network study on uncrosslinked and crosslinked cis-polyisoprene polymers. Polymer 2011, 52, 5867–5878. [Google Scholar] [CrossRef]
- Zhou, Q.; Larson, R.G. Primitive path identification and statistics in molecular dynamics simulations of entangled polymer melts. Macromolecules 2005, 38, 5761–5765. [Google Scholar] [CrossRef]
- Shanbhag, S.; Kröger, M. Primitive path networks generated by annealing and geometrical methods: insights into differences. Macromolecules 2007, 40, 2897–2903. [Google Scholar] [CrossRef]
- Hill, T.L. Thermodynamics of Small Systems, Part I and Part II; Dover: Mineola, NY, USA, 2002. [Google Scholar]
- Duiser, J.A. Het Visco-Elastische Gedrag van Twee Polycarbonzuren in Water. Ph.D. Thesis, Rijksuniversiteit Leiden, Leiden, The Netherlands, 1965. [Google Scholar]
- Graessley, W.W. Statistical mechanics of random coil networks. Macromolecules 1975, 8, 186–190. [Google Scholar] [CrossRef]
- Graessley, W.W. Elasticity and chain dimensions in Gaussian networks. Macromolecules 1975, 8, 865–868. [Google Scholar] [CrossRef]
- Flory, P.J.; Gordon, M.; McCrum, N.G. Statistical thermodynamics of random networks [and discussion]. Proc. R. Soc. Lond. A 1976, 351, 351–380. [Google Scholar] [CrossRef]
- Staverman, A.J. Properties of phantom networks and real networks. Adv. Polym. Sci. 1982, 44, 73–101. [Google Scholar]
- Larson, R.G.; Sridhar, T.; Leal, L.G.; McKinley, G.H.; Likhtman, A.E.; McLeish, T.C.B. Definitions of entanglement spacing and time constants in the tube model. J. Rheol. 2003, 47, 809–818. [Google Scholar] [CrossRef]
- Masubuchi, Y.; Ianniruberto, G.; Greco, F.; Marrucci, G. Entanglement molecular weight and frequency response of sliplink networks. J. Chem. Phys. 2003, 119, 6925–6930. [Google Scholar] [CrossRef]
- Everaers, R. Topological versus rheological entanglement length in primitive-path analysis protocols, tube models, and slip-link models. Phys. Rev. E 2012, 86, 022801:1–022801:5. [Google Scholar] [CrossRef] [PubMed]
- Janeschitz-Kriegl, H. Polymer Melt Rheology and Flow Birefringence; Springer-Verlag: Berlin, Germany, 1983. [Google Scholar]
- Ramírez, J.; Sukumaran, S.K.; Likhtman, A.E. Significance of cross correlations in the stress relaxation of polymer melts. J. Chem. Phys. 2007, 126, 244904:1–244904:6. [Google Scholar] [CrossRef] [PubMed]
- Chandler, D. Introduction to Modern Statistical Mechanics; Oxford University Press: New York, NY, USA, 1987; Chapter 8. [Google Scholar]
- Indei, T.; Schieber, J.D.; Takimoto, J. Effects of fluctuations of cross-linking points on viscoelastic properties of associating polymer networks. Rheol. Acta 2012, 51, 1021–1039. [Google Scholar] [CrossRef]
- Biot, M.A. Variational principles in irreversible thermodynamics with application to viscoelasticity. Phys. Rev. 1955, 97, 1463–1469. [Google Scholar] [CrossRef]
- Marrucci, G. The free energy constitutive equation for polymer solutions from the dumbbell model. Trans. Soc. Rheol. 1972, 16, 321–330. [Google Scholar] [CrossRef]
- Doi, M. Variational principle for the Kirkwood theory for the dynamics of polymer solutions and suspensions. J. Chem. Phys. 1983, 79, 5080–5087. [Google Scholar] [CrossRef]
- Schieber, J.D.; Öttinger, H.C. On consistency criteria for stress tensors in kinetic theory models. J. Rheol. 1994, 38, 1909–1924. [Google Scholar] [CrossRef]
- Kaufman, A.N. Dissipative Hamiltonian systems: A unifying principle. Phys. Lett. A 1984, 100, 419–422. [Google Scholar] [CrossRef]
- Grmela, M.; Öttinger, H.C. Dynamics and thermodynamics of complex fluids. I. Development of a general formalism. Phys. Rev. E 1997, 56, 6620–6632. [Google Scholar] [CrossRef]
- Öttinger, H.C.; Grmela, M. Dynamics and thermodynamics of complex fluids. II. Illustrations of a general formalism. Phys. Rev. E 1997, 56, 6633–6655. [Google Scholar] [CrossRef]
- Öttinger, H.C. General projection operator formalism for the dynamics and thermodynamics of complex fluids. Phys. Rev. E 1998, 57, 1416–1420. [Google Scholar] [CrossRef]
- Öttinger, H.C. Beyond Equilibrium Thermodynamics; Wiley-Interscience: Hoboken, NJ, USA, 2005. [Google Scholar]
- Ronca, G.; Allegra, G. An approach to rubber elasticity with internal constraints. J. Chem. Phys. 1975, 63, 4990–4997. [Google Scholar] [CrossRef]
- Treloar, L.R.G. The Physics of Rubber Elasticity, 2nd ed.; Clarendon Press: Oxford, NY, USA, 1958. [Google Scholar]
- Mead, D.W.; Leal, L.G. The reptation model with segmental stretch I. Basic equations and general properties. Rheol. Acta 1995, 34, 339–359. [Google Scholar] [CrossRef]
- Luap, C.; Karlina, M.; Schweizer, T.; Venerus, D.C. Limit of validity of the stress-optical rule for polystyrene melts: Influence of polydispersity. J. Non-Newtonian Fluid Mech. 2006, 138, 197–203. [Google Scholar] [CrossRef]
- Fuller, G.G. Optical Rheometry of Complex Fluids; Topics in Chemical Engineering, Oxford University Press: New York, NY, USA, 1995. [Google Scholar]
- Kubo, R.; Toda, M.; Hashitsume, N. Statistical Physics II: Nonequilibrium Statistical Mechanics; Springer-Verlag: Berlin, Germany, 1985. [Google Scholar]
- Heinrich, G.; Straube, E.; Helmis, G. Rubber elasticity of polymer networks: Theories. Adv. Polym. Sci. 1988, 85, 33–87. [Google Scholar]
- Rubinstein, M.; Panyukov, S. Nonaffine deformation and elasticity of polymer networks. Macromolecules 1997, 30, 8036–8044. [Google Scholar] [CrossRef]
- Rubinstein, M.; Panyukov, S. Elasticity of polymer networks. Macromolecules 2002, 35, 6670–6686. [Google Scholar] [CrossRef]
- Everaers, R. Constrained fluctuation theories of rubber elasticity: General results and an exactly solvable model. Eur. Phys. J. B 1998, 4, 341–350. [Google Scholar] [CrossRef]
- Steenbakkers, R.J.A.; Tzoumanekas, C.; Li, Y.; Liu, W.K.; Kröger, M.; Schieber, J.D. Primitive-path statistics of entangled polymers: Mapping multi-chain simulations onto single-chain mean-field models. 2013. to be submitted for publication. [Google Scholar] [CrossRef]
- Basu, A.; Wen, Q.; Mao, X.; Lubensky, T.C.; Janmey, P.A.; Yodh, A.G. Nonaffine displacements in flexible polymer networks. Macromolecules 2011, 44, 1671–1679. [Google Scholar] [CrossRef]
- Öttinger, H.C. Thermodynamically admissible reptation models with anisotropic tube cross sections and convective constraint release. J. Non-Newtonian Fluid Mech. 2000, 89, 165–185. [Google Scholar] [CrossRef]
- Schieber, J.D.; Neergaard, J.; Gupta, S. A full-chain, temporary network model with sliplinks, chain-length fluctuations, chain connectivity and chain stretching. J. Rheol. 2003, 47, 213–233. [Google Scholar] [CrossRef]
- Likhtman, A.E. Single-chain slip-link model of entangled polymers: Simultaneous description of neutron spin-echo, rheology, and diffusion. Macromolecules 2005, 38, 6128–6139. [Google Scholar] [CrossRef]
- Masubuchi, Y.; Takimoto, J.; Koyama, K.; Ianniruberto, G.; Marrucci, G.; Greco, F. Brownian simulations of a network of reptating primitive chains. J. Chem. Phys. 2001, 115, 4387–4394. [Google Scholar] [CrossRef]
- Ianniruberto, G.; Marrucci, G. Stress tensor and stress-optical law in entangled polymers. J. Non-Newtonian Fluid Mech. 1998, 79, 225–234. [Google Scholar] [CrossRef]
- Öttinger, H.C.; Beris, A.N. Thermodynamically consistent reptation model without independent alignment. J. Chem. Phys. 1999, 110, 6593–6596. [Google Scholar] [CrossRef]
- Milner, S.T. Thermodynamic admissibility of the reptation model. J. Rheol. 2004, 48, 53–67. [Google Scholar] [CrossRef]
- Edwards, B.J. Letter to the editor: Comments on “Thermodynamic admissibility of the reptation model” [J. Rheol. 48, 53 (2004)]. J. Rheol. 2004, 48, 705–708. [Google Scholar] [CrossRef]
- Wagner, M.H.; Rubio, P.; Bastian, H. The molecular stress function model for polydisperse polymer melts with dissipative convective constraint release. J. Rheol. 2001, 45, 1387–1412. [Google Scholar] [CrossRef]
- Wagner, M.H. The effect of dynamic tube dilation on chain stretch in nonlinear polymer melt rheology. J. Non-Newtonian Fluid Mech. 2011, 166, 915–924. [Google Scholar] [CrossRef]
- Marrucci, G.; Ianniruberto, G. Interchain pressure effect in extensional flows of entangled polymer melts. Macromolecules 2004, 37, 3934–3942. [Google Scholar] [CrossRef]
- Leygue, A.; Bailly, C.; Keunings, R. A tube-based constitutive equation for polydisperse entangled linear polymers. J. Non-Newtonian Fluid Mech. 2006, 136, 1–16. [Google Scholar] [CrossRef]
- Winnik, M.A.; Yekta, A. Associative polymers in aqueous solution. Curr. Opin. Colloid Interface Sci. 1997, 2, 424–436. [Google Scholar] [CrossRef]
- Chassenieux, C.; Nicolai, T.; Benyahia, L. Rheology of associative polymer solutions. Curr. Opin. Colloid Interface Sci. 2011, 16, 18–26. [Google Scholar] [CrossRef]
- Tanaka, F.; Edwards, S.F. Viscoelastic properties of physically crosslinked networks. 1. Transient network theory. Macromolecules 1992, 25, 1516–1523. [Google Scholar] [CrossRef]
- Tanaka, F.; Edwards, S.F. Viscoelastic properties of physically crosslinked networks. Part 1. Non-linear stationary viscoelasticity. J. Non-Newtonian Fluid Mech. 1992, 43, 247–271. [Google Scholar] [CrossRef]
- Tanaka, F.; Edwards, S.F. Viscoelastic properties of physically crosslinked networks. Part 2. Dynamic mechanical moduli. J. Non-Newtonian Fluid Mech. 1992, 43, 273–288. [Google Scholar] [CrossRef]
- Tanaka, F.; Edwards, S.F. Viscoelastic properties of physically crosslinked networks. Part 3. Time-dependent phenomena. J. Non-Newtonian Fluid Mech. 1992, 43, 289–309. [Google Scholar] [CrossRef]
- Green, M.S.; Tobolsky, A.V. A new approach to the theory of relaxing polymeric media. J. Chem. Phys. 1946, 14, 80–92. [Google Scholar] [CrossRef]
- Lodge, A.S. A network theory of flow birefringence and stress in concentrated polymer solutions. Trans. Faraday Soc. 1956, 52, 120–130. [Google Scholar] [CrossRef]
- Yamamoto, M. The visco-elastic properties of network structure I. General formalism. J. Phys. Soc. Jpn. 1956, 11, 413–421. [Google Scholar] [CrossRef]
- Yamamoto, M. The visco-elastic properties of network structure II. Structural viscosity. J. Phys. Soc. Jpn. 1957, 12, 1148–1158. [Google Scholar] [CrossRef]
- Yamamoto, M. The visco-elastic properties of network structure III. Normal stress effect (Weissenberg effect). J. Phys. Soc. Jpn. 1958, 13, 1200–1211. [Google Scholar] [CrossRef]
- Bird, R.B.; Curtiss, C.F.; Armstrong, R.C.; Hassager, O. Dynamics of Polymeric Liquids Volume II: Kinetic Theory; Wiley-Interscience: New York, NY, USA, 1987; Chapter 20. [Google Scholar]
- Wang, S.Q. Transient network theory for shear-thickening fluids and physically crosslinked networks. Macromolecules 1992, 25, 7003–7010. [Google Scholar] [CrossRef]
- Vaccaro, A.; Marrucci, G. A model for the nonlinear rheology of associating polymers. J. Non-Newtonian Fluid Mech. 2000, 92, 261–273. [Google Scholar] [CrossRef]
- Tripathi, A.; Tam, K.C.; McKinley, G.H. Rheology and dynamics of associative polymers in shear and extension: theory and experiments. Macromolecules 2006, 39, 1981–1999. [Google Scholar] [CrossRef]
- Indei, T.; Koga, T.; Tanaka, F. Theory of shear-thickening in transient networks of associating polymers. Macromol. Rapid Commun. 2005, 26, 701–706. [Google Scholar] [CrossRef]
- Cifre, J.G.H.; Barenbrug, T.M.A.O.M.; Schieber, J.D.; van den Brule, B.H.A.A. Brownian dynamics simulation of reversible polymer networks under shear using a non-interacting dumbbell model. J. Non-Newtonian Fluid Mech. 2003, 113, 73–96. [Google Scholar] [CrossRef]
- Schieber, J.D.; Horio, K. Fluctuation in entanglement positions via elastic slip-links. J. Chem. Phys. 2010, 132, 074905:1–074905:11. [Google Scholar] [CrossRef] [PubMed]
- Indei, T.; Takimoto, J. Linear viscoelastic properties of transient networks formed by associating polymers with multiple stickers. J. Chem. Phys. 2010, 133, 194902:1–194902:13. [Google Scholar] [CrossRef] [PubMed]
- Jongschaap, R.J.J.; Wientjes, R.H.W.; Duits, M.H.G.; Mellema, J. A generalized transient network model for associative polymer networks. Macromolecules 2001, 34, 1031–1038. [Google Scholar] [CrossRef]
- Rubinstein, M.; Semenov, A.N. Thermoreversible gelation in solutions of associating polymers. 2. Linear dynamics. Macromolecules 1998, 31, 1386–1397. [Google Scholar] [CrossRef]
- Indei, T.; Schieber, J.D. Correction of Doi–Edwards’ Green function for a chain in a harmonic potential and its implication for the stress-optical rule. Available online: http://arxiv.org/abs/1302.5151 (accessed on 28 May 2013).
- Chassenieux, C.; Tassin, J.F.; Gohy, J.F.; Jérôme, R. Elongation of telechelic ionomers under shear: A rheological and rheo-optical study. Macromolecules 2000, 33, 1796–1800. [Google Scholar] [CrossRef]
- Pellens, L.; Vermant, J.; Mewis, J. Deviations from the stress-optical rule in telechelic associative polymer solutions. Macromolecules 2005, 38, 1911–1918. [Google Scholar] [CrossRef]
- Hua, C.C.; Schieber, J.D. Segment connectivity, chain-length breathing, segmental stretch, and constraint release in reptation models. I. Theory and single-step strain predictions. J. Chem. Phys. 1998, 109, 10018–10027. [Google Scholar] [CrossRef]
- Hua, C.C.; Schieber, J.D.; Venerus, D.C. Segment connectivity, chain-length breathing, segmental stretch, and constraint release in reptation models. II. Double-step strain predictions. J. Chem. Phys. 1998, 109, 10028–10032. [Google Scholar] [CrossRef]
- Hua, C.C.; Schieber, J.D.; Venerus, D.C. Segment connectivity, chain-length breathing, segmental stretch, and constraint release in reptation models. III. Shear flows. J. Rheol. 1999, 43, 701–717. [Google Scholar] [CrossRef]
- Schieber, J.D. GENERIC compliance of a temporary network model with sliplinks, chain-length fluctuations, segment-connectivity and constraint release. J. Non-Equilib. Thermodyn. 2003, 28, 179–188. [Google Scholar] [CrossRef]
- Schieber, J.D. Fluctuations in entanglements of polymer liquids. J. Chem. Phys. 2003, 118, 5162–5166. [Google Scholar] [CrossRef]
- Nair, D.; Schieber, J.D. Linear viscoelastic predictions of a consistently unconstrained Brownian slip-link model. Macromolecules 2006, 39, 3386–3397. [Google Scholar] [CrossRef]
- Chappa, V.C.; Morse, D.C.; Zippelius, A.; Müller, M. Translationally invariant slip-spring model for entangled polymer dynamics. Phys. Rev. Lett. 2012, 109, 148302. [Google Scholar] [CrossRef] [PubMed]
- Uneyama, T.; Masubuchi, Y. Multi-chain slip-spring model for entangled polymer dynamics. J. Chem. Phys. 2012, 137, 154902:1–154902:13. [Google Scholar] [CrossRef] [PubMed]
- Uneyama, T.; Masubuchi, Y. Detailed balance condition and effective free energy in the primitive chain network model. J. Chem. Phys. 2011, 135, 184904:1–184904:17. [Google Scholar] [CrossRef] [PubMed]
- James, H.M.; Guth, E. Theory of the elastic properties of rubber. J. Chem. Phys. 1943, 11, 455–481. [Google Scholar] [CrossRef]
- James, H.M. Statistical properties of networks of flexible chains. J. Chem. Phys. 1947, 15, 651–668. [Google Scholar] [CrossRef]
- James, H.M.; Guth, E. Simple presentation of network theory of rubber, with a discussion of other theories. J. Polym. Sci. B Polym. Phys. 1949, 4, 153–182. [Google Scholar] [CrossRef]
- Edwards, S.F. The statistical mechanics of polymerized material. Proc. Phys. Soc. 1967, 92, 9–16. [Google Scholar] [CrossRef]
- Steenbakkers, R.J.A.; Schieber, J.D. Derivation of free energy expressions for tube models from coarse-grained slip-link models. J. Chem. Phys. 2012, 137, 034901:1–034901:19. [Google Scholar] [CrossRef] [PubMed]
- Jensen, M.K.; Khaliullin, R.; Schieber, J.D. Self-consistent modeling of entangled network strands and linear dangling structures in a single-strand mean-field slip-link model. Rheol. Acta 2012, 51, 21–35. [Google Scholar] [CrossRef]
- Steenbakkers, R.J.A.; Schieber, J.D. Thermodynamically consistent incorporation of entanglement spatial fluctuations in the slip-link model. 2013. to be submitted for publication. [Google Scholar]
- Van Heel, A.P.G.; Hulsen, M.A.; van den Brule, B.H.A.A. Simulation of the Doi–Edwards model in complex flow. J. Rheol. 1999, 43, 1239–1260. [Google Scholar] [CrossRef]
- Peters, E.A.J.F.; van Heel, A.P.G.; Hulsen, M.A.; van den Brule, B.H.A.A. Generalization of the deformation field method to simulate advanced reptation models in complex flows. J. Rheol. 2000, 44, 811–829. [Google Scholar] [CrossRef]
- Read, D.J.; Jagannathan, K.; Likhtman, A.E. Entangled polymers: Constraint release, mean paths, and tube bending energy. Macromolecules 2008, 41, 6843–6853. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).