A Multiscale Mechanical Model for Plant Tissue Stiffness
Abstract
:1. Introduction

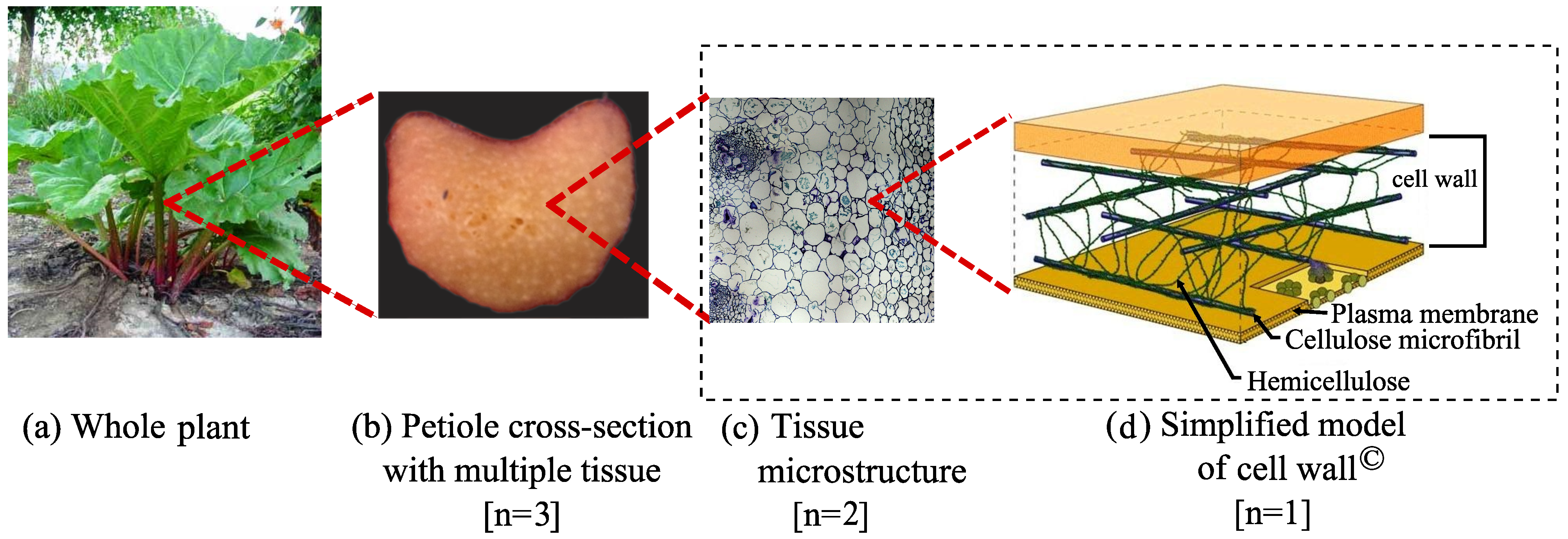
2. Methodology
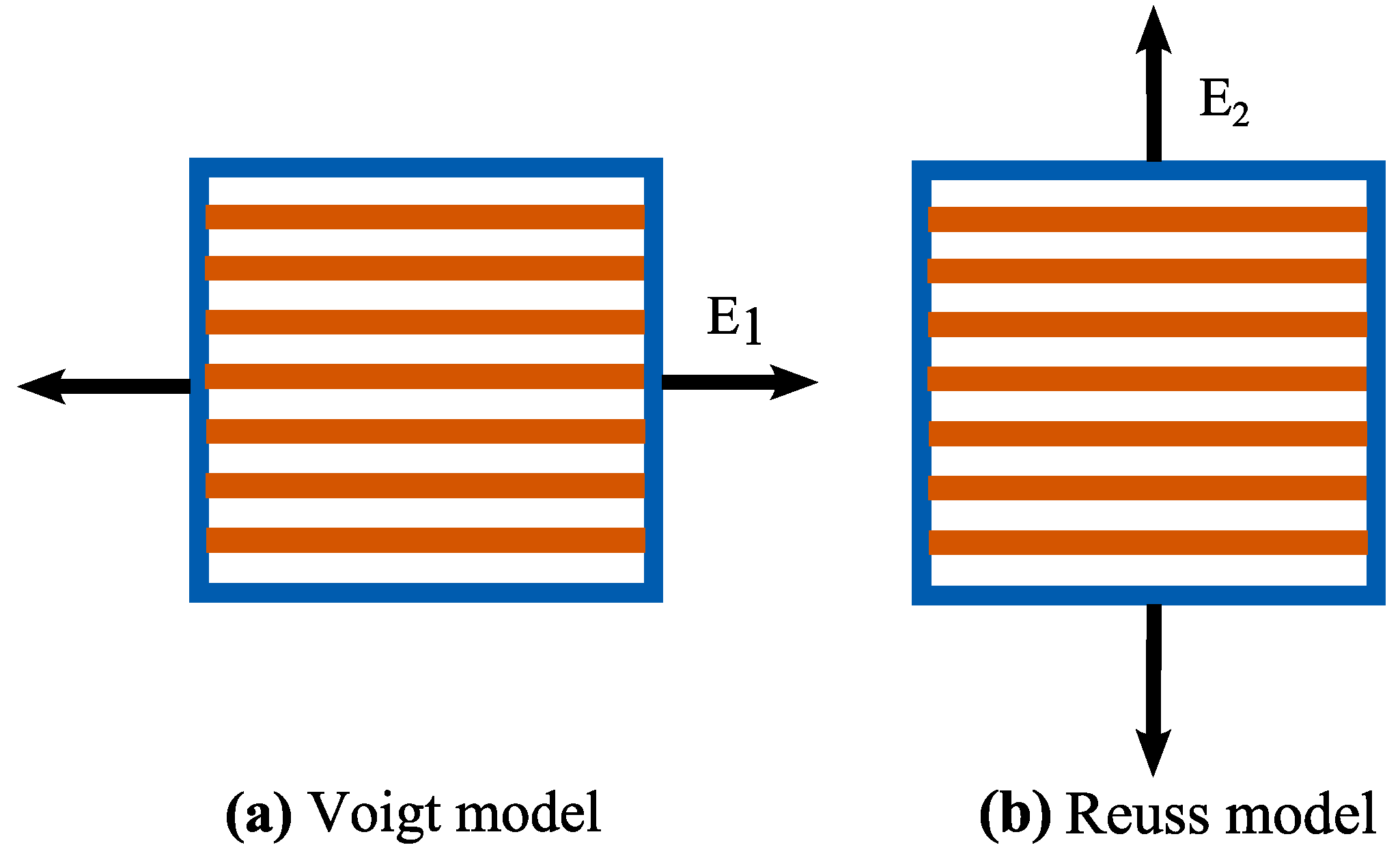
2.1. Stiffness of Cell Wall via Micromechanics Theory
| Properties | CMF | Lignin | Hemicellulose |
|---|---|---|---|
| (GPa) | 134 | 2.0 | 2.0 |
| G (GPa) | 4.4 | 1.0 | 0.6 |
| ν | 0.1 | 0.2 | 0.3 |
2.2. Constitutive Properties of Cell Wall using Macromechanics

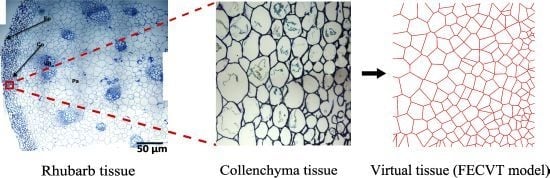
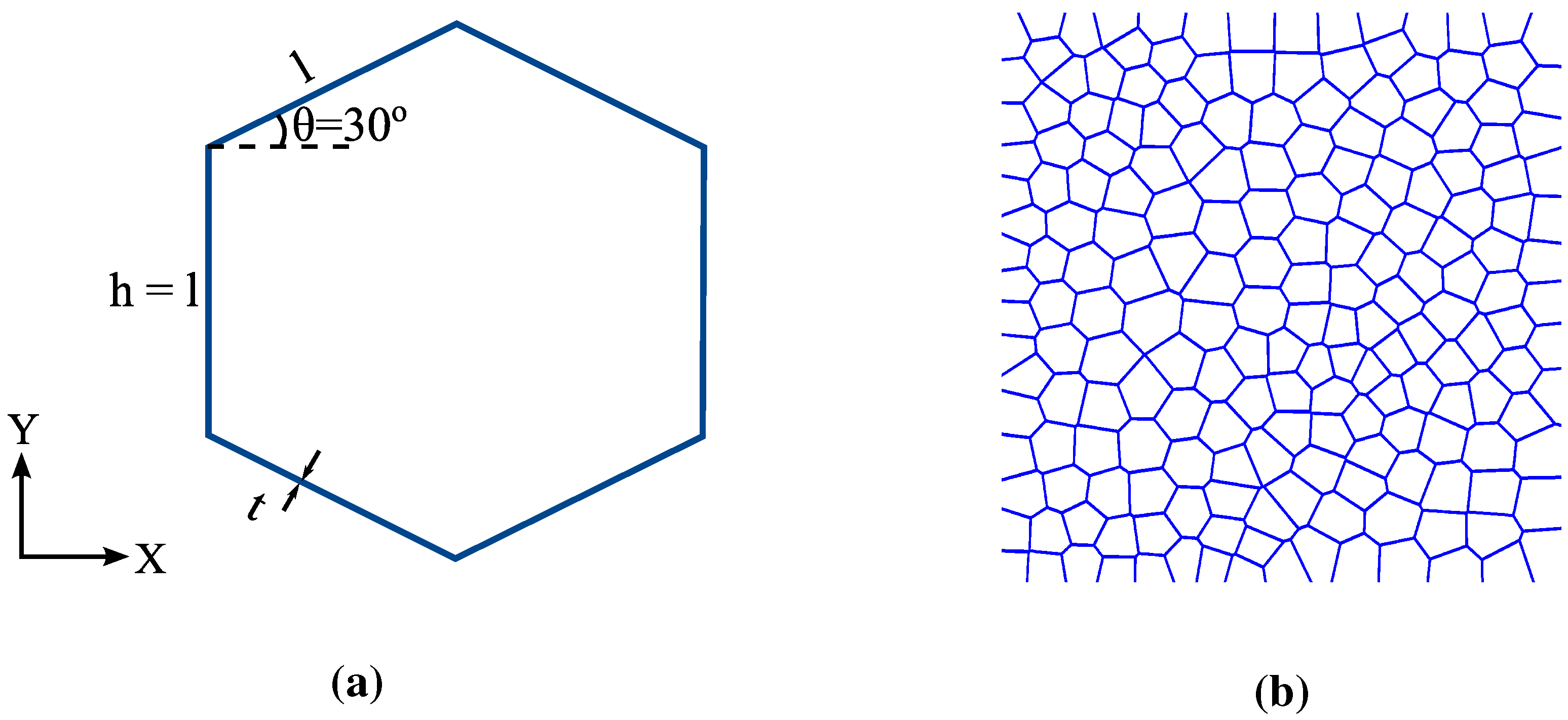
2.3. Geometric Modeling
2.4. Finite Element (FE) Modeling
2.4.1. Boundary Conditions

2.4.2. Determination of Apparent Tissue Stiffness
3. Results and Discussion
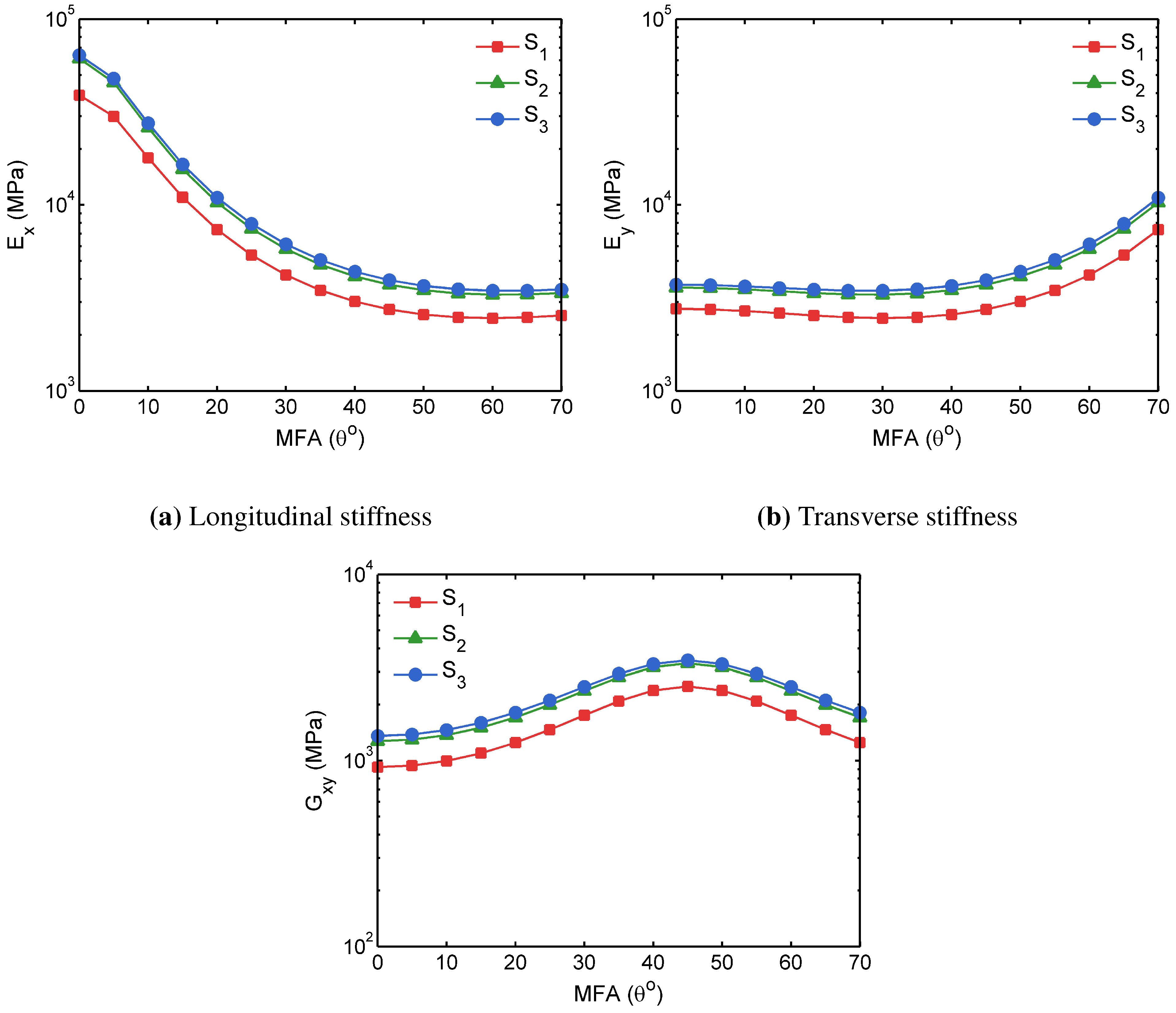
3.1. Stiffness of Cell Wall
| Cell wall layer | CMF (%) | Lignin (%) | Hemicellulose (%) |
|---|---|---|---|
| S | 28 | 45 | 27 |
| S | 45 | 20 | 35 |
| S | 47 | 15 | 38 |
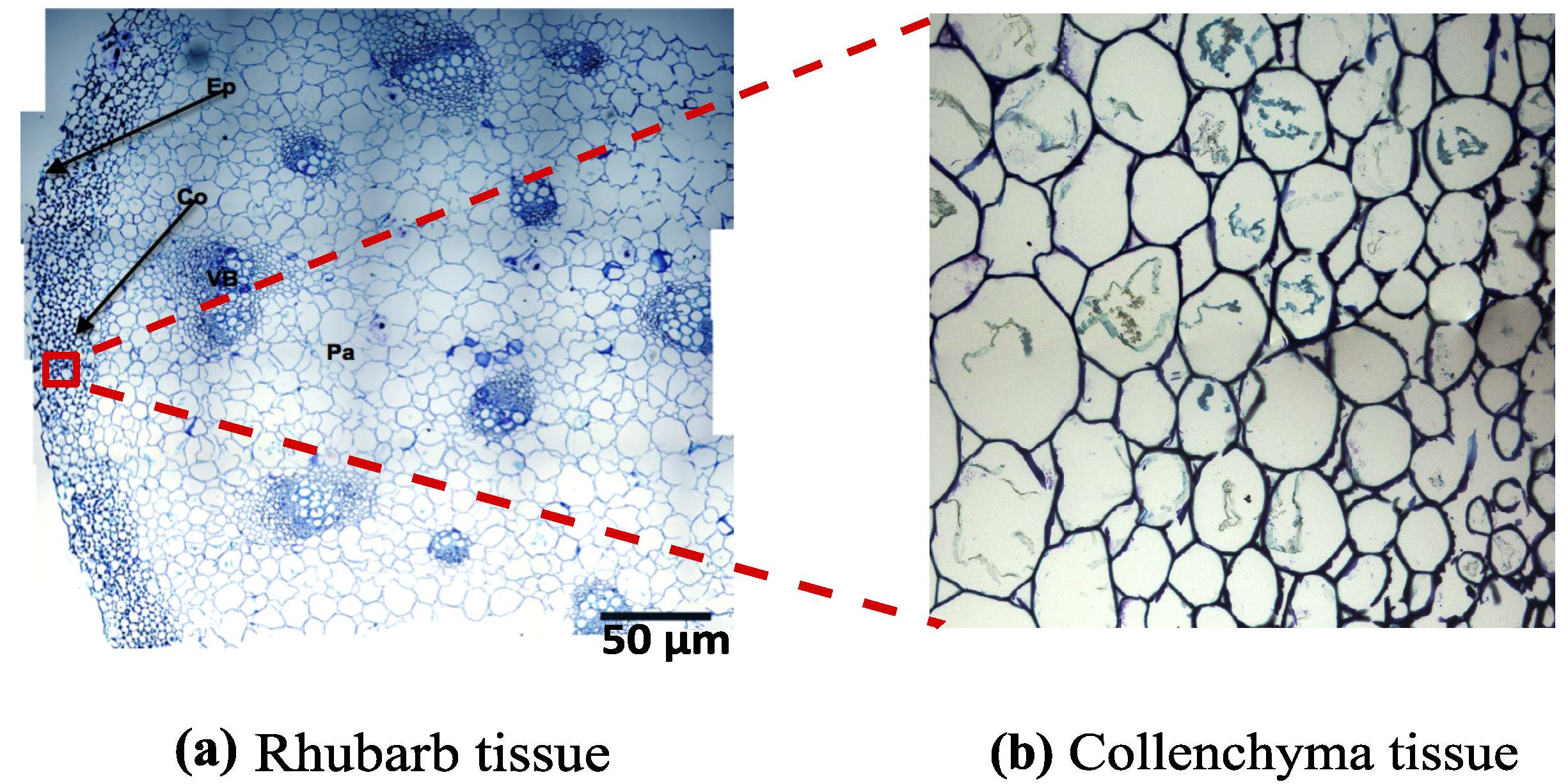
3.2. FECVT Modeling of the Tissue Microstructure
| (GPA) | (GPA) | (GPA) | |||
|---|---|---|---|---|---|
| Cell wall | 11.834 | 2.489 | 1.339 | 0.3680 | 0.0774 |

| Sum of squares | df | Mean square | F | Sig. | |
|---|---|---|---|---|---|
| Between Groups | 0.651 | 2 | 0.321 | 0.172 | 0.837 |
| Within Groups | 1146.397 | 603 | 1.863 | – | – |
| Total | 1147.058 | 605 | – | – | – |
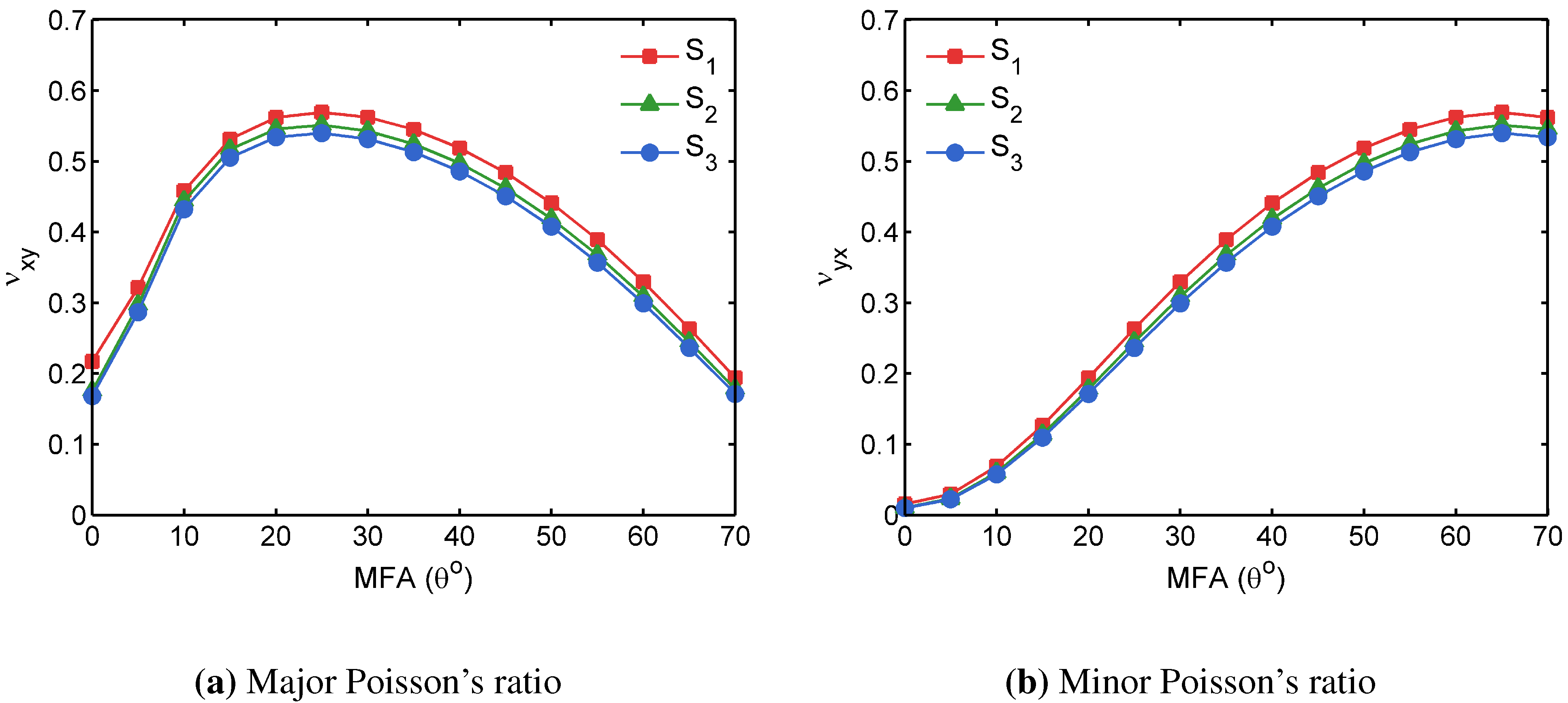
3.3. Apparent Tissue Stiffness through FEA
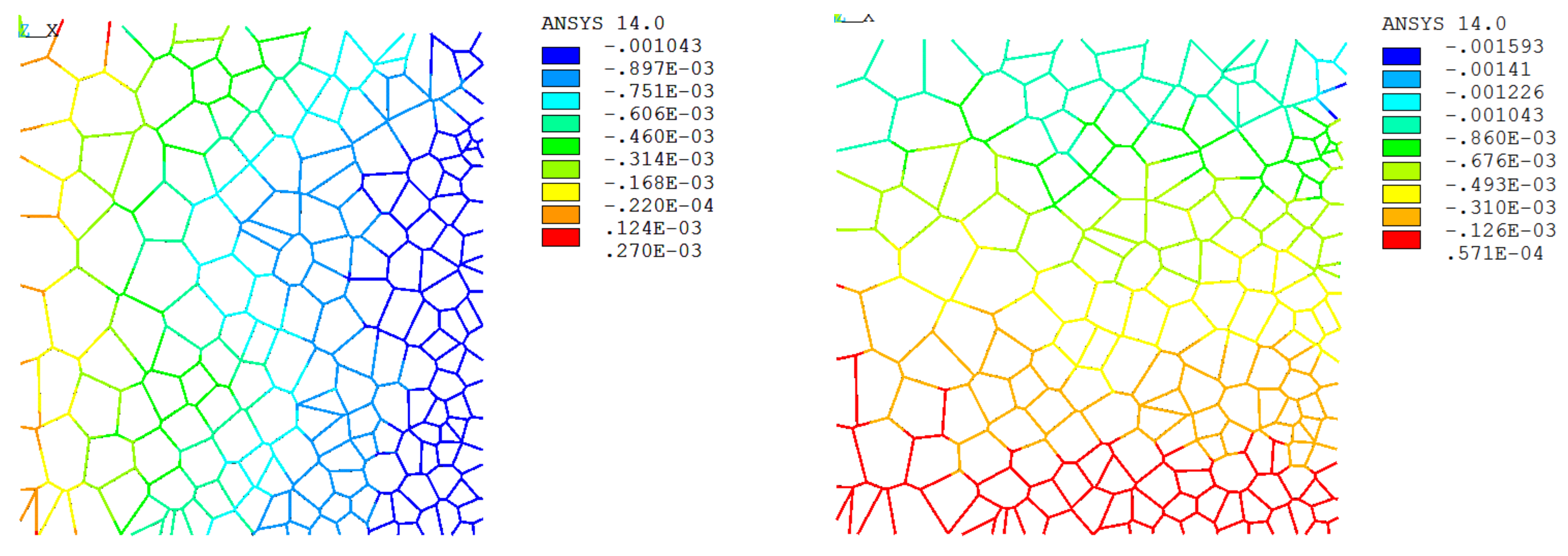
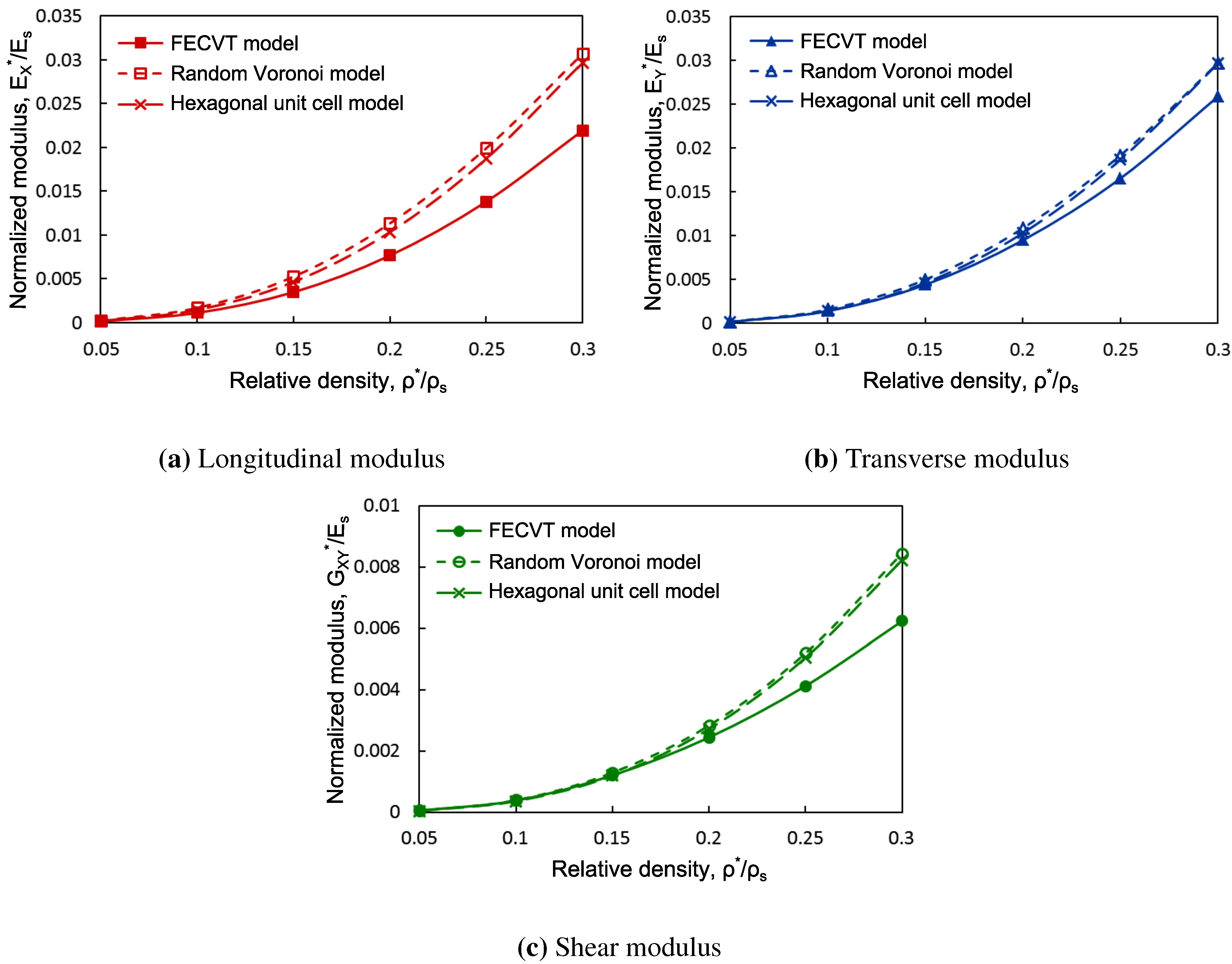
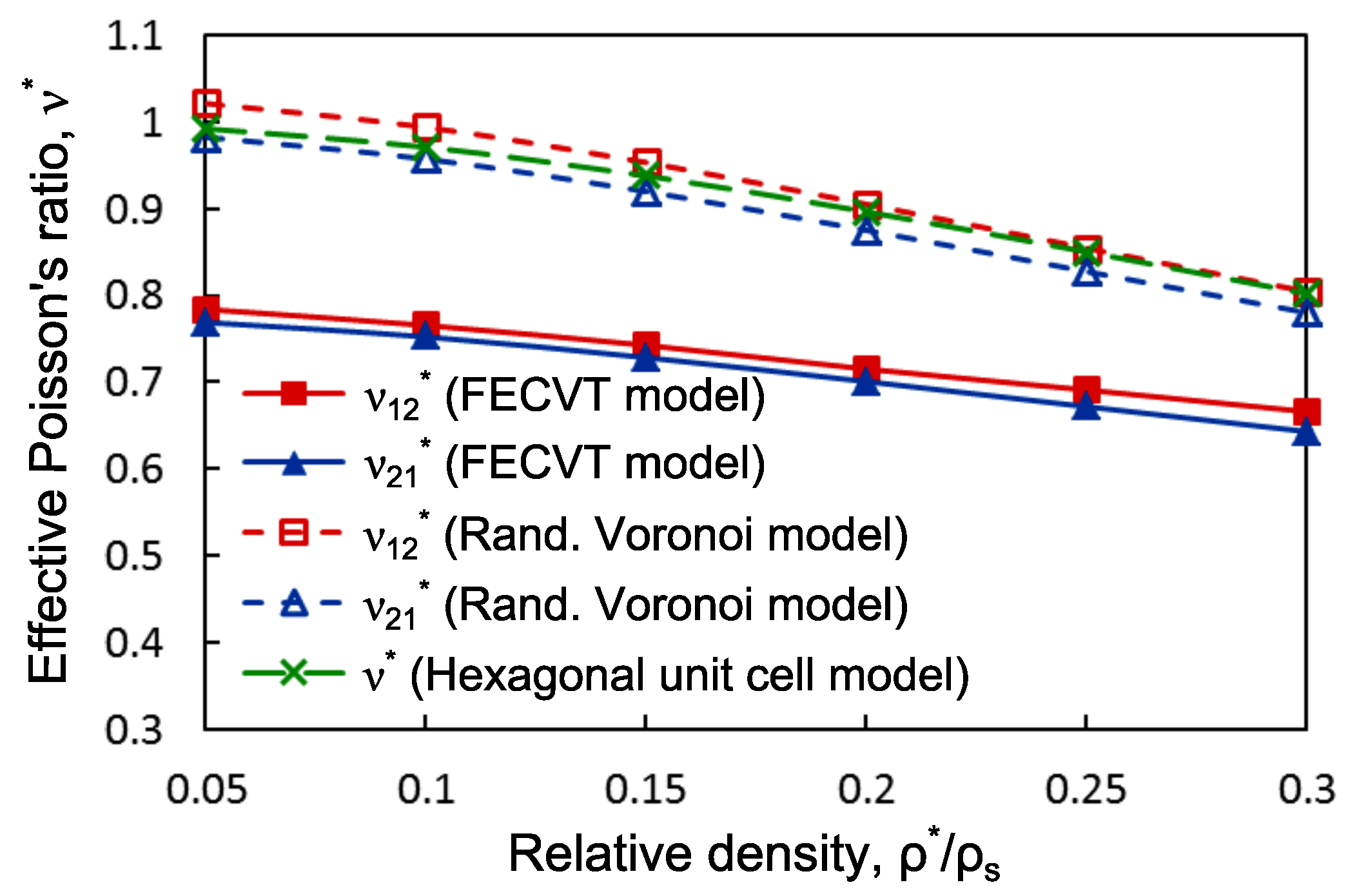
4. Conclusions
Acknowledgements
Conflict of Interest
References
- Kutschera, U. The growing outer epidermal wall: Design and physiological role of a composite structure. Ann. Bot. 2008, 101, 615–621. [Google Scholar] [CrossRef] [PubMed]
- Carpita, N.C.; Gibeaut, D.M. Structural models of primary-cell walls in flowering plants: Consistency of molecular-structure with the physical-properties of the walls during growth. Plant J. 1993, 3, 1–30. [Google Scholar] [CrossRef] [PubMed]
- Fahlen, J.; Salmen, L. Pore and matrix distribution in the fiber wall revealed by atomic force microscopy and image analysis. Biomacromolecules 2005, 6, 433–438. [Google Scholar] [CrossRef] [PubMed]
- Fengel, D.; Wegener, G. Wood: Chemistry, Ultrastructure, Reactions; Walter de Gruyter: Berlin, Germany, 1984. [Google Scholar]
- McNeil, M.; Darvill, A.G.; Fry, S.C.; Albersheim, P. Structure and function of the primary-cell walls of plants. Annu. Rev. Biochem. 1984, 53, 625–663. [Google Scholar] [CrossRef] [PubMed]
- Kha, H.; Tuble, S.; Kalyanasundaram, S.; Williamson, R.E. Finite Element Analysis of Plant Cell Wall Materials. In Advanced Materials Research; Bell, J., Yan, C., Ye, L., Zhang, L., Eds.; Trans Tech Publications Ltd.: Stafa-Zurich, Switzerland, 2008; Volume 32, pp. 197–201. [Google Scholar]
- Niklas, K.J. The Effect of Geometry on Mechanical Behavior. In Plant Biomechanics; The University of Chicago Press: Chicago, IL, USA, 1992; pp. 123–189. [Google Scholar]
- Fratzl, P.; Burgert, I.; Gupta, H.S. On the role of interface polymers for the mechanics of natural polymeric composites. Phys. Chem. Chem. Phys. 2004, 6, 5575–5579. [Google Scholar] [CrossRef]
- Kerstens, S.; Decraemer, W.F.; Verbelen, J.P. Cell walls at the plant surface behave mechanically like fiber-reinforced composite materials. Plant Physiol. 2001, 127, 381–385. [Google Scholar] [CrossRef] [PubMed]
- Salmen, L. Micromechanical understanding of the cell-wall structure. C. R. Biologies 2004, 327, 873–880. [Google Scholar] [CrossRef] [PubMed]
- Bergander, A.; Salmen, L. Cell wall properties and their effects on the mechanical properties of fibers. J. Mater. Sci. 2002, 37, 151–156. [Google Scholar] [CrossRef]
- Burgert, I.; Dunlop, J.W.C. Micromechanics of Cell Walls. In Mechanical Integration of Plant Cells and Plants; Wojtaszek, P., Ed.; Springer: Berlin, Germany, 2011; Volume 9, pp. 27–52. [Google Scholar]
- Niklas, K.J. Voigt and reuss models for predicting changes in Young’s modulus of dehydrating plant organs. Ann. Bot. 1992, 70, 347–355. [Google Scholar]
- Keckes, J.; Burgert, I.; Frühmann, K.; Müller, M.; Kölln, K.; Hamilton, M.; Burghammer, M.; Roth, S.V.; Stanzl-Tschegg, S.; Fratzl, P. Cell-wall recovery after irreversible deformation of wood. Nat. Mater. 2003, 2, 810–813. [Google Scholar] [CrossRef] [PubMed]
- Qing, H.; Mishnaevsky, L., Jr. 3D multiscale micromechanical model of wood: From annual rings to microfibrils. Int. J. Solids Struct. 2011, 43, 487–495. [Google Scholar] [CrossRef]
- Qing, H.; Mishnaevsky, L., Jr. A 3D multilevel model of damage and strength of wood: Analysis of microstructural effects. Mech. Mater. 2010, 47, 1253–1267. [Google Scholar] [CrossRef]
- Gindl, W.; Schoberl, T. The significance of the elastic modulus of wood cell walls obtained from nanoindentation measurements. Compos. A Appl. Sci. Manuf. 2004, 35, 1345–1349. [Google Scholar] [CrossRef]
- Gindl, W.; Gupta, H.S.; Schöberl, T.; Lichtenegger, H.C.; Fratzl, P. Mechanical properties of spruce wood cell walls by nanoindentation. Appl. Phys. A Mater. Sci. Process. 2004, 79, 2069–2073. [Google Scholar] [CrossRef]
- U.S. Department of Energy Genome Program. Avaliable online: http://genomics.energy.gov/ (accessed on 30 May 2013).
- Ghosh, S.; Lee, K.; Moorthy, S. Two scale analysis of heterogeneous elastic-plastic materials with asymptotic homogenization and Voronoi cell finite element model. Comput. Methods Appl. Mech. Eng. 1996, 132, 63–116. [Google Scholar] [CrossRef]
- Ghysels, P.; Samaey, G.; Tijskens, B.; van Liedekerke, P.; Ramon, H.; Roose, D. Multi-scale simulation of plant tissue deformation using a model for individual cell mechanics. Phys. Biol. 2009, 6, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Pasini, D. On the biological shape of the polygonaceae rheum rhabarbarum petiole. Int. J. Des. Nat. Ecodyn. 2008, 3, 1–25. [Google Scholar] [CrossRef] [PubMed]
- Faisal, T.R.; KhalilAbad, E.M.; Hristozov, N.; Pasini, D. The impact of tissue morphology, cross-section and turgor pressure on the mechanical properties of the leaf petiole in plants. J. Bionic Eng. 2010, 7, S11–S23. [Google Scholar]
- Rey, A.D.; Pasini, D.; Murugesan, Y.K. Multiscale Modeling of Plant Cell Wall Architecture and Tissue Mechanics for Biomimetic Applications. In Biomimetics: Nature-Based Innovation; Bar-Cohen, Y., Ed.; CRC Press: New York, NY, USA, 2011; pp. 131–168. [Google Scholar]
- Gibson, L.J.; Ashby, M.F.; Schajer, G.S.; Robertson, C.I. The mechanics of two-dimensional cellular materials. Proc. R. Soc. Lond. A 1982, 382, 25–42. [Google Scholar]
- Gibson, L.J.; Ashby, M.F. The Mechanics of Foams: Basic Results. In Cellular Solids: Structure and Properties, 2nd ed.; Cambridge University Press: Cambridge, MA, USA, 1999; pp. 175–234. [Google Scholar]
- Silva, M.J.; Hayes, W.C.; Gibson, L.J. The effects of nonperiodic microstructure on the elastic properties of 2-dimensional cellular solids. Int. J. Mech. Sci. 1995, 37, 1161–1177. [Google Scholar]
- Li, K.; Gao, X.L.; Subhash, G. Effects of cell shape and cell wall thickness variations on the elastic properties of two-dimensional cellular solids. Int. J. Solids Struct. 2005, 42, 1777–1795. [Google Scholar]
- Silva, M.J.; Gibson, L.J. The effects of non-periodic microstructure and defects on the compressive strength of two-dimensional cellular solids. Int. J. Mech. Sci. 1997, 39, 549–563. [Google Scholar]
- Cailletaud, G.; Forest, S.; Jeulin, D.; Feyel, F.; Galliet, I.; Mounoury, V.; Quilici, S. Some elements of microstructural mechanics. Comput. Mater. Sci. 2003, 27, 351–374. [Google Scholar]
- Hussain, K.; de los Rios, E.R.; Navarro, A. A two-stage micromechanics model for short fatigue cracks. Eng. Fract. Mech. 1993, 44, 425–436. [Google Scholar]
- Mattea, M.; Urbicain, M.J.; Rotstein, E. Computer model of shrinkage and deformation of cellular tissue during dehydration. Chem. Eng. Sci. 1989, 44, 2853–2859. [Google Scholar]
- Roudot, A.C.; Duprat, F.; Pietri, E. Simulation of a penetrometric test on apples using Voronoi-Delaunay tessellation. Food Struct. 1990, 9, 215–222. [Google Scholar]
- Ntenga, R.; Beakou, A. Structure, morphology and mechanical properties of Rhectophyllum camerunense (RC) plant-fiber. Part I: Statistical description and image-based reconstruction of the cross-section. Comput. Mater. Sci. 2011, 50, 1442–1449. [Google Scholar]
- Beakou, A.; Ntenga, R. Structure, morphology and mechanical properties of Rhectophyllum camerunense (RC) plant fiber. Part II: Computational homogenization of the anisotropic elastic properties. Comput. Mater. Sci. 2011, 50, 1550–1558. [Google Scholar]
- Faisal, T.R.; Hristozov, N.; Rey, A.D.; Western, T.L.; Pasini, D. Experimental determination of Philodendron melinonii and Arabidopsis thaliana tissue microstructure and geometric modeling via finite-edge centroidal Voronoi tessellation. Phys. Rev. E 2012, 86, 031921:1–031921:10. [Google Scholar]
- Fazekas, A.; Dendievel, R.; Salvo, L.; Brechet, Y. Effect of microstructural topology upon the stiffness and strength of 2D cellular structures. Int. J. Mech. Sci. 2002, 44, 2047–2066. [Google Scholar]
- Roberts, A.P.; Garboczi, E.J. Elastic moduli of model random three-dimensional closed-cell cellular solids. Acta Mater. 2001, 49, 189–197. [Google Scholar]
- Faisal, T.R.; Rey, A.D.; Pasini, D. Hierarchical microstructure and elastic properties of leaf petiole tissue in philodendron melinonii. MRS Proc. 2011, 1420, 1–6. [Google Scholar]
- Gillis, P.P. Effect of hydrogen bonds on the axial stiffnes of crystalline native cellulose. J. Polym. Sci. A Polym. Phys. 1969, 7, 783–794. [Google Scholar]
- Bodig, J.; Jayne, B.A.T. Mechanics of Wood and Wood Composites, 2nd revised ed.; Krieger Publishing Company: New York, NY, USA, 1993. [Google Scholar]
- Sakurada, I.; Kaji, K. Relation between the polymer conformation and the elastic modulus of the crystalline region of polymer. J. Polym. Sci. C Polym. Symp. 1970, 31, 57–76. [Google Scholar]
- Sakurada, I.; Nukushina, Y.; Ito, T. Experimental determination of the elastic modulus of crystalline regions in oriented polymers. J. Polym. Sci. 1962, 57, 651–660. [Google Scholar]
- Satcurada, I.; Ito, T.; Nakamae, K. Elastic moduli of the crystal lattices of polymers. J. Polym. Sci. C Polym. Symp. 1967, 15, 75–91. [Google Scholar]
- Tashiro, K.; Kobayashi, M. Theoretical evaluation of three-dimensional elastic constants of native and regenerated celluloses: Role of hydrogen bonds. Polymer 1967, 32, 1516–1526. [Google Scholar]
- Cousins, W.J. Young’s modulus of hemicellulose as related to moisture content. Wood Sci. Technol. 1978, 12, 161–167. [Google Scholar]
- Cousins, W.J. Elastic modulus of lignin as related to moisture content. Wood Sci. Technol. 1976, 10, 9–17. [Google Scholar]
- Cousins, W.J.; Armstrong, R.W.; Robinson, W.H. Young’s modulus of lignin from a continuous indentation test. J. Mater. Sci. 1975, 10, 1655–1658. [Google Scholar]
- Canny, J. A computational approach to edge detection. IEEE Trans. Pattern Anal. Mach. Intell. 1986, 8, 679–699. [Google Scholar]
- Barber, C.B.; Dobkin, D.P.; Huhdanpaa, H. The Quickhull algorithm for convex hulls. ACM Trans. Math. Softw. 1996, 22, 469–483. [Google Scholar]
- Zhu, H.X.; Knott, J.F.; Mills, N.J. Analysis of the elastic properties of open-cell foams with tetrakaidecahedral cells. J. Mech. Phys. Solids 1997, 45, 319–343. [Google Scholar]
- Van der Burg, M.W.D.; Shulmeister, V.; van der Geissen, E.; Marissen, R. On the linear elastic properties of regular and random open-cell foam models. J. Cell. Plast. 1997, 33, 31–54. [Google Scholar]
- Cave, I.D. Theory of X-ray measurement of microfibril angle in wood. Part 1. The condition for reflection X-ray diffraction by materials with dibre type symmetry. Wood Sci. Technol. 1997, 31, 143–152. [Google Scholar]
- Cave, I.D. Theory of X-ray measurement of microfibril angle in wood. Part 2. The diffraction diagram X-ray diffraction by materials with fibre type symmetry. Wood Sci. Technol. 1997, 31, 225–234. [Google Scholar]
- Barnett, J.R.; Bonham, V. A. Cellulose microfibril angle in the cell wall of wood fibres. Biol. Rev. 2007, 79, 461–472. [Google Scholar]
- Niklas, K.J.; Spatz, H. Plant Physiology; University of Chicago Press: Chicago, IL, USA, 2012. [Google Scholar]
- Roelofsen, P.A. The Plant Cell Wall. In Handbuch der Pflanzenanatomie; von Lindbauer, K., Ed.; Borntraeger: Berlin, Germany, 1959. [Google Scholar]
- Leroux, O. Collenchyma: A versatile mechanical tissue with dynamic cell walls. Ann. Bot. 2012, 110, 1083–1098. [Google Scholar]
- Kerr, T.; Bailey, I.W. The cambium and its derivative tissue. X. Structure, optical properties and chemical composition of the so-called middle lamella. J. Arnold Arboretum 1934, 15, 329–349. [Google Scholar]
- Beer, M.; Setterfield, G. Fine structure in thickened primary walls of collenchyma cells of celery petioles. Am. J. Bot. 1958, 45, 571–580. [Google Scholar]
- Roland, J.C. Infrastructure des membranes du collenchyme. C. R. Acad. Sci. 1964, 259, 4331–4334. [Google Scholar]
- Roland, J.C. Edification et infrastructure de la membrane collenchymateuse. Son remaniement lors de la sclerification. C. R. Acad. Sci. 1965, 260, 950–953. [Google Scholar]
- Roland, J.C. Organisation de la membrane paraplasmique du collenchyme. J. Microsc. 1966, 5, 323–348. [Google Scholar]
- Chafe, S.C. The fine structure of the collenchyma cell wall. Planata 1969, 90, 12–21. [Google Scholar]
- Gupta, G.P. Plant Cell Biology; Discovery Publishing House Pvt. Ltd.: New Delhi, India, 2004. [Google Scholar]
- Stevens, C.; Müssig, J. What Are Natural Fibres? In Industrial Applications of Natural Fibres: Structure, Properties and Technical Applications; Müssig, J., Ed.; John Wiley & Sons, Limited: London, UK, 2010; pp. 13–48. [Google Scholar]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Faisal, T.R.; Rey, A.D.; Pasini, D. A Multiscale Mechanical Model for Plant Tissue Stiffness. Polymers 2013, 5, 730-750. https://doi.org/10.3390/polym5020730
Faisal TR, Rey AD, Pasini D. A Multiscale Mechanical Model for Plant Tissue Stiffness. Polymers. 2013; 5(2):730-750. https://doi.org/10.3390/polym5020730
Chicago/Turabian StyleFaisal, Tanvir R., Alejandro D. Rey, and Damiano Pasini. 2013. "A Multiscale Mechanical Model for Plant Tissue Stiffness" Polymers 5, no. 2: 730-750. https://doi.org/10.3390/polym5020730
APA StyleFaisal, T. R., Rey, A. D., & Pasini, D. (2013). A Multiscale Mechanical Model for Plant Tissue Stiffness. Polymers, 5(2), 730-750. https://doi.org/10.3390/polym5020730