Temperature Dependence of Nonlinear Elastic Moduli of Polystyrene
Abstract
1. Introduction
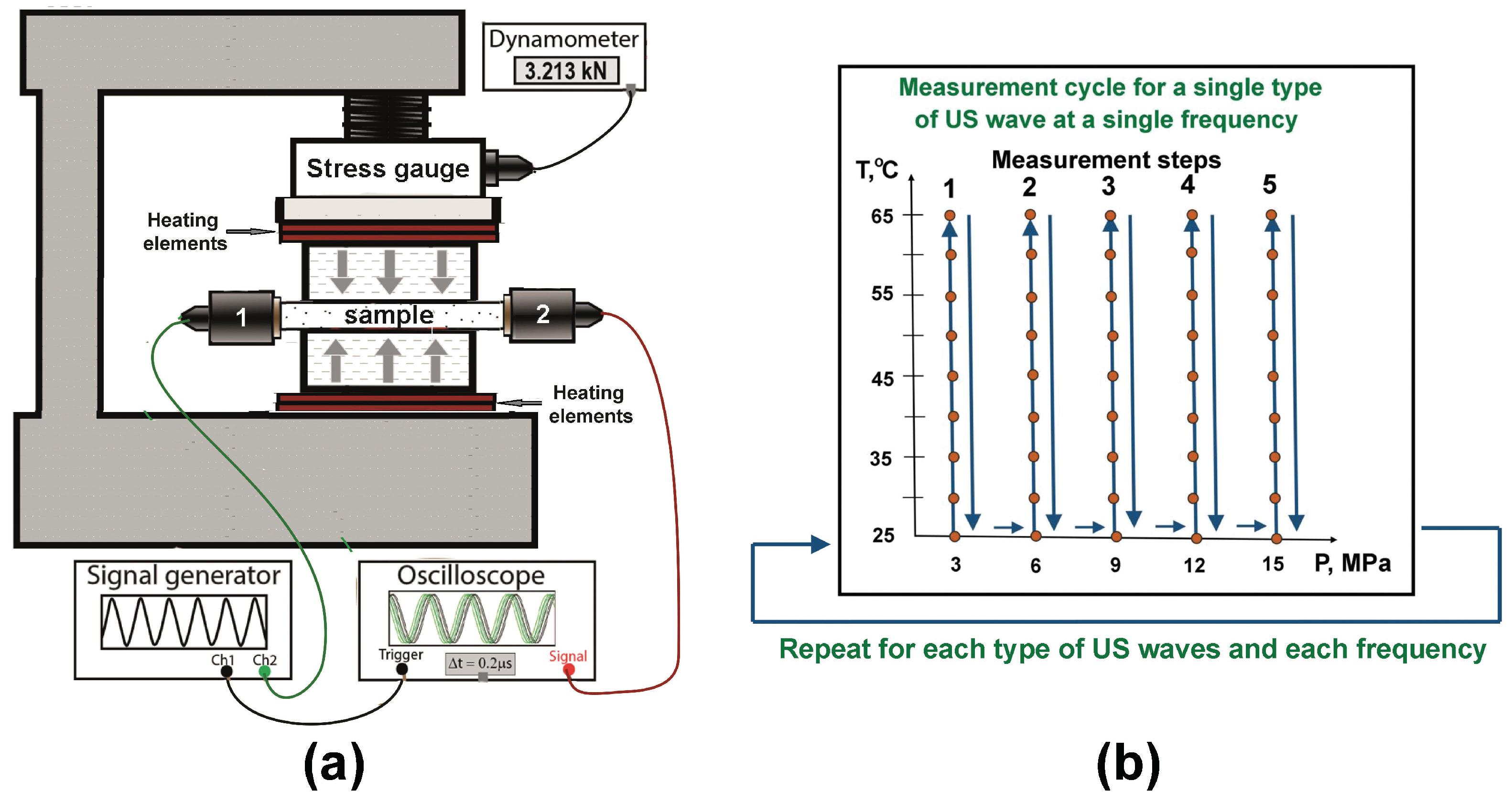
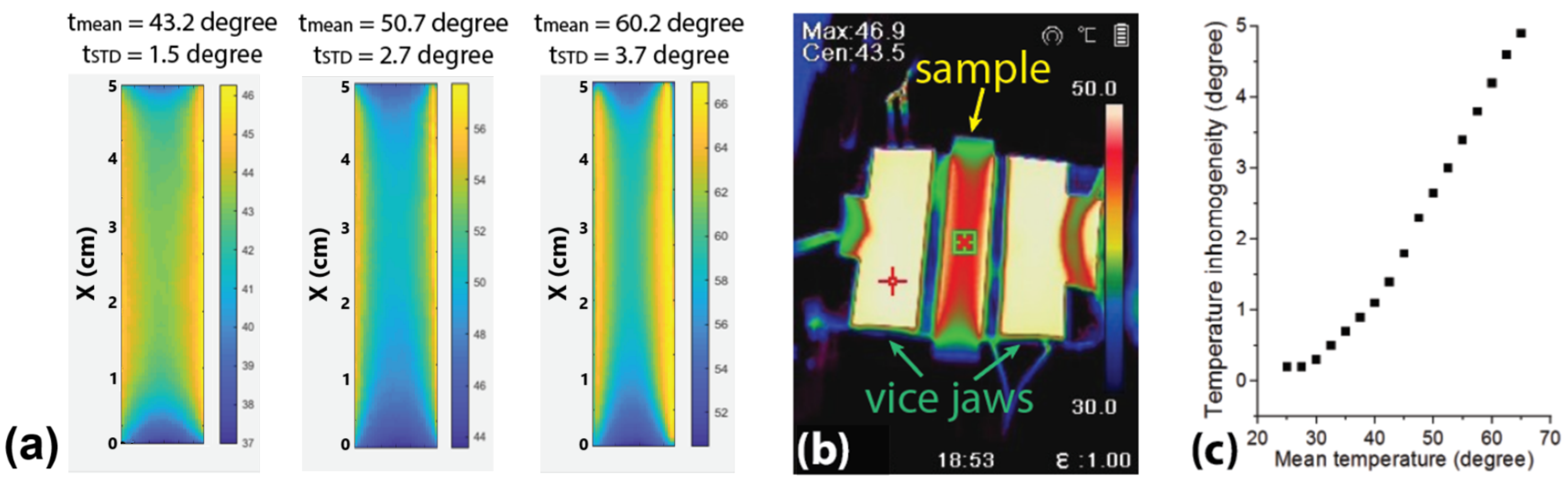
2. Material and Method
3. Results and Discussion
3.1. Temperature Dependence of Ultrasonic Wave Velocities at Zero Pressure
3.2. Temperature Dependence of Nonlinear Elastic Moduli
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Grosberg, A.Y.; Khokhlov, A.R. Giant Molecules: Here, There, and Everywhere, 2nd ed.; World Scientific: Singapore, 2011. [Google Scholar]
- Osswald, T.A.; Menges, G. Material Science of Polymers for Engineers, 3rd ed.; Hanser: Munich, Germany, 2012. [Google Scholar]
- Mai, Y.W.; Yu, Z.Z. Polymer Nanocomposites; Woodhead Publishing: Sawston, UK, 2006. [Google Scholar]
- Peters, S.T. (Ed.) Handbook of Composites, 2nd ed.; Springer: New York, NY, USA, 1998. [Google Scholar] [CrossRef]
- Moskalyuk, O.A.; Belashov, A.V.; Beltukov, Y.M.; Ivan’kova, E.M.; Popova, E.N.; Semenova, I.V.; Yelokhovsky, V.Y.; Yudin, V.E. Polystyrene-Based Nanocomposites with Di erent Fillers: Fabrication and Mechanical Properties. Polymers 2020, 12, 2457. [Google Scholar] [CrossRef]
- Belashov, A.V.; Zhikhoreva, A.A.; Moskalyuk, O.A.; Beltukov, Y.M.; Semenova, I.V. Linear and Nonlinear Elastic Properties of Polystyrene-Based Nanocomposites with Allotropic Carbon Fillers and Binary Mixtures. Polymers 2022, 14, 5462. [Google Scholar] [CrossRef] [PubMed]
- Naskar, A.K.; Keum, J.K.; Boeman, R.G. Polymer Matrix Nanocomposites for Automotive Structural Components. Nat. Nanotechnol. 2016, 11, 1026–1030. [Google Scholar] [CrossRef]
- Joshi, M.; Chatterjee, U. Polymer Nanocomposite: An Advanced Material for Aerospace Applications. In Advanced Composite Materials for Aerospace Engineering; Rana, S., Fangueiro, R., Eds.; Elsevier: Amsterdam, The Netherlands, 2016; pp. 241–264. [Google Scholar] [CrossRef]
- Hussain, A.; Jabeen, N.; Tabassum, A.; Ali, J. 3D-Printed Conducting Polymers for Solid Oxide Fuel Cells. In 3D Printed Conducting Polymers; Gupta, R.K., Ed.; Elsevier: Amsterdam, The Netherlands, 2024; Chapter 12. [Google Scholar] [CrossRef]
- Ma, P.C.; Zhang, Y. Perspectives of carbon nanotubes/polymer nanocomposites for wind blade materials. Renew. Sustain. Energy Rev. 2014, 30, 651–660. [Google Scholar] [CrossRef]
- Mashkov, Y.K.; Egorova, V.A.; Chemisenko, O.V.; Maliy, O.V. Polymer Nanocomposites Development and Research for Petrochemical and Oil and Gas Production Equipment. Procedia Eng. 2016, 152, 545–550. [Google Scholar] [CrossRef][Green Version]
- Siviour, C.R.; Jordan, J.L. High Strain Rate Mechanics of Polymers: A Review. J. Dyn. Behav. Mater. 2016, 2, 15–32. [Google Scholar] [CrossRef]
- Capodagli, J.; Lakes, R. Isothermal Viscoelastic Properties of PMMA and LDPE over 11 Decades of Frequency and Time: A Test of Time—Temperature Superposition. Rheol. Acta 2008, 47, 777–786. [Google Scholar] [CrossRef]
- Yadav, P.; Chrysochoos, A.; Arnould, O.; Bardet, S. Effect of Thermomechanical Couplings on Viscoelastic Behaviour of Polystyrene. In Dynamic Behavior of Materials, Volume 1: Proceedings of the 2019 Annual Conference on Experimental and Applied Mechanics, Reno, NV, USA, 3–6 June 2019; Lamberson, L.E., Ed.; Springer International Publishing: Berlin/Heidelberg, Germany, 2020; pp. 17–24. [Google Scholar] [CrossRef]
- Ionita, D.; Cristea, M.; Gaina, C. Prediction of Polyurethane Behaviour via Time-Temperature Superposition: Meanings and Limitations. Polym. Test. 2020, 83, 106340. [Google Scholar] [CrossRef]
- Arrigo, R.; Malucelli, G. Rheological Behavior of Polymer/Carbon Nanotube Composites: An Overview. Materials 2020, 13, 2771. [Google Scholar] [CrossRef]
- Filippone, G.; Salzano De Luna, M. A Unifying Approach for the Linear Viscoelasticity of Polymer Nanocomposites. Macromolecules 2012, 45, 8853–8860. [Google Scholar] [CrossRef]
- Hu, X.L.; Luo, W.B.; Liu, X.; Li, M.; Huang, Y.J.; Bu, J.L. Temperature and Frequency Dependent Rheological Behaviour of Carbon Black Filled Natural Rubber. Plast. Rubber Compos. 2013, 42, 416–420. [Google Scholar] [CrossRef]
- Wang, J.; Guo, Y.; Yu, W.; Zhou, C.; Steeman, P. Linear and Nonlinear Viscoelasticity of Polymer/Silica Nanocomposites: An Understanding from Modulus Decomposition. Rheol. Acta 2016, 55, 37–50. [Google Scholar] [CrossRef]
- Fu, Y.B.; Ogden, R.W. (Eds.) Nonlinear Elasticity: Theory and Applications; Number 283 in London Mathematical Society Lecture Note Series; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Astorga, A.; Guéguen, P.; Kashima, T. Nonlinear Elasticity Observed in Buildings during a Long Sequence of Earthquakes. Bull. Seismol. Soc. Am. 2018, 108, 1185–1198. [Google Scholar] [CrossRef]
- Beresnev, I.A.; Wen, K.L. Nonlinear Soil Response—A Reality? Bull. Seismol. Soc. Am. 1996, 86, 1964–1978. [Google Scholar] [CrossRef]
- Field, E.H.; Johnson, P.A.; Beresnev, I.A.; Zeng, Y. Nonlinear Ground-Motion Amplification by Sediments during the 1994 Northridge Earthquake. Nature 1997, 390, 599–602. [Google Scholar] [CrossRef]
- Renaud, G.; Rivière, J.; Larmat, C.; Rutledge, J.; Lee, R.; Guyer, R.; Stokoe, K.; Johnson, P. In Situ Characterization of Shallow Elastic Nonlinear Parameters with Dynamic Acoustoelastic Testing. J. Geophys. Res. Solid Earth 2014, 119, 6907–6923. [Google Scholar] [CrossRef]
- Ogden, R.W. Nonlinear Elasticity, Anisotropy, Material Stability and Residual Stresses in Soft Tissue. In Biomechanics of Soft Tissue in Cardiovascular Systems; Holzapfel, G.A., Ogden, R.W., Eds.; Springer: Vienna, Austria, 2003; pp. 65–108. [Google Scholar] [CrossRef]
- Storm, C.; Pastore, J.J.; MacKintosh, F.C.; Lubensky, T.C.; Janmey, P.A. Nonlinear Elasticity in Biological Gels. Nature 2005, 435, 191–194. [Google Scholar] [CrossRef]
- Philipp, M.; Müller, U.; Aleksandrova, R.; Sanctuary, R.; Müller-Buschbaum, P.; Krüger, J.K. Immense Elastic Nonlinearities at the Demixing Transition of Aqueous PNIPAM Solutions. Soft Matter 2013, 9, 5034. [Google Scholar] [CrossRef]
- Hughes, D.S.; Kelly, J.L. Second-Order Elastic Deformation of Solids. Phys. Rev. 1953, 92, 1145–1149. [Google Scholar] [CrossRef]
- Rivière, J.; Renaud, G.; Guyer, R.A.; Johnson, P.A. Pump and Probe Waves in Dynamic Acousto-Elasticity: Comprehensive Description and Comparison with Nonlinear Elastic Theories. J. Appl. Phys. 2013, 114, 54905. [Google Scholar] [CrossRef]
- Lott, M.; Remillieux, M.C.; Garnier, V.; Le Bas, P.Y.; Ulrich, T.J.; Payan, C. Nonlinear Elasticity in Rocks: A Comprehensive Three-Dimensional Description. Phys. Rev. Mater. 2017, 1, 23603. [Google Scholar] [CrossRef]
- Matlack, K.H.; Kim, J.Y.; Jacobs, L.J.; Qu, J. Review of Second Harmonic Generation Measurement Techniques for Material State Determination in Metals. J. Nondestruct. Eval. 2015, 34, 273. [Google Scholar] [CrossRef]
- Krüger, J.K.; Grammes, C.; Stockem, K.; Zietz, R.; Dettenmaier, M. Nonlinear Elastic Properties of Solid Polymers as Revealed by Brillouin Spectroscopy. Colloid Polym. Sci. 1991, 269, 764–771. [Google Scholar] [CrossRef]
- Payan, C.; Garnier, V.; Moysan, J.; Johnson, P.A. Determination of Third Order Elastic Constants in a Complex Solid Applying Coda Wave Interferometry. Appl. Phys. Lett. 2009, 94, 11904. [Google Scholar] [CrossRef]
- Garbuzov, F.E.; Samsonov, A.M.; Semenov, A.A.; Shvartz, A.G. Determination of Third-Order Elastic Moduli via Parameters of Bulk Strain Solitons. Tech. Phys. Lett. 2016, 42, 121–123. [Google Scholar] [CrossRef]
- Bermes, C.; Kim, J.Y.; Qu, J.; Jacobs, L.J. Experimental Characterization of Material Nonlinearity Using Lamb Waves. Appl. Phys. Lett. 2007, 90, 21901. [Google Scholar] [CrossRef]
- Masurkar, F.; Tse, P. Analyzing the Features of Material Nonlinearity Evaluation in a Rectangular Aluminum Beam Using Rayleigh Waves: Theoretical and Experimental Study. J. Phys. Commun. 2019, 3, 55002. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Theory of Elasticity; Wiley: New York, NY, USA, 1956. [Google Scholar]
- Murnaghan, E.D. Finite Deformation of an Elastic Solid; Wiley: New York, NY, USA, 1951. [Google Scholar]
- Thurston, R.N.; Brugger, K. Third-Order Elastic Constants and the Velocity of Small Amplitude Elastic Waves in Homogeneously Stressed Media. Phys. Rev. 1964, 133, A1604–A1610. [Google Scholar] [CrossRef]
- Nagy, P.B. Fatigue Damage Assessment by Nonlinear Ultrasonic Materials Characterization. Ultrasonics 1998, 36, 375–381. [Google Scholar] [CrossRef]
- Wallace, D.C. Thermoelastic Theory of Stressed Crystals and Higher-Order Elastic Constants. In Solid State Physics; Elsevier: Amsterdam, The Netherlands, 1970; Volume 25, pp. 301–404. [Google Scholar] [CrossRef]
- Matlack, K.; Kim, J.Y.; Wall, J.; Qu, J.; Jacobs, L.; Sokolov, M. Sensitivity of Ultrasonic Nonlinearity to Irradiated, Annealed, and Re-Irradiated Microstructure Changes in RPV Steels. J. Nucl. Mater. 2014, 448, 26–32. [Google Scholar] [CrossRef]
- Jhang, K.Y. Nonlinear Ultrasonic Techniques for Nondestructive Assessment of Micro Damage in Material: A Review. Int. J. Precis. Eng. Manuf. 2009, 10, 123–135. [Google Scholar] [CrossRef]
- Ferry, J.D. Viscoelastic Properties of Polymers, 3rd ed.; Wiley: New York, NY, USA, 1980. [Google Scholar]
- Hyun, K.; Wilhelm, M.; Klein, C.O.; Cho, K.S.; Nam, J.G.; Ahn, K.H.; Lee, S.J.; Ewoldt, R.H.; McKinley, G.H. A review of nonlinear oscillatory shear tests: Analysis and application of large amplitude oscillatory shear (LAOS). Prog. Polym. Sci. 2011, 36, 1697–1753. [Google Scholar] [CrossRef]
- Song, H.Y.; Faust, L.; Son, J.; Kim, M.; Park, S.J.; Kyun Ahn, S.; Wilhelm, M.; Hyun, K. Small and Medium Amplitude Oscillatory Shear Rheology of Model Branched Polystyrene (PS) Melts. Polymers 2020, 12, 365. [Google Scholar] [CrossRef]
- Ewoldt, R.H.; Bharadwaj, N.A. Low-Dimensional Intrinsic Material Functions for Nonlinear Viscoelasticity. Rheol. Acta 2013, 52, 201–219. [Google Scholar] [CrossRef]
- Ward, I.M.; Sweeney, J. Non-Linear Viscoelastic Behaviour. In Mechanical Properties of Solid Polymers; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2012; Chapter 11; pp. 285–318. [Google Scholar] [CrossRef]
- Findley, W.N.; Lai, J.S.; Onaran, K. Creep and Relaxation of Nonlinear Viscoelastic Materials: With an Introduction to Linear Viscoelasticity; Dover Books on Engineering, Dover: New York, NY, USA, 1989. [Google Scholar]
- Mangalara, S.C.H.; McKenna, G.B. Large-Amplitude Oscillatory Shear to Investigate the Nonlinear Rheology of Polymer Glasses—PMMA. Mech.-Time-Depend. Mater. 2023, 27, 99–117. [Google Scholar] [CrossRef]
- Mangalara, S.C.H.; McKenna, G.B. Mechanical Hole-Burning Spectroscopy of PMMA Deep in the Glassy State. J. Chem. Phys. 2020, 152, 074508. [Google Scholar] [CrossRef] [PubMed]
- Mangalara, S.C.H.; Paudel, S.; McKenna, G.B. Mechanical Spectral Hole Burning in Glassy Polymers—Investigation of Polycarbonate, a Material with Weak β-Relaxation. J. Chem. Phys. 2021, 154, 124904. [Google Scholar] [CrossRef] [PubMed]
- Klompen, E.; Govaert, L. Nonlinear Viscoelastic Behaviour of Thermorheologically Complex Materials. Mech.-Time-Depend. Mater. 1999, 3, 49–69. [Google Scholar] [CrossRef]
- Caruthers, J.M.; Adolf, D.B.; Chambers, R.S.; Shrikhande, P. A Thermodynamically Consistent, Nonlinear Viscoelastic Approach for Modeling Glassy Polymers. Polymer 2004, 45, 4577–4597. [Google Scholar] [CrossRef]
- Wang, Q.; Saunders, G.; Senin, H.; Lambson, E. Temperature Dependences of the Third-Order Elastic Constants and Acoustic Mode Vibrational Anharmonicity of Vitreous Silica. J.-Non-Cryst. Solids 1992, 143, 65–74. [Google Scholar] [CrossRef]
- Mohrbacher, H.; Salama, K. The Temperature Dependence of Third-Order Elastic Constants in Metal-Matrix Composites. In Review of Progress in Quantitative Nondestructive Evaluation: Volumes 12A and 12B; Thompson, D.O., Chimenti, D.E., Eds.; Springer: Boston, MA, USA, 1993; pp. 2091–2097. [Google Scholar] [CrossRef]
- Nucera, C.; Lanza Di Scalea, F. Nonlinear Wave Propagation in Constrained Solids Subjected to Thermal Loads. J. Sound Vib. 2014, 333, 541–554. [Google Scholar] [CrossRef]
- Meeks, E.L.; Arnold, R.T. Temperature Dependence of the Third-Order Elastic Constants of SrTiO3. Phys. Rev. 1970, 1, 982–988. [Google Scholar] [CrossRef]
- Wang, K.; Cao, W.; Liu, M.; Li, Y.; Zhou, P.; Su, Z. Advancing Elastic Wave Imaging Using Thermal Susceptibility of Acoustic Nonlinearity. Int. J. Mech. Sci. 2020, 175, 105509. [Google Scholar] [CrossRef]
- Belashov, A.V.; Beltukov, Y.M.; Moskalyuk, O.A.; Semenova, I.V. Relative Variations of Nonlinear Elastic Moduli in Polystyrene-Based Nanocomposites. Polym. Test. 2021, 95, 107132. [Google Scholar] [CrossRef]
- Belashov, A.V.; Zhikhoreva, A.A.; Beltukov, Y.M.; Semenova, I.V. Frequency Dependence of Nonlinear Elastic Moduli of Polystyrene. Int. J. -Non-Linear Mech. 2024, 167, 104913. [Google Scholar] [CrossRef]
- Lamberson, D.L.; Asay, J.R.; Guenther, A.H. Equation of State of Polystyrene and Polymethylmethacrylate from Ultrasonic Measurements at Moderate Pressures. J. Appl. Phys. 1972, 43, 976. [Google Scholar] [CrossRef]
- Hughes, D.S.; Blankenship, E.B.; Mims, R.L. Variation of Elastic Moduli and Wave Velocity with Pressure and Temperature in Plastics. J. Appl. Phys. 1950, 21, 294. [Google Scholar] [CrossRef]




| Temperature | (m/s) | (m/s) | (g/cm3) | (GPa) | (GPa) |
|---|---|---|---|---|---|
| 25 °C | 2240 ± 18 | 1173 ± 8 | 1.06 | 1.46 ± 0.01 | 2.41 ± 0.01 |
| 35 °C | 2220 ± 18 | 1162 ± 8 | 1.06 | 1.43 ± 0.01 | 2.36 ± 0.01 |
| 45 °C | 2200 ± 18 | 1155 ± 8 | 1.06 | 1.41 ± 0.01 | 2.31 ± 0.01 |
| 55 °C | 2182 ± 18 | 1148 ± 8 | 1.06 | 1.39 ± 0.01 | 2.26 ± 0.01 |
| 65 °C | 2160 ± 18 | 1135 ± 8 | 1.06 | 1.37 ± 0.01 | 2.21 ± 0.01 |
| Temperature | l (GPa) | m (GPa) | n (GPa) | |||
|---|---|---|---|---|---|---|
| 0.7 MHz | 3 MHz | 0.7 MHz | 3 MHz | 0.7 MHz | 3 MHz | |
| 25 °C | ||||||
| 30 °C | ||||||
| 35 °C | ||||||
| 40 °C | ||||||
| 45 °C | ||||||
| 50 °C | ||||||
| 55 °C | ||||||
| 60 °C | ||||||
| 65 °C | ||||||
| Temperature Susceptibility | Value (GPa/°C) |
|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Belashov, A.V.; Zhikhoreva, A.A.; Beltukov, Y.M.; Semenova, I.V. Temperature Dependence of Nonlinear Elastic Moduli of Polystyrene. Polymers 2025, 17, 1008. https://doi.org/10.3390/polym17081008
Belashov AV, Zhikhoreva AA, Beltukov YM, Semenova IV. Temperature Dependence of Nonlinear Elastic Moduli of Polystyrene. Polymers. 2025; 17(8):1008. https://doi.org/10.3390/polym17081008
Chicago/Turabian StyleBelashov, Andrey V., Anna A. Zhikhoreva, Yaroslav M. Beltukov, and Irina V. Semenova. 2025. "Temperature Dependence of Nonlinear Elastic Moduli of Polystyrene" Polymers 17, no. 8: 1008. https://doi.org/10.3390/polym17081008
APA StyleBelashov, A. V., Zhikhoreva, A. A., Beltukov, Y. M., & Semenova, I. V. (2025). Temperature Dependence of Nonlinear Elastic Moduli of Polystyrene. Polymers, 17(8), 1008. https://doi.org/10.3390/polym17081008






