Patch-Based Recycled Composites: Experimental Investigation and Modeling Techniques on Four-Point Bending and Curved Beam Traction Tests
Abstract
1. Introduction
2. Materials and Methods
2.1. Prepreg Patches and Architecture
- the first one is created by placing each patch side by side with no gaps between them until the whole surface is covered;
- the second one is laid on top of the first, shifted by half the size of the patch in both plane directions, ensuring no gaps between patches.
2.2. Sample Preparation and Testing
2.3. Modeling
- 4PB sample models are patch-based, and therefore, they include each patch they are actually made of;
- curved beam sample models are equivalent-lamina based, and therefore, each single layer is modeled as an individual equivalent lamina.
2.3.1. 4PB Specimen Modeling
- the first approach relates the interaction between patches from consecutive layers that are in contact on the long side. This interaction was modeled as a cohesive interface, referred to as the “Cohesive interface” in Figure 3, the properties of which were determined through an experimental campaign on the original material mentioned earlier: Double cantilever beam (DCB) and 4-point end notched flexure (4ENF) tests were conducted to determine the parameters for defining the interface properties. While fracture toughness values were directly obtained from experiments (Table 1), the penalty stiffness and the normal cohesive strength were set to 40,000 MPa/mm and 27 MPa, respectively, as a result of the fitting procedure;
- the second approach addresses the interaction between patches within the same layer, in contact along the short edge. In this scenario, the contact area is in reality a resin pocket, as illustrated in Figure 4.
2.3.2. Curved Beam Specimen Modeling
3. Results and Discussion
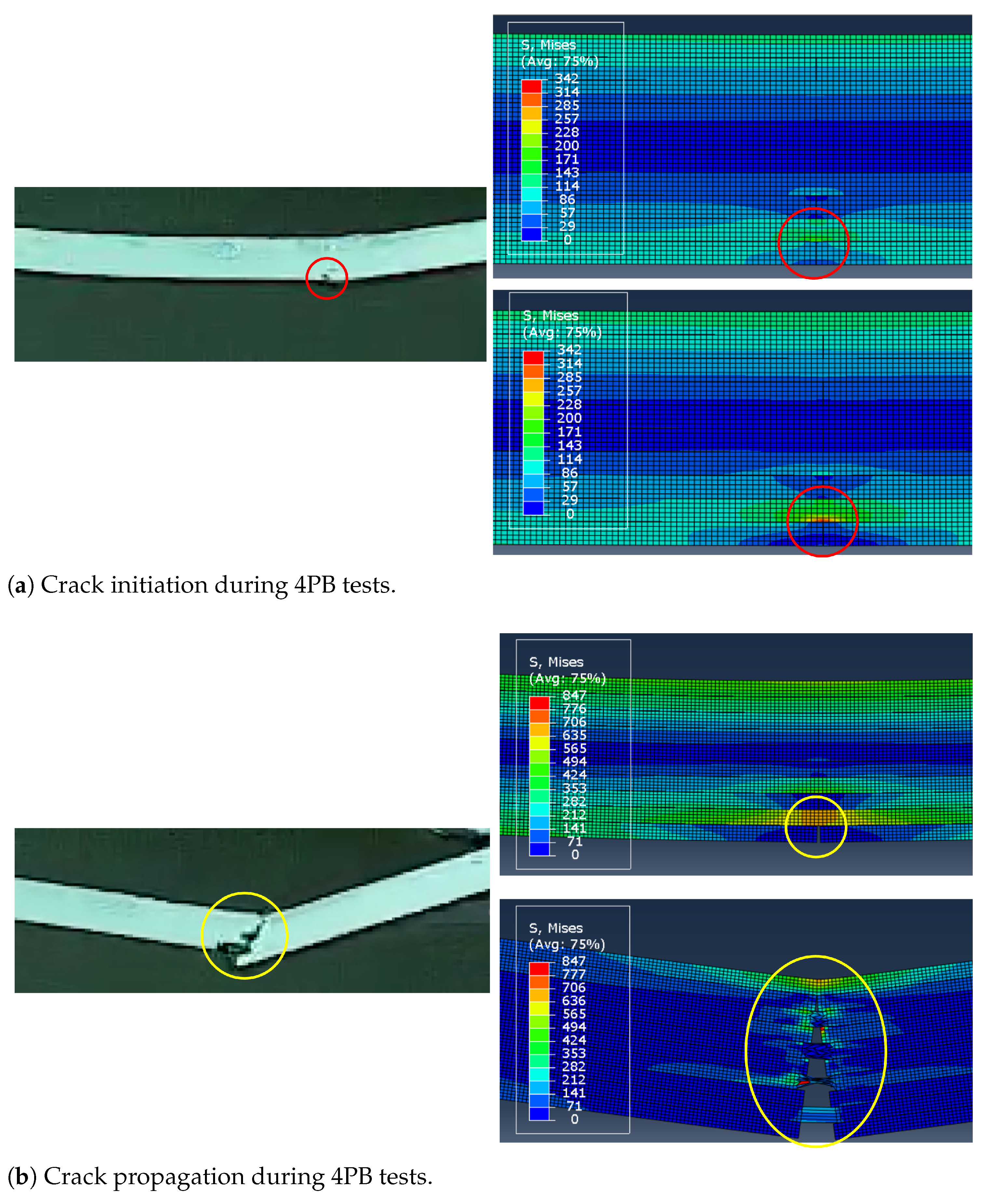
3.1. Experiments
- evaluating mechanical properties of the patch-based material to assess its potential to be used for load-bearing components;
- building up the necessary data set for numerical modeling;
- assessing the patch-based laminate properties under different testing configurations.
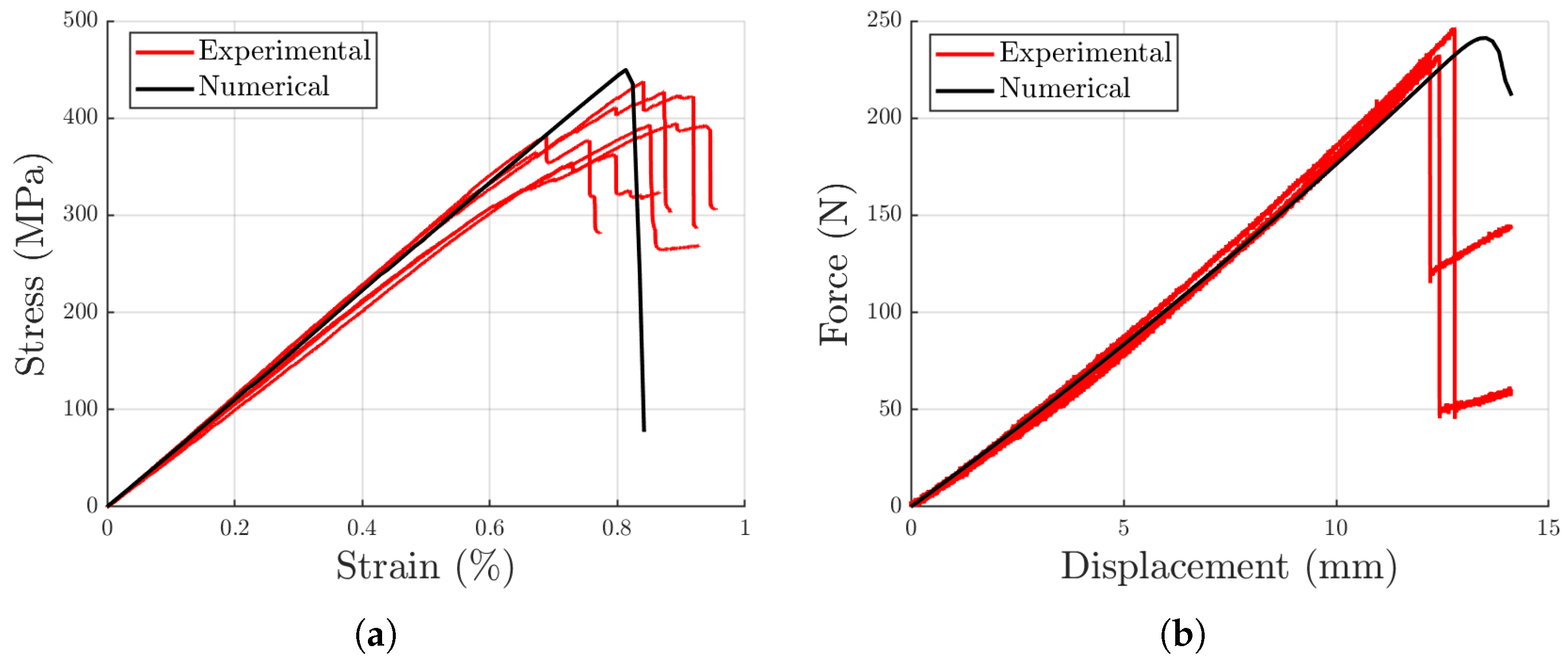
3.2. Numerical Simulations
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Bhong, M.; Khan, T.K.; Devade, K.; Vijay Krishna, B.; Sura, S.; Eftikhaar, H.; Pal Thethi, H.; Gupta, N. Review of composite materials and applications. Mater. Today Proc. 2023. [CrossRef]
- Zhang, J.; Lin, G.; Vaidya, U.; Wang, H. Past, Present and Future Prospective of Global Carbon Fibre Composite Developments and Applications. Compos. Part Eng. 2022, 250, 110463. [Google Scholar] [CrossRef]
- Nilakantan, G.; Nutt, S. Reuse and upcycling of thermoset prepreg scrap: Case study with out-of-autoclave carbon fiber/epoxy prepreg. J. Compos. Mater. 2018, 52, 341–360. [Google Scholar] [CrossRef]
- Wu, M.S.; Centea, T.; Nutt, S. Compression molding of reused in-process waste—Effects of material and process factors. Adv. Manuf. Polym. Compos. Sci. 2018, 4, 1–12. [Google Scholar] [CrossRef]
- Krauklis, A.; Karl, C.; Gagani, A.; Jørgensen, J. Composite Material Recycling Technology—State-of-the-Art and Sustainable Development for the 2020s. J. Compos. Sci. 2021, 5, 28. [Google Scholar] [CrossRef]
- Spini, F.; Bettini, P. End-of-Life wind turbine blades: Review on recycling strategies. Compos. Part Eng. 2024, 275, 111290. [Google Scholar] [CrossRef]
- Pickering, S.J. Recycling technologies for thermoset composite materials—Current status. Compos. Part Appl. Sci. Manuf. 2006, 37, 1206–1215. [Google Scholar] [CrossRef]
- Naqvi, S.; Prabhakara, H.M.; Bramer, E.; Dierkes, W.; Akkerman, R.; Brem, G. A critical review on recycling of end-of-life carbon fibre/glass fibre reinforced composites waste using pyrolysis towards a circular economy. Resour. Conserv. Recycl. 2018, 136, 118–129. [Google Scholar] [CrossRef]
- Ali, Z.; Asmatulu, E. Effects of Acid Treatment on The Recovery of Outdated Pre-preg Composite Fibers. Res. Squadre 2021. [Google Scholar] [CrossRef]
- Bettini, P.; Calervo, L.; Palazzetti, R. Experimental study on a new generation of recycled composite laminates. Compos. Part Open Access 2025, 16, 100571. [Google Scholar] [CrossRef]
- Aranke, S.; Pipes, R. Platelet critical length for Prepreg Platelet Molded Composites. Compos. Part Appl. Sci. Manuf. 2024, 181, 108142. [Google Scholar] [CrossRef]
- Jin, B.; Li, X.; Jain, A.; González, C.; LLorca, J.; Nutt, S. Optimization of microstructures and mechanical properties of composite oriented strand board from reused prepreg. Compos. Struct. 2017, 174, 389–398. [Google Scholar] [CrossRef]
- Ko, S.; Yang, J.; Tuttle, M.; Salviato, M. Effect of the platelet size on the fracturing behavior and size effect of discontinuous fiber composite structures. Compos. Struct. 2019, 227, 111245. [Google Scholar] [CrossRef]
- De Souza, C.; Opelt, C.; Cândido, G.; De Souza, S.B.; Botelho, E.; Fernandes Marlet, J.; Rezende, M. Reuse of Uncured Carbon Fiber/Epoxy Resin Prepreg Scraps: Mechanical Behavior and Environmental Response. Acs Sustain. Chem. Eng. 2019, 7, 2200–2206. [Google Scholar] [CrossRef]
- Bao, L.; Sun, Y.; Ruan, F.; Murakami, Y.; Yu, Y. Development of a method for recycling factory waste carbon fiber prepregs and increasing the added value of the collected material. Polym. Compos. 2023, 44, 2071–2079. [Google Scholar] [CrossRef]
- Nakagawa, T.; Ko, S.; Slaughter, C.; Abdullah, T.; Houser, G.; Salviato, M. Effects of aging on the mechanical and fracture properties of chopped fiber composites made from repurposed aerospace prepreg scrap and waste. Sustain. Mater. Technol. 2022, 33, e00470. [Google Scholar] [CrossRef]
- Nakagawa, T.; Ko, S.; Houser, G.; Yang, J.; Salviato, M. Flexural Performance of Hybrid Discontinuous Fiber Composites Made of Repurposed Aerospace Prepreg. In Proceedings of the American Society for Composites—37th Technical Conference, ASC 2022, Tucson, AZ, USA, 9–21 September 2022. [Google Scholar] [CrossRef]
- Ko, S.; Yang, J.; Tuttle, M.; Salviato, M. Stochastic Computational Modeling of the Fracturing Behavior in Discontinuous Fiber Composite Structures. SAMPE Virtual Conf. Proc. 2020. [Google Scholar] [CrossRef]
- Ko, S.; Nakagawa, T.; Chen, Z.; Davey, J.; Abdullah, T.; Kuklenski, L.; Adams, E.; Soja, M.; Park, C.; Avery, W.; et al. Experimental and Numerical Investigations of Stochastic Thickness Effects in Discontinuous Fiber Composites. In Proceedings of the American Society for Composites—Thirty-Sixth Technical Conference on Composite Materials, Virtual Conference, 20–22 September 2021. [Google Scholar] [CrossRef]
- Nachtane, M.; Meraghni, F.; Chatzigeorgiou, G.; Harper, L.; Pelascini, F. Multiscale viscoplastic modeling of recycled glass fiber-reinforced thermoplastic composites: Experimental and numerical investigations. Compos. Part Eng. 2022, 242, 110087. [Google Scholar] [CrossRef]
- Harper, L.; Qian, C.; Luchoo, R.; Warrior, N. 3D geometric modelling of discontinuous fibre composites using a force-directed algorithm. J. Compos. Mater. 2016, 51, 2722. [Google Scholar] [CrossRef]
- Belliveau, R.; Landry, B.; Laplante, G. A 3D finite element model to simulate progressive damage in unidirectional- and woven-fibre thermoplastic discontinuous-long-fibre composites. J. Thermoplast. Compos. Mater. 2023, 36, 089270572311585. [Google Scholar] [CrossRef]
- Alves, M.; Martulli, L.; Kerschbaum, M.; Swolfs, Y.; Lomov, S.; Pimenta, S. A 3D finite element stochastic framework for the failure of tow-based discontinuous composites. Compos. Sci. Technol. 2022, 232, 109846. [Google Scholar] [CrossRef]
- Kravchenko, S.G.; Sommer, D.E.; Denos, B.R.; Avery, W.B.; Pipes, R.B. Structure-property relationship for a prepreg platelet molded composite with engineered meso-morphology. Compos. Struct. 2019, 210, 430–445. [Google Scholar] [CrossRef]
- ASTM D7264; Standard Test Method for Flexural Properties of Polymer Matrix Composite Materials. ASTM: West Conshohocken, PA, USA, 2007.
- Baldi, A.; Airoldi, A.; Belotti, P.; Bettini, P.; Sala, G. Numerical and experimental analyses of multiple delaminations in curved composite laminates. In Proceedings of the 19th International Conference on Composite Materials, Montréal, QC, Canada, 28 July–2 August 2013; Volume 2013, pp. 1873–1884. [Google Scholar]
- Jackson, W.; Martin, R. An interlaminar tensile strength specimen. Compos. Mater. Test. Des. 1993, 11, 333–354. [Google Scholar]
- Falk, M.; Needleman, A.; Rice, J. A critical evaluation of dynamic fracture simulations using cohesive surfaces. arXiv 2021, arXiv:cond-mat/0106304. [Google Scholar] [CrossRef]
- Yu, H.; Longana, M.L.; Jalalvand, M.; Wisnom, M.R.; Potter, K.D. Pseudo-ductility in intermingled carbon/glass hybrid composites with highly aligned discontinuous fibres. Compos. Part Appl. Sci. Manuf. 2015, 73, 35–44. [Google Scholar] [CrossRef]
- Yu, H.; Potter, K.; Wisnom, M. A novel manufacturing method for aligned discontinuous fibre composites (High Performance-Discontinuous Fibre method). Compos. Part Appl. Sci. Manuf. 2014, 65, 175–185. [Google Scholar] [CrossRef]









| Property | Value |
|---|---|
| Young Modulus | 64.3 GPa |
| Strength | 700 MPa |
| 1.356 kJ/m2 | |
| 2.378 kJ/m2 |
| This Work | [14] | [17] | [17] | |
|---|---|---|---|---|
| Material | HEMT-3 CC610E | HexPlyF155 W3T282 | T800S/3900 | T800S/3900 |
| Platelet size (mm2) | 2500 | 15,000 | 114 | 285 |
| Bending Strength (MPa) | 400 ± 28 | 371 ± 55 | 233 ± 60 | 456 ± 116 |
| Strength retention | 57% | 44% | 8% | 15% |
| Bending Stiffness (GPa) | 55 ± 3 | 55 ± 3 | 32 ± 4 | 39 ± 2 |
| Stiffness retention | 85% | 91% | 22% | 26% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Palazzetti, R.; Calervo, L.; Milite, A.; Bettini, P. Patch-Based Recycled Composites: Experimental Investigation and Modeling Techniques on Four-Point Bending and Curved Beam Traction Tests. Polymers 2025, 17, 757. https://doi.org/10.3390/polym17060757
Palazzetti R, Calervo L, Milite A, Bettini P. Patch-Based Recycled Composites: Experimental Investigation and Modeling Techniques on Four-Point Bending and Curved Beam Traction Tests. Polymers. 2025; 17(6):757. https://doi.org/10.3390/polym17060757
Chicago/Turabian StylePalazzetti, Roberto, Lorenzo Calervo, Alessandro Milite, and Paolo Bettini. 2025. "Patch-Based Recycled Composites: Experimental Investigation and Modeling Techniques on Four-Point Bending and Curved Beam Traction Tests" Polymers 17, no. 6: 757. https://doi.org/10.3390/polym17060757
APA StylePalazzetti, R., Calervo, L., Milite, A., & Bettini, P. (2025). Patch-Based Recycled Composites: Experimental Investigation and Modeling Techniques on Four-Point Bending and Curved Beam Traction Tests. Polymers, 17(6), 757. https://doi.org/10.3390/polym17060757








