Microstructural Deformation and Failure of Highly Explosive-Filled Polymer Composites Under Dynamic Compression
Abstract
1. Introduction
2. Constructive Model
2.1. Elastic Model for Particles
2.2. Viscoelastic Model for Polymer Binder
2.3. Bilinear Cohesive Law for Interface
3. Modeling the Micromechanics of PBXs
3.1. Numerical Simulation Model
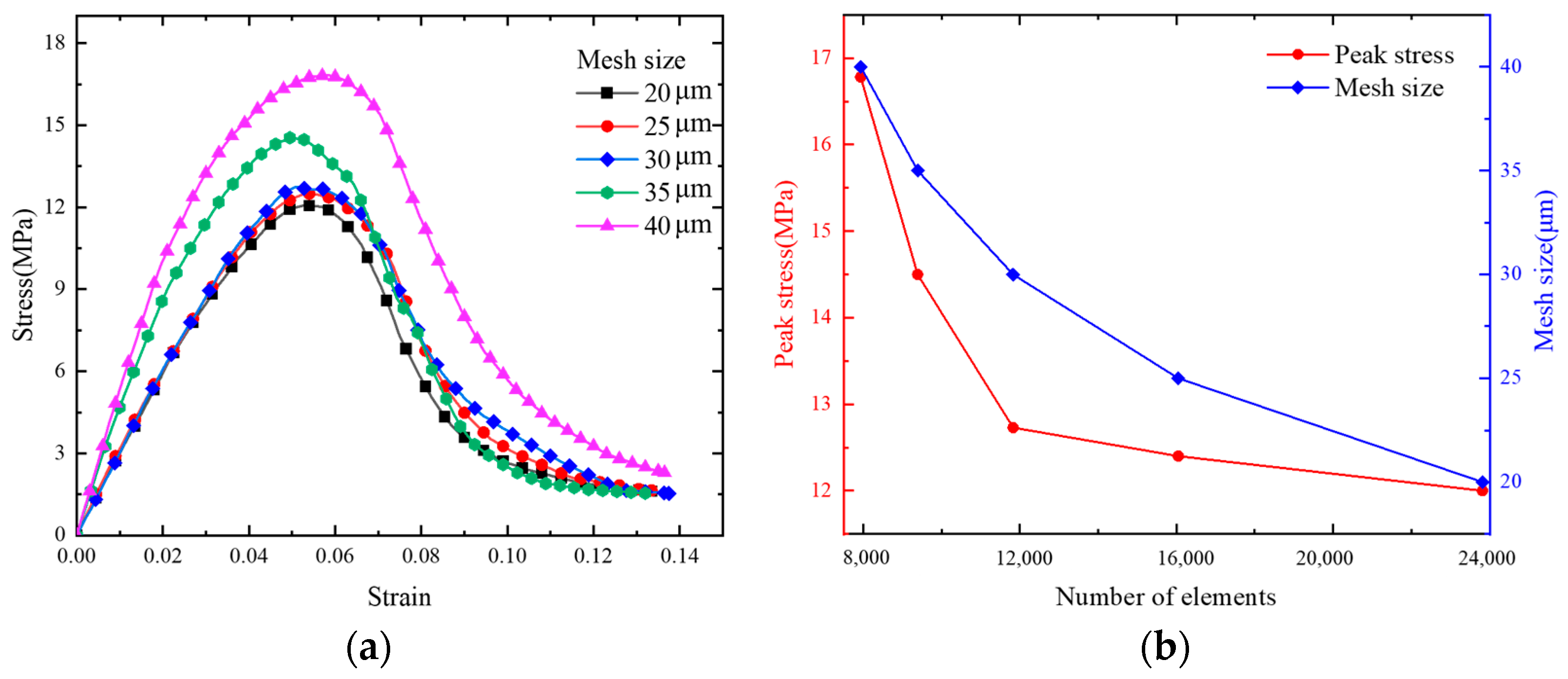
3.2. Mesh Size Study
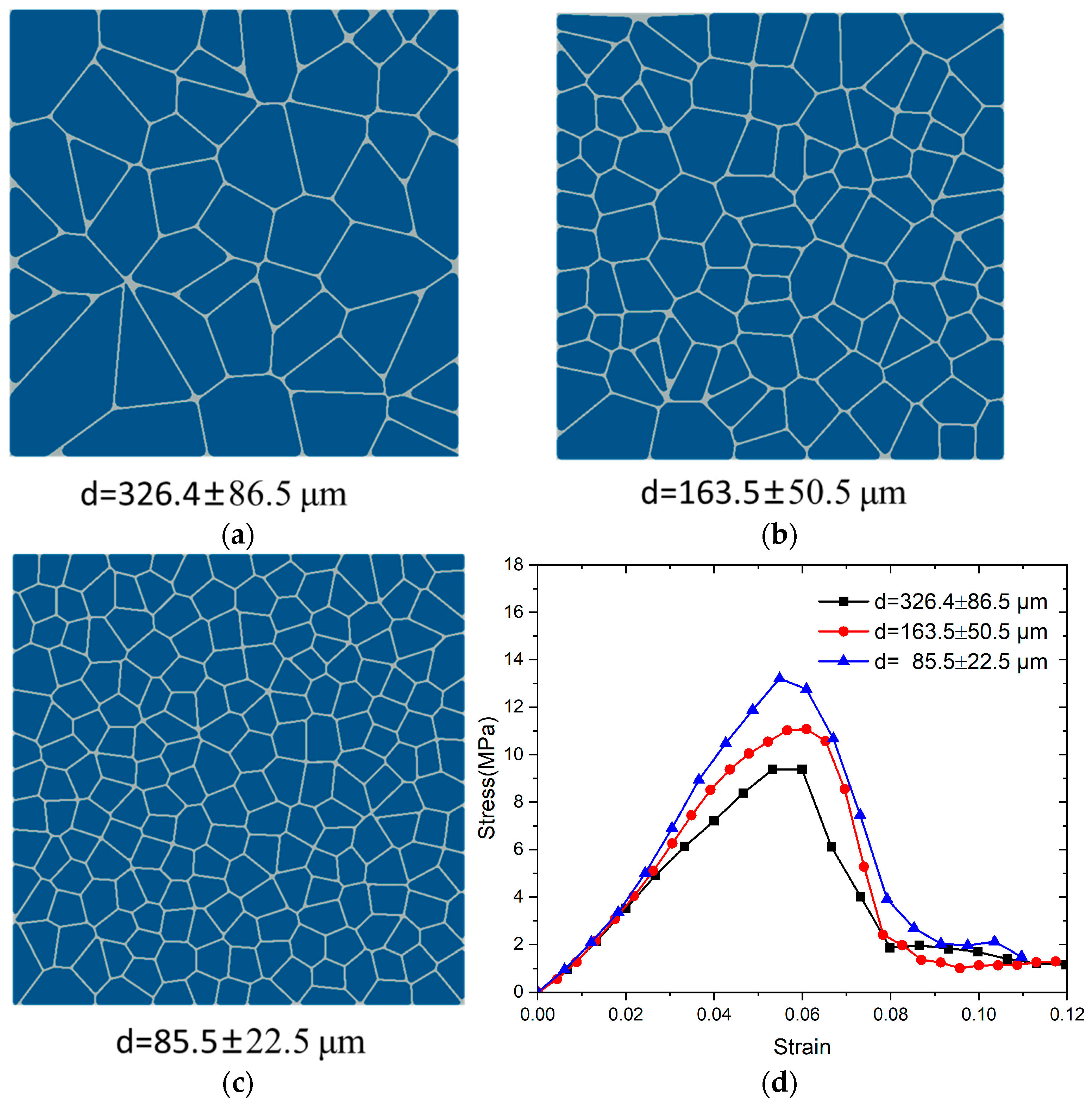
3.3. Particle Size Study
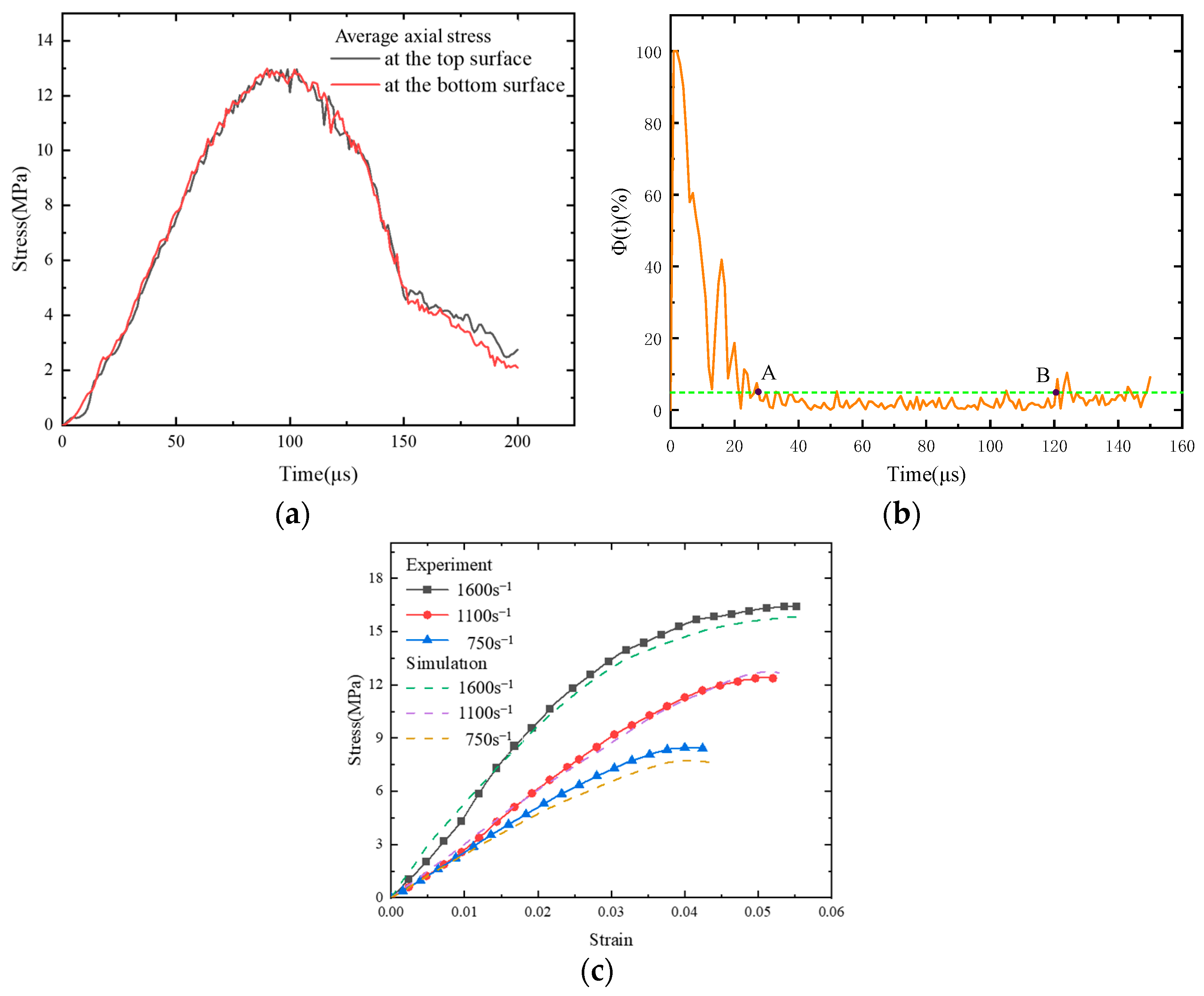
3.4. Stress Equilibrium and Model Verification
4. Results and Discussion
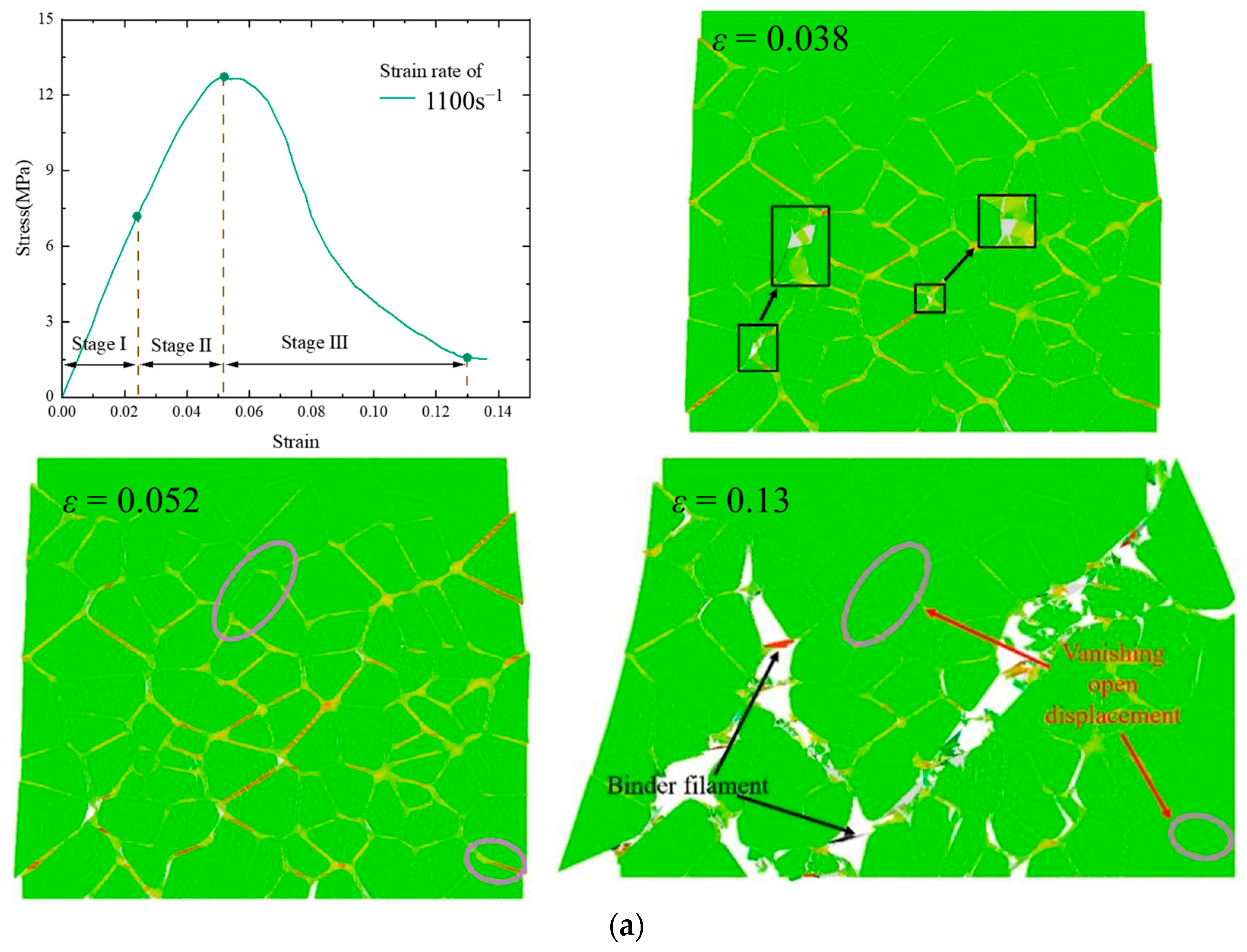
4.1. Mechanical Response and Failure Mechanism
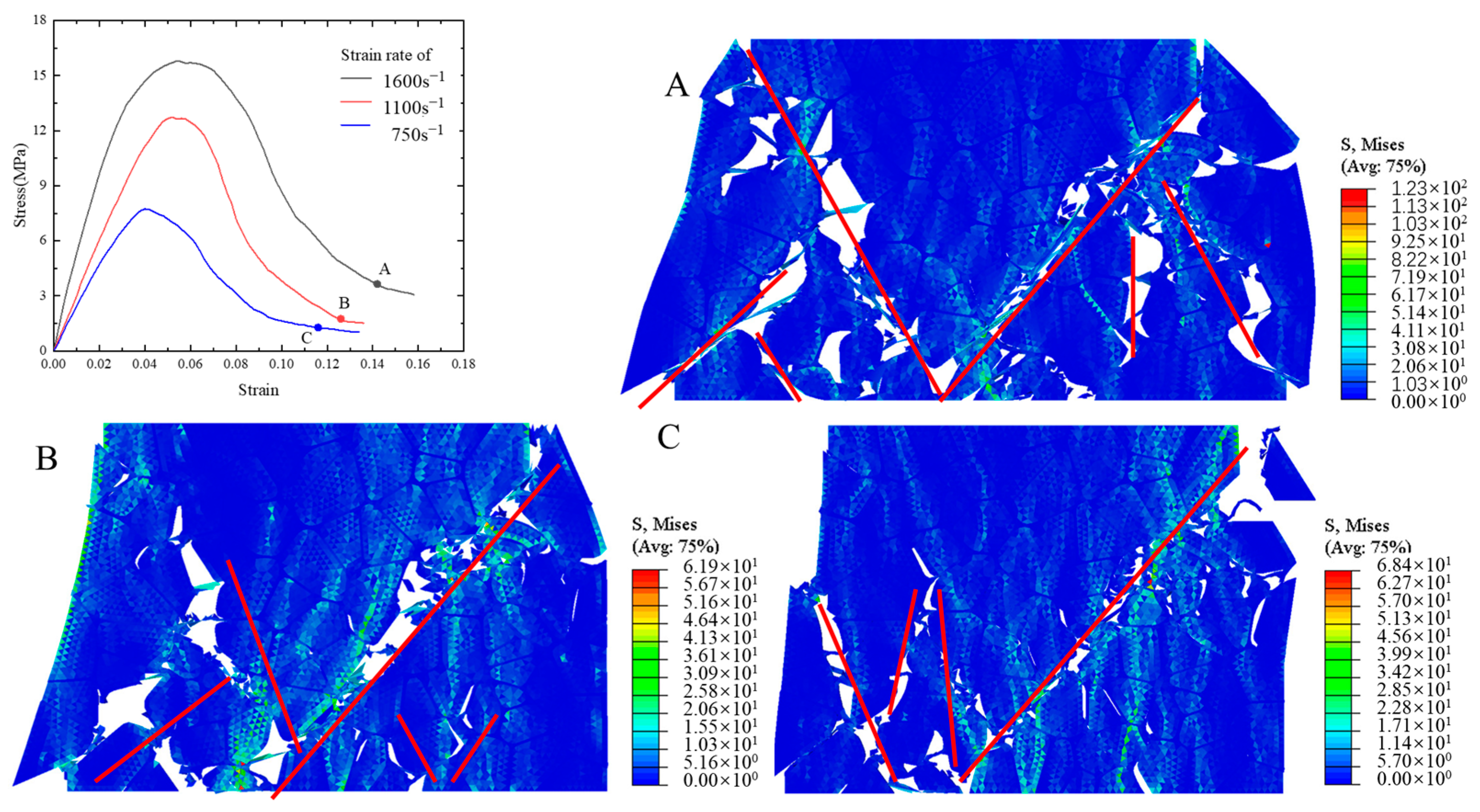
4.2. Effect of Strain Rate on Mechanical Behavior and Damage
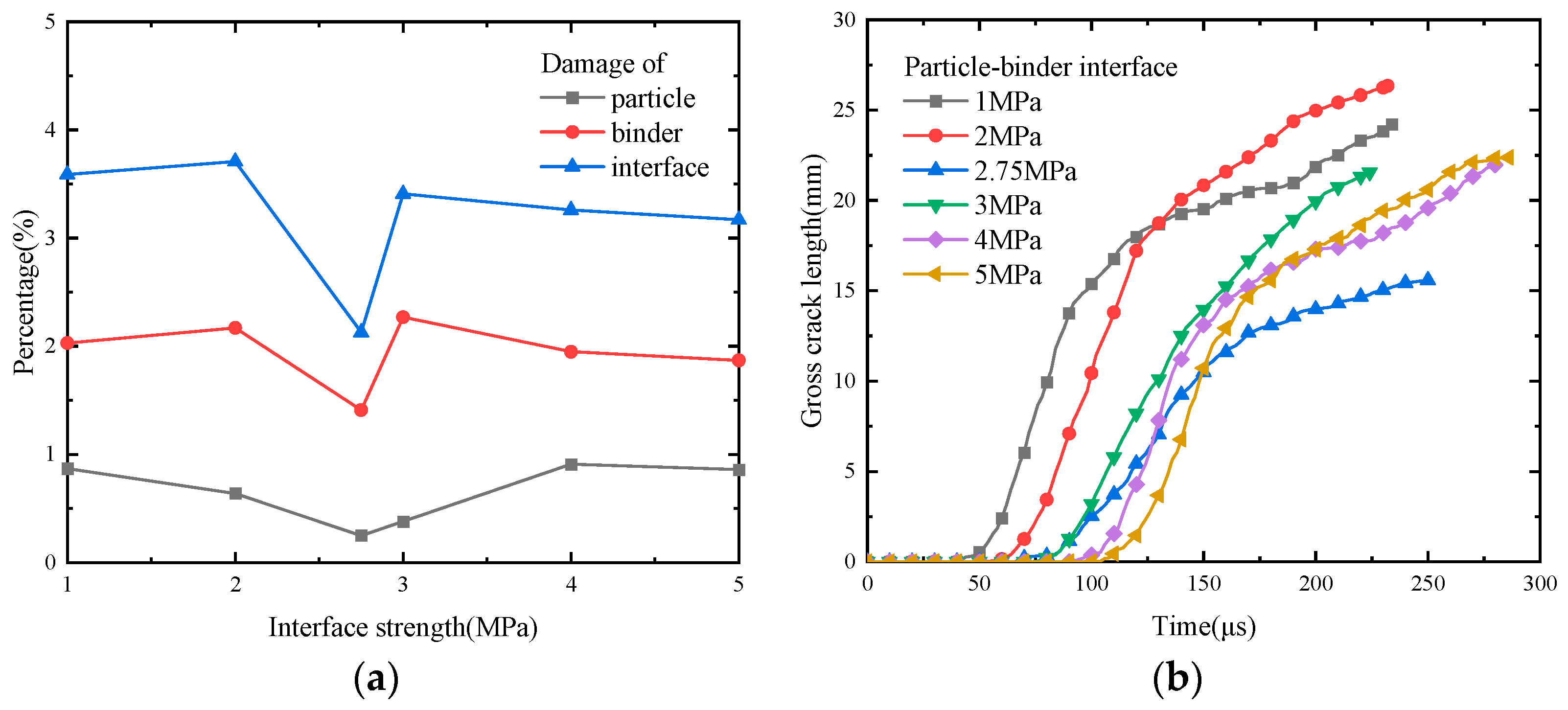
4.3. Effect of Interface Strength on Mechanical Properties and Damage
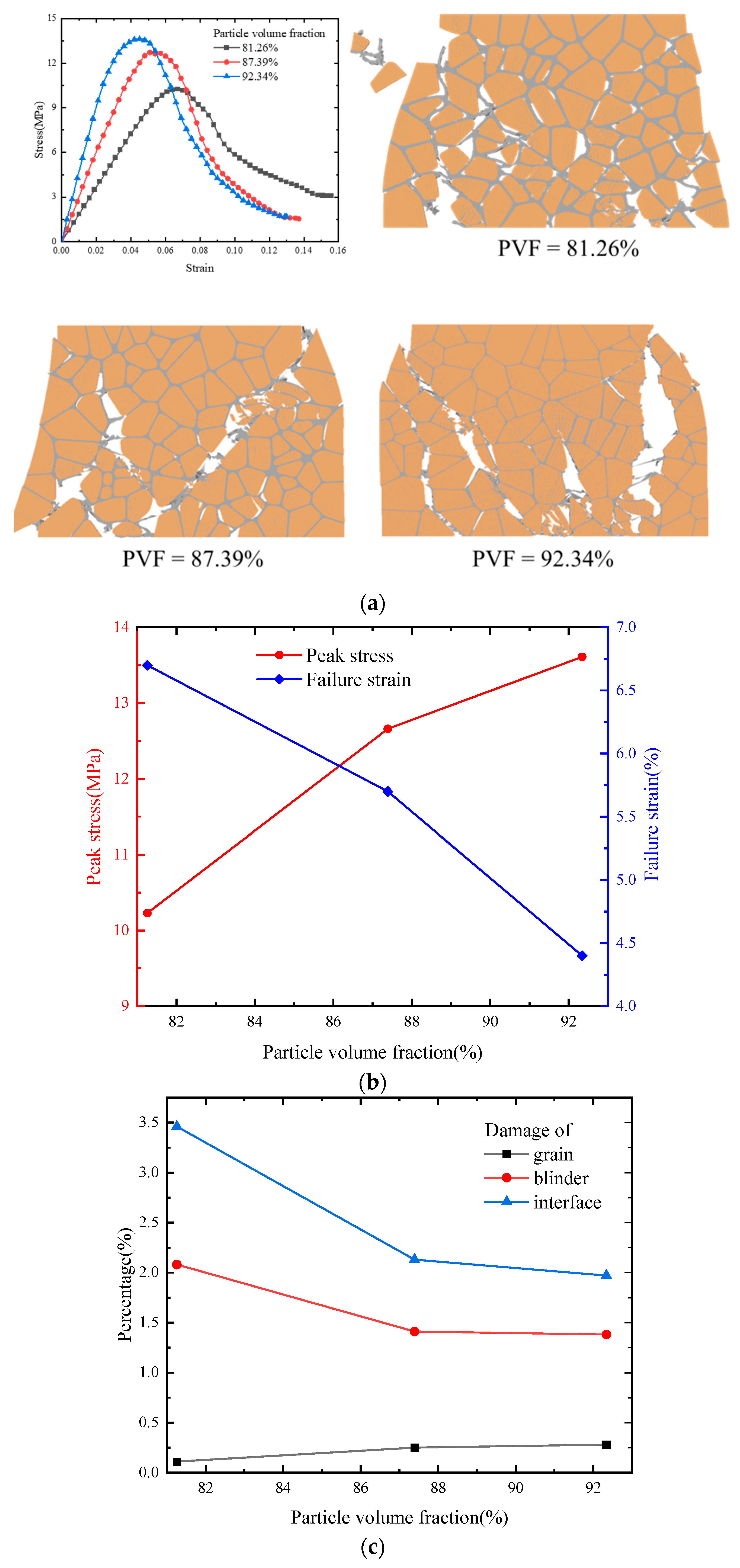
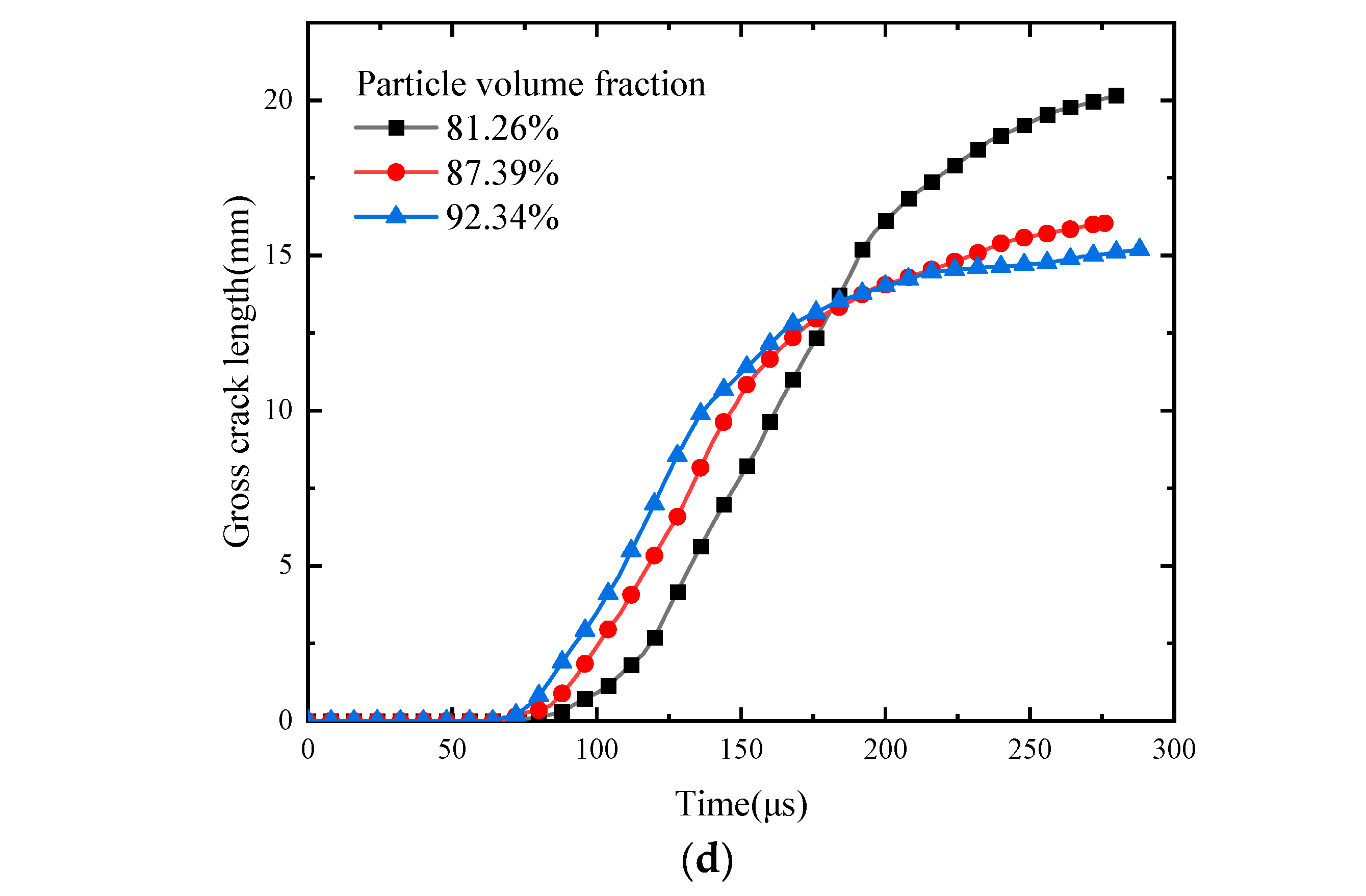
4.4. Effect of Particle Volume Fraction on Mechanical Properties and Damage
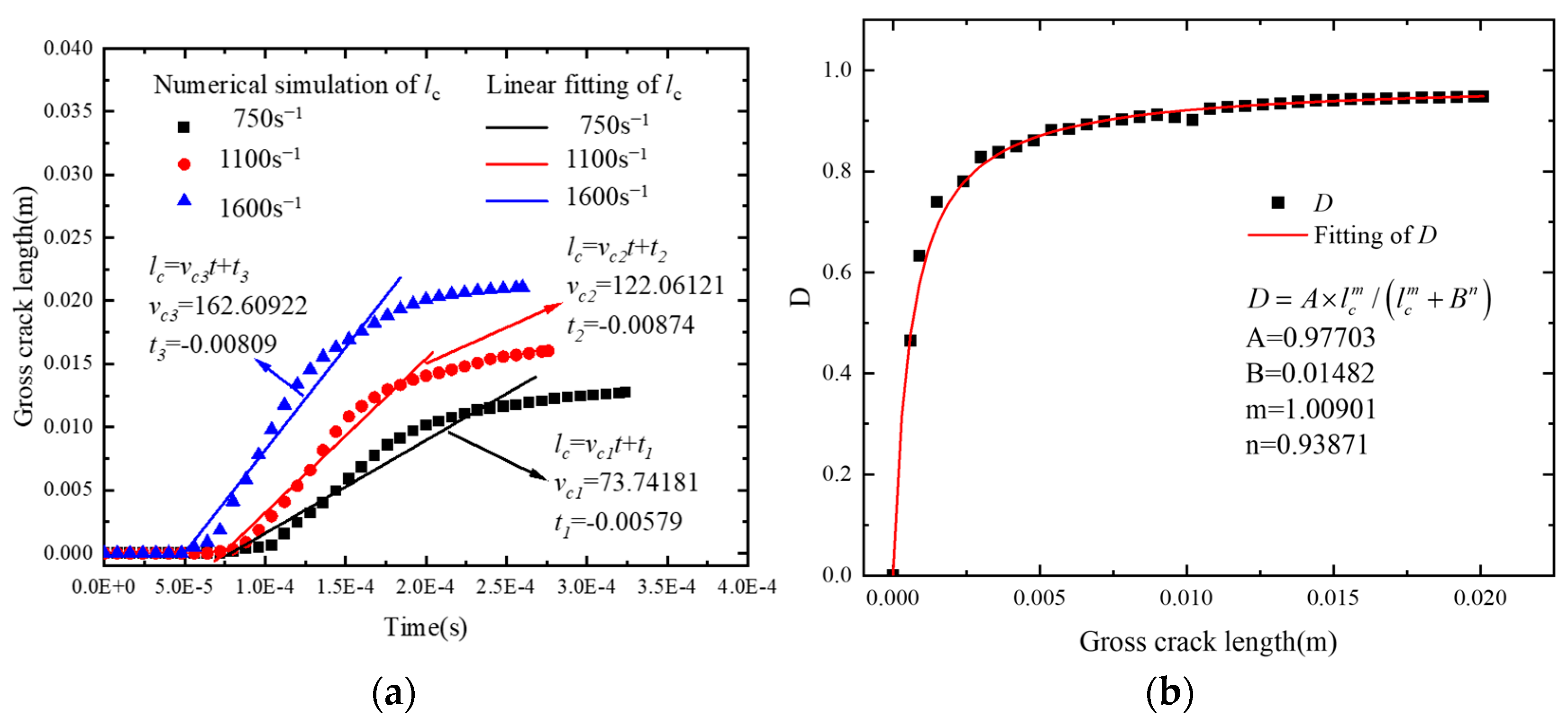
5. Damage Evolution Equation Based on Microcracks
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Clements, B.; Mas, E. A theory for plastic-bonded materials with a bimodal size distribution of filler particles. Model. Simul. Mater. Sci. 2004, 12, 407. [Google Scholar]
- Barua, A.; Zhou, M. Computational analysis of temperature rises in microstructures of HMX-Estane PBXs. Comput. Mech. 2013, 52, 151–159. [Google Scholar]
- Xiao, Y.; Sun, Y.; Zhen, Y.; Guo, L.; Yao, L. Characterization, modeling and simulation of the impact damage for polymer bonded explosives. Int. J. Impact Eng. 2017, 103, 149–158. [Google Scholar]
- Hang, G.-Y.; Yu, W.-L.; Wang, T.; Wang, J.-T.; Li, Z. Comparative studies on structures, mechanical properties, sensitivity, stabilities and detonation performance of CL-20/TNT cocrystal and composite explosives by molecular dynamics simulation. J. Mol. Model. 2017, 23, 281. [Google Scholar]
- Chen, P.; Xie, H.; Huang, F.; Huang, T.; Ding, Y. Deformation and failure of polymer bonded explosives under diametric compression test. Polym. Test. 2006, 25, 333–341. [Google Scholar] [CrossRef]
- Chen, P.; Huang, F.; Ding, Y. Microstructure, deformation and failure of polymer bonded explosives. J. Mater. Sci. 2007, 42, 5272–5280. [Google Scholar]
- Chen, P.; Huang, F.; Dai, K.; Ding, Y. Detection and Characterization of Long-Pulse Low-Velocity Impact Damage in Plastic Bonded Explosives. Int. J. Impact Eng. 2005, 31, 497–508. [Google Scholar]
- Mares, J.; Miller, J.; Sharp, N.; Moore, D.; Adams, D.; Groven, L.; Rhoads, J.; Son, S.F. Thermal and mechanical response of PBX 9501 under contact excitation. J. Appl. Phys. 2013, 113, 084904. [Google Scholar]
- Anderson, E.K.; Chiquete, C.; Jackson, S.I.; Chicas, R.I.; Short, M. The comparative effect of HMX content on the detonation performance characterization of PBX 9012 and PBX 9501 high explosives. Combust. Flame 2021, 230, 111415. [Google Scholar]
- Palmer, S.; Field, J.E.; Huntley, J. Deformation, strengths and strains to failure of polymer bonded explosives. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1993, 440, 399–419. [Google Scholar]
- Rae, P.; Goldrein, H.; Palmer, S.; Field, J.; Lewis, A. Quasi–static studies of the deformation and failure of β–HMX based polymer bonded explosives. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 2002, 458, 743–762. [Google Scholar]
- Skidmore, C.; Phillips, D.; Howe, P.; Mang, J.; Romero, J. The Evolution of Microstructural Changes in Pressed HMX Explosives; Los Alamos National Laboratory (LANL): Los Alamos, NM, USA, 1998.
- Rae, P.; Palmer, S.; Goldrein, H.; Lewis, A.; Field, J. White-light digital image cross-correlation (DICC) analysis of the deformation of composite materials with random microstructure. Opt. Laser. Eng. 2004, 41, 635–648. [Google Scholar]
- Goldrein, H.; Ra e, P.; Palmer, S.; Field, J. Construction of a high-resolution moiré interferometer for investigating microstructural displacement fields in materials. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 2002, 360, 939–952. [Google Scholar]
- Zhou, Z.; Chen, P.; Huang, F.; Liu, S. Experimental study on the micromechanical behavior of a PBX simulant using SEM and digital image correlation method. Opt. Laser. Eng. 2011, 49, 366–370. [Google Scholar]
- Liu, Z.; Xie, H.; Li, K.; Chen, P.; Huang, F. Fracture behavior of PBX simulation subject to combined thermal and mechanical loads. Polym. Test. 2009, 28, 627–635. [Google Scholar]
- Wu, H.M. Researches on the Constitutive Behavior of Three Kinds of Energetic Materials. Master’s Thesis, National University of Defence Technology, Changsha, China, 2003. [Google Scholar]
- Zhang, H.-N.; Chang, H.; Li, X.-J.; Wu, X.-G.; He, Q.-W. The effect of strain rate on compressive behavior and failure mechanism of CMDB propellant. Def. Technol. 2022, 18, 467–475. [Google Scholar]
- Chen, L.; Han, D.; Bai, S.-L.; Zhao, F.; Li, K.-W.; Chen, J.-K. Mechanical Behavior of a PBX Substitute Material under Static and Dynamic Loading. J. Test. Eval. 2019, 47, 1182–1192. [Google Scholar]
- Ravindran, S.; Tessema, A.; Kidane, A. Multiscale damage evolution in polymer bonded sugar under dynamic loading. Mech. Mater. 2017, 114, 97–106. [Google Scholar]
- Zhang, R.; Mohammed, I.K.; Taylor, A.C.; Charalambides, M.N. A microstructure image-based numerical model for predicting the fracture toughness of alumina trihydrate (ATH) filled poly (methyl methacrylate)(PMMA) composites. Compos. Part B-Eng. 2022, 232, 109632. [Google Scholar]
- Karimi, D.; Milani, A.; Alavi, F. Recycled Stone/ABS particulate composite: Micromechanical finite element fracture analysis. Compos. Part B-Eng. 2019, 177, 107315. [Google Scholar]
- Guo, Y.; Liu, R.; Chen, P.; Zhou, B.; Hu, G.; Han, C.; Lv, K.; Zhu, S. Mechanical behavior of PBX with different HMX crystal size during die pressing: Experimental study and DEM simulation. Compos. Sci. Technol. 2022, 222, 109378. [Google Scholar] [CrossRef]
- Kang, G.; Ning, Y.; Chen, P.; Ni, K. Meso-structure construction and effective modulus simulation of PBXs. J. Energ. Mater. 2020, 38, 261–282. [Google Scholar] [CrossRef]
- Dastgerdi, J.N.; Anbarlooie, B.; Marzban, S.; Marquis, G. Mechanical and real microstructure behavior analysis of particulate-reinforced nanocomposite considering debonding damage based on cohesive finite element method. Compos. Struct. 2015, 122, 518–525. [Google Scholar] [CrossRef]
- Xiao, Y.; Gong, T.; Zhang, X.; Sun, Y. Multiscale modeling for dynamic compressive behavior of polymer bonded explosives. Int. J. Mech. Sci. 2023, 242, 108007. [Google Scholar] [CrossRef]
- Huang, K.; Yan, J.; Shen, R.; Wan, Y.; Li, Y.; Ge, H.; Yu, H.; Guo, L. Investigation on fracture behavior of polymer-bonded explosives under compression using a viscoelastic phase-field fracture method. Eng. Fract. Mech. 2022, 266, 108411. [Google Scholar] [CrossRef]
- Li, P.; Hao, Z.; Zhen, W. A stabilized non-ordinary state-based peridynamic model. Comput. Methods Appl. Mech. Eng. 2018, 339, 262–280. [Google Scholar] [CrossRef]
- Wang, X.; Wu, Y.; Huang, F. Numerical mesoscopic investigations of dynamic damage and failure mechanisms of polymer bonded explosives. Int. J. Solids Struct. 2017, 129, 28–39. [Google Scholar] [CrossRef]
- Hudson, R.J.; Zioupos, P.; Gill, P.P. Investigating the Mechanical Properties of RDX Crystals Using Nano-Indentation. Propell. Explos. Pyrot. 2012, 37, 191–197. [Google Scholar] [CrossRef]
- LaBarbera, D.; Zikry, M. Heterogeneous thermo-mechanical behavior and hot spot formation in RDX–estane energetic aggregates. Int. J. Solids Struct. 2015, 62, 91–103. [Google Scholar] [CrossRef]
- Shukla, A.; Joshi, Y.M. Boltzmann superposition principle for a time-dependent soft material: Assessment under creep flow field. Rheol. Acta 2017, 56, 927–940. [Google Scholar] [CrossRef]
- Xiao, Y.; Fan, C.; Wang, Z.; Sun, Y. Visco-hyperelastic constitutive modeling of the dynamic mechanical behavior of HTPB casting explosive and its polymer binder. Acta Mech. 2020, 231, 2257–2272. [Google Scholar]
- Oliveira, L.A.; Donadon, M.V. Delamination analysis using cohesive zone model: A discussion on traction-separation law and mixed-mode criteria. Eng. Fract. Mech. 2020, 228, 106922. [Google Scholar]
- Hashin, Z. The spherical inclusion with imperfect interface. J. Appl. Mech. 1991, 58, 444–449. [Google Scholar]
- Lissenden, C.; Herakovich, C. Engineering Numerical modelling of damage development and viscoplasticity in metal matrix composites. Comput. Methods Appl. Mech. Eng. 1995, 126, 289–303. [Google Scholar]
- Scheider, I.; Brocks, W. The effect of the traction separation law on the results of cohesive zone crack propagation analyses. Key Eng. Mater. 2003, 251, 313–318. [Google Scholar]
- Yang, Z.; Kang, G.; Liu, R.; Chen, P. Predicting the mechanical behaviour of highly particle-filled polymer composites using the nonlinear finite element method. Compos. Struct. 2022, 286, 115275. [Google Scholar]
- Dai, K.; Lu, B.; Chen, P.; Chen, J. Modelling microstructural deformation and the failure process of plastic bonded explosives using the cohesive zone model. Materials 2019, 12, 3661. [Google Scholar] [CrossRef]
- van der Heijden, A.E.; Bouma, R.H.; van der Steen, A.C. Physicochemical Parameters of Nitramines Influencing Shock Sensitivity. Propell. Explos. Pyrot. 2004, 29, 304–313. [Google Scholar] [CrossRef]
- Olokun, A.; Prakash, C.; Gunduz, I.; Tomar, V. The role of microstructure in the impact induced temperature rise in hydroxyl terminated polybutadiene (HTPB)–cyclotetramethylene–tetranitramine (HMX) energetic materials using the cohesive finite element method. J. Appl. Phys. 2020, 128, 065901. [Google Scholar]
- Annapragada, S.R.; Sun, D.; Garimella, S.V. Prediction of effective thermos-mechanical properties of particulate composites. Comp. Mater. Sci. 2007, 40, 255–266. [Google Scholar] [CrossRef]
- Xiao, Y.; Xiao, X.; Xiong, Y.; Fan, C.; Wang, Z.; Sun, Y. Mechanical behavior of a typical polymer bonded explosive under compressive loads. J. Energ. Mater. 2023, 41, 378–410. [Google Scholar]
- Ravichandran, G.; Subhash, G. Critical appraisal of limiting strain rates for compression testing of ceramics in a split Hopkinson pressure bar. J. Am. Ceram. Soc. 1994, 77, 263–267. [Google Scholar] [CrossRef]
- Wu, P.; Wang, X. Experimental and Numerical Simulation on the Damage Process of HTPB Propellant at the Crack Tip. Chin. J. Energ. Mater. 2020, 28, 514–521. [Google Scholar]
- Tan, H.; Liu, C.; Huang, Y.; Geubelle, P.H. The cohesive law for the particle/matrix interfaces in high explosives. J. Mech. Phys. Solid. 2005, 53, 1892–1917. [Google Scholar]
- Idar, D.; Thompson, D.; Gray Iii, G.; Blumenthal, W.; Cady, C.; Peterson, P.; Roemer, E.; Wright, W.; Jacquez, B. Influence of polymer molecular weight, temperature, and strain rate on the mechanical properties of PBX 9501. In AIP Conference Proceedings; American Institute of Physics: Melville, NY, USA, 2002; pp. 821–824. [Google Scholar]
- Gray, G.; Blumenthal, W.; Idar, D.; Cady, C. Influence of temperature on the high-strain-rate mechanical behavior of PBX 9501. In AIP Conference Proceedings; AIP Publishing: New York, NY, USA, 1998; pp. 583–586. [Google Scholar]
- Barua, A. Mesoscale Computational Prediction and Quantification of Thermomechanical Ignition Behavior of Polymer-Bonded Explosives (PBXs); Georgia Institute of Technology: Atlanta, GA, USA, 2013. [Google Scholar]
- Kang, G.; Chen, P.; Guo, X.; Ma, G.; Ning, Y. Simulations of meso-scale deformation and damage of polymer bonded explosives by the numerical manifold method. Eng. Anal. Bound. Elem. 2018, 96, 123–137. [Google Scholar]
- Li, X.; Liu, Y.; Sun, Y. Dynamic Mechanical Damage and Non-Shock initiation of a New Polymer Bonded Explosive during Penetration. Polymers 2020, 12, 1342. [Google Scholar] [CrossRef]
- Liu, R.; Wang, X.-J.; Chen, P.-W.; Kang, G.; Zhu, S.-P.; Guo, Y.-S. The role of tension–compression asymmetrical microcrack evolution in the ignition of polymer-bonded explosives under low-velocity impact. J. Appl. Phys. 2021, 129, 175108. [Google Scholar]
- Dienes, J.; Zuo, Q.; Kershner, J. Impact initiation of explosives and propellants via statistical crack mechanics. J. Mech. Phys. Solid. 2006, 54, 1237–1275. [Google Scholar]






| Log τi | Log Ei | Log Ki | Log Gi | Log τi | Log Ei | Log Ki | Log Gi | ||
|---|---|---|---|---|---|---|---|---|---|
| 1 | −9 | 1.708 | 2.231 | 1.246 | 9 | −1 | 0.344 | 0.867 | −0.118 |
| 2 | −8 | 1.543 | 2.066 | 1.081 | 10 | 0 | 0.096 | 0.619 | −0.366 |
| 3 | −7 | 1.467 | 1.990 | 1.005 | 11 | 1 | −0.534 | −0.011 | −0.996 |
| 4 | −6 | 1.316 | 1.839 | 0.854 | 12 | 2 | −0.285 | 0.238 | −0.747 |
| 5 | −5 | 1.134 | 1.657 | 0.672 | 13 | 3 | −1.193 | −0.670 | −1.655 |
| 6 | −4 | 0.996 | 1.519 | 0.534 | 14 | 4 | −0.632 | −0.109 | −1.094 |
| 7 | −3 | 0.775 | 1.298 | 0.313 | 15 | 5 | −1.472 | −0.949 | −1.934 |
| 8 | −2 | 0.616 | 1.139 | 0.157 |
| Cohesive Element Type | K (MPa/mm) | σ (MPa) | G (N/mm) |
|---|---|---|---|
| Particle | 1800 | 6 | 0.01 |
| Binder | 900 | 7.5 | 0.15 |
| Particle–binder interface | 800 | 2.75 | 0.012 |
| Element | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| (s) | 1 × 108 | 1 × 107 | 1 × 106 | 1 × 105 | ∞ |
| (MPa) | 297.17 | 221.82 | 175.39 | 78.34 | 1.66 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Zhao, H.; Yu, W.; Zhang, Q.; Sun, Y.; Xiao, Y. Microstructural Deformation and Failure of Highly Explosive-Filled Polymer Composites Under Dynamic Compression. Polymers 2025, 17, 867. https://doi.org/10.3390/polym17070867
Zhang X, Zhao H, Yu W, Zhang Q, Sun Y, Xiao Y. Microstructural Deformation and Failure of Highly Explosive-Filled Polymer Composites Under Dynamic Compression. Polymers. 2025; 17(7):867. https://doi.org/10.3390/polym17070867
Chicago/Turabian StyleZhang, Xiaowei, Heming Zhao, Wanqian Yu, Qiao Zhang, Yi Sun, and Youcai Xiao. 2025. "Microstructural Deformation and Failure of Highly Explosive-Filled Polymer Composites Under Dynamic Compression" Polymers 17, no. 7: 867. https://doi.org/10.3390/polym17070867
APA StyleZhang, X., Zhao, H., Yu, W., Zhang, Q., Sun, Y., & Xiao, Y. (2025). Microstructural Deformation and Failure of Highly Explosive-Filled Polymer Composites Under Dynamic Compression. Polymers, 17(7), 867. https://doi.org/10.3390/polym17070867





