Chain Size and Knots of Ring Polymers in All-Crossing and Intra-Crossing Melts
Abstract
1. Introduction
2. Simulation Method and Model
2.1. Simulation Method
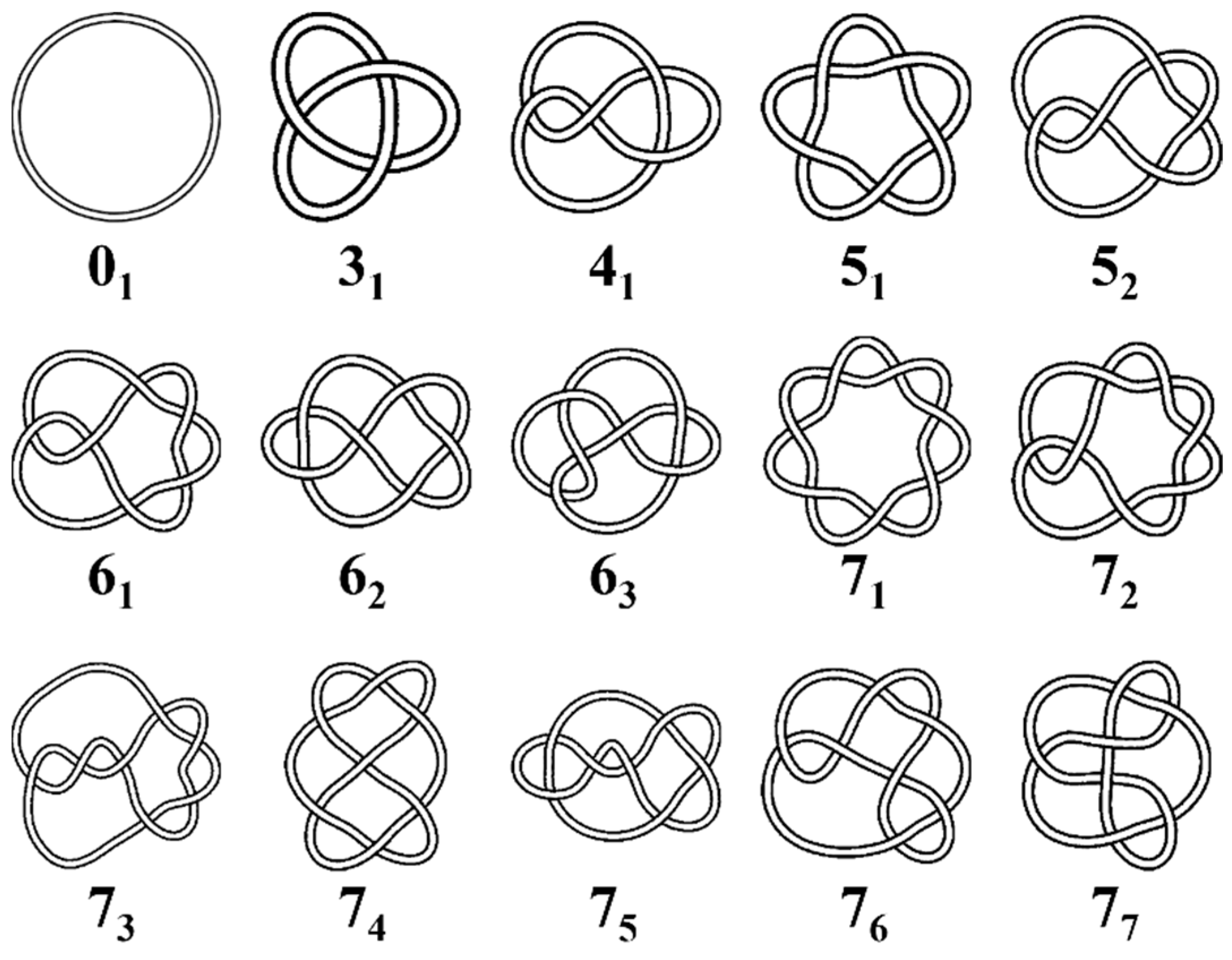
2.2. Identification of Knots
3. Results and Discussion
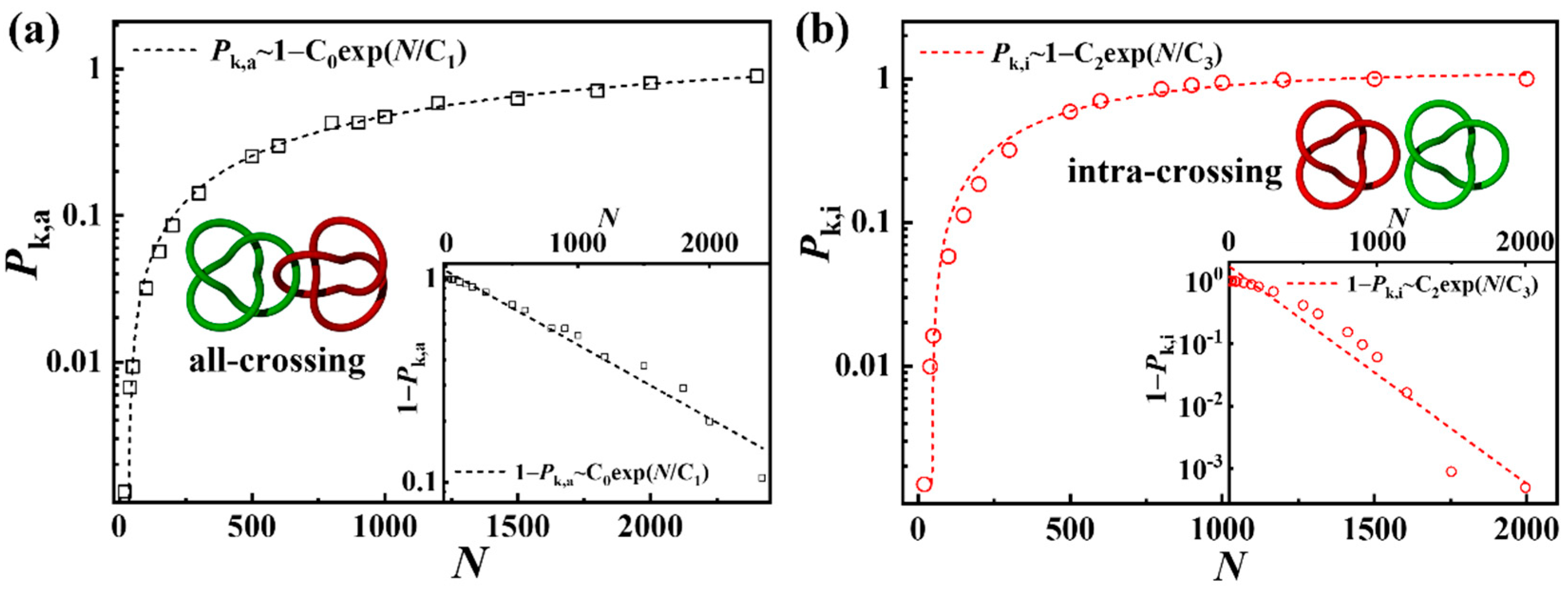
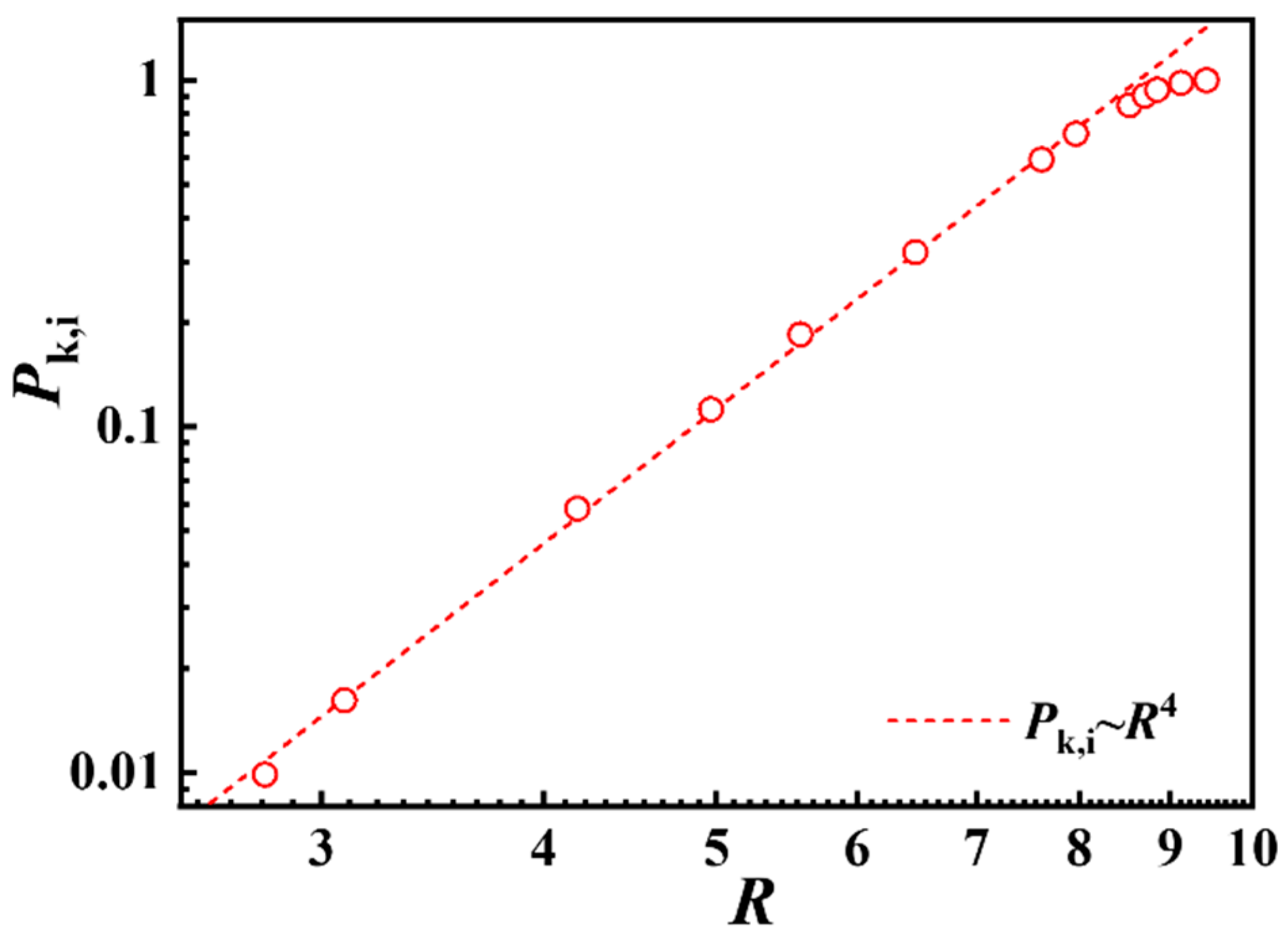
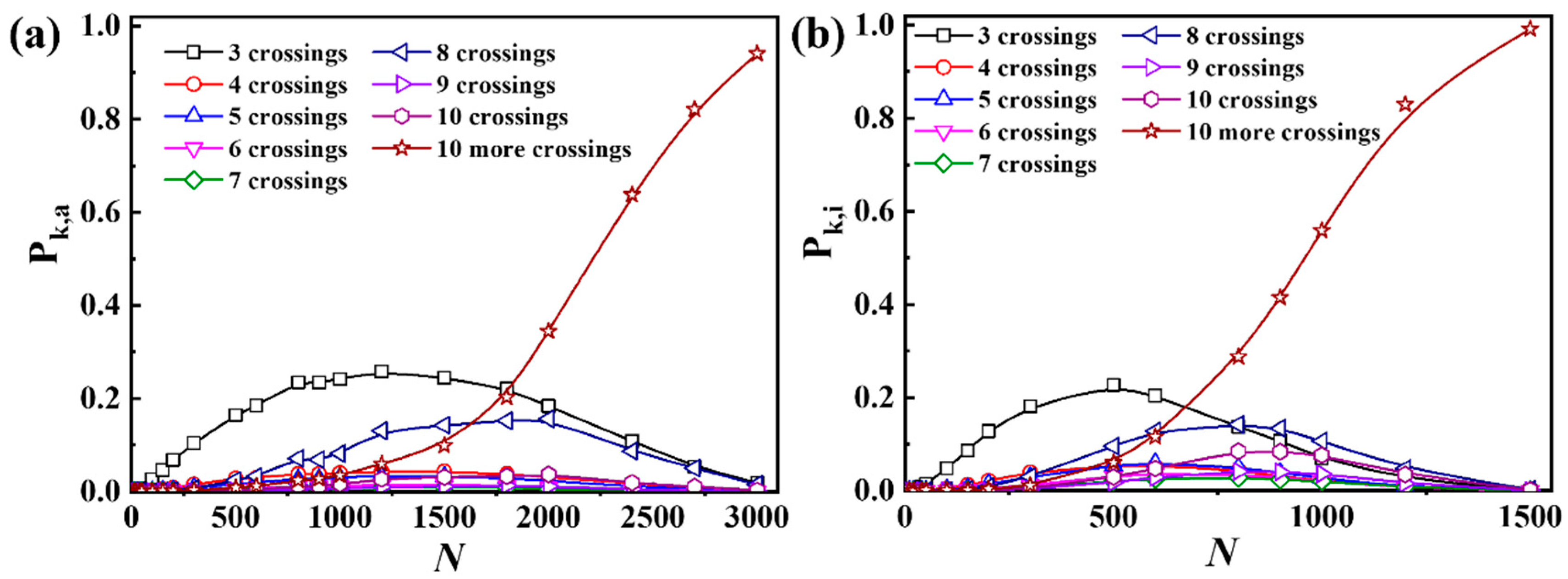
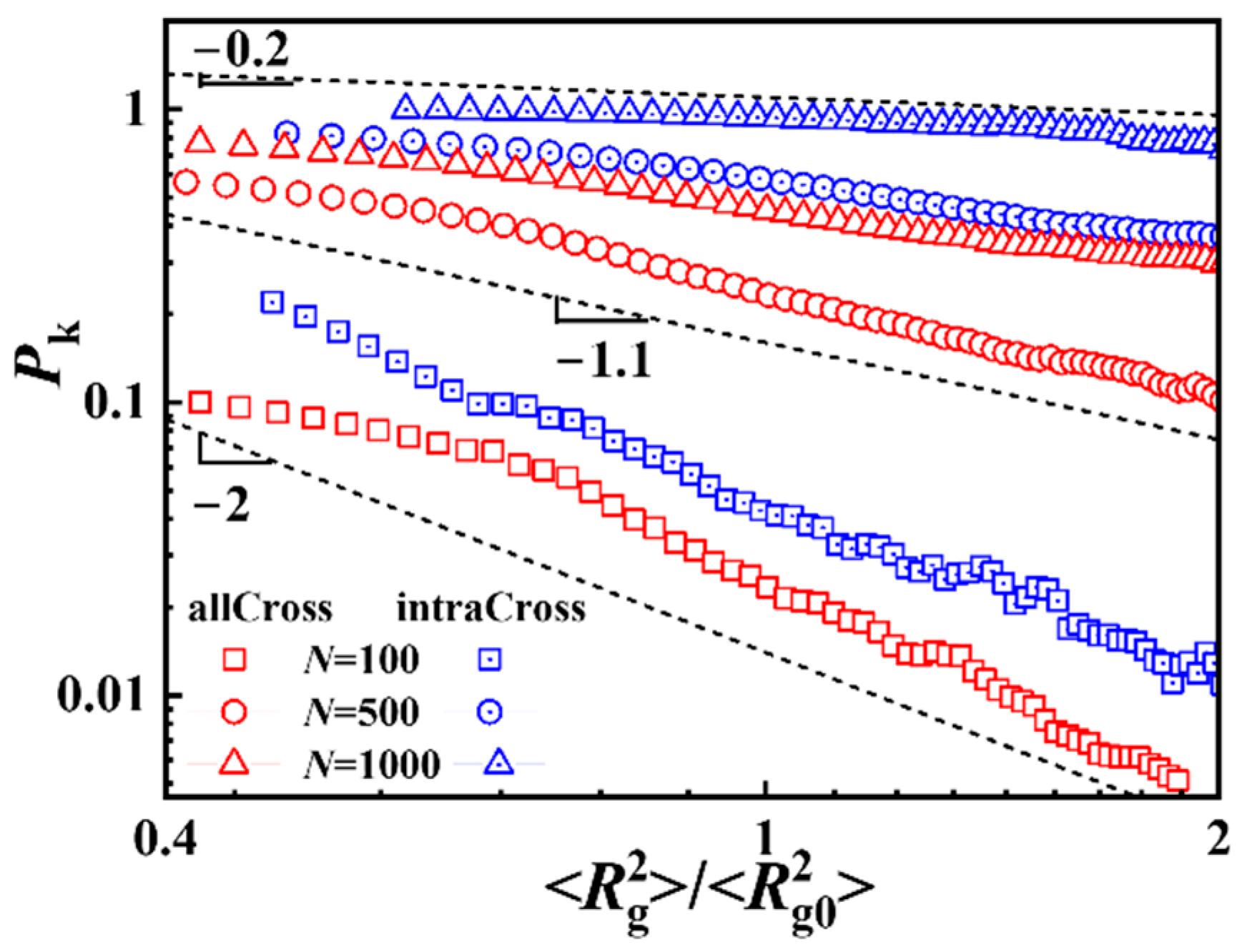
3.1. Knotting Probability of Ring Polymers
3.2. Interchain Constraint Contribution to the Free Energy
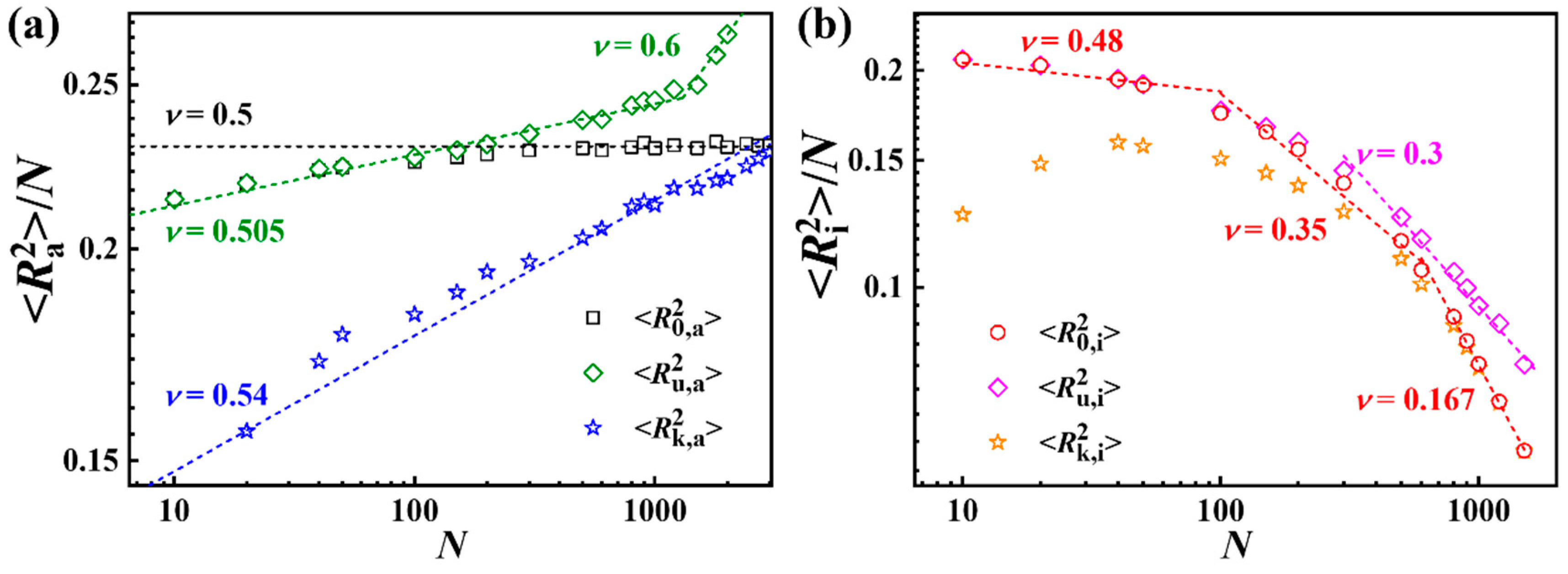
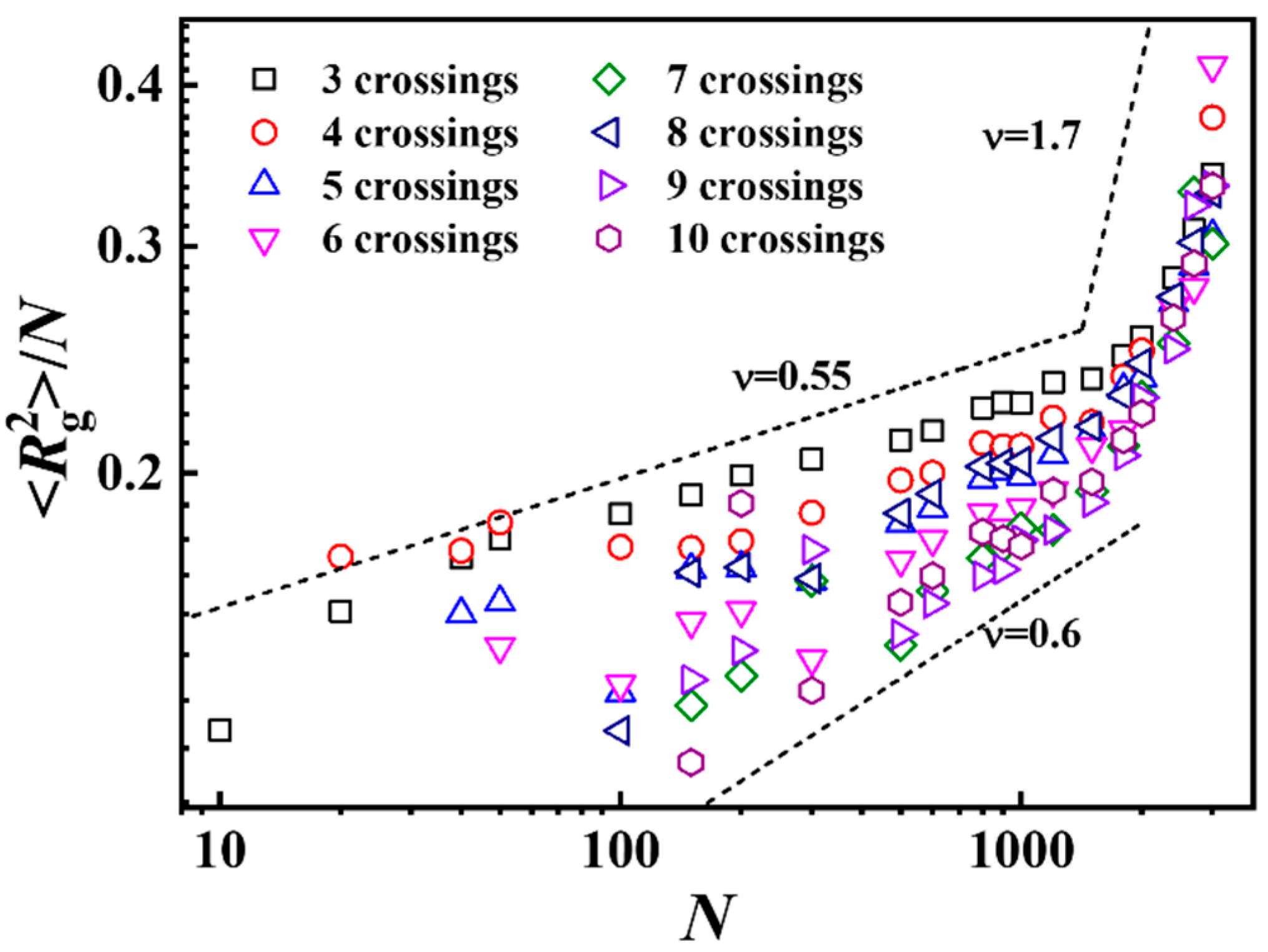
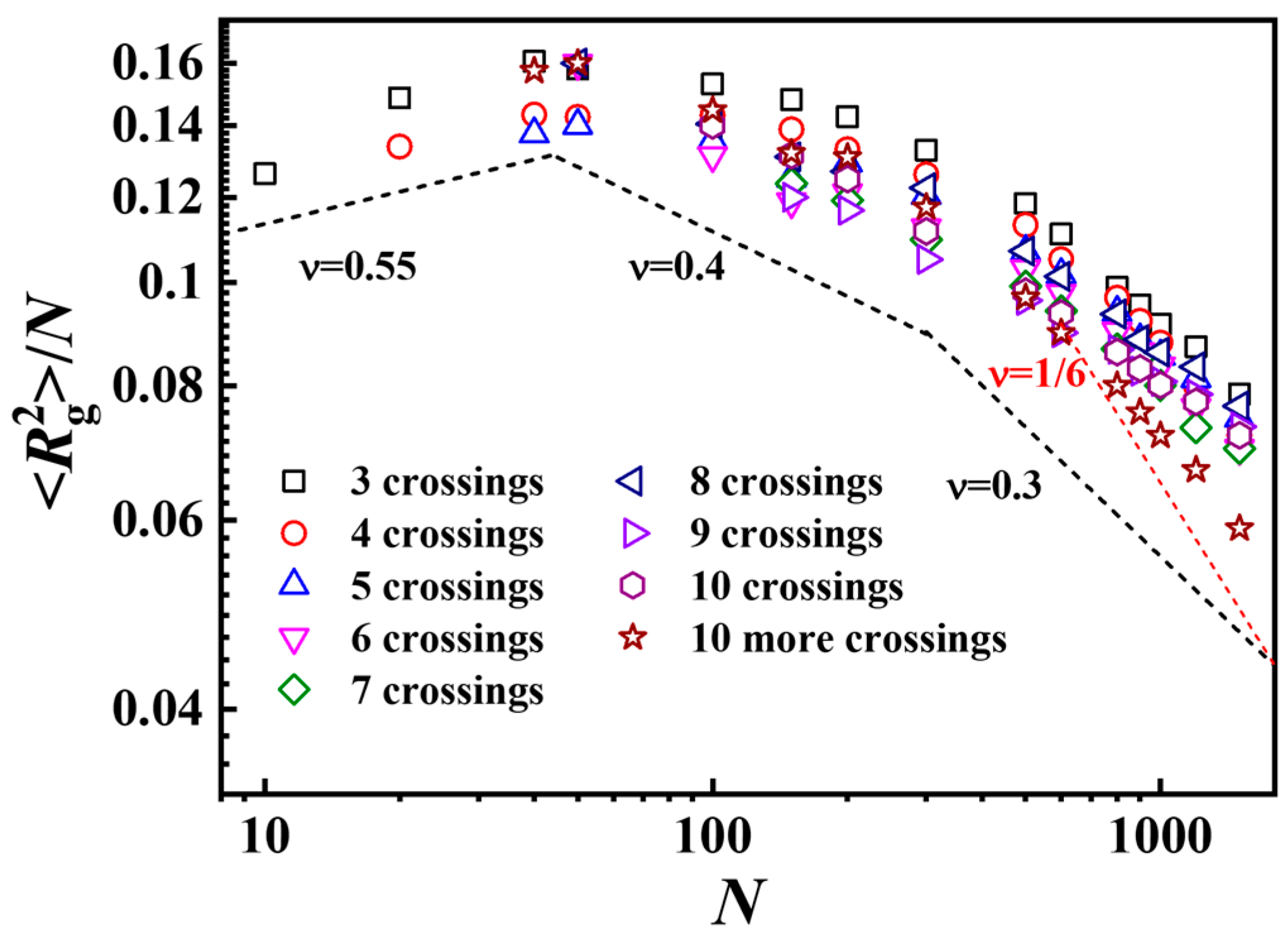
3.3. Probability and Sizes of Different Types of Knotting Rings
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Halverson, J.D.; Lee, W.B.; Grest, G.S.; Grosberg, A.Y.; Kremer, K. Molecular dynamics simulation study of nonconcatenated ring polymers in a melt. I. Statics. J. Chem. Phys. 2011, 134, 204904. [Google Scholar] [CrossRef] [PubMed]
- Halverson, J.D.; Lee, W.B.; Grest, G.S.; Grosberg, A.Y.; Kremer, K. Molecular dynamics simulation study of nonconcatenated ring polymers in a melt. II. Dynamics. J. Chem. Phys. 2011, 134, 204905. [Google Scholar] [CrossRef] [PubMed]
- Parisi, D.; Costanzo, S.; Jeong, Y.; Ahn, J.; Chang, T.; Vlassopoulos, D.; Halverson, J.D.; Kremer, K.; Ge, T.; Rubinstein, M.; et al. Nonlinear shear rheology of entangled polymer rings. Macromolecules 2021, 54, 2811–2827. [Google Scholar] [CrossRef]
- Jacob, F.; Wollman, E.L. Genetic and physical determinations of chromosomal segments in Escherichia coli. Symp. Soc. Exp. Biol. 1958, 12, 75–92. [Google Scholar]
- Freifelder, D.; Kleinschmidt, A.K.; Sinsheimer, R.L. Electron Microscopy of Single-Stranded DNA: Circularity of DNA of Bacteriophage φX174. Science 1964, 146, 254–255. [Google Scholar] [CrossRef]
- Arrighi, V.; Gagliardi, S.; Dagger, A.C.; Semlyen, J.A.; Higgins, J.S.; Shenton, M.J. Conformation of cyclics and linear chain polymers in bulk by SANS. Macromolecules 2004, 37, 8057–8065. [Google Scholar] [CrossRef]
- Brás, A.R.; Gooßen, S.; Krutyeva, M.; Radulescu, A.; Farago, B.; Allgaier, J.; Pyckhout-Hintzen, W.; Wischnewski, A.; Richter, D. Compact structure and non-Gaussian dynamics of ring polymer melts. Soft Matter 2014, 10, 3649–3655. [Google Scholar] [CrossRef]
- Brás, A.R.; Pasquino, R.; Koukoulas, T.; Tsolou, G.; Holderer, O.; Radulescu, A.; Allgaier, J.; Mavrantzas, V.G.; Pyckhout-Hintzen, W.; Wischnewski, A.; et al. Structure and dynamics of polymer rings by neutron scattering: Breakdown of the Rouse model. Soft Matter 2011, 7, 11169–11176. [Google Scholar] [CrossRef]
- Gooßen, S.; Brás, A.R.; Krutyeva, M.; Sharp, M.; Falus, P.; Feoktystov, A.; Gasser, U.; Pyckhout-Hintzen, W.; Wischnewski, A.; Richter, D. Molecular scale dynamics of large ring polymers. Phys. Rev. Lett. 2014, 113, 168302. [Google Scholar] [CrossRef]
- Iwamoto, T.; Doi, Y.; Kinoshita, K.; Ohta, Y.; Takano, A.; Takahashi, Y.; Nagao, M.; Matsushita, Y. Conformations of ring polystyrenes in bulk studied by SANS. Macromolecules 2018, 51, 1539–1548. [Google Scholar] [CrossRef]
- Richter, D.; Gooßen, S.; Wischnewski, A. Celebrating soft matter’s 10th anniversary: Topology matters: Structure and dynamics of ring polymers. Soft Matter 2015, 11, 8535–8549. [Google Scholar] [CrossRef]
- Cates, M.E.; Deutsch, J.M. Conjectures on the statistics of ring polymers. J. Phys. 1986, 47, 2121–2128. [Google Scholar] [CrossRef]
- Ge, T.; Panyukov, S.; Rubinstein, M. Self-similar conformations and dynamics in entangled melts and solutions of nonconcatenated ring polymers. Macromolecules 2016, 49, 708–722. [Google Scholar] [CrossRef]
- Grosberg, A.Y. Annealed lattice animal model and Flory theory for the melt of non-concatenated rings: Towards the physics of crumpling. Soft Matter 2014, 10, 560–565. [Google Scholar] [CrossRef] [PubMed]
- Lang, M.; Fischer, J.; Sommer, J.-U. Effect of topology on the conformations of ring polymers. Macromolecules 2012, 45, 7642–7648. [Google Scholar] [CrossRef]
- Obukhov, S.; Johner, A.; Baschnagel, J.; Meyer, H.; Wittmer, J.P. Melt of polymer rings: The decorated loop model. Europhys. Lett. 2014, 105, 48005. [Google Scholar] [CrossRef]
- Sakaue, T. Ring polymers in melts and solutions: Scaling and crossover. Phys. Rev. Lett. 2011, 106, 167802. [Google Scholar] [CrossRef]
- Sakaue, T. Statistics and geometrical picture of ring polymer melts and solutions. Phys. Rev. E 2012, 85, 021806. [Google Scholar] [CrossRef]
- Suzuki, J.; Takano, A.; Deguchi, T.; Matsushita, Y. Dimension of ring polymers in bulk studied by Monte-Carlo simulation and self-consistent theory. J. Chem. Phys. 2009, 131, 144902. [Google Scholar] [CrossRef]
- Müller, M.; Wittmer, J.P.; Cates, M.E. Topological effects in ring polymers: A computer simulation study. Phys. Rev. E 1996, 53, 5063–5074. [Google Scholar] [CrossRef] [PubMed]
- Suzuki, J.; Takano, A.; Matsushita, Y. Topological effect in ring polymers investigated with Monte Carlo simulation. J. Chem. Phys. 2008, 129, 034903. [Google Scholar] [CrossRef] [PubMed]
- Tsolou, G.; Stratikis, N.; Baig, C.; Stephanou, P.S.; Mavrantzas, V.G. Melt structure and dynamics of unentangled polyethylene rings: Rouse theory, atomistic molecular dynamics simulation, and comparison with the linear analogues. Macromolecules 2010, 43, 10692–10713. [Google Scholar] [CrossRef]
- Vettorel, T.; Grosberg, A.Y.; Kremer, K. Statistics of polymer rings in the melt: A numerical simulation study. Phys. Biol. 2009, 6, 025013. [Google Scholar] [CrossRef]
- Vettorel, T.; Reigh, S.Y.; Yoon, D.Y.; Kremer, K. Monte-Carlo method for simulations of ring polymers in the melt. Macromol. Rapid Commun. 2009, 30, 345–351. [Google Scholar] [CrossRef] [PubMed]
- Parisi, D.; Ahn, J.; Chang, T.; Vlassopoulos, D.; Rubinstein, M. Stress relaxation in symmetric ring-linear polymer blends at low ring fractions. Macromolecules 2020, 53, 1685–1693. [Google Scholar] [CrossRef]
- Tsalikis, D.G.; Koukoulas, T.; Mavrantzas, V.G.; Pasquino, R.; Vlassopoulos, D.; Pyckhout-Hintzen, W.; Wischnewski, A.; Monkenbusch, M.; Richter, D. Microscopic structure, conformation, and dynamics of ring and linear poly(ethylene oxide) melts from detailed atomistic molecular dynamics simulations: Dependence on chain length and direct comparison with experimental data. Macromolecules 2017, 50, 2565–2584. [Google Scholar] [CrossRef]
- Hur, K.; Winkler, R.G.; Yoon, D.Y. Comparison of ring and linear polyethylene from molecular dynamics simulations. Macromolecules 2006, 39, 3975–3977. [Google Scholar] [CrossRef]
- Pakula, T.; Geyler, S. Cooperative relaxations in condensed macromolecular systems. 3. Computer-simulated melts of cyclic polymers. Macromolecules 1988, 21, 1665–1670. [Google Scholar] [CrossRef]
- Brown, S.; Szamel, G. Structure and dynamics of ring polymers. J. Chem. Phys. 1998, 108, 4705–4708. [Google Scholar] [CrossRef]
- Mo, J.; Wang, J.; Wang, Z.; Lu, Y.; An, L. Size and dynamics of a tracer ring polymer embedded in a linear polymer chain melt matrix. Macromolecules 2022, 55, 1505–1514. [Google Scholar] [CrossRef]
- Mo, J.; Wang, Z.; Lu, Y.; An, L. Size and Dynamics of Ring Polymers under Different Topological Constraints. Chin. J. Polym. Sci. 2022, 41, 516–524. [Google Scholar] [CrossRef]
- Obukhov, S.P.; Rubinstein, M.; Duke, T. Dynamics of a ring polymer in a gel. Phys. Rev. Lett. 1994, 73, 1263–1266. [Google Scholar] [CrossRef]
- Grosberg, A.; Rabin, Y.; Havlin, S.; Neer, A. Crumpled globule model of the three-dimensional structure of DNA. Europhys. Lett. 1993, 23, 373. [Google Scholar] [CrossRef]
- Grosberg, A.Y.; Nechaev, S.K.; Shakhnovich, E.I. The role of topological constraints in the kinetics of collapse of macromolecules. J. Phys. Fr. 1988, 49, 2095–2100. [Google Scholar] [CrossRef]
- Khokhlov, A.R.; Nechaev, S.K. Polymer chain in an array of obstacles. Phys. Lett. A 1985, 112, 156–160. [Google Scholar] [CrossRef]
- Lang, M. Ring conformations in bidisperse blends of ring polymers. Macromolecules 2013, 46, 1158–1166. [Google Scholar] [CrossRef]
- Tang, J.; Du, N.; Doyle, P.S. Compression and self-entanglement of single DNA molecules under uniform electric field. Proc. Natl. Acad. Sci. USA 2011, 108, 16153–16158. [Google Scholar] [CrossRef] [PubMed]
- Christian, T.; Sakaguchi, R.; Perlinska, A.P.; Lahoud, G.; Ito, T.; Taylor, E.A.; Yokoyama, S.; Sulkowska, J.I.; Hou, Y.-M. Methyl transfer by substrate signaling from a knotted protein fold. Nat. Struct. Mol. Biol. 2016, 23, 941–948. [Google Scholar] [CrossRef]
- Rosa, A.; Di Ventra, M.; Micheletti, C. Topological Jamming of Spontaneously Knotted Polyelectrolyte Chains Driven Through a Nanopore. Phys. Rev. Lett. 2012, 109, 118301. [Google Scholar] [CrossRef]
- Arai, Y.; Yasuda, R.; Akashi, K.-i.; Harada, Y.; Miyata, H.; Kinosita, K.; Itoh, H. Tying a molecular knot with optical tweezers. Nature 1999, 399, 446–448. [Google Scholar] [CrossRef]
- Deguchi, T.; Tsurusaki, K. A Statistical Study of Random Knotting Using the Vassiliev Invariants. J. Knot Theory Its Ramif. 1994, 3, 321–353. [Google Scholar] [CrossRef]
- Deguchi, T.; Tsurusaki, K. Universality of random knotting. Phys. Rev. E 1997, 55, 6245–6248. [Google Scholar] [CrossRef]
- Moore, N.T.; Lua, R.C.; Grosberg, A.Y. Topologically driven swelling of a polymer loop. Proc. Natl. Acad. Sci. USA 2004, 101, 13431–13435. [Google Scholar] [CrossRef] [PubMed]
- Shaffer, J.S. Effects of chain topology on polymer dynamics: Bulk melts. J. Chem. Phys. 1994, 101, 4205–4213. [Google Scholar] [CrossRef]
- Shaffer, J.S. Effects of chain topology on polymer dynamics: Configurational relaxation in polymer melts. J. Chem. Phys. 1995, 103, 761–772. [Google Scholar] [CrossRef]
- Carmesin, I.; Kremer, K. The bond fluctuation method: A new effective algorithm for the dynamics of polymers in all spatial dimensions. Macromolecules 1988, 21, 2819–2823. [Google Scholar] [CrossRef]
- Shaffer, J.S. Dynamics of confined polymer melts: Topology and entanglement. Macromolecules 1996, 29, 1010–1013. [Google Scholar] [CrossRef]
- Brown, S.; Szamel, G. Computer simulation study of the structure and dynamics of ring polymers. J. Chem. Phys. 1998, 109, 6184–6192. [Google Scholar] [CrossRef]
- Yang, Y.; Sun, Z.; Fu, C.; An, L.; Wang, Z.-G. Monte Carlo simulation of a single ring among linear chains: Structural and dynamic heterogeneity. J. Chem. Phys. 2010, 133, 064901. [Google Scholar] [CrossRef]
- Wang, J.; Song, J.; Lu, Y.; Ruan, Y.; An, L. Phase behavior and interfacial properties of diblock copolymer-homopolymer ternary mixtures: Influence of volume fraction of copolymers and interaction energy. Chin. J. Polym. Sci. 2017, 35, 874–886. [Google Scholar] [CrossRef]
- Subramanian, G.; Shanbhag, S. Self-diffusion in binary blends of cyclic and linear polymers. Macromolecules 2008, 41, 7239–7242. [Google Scholar] [CrossRef]
- Subramanian, G.; Shanbhag, S. Conformational properties of blends of cyclic and linear polymer melts. Phys. Rev. E 2008, 77, 011801. [Google Scholar] [CrossRef]
- Shanbhag, S. Unusual dynamics of ring probes in linear matrices. J. Polym. Sci. Part B Polym. Phys. 2017, 55, 169–177. [Google Scholar] [CrossRef]
- Paul, W.; Binder, K.; Heermann, D.W.; Kremer, K. Dynamics of polymer solutions and melts. reptation predictions and scaling of relaxation times. J. Chem. Phys. 1991, 95, 7726–7740. [Google Scholar] [CrossRef]
- Rolfsen, D. Knots and Links; American Mathematical Society: Providence, RI, USA, 1976. [Google Scholar]
- Micheletti, C.; Marenduzzo, D.; Orlandini, E. Polymers with spatial or topological constraints: Theoretical and computational results. Phys. Rep. 2011, 504, 1–73. [Google Scholar] [CrossRef]
- Koniaris, K.; Muthukumar, M. Knottedness in ring polymers. Phys. Rev. Lett. 1991, 66, 2211–2214. [Google Scholar] [CrossRef]
- Dai, L.; Doyle, P.S. Universal Knot Spectra for Confined Polymers. Macromolecules 2018, 51, 6327–6333. [Google Scholar] [CrossRef]
- Mansfield, M.L.; Douglas, J.F. Properties of knotted ring polymers. I. Equilibrium dimensions. J. Chem. Phys. 2010, 133, 044903. [Google Scholar] [CrossRef] [PubMed]
| Interchain Constraint Contribution Finter | Intrachain Constraint Contribution Fintra | Scaling Exponents ν | |
|---|---|---|---|
| Cates and Deutsch [12] | 2/5 | ||
| Suzuki et al. [19] | 1/3 | ||
| Sakaue [17,18] | 1/2 2/5~1/3 | ||
| Lang et al. [15,36] | 2/5 | ||
| 3/8 | |||
| 4/9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mo, J.; Guo, J.; Yu, X.; Yang, J.; Hu, G.; Xin, J.; Yan, M.; Wang, Y.; Mo, Y.; Jia, Y.; et al. Chain Size and Knots of Ring Polymers in All-Crossing and Intra-Crossing Melts. Polymers 2025, 17, 854. https://doi.org/10.3390/polym17070854
Mo J, Guo J, Yu X, Yang J, Hu G, Xin J, Yan M, Wang Y, Mo Y, Jia Y, et al. Chain Size and Knots of Ring Polymers in All-Crossing and Intra-Crossing Melts. Polymers. 2025; 17(7):854. https://doi.org/10.3390/polym17070854
Chicago/Turabian StyleMo, Jiangyang, Jingqiao Guo, Xue Yu, Jianlei Yang, Guodong Hu, Jianhui Xin, Mengxia Yan, Yuan Wang, Yongjie Mo, Yuxi Jia, and et al. 2025. "Chain Size and Knots of Ring Polymers in All-Crossing and Intra-Crossing Melts" Polymers 17, no. 7: 854. https://doi.org/10.3390/polym17070854
APA StyleMo, J., Guo, J., Yu, X., Yang, J., Hu, G., Xin, J., Yan, M., Wang, Y., Mo, Y., Jia, Y., Wu, L., & Ruan, Y. (2025). Chain Size and Knots of Ring Polymers in All-Crossing and Intra-Crossing Melts. Polymers, 17(7), 854. https://doi.org/10.3390/polym17070854





