Metamortar Composites Reinforced with Re-Entrant Auxetic Cells: Mechanical Performance and Enhanced Energy Absorption
Abstract
1. Introduction
2. Materials and Methods
2.1. Auxetic Structures Manufactured with an FDM System
2.2. Experimental Testing
2.3. Specific Energy Absorption
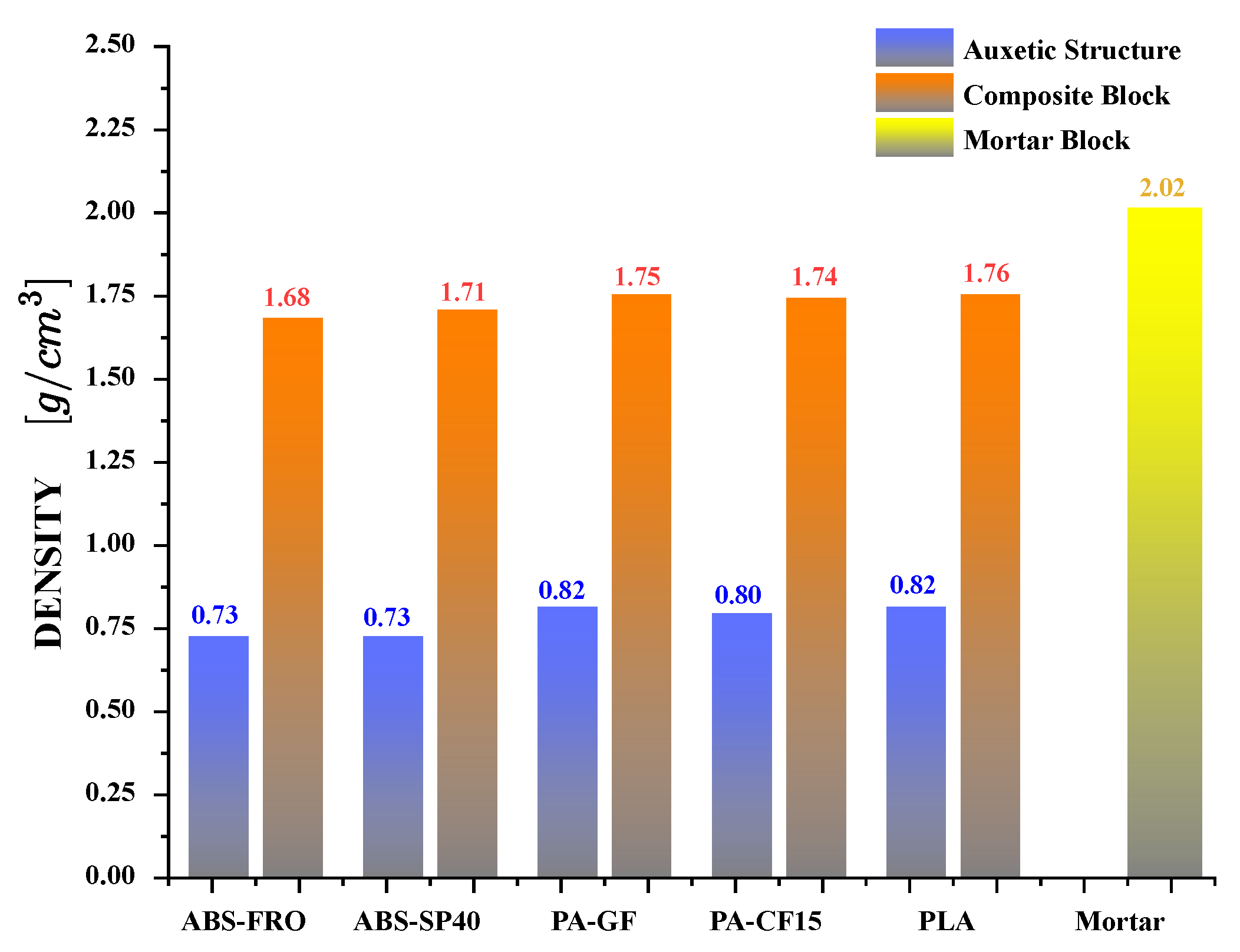
3. Results and Discussion
4. Conclusions
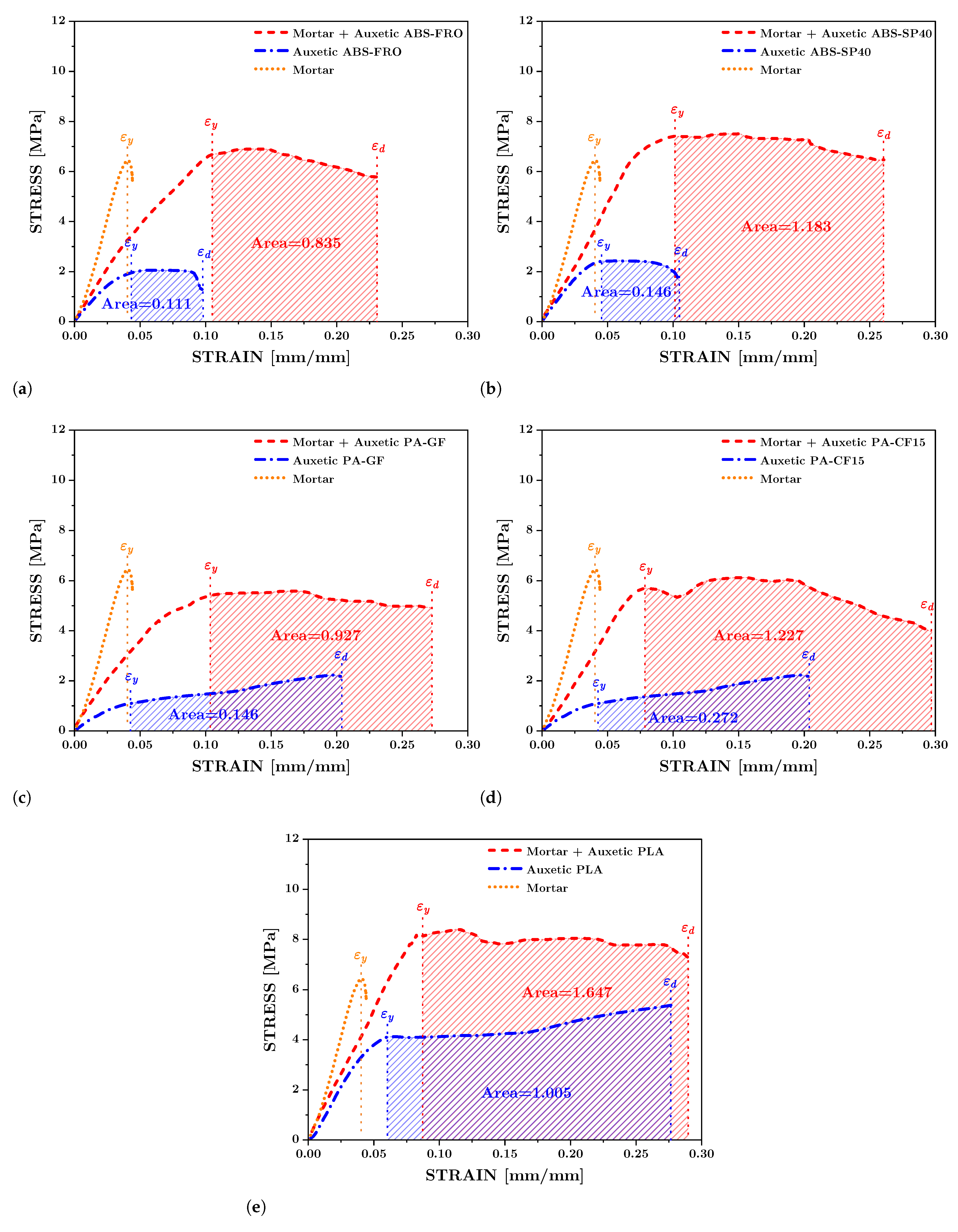
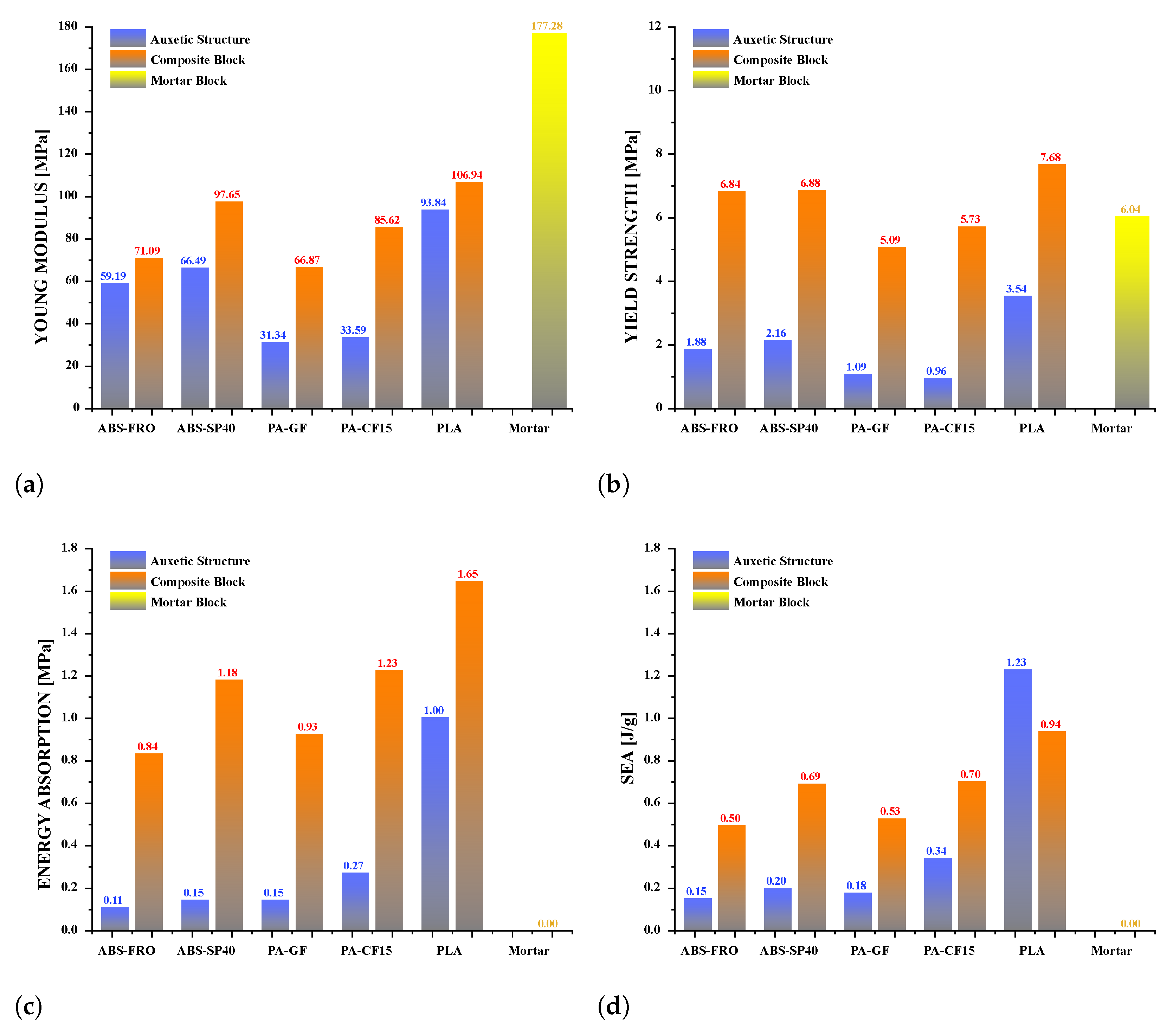
- The inclusion of auxetic structures significantly enhanced the energy dissipation capacity of the mortar. The most effective reinforcement was the -based structure, which achieved an energy absorption of 1.56 MPa, representing a 78% increase compared to plain mortar.
- While plain mortar exhibited brittle failure at 4.4% strain, the auxetic composites demonstrated superior ductility, achieving failure strains between 23% and 30%. This confirms that the auxetic core effectively delays catastrophic failure.
- As expected, the introduction of the polymeric core reduced the Young’s modulus of the composite by 39% to 62% compared to pure mortar. However, the yield strength was largely maintained, with composites showing a 27% increase in yield strength.
- Among the five filaments tested, provided the optimal balance between stiffness and ductility for this specific application, outperforming the carbon-fiber- and glass-fiber-reinforced polyamides (-, -), which proved too stiff to fully exploit the auxetic deformation mechanism before matrix failure.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, T.; Wang, L. Bending behavior of sandwich composite structures with tunable 3D-printed core materials. Compos. Struct. 2017, 175, 46–57. [Google Scholar] [CrossRef]
- Ríos, I.; Duchêne, L.; Habraken, A.M.; Oñate, A.; Valle, R.; Mertens, A.; Garrido, C.; Pincheira, G.; Tuninetti, V. Compressive Behavior of 316L Stainless Steel Lattice Structures for Additive Manufacturing: Experimental Characterization and Numerical Modeling. Biomimetics 2025, 10, 680. [Google Scholar] [CrossRef]
- Tuninetti, V.; Castro, J.; Valle, R.; Bustos, F.; Saggionetto, E.; Garrido, C.; Oñate, A.; Salas, A.; Medina, C.; Pincheira, G.; et al. Ultra-High Damping Efficiency in LPBF Kelvin Metamaterials for Hysteretic Applications. Adv. Eng. Mater. 2025, in press. [Google Scholar] [CrossRef]
- Wang, L.; Sun, J.; Ding, T.; Liang, Y.; Ho, J.; Lai, M. Manufacture and behaviour of innovative 3D printed auxetic composite panels subjected to low-velocity impact load. Structures 2022, 38, 910–933. [Google Scholar] [CrossRef]
- Korkmaz, M.E.; Gupta, M.K.; Robak, G.; Moj, K.; Krolczyk, G.M.; Kuntoğlu, M. Development of lattice structure with selective laser melting process: A state of the art on properties, future trends and challenges. J. Manuf. Processes 2022, 81, 1040–1063. [Google Scholar] [CrossRef]
- Han, Y.; Lu, W. Evolutionary design of nonuniform cellular structures with optimized Poisson’s ratio distribution. Mater. Des. 2018, 141, 384–394. [Google Scholar] [CrossRef]
- Harris, J.; Winter, R.; McShane, G. Impact response of additively manufactured metallic hybrid lattice materials. Int. J. Impact Eng. 2017, 104, 177–191. [Google Scholar] [CrossRef]
- Ufodike, C.O.; Ahmed, M.F.; Dolzyk, G. Additively manufactured biomorphic cellular structures inspired by wood microstructure. J. Mech. Behav. Biomed. Mater. 2021, 123, 104729. [Google Scholar] [CrossRef] [PubMed]
- Castro, J.; Valle, R.; Leiva, J.; Oñate, A.; Saggionetto, E.; Mertens, A.; Tuninetti, V. Density-Based Topology-Optimized 3D-Printed Fixtures for Cyclic Mechanical Testing of Lattice Structures. Polymers 2025, 17, 2468. [Google Scholar] [CrossRef]
- Tuninetti, V.; Narayan, S.; Ríos, I.; Menacer, B.; Valle, R.; Al-lehaibi, M.; Kaisan, M.U.; Samuel, J.; Oñate, A.; Pincheira, G.; et al. Biomimetic Lattice Structures Design and Manufacturing for High Stress, Deformation, and Energy Absorption Performance. Biomimetics 2025, 10, 458. [Google Scholar] [CrossRef]
- Narayan, S.; Menacer, B.; Kaisan, M.U.; Samuel, J.; Al-Lehaibi, M.; Mahroogi, F.O.; Tuninetti, V. Global Research Trends in Biomimetic Lattice Structures for Energy Absorption and Deformation: A Bibliometric Analysis (2020–2025). Biomimetics 2025, 10, 477. [Google Scholar] [CrossRef]
- Egan, P.F.; Khatri, N.R.; Parab, M.A.; Arefin, A.M.E. Mechanics of 3D-Printed Polymer Lattices with Varied Design and Processing Strategies. Polymers 2022, 14, 5515. [Google Scholar] [CrossRef]
- Bustihan, A.; Botiz, I.; Branco, R.; Martins, R.F. Enhancing Mechanical Energy Absorption of Honeycomb and Triply Periodic Minimal Surface Lattice Structures Produced by Fused Deposition Modelling in Reusable Polymers. Polymers 2025, 17, 1111. [Google Scholar] [CrossRef]
- Wang, Z.; Xu, M.; Du, J.; Jin, Y. Experimental and Numerical Investigation of Polymer-Based 3D-Printed Lattice Structures with Largely Tunable Mechanical Properties Based on Triply Periodic Minimal Surface. Polymers 2024, 16, 711. [Google Scholar] [CrossRef]
- Széles, L.; Horváth, R.; Cveticanin, L. Analysis of Mechanical Properties and Parameter Dependency of Novel, Doubly Re-Entrant Auxetic Honeycomb Structures. Polymers 2024, 16, 2524. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Shi, B.Q.; Wang, B.; Yu, G.Q. Crushing Response and Optimization of a Modified 3D Re-Entrant Honeycomb. Materials 2024, 17, 2083. [Google Scholar] [CrossRef]
- Baroutaji, A.; Nikkhah, H.; Arjunan, A.; Pirmohammad, S.; Robinson, J. In-Plane Compressive Responses of Non-Homogenous Re-Entrant Honeycombs Fabricated by Fused Deposition Modelling. Micromachines 2024, 15, 694. [Google Scholar] [CrossRef]
- Tashkinov, M.; Tarasova, A.; Vindokurov, I.; Silberschmidt, V.V. Composites with Re-Entrant Lattice: Effect of Filler on Auxetic Behaviour. Polymers 2023, 15, 4076. [Google Scholar] [CrossRef]
- Plewa, J.; Płońska, M.; Feliksik, K.; Junak, G. Experimental Study of Auxetic Structures Made of Re-Entrant (“Bow-Tie”) Cells. Materials 2024, 17, 3061. [Google Scholar] [CrossRef] [PubMed]
- Gao, D.; Zhang, J.; Zhang, C.; You, Y. Dynamic Compressive and Flexural Behaviour of Re-Entrant Auxetics: A Numerical Study. Materials 2023, 16, 5219. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y.; Kim, Y.; Libonati, F.; Ryu, S. Designing tough isotropic structural composite using computation, 3D printing and testing. Compos. Part B Eng. 2019, 167, 736–745. [Google Scholar] [CrossRef]
- Wang, S.; Wang, Y.; Yu, F.; Yang, Y.; Huang, Z.; Ding, Y. Evaluation of in-plane crushing performance of printed randomly polymeric honeycombs filled with foamed concrete. Constr. Build. Mater. 2021, 310, 125291. [Google Scholar] [CrossRef]
- Maj, M.; Ubysz, A. The reasons for the loss of polyurea coatings adhesion to the concrete substrate in chemically aggressive water tanks. Eng. Fail. Anal. 2022, 142, 106774. [Google Scholar] [CrossRef]
- Zhao, G.; Fan, Y.; Tang, C.; Wei, Y.; Hao, W. Preparation and compressive properties of cementitious composites reinforced by 3D printed cellular structures with a negative Poisson’s ratio. Dev. Built Environ. 2024, 17, 100362. [Google Scholar] [CrossRef]
- Donoghue, J.P.; Alderson, K.L.; Evans, K.E. The fracture toughness of composite laminates with a negative Poisson’s ratio. Phys. Status Solidi (B) 2009, 246, 2011–2017. [Google Scholar] [CrossRef]
- Li, C.F.; Chen, G.P.; Zhu, S.W. Study on the properties of straw fiber reinforced cement-based composite. Appl. Mech. Mater. 2013, 368, 997–1000. [Google Scholar] [CrossRef]
- Zhang, J.; Lu, G.; You, Z. Large deformation and energy absorption of additively manufactured auxetic materials and structures: A review. Compos. Part B Eng. 2020, 201, 108340. [Google Scholar] [CrossRef]
- Zhu, X.F.; Lv, D.W. Application and research of high-strength steel fiber reinforced concrete in a project. Adv. Mater. Res. 2011, 261, 436–440. [Google Scholar] [CrossRef]
- Tayfur, S.; Alver, N.; Abdi, S.; Saatcı, S.; Ghiami, A. Characterization of concrete matrix/steel fiber de-bonding in an SFRC beam: Principal component analysis and k-mean algorithm for clustering AE data. Eng. Fract. Mech. 2018, 194, 73–85. [Google Scholar] [CrossRef]
- Liu, J.; Jia, Y.; Wang, J. Experimental study on mechanical and durability properties of glass and polypropylene fiber reinforced concrete. Fibers Polym. 2019, 20, 1900–1908. [Google Scholar] [CrossRef]
- Enfedaque, A.; Alberti, M.G.; Gálvez, J.C. Analysis of the Versatility of Multi-Linear Softening Functions Applied in the Simulation of Fracture Behaviour of Fibre-Reinforced Cementitious Materials. Materials 2019, 12, 3656. [Google Scholar] [CrossRef]
- Kizilkanat, A.B. Experimental evaluation of mechanical properties and fracture behavior of carbon fiber reinforced high strength concrete. Period. Polytech. Civ. Eng. 2016, 60, 289–296. [Google Scholar] [CrossRef]
- Heo, G.H.; Park, J.G.; Seo, D.J.; Jun, H.M.; Koh, S.G. An Experimental Investigation on the Mechanical Properties including Strength and Flexural Toughness of Mortar Reinforced with Steel-Carbon Hybrid Fibers. Adv. Civ. Eng. 2021, 2021, 8618716. [Google Scholar] [CrossRef]
- De Schutter, G.; Lesage, K.; Mechtcherine, V.; Nerella, V.N.; Habert, G.; Agusti-Juan, I. Vision of 3D printing with concrete—Technical, economic and environmental potentials. Cem. Concr. Res. 2018, 112, 25–36. [Google Scholar] [CrossRef]
- Chen, M.; Chen, Z.; Xuan, Y.; Zhang, T.; Zhang, M. Static and dynamic compressive behaviour of 3D printed auxetic lattice reinforced ultra-high performance concrete. Cem. Concr. Compos. 2023, 139, 105046. [Google Scholar] [CrossRef]
- Vitalis, T.; Gross, A.; Tzortzinis, G.; Schagen, B.; Gerasimidis, S. Enhancing mortar composite matrices with three-dimensional auxetic truss lattice materials for reinforced concrete structures. Constr. Build. Mater. 2024, 457, 139165. [Google Scholar] [CrossRef]
- Luo, C.; Ren, X.; Han, D.; Zhang, X.G.; Zhong, R.; Zhang, X.Y.; Xie, Y.M. A novel concrete-filled auxetic tube composite structure: Design and compressive characteristic study. Eng. Struct. 2022, 268, 114759. [Google Scholar] [CrossRef]
- Tzortzinis, G.; Gross, A.; Gerasimidis, S. Auxetic boosting of confinement in mortar by 3D reentrant truss lattices for next generation steel reinforced concrete members. Extrem. Mech. Lett. 2022, 52, 101681. [Google Scholar] [CrossRef]
- Andrew, J.J.; Ubaid, J.; Hafeez, F.; Schiffer, A.; Kumar, S. Impact performance enhancement of honeycombs through additive manufacturing-enabled geometrical tailoring. Int. J. Impact Eng. 2019, 134, 103360. [Google Scholar] [CrossRef]
- Li, T.; Jarrar, F.; Abu Al-Rub, R.; Cantwell, W. Additive manufactured semi-plate lattice materials with high stiffness, strength and toughness. Int. J. Solids Struct. 2021, 230–231, 111153. [Google Scholar] [CrossRef]
- J, J.A.; Schneider, J.; Schiffer, A.; Hafeez, F.; Kumar, S. Dynamic crushing of tailored honeycombs realized via additive manufacturing. Int. J. Mech. Sci. 2022, 219, 107126. [Google Scholar] [CrossRef]
- Garner, E.; Kolken, H.M.; Wang, C.C.; Zadpoor, A.A.; Wu, J. Compatibility in microstructural optimization for additive manufacturing. Addit. Manuf. 2019, 26, 65–75. [Google Scholar] [CrossRef]
- Li, T.; Chen, Y.; Hu, X.; Li, Y.; Wang, L. Exploiting negative Poisson’s ratio to design 3D-printed composites with enhanced mechanical properties. Mater. Des. 2018, 142, 247–258. [Google Scholar] [CrossRef]
- Alkhader, M.; Vural, M. Mechanical response of cellular solids: Role of cellular topology and microstructural irregularity. Int. J. Eng. Sci. 2008, 46, 1035–1051. [Google Scholar] [CrossRef]
- Chen, Y.; Li, T.; Jia, Z.; Scarpa, F.; Yao, C.W.; Wang, L. 3D printed hierarchical honeycombs with shape integrity under large compressive deformations. Mater. Des. 2018, 137, 226–234. [Google Scholar] [CrossRef]
- Zhang, L.; Song, B.; Zhao, A.; Liu, R.; Yang, L.; Shi, Y. Study on mechanical properties of honeycomb pentamode structures fabricated by laser additive manufacturing: Numerical simulation and experimental verification. Compos. Struct. 2019, 226, 111199. [Google Scholar] [CrossRef]
- Yang, H.; Wang, B.; Ma, L. Mechanical properties of 3D double-U auxetic structures. Int. J. Solids Struct. 2019, 180–181, 13–29. [Google Scholar] [CrossRef]
- Harinarayana, V.; Shin, Y. Design and evaluation of three–dimensional axisymmetric mechanical metamaterial exhibiting negative Poisson’s ratio. J. Mater. Res. Technol. 2022, 19, 1390–1406. [Google Scholar] [CrossRef]
- Sahariah, B.J.; Namdeo, A.; Khanikar, P. Composite-inspired multilattice metamaterial structure: An auxetic lattice design with improved strength and energy absorption. Mater. Today Commun. 2022, 30, 103159. [Google Scholar] [CrossRef]
- Wang, X.T.; Wang, B.; Li, X.W.; Ma, L. Mechanical properties of 3D re-entrant auxetic cellular structures. Int. J. Mech. Sci. 2017, 131–132, 396–407. [Google Scholar] [CrossRef]
- Novak, N.; Biasetto, L.; Rebesan, P.; Zanini, F.; Carmignato, S.; Krstulović-Opara, L.; Vesenjak, M.; Ren, Z. Experimental and computational evaluation of tensile properties of additively manufactured hexa- and tetrachiral auxetic cellular structures. Addit. Manuf. 2021, 45, 102022. [Google Scholar] [CrossRef]
- Pei, L.Z.; Qi, C.; Yang, S.; Ma, Y.H.; Wu, P.C. A hierarchical fabrication method and crushing response of metallic 3D re-entrant honeycomb. Thin-Walled Struct. 2022, 176, 109369. [Google Scholar] [CrossRef]
- Wang, S.; Deng, C.; Ojo, O.; Akinrinlola, B.; Kozub, J.; Wu, N. Design and modeling of a novel three dimensional auxetic reentrant honeycomb structure for energy absorption. Compos. Struct. 2022, 280, 114882. [Google Scholar] [CrossRef]
- Yang, L.; Harrysson, O.; West, H.; Cormier, D. Mechanical properties of 3D re-entrant honeycomb auxetic structures realized via additive manufacturing. Int. J. Solids Struct. 2015, 69–70, 475–490. [Google Scholar] [CrossRef]
- Yang, L.; Harrysson, O.; West, H.; Cormier, D. Compressive properties of Ti–6Al–4V auxetic mesh structures made by electron beam melting. Acta Mater. 2012, 60, 3370–3379. [Google Scholar] [CrossRef]
- Genç, O.K.; Kong, Z.; Keshtegar, B.; Thai, D.K. Blast-Resistant Design of Reinforced Concrete Slabs with Auxetic-Shaped Reinforcement Layout. Buildings 2024, 14, 3392. [Google Scholar] [CrossRef]
- Hematibahar, M.; Hasanzadeh, A.; Kharun, M.; Beskopylny, A.N.; Stel’makh, S.A.; Shcherban’, E.M. The Influence of Three-Dimensionally Printed Polymer Materials as Trusses and Shell Structures on the Mechanical Properties and Load-Bearing Capacity of Reinforced Concrete. Materials 2024, 17, 3413. [Google Scholar] [CrossRef] [PubMed]
- Zhong, R.; Ren, X.; Zhang, X.Y.; Luo, C.; Zhang, Y.; Xie, Y.M. Mechanical properties of concrete composites with auxetic single and layered honeycomb structures. Constr. Build. Mater. 2022, 322, 126453. [Google Scholar] [CrossRef]
- Choudhry, N.K.; Nguyen, T.K.; Nguyen-Van, V.; Panda, B.; Tran, P. Auxetic lattice reinforcement for tailored mechanical properties in cementitious composite: Experiments and modelling. Constr. Build. Mater. 2024, 438, 137252. [Google Scholar] [CrossRef]
- Salazar, B.; Aghdasi, P.; Williams, I.D.; Ostertag, C.P.; Taylor, H.K. Polymer lattice-reinforcement for enhancing ductility of concrete. Mater. Des. 2020, 196, 109184. [Google Scholar] [CrossRef]
- Xu, Y.; Meng, Z.; Bol, R.J.; Šavija, B. Spring-like behavior of cementitious composite enabled by auxetic hyperelastic frame. Int. J. Mech. Sci. 2024, 275, 109364. [Google Scholar] [CrossRef]
- Momoh, E.O.; Jayasinghe, A.; Hajsadeghi, M.; Vinai, R.; Evans, K.E.; Kripakaran, P.; Orr, J. A state-of-the-art review on the application of auxetic materials in cementitious composites. Thin-Walled Struct. 2024, 196, 111447. [Google Scholar] [CrossRef]
- Hematibahar, M.; Milani, A.; Fediuk, R.; Amran, M.; Bakhtiary, A.; Kharun, M.; Mousavi, M.S. Optimization of 3D-printed reinforced concrete beams with four types of reinforced patterns and different distances. Eng. Fail. Anal. 2025, 168, 109096. [Google Scholar] [CrossRef]
- Laureijs, R.E.; Roca, J.B.; Narra, S.P.; Montgomery, C.; Beuth, J.L.; Fuchs, E.R. Metal additive manufacturing: Cost competitive beyond low volumes. J. Manuf. Sci. Eng. 2017, 139, 081010. [Google Scholar] [CrossRef]
- Xu, A.; Saleh, M.; Bhattacharyya, D. Experimental and computational analysis of the in situ tensile deformation of 2D honeycomb lattice structures in Ni single crystals. Compos. Part B Eng. 2020, 186, 107823. [Google Scholar] [CrossRef]
- Xu, F.; Yu, K.; Hua, L. In-plane dynamic response and multi-objective optimization of negative Poisson’s ratio (NPR) honeycomb structures with sinusoidal curve. Compos. Struct. 2021, 269, 114018. [Google Scholar] [CrossRef]
- Nguyen-Van, V.; Liu, J.; Li, S.; Zhang, G.; Nguyen-Xuan, H.; Tran, P. Modelling of 3D-printed bio-inspired Bouligand cementitious structures reinforced with steel fibres. Eng. Struct. 2023, 274, 115123. [Google Scholar] [CrossRef]
- Guo, P.; Zhang, Y.; Xi, Y.; Saleem, K.; El-Meligy, M.; Safarpour, H. Nonlinear transient deflections of multi-layer sector plate structures on auxetic concrete foundation: Introducing an artificial intelligence algorithm for nonlinear problems. Structures 2024, 70, 107563. [Google Scholar] [CrossRef]
- Valle, R.; Pincheira, G.; Tuninetti, V. Design of an auxetic cellular structure with different elastic properties in its three orthogonal directions. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2021, 235, 1341–1350. [Google Scholar] [CrossRef]
- Valle, R.; Pincheira, G.; Tuninetti, V.; Fernandez, E.; Uribe-Lam, E. Design and Characterization of Asymmetric Cell Structure of Auxetic Material for Predictable Directional Mechanical Response. Materials 2022, 15, 1841. [Google Scholar] [CrossRef] [PubMed]
- Valle, R.; Pincheira, G.; Tuninetti, V.; Garrido, C.; Treviño, C.; Morales, J. Evaluation of the Orthotropic Behavior in an Auxetic Structure Based on a Novel Design Parameter of a Square Cell with Re-Entrant Struts. Polymers 2022, 14, 4325. [Google Scholar] [CrossRef]
- Garrido, C.; Pincheira, G.; Valle, R.; Fernández, J.; Tuninetti, V. Plastic deformation behavior and energy absorption performance of a composite metamaterial based on asymmetric auxetic lattices. Compos. Struct. 2024, 346, 118410. [Google Scholar] [CrossRef]
- Wang, Z.; Lei, Z.; Li, Z.; Yuan, K.; Wang, X. Mechanical reinforcement mechanism of a hierarchical Kagome honeycomb. Thin-Walled Struct. 2021, 167, 108235. [Google Scholar] [CrossRef]
- Zamani, M.H.; Heidari-Rarani, M.; Torabi, K. Optimal design of a novel graded auxetic honeycomb core for sandwich beams under bending using digital image correlation (DIC). Compos. Struct. 2022, 286, 115310. [Google Scholar] [CrossRef]
- Zhang, X.c.; Ding, H.m.; An, L.q.; Wang, X.l. Numerical Investigation on Dynamic Crushing Behavior of Auxetic Honeycombs with Various Cell-Wall Angles. Adv. Mech. Eng. 2014, 7, 679678. [Google Scholar] [CrossRef]
- Zhang, H.; Lin, G.; Sun, W. Structural design and tunable mechanical properties of novel corrugated 3D lattice metamaterials by geometric tailoring. Thin-Walled Struct. 2023, 184, 110495. [Google Scholar] [CrossRef]
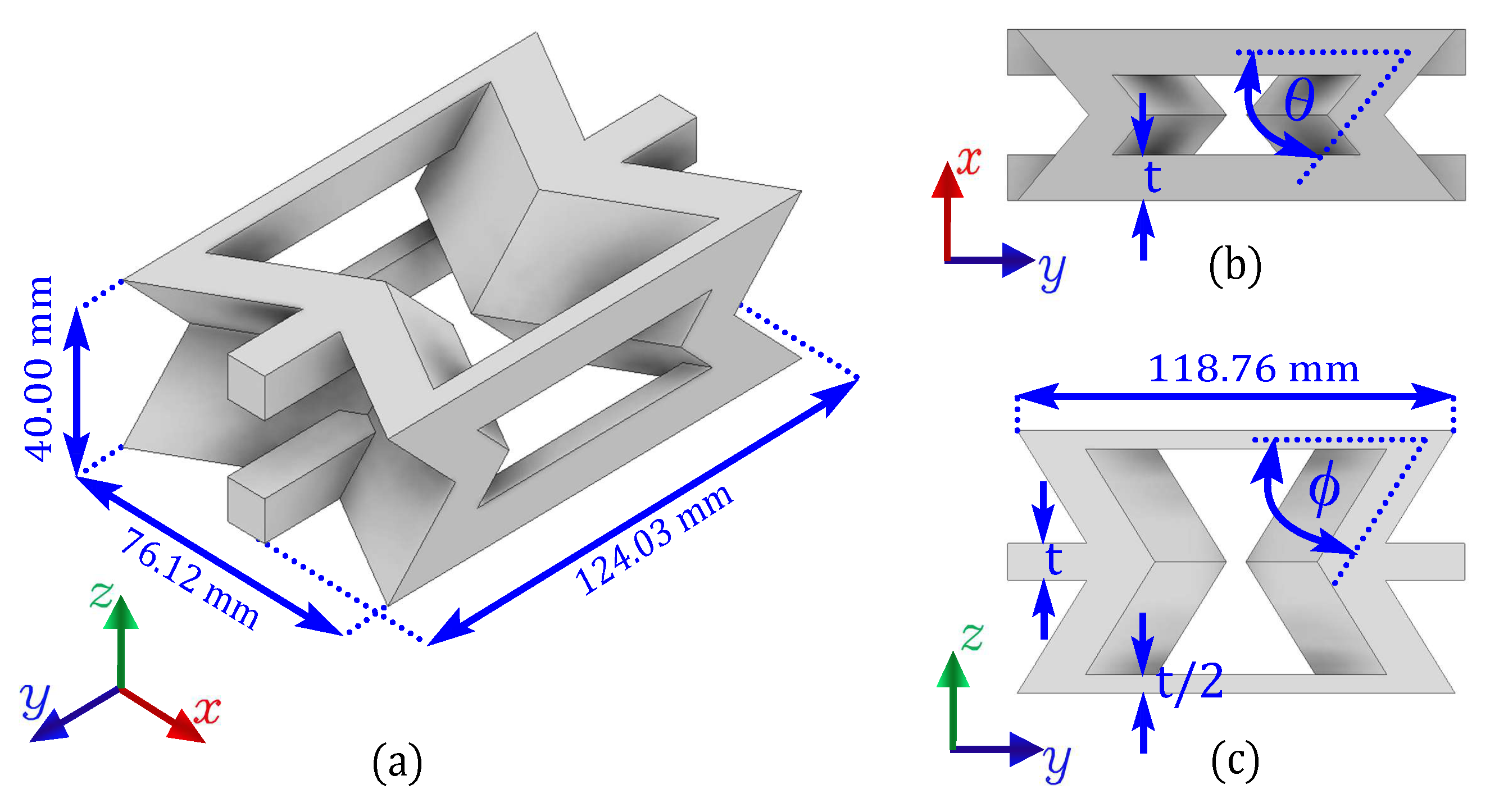



| Filament | Extrusion Temp. [°C] | Bed Temp. [°C] | Refrigeration [%] |
|---|---|---|---|
| 220 | 60 | 100 | |
| - | 235 | 100 | 0 |
| - | 235 | 100 | 0 |
| - | 250 | 100 | 0 |
| - | 250 | 100 | 0 |
| Sample | Maximum Strain | ||
|---|---|---|---|
| Mortar |  | ||
| COMPOSITE BLOCKS |  | ||
 | |||
 | |||
 | |||
 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fernández, J.; Garrido, C.; Muñoz, L.; Nuñez, F.; Valle, R.; Tuninetti, V. Metamortar Composites Reinforced with Re-Entrant Auxetic Cells: Mechanical Performance and Enhanced Energy Absorption. Polymers 2025, 17, 3153. https://doi.org/10.3390/polym17233153
Fernández J, Garrido C, Muñoz L, Nuñez F, Valle R, Tuninetti V. Metamortar Composites Reinforced with Re-Entrant Auxetic Cells: Mechanical Performance and Enhanced Energy Absorption. Polymers. 2025; 17(23):3153. https://doi.org/10.3390/polym17233153
Chicago/Turabian StyleFernández, Jorge, César Garrido, Luis Muñoz, Felipe Nuñez, Rodrigo Valle, and Víctor Tuninetti. 2025. "Metamortar Composites Reinforced with Re-Entrant Auxetic Cells: Mechanical Performance and Enhanced Energy Absorption" Polymers 17, no. 23: 3153. https://doi.org/10.3390/polym17233153
APA StyleFernández, J., Garrido, C., Muñoz, L., Nuñez, F., Valle, R., & Tuninetti, V. (2025). Metamortar Composites Reinforced with Re-Entrant Auxetic Cells: Mechanical Performance and Enhanced Energy Absorption. Polymers, 17(23), 3153. https://doi.org/10.3390/polym17233153






