Simulation of the Melt Conveying Zone of a Single-Screw Extruder for Mixed Polymer Materials Using an Isothermal Analytical Flat Plate Model
Abstract
1. Introduction
2. Materials and Methods
2.1. Production of Polymer Blends
2.2. Acquisition of Input Data for the Simulation
2.2.1. Material Data
2.2.2. Extrusion Experiments
2.3. Simulation of the Melt Conveying Zone
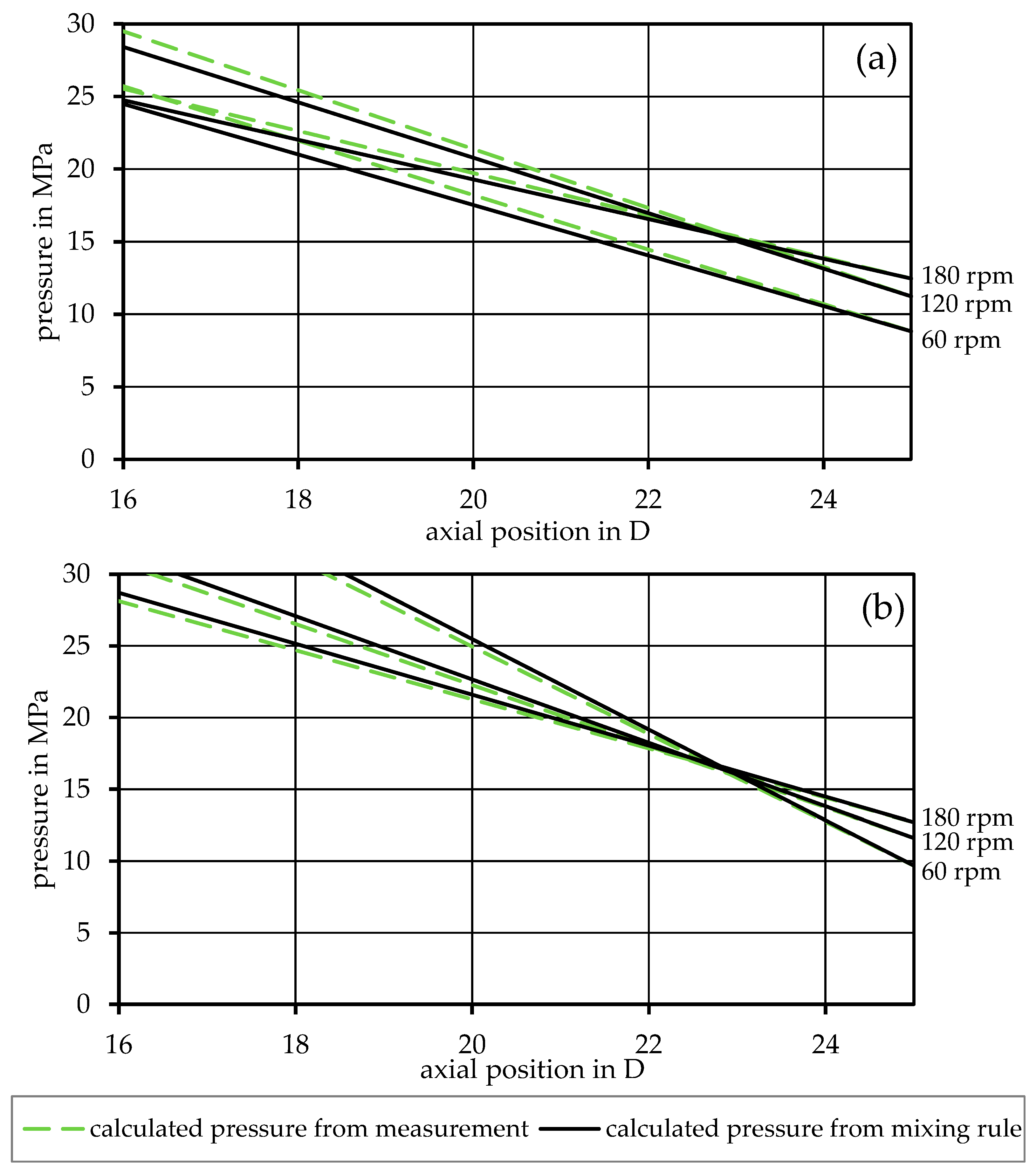
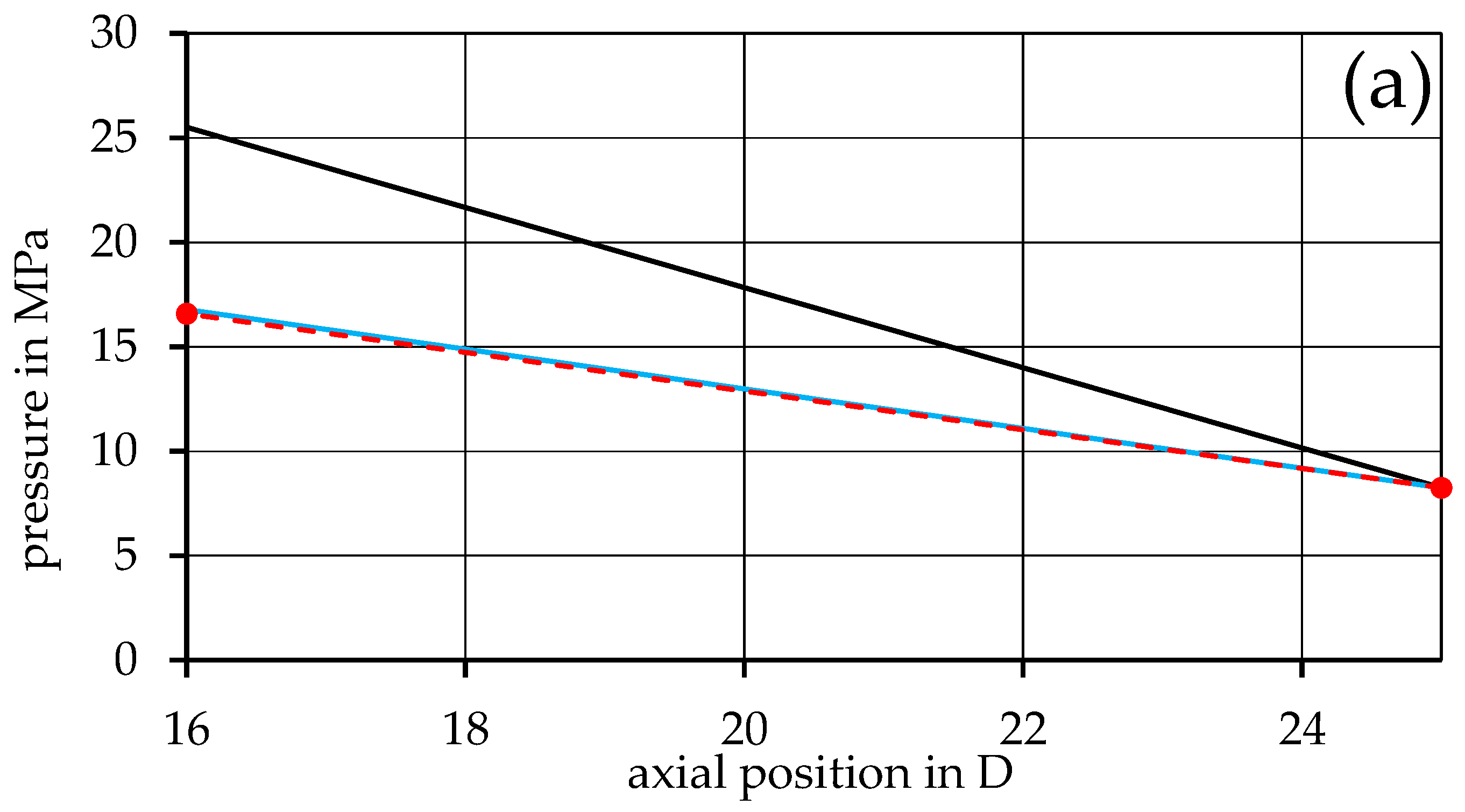
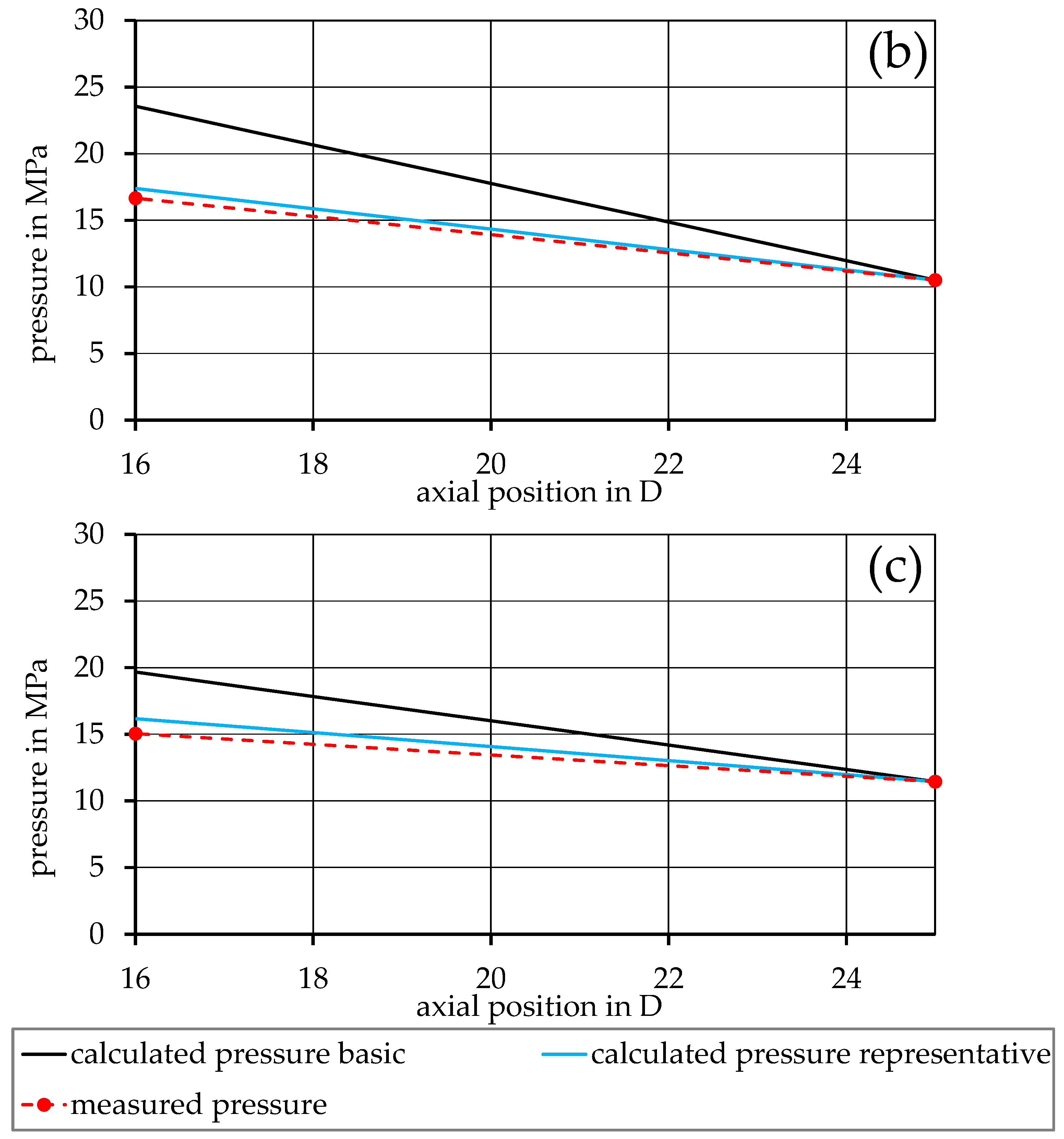
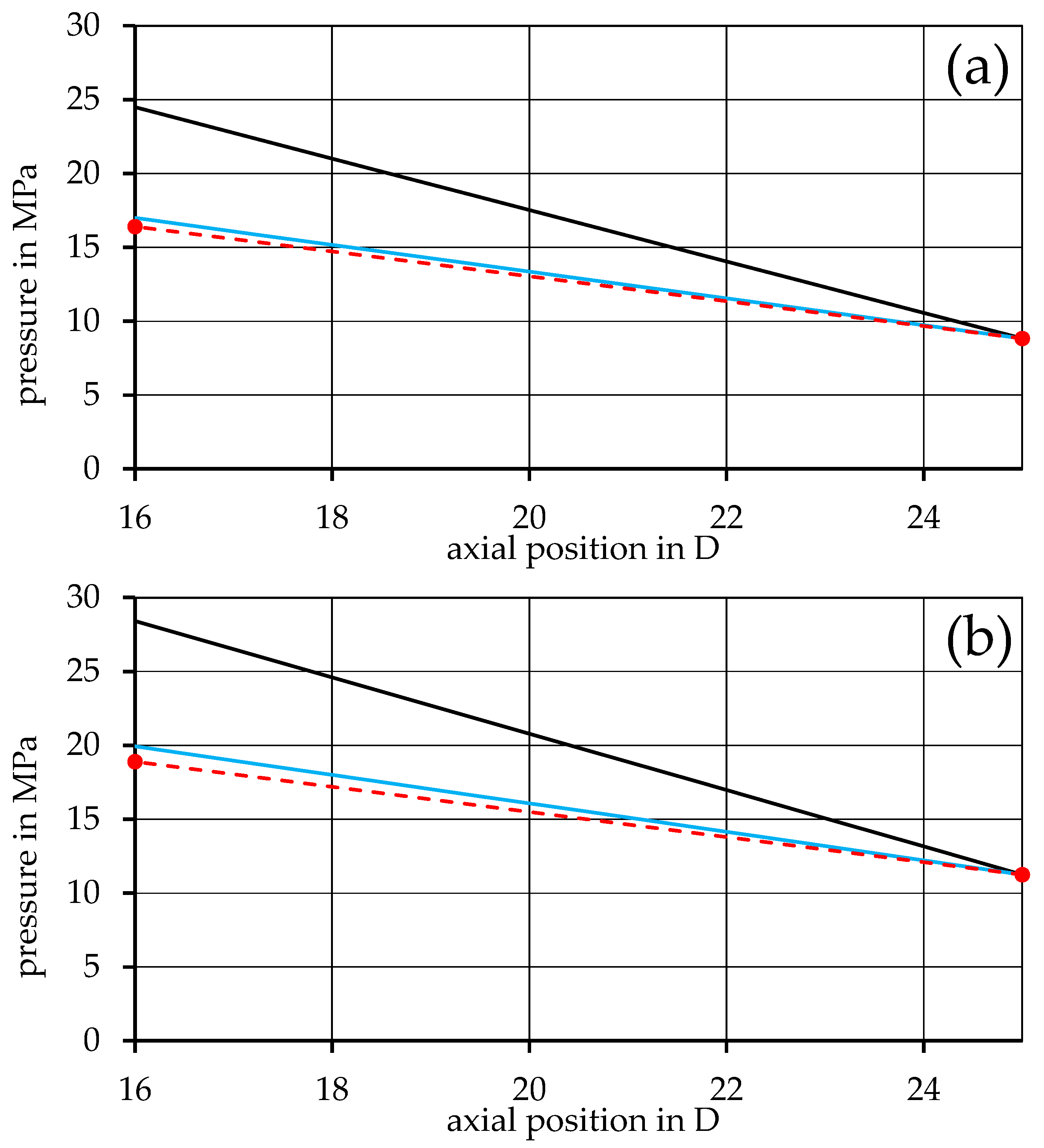
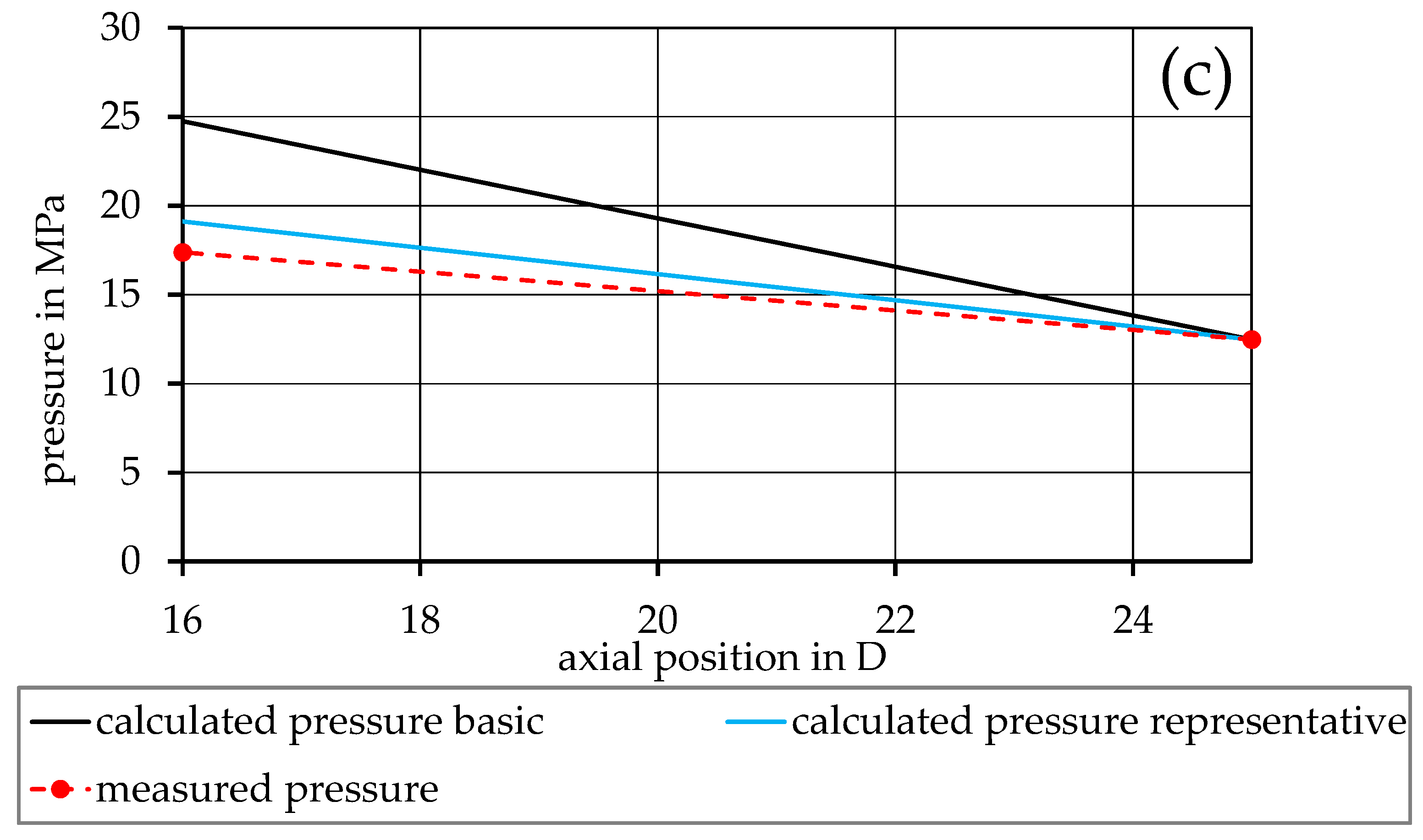
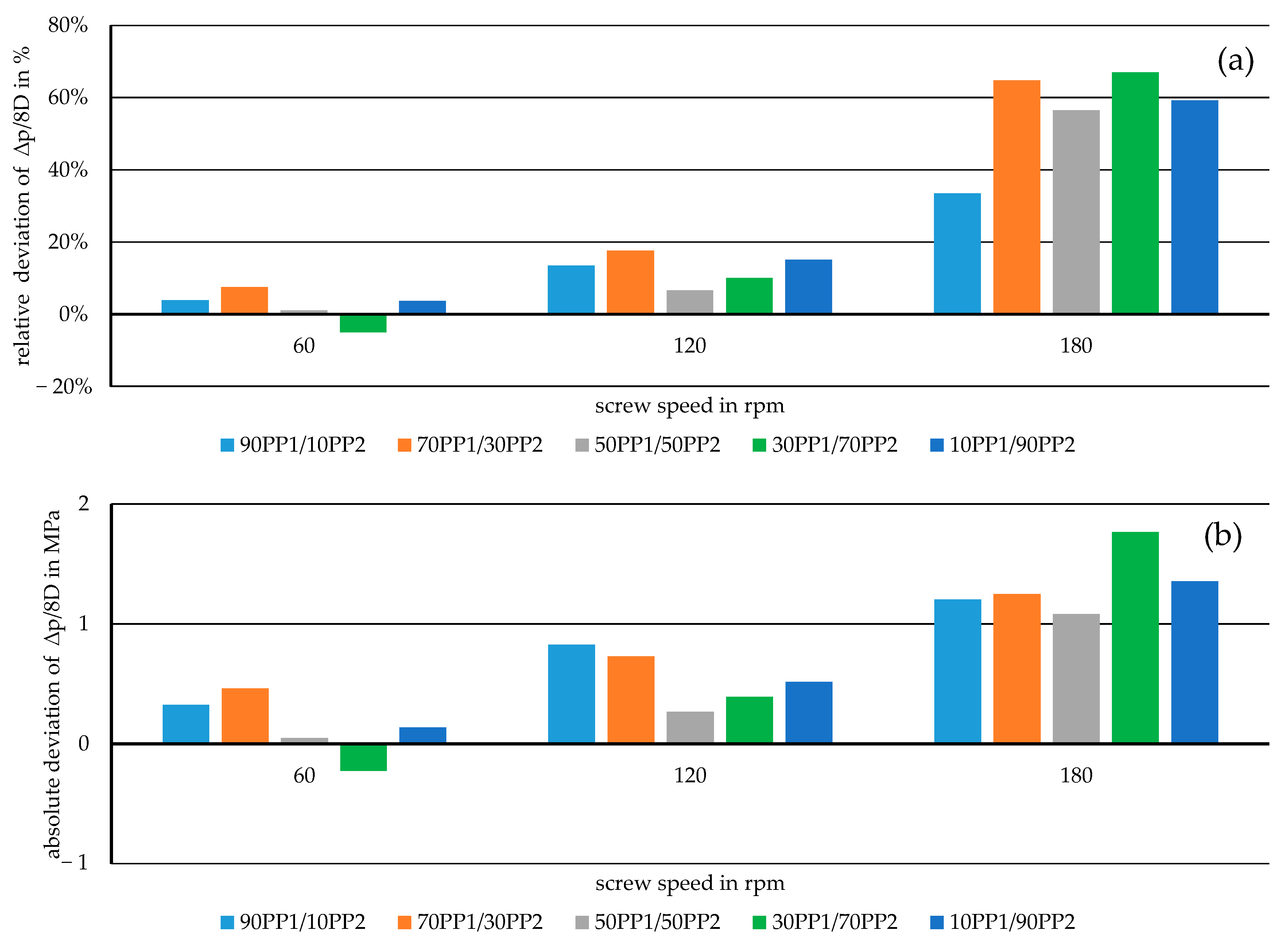
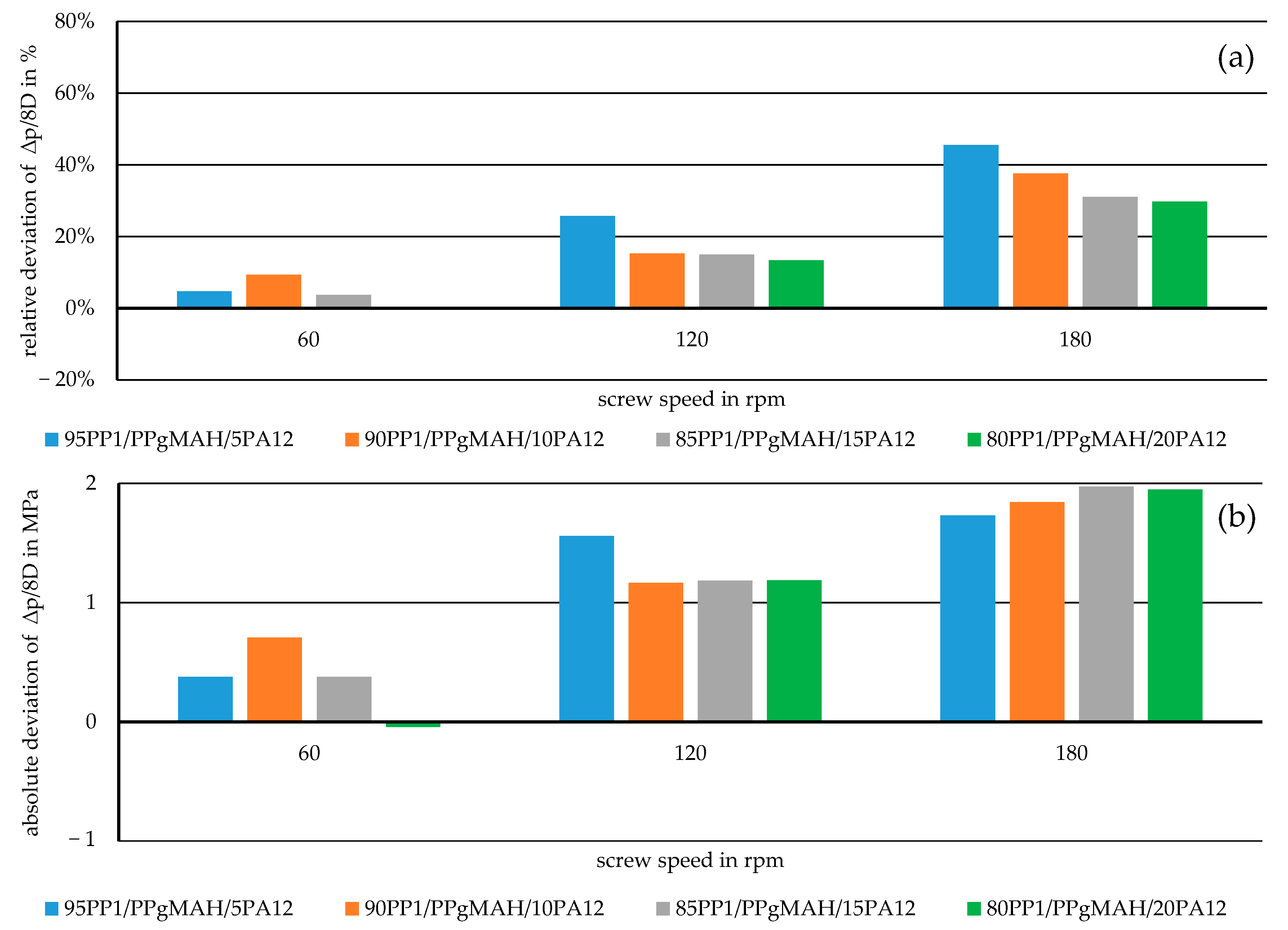
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding

Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| PP1 200 °C | η PP1 200 °C | PP2 200 °C | η PP2 200 °C | PP1 230 °C | η PP1 230 °C | PP2 230 °C | η PP2 230 °C |
|---|---|---|---|---|---|---|---|
| 11.16 | 2232.93 | 10.51 | 1054.75 | 11.04 | 1957.08 | 10.36 | 628.91 |
| 28.65 | 1284.30 | 24.67 | 757.27 | 27.91 | 1183.19 | 23.79 | 518.47 |
| 66.05 | 783.48 | 56.13 | 530.42 | 64.21 | 735.00 | 54.11 | 392.09 |
| 153.17 | 452.61 | 130.53 | 349.94 | 146.25 | 441.12 | 123.19 | 275.21 |
| 341.96 | 260.99 | 308.89 | 208.92 | 331.14 | 258.06 | 285.65 | 178.33 |
| 802.71 | 142.49 | 736.65 | 116.15 | 756.67 | 145.96 | 684.26 | 104.17 |
| 1964.28 | 70.55 | 1742.50 | 61.83 | 1770.23 | 78.27 | 1640.65 | 56.40 |
| 4413.11 | 36.85 | 4085.47 | 32.17 | 4418.68 | 37.98 | 3822.34 | 30.13 |
| 9667.29 | 19.81 | 9461.38 | 16.51 | 11,241.05 | 17.17 | 9015.37 | 15.54 |
| 16,904.08 | 13.21 | 16,742.36 | 10.91 | 19,808.35 | 10.93 | 16,416.06 | 10.04 |
| PP1/PPgMAH 230 °C | η PP1/PPgMAH 230 °C | PA12 230 °C | η PA12 230 °C | PP1/PPgMAH 250 °C | η PP1/PPgMAH 250 °C | PA12 250 °C | η PA12 250 °C |
|---|---|---|---|---|---|---|---|
| 10.38 | 1412.35 | 19.58 | 1585.16 | 10.80 | 1189.36 | 8.24 | 2148.32 |
| 25.99 | 1064.44 | 46.85 | 1523.74 | 25.58 | 814.29 | 17.71 | 1757.46 |
| 61.74 | 652.26 | 108.22 | 1261.41 | 58.83 | 562.47 | 38.64 | 1385.98 |
| 142.06 | 401.29 | 251.82 | 899.55 | 138.02 | 347.63 | 84.95 | 1065.02 |
| 329.13 | 231.52 | 603.50 | 565.40 | 320.93 | 203.55 | 190.67 | 765.44 |
| 757.00 | 130.03 | 1478.09 | 307.94 | 733.86 | 116.28 | 441.92 | 499.65 |
| 1762.59 | 70.03 | 2957.63 | 195.87 | 1676.36 | 64.87 | 1071.40 | 285.17 |
| 4144.25 | 36.18 | 5849.49 | 145.42 | 4007.33 | 33.68 | 2712.68 | 143.32 |
| 12,936.16 | 13.75 | 10,003.69 | 16.01 | 6487.90 | 71.19 | ||
| 36,861.17 | 5.43 | 18,172.23 | 10.08 |
| 90PP1/10PP2 200 °C | η 90PP1/10PP2 200 °C | 70PP1/30PP2 200 °C | η 70PP1/30PP2 200 °C | 50PP1/50PP2 200 °C | η 50PP1/50PP2 200 °C | 30PP1/70PP2 200 °C | η 30PP1/70PP2 200 °C | 10PP1/90PP2 200 °C | η 10PP1/90PP2 200 °C |
|---|---|---|---|---|---|---|---|---|---|
| 22.88 | 1371.27 | 11.08 | 2036.03 | 10.99 | 1611.33 | 22.30 | 975.10 | 22.31 | 794.66 |
| 62.20 | 765.16 | 29.18 | 1167.16 | 25.71 | 1066.53 | 57.64 | 621.41 | 55.52 | 568.03 |
| 147.80 | 443.14 | 65.29 | 710.51 | 60.79 | 723.14 | 135.50 | 387.95 | 133.94 | 355.43 |
| 337.98 | 253.31 | 147.19 | 434.26 | 144.73 | 418.97 | 316.94 | 228.79 | 311.27 | 210.94 |
| 776.74 | 141.21 | 337.98 | 247.99 | 331.32 | 243.59 | 738.55 | 128.72 | 734.70 | 119.15 |
| 1891.64 | 71.79 | 752.22 | 142.51 | 737.86 | 140.87 | 1651.40 | 72.84 | 1700.51 | 64.73 |
| 4404.70 | 36.31 | 1803.28 | 75.34 | 1760.32 | 75.57 | 3908.87 | 38.75 | 3835.44 | 35.59 |
| 12,867.65 | 14.71 | 4386.00 | 36.87 | 4342.20 | 36.75 | 9402.64 | 19.19 | 9026.72 | 18.40 |
| 9910.65 | 19.08 | 10,085.44 | 18.48 | 16,691.30 | 12.67 | 16,470.85 | 11.85 | ||
| 17,179.09 | 12.78 | 17,565.97 | 12.24 |
| 90PP1/10PP2 230 °C | η 90PP1/10PP2 230 °C | 70PP1/30PP2 230 °C | η 70PP1/30PP2 230 °C | 50PP1/50PP2 230 °C | η 50PP1/50PP2 230 °C | 30PP1/70PP2 230 °C | η 30PP1/70PP2 230 °C | 10PP1/90PP2 230 °C | η 10PP1/90PP2 230 °C |
|---|---|---|---|---|---|---|---|---|---|
| 10.88 | 1412.30 | 10.71 | 1234.29 | 10.74 | 1096.01 | 10.33 | 745.83 | 10.20 | 574.38 |
| 26.25 | 923.46 | 25.25 | 869.82 | 24.92 | 772.13 | 23.80 | 619.60 | 23.18 | 506.79 |
| 60.57 | 607.76 | 59.06 | 589.92 | 57.24 | 547.73 | 53.77 | 465.84 | 52.84 | 396.95 |
| 140.42 | 372.61 | 138.58 | 362.04 | 134.65 | 346.85 | 126.85 | 318.33 | 122.06 | 280.86 |
| 323.74 | 218.22 | 319.38 | 213.53 | 310.95 | 207.23 | 301.58 | 192.19 | 288.14 | 179.64 |
| 772.77 | 119.07 | 736.61 | 121.57 | 722.21 | 119.09 | 710.95 | 109.83 | 692.25 | 103.30 |
| 1767.91 | 64.04 | 1708.62 | 66.39 | 1648.27 | 66.48 | 1626.89 | 61.58 | 1615.21 | 57.29 |
| 4077.20 | 34.11 | 3977.52 | 35.10 | 3791.35 | 36.30 | 3753.18 | 33.68 | 3732.45 | 31.27 |
| 9543.84 | 17.27 | 9722.46 | 17.21 | 9331.12 | 17.92 | 8834.44 | 17.44 | 8854.92 | 16.12 |
| 16,823.99 | 11.46 | 17,843.72 | 10.77 | 17,303.28 | 11.19 | 16,007.48 | 11.42 | 16,172.53 | 10.44 |
| 95PP1/PPgMAH/5PA12 230 °C | η 95PP1/PPgMAH/5PA12 230 °C | 90PP1/PPgMAH/10PA12 230 °C | η 90PP1/PPgMAH/10PA12 230 °C | 85PP1/PPgMAH/15PA12 230 °C | η 85PP1/PPgMAH/15PA12 230 °C | 80PP1/PPgMAH/20PA12 230 °C | η 80PP1/PPgMAH/20PA12 230 °C |
|---|---|---|---|---|---|---|---|
| 10.97 | 1564.79 | 10.64 | 1712.37 | 11.07 | 1691.22 | 10.99 | 1807.83 |
| 26.95 | 993.20 | 26.36 | 1192.64 | 26.70 | 1063.02 | 27.52 | 1119.55 |
| 61.29 | 648.47 | 62.53 | 740.10 | 61.57 | 701.99 | 62.70 | 710.60 |
| 142.01 | 395.85 | 144.59 | 444.09 | 143.60 | 418.52 | 142.68 | 435.84 |
| 327.63 | 229.52 | 333.45 | 255.71 | 330.80 | 242.57 | 332.36 | 250.91 |
| 746.47 | 130.55 | 781.32 | 139.96 | 770.16 | 134.08 | 773.87 | 137.79 |
| 1742.62 | 70.70 | 1852.57 | 72.75 | 1773.18 | 72.34 | 1691.48 | 78.38 |
| 4183.34 | 35.84 | 4339.74 | 37.12 | 4056.73 | 38.54 | 3752.81 | 44.31 |
| 11,361.95 | 15.52 | 11,601.36 | 16.27 | 9610.83 | 19.42 | 12,319.38 | 16.63 |
| 22,425.61 | 8.66 | 22,980.69 | 9.02 | 17,343.03 | 12.45 |
| 95PP1/PPgMAH/5PA12 250 °C | η 95PP1/PPgMAH/5PA12 250 °C | 90PP1/PPgMAH/10PA12 250 °C | η 90PP1/PPgMAH/10PA12 250 °C | 85PP1/PPgMAH/15PA12 250 °C | η 85PP1/PPgMAH/15PA12 250 °C | 80PP1/PPgMAH/20PA12 250 °C | η 80PP1/PPgMAH/20PA12 250 °C |
|---|---|---|---|---|---|---|---|
| 10.93 | 1322.41 | 11.02 | 1383.71 | 11.00 | 1451.30 | 10.96 | 1438.56 |
| 26.67 | 854.35 | 26.82 | 874.38 | 26.73 | 923.44 | 26.89 | 917.96 |
| 60.82 | 562.02 | 60.47 | 583.10 | 61.94 | 600.94 | 62.02 | 591.61 |
| 139.29 | 348.70 | 139.53 | 361.31 | 142.24 | 362.84 | 140.62 | 363.69 |
| 320.02 | 206.56 | 320.78 | 212.82 | 320.30 | 217.49 | 315.78 | 220.48 |
| 732.93 | 118.09 | 731.11 | 122.36 | 720.29 | 127.16 | 730.69 | 126.24 |
| 1693.41 | 65.09 | 1707.39 | 66.82 | 1718.32 | 68.64 | 1744.21 | 67.03 |
| 4024.87 | 33.77 | 4100.18 | 34.10 | 4242.49 | 33.72 | 4248.64 | 33.41 |
| 12,306.15 | 13.16 | 10,033.85 | 16.48 | 9871.78 | 16.98 | 9590.90 | 17.31 |
| 31,211.24 | 5.74 | 18,075.70 | 10.47 | 17,178.96 | 11.33 |
References
- EU. European Commission Directive (Eu) 2018/852 of the European Parliament and of the Council of 30 May 2018 Amending 94/62/EC on Packaging and Packaging Waste. Off. J. Eur. Union 2018, 61, 141–154. [Google Scholar]
- Gogos, C.G.; Tadmor, Z. Principles of Polymer Processing; Wiley-Interscience: Hoboken, NJ, USA, 2014. [Google Scholar]
- Rauwendaal, C. Polymer Extrusion, 5th ed.; Carl Hanser Verlag: Munich, Germany, 2014. [Google Scholar]
- Giles, H.F.; Wagner, J.R.; Mount, E.M. Extrusion: The Definitive Processing Guide and Handbook; William Andrew Pub: Norwich, CT, USA, 2004. [Google Scholar]
- Ehrenstein, G.W. Polymer-Werkstoffe: Struktur—Eigenschaften—Anwendung, 3rd ed.; Carl Hanser Verlag: Munich, Germany, 2011. [Google Scholar]
- Lamtai, A.; Elkoun, S.; Robert, M.; Mighri, F.; Diez, C. Mechanical Recycling of Thermoplastics: A Review of Key Issues. Waste 2023, 1, 860–883. [Google Scholar] [CrossRef]
- Rudolph, N.; Kiesel, R.; Aumnate, C. Einführung Kunststoffrecycling: Ökonomische, Ökologische und Technische Aspekte der Kunststoffabfallverwertung; Carl Hanser Verlag: Munich, Germany, 2020; ISBN 9783446458802. [Google Scholar]
- Naderi Kalali, E.; Lotfian, S.; Entezar Shabestari, M.; Khayatzadeh, S.; Zhao, C.; Yazdani Nezhad, H. A Critical Review of the Current Progress of Plastic Waste Recycling Technology in Structural Materials. Curr. Opin. Green Sustain. Chem. 2023, 40, 100763. [Google Scholar] [CrossRef]
- Tamizhdurai, P.; Mangesh, V.L.; Santhosh, S.; Vedavalli, R.; Kavitha, C.; Bhutto, J.K.; Alreshidi, M.A.; Yadav, K.K.; Kumaran, R. A State-of-the-Art Review of Multilayer Packaging Recycling: Challenges, Alternatives, and Outlook. J. Clean. Prod. 2024, 447, 141403. [Google Scholar] [CrossRef]
- DeLassus, P. Barrier Polymers. In Kirk-Othmer Encyclopedia of Chemical Technology, 3rd ed.; Wiley: Hoboken, NJ, USA, 2002; Volume 3, pp. 480–502. [Google Scholar]
- Valentas, K.J.; Rotstein, E.; Singh, R.P. Handbook of Food Engineering Practice; CRC Press: Boca Raton, FL, USA, 1997. [Google Scholar]
- Knudsen, M. Die Molekularströmung der Gase durch Öffnungen und die Effusion. Ann. Phys. 1909, 333, 999–1016. [Google Scholar] [CrossRef]
- Knudsen, M. Die Gesetze der Molekularströmung und der inneren Reibungsströmung der Gase durch Röhren. Ann. Phys. 1909, 333, 75–130. [Google Scholar] [CrossRef]
- Perrin, D.; Mantaux, O.; Ienny, P.; Léger, R.; Dumon, M.; Lopez-Cuesta, J.M. Influence of Impurities on the Performances of HIPS Recycled from Waste Electric and Electronic Equipment (WEEE). Waste Manag. 2016, 56, 438–445. [Google Scholar] [CrossRef]
- Signoret, C.; Caro-Bretelle, A.S.; Lopez-Cuesta, J.M.; Ienny, P.; Perrin, D. Impact of Pp Impurities on Abs Tensile Properties: Computational Mechanical Modelling Aspects. Polymers 2021, 13, 1647. [Google Scholar] [CrossRef]
- Aurrekoetxea, J.; Sarrionandia, M.A.; Urrutibeascoa, I.; Maspoch, M.L.I. Effects of Recycling on the Microstructure and the Mechanical Properties of Isotactic Polypropylene. J. Mater. Sci. 2001, 36, 2607–2613. [Google Scholar] [CrossRef]
- Incarnato, L.; Scarfato, P.; Acierno, D. Rheological and Mechanical Properties of Recycled Polypropylene. Polym. Eng. Sci. 1999, 39, 749–755. [Google Scholar] [CrossRef]
- Bahlouli, N.; Pessey, D.; Raveyre, C.; Guillet, J.; Ahzi, S.; Dahoun, A.; Hiver, J.M. Recycling Effects on the Rheological and Thermomechanical Properties of Polypropylene-Based Composites. Mater. Des. 2012, 33, 451–458. [Google Scholar] [CrossRef]
- Hensen, F.; Knappe, H.; Potente, H. Handbuch der Kunststoff-Extrusionstechnik: Extrusionsanlagen, 1st ed.; Carl Hanser Verlag: Munich, Germany, 1989. [Google Scholar]
- Grellmann, W.; Seidler, S. Kunststoffprüfung, 4th ed.; Carl Hanser Verlag: Munich, Germany, 2024. [Google Scholar]
- Osswald, T.A.; Rudolph, N.S. Polymer Rheology: Fundamentals and Applications; Hanser Publications: Cincinnati, OH, USA, 2015; ISBN 9781569905234. [Google Scholar]
- Bagley, E.B. End Corrections in the Capillary Flow of Polyethylene. J. Appl. Phys. 1957, 28, 624–627. [Google Scholar] [CrossRef]
- Rabinowitsch, B. Über die Viskosität und Elastizität von Solen. Z. Für Phys. Chem. 1929, 145A, 1–26. [Google Scholar] [CrossRef]
- Kneidinger, C.; Wagner, E.; Längauer, M.; Zitzenbacher, G. Estimation of the Shear Viscosity of Mixed-Polymer Materials for Screw Extrusion-Based Recycling Process Modeling. Polymers 2024, 16, 1339. [Google Scholar] [CrossRef]
- Heitmiller, R.F.; Naar, R.Z.; Zabusky, H.H. Effect of Homogeneity on Viscosity in Capillary Extrusion of Polyethylene. J. Appl. Polym. Sci. 1964, 8, 873–880. [Google Scholar] [CrossRef]
- Bingham, E.C. The Viscosity of Binary Mixtures. J. Phys. Chem. 1914, 18, 157–165. [Google Scholar] [CrossRef]
- Arrhenius, S. Über Die innere Reibung verdünnter wässeriger Lösungen. Z. Für Phys. Chem. 1887, 1U, 285–298. [Google Scholar] [CrossRef]
- Bersted, B.H.; Slee, J.D.; Richter, C.A. Prediction of Rheological Behavior of Branched Polyethylene from Molecular Structure. J. Appl. Polym. Sci. 1981, 26, 1001–1014. [Google Scholar] [CrossRef]
- Tsenoglou, C. Viscoelasticity of Binary Homopolymer Blends. ASC Polym. Prepr. 1987, 28, 185–186. [Google Scholar]
- Kendall, J.; Monroe, K.P. The Viscosity of Liquids. II. The Viscosity-Composition Curve for Ideal Liquid Mixtures. J. Am. Chem. Soc. 1917, 39, 1787–1802. [Google Scholar] [CrossRef]
- Leherbauer, D.; Wager, E.; Kneidinger, C.; Hehenberger, P. Model-Based Electricity Consumption Quantification of Polymer Extruders for Mechanical Recycling Applications. Procedia CIRP 2025, 135, 630–635. [Google Scholar] [CrossRef]
- Kneidinger, C. Solids Conveying, Melting and Melt Conveying in Single Screw Extruders and Extrusion Dies. Ph.D. Thesis, JKU Johannes Kepler Universität, Linz, Austria, 2021. [Google Scholar]
- Kneidinger, C.; Schroecker, E.; Zitzenbacher, G.; Miethlinger, J. Melting Behavior of Heterogeneous Polymer Bulk Solids Related to Flood Fed Single Screw Extruders. Polymers 2020, 12, 2893. [Google Scholar] [CrossRef]
- Zitzenbacher, G. Berechnung Der Rotatorischen Strömung, Verweilzeit und Deformation in der Meteringzone Eines Einschneckenextruders. Master’s Thesis, Montanuniversität Leoben, Leoben, Austria, 1998. [Google Scholar]
- Yasuda, K. Investigation of the Analogies Between Viscometric and Linear Viscoelastic Properties of Polystyrene Fluids. Ph.D. Thesis, MIT-Massachusetts Institute of Technology, Cambridge, MA, USA, 1979. [Google Scholar]
- Arrhenius, S. Über die Dissociationswärme und den Einfluss der Temperatur auf den Dissociationsgrad der Elektrolyte. Z. Für Phys. Chem. 1889, 4U, 96–116. [Google Scholar] [CrossRef]
- Giesekus, H.; Langer, G. Die Bestimmung der wahren Fließkurven nicht-Newtonscher Flüssigkeiten und plastischer Stoffe mit der Methode der Repräsentativen Viskosität. Rheol. Acta 1977, 16, 1–22. [Google Scholar] [CrossRef]
- Binder, W. Modellierung der Transportvorgänge in Einschneckenextrudern. Ph.D. Thesis, Montanuniversität Leoben, Leoben, Austria, 1999. [Google Scholar]
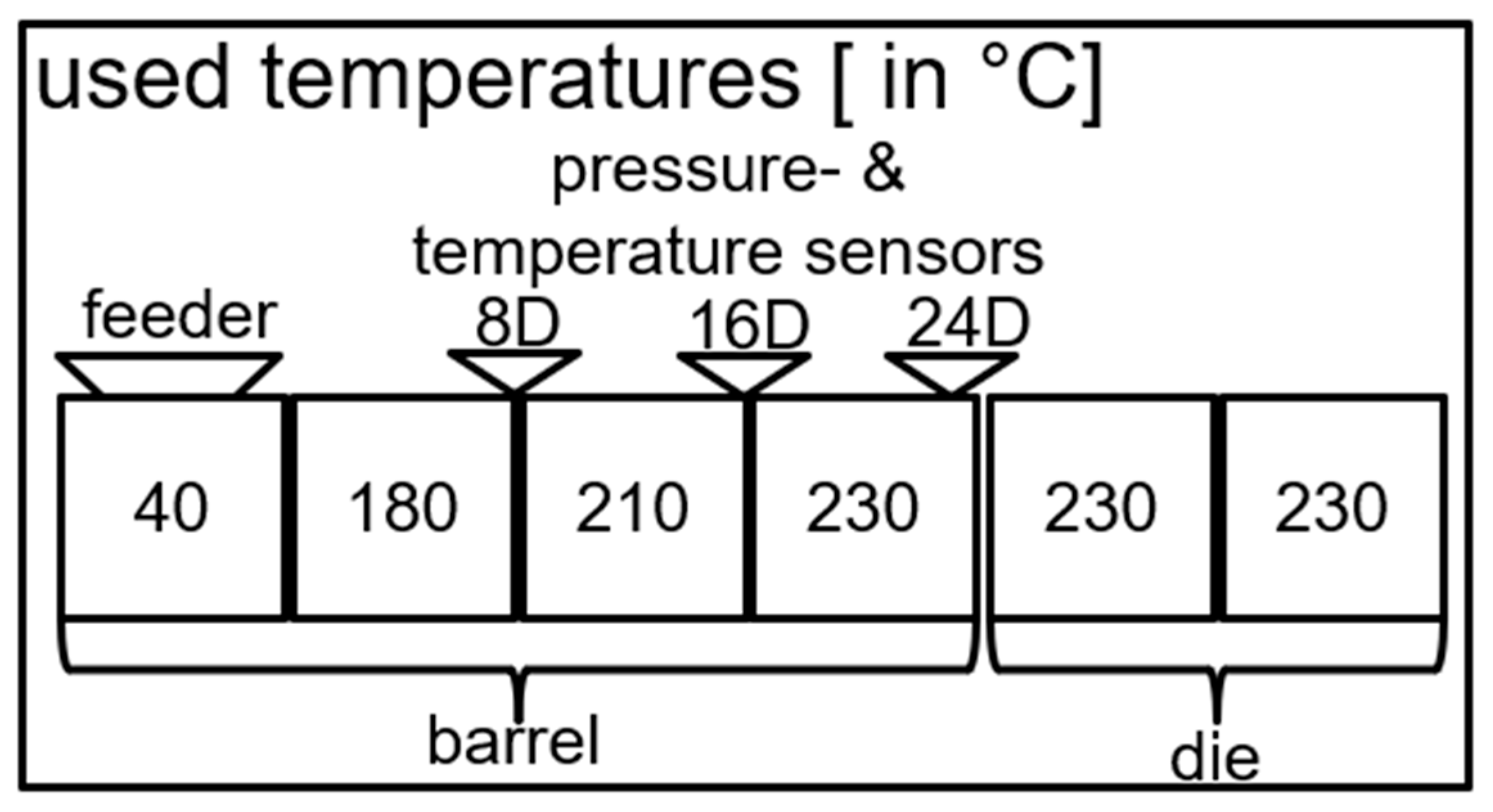
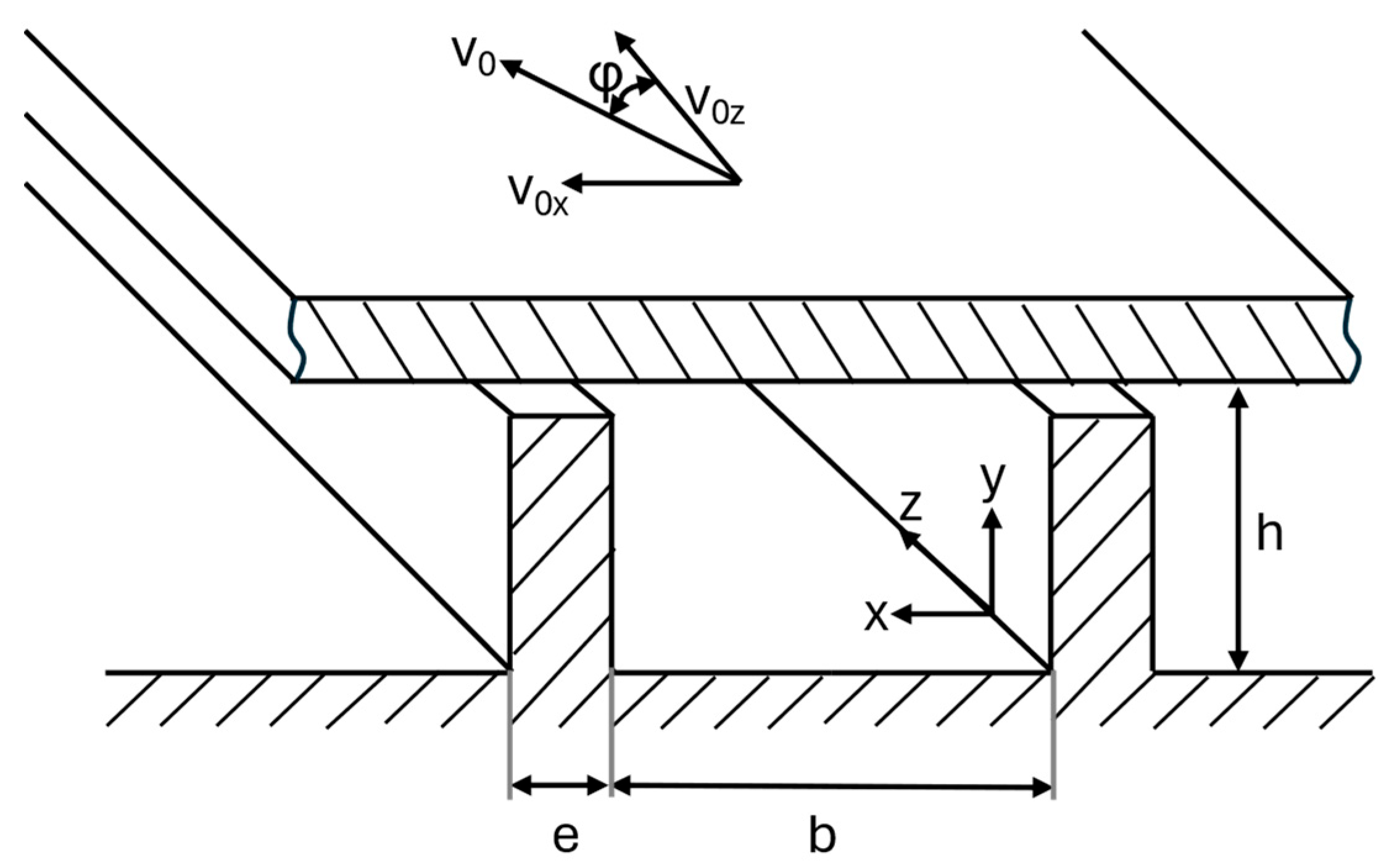
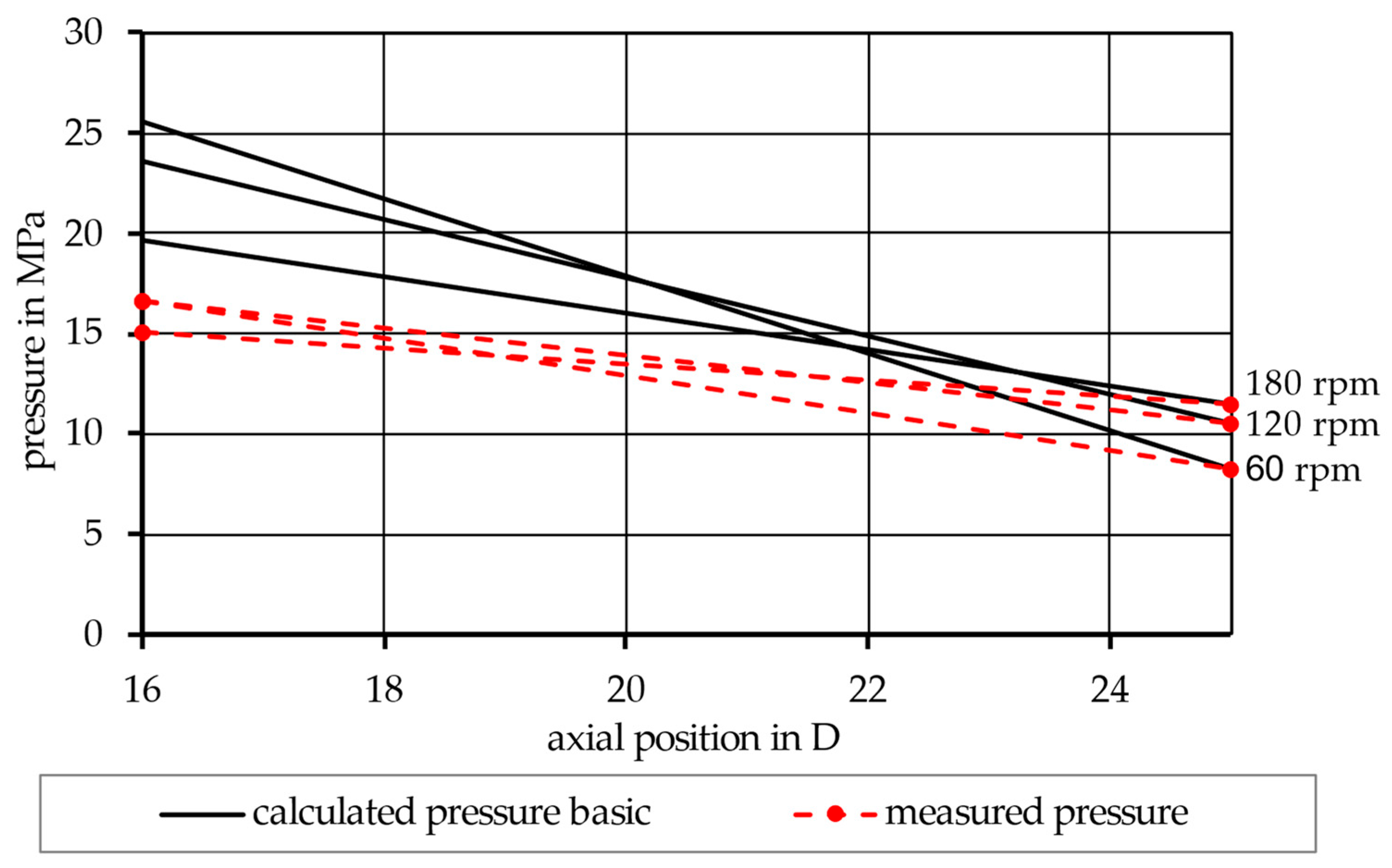

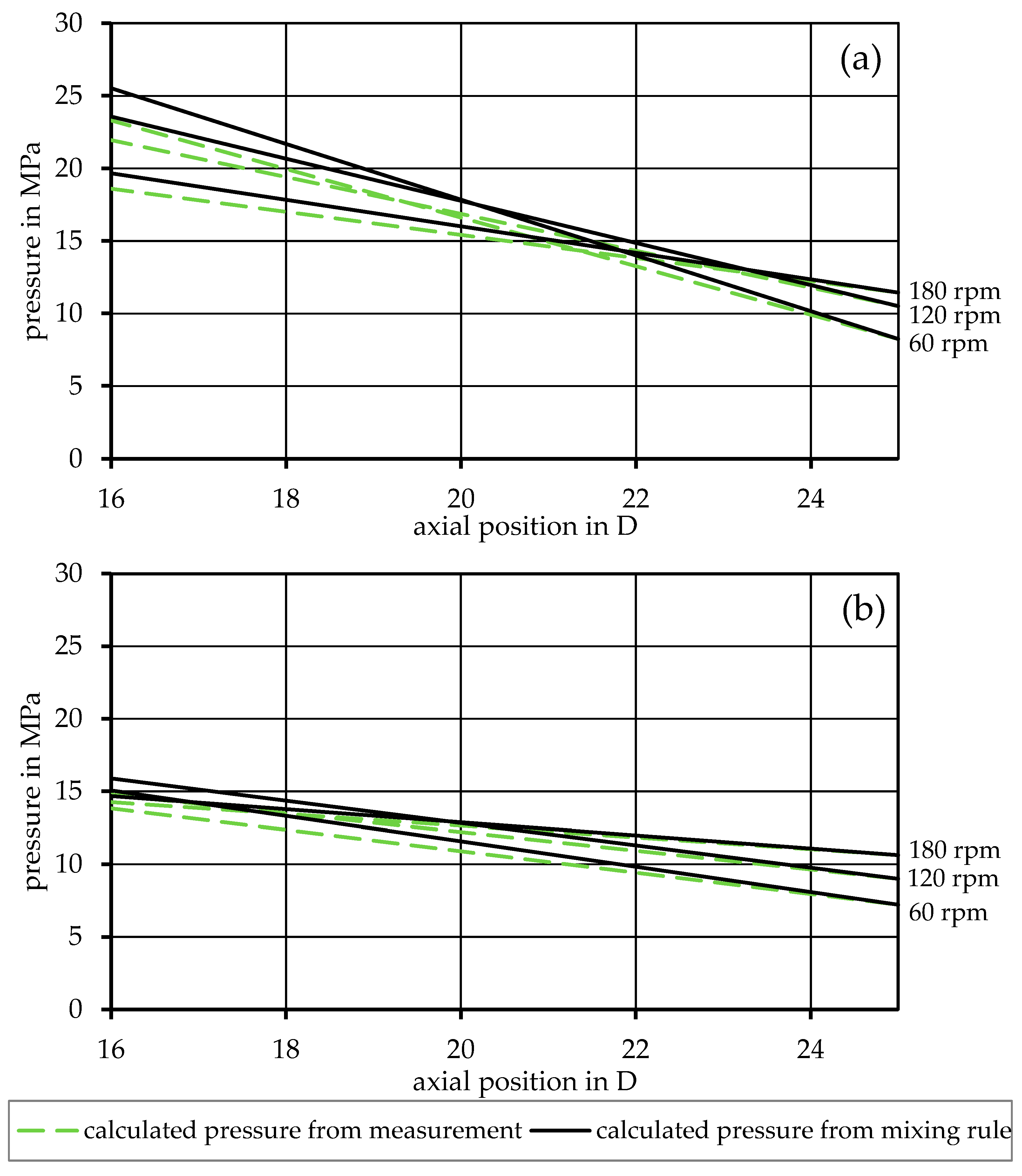
| Base Polymer | Concentration Base Polymer (wt%) | Contaminating Polymer | Concentration Contaminating Polymer (wt%) |
|---|---|---|---|
| PP1 | 100 | - | - |
| PP1 | 90 | PP2 | 10 |
| PP1 | 70 | PP2 | 30 |
| PP1 | 50 | PP2 | 50 |
| PP1 | 30 | PP2 | 70 |
| PP1 | 10 | PP2 | 90 |
| PP2 | 100 | - | - |
| PP1 | 96 | PPgMAH | 4 |
| PP1/PPgMAH * | 95 | PA12 | 5 |
| PP1/PPgMAH * | 90 | PA12 | 10 |
| PP1/PPgMAH * | 85 | PA12 | 15 |
| PP1/PPgMAH * | 80 | PA12 | 20 |
| PA12 | 100 | - | - |
| Geometric Aspect | Screw Dimensions |
|---|---|
| Diameter (mm) | 20 |
| Length (L/D) | 25 |
| Pitch (L/D) | 1 |
| Flight width (mm) | 2.5 |
| Flight clearance (mm) | 0.015 |
| Feeding zone | |
| Length (L/D) | 10 |
| Channel depth (mm) | 4 |
| Compression zone | |
| Length (L/D) | 6 |
| Channel depth ratio | 3.64 |
| Melt conveying zone | |
| Length (L/D) | 9 |
| Channel depth (mm) | 1.1 |
| Mixture | Source | η0 (Pa s) | B (s) | n | a | E0 (J/mol) | TB (K) | Deviation |
|---|---|---|---|---|---|---|---|---|
| 100PP1 | Measurement | 12,596.904 | 0.198 | 0.1666 | 0.445 | 37,311.25 | 473.150 | 0.019 |
| 90PP1/10PP2 | Measurement | 11,583.003 | 0.168 | 0.1583 | 0.427 | 37,946.07 | 473.150 | 0.019 |
| Mixing Rule | 5882.389 | 0.111 | 0.1876 | 0.539 | 39,869.22 | 473.150 | 0.015 | |
| 70PP1/300PP2 | Measurement | 6843.851 | 0.073 | 0.1271 | 0.426 | 34,920.43 | 473.150 | 0.025 |
| Mixing Rule | 5309.360 | 0.105 | 0.1980 | 0.550 | 42,576.17 | 473.150 | 0.017 | |
| 50PP1/50PP2 | Measurement | 5187.324 | 0.077 | 0.1642 | 0.474 | 36,661.24 | 473.150 | 0.018 |
| Mixing Rule | 5543.623 | 0.073 | 0.1577 | 0.435 | 39,483.40 | 473.150 | 0.011 | |
| 30PP1/70PP2 | Measurement | 4247.685 | 0.055 | 0.1485 | 0.444 | 35,361.64 | 473.150 | 0.015 |
| Mixing Rule | 2961.148 | 0.039 | 0.1645 | 0.485 | 42,216.90 | 473.150 | 0.019 | |
| 10PP1/90PP2 | Measurement | 2470.133 | 0.029 | 0.1325 | 0.483 | 36,652.37 | 473.150 | 0.012 |
| Mixing Rule | 2016.089 | 0.019 | 0.1091 | 0.482 | 41,503.27 | 473.150 | 0.027 | |
| 100PP2 | Measurement | 2047.812 | 0.020 | 0.1058 | 0.479 | 37,212.15 | 473.150 | 0.019 |
| 100PP1/PPgMAH | Measurement | 15,939.316 | 0.05 | 0.0125 | 0.264 | 47,166.06 | 503.150 | 0.023 |
| 95PP1/PPgMAH/05PA12 | Measurement | 4129.580 | 0.063 | 0.1666 | 0.501 | 38,160.74 | 503.150 | 0.019 |
| Mixing Rule | 14,153.343 | 0.048 | 0.0114 | 0.273 | 38,853.59 | 503.150 | 0.013 | |
| 90PP1/PPgMAH/10PA12 | Measurement | 4215.396 | 0.062 | 0.1694 | 0.499 | 37,977.38 | 503.150 | 0.019 |
| Mixing Rule | 16,993.074 | 0.057 | 0.0125 | 0.280 | 66,253.97 | 503.150 | 0.011 | |
| 85PP1/PPgMAH/15PA12 | Measurement | 4465.000 | 0.063 | 0.1676 | 0.487 | 37,431.24 | 503.150 | 0.018 |
| Mixing Rule | 22,459.861 | 0.072 | 0.0274 | 0.250 | 37,121.16 | 503.150 | 0.013 | |
| 80PP1/PPgMAH/20PA12 | Measurement | 5366.491 | 0.073 | 0.1713 | 0.457 | 40,986.60 | 503.150 | 0.016 |
| Mixing Rule | 27,675.946 | 0.093 | 0.0366 | 0.246 | 50,773.06 | 503.150 | 0.013 | |
| 100PA12 | Measurement | 4217.026 | 0.030 | 0.3293 | 0.622 | 50,157.67 | 503.150 | 0.106 |
| Mixture | Screw Speed (rpm) | Mass Throughput (kg/h) | Mass Temperature (°C) | Melt Density at 230 °C (kg/m3) |
|---|---|---|---|---|
| 100PP1 | 60 | 1.549 | 229.290 | 740 |
| 120 | 2.694 | 228.725 | 740 | |
| 180 | 3.928 | 228.548 | 740 | |
| 90PP1/10PP2 | 60 | 1.560 | 228.774 | 740 |
| 120 | 2.845 | 228.064 | 740 | |
| 180 | 3.997 | 227.371 | 740 | |
| 70PP1/300PP2 | 60 | 1.494 | 228.274 | 740 |
| 120 | 2.741 | 228.161 | 740 | |
| 180 | 3.904 | 227.612 | 740 | |
| 50PP1/50PP2 | 60 | 1.435 | 228.967 | 740 |
| 120 | 2.727 | 228.096 | 740 | |
| 180 | 3.912 | 228.338 | 740 | |
| 30PP1/70PP2 | 60 | 1.441 | 227.741 | 740 |
| 120 | 2.839 | 229.467 | 740 | |
| 180 | 4.081 | 230.016 | 740 | |
| 10PP1/90PP2 | 60 | 1.495 | 227.887 | 740 |
| 120 | 2.777 | 229.209 | 740 | |
| 180 | 4.057 | 229.483 | 740 | |
| 100PP2 | 60 | 1.450 | 229.338 | 740 |
| 120 | 2.651 | 228.242 | 740 | |
| 180 | 3.982 | 228.693 | 740 | |
| 100PP1/PPgMAH | 60 | 1.540 | 228.612 | 741 |
| 120 | 2.773 | 228.322 | 741 | |
| 180 | 3.943 | 228.532 | 741 | |
| 95PP1/PPgMAH/05PA12 | 60 | 1.561 | 229.290 | 746 |
| 120 | 2.919 | 229.596 | 746 | |
| 180 | 4.097 | 229.387 | 746 | |
| 90PP1/PPgMAH/10PA12 | 60 | 1.558 | 230.629 | 753 |
| 120 | 3.010 | 229.129 | 753 | |
| 180 | 4.221 | 231.903 | 753 | |
| 85PP1/PPgMAH/15PA12 | 60 | 1.659 | 228.645 | 758 |
| 120 | 3.030 | 227.709 | 758 | |
| 180 | 4.369 | 228.677 | 758 | |
| 80PP1/PPgMAH/20PA12 | 60 | 1.783 | 230.003 | 764 |
| 120 | 3.099 | 228.766 | 764 | |
| 180 | 4.390 | 230.383 | 764 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wagner, E.; Kneidinger, C.; Burgstaller, C.; Zitzenbacher, G. Simulation of the Melt Conveying Zone of a Single-Screw Extruder for Mixed Polymer Materials Using an Isothermal Analytical Flat Plate Model. Polymers 2025, 17, 3145. https://doi.org/10.3390/polym17233145
Wagner E, Kneidinger C, Burgstaller C, Zitzenbacher G. Simulation of the Melt Conveying Zone of a Single-Screw Extruder for Mixed Polymer Materials Using an Isothermal Analytical Flat Plate Model. Polymers. 2025; 17(23):3145. https://doi.org/10.3390/polym17233145
Chicago/Turabian StyleWagner, Emil, Christian Kneidinger, Christoph Burgstaller, and Gernot Zitzenbacher. 2025. "Simulation of the Melt Conveying Zone of a Single-Screw Extruder for Mixed Polymer Materials Using an Isothermal Analytical Flat Plate Model" Polymers 17, no. 23: 3145. https://doi.org/10.3390/polym17233145
APA StyleWagner, E., Kneidinger, C., Burgstaller, C., & Zitzenbacher, G. (2025). Simulation of the Melt Conveying Zone of a Single-Screw Extruder for Mixed Polymer Materials Using an Isothermal Analytical Flat Plate Model. Polymers, 17(23), 3145. https://doi.org/10.3390/polym17233145











