Moisture Content Distribution in Cross-Section of Cylindrical Wood Components
Abstract
1. Introduction
2. Experimental Study
2.1. Experimental Design
2.2. Permeability Experiment
2.3. Measurement Scheme
3. Experimental Results
3.1. Average Moisture Content
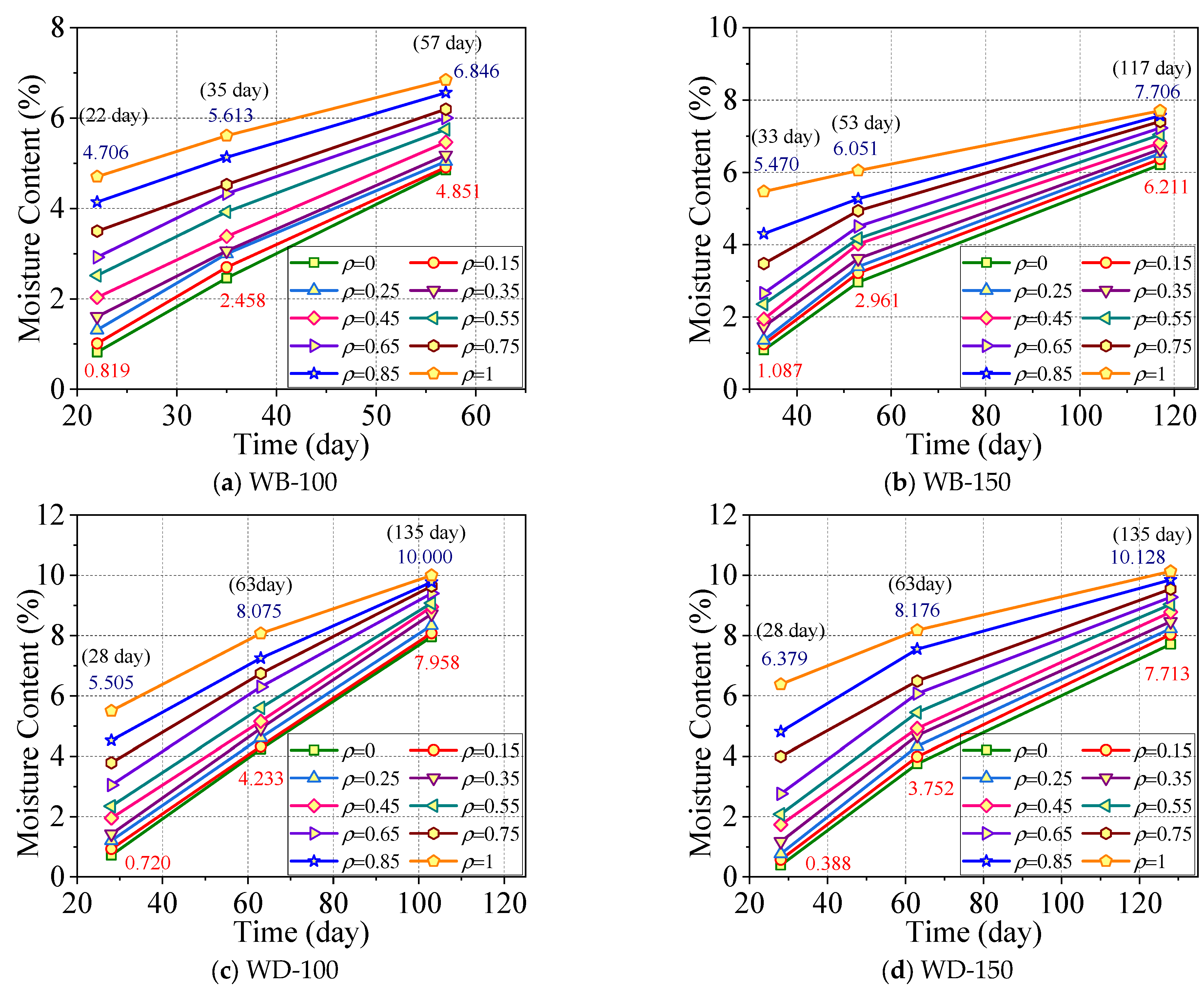
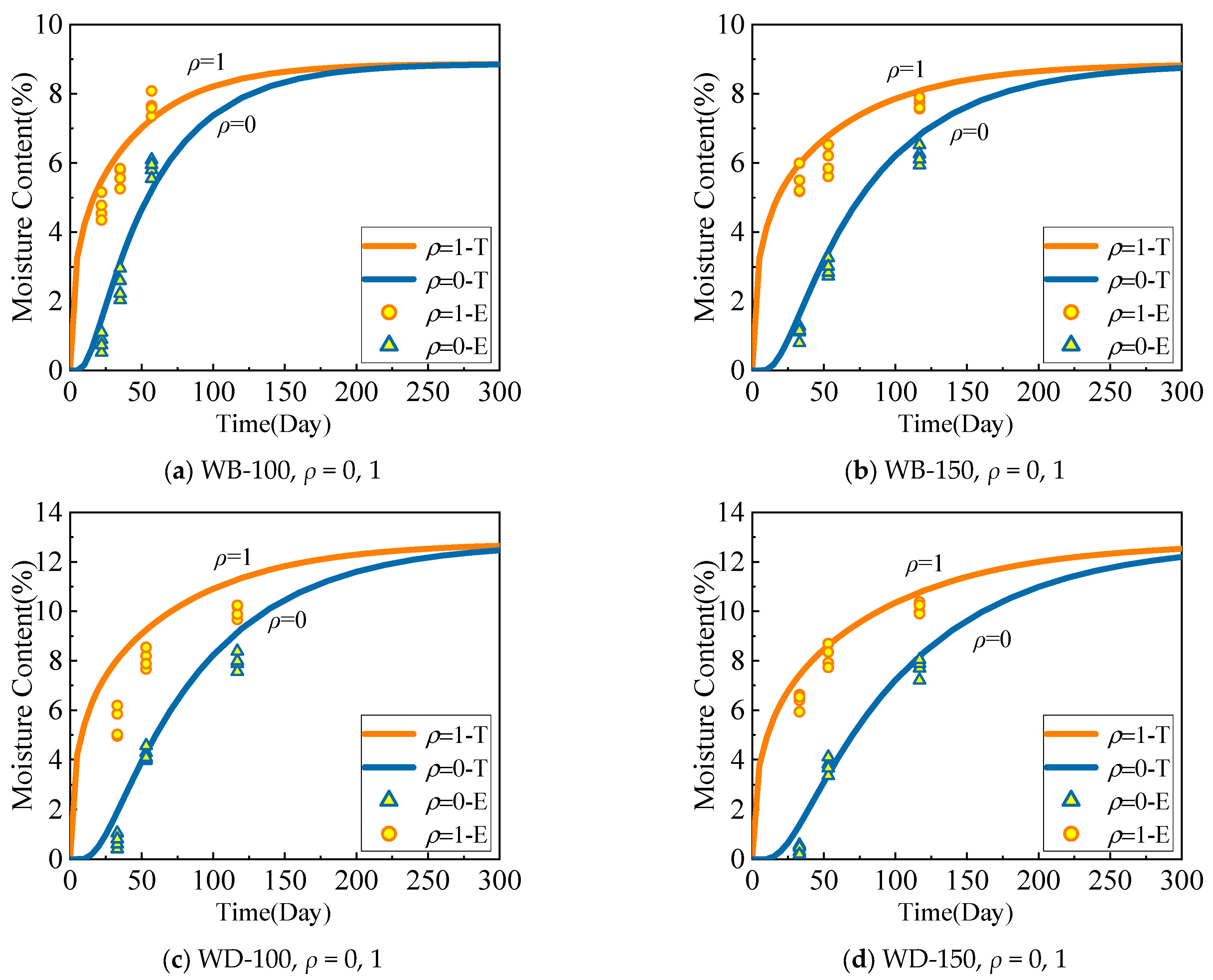
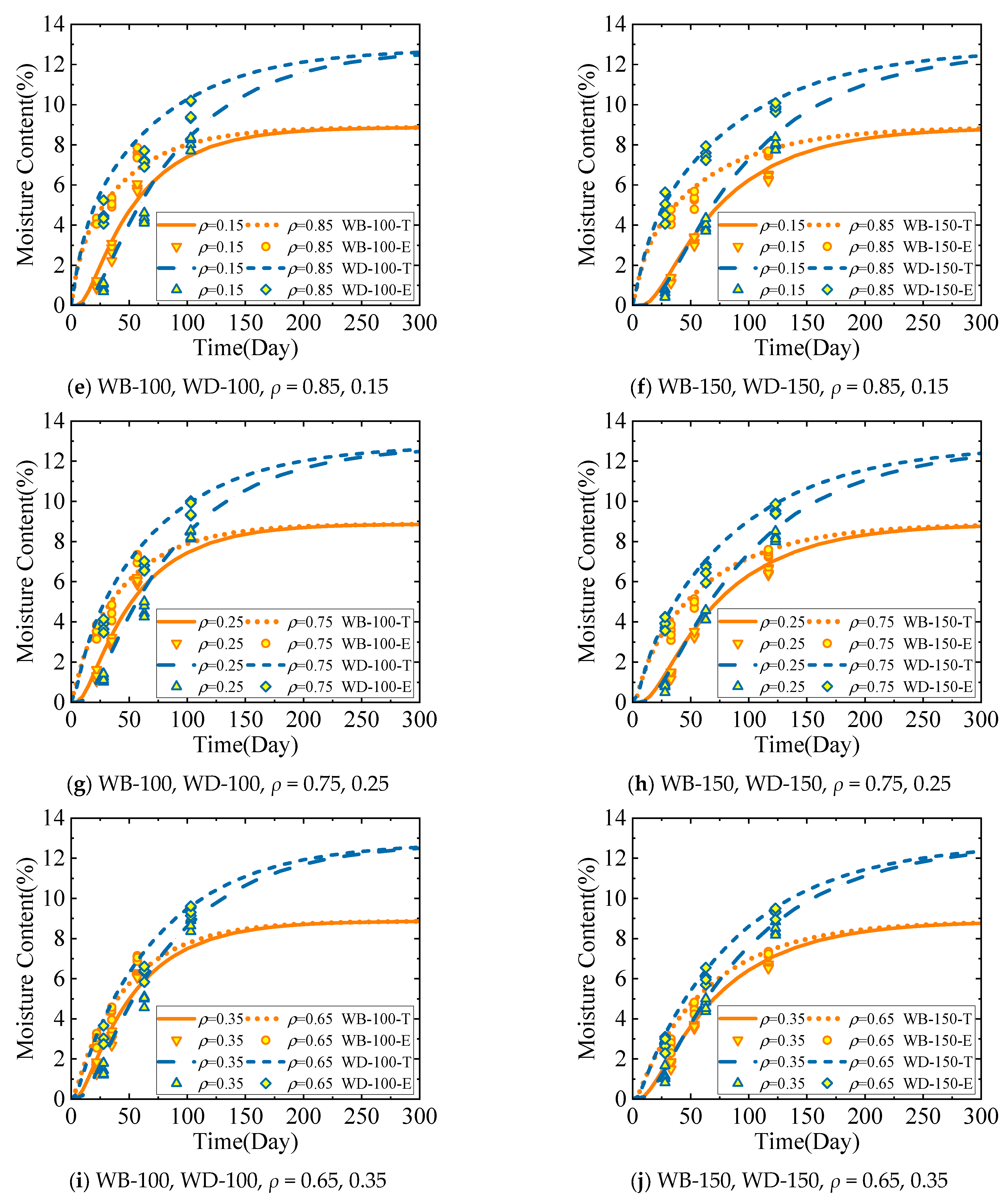
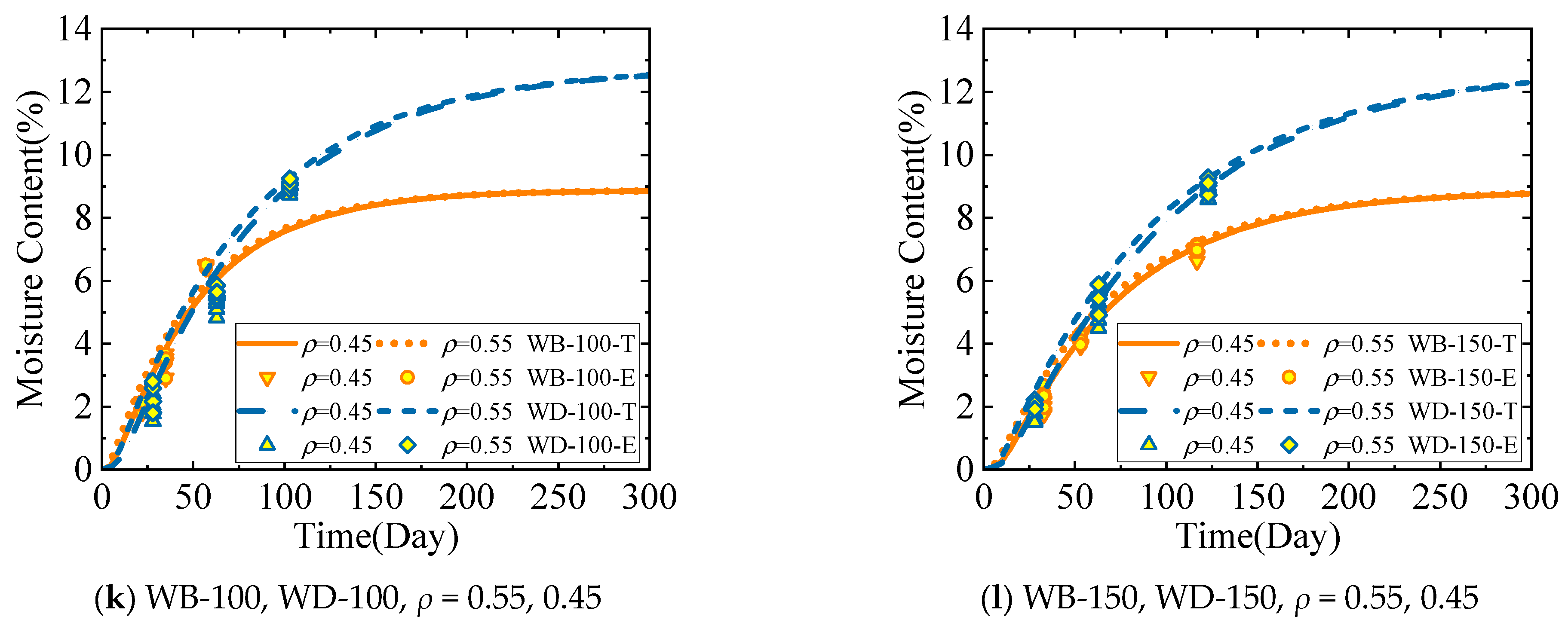
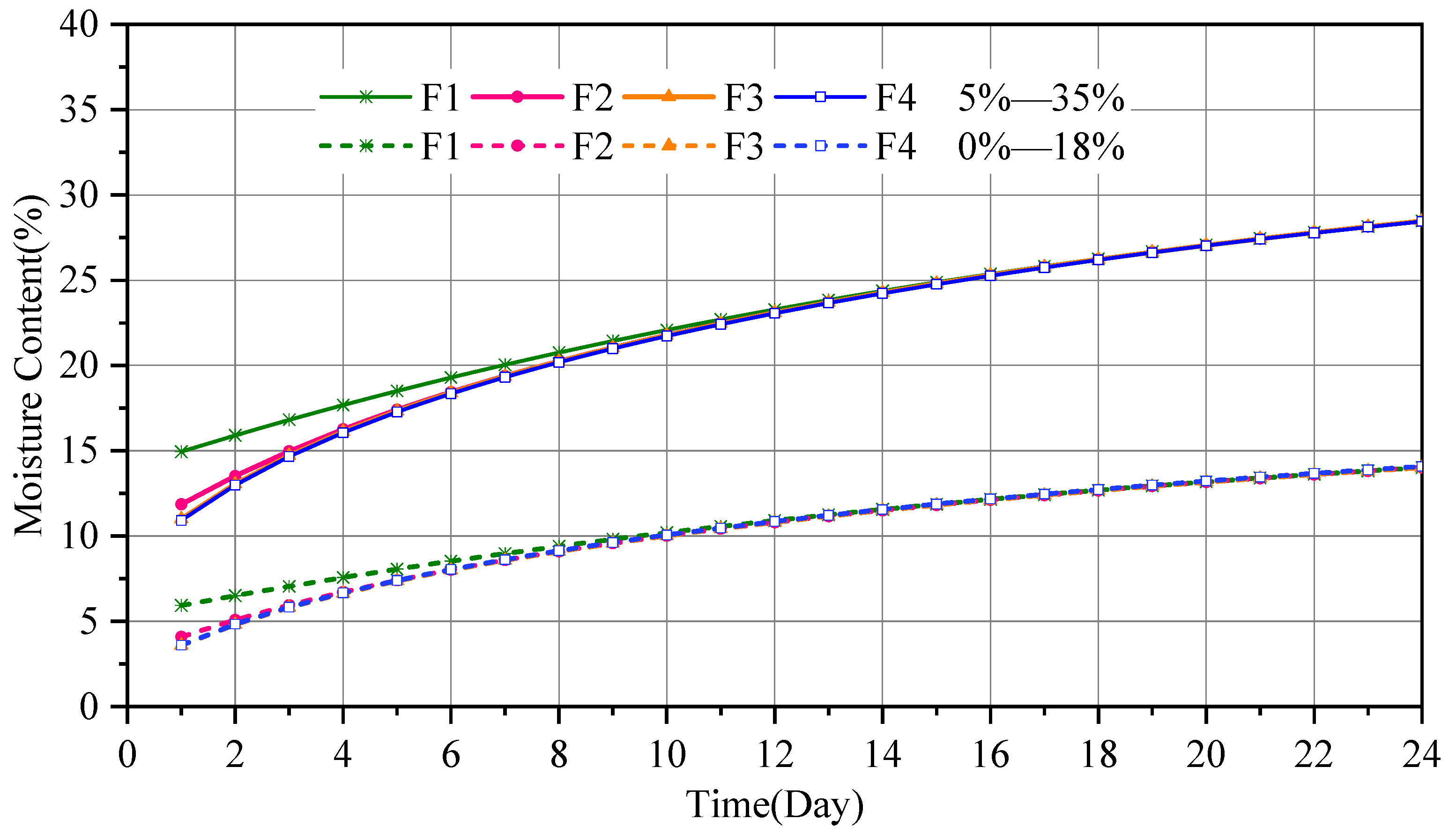
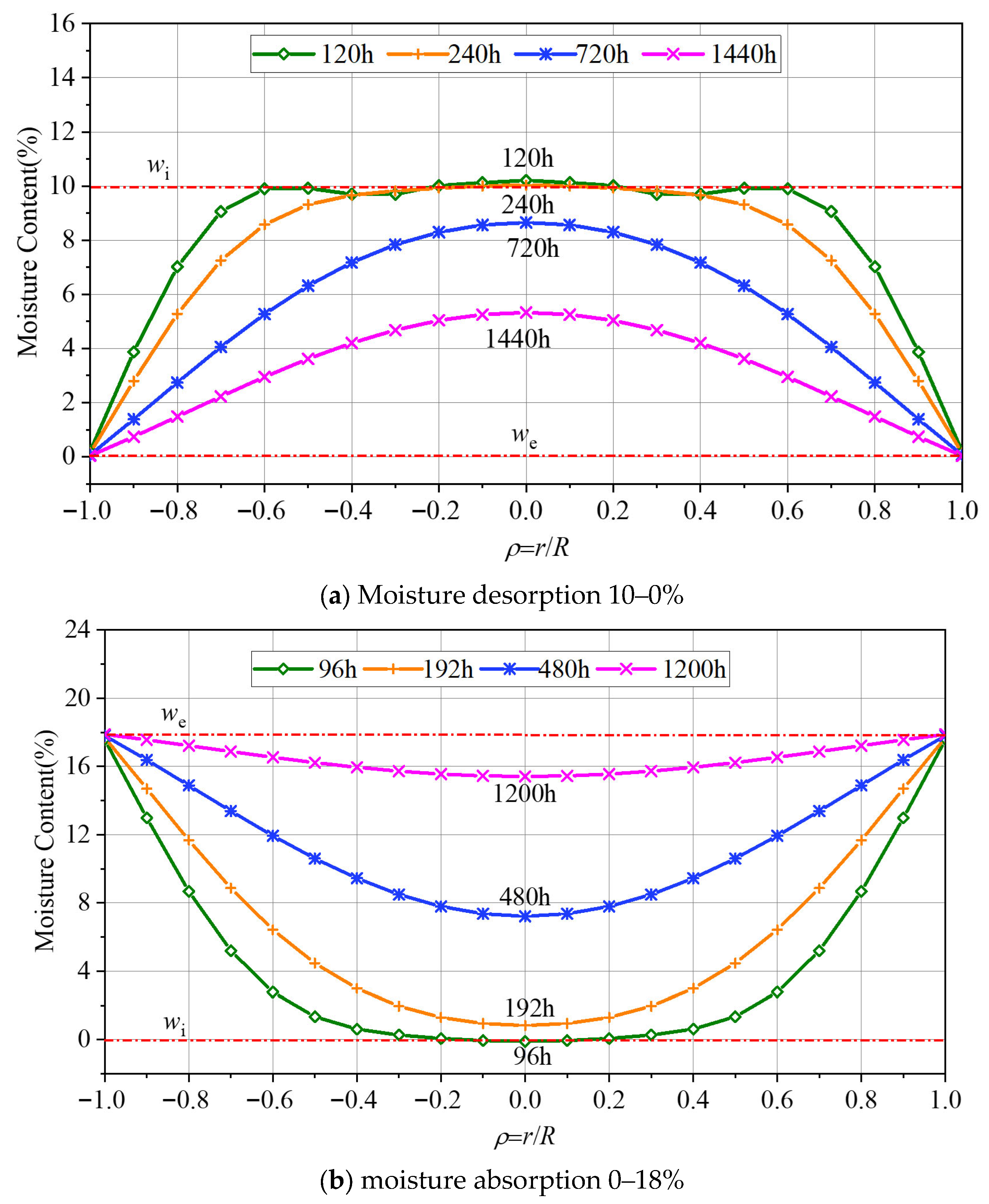
3.2. Moisture Distribution in Space
3.3. Moisture Distribution over Time
3.4. Calculation of Parameters D and S
4. Theoretical Analysis
5. Comparison
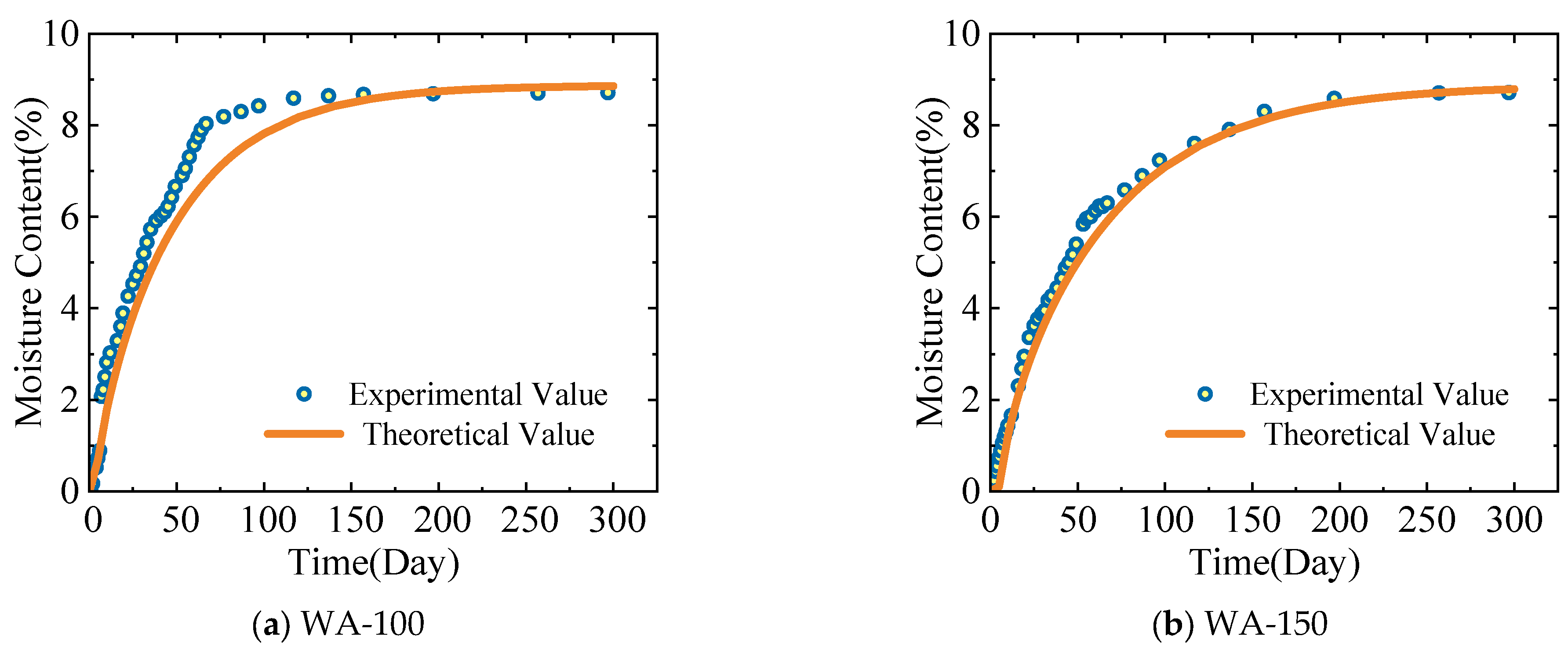
5.1. Average Moisture Content
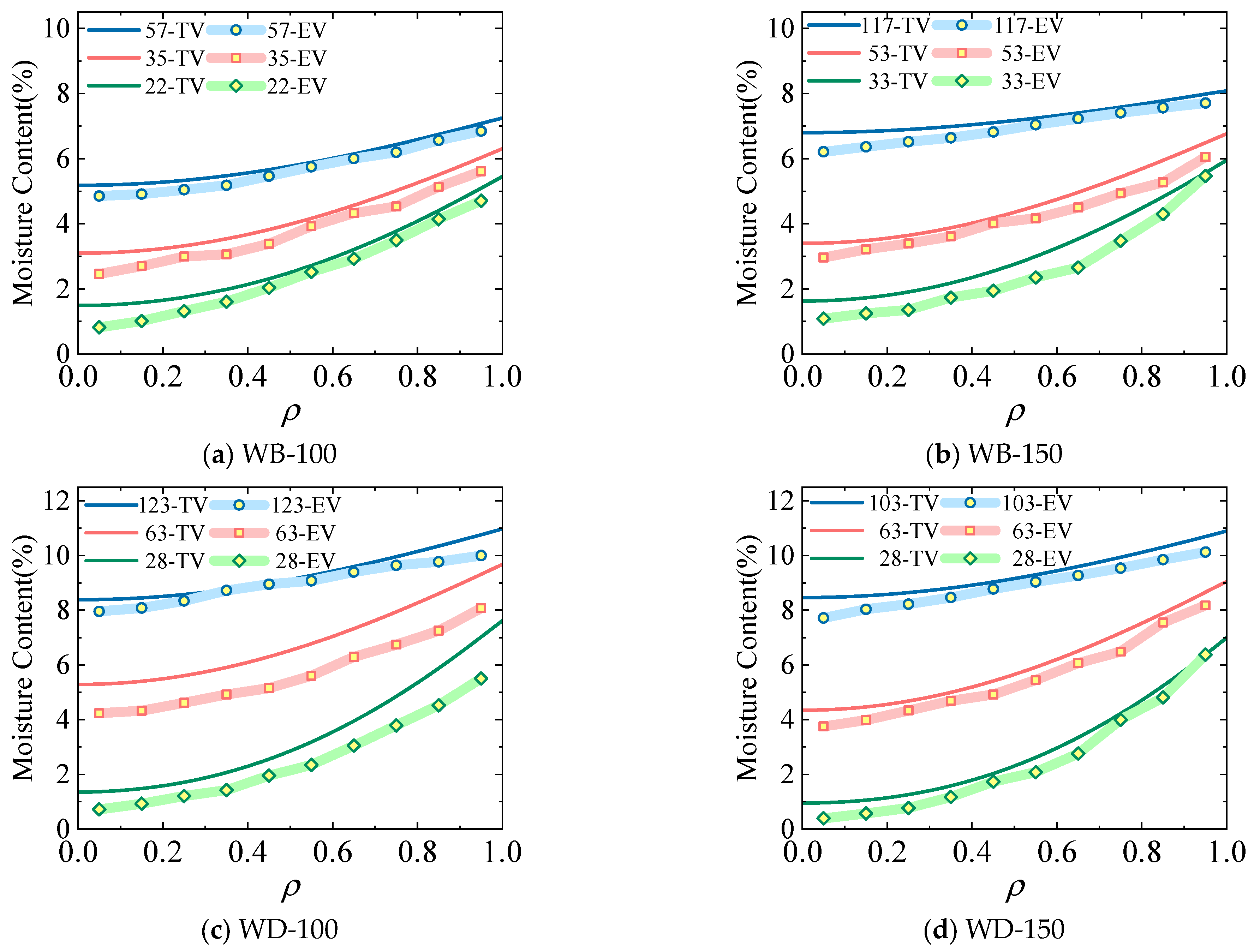
5.2. Moisture Distribution in Space
5.3. Moisture Distribution over Time
6. Discussion
6.1. Root of the Order μn
6.2. Component Size R
6.3. Position in the Component ρ
7. Conclusions
- (1)
- It is feasible to establish a moisture field model of wood components by referring to the theory of food drying and using a temperature field model. Comparison with experimental data reveals that the established time-varying moisture field model for cylindrical wood components has high accuracy. This model can provide a relatively accurate reference for predicting the change in the average moisture content of wood components, the change in moisture content over time, and its distribution law in space.
- (2)
- During moisture absorption, the distribution of the average moisture content of wood components increased continuously with time, and the growth rate of the average moisture content gradually decreased. Both the average moisture content and the radius of the specimen affected the moisture absorption efficiency of wood components. Under similar environmental conditions, specimens with a smaller radius have a higher moisture absorption efficiency. When the radii of the specimens are the same, specimens with a lower average moisture content have a higher moisture absorption efficiency.
- (3)
- During moisture absorption and desorption in cylindrical components, the greater the moisture content difference, the faster the equilibrium moisture content is reached. Moreover, the time for the outer part to reach the equilibrium moisture content was much shorter than that for the inner part of the component.
- (4)
- When the external moisture content changed, the change range of the moisture content was smaller closer to the inside of the wood component, and hysteresis was more evident; the method of directly replacing the moisture content of wood components with the equilibrium moisture content of the external environment was inaccurate. At the initial stage of the experiment, the surface moisture content was high, whereas the internal moisture content was low. As the experiment progressed, the difference in the moisture content gradient between the inside and the surface of the specimen became increasingly smaller, and the moisture content of the entire cross-section of the specimen approached the equilibrium moisture content.
- (5)
- When calculating the model for the average moisture content of cylindrical components and using the models depicting the spatial variation and temporal evolution of the moisture content, it is sufficient to take the first three orders of the roots μn of the characteristic equation of the Bessel function of the first type J in the theoretical model for long time of diffusion, which can achieve a high level of accuracy. For wood components with dimensions commonly used in engineering, when calculating their moisture content over a short period (i.e., a dozen days), a higher order of the roots μn of the characteristic equation of the Bessel function of the first type J results in greater calculation accuracy.
- (6)
- When the diameter of cylindrical components is equal to the thickness of laminate components, the rates of moisture absorption and desorption of cylindrical components are higher than those of laminate components. Regardless of the moisture absorption or desorption process, the exterior of the components reached the equilibrium moisture content much earlier than the interior of the components.
8. Limitations and Future Work
- (1)
- The experiments were only conducted on a single type of Chinese fir. This narrow scope restricts the generalizability of the results, as different wood species may exhibit distinct moisture diffusion behaviors under the same conditions.
- (2)
- The Bessel function-based model assumes constant diffusion coefficients and constant temperature. In practical applications, however, wood diffusivity varies significantly with both moisture content and temperature, which may restrict the model accuracy in predicting moisture transfer behaviors. Additionally, the current calculation methods for the moisture diffusivity D and sorption coefficient S have limitations. The preliminary estimation equations for these parameters were originally derived for wood slabs. When applied directly to cylindrical components, these equations may introduce deviations. This further affects the prediction reliability of the model.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| we | equilibrium moisture content (%) |
| w | moisture content (%) |
| T | ambient temperature (°C) |
| RH | relative humidity (%) |
| r | radius of specimen (mm) |
| L | length of specimen (mm) |
| θ | angle of specimen (°) |
| mw | mass of the specimen at a certain measurement time point (g) |
| m0 | mass of the permeability specimen at absolute dry time (g) |
| mP | mass of the permeability specimen at initial state (g) |
| m1,m2,m3.. | mass of the cut specimen at initial state (g) |
| m1′,m2′,m3′… | mass of the cut specimen at absolute dry time (g) |
| EV | experimental value |
| MV | mean value |
| ρ | relative distance of the cross-section |
| t0.5 | time required to reach half of the total adsorption capacity |
| t | time required to reach the total adsorption capacity |
| D | moisture diffusivity (mm2/day) |
| S | surface emission coefficient (mm/day) |
| ϕ | relative moisture content |
| wi | initial moisture content (%) |
| r | distance from any point to the center |
| R | half the radial length of component |
| ws | moisture content of the wood surface |
| J | the first-class Bessel Function |
| μn | the root of the characteristic equation |
| ν | shape factor of the Bessel Function |
| Bi | Biot number for mass transfer |
| Fo | Fourier number |
References
- Thybring, E.E.; Fredriksson, M.; Zelinka, S.L.; Glass, S.V. Water in Wood: A Review of Current Understanding and Knowledge Gaps. Forests 2022, 13, 2051. [Google Scholar] [CrossRef]
- Arriaga, F.; Wang, X.; Íñiguez-González, G.; Llana, D.F.; Esteban, M.; Niemz, P. Mechanical Properties of Wood: A Review. Forests 2023, 14, 1202. [Google Scholar] [CrossRef]
- Li, W.; Chen, M.; Dai, Y.; Ke, L.-L. Analysis on moisture-induced stresses in wood cell wall considering periodically graded microstructures. Int. J. Solids Struct. 2025, 312, 113277. [Google Scholar] [CrossRef]
- Gao, Y.; Fu, Z.; Fu, F.; Zhou, Y.; Gao, X.; Zhou, F. The formation mechanism of microcracks and fracture morphology of wood during drying. Dry. Technol. 2023, 41, 1268–1277. [Google Scholar] [CrossRef]
- Stéphan, A.; Perré, P.; L’hOstis, C.; Rémond, R. The fork device: A test for estimating the memory creep of wood under load during moisture variation. Wood Sci. Technol. 2025, 59, 22. [Google Scholar] [CrossRef]
- Vergara, P.M.; Carreño-Chovan, C.; Quiroz, M.; Alaniz, A.J.; Fierro, A.; Saavedra, M.; Hidalgo-Corrotea, C.M.; Zúñiga, A.H.; Carvajal, M.A.; Borquez, C.; et al. The internal decay of wood is driven by the interplay between foraging Magellanic woodpeckers and environmental conditions. Sci. Total Environ. 2024, 955, 177133. [Google Scholar] [CrossRef]
- Yi, W. Research on the Intelligent Wood Moisture Content Measuring Instrument; Harbin Engineering University: Harbin, China, 2011. [Google Scholar]
- Fredriksson, M.; Wadsö, L.; Johansson, P. Small resistive wood moisture sensors: A method for moisture content determination in wood structures. Eur. J. Wood Wood Prod. 2013, 71, 515–524. [Google Scholar] [CrossRef]
- Hafsa, W.; Nguyen, T.A.; Angellier, N.; Ulmet, L.; Takarli, M.; Pop, O.; Dubois, F. Assessment of moisture content profile in Douglas-fir wood using electrical resistivity-based tomography. Constr. Build. Mater. 2023, 366, 130193. [Google Scholar] [CrossRef]
- Uwizeyimana, P.; Perrin, M.; Eyma, F. Moisture monitoring in glulam timber structures with embedded resistive sensors: Study of influence parameters. Wood Sci. Technol. 2020, 54, 1463–1478. [Google Scholar] [CrossRef]
- Brischke, C.; Rapp, A.O.; Bayerbach, R. Measurement system for long-term recording of wood moisture content with internal conductively glued electrodes. Build. Environ. 2008, 43, 1566–1574. [Google Scholar] [CrossRef]
- Hao, L. Theories and Factors of Wood Moisture Content Testing Based on Stress Wave Technology; Beijing Forestry University: Beijing, China, 2014. [Google Scholar]
- Mai, T.C.; Razafindratsima, S.; Sbartaï, Z.M.; Demontoux, F.; Bos, F. Non-destructive evaluation of moisture content of wood material at GPR frequency. Constr. Build. Mater. 2015, 77, 213–217. [Google Scholar] [CrossRef]
- Rahimi, S.; Avramidis, S.; Sassani, F.; Nasir, V. Machine learning-based prediction of internal moisture variation in kiln-dried timber. Wood Mater. Sci. Eng. 2023, 19, 499–510. [Google Scholar] [CrossRef]
- Suekuni, M.T.; D’Souza, N.; Allgeier, A.M. NMR Relaxometry Studies on the Drying Kinetics of Cellulose Nanofibers. Ind. Eng. Chem. Res. 2022, 61, 5475–5483. [Google Scholar] [CrossRef]
- Silva, J.V.F.; Cogulet, A.; Blanchet, P.; Pechon, Q. Effect of Relative Humidity Level on Bonding Properties of Black Spruce Glulam. BioResources 2025, 20, 2922–2932. [Google Scholar] [CrossRef]
- Awais, M.; Altgen, M.; Mäkelä, M.; Belt, T.; Rautkari, L. Quantitative prediction of moisture content distribution in acetylated wood using near-infrared hyperspectral imaging. J. Mater. Sci. 2022, 57, 3416–3429. [Google Scholar] [CrossRef]
- Xu, Z.; Ding, T.; Ding, J.; Wang, H. Moisture content measuring of wood with commutated tomography. Wood Process. Mach. 2009, 20, 7–9. [Google Scholar]
- Aira-Zunzunegui, J.R.; Sánchez-Aparicio, M.; Sánchez-Aparicio, L.J.; Pinilla-Melo, J.; García-Morales, S. Determination of wood moisture content with terrestrial laser scanner. Constr. Build. Mater. 2022, 350, 128834. [Google Scholar] [CrossRef]
- Arends, T.; Barakat, A.J.; Pel, L. Moisture transport in pine wood during one-sided heating studied by NMR. Exp. Therm. Fluid Sci. 2018, 99, 259–271. [Google Scholar] [CrossRef]
- Chiniforush, A.; Valipour, H.; Akbarnezhad, A. Water vapor diffusivity of engineered wood: Effect of temperature and moisture content. Constr. Build. Mater. 2019, 224, 1040–1055. [Google Scholar] [CrossRef]
- Chen, K.; Qiu, H.; Sun, M.; Lam, F. Experimental and numerical study of moisture distribution and shrinkage crack propagation in cross section of timber members. Constr. Build. Mater. 2019, 221, 219–231. [Google Scholar] [CrossRef]
- Svensson, S.; Turk, G.; Hozjan, T. Predicting moisture state of timber members in a continuously varying climate. Eng. Struct. 2011, 33, 3064–3070. [Google Scholar] [CrossRef]
- Niklewski, J.; Fredriksson, M.; Isaksson, T. Moisture content prediction of rain-exposed wood: Test and evaluation of a simple numerical model for durability applications. Build. Environ. 2016, 97, 126–136. [Google Scholar] [CrossRef]
- Zheng, Z.; Liping, S.; Bin, J. Three-Dimensional Computational Model for Wood Moisture Content and Density Based on Finite Element Method. J. Northeast. For. Univ. 2014, 2, 133–135. [Google Scholar]
- Autengruber, M.; Lukacevic, M.; Gröstlinger, C.; Eberhardsteiner, J.; Füssl, J. Numerical assessment of wood moisture content-based assignments to service classes in EC 5 and a prediction concept for moisture-induced stresses solely using relative humidity data. Eng. Struct. 2021, 245, 112849. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, L.; Ma, F. Finite element method with nonlocal boundary condition for solving the nondestructive testing problem of wood moisture content. Appl. Math. Comput. 2015, 250, 432–443. [Google Scholar] [CrossRef]
- He, Z.; Qian, J.; Qu, L.; Wang, Z.; Yi, S. Simulation of moisture transfer during wood vacuum drying. Results Phys. 2019, 12, 1299–1303. [Google Scholar] [CrossRef]
- Autengruber, M.; Lukacevic, M.; Füssl, J. Finite-element-based moisture transport model for wood including free water above the fiber saturation point. Int. J. Heat Mass Transf. 2020, 161, 120228. [Google Scholar]
- Afshari, Z.; Malek, S. Moisture transport in laminated wood and bamboo composites bonded with thin adhesive layers—A numerical study. Constr. Build. Mater. 2022, 340, 127597. [Google Scholar] [CrossRef]
- Xia, C.; Wang, P.; Zhang, Y. Prediction of Moisture Content of Wood Based on Deep Learning. J. Hangzhou Dianzi Univ. (Nat. Sci.) 2015, 35, 32–35. [Google Scholar]
- Daassi-Gnaba, H.; Oussar, Y.; Merlan, M.; Ditchi, T.; Géron, E.; Holé, S. Wood moisture content prediction using feature selection techniques and a kernel method. Neurocomputing 2017, 237, 79–91. [Google Scholar] [CrossRef]
- Elustondo, D.; Matan, N.; Langrish, T.; Pang, S. Advances in wood drying research and development. Dry. Technol. 2023, 41, 890–914. [Google Scholar] [CrossRef]
- Hajian, E.; Couceiro, J.; Hansson, L.; Sandberg, D. Drying Behaviour of Western Hemlock with Schedules Developed for Norway Spruce and Scots Pine. Appl. Sci. 2023, 13, 11083. [Google Scholar] [CrossRef]
- Simpson, W.T.; Liu, J.Y. Dependence of the water vapor diffusion coefficient of aspen (Populus spec.) on moisture content. Wood Sci. Technol. 1991, 26, 9–21. [Google Scholar] [CrossRef]
- Fortino, S.; Mirianon, F.; Toratti, T. A 3D moisture-stress FEM analysis for time dependent problems in timber structures. Mech. Time-Depend. Mater. 2009, 13, 333–356. [Google Scholar] [CrossRef]
- Dinçer, İ.; Zamfirescu, C. Drying Phenomena; University of Ontario Institute of Technology: Oshawa, ON, Canada, 2016; pp. 192–206. [Google Scholar]
- Adebiyi, G.A. Single expression for the solution of the one-dimensional transient conduction equation for the simple regular-shaped solids. J. Heat Transf. 1995, 117, 158–160. [Google Scholar] [CrossRef]
- Simpson, W.T. Determination and use of moisture diffusion coefficient to characterize dring of northern red oak. Wood Sci. Technol. 1993, 27, 409–420. [Google Scholar] [CrossRef]



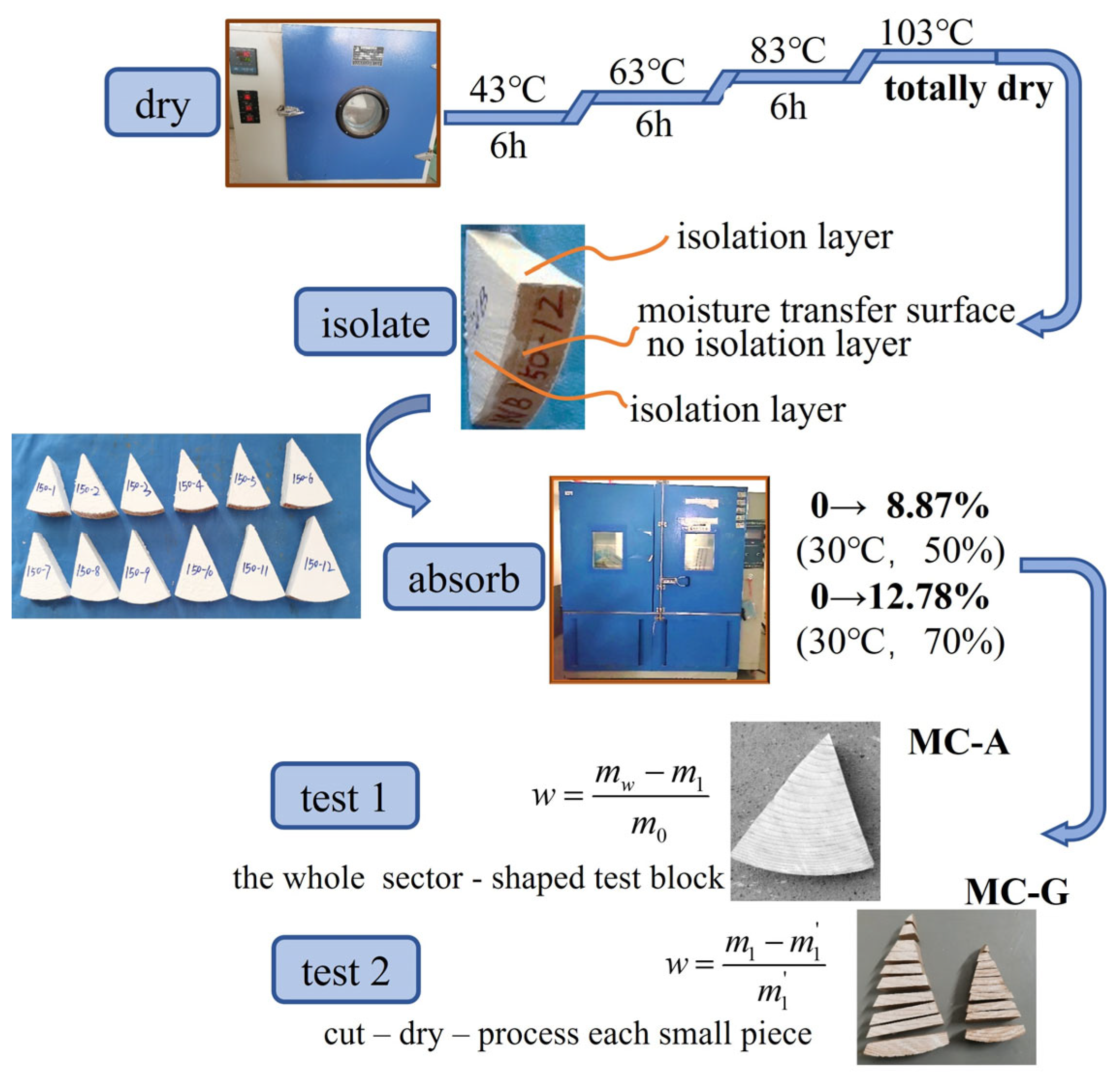







| No. | Specimen Size | Number | Environment | Test Purpose | ||||
|---|---|---|---|---|---|---|---|---|
| Radius R (mm) | Length L (mm) | Angle θ (°) | T (°C) | RH (%) | We (%) | |||
| WA-100 | 100 | 40 | 45 | 12 | 30 | 50 | 8.87 | MC-A |
| WA-150 | 150 | 40 | 45 | 12 | 30 | 50 | 8.87 | MC-A |
| WC-100 | 100 | 40 | 45 | 12 | 30 | 70 | 12.78 | MC-A |
| WC-150 | 150 | 40 | 45 | 12 | 30 | 70 | 12.78 | MC-A |
| WB-100 | 100 | 40 | 45 | 12 | 30 | 50 | 8.87 | MC-G |
| WB-150 | 150 | 40 | 45 | 12 | 30 | 50 | 8.87 | MC-G |
| WD-100 | 100 | 40 | 45 | 12 | 30 | 70 | 12.78 | MC-G |
| WD-150 | 150 | 40 | 45 | 12 | 30 | 70 | 12.78 | MC-G |
| No. | Direction | m0 (g) | mP (g) | w = (mP – m0)/m0 (%) |
|---|---|---|---|---|
| W1 | Longitudinal | 98.29 | 99.06 | 0.78% |
| W2 | Tangential | 185.23 | 187.45 | 1.19% |
| W3 | Radial | 134.63 | 135.97 | 0.99% |
| No. | Diameter (mm) | we (%) | t (day) | t0.5 (day) | D (mm2/day) | S (mm/day) |
|---|---|---|---|---|---|---|
| WA-100 | 200 | 8.87 | 86.92 | 24.96 | 78.53 | 1.13 |
| WA-150 | 300 | 8.87 | 136.92 | 38.17 | 115.54 | 1.06 |
| WC-100 | 200 | 12.78 | 143 | 40.9 | 47.92 | 0.68 |
| WC-150 | 300 | 12.78 | 170 | 46.1 | 95.66 | 0.85 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, P.; Zhang, H.; Han, J.; Zhao, Y.; Han, X. Moisture Content Distribution in Cross-Section of Cylindrical Wood Components. Polymers 2025, 17, 2994. https://doi.org/10.3390/polym17222994
Tian P, Zhang H, Han J, Zhao Y, Han X. Moisture Content Distribution in Cross-Section of Cylindrical Wood Components. Polymers. 2025; 17(22):2994. https://doi.org/10.3390/polym17222994
Chicago/Turabian StyleTian, Panpan, Heng Zhang, Jianhong Han, Yu Zhao, and Xia Han. 2025. "Moisture Content Distribution in Cross-Section of Cylindrical Wood Components" Polymers 17, no. 22: 2994. https://doi.org/10.3390/polym17222994
APA StyleTian, P., Zhang, H., Han, J., Zhao, Y., & Han, X. (2025). Moisture Content Distribution in Cross-Section of Cylindrical Wood Components. Polymers, 17(22), 2994. https://doi.org/10.3390/polym17222994





