The Role of Cross-Sectional Design and Orientation in Governing Energy Absorption of Additively Manufactured Polyamide 12 (PA12) Octet Lattices
Abstract
1. Introduction
2. Materials and Methods
2.1. Lattice Parent Material
2.2. Design and Geometry of Lattice Structures
2.3. Fabrication of Specimens
2.4. Experimental Testing Set-Up
2.5. Assessment of Crashworthiness Criteria
2.6. Second Moment of Area and Member Stability
- Orientation Effect
- Implications for Lattice Performance
3. Results and Discussion
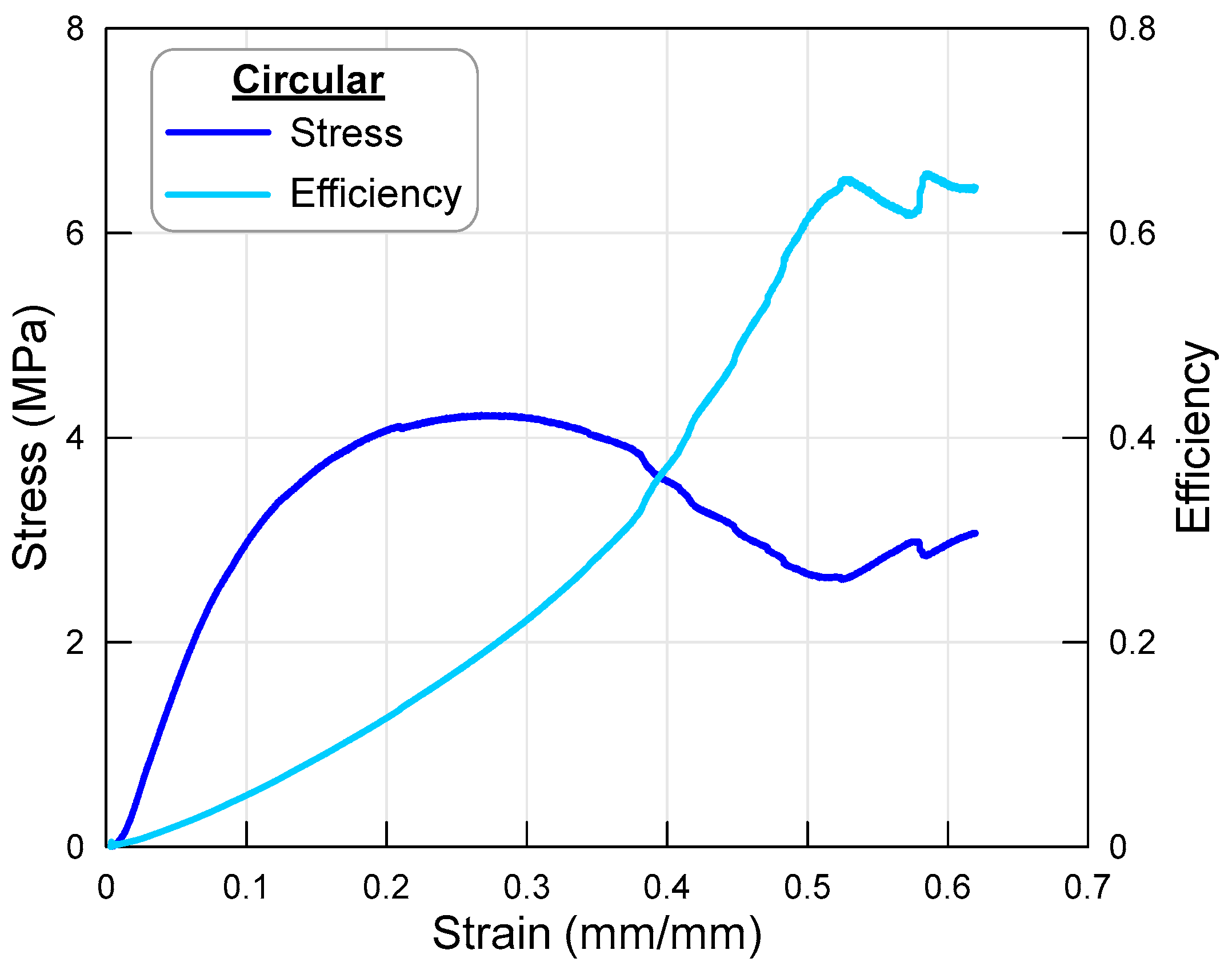
3.1. Circular Cross-Section
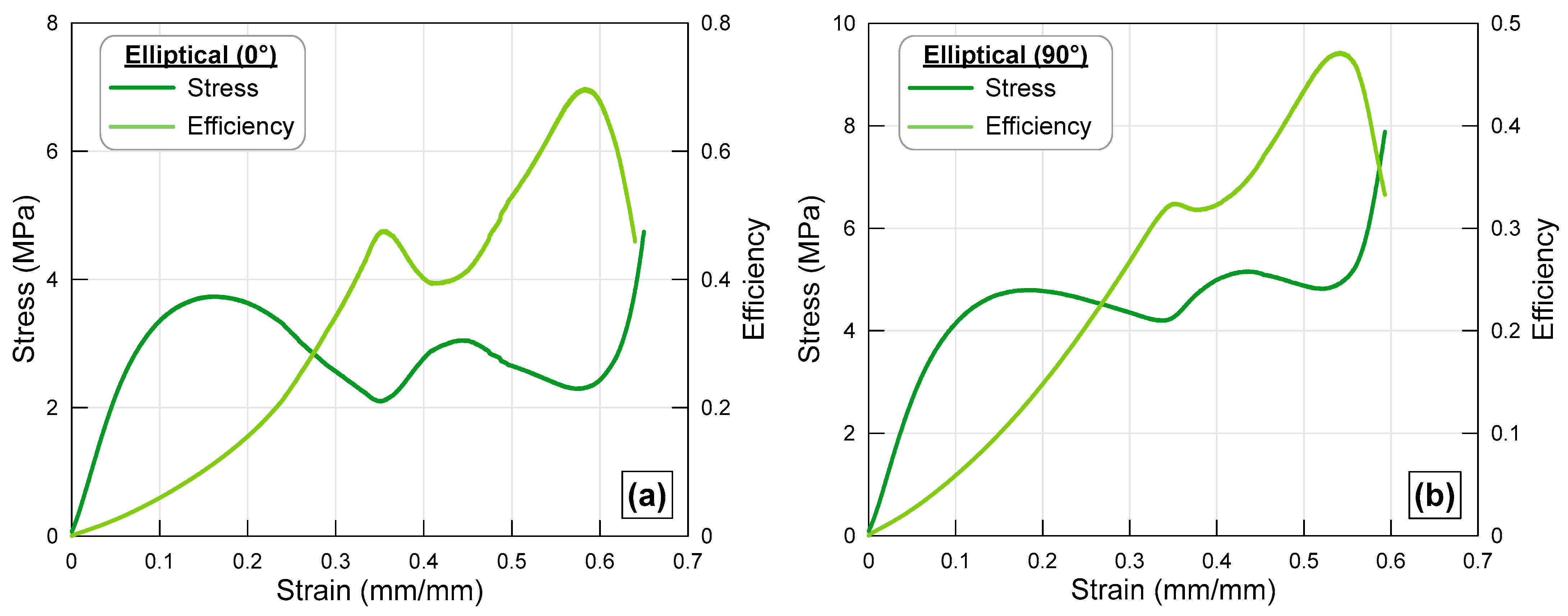
3.2. Elliptical Cross-Section
3.3. Rectangular Cross-Section
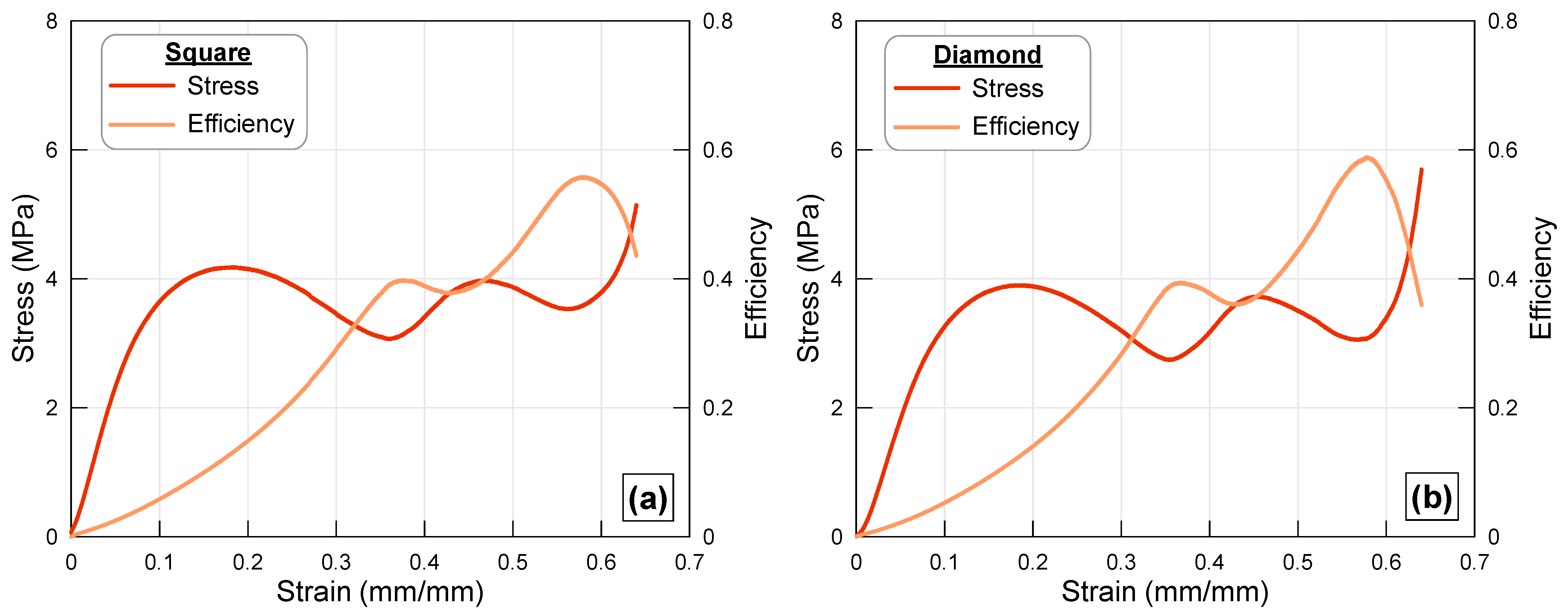
3.4. Square Cross-Section
3.5. Discussion of Comparative Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, X.; Qin, R.; Chen, B. Mechanical properties and energy absorption capability of a topology-optimized lattice structure manufactured via selective laser melting under axial and offset loading. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2022, 236, 10221–10236. [Google Scholar] [CrossRef]
- Yalçın, M.M. Flexural Behavior of 3D-Printed Carbon Fiber-Reinforced Nylon Lattice Beams. Polymers 2024, 16, 2991. [Google Scholar] [CrossRef]
- Yao, J.; Ding, R.; Li, K.; Du, B.; Zhao, L.; Yuan, Y. Study on the impact behavior of arch micro-strut (ARCH) lattice structure by selective laser melting (SLM). Rapid Prototyp. J. 2022, 28, 1541–1557. [Google Scholar] [CrossRef]
- Shi, W.; Lin, Y.; Li, J.; Liu, S.; Han, Y.; Liu, B. Mechanical Response and Energy Absorption of 316L Stainless Steel Body-Centered-Cubic Functionally Graded Lattice Structures under Quasistatic Compressive Test. Adv. Eng. Mater. 2023, 25, 2300451. [Google Scholar] [CrossRef]
- Zhao, M.; Liu, F.; Fu, G.; Zhang, D.Z.; Zhang, T.; Zhou, H. Improved Mechanical Properties and Energy Absorption of BCC Lattice Structures with Triply Periodic Minimal Surfaces Fabricated by SLM. Materials 2018, 11, 2411. [Google Scholar] [CrossRef]
- Lin, Y.; Shi, W.; Sun, X.; Liu, S.; Li, J.; Zhou, Y.; Han, Y. Influence of Density Gradient on the Compression of Functionally Graded BCC Lattice Structure. Materials 2023, 16, 520. [Google Scholar] [CrossRef]
- Bernard, A.R.; Yalcin, M.M.; ElSayed, M.S. Crashworthiness investigations for 3D printed multi-layer multi-topology carbon fiber nylon lattice materials. J. Reinf. Plast. Compos. 2024, 44, 634–649. [Google Scholar] [CrossRef]
- Bernard, A.R.; Yalcin, M.M.; ElSayed, M.S. Shape transformers for crashworthiness of additively manufactured engineering resin lattice structures: Experimental and numerical investigations. Mech. Mater. 2024, 190, 104925. [Google Scholar] [CrossRef]
- Emir, E.; Bahçe, E. Investigation of the mechanical properties triple periodic minimal surfaces lattice structures with functional graded of porosity. J. Cell. Plast. 2023, 59, 251–268. [Google Scholar] [CrossRef]
- Ganapathy, S.B.; Sakthivel, A.R. Investigation on the Compressive Characteristics and Optimization of Design Parameters of a Novel Functionally Graded Cell Structure. Funct. Compos. Struct. 2024, 6, 015009. [Google Scholar] [CrossRef]
- Liang, Y.; Zhou, W.; Liu, Y.; Li, Z.; Yang, Y.; Xi, H.; Wu, Z. Energy Absorption and Deformation Behavior of 3D Printed Triply Periodic Minimal Surface Stainless Steel Cellular Structures under Compression. Steel Res. Int. 2021, 92, 2000411. [Google Scholar] [CrossRef]
- Shi, X.; Liao, W.; Li, P.; Zhang, C.; Liu, T.; Wang, C.; Wu, J. Comparison of Compression Performance and Energy Absorption of Lattice Structures Fabricated by Selective Laser Melting. Adv. Eng. Mater. 2020, 22, 2000453. [Google Scholar] [CrossRef]
- Okutan, M.S.; Yalçın, M.M.; ElSayed, M.S.; Genel, K. Lateral deformation behavior of internally fin-stiffened tubes. Int. J. Mech. Sci. 2025, 300, 110446. [Google Scholar] [CrossRef]
- Yalçın, M.M. Experimental investigation on energy absorption capability of 3D printed onyx nested rings under lateral loading. J. Reinf. Plast. Compos. 2024. [Google Scholar] [CrossRef]
- Qi, D.; Yu, H.; Liu, M.; Huang, H.; Xu, S.; Xia, Y.; Qian, G.; Wu, W. Mechanical behaviors of SLM additive manufactured octet-truss and truncated-octahedron lattice structures with uniform and taper beams. Int. J. Mech. Sci. 2019, 163, 105091. [Google Scholar] [CrossRef]
- Al-Saedi, D.S.J.; Masood, S.H.; Faizan-Ur-Rab, M.; Alomarah, A.; Ponnusamy, P. Mechanical properties and energy absorption capability of functionally graded F2BCC lattice fabricated by SLM. Mater. Des. 2018, 144, 32–44. [Google Scholar] [CrossRef]
- Yang, Z.; Yu, Y.; Wei, Y.; Huang, C. Crushing behavior of a thin-walled circular tube with internal gradient grooves fabricated by SLM 3D printing. Thin-Walled Struct. 2017, 111, 1–8. [Google Scholar] [CrossRef]
- Bernard, A.R.; Yalçın, M.M.; ElSayed, M.S.A. Crashworthiness Investigations for 3D-Printed Multi-Layer Multi-Topology Engineering Resin Lattice Materials. Materials 2024, 17, 4844. [Google Scholar] [CrossRef]
- Li, Y.; Gu, H.; Pavier, M.; Coules, H. Compressive behaviours of octet-truss lattices. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2020, 234, 3257–3269. [Google Scholar] [CrossRef]
- Surjadi, J.U.; Feng, X.; Zhou, W.; Lu, Y. Optimizing film thickness to delay strut fracture in high-entropy alloy composite microlattices. Int. J. Extreme Manuf. 2021, 3, 025101. [Google Scholar] [CrossRef]
- Després, N.; Cyr, E.; Mohammadi, M. A performance metric for additively manufactured microlattice structures under different loading conditions. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2019, 233, 1814–1829. [Google Scholar] [CrossRef]
- Khan, M.; Haq, M.R.U.; Khan, M.S.; Butt, S.I.; Nazir, A.; Jan, A. Design for Additive Manufacturing Driven Multi-Layered Hybrid Mechanical Metamaterials for Improved Mechanical Performance. Adv. Eng. Mater. 2025, 27, 2402737. [Google Scholar] [CrossRef]
- Adel, A.; Adly, M.A.; Reda, R.; Abdelkawy, A. Comparative Structural and Mechanical Characterization of FDM 3D-Printed PLA Scaffolds for Bone Tissue Engineering Applications. Polym. Adv. Technol. 2025, 36, e70257. [Google Scholar] [CrossRef]
- Zhao, P.; Huang, D.; Zhang, Y.; Zhang, H.; Chen, W. Microstructure and Properties of Hollow Octet Nickel Lattice Materials. Materials 2022, 15, 8417. [Google Scholar] [CrossRef]
- Kalia, B.; Singh, R.; Pabla, B.S.; Singh, G. On 17-4PH stainless steel dental implant for premolar 4 in canine under compressive loading: Effect of solid and octet metastructure. Explor. BioMat-X 2024, 1, 202–214. [Google Scholar] [CrossRef]
- Vangelatos, Z.; Komvopoulos, K.; Grigoropoulos, C. Vacancies for controlling the behavior of microstructured three-dimensional mechanical metamaterials. Math. Mech. Solids 2019, 24, 511–524. [Google Scholar] [CrossRef]
- Khiavi, S.G.; Sadeghi, B.M.; Divandari, M. Effect of topology on strength and energy absorption of PA12 non-auxetic strut-based lattice structures. J. Mater. Res. Technol. 2022, 21, 1595–1613. [Google Scholar] [CrossRef]
- Zhao, J.; Liu, R.; Cai, J.; Estakhrianhaghighi, E.; Sasmito, A.P.; Hou, J.; Akbarzadeh, A. Enhanced Mechanical Properties of Lattice Structures Enabled by Tailoring Oblique Truss Orientation Angle. Adv. Eng. Mater. 2024, 26, 2301646. [Google Scholar] [CrossRef]
- Poddar, P.; Olles, M.; Cormier, D. Mechanical Response of Carbon Composite Octet Truss Structures Produced via Axial Lattice Extrusion. Polymers 2022, 14, 3553. [Google Scholar] [CrossRef]
- Chen, A.Y.-J.; Chen, A.; Fitzhugh, A.; Hartman, A.; Kaiser, P.; Nwaogwugwu, I.; Zeng, J.; Gu, G.X. Multi Jet Fusion printed lattice materials: Characterization and prediction of mechanical performance. Mater. Adv. 2023, 4, 1030–1040. [Google Scholar] [CrossRef]
- HP 3D High Reusability PA 12 Strong, Lowest Cost, 1 Quality Parts Picture Taken After Graphite Post-Processing. 2017. Available online: https://proto3000.com/wp-content/uploads/2021/07/Proto3000_HP-PA12-material-datasheet-1.pdf (accessed on 1 September 2025).
- ASTM D3418-21; Standard Test Method for Transition Temperatures and Enthalpies of Fusion and Crystallization of Polymers by Differential Scanning Calorimetry. ASTM: West Conshohocken, PA, USA, 2021.
- ASTM D3451-06(2017); Standard Guide for Testing Coating Powders and Powder Coatings. ASTM: West Conshohocken, PA, USA, 2024.
- ASTM D1895-17; Standard Test Methods for Apparent Density, Bulk Factor, and Pourability of Plastic Materials. ASTM: West Conshohocken, PA, USA, 2024.
- ASTM D792-20; Standard Test Methods for Density and Specific Gravity (Relative Density) of Plastics by Displacement. ASTM: West Conshohocken, PA, USA, 2020.
- ASTM D638-14; Standard Test Method for Tensile Properties of Plastics. ASTM: West Conshohocken, PA, USA, 2022.
- ASTM D790-17; Standard Test Methods for Flexural Properties of Unreinforced and Reinforced Plastics and Electrical Insulating Materials. ASTM: West Conshohocken, PA, USA, 2017.
- ASTM D256-24; Standard Test Methods for Determining the Izod Pendulum Impact Resistance of Plastics. ASTM: West Conshohocken, PA, USA, 2025.
- Yang, C.; Li, Q. Advanced lattice material with high energy absorption based on topology optimisation. Mech. Mater. 2020, 148, 103536. [Google Scholar] [CrossRef]
- Bernard, A.R.; ElSayed, M.S. Impact Resistance and Specific Energy Absorption Efficiency Limits of Periodic Cellular Solids. AIAA Sci. Technol. Forum Expo. 2022, 2022, 1–15. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, Z.; Zhou, S.; Shao, J.; Wu, X. Novel negative poisson’s ratio lattice structures with enhanced stiffness and energy absorption capacity. Materials 2018, 11, 1095. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.M.; Magkiriadis, I.; Harrigan, J.J. Compressive strain at the onset of densification of cellular solids. J. Cell. Plast. 2006, 42, 371–392. [Google Scholar] [CrossRef]
- Ha, N.S.; Lu, G. Thin-walled corrugated structures: A review of crashworthiness designs and energy absorption characteristics. Thin-Walled Struct. 2020, 157, 106995. [Google Scholar] [CrossRef]
- Kahraman, M.F.; Genel, K. Bending performance of the AuxOcta multi-cellular beam structure. Eng. Struct. 2023, 294, 116737. [Google Scholar] [CrossRef]
- Kahraman, M.F.; Genel, K. Effect of angle and thickness of cell wall on bending behavior of auxetic beam. Mater. Today Commun. 2024, 38, 108339. [Google Scholar] [CrossRef]
- Kahraman, M.F.; İrIç, S.; Genel, K. Comparative failure behavior of metal honeycomb structures under bending: A finite element-based study. Eng. Fail. Anal. 2024, 157, 107963. [Google Scholar] [CrossRef]
- Ozdemir, Z.; Tyas, A.; Goodall, R.; Askes, H. Energy absorption in lattice structures in dynamics: Nonlinear FE simulations. Int. J. Impact Eng. 2017, 102, 1–15. [Google Scholar] [CrossRef]
- Nasrullah, A.I.H.; Santosa, S.P.; Dirgantara, T. Design and optimization of crashworthy components based on lattice structure configuration. Structures 2020, 26, 969–981. [Google Scholar] [CrossRef]
- Campanelli, S.L.; Contuzzi, N.; Ludovico, A.D.; Caiazzo, F.; Cardaropoli, F.; Sergi, V. Manufacturing and characterization of Ti6Al4V lattice components manufactured by selective laser melting. Materials 2014, 7, 4803–4822. [Google Scholar] [CrossRef] [PubMed]
- Cronau, J.; Engstler, F. Energy absorption of 3D printed stochastic lattice structures under impact loading—Design parameters, manufacturing, and testing. Prog. Addit. Manuf. 2025, 10, 3145–3156. [Google Scholar] [CrossRef]
- Schneider, J.; Kumar, S. Comparative performance evaluation of microarchitected lattices processed via SLS, MJ, and DLP 3D printing methods: Experimental investigation and modelling. J. Mater. Res. Technol. 2023, 26, 7182–7198. [Google Scholar] [CrossRef]
- Nasim, M.; Galvanetto, U. Mechanical characterisation of additively manufactured PA12 lattice structures under quasi-static compression. Mater. Today Commun. 2021, 29, 102902. [Google Scholar] [CrossRef]
- Osswald, P.V.; Obst, P.; Capote, G.A.M.; Friedrich, M.; Rietzel, D.; Witt, G. Failure criterion for PA 12 multi-jet fusion additive manufactured parts. Addit. Manuf. 2021, 37, 101668. [Google Scholar] [CrossRef]
- Calignano, F.; Giuffrida, F.; Galati, M. Effect of the build orientation on the mechanical performance of polymeric parts produced by multi jet fusion and selective laser sintering. J. Manuf. Process. 2021, 65, 271–282. [Google Scholar] [CrossRef]
- Koh, Z.H.; Chen, K.; Du, H.; Zeng, J.; Zhou, K. Long-term ageing effect on mechanical properties of polyamide 12 printed by Multi-Jet-Fusion. Int. J. Mech. Sci. 2023, 256, 108513. [Google Scholar] [CrossRef]
- Khorasani, M.; MacDonald, E.; Downing, D.; Ghasemi, A.; Leary, M.; Dash, J.; Sharabian, E.; Almalki, A.; Brandt, M.; Bateman, S. Multi Jet Fusion (MJF) of polymeric components: A review of process, properties and opportunities. Addit. Manuf. 2024, 91, 104331. [Google Scholar] [CrossRef]
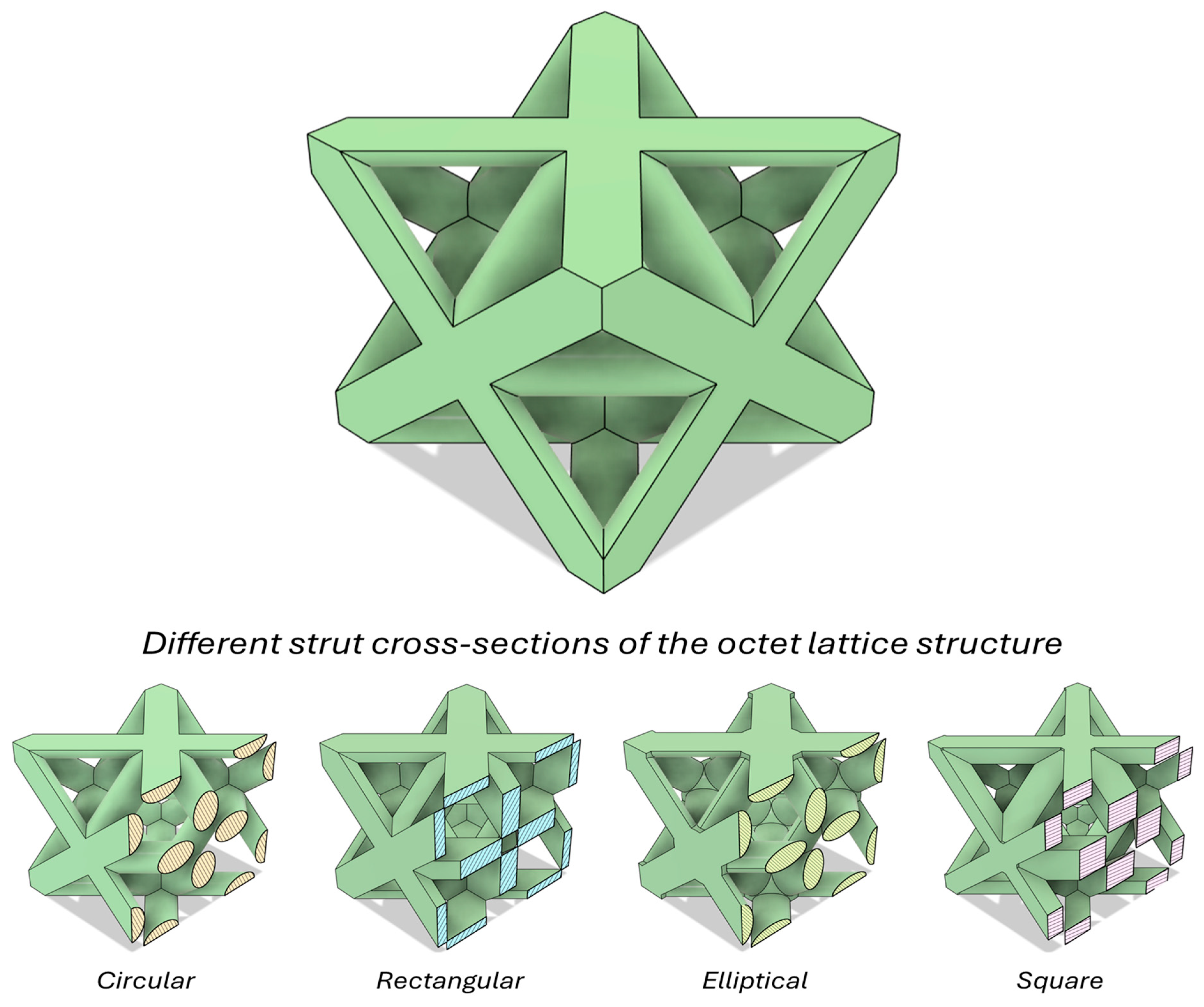



| Category | Measurement | Value | Method |
|---|---|---|---|
| General properties | Powder melting point (DSC) | 187 °C | ASTM D3418 [32] |
| Particle size | 60 µm | ASTM D3451 [33] | |
| Bulk density of powder | 0.425 g/cm3 | ASTM D1895 [34] | |
| Density of parts | 1.01 g/cm3 | ASTM D792 [35] | |
| Mechanical properties | Tensile strength, max load, XY | 48 MPa | ASTM D638 [36] |
| Tensile strength, max load, Z | 48 MPa | ASTM D638 [36] | |
| Tensile modulus, XY | 1700 MPa | ASTM D638 [36] | |
| Tensile modulus, Z | 1800 MPa | ASTM D638 [36] | |
| Elongation at break, XY | 20% | ASTM D638 [36] | |
| Elongation at break, Z | 15% | ASTM D638 [36] | |
| Flexural strength (@ 5%), XY | 65 MPa | ASTM D790 [37] | |
| Flexural strength (@ 5%), Z | 70 MPa | ASTM D790 [37] | |
| Flexural modulus, XY | 1730 MPa | ASTM D790 [37] | |
| Flexural modulus, Z | 1730 MPa | ASTM D790 [37] | |
| Izod impact notched (@ 3.2 mm, 23 °C), XYZ | 3.5 kJ/m2 | ASTM D256 [38] |
| Strut Geometry | Densification Strain (mm/mm) | Mass (g) | σmean | σmax | Energy Absorbed | CSE | SEA |
|---|---|---|---|---|---|---|---|
| (MPa) | (MPa) | (J) | (MPa/MPa) | (J/g) | |||
| Circular | 0.62 | 2.5 | 3.24 | 4.22 | 2.01 | 0.77 | 0.79 |
| S.D. | ±0.01 | ±0.01 | ±0.00 | ±0.02 | ±0.03 | ±0.01 | ±0.03 |
| Elliptical_0° | 0.59 | 2.5 | 2.74 | 3.74 | 1.62 | 0.74 | 0.63 |
| S.D. | ±0.01 | ±0.01 | ±0.00 | ±0.03 | ±0.03 | ±0.01 | ±0.03 |
| Elliptical_90° | 0.55 | 2.5 | 4.29 | 5.16 | 2.36 | 0.84 | 0.92 |
| S.D. | ±0.01 | ±0.01 | ±0.01 | ±0.02 | ±0.04 | ±0.01 | ±0.04 |
| Rectangular_0° | 0.6 | 2.5 | 3.52 | 4.41 | 2.11 | 0.8 | 0.82 |
| S.D. | ±0.01 | ±0.00 | ±0.01 | ±0.02 | ±0.03 | ±0.01 | ±0.03 |
| Rectangular_90° | 0.53 | 2.5 | 4.36 | 5.19 | 2.31 | 0.84 | 0.9 |
| S.D. | ±0.01 | ±0.00 | ±0.01 | ±0.02 | ±0.04 | ±0.01 | ±0.04 |
| Square | 0.58 | 2.5 | 3.48 | 4.18 | 2.02 | 0.83 | 0.79 |
| S.D. | ±0.01 | ±0.00 | ±0.01 | ±0.03 | ±0.03 | ±0.01 | ±0.03 |
| Diamond | 0.59 | 2.5 | 3.1 | 3.9 | 1.83 | 0.8 | 0.72 |
| S.D. | ±0.01 | ±0.00 | ±0.01 | ±0.03 | ±0.03 | ±0.01 | ±0.03 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yalçın, M.M.; İriç, S.; İriç, D.; Elsayed, M.S.A. The Role of Cross-Sectional Design and Orientation in Governing Energy Absorption of Additively Manufactured Polyamide 12 (PA12) Octet Lattices. Polymers 2025, 17, 2817. https://doi.org/10.3390/polym17212817
Yalçın MM, İriç S, İriç D, Elsayed MSA. The Role of Cross-Sectional Design and Orientation in Governing Energy Absorption of Additively Manufactured Polyamide 12 (PA12) Octet Lattices. Polymers. 2025; 17(21):2817. https://doi.org/10.3390/polym17212817
Chicago/Turabian StyleYalçın, Muhammet Muaz, Sedat İriç, Derya İriç, and Mostafa S. A. Elsayed. 2025. "The Role of Cross-Sectional Design and Orientation in Governing Energy Absorption of Additively Manufactured Polyamide 12 (PA12) Octet Lattices" Polymers 17, no. 21: 2817. https://doi.org/10.3390/polym17212817
APA StyleYalçın, M. M., İriç, S., İriç, D., & Elsayed, M. S. A. (2025). The Role of Cross-Sectional Design and Orientation in Governing Energy Absorption of Additively Manufactured Polyamide 12 (PA12) Octet Lattices. Polymers, 17(21), 2817. https://doi.org/10.3390/polym17212817






