From Research Trend to Performance Prediction: Metaheuristic-Driven Machine Learning Optimization for Cement Pastes Containing Bio-Based Phase Change Materials
Abstract
1. Introduction
2. Techniques and Methodology
2.1. Bibliometric Analysis
2.1.1. Literature Retrieval
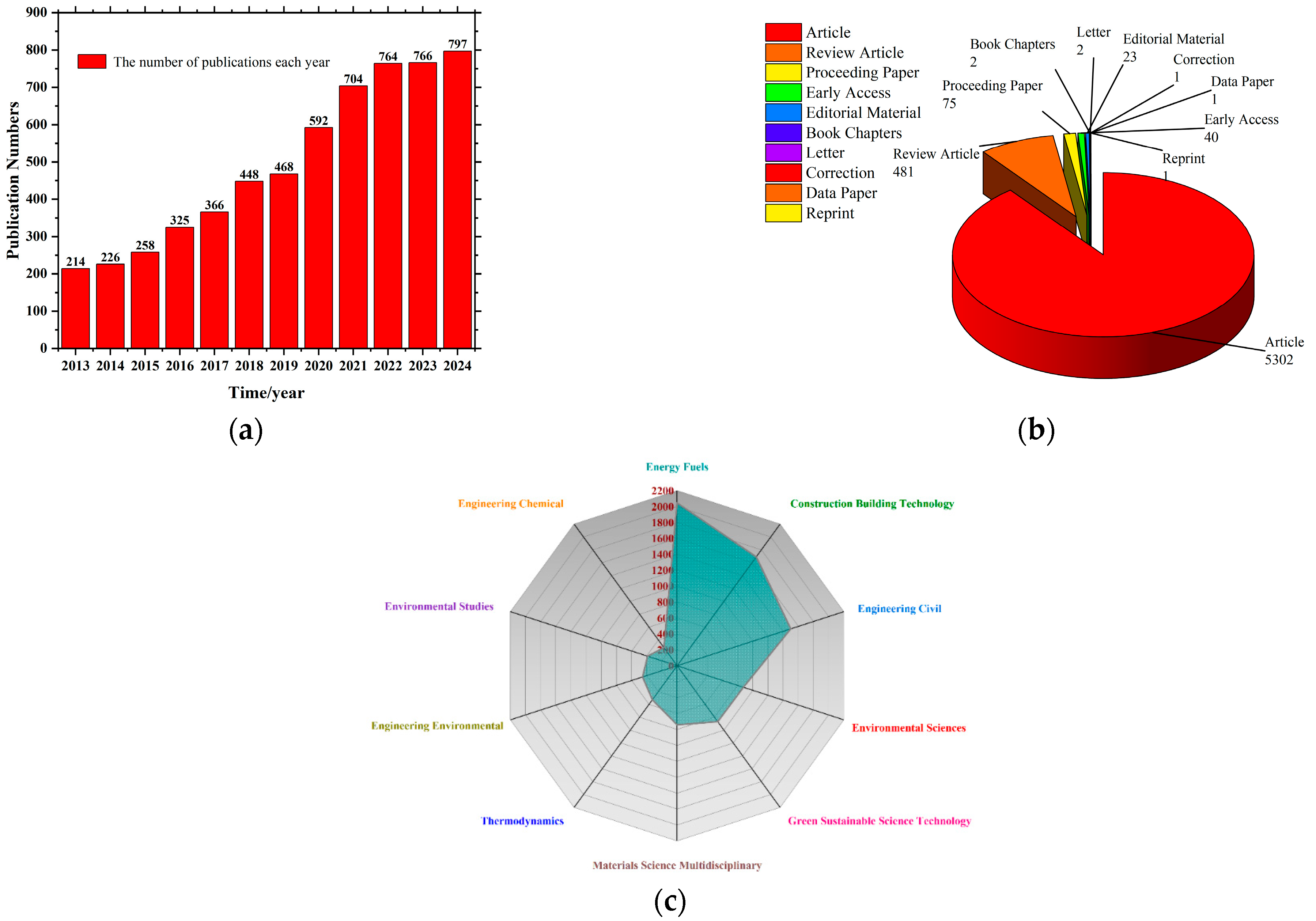
2.1.2. Publication Trends
2.1.3. Knowledge Network Analysis
- (1)
- Country Collaboration Network
- (2)
- Institutional Collaboration Network
- (3)
- High-Impact Literature and Knowledge Diffusion
- (4)
- Author Co-Citation Analysis
- (5)
- Author Collaboration Network
- (6)
- Journal Co-Citation Analysis
2.2. Evolution of Research Trends
2.2.1. Main Terms Analysis
2.2.2. Performance Evaluation of Bio-Based Phase Change Materials
2.2.3. Analysis of Thermal and Mechanical Characteristics in Cement Pastes with Different BPCMs
2.3. Machine Learning Model
2.3.1. Support Vector Regression (SVR)
2.3.2. Random Forest (RF)
2.3.3. Extreme Gradient Boosting (XGBoost)
2.3.4. Categorical Boosting (CatBoost)
2.4. Optimization Algorithms
2.4.1. Genetic Algorithm (GA)
2.4.2. Particle Swarm Optimization (PSO)
2.4.3. Whale Optimization Algorithm (WOA)
2.4.4. Grey Wolf Optimizer (GWO)
2.4.5. Firefly Algorithm (FFA)
2.5. Development of Predictive Models
3. Results and Discussion
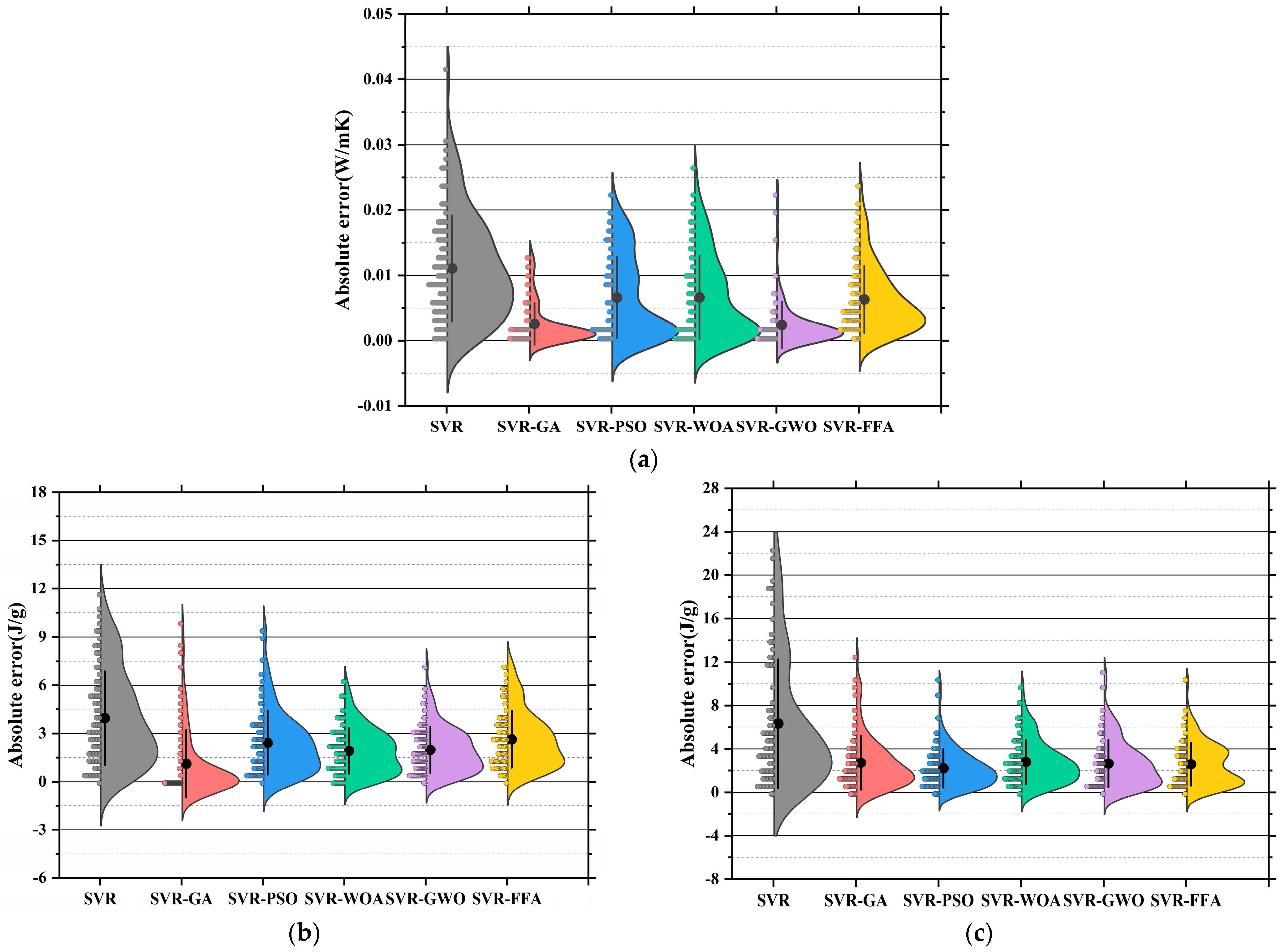
3.1. Performance Prediction Based on Support Vector Regression and Optimized Hybrid Models
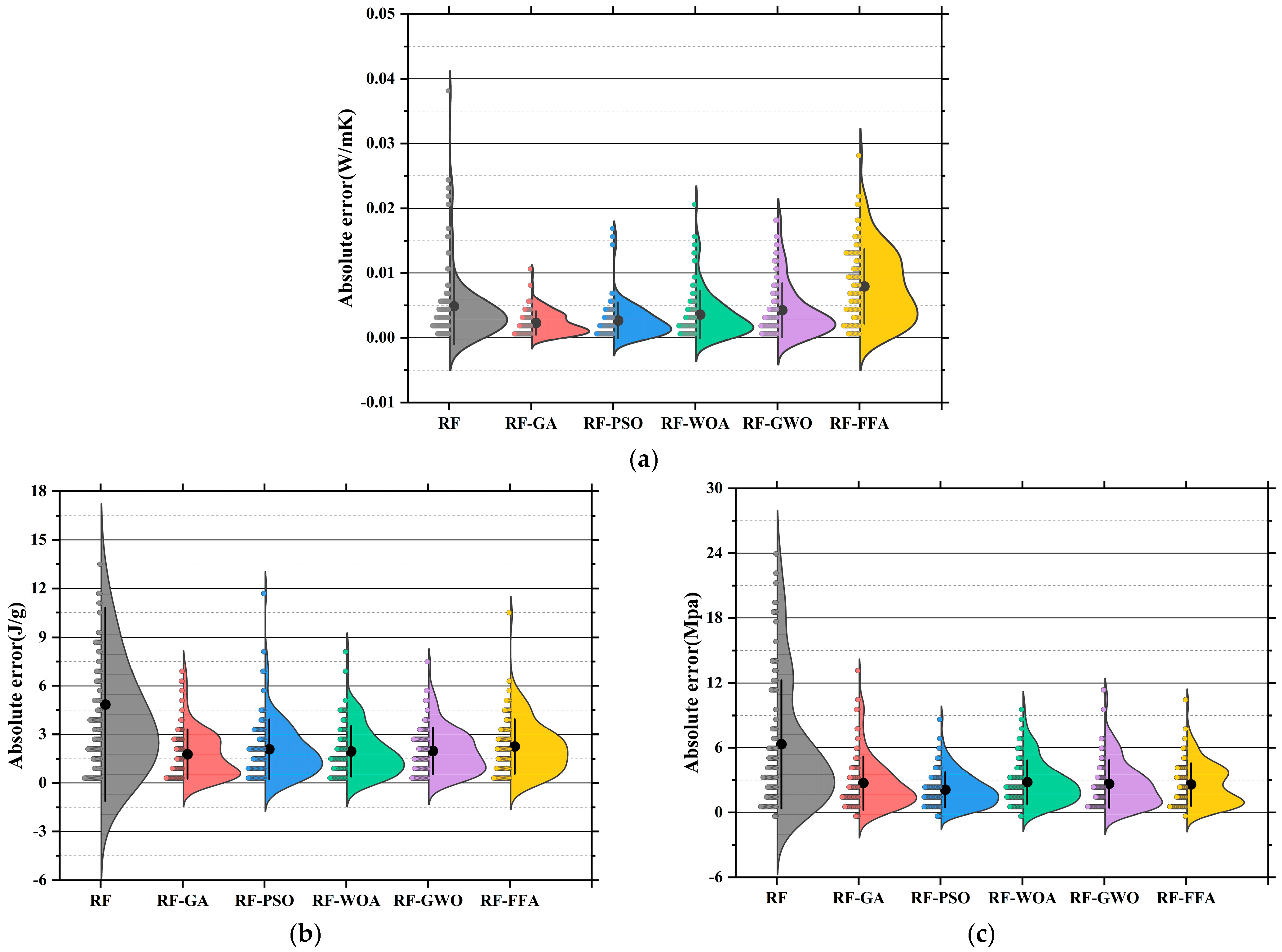
3.2. Performance Prediction Based on Random Forest and Optimized Hybrid Models
3.3. Performance Prediction Based on Extreme Gradient Boosting and Optimized Hybrid Models
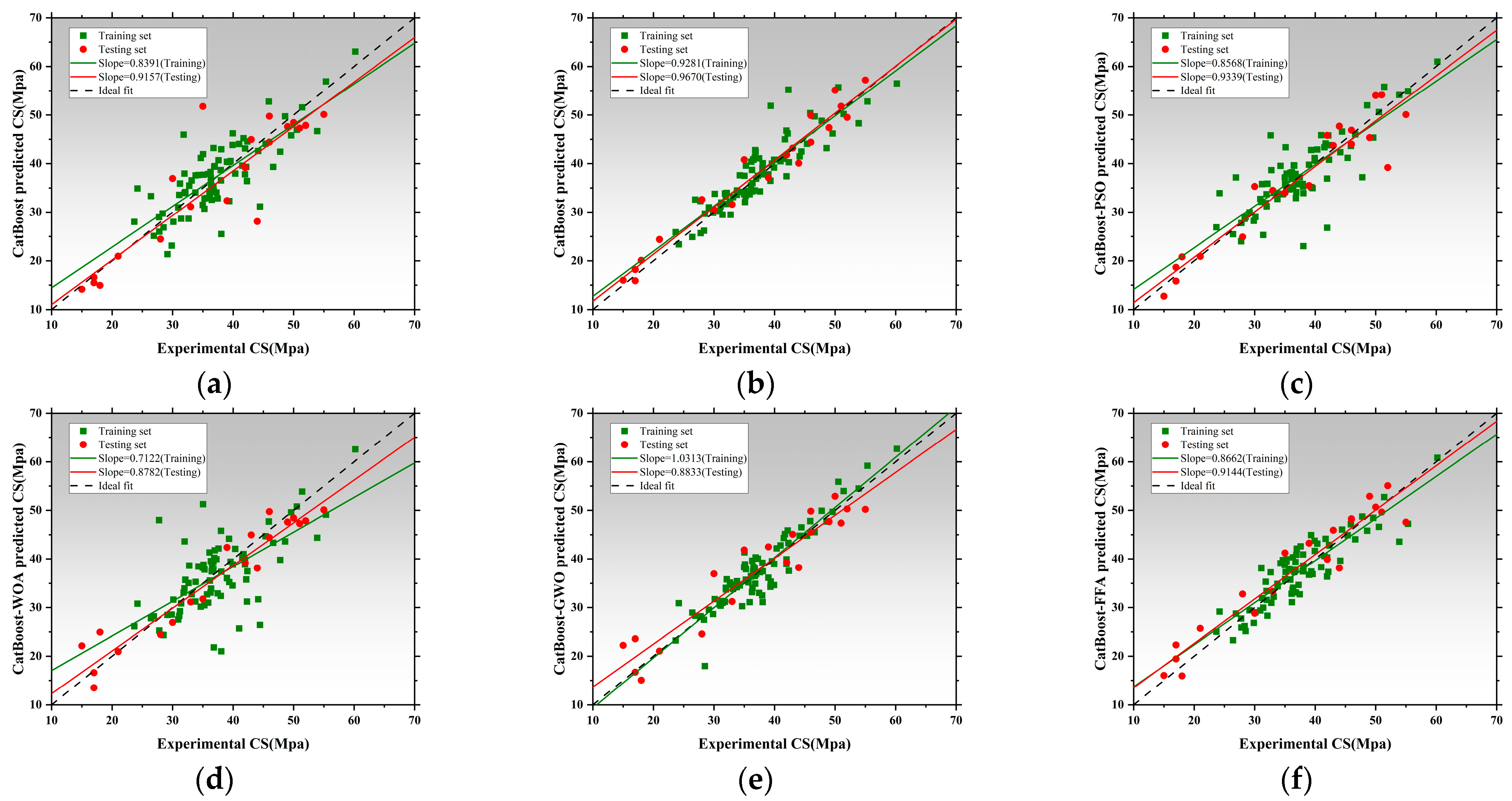
3.4. Performance Prediction Based on Categorical Boosting and Optimized Hybrid Models
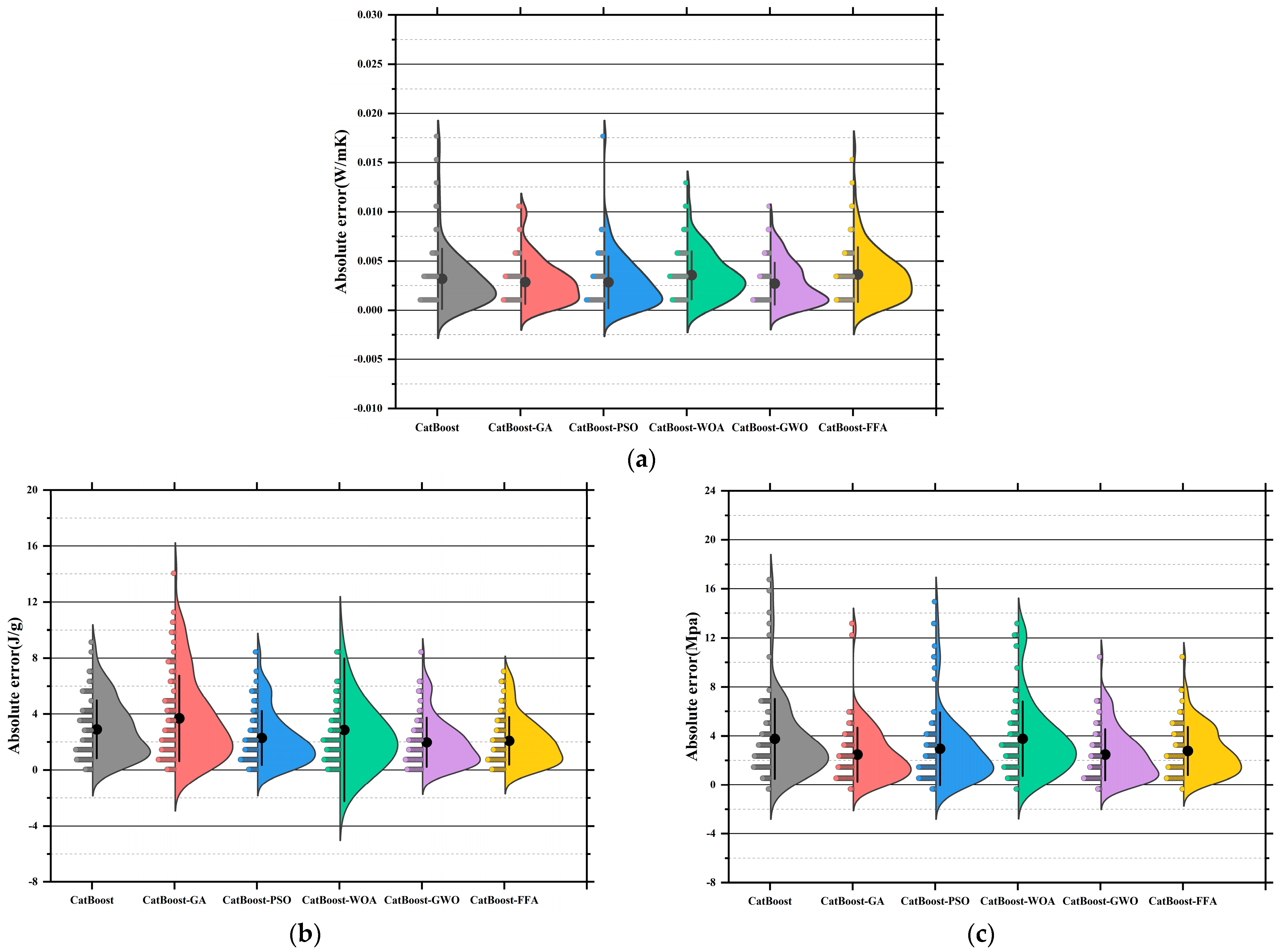
3.5. Comparative Evaluation of Model Accuracy
3.6. Future Improvements
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Osibodu, S.J.; Adeyinka, A.M.; Mbelu, O.V. Phase Change Material Integration in Concrete for Thermal Energy Storage: Techniques and Applications in Sustainable Building. Sustain. Energy Res. 2024, 11, 45. [Google Scholar] [CrossRef]
- Yadav, A.; Samykano, M.; Pandey, A.K.; Tyagi, V.V.; Devarajan, R.; Sudhakar, K.; Noor, M.M. A Systematic Review on Bio-Based Phase Change Materials. Int. J. Automot. Mech. Eng. 2023, 20, 10547–10558. [Google Scholar] [CrossRef]
- Yu, Z.; Shao, R.; Li, J.; Wu, C. An In-Depth Review of Phase Change Materials in Concrete for Enhancing Building Energy-Efficient Temperature Control Systems. J. Energy Storage 2024, 104, 114533. [Google Scholar] [CrossRef]
- Ling, T.-C.; Poon, C.-S. Use of Phase Change Materials for Thermal Energy Storage in Concrete: An Overview. Constr. Build. Mater. 2013, 46, 55–62. [Google Scholar] [CrossRef]
- Rathore, P.K.S.; Shukla, S.K. Potential of Macroencapsulated PCM for Thermal Energy Storage in Buildings: A Comprehensive Review. Constr. Build. Mater. 2019, 225, 723–744. [Google Scholar] [CrossRef]
- Eddhahak-Ouni, A.; Drissi, S.; Colin, J.; Neji, J.; Care, S. Experimental and Multi-Scale Analysis of the Thermal Properties of Portland Cement Concretes Embedded with Microencapsulated Phase Change Materials (PCMs). Appl. Therm. Eng. 2014, 64, 32–39. [Google Scholar] [CrossRef]
- Ramakrishnan, S.; Sanjayan, J.; Wang, X.; Alam, M.; Wilson, J. A Novel Paraffin/Expanded Perlite Composite Phase Change Material for Prevention of PCM Leakage in Cementitious Composites. Appl. Energy 2015, 157, 85–94. [Google Scholar] [CrossRef]
- Jeon, I.K.; Azzam, A.; Al Jebaei, H.; Kim, Y.R.; Aryal, A.; Baltazar, J.C. Effects of Shape-Stabilized Phase Change Materials in Cementitious Composites on Thermal-Mechanical Properties and Economic Benefits. Appl. Therm. Eng. 2023, 219, 119444. [Google Scholar] [CrossRef]
- Marchi, S.; Pagliolico, S.; Sassi, G. Characterization of Panels Containing Micro-Encapsulated Phase Change Materials. Energy Convers. Manag. 2013, 74, 261–268. [Google Scholar] [CrossRef]
- Rashid, F.L.; Al-Obaidi, M.A.; Dulaimi, A.; Mahmood, D.M.N.; Sopian, K. A Review of Recent Improvements, Developments, and Effects of Using Phase-Change Materials in Buildings to Store Thermal Energy. Design 2023, 7, 90. [Google Scholar] [CrossRef]
- Nalla, B.T.; Subbiah, G.; Das, S.N.; Kumar, S.; Swarnkar, S.K.; Kaliappan, N. Bio-Based Phase-Change Materials for Thermal Energy Storage: Recent Advances, Challenges, and Outlook. Results Eng. 2025, 28, 107087. [Google Scholar]
- Siddesh, J.S.; Shivaprasad, K.N.; Yang, H.M. Enhancing the Thermal Performance of Cementitious Composites: A Comprehensive Review of Phase Change Material Integration. Appl. Therm. Eng. 2025, 268, 125849. [Google Scholar] [CrossRef]
- Kumar, N.; Thapliyal, P.C.; Kumar, A.; Kumar, A. A Mini Review on Paraffin-Graphene and Related Hybrid Phase Change Materials for Building Energy Applications. Energy Storage 2023, 5, e350. [Google Scholar]
- Zadshir, M.; Kim, B.W.; Yin, H. Bio-Based Phase Change Materials for Sustainable Development. Materials 2024, 17, 4816. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.; Han, J.; Shen, Y.; Khan, S.Y.; Ji, W.; Jin, H.; Kumar, M. The Contribution of Artificial Intelligence to Phase Change Materials in Thermal Energy Storage: From Prediction to Optimization. Renew. Energy 2025, 238, 121973. [Google Scholar] [CrossRef]
- da Cunha, S.R.L.; de Aguiar, J.L.B. Phase Change Materials and Energy Efficiency of Buildings: A Review of Knowledge. J. Energy Storage 2020, 27, 101083. [Google Scholar] [CrossRef]
- Liu, L.; Hammami, N.; Trovalet, L.; Bigot, D.; Habas, J.P.; Malet-Damour, B. Description of Phase Change Materials (PCMs) Used in Buildings under Various Climates: A Review. J. Energy Storage 2022, 56, 105760. [Google Scholar] [CrossRef]
- Mehrizi, A.A.; Karimi-Maleh, H.; Naddafi, M.; Karimi, F. Application of bio-based phase change materials for effective heat management. J. Energy Storage 2023, 61, 106859. [Google Scholar] [CrossRef]
- Shi, T.; Liu, Y.; Hu, Z.; Cen, M.; Zeng, C.; Xu, J.; Zhao, Z. Deformation Performance and Fracture Toughness of Carbon Nanofiber-Modified Cement-Based Materials. ACI Mater. J. 2022, 119, 119–128. [Google Scholar]
- Yang, H.; Cui, H.; Tang, W.; Li, Z.; Han, N.; Xing, F. A Critical Review on Research Progress of Graphene/Cement Based Composites. Compos. Part A Appl. Sci. Manuf. 2017, 102, 273–296. [Google Scholar] [CrossRef]
- Janjaroen, T.; Khammahong, S.; Tuichai, W.; Karaphun, A.; Phrompet, C.; Sriwong, C.; Ruttanapun, C. The Mechanical and Thermal Properties of Cement CAST Mortar/Graphene Oxide Composites Materials. Int. J. Concr. Struct. Mater. 2022, 16, 34. [Google Scholar] [CrossRef]
- Yadav, A.; Pandey, A.K.; Samykano, M.; Kalidasan, B.; Said, Z. A Review of Organic Phase Change Materials and Their Adaptation for Thermal Energy Storage. Int. Mater. Rev. 2024, 69, 380–446. [Google Scholar] [CrossRef]
- Marani, A.; Nehdi, M.L. Machine Learning Prediction of Compressive Strength for Phase Change Materials Integrated Cementitious Composites. Constr. Build. Mater. 2020, 265, 120286. [Google Scholar] [CrossRef]
- Shafaie, V.; Rad, M.M. DEM-driven investigation and AutoML-enhanced prediction of macroscopic behavior in cementitious composites with variable frictional parameters. Mater. Des. 2025, 254, 114069. [Google Scholar] [CrossRef]
- Al-Taai, S.R.; Azize, N.M.; Thoeny, Z.A.; Imran, H.; Bernardo, L.F.; Al-Khafaji, Z. XGBoost Prediction Model Optimized with Bayesian for the Compressive Strength of Eco-Friendly Concrete Containing Ground Granulated Blast Furnace Slag and Recycled Coarse Aggregate. Appl. Sci. 2023, 13, 8889. [Google Scholar] [CrossRef]
- Ahmad, A.; Ostrowski, K.A.; Maślak, M.; Farooq, F.; Mehmood, I.; Nafees, A. Comparative Study of Supervised Machine Learning Algorithms for Predicting the Compressive Strength of Concrete at High Temperature. Materials 2021, 14, 4222. [Google Scholar] [CrossRef]
- Hassan, R.; Baghban, A. Pioneering Machine Learning Techniques to Estimate Thermal Conductivity of Carbon-Based Phase Change Materials: A Comprehensive Modeling Framework. Case Stud. Therm. Eng. 2025, 73, 106648. [Google Scholar] [CrossRef]
- Moein, M.M.; Saradar, A.; Rahmati, K.; Mousavinejad, S.H.G.; Bristow, J.; Aramali, V.; Karakouzian, M. Predictive Models for Concrete Properties Using Machine Learning and Deep Learning Approaches: A Review. J. Build. Eng. 2023, 63, 105444. [Google Scholar]
- Li, Y.; Shen, J.; Lin, H.; Li, Y. Optimization Design for Alkali-Activated Slag-Fly Ash Geopolymer Concrete Based on Artificial Intelligence Considering Compressive Strength, Cost, and Carbon Emission. J. Build. Eng. 2023, 75, 106929. [Google Scholar]
- Bragalia, M.; Lamastra, F.R.; Berrocal, J.A.; Paleari, L.; Nanni, F. Sustainable phase change materials (PCMs): Waste fat from cooking pork meat confined in polypropylene fibrous mat from waste surgical mask and porous bio-silica. Mater. Today Sustain. 2023, 23, 100454. [Google Scholar] [CrossRef]
- Lomada, R.R.; Sergei, S.; Vatin, N.I.; Joshi, A. ML Prediction and ANN-PSO Based Optimization for Compressive Strength of Blended Concrete. Cogent Eng. 2024, 11, 2380347. [Google Scholar] [CrossRef]
- Nguyen, H.; Cao, M.T.; Tran, X.L.; Tran, T.H.; Hoang, N.D. A Novel Whale Optimization Algorithm Optimized XGBoost Regression for Estimating Bearing Capacity of Concrete Piles. Neural Comput. Appl. 2023, 35, 3825–3852. [Google Scholar] [CrossRef]
- Urkude, N.; Hora, M.S.; Utkarsh. Enhancing Machine Learning Models with Metaheuristic Optimization Techniques for Accurate Prediction of PSC in FRP-Reinforced Concrete Slabs. Mech. Adv. Mater. Struct. 2024, 32, 3591–3607. [Google Scholar] [CrossRef]
- Yang, P.; Li, C.; Qiu, Y. Metaheuristic Optimization of Random Forest for Predicting Punch Shear Strength of FRP-Reinforced Concrete Beams. Materials 2023, 16, 4034. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, G.; Zhang, H.; Zhang, Y.; Yang, X. Predicting the Compressive Strength of Environmentally Friendly Concrete Using Multiple Machine Learning Algorithms. Buildings 2024, 14, 190. [Google Scholar] [CrossRef]
- Karimi Sharafshadeh, B.; Ketabdari, M.J.; Azarsina, F.; Amiri, M.; Nehdi, M.L. New Fuzzy-Heuristic Methodology for Analyzing Compression Load Capacity of Composite Columns. Buildings 2023, 13, 125. [Google Scholar] [CrossRef]
- Donthu, N.; Kumar, S.; Mukherjee, D.; Pandey, N.; Lim, W.M. How to Conduct a Bibliometric Analysis: An Overview and Guidelines. J. Bus. Res. 2021, 133, 285–296. [Google Scholar] [CrossRef]
- Marzi, G.; Balzano, M.; Caputo, A.; Pellegrini, M.M. Guidelines for Bibliometric-Systematic Literature Reviews: 10 Steps to Combine Analysis, Synthesis and Theory Development. Int. J. Manag. Rev. 2025, 27, 81–103. [Google Scholar] [CrossRef]
- Kumar, R. Bibliometric Analysis: Comprehensive Insights into Tools, Techniques, Applications, and Solutions for Research Excellence. Spectr. Eng. Manag. Sci. 2025, 3, 45–62. [Google Scholar] [CrossRef]
- Arachchi, K.K.; Mirza, O.; Mashiri, F.; Pathirana, S. Systematic Review of the Use of Phase Change Material (PCM) in Concrete and the Fire Performance of PCM in Concrete. Aust. J. Struct. Eng. 2025, 26, 175–188. [Google Scholar] [CrossRef]
- Al-Yasiri, Q.; Szabó, M. Case study on the optimal thickness of phase change material incorporated composite roof under hot climate conditions. Case Stud. Constr. Mater. 2021, 14, e00522. [Google Scholar] [CrossRef]
- Al-Yasiri, Q.; Szabó, M. Incorporation of phase change materials into building envelope for thermal comfort and energy saving: A comprehensive analysis. J. Build. Eng. 2021, 36, 102122. [Google Scholar] [CrossRef]
- Baetens, R.; Jelle, B.P.; Gustavsen, A. Phase change materials for building applications: A state-of-the-art review. Energy Build. 2010, 42, 1361–1368. [Google Scholar] [CrossRef]
- Boussaba, L.; Makhlouf, S.; Foufa, A.; Lefebvre, G.; Royon, L. vegetable fat: A low-cost bio-based phase change material for thermal energy storage in buildings. J. Build. Eng. 2019, 21, 222–229. [Google Scholar] [CrossRef]
- Chen, F.; Wolcott, M. Polyethylene/paraffin binary composites for phase change material energy storage in building: A morphology, thermal properties, and paraffin leakage study. Sol. Energy Mater. Sol. Cells 2015, 137, 79–85. [Google Scholar] [CrossRef]
- Qin, Y.; Ghalambaz, M.; Sheremet, M.; Fteiti, M.; Alresheedi, F. A bibliometrics study of phase change materials (PCMs). J. Energy Storage 2023, 73, 108987. [Google Scholar] [CrossRef]
- Alipour, A.; Eslami, F.; Sadrameli, S.M. A novel bio-based phase change material of methyl palmitate and decanoic acid eutectic mixture: Thermodynamic modeling and thermal performance. Chem. Thermodyn. Therm. Anal. 2023, 10, 100111. [Google Scholar] [CrossRef]
- Wu, D.; Rahim, M.; El Ganaoui, M.; Bennacer, R.; Liu, B. Multilayer assembly of phase change material and bio-based concrete: A passive envelope to improve the energy and hygrothermal performance of buildings. Energy Convers. Manag. 2022, 257, 115454. [Google Scholar] [CrossRef]
- Das, D.; Crosby, R.; Paul, M.C. A comprehensive review on the form stable phase change materials for storing renewable heat preparation, characterization and application. J. Energy Storage 2025, 110, 115284. [Google Scholar] [CrossRef]
- Li, Y.; Nord, N.; Xiao, Q.; Tereshchenko, T. Building heating applications with phase change material: A comprehensive review. J. Energy Storage 2020, 31, 101634. [Google Scholar] [CrossRef]
- Cai, R.; Sun, Z.; Yu, H.; Meng, E.; Wang, J.; Dai, M. Review on optimization of phase change parameters in phase change material building envelopes. J. Build. Eng. 2021, 35, 101979. [Google Scholar] [CrossRef]
- Song, M.; Niu, F.; Mao, N.; Hu, Y.; Deng, S. Review on building energy performance improvement using phase change materials. Energy Build. 2018, 158, 776–793. [Google Scholar] [CrossRef]
- Benhorma, A.; Bensenouci, A.; Teggar, M.; Ismail, K.A.R.; Arıcı, M.; Mezaache, E.; Laouer, A.; Lino, F.A.M. Prospects and challenges of bio-based phase change materials: An up to date review. J. Energy Storage 2024, 90, 111713. [Google Scholar] [CrossRef]
- Chen, H.; Tsang, Y.P.; Wu, C.H. When text mining meets science mapping in the bibliometric analysis: A review and future opportunities. Int. J. Eng. Bus. Manag. 2023, 15, 18479790231222349. [Google Scholar] [CrossRef]
- Mabrouk, R.; Naji, H.; Benim, A.C.; Dhahri, H. A state of the art review on sensible and latent heat thermal energy storage processes in porous media: Mesoscopic simulation. Appl. Sci. 2022, 12, 6995. [Google Scholar] [CrossRef]
- Li, C.; Sun, Z.; Wang, Y.; Zhu, J.; Wu, J.; Feng, L.; Wen, X.; Cai, W.; Yu, H.; Wang, M.; et al. A novel biogenic porous core/shell-based shape-stabilized phase change material for building energy saving. J. Energy Storage 2024, 95, 112504. [Google Scholar] [CrossRef]
- Rmili, Y.; Ndiaye, K.; Plancher, L.; Tahar, Z.E.A.; Cousture, A.; Melinge, Y. Properties and durability of cementitious composites incorporating solid-solid phase change materials. Appl. Sci. 2024, 14, 2040. [Google Scholar] [CrossRef]
- Li, D.; Zhuang, B.; Chen, Y.; Li, B.; Landry, V.; Kaboorani, A.; Wang, X.A. Incorporation technology of bio-based phase change materials for building envelope: A review. Energy Build. 2022, 260, 111920. [Google Scholar] [CrossRef]
- Dams, B.; Maskell, D.; Shea, A.; Allen, S.; Cascione, V.; Walker, P. Upscaling bio-based construction: Challenges and opportunities. Build. Res. Inf. 2023, 51, 764–782. [Google Scholar] [CrossRef]
- Rathore, P.K.S.; Gupta, N.K.; Yadav, D.; Shukla, S.K.; Kaul, S. Thermal performance of the building envelope integrated with phase change material for thermal energy storage: An updated review. Sustain. Cities Soc. 2022, 79, 103690. [Google Scholar] [CrossRef]
- Huang, J.; Li, M.; Fan, D. Core-shell particles for devising high-performance full-day radiative cooling paint. Appl. Mater. Today 2021, 25, 101209. [Google Scholar] [CrossRef]
- Cao, V.D.; Pilehvar, S.; Salas-Bringas, C.; Szczotok, A.M.; Bui, T.Q.; Carmona, M.; Rodriguez, J.F.; Kjøniksen, A.-L. Thermal analysis of geopolymer concrete walls containing microencapsulated phase change materials for building applications. Sol. Energy 2019, 178, 295–307. [Google Scholar] [CrossRef]
- Jin Ong, P.; Leow, Y.; Yun Debbie Soo, X.; Chua, M.H.; Ni, X.; Suwardi, A.; Tan, C.K.I.; Zheng, R.; Wei, F.; Xu, J.; et al. Valorization of Spent coffee Grounds: A sustainable resource for Bio-based phase change materials for thermal energy storage. Waste Manag. 2023, 157, 339–347. [Google Scholar] [CrossRef] [PubMed]
- Mondal, S. Phase change materials for smart textiles–An overview. Appl. Therm. Eng. 2008, 28, 1536–1550. [Google Scholar] [CrossRef]
- Fabiani, C.; Pisello, A.L.; Barbanera, M.; Cabeza, L.F. Palm Oil-Based Bio-PCM for Energy Efficient Building Applications: Multipurpose Thermal Investigation and Life Cycle Assessment. J. Energy Storage 2020, 28, 101129. [Google Scholar] [CrossRef]
- Sarcinella, A.; Cunha, S.; Aguiar, I.; Aguiar, J.; Frigione, M. Sustainable organic phase change materials for sustainable energy efficiency solutions. Polymers 2025, 17, 1343. [Google Scholar] [CrossRef]
- Pinheiro, C.; Landi Jr, S.; Lima Jr, O.; Ribas, L.; Hammes, N.; Segundo, I.R.; Carneiro, J. Advancements in phase change materials in asphalt pavements for mitigation of urban heat island effect: Bibliometric analysis and systematic review. Sensors 2023, 23, 7741. [Google Scholar] [CrossRef]
- Xu, L.; Yang, R. Stearic acid/inorganic porous matrix phase change composite for hot water systems. Molecules 2019, 24, 1482. [Google Scholar] [CrossRef]
- Reddy, V.J.; Ghazali, M.F.; Kumarasamy, S. Innovations in phase change materials for diverse industrial applications: A comprehensive review. Results Chem. 2024, 8, 101552. [Google Scholar] [CrossRef]
- Rashid, F.L.; Al-Obaidi, M.A.; Dulaimi, A.; Bernardo, L.F.A.; Eleiwi, M.A.; Mahood, H.B.; Hashim, A. A review of recent improvements, developments, effects, and challenges on using phase-change materials in concrete for thermal energy storage and release. J. Compos. Sci. 2023, 7, 352. [Google Scholar] [CrossRef]
- Bao, X.; Memon, S.A.; Yang, H.; Dong, Z.; Cui, H. Thermal Properties of Cement-Based Composites for Geothermal Energy Applications. Materials 2017, 10, 462. [Google Scholar] [CrossRef]
- Sharma, R.; Jang, J.G.; Hu, J.W. Phase-Change Materials in Concrete: Opportunities and Challenges for Sustainable Construction and Building Materials. Materials 2022, 15, 335. [Google Scholar] [CrossRef] [PubMed]
- Junaid, M.F.; ur Rehman, Z.; Ijaz, N.; Farooq, R.; Khalid, U.; Ijaz, Z. Performance evaluation of cement-based composites containing phase change materials from energy management and construction standpoints. Constr. Build. Mater. 2024, 416, 135108. [Google Scholar] [CrossRef]
- Przybek, A.; Łach, M.; Romańska, P.; Ciemnicka, J.; Prałat, K.; Koper, A. Geopolymer Concretes with Organic Phase Change Materials—Analysis of Thermal Properties and Microstructure. Materials 2025, 18, 2557. [Google Scholar] [CrossRef]
- Jiao, K.; Lu, L.; Zhao, L.; Wang, G. Towards passive building thermal regulation: A state-of-the-art review on recent progress of PCM-integrated building envelopes. Sustainability 2024, 16, 6482. [Google Scholar] [CrossRef]
- Said, Z.; Pandey, A.K.; Tiwari, A.K.; Kalidasan, B.; Jamil, F.; Thakur, A.K.; Tyagi, V.; Sarı, A.; Ali, H.M. Nano-enhanced phase change materials: Fundamentals and applications. Prog. Energy Combust. Sci. 2024, 104, 101162. [Google Scholar] [CrossRef]
- Mishra, R.K.; Verma, K.; Mishra, V.; Chaudhary, B. A review on carbon-based phase change materials for thermal energy storage. J. Energy Storage 2022, 50, 104166. [Google Scholar] [CrossRef]
- Amaral, C.; Vicente, R.; Marques, P.A.A.P.; Barros-Timmons, A. Phase change materials and carbon nanostructures for thermal energy storage: A literature review. Renew. Sustain. Energy Rev. 2017, 79, 1212–1228. [Google Scholar] [CrossRef]
- Šavija, B.; Zhang, H.; Schlangen, E. Influence of microencapsulated phase change material (PCM) addition on (micro) mechanical properties of cement paste. Materials 2017, 10, 863. [Google Scholar] [CrossRef]
- Dehmous, M.; Franquet, E.; Lamrous, N. Mechanical and Thermal Characterizations of Various Thermal Energy Storage Concretes Including Low-Cost Bio-Sourced PCM. Energy Build. 2021, 241, 110878. [Google Scholar] [CrossRef]
- Sun, H.; Yu, K.; Jia, M.; Wang, Z.; Yang, Y.; Liu, Y. Heat-Stored Engineered Cementitious Composite Containing Microencapsulated n-Octadecane with Cenosphere Shell. Coatings 2025, 15, 128. [Google Scholar] [CrossRef]
- Orsini, F.; Marrone, P.; Santini, S.; Sguerri, L.; Asdrubali, F.; Baldinelli, G.; Bianchi, F.; Presciutti, A. Smart materials: Cementitious mortars and PCM mechanical and thermal characterization. Materials 2021, 14, 4163. [Google Scholar] [CrossRef] [PubMed]
- Zhu, M.; Li, J.; Wang, Y.; Meng, F. Experimental Study on Fire Resistance of Phase Change Energy Storage Concrete Partition Walls. Fire 2025, 8, 128. [Google Scholar] [CrossRef]
- Hassan, A.; Laghari, M.S.; Rashid, Y. Micro-encapsulated phase change materials: A review of encapsulation, safety and thermal characteristics. Sustainability 2016, 8, 1046. [Google Scholar] [CrossRef]
- Jha, S.K.; Sankar, A.; Zhou, Y.; Ghosh, A. Incorporation of phase change materials in buildings. Constr. Mater. 2024, 4, 676–703. [Google Scholar] [CrossRef]
- Mandal, S. Advancements in Phase Change Materials: Stabilization Techniques and Applications. Prabha Mater. Sci. Lett. 2024, 3, 254–267. [Google Scholar] [CrossRef]
- Min, L.; Liu, Y.; Wang, C.; Du, Y.; Fang, H. A novel stereotyped phase change material with a low leakage rate for new energy storage building applications. Constr. Build. Mater. 2024, 433, 136757. [Google Scholar] [CrossRef]
- Navarro, L.; Solé, A.; Martín, M.; Barreneche, C.; Olivieri, L.; Tenorio, J.A.; Cabeza, L.F. Benchmarking of useful phase change materials for a building application. Energy Build. 2019, 182, 45–50. [Google Scholar] [CrossRef]
- Abhat, A. Low temperature latent heat thermal energy storage: Heat storage materials. Sol. Energy 1983, 30, 313–332. [Google Scholar] [CrossRef]
- Li, G.; Xu, G.; Tao, Z. Effect on the thermal properties of building mortars with microencapsulated phase change materials for radiant floors. Buildings 2023, 13, 2476. [Google Scholar] [CrossRef]
- Zhang, X.; Han, Z.; Liu, L.; Xia, X.; Liu, Q.; Duan, Y.; Wang, X. Experimental Study on Mechanical and Thermal Properties of Backfill Body with Paraffin Added. Energies 2023, 17, 217. [Google Scholar] [CrossRef]
- Gbekou, F.K.; Benzarti, K.; Boudenne, A.; Eddhahak, A.; Duc, M. Mechanical and thermophysical properties of cement mortars including bio-based microencapsulated phase change materials. Constr. Build. Mater. 2022, 352, 129056. [Google Scholar] [CrossRef]
- Cui, H.; Yang, S.; Memon, S.A. Development of carbon nanotube modified cement paste with microencapsulated phase-change material for structural-functional integrated application. Int. J. Mol. Sci. 2015, 16, 8027–8039. [Google Scholar] [CrossRef]
- Liu, F.; Wang, J.; Qian, X. Integrating phase change materials into concrete through microencapsulation using cenospheres. Cem. Concr. Compos. 2017, 80, 317–325. [Google Scholar] [CrossRef]
- Cabeza, L.F.; Castell, A.; Barreneche, C.D.; De Gracia, A.; Fernández, A.I. Materials used as PCM in thermal energy storage in buildings: A review. Renew. Sustain. Energy Rev. 2011, 15, 1675–1695. [Google Scholar] [CrossRef]
- Su, X.; Jiang, H.; Qin, T.; Lin, G. Particle Swarm Optimization-Support Vector Regression (PSO-SVR)-Based Rapid Prediction Method for Radiant Heat Transfer for a Spacecraft Vacuum Thermal Test. Appl. Sci. 2024, 14, 9407. [Google Scholar] [CrossRef]
- Nazir, K.; Memon, S.A.; Saurbayeva, A. Predicting the PCM-incorporated building’s performance using optimized linear kernel and tree-based machine learning methods. J. Energy Storage 2024, 94, 112495. [Google Scholar] [CrossRef]
- Cunha, S.; Parente, M.; Tinoco, J.; Aguiar, J. Leveraging machine learning for designing sustainable mortars with non-encapsulated PCMs. Sustainability 2024, 16, 6775. [Google Scholar] [CrossRef]
- Farooq, F.; Amin, M.N.; Khan, K.; Sadiq, M.R.; Javed, M.F.; Aslam, F.; Alyousef, R. A comparative study of random forest and genetic engineering programming for the prediction of compressive strength of high strength concrete (HSC). Appl. Sci. 2020, 10, 7330. [Google Scholar] [CrossRef]
- Liang, B.; Qin, W.; Liao, Z. A Differential Evolutionary-Based XGBoost for Solving Classification of Physical Fitness Test Data of College Students. Mathematics 2025, 13, 1405. [Google Scholar] [CrossRef]
- Chou, J.S.; Tsai, C.F.; Pham, A.D.; Lu, Y.H. Machine learning in concrete strength simulations: Multi-nation data analytics. Constr. Build. Mater. 2014, 73, 771–780. [Google Scholar] [CrossRef]
- Cook, R.; Lapeyre, J.; Ma, H.; Kumar, A. Prediction of compressive strength of concrete: Critical comparison of performance of a hybrid machine learning model with standalone models. J. Mater. Civ. Eng. 2019, 31, 04019255. [Google Scholar] [CrossRef]
- Ebid, A.; Deifalla, A. Using artificial intelligence techniques to predict punching shear capacity of lightweight concrete slabs. Materials 2022, 15, 2732. [Google Scholar] [CrossRef]
- Chen, D.; Luo, H.; Liu, Z.; Pan, J.; Wu, Y.; Wang, E.; Lu, C.; Wang, L.; Wang, W.; Ou, G. A Dual-Variable Selection Framework for Enhancing Forest Aboveground Biomass Estimation via Multi-Source Remote Sensing. Remote Sens. 2025, 15, 12939. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, T.; Tian, L.; Huang, B.; Yang, J.; Zeng, Z. Ada-xg-CatBoost: A combined forecasting model for gross ecosystem product (GEP) prediction. Sustainability 2024, 16, 7203. [Google Scholar] [CrossRef]
- Mehdary, A.; Chehri, A.; Jakimi, A.; Saadane, R. Hyperparameter optimization with genetic algorithms and XGBoost: A step forward in smart grid fraud detection. Sensors 2024, 24, 1230. [Google Scholar] [CrossRef] [PubMed]
- Al-Mudhafar, W.J.; Hasan, A.A.; Abbas, M.A.; Wood, D.A. Machine learning with hyperparameter optimization applied in facies-supported permeability modeling in carbonate oil reservoirs. Sci. Rep. 2025, 15, 12939. [Google Scholar] [CrossRef]
- Zheng, J.; Yao, T.; Yue, J.; Wang, M.; Xia, S. Compressive strength prediction of BFRC based on a novel hybrid machine learning model. Buildings 2023, 13, 1934. [Google Scholar] [CrossRef]
- Malashin, I.; Tynchenko, V.; Gantimurov, A.; Nelyub, V.; Borodulin, A. Boosting-Based Machine Learning Applications in Polymer Science: A Review. Polymers 2025, 17, 499. [Google Scholar] [CrossRef]
- Zhuo, H.; Li, T.; Lu, W.; Zhang, Q.; Ji, L.; Li, J. Prediction model for spontaneous combustion temperature of coal based on PSO-XGBoost algorithm. Sci. Rep. 2025, 15, 2752. [Google Scholar] [CrossRef]
- Zhao, Y.; Chen, Z.; Jian, X. A High-generalizability machine learning framework for analyzing the homogenized properties of short fiber-reinforced polymer composites. Polymers 2023, 15, 3962. [Google Scholar] [CrossRef]
- He, P.; Wu, W. Levy flight-improved grey wolf optimizer algorithm-based support vector regression model for dam deformation prediction. Front. Earth Sci. 2023, 11, 1122937. [Google Scholar] [CrossRef]
- Mabdeh, A.N.; Ajin, R.S.; Razavi-Termeh, S.V.; Ahmadlou, M.; Al-Fugara, A.K. Enhancing the performance of machine learning and deep learning-based flood susceptibility models by integrating grey wolf optimizer (GWO) algorithm. Remote Sens. 2024, 16, 2595. [Google Scholar] [CrossRef]
- Ahmed, H.U.; Mostafa, R.R.; Mohammed, A.; Sihag, P.; Qadir, A. Support vector regression (SVR) and grey wolf optimization (GWO) to predict the compressive strength of GGBFS-based geopolymer concrete. Neural Comput. Appl. 2023, 35, 2909–2926. [Google Scholar] [CrossRef]
- Huang, J.; Sabri, M.M.S.; Ulrikh, D.V.; Ahmad, M.; Alsaffar, K.A.M. Predicting the compressive strength of the cement-fly ash-slag ternary concrete using the firefly algorithm (FA) and random forest (RF) hybrid machine-learning method. Materials 2022, 15, 4193. [Google Scholar] [CrossRef]
- Wang, Q.A.; Zhang, J.; Huang, J. Simulation of the compressive strength of cemented tailing backfill through the use of firefly algorithm and random forest model. Shock Vib. 2021, 2021, 5536998. [Google Scholar] [CrossRef]
- Rahamathulla, M.Y.; Ramaiah, M. Optimizing Anomaly Detection Models for Edge IIoT with an Enhanced Firefly Algorithm-Based Hyperparameter Tuning Strategy. Results Eng. 2025, 27, 105843. [Google Scholar] [CrossRef]
- GB/T 50081-2019; Ministry of Housing and Urban-Rural Development of the People’s Republic of China. Standard for Test Methods of Physical and Mechanical Properties of Concrete. China Architecture & Building Press: Beijing, China, 2019.
- Nikbin, I.M.; Beygi, M.H.A.; Kazemi, M.T.; Amiri, J.V.; Rabbanifar, S.; Rahmani, E.; Rahimi, S. A comprehensive investigation into the effect of water to cement ratio and powder content on mechanical properties of self-compacting concrete. Constr. Build. Mater. 2014, 57, 69–80. [Google Scholar] [CrossRef]
- Sánchez-Mendieta, C.; Galán-Díaz, J.J.; Martinez-Lage, I. Relationships between density, porosity, compressive strength and permeability in porous concretes: Optimization of properties through control of the water-cement ratio and aggregate type. J. Build. Eng. 2024, 97, 110858. [Google Scholar] [CrossRef]
- Badarloo, B.; Lehner, P. Practical Aspects of Correlation Analysis of Compressive Strength from Destructive and Non-Destructive Methods in Different Directions. Infrastructures 2023, 8, 155. [Google Scholar] [CrossRef]
- Sayyar, M.; Weerasiri, R.R.; Soroushian, P.; Lu, J. Experimental and numerical study of shape-stable phase-change nanocomposite toward energy-efficient building constructions. Energy Build. 2014, 75, 249–255. [Google Scholar] [CrossRef]
- Sukontasukkul, P.; Uthaichotirat, P.; Sangpet, T.; Sisomphon, K.; Newlands, M.; Siripanichgorn, A.; Chindaprasirt, P. Thermal properties of lightweight concrete incorporating high contents of phase change materials. Constr. Build. Mater. 2019, 207, 431–439. [Google Scholar] [CrossRef]
- Suttaphakdee, P.; Dulsang, N.; Lorwanishpaisarn, N.; Kasemsiri, P.; Posi, P.; Chindaprasirt, P. Optimizing mix proportion and properties of lightweight concrete incorporated phase change material paraffin/recycled concrete block composite. Constr. Build. Mater. 2016, 127, 475–483. [Google Scholar] [CrossRef]
- Cunha, S.; Lima, M.; Aguiar, J.B. Influence of adding phase change materials on the physical and mechanical properties of cement mortars. Constr. Build. Mater. 2016, 127, 1–10. [Google Scholar] [CrossRef]
- Zalba, B.; Marín, J.M.; Cabeza, L.F.; Mehling, H. Review on thermal energy storage with phase change: Materials, heat transfer analysis and applications. Appl. Therm. Eng. 2003, 23, 251–283. [Google Scholar] [CrossRef]
- Zhang, C.; Pang, C.; Mao, Y.; Tang, Z. Effect and mechanism of polyethylene glycol (PEG) used as a phase change composite on cement paste. Materials 2022, 15, 2749. [Google Scholar] [CrossRef]
- Chem, Y.; Jiang, Q.H.; Xin, L.I. Research status and application of phase change materials. J. Mater. Eng. 2019, 47, 1–10. [Google Scholar]
- Shi, J.; Chen, Z.; Shao, S.; Zheng, J. Experimental and numerical study on effective thermal conductivity of novel form-stable basalt fiber composite concrete with PCMs for thermal storage. Appl. Therm. Eng. 2014, 66, 156–161. [Google Scholar] [CrossRef]
- Niall, D.; Kinnane, O.; West, R.P.; McCormack, S. Mechanical and thermal evaluation of different types of PCM-concrete composite panels. J. Struct. Integr. Maint. 2017, 2, 100–108. [Google Scholar] [CrossRef]
- Yang, J.; Zhou, J.; Nie, Z.; Liu, L. Preparation and Property Analysis of Phase Change Concrete PEG/SiO2-CPCM. J. Compos. Adv. Mater. 2019, 29, 21–26. [Google Scholar] [CrossRef]
- Ping, Z.H.; Nguyen, Q.T.; Chen, S.M.; Zhou, J.Q.; Ding, Y.D. States of water in different hydrophilic polymers-DSC and FTIR studies. Polymer 2001, 42, 8461–8467. [Google Scholar] [CrossRef]
- Alqurashi, M. Data-Driven Insights into Concrete Flow and Strength: Advancing Smart Material Design Using Machine Learning Strategies. Buildings 2025, 15, 2244. [Google Scholar] [CrossRef]
- Ghosh, A.; Ransinchung, G.D. Application of machine learning algorithm to assess the efficacy of varying industrial wastes and curing methods on strength development of geopolymer concrete. Constr. Build. Mater. 2022, 341, 127828. [Google Scholar] [CrossRef]
- Vakharia, V.; Gujar, R. Prediction of compressive strength and portland cement composition using cross-validation and feature ranking techniques. Constr. Build. Mater. 2019, 225, 292–301. [Google Scholar] [CrossRef]
- Ahmad, W.; Veeraghantla, V.S.S.C.S.; Byrne, A. Advancing sustainable concrete using biochar: Experimental and modelling study for mechanical strength evaluation. Sustainability 2025, 17, 2516. [Google Scholar] [CrossRef]
- Nafees, A.; Amin, M.N.; Khan, K.; Nazir, K.; Ali, M.; Javed, M.F.; Aslam, F.; Musarat, M.A.; Vatin, N.I. Modeling of mechanical properties of silica fume-based green concrete using machine learning techniques. Polymers 2021, 14, 30. [Google Scholar] [CrossRef]
- Chen, L.; Wang, Z.; Khan, A.A.; Khan, M.; Javed, M.F.; Alaskar, A.; Eldin, S.M. Development of predictive models for sustainable concrete via genetic programming-based algorithms. J. Mater. Res. Technol. 2023, 24, 6391–6410. [Google Scholar] [CrossRef]
- Shah, M.I.; Javed, M.F.; Aslam, F.; Alabduljabbar, H. Machine learning modeling integrating experimental analysis for predicting the properties of sugarcane bagasse ash concrete. Constr. Build. Mater. 2022, 314, 125634. [Google Scholar] [CrossRef]
- Ghazvinian, H.; Mousavi, S.F.; Karami, H.; Farzin, S.; Ehteram, M.; Hossain, M.S.; Fai, C.M.; Bin Hashim, H.; Singh, V.P.; Ros, F.C.; et al. Integrated support vector regression and an improved particle swarm optimization-based model for solar radiation prediction. PLoS ONE 2019, 14, e0217634. [Google Scholar] [CrossRef] [PubMed]
- Zhu, S.P.; Keshtegar, B.; Seghier, M.E.A.B.; Zio, E.; Taylan, O. Hybrid and enhanced PSO: Novel first order reliability method-based hybrid intelligent approaches. Comput. Methods Appl. Mech. Eng. 2022, 393, 114730. [Google Scholar] [CrossRef]
- Chen, W.; Hasanipanah, M.; Nikafshan Rad, H.; Jahed Armaghani, D.; Tahir, M.M. A new design of evolutionary hybrid optimization of SVR model in predicting the blast-induced ground vibration. Eng. Comput. 2021, 37, 1455–1471. [Google Scholar] [CrossRef]
- Chaabene, W.B.; Flah, M.; Nehdi, M.L. Machine learning prediction of mechanical properties of concrete: Critical review. Constr. Build. Mater. 2020, 260, 119889. [Google Scholar] [CrossRef]
- Xu, J.; Zhao, X.; Yu, Y.; Xie, T.; Yang, G.; Xue, J. Parametric sensitivity analysis and modelling of mechanical properties of normal-and high-strength recycled aggregate concrete using grey theory, multiple nonlinear regression and artificial neural networks. Constr. Build. Mater. 2019, 211, 479–491. [Google Scholar] [CrossRef]
- Bakouri, M.; Sultan, H.S.; Samad, S.; Togun, H.; Goodarzi, M. Predicting thermophysical properties enhancement of metal-based phase change materials using various machine learning algorithms. J. Taiwan Inst. Chem. Eng. 2023, 148, 104934. [Google Scholar] [CrossRef]
- Kottala, R.K.; Chigilipalli, B.K.; Mukuloth, S.; Shanmugam, R.; Kantumuchu, V.C.; Ainapurapu, S.B.; Cheepu, M. Thermal degradation studies and machine learning modelling of nano-enhanced sugar alcohol-based phase change materials for medium temperature applications. Energies 2023, 16, 2187. [Google Scholar] [CrossRef]
- Goud, M. A comprehensive investigation and artificial neural network modeling of shape stabilized composite phase change material for solar thermal energy storage. J. Energy Storage 2022, 48, 103992. [Google Scholar] [CrossRef]
- Goud, M.; Raval, F. A sustainable biochar-based shape stable composite phase change material for thermal management of a lithium-ion battery system and hybrid neural network modeling for heat flow prediction. J. Energy Storage 2022, 56, 106163. [Google Scholar]
- Wei, H.; Luo, K.; Xing, J.; Fan, J. Predicting co-pyrolysis of coal and biomass using machine learning approaches. Fuel 2022, 310, 122248. [Google Scholar] [CrossRef]
- Ozawa, T. A new method of analyzing thermogravimetric data. Bull. Chem. Soc. Jpn. 1965, 38, 1881–1886. [Google Scholar] [CrossRef]
- Starink, M.J. A new method for the derivation of activation energies from experiments performed at constant heating rate. Thermochim. Acta 1996, 288, 97–104. [Google Scholar] [CrossRef]
- Mavromatidis, L.E.; Bykalyuk, A.; Lequay, H. Development of polynomial regression models for composite dynamic envelopes’ thermal performance forecasting. Appl. Energy 2013, 104, 379–391. [Google Scholar] [CrossRef]
- Stergiou, K.; Ntakolia, C.; Varytis, P.; Koumoulos, E.; Karlsson, P.; Moustakidis, S. Enhancing property prediction and process optimization in building materials through machine learning: A review. Comput. Mater. Sci. 2023, 220, 112031. [Google Scholar] [CrossRef]
- Butler, K.T.; Davies, D.W.; Cartwright, H.; Isayev, O.; Walsh, A. Machine learning for molecular and materials science. Nature 2018, 559, 547–555. [Google Scholar] [CrossRef]
- Seghier, M.E.A.B.; Plevris, V.; Solorzano, G. Random forest-based algorithms for accurate evaluation of ultimate bending capacity of steel tubes. Structures 2022, 44, 261–273. [Google Scholar] [CrossRef]
- Abualigah, L. Particle Swarm Optimization: Advances, Applications, and Experimental Insights. Comput. Mater. Contin. 2025, 82, 2. [Google Scholar] [CrossRef]
- Krzywanski, J.; Sosnowski, M.; Grabowska, K.; Zylka, A.; Lasek, L.; Kijo-Kleczkowska, A. Advanced computational methods for modeling, prediction and optimization-a review. Materials 2024, 17, 3521. [Google Scholar] [CrossRef] [PubMed]
- Sarker, I.H. Data science and analytics: An overview from data-driven smart computing, decision-making and applications perspective. SN Comput. Sci. 2021, 2, 377. [Google Scholar] [CrossRef]
- Efendigil, T.; Önüt, S.; Kahraman, C. A decision support system for demand forecasting with artificial neural networks and neuro-fuzzy models: A comparative analysis. Expert Syst. Appl. 2009, 36, 6697–6707. [Google Scholar] [CrossRef]
- Abualigah, L.; Sheikhan, A.; Ikotun, A.M.; Zitar, R.A.; Alsoud, A.R.; Al-Shourbaji, I.; Jia, H. Particle swarm optimization algorithm: Review and applications. Metaheuristic Optim. Algorithms 2024, 1–14. [Google Scholar] [CrossRef]
- Marini, F.; Walczak, B. Particle swarm optimization (PSO). A tutorial. Chemom. Intell. Lab. Syst. 2015, 149, 153–165. [Google Scholar] [CrossRef]
- Piotrowski, A.P.; Napiorkowski, J.J.; Piotrowska, A.E. Particle swarm optimization or differential evolution-A comparison. Eng. Appl. Artif. Intell. 2023, 121, 106008. [Google Scholar]
- Zhang, X.; Liu, H.; Tu, L. A modified particle swarm optimization for multimodal multi-objective optimization. Eng. Appl. Artif. Intell. 2020, 95, 103905. [Google Scholar] [CrossRef]
- Zhou, J.; Huang, S.; Qiu, Y. Optimization of random forest through the use of MVO, GWO and MFO in evaluating the stability of underground entry-type excavations. Tunn. Undergr. Space Technol. 2022, 124, 104494. [Google Scholar] [CrossRef]
- Luo, X.; Yuan, Y.; Chen, S.; Zeng, N.; Wang, Z. Position-transitional particle swarm optimization-incorporated latent factor analysis. IEEE Trans. Knowl. Data Eng. 2020, 34, 3958–3970. [Google Scholar] [CrossRef]
- Yue, Y.; Cao, L.; Lu, D.; Hu, Z.; Xu, M.; Wang, S.; Ding, H. Review and empirical analysis of sparrow search algorithm. Artif. Intell. Rev. 2023, 56, 10867–10919. [Google Scholar] [CrossRef]
- Adnan, R.M.; Mostafa, R.R.; Kisi, O.; Yaseen, Z.M.; Shahid, S.; Zounemat-Kermani, M. Improving streamflow prediction using a new hybrid ELM model combined with hybrid particle swarm optimization and grey wolf optimization. Knowl.-Based Syst. 2021, 230, 107379. [Google Scholar] [CrossRef]
- Chou, J.S.; Pham, A.D. Enhanced artificial intelligence for ensemble approach to predicting high performance concrete compressive strength. Constr. Build. Mater. 2013, 49, 554–563. [Google Scholar] [CrossRef]
- Qi, C.; Fourie, A.; Chen, Q. Neural network and particle swarm optimization for predicting the unconfined compressive strength of cemented paste backfill. Constr. Build. Mater. 2018, 159, 473–478. [Google Scholar] [CrossRef]
- Wei, H.; Zhao, S.; Rong, Q.; Bao, H. Predicting the effective thermal conductivities of composite materials and porous media by machine learning methods. Int. J. Heat Mass Transf. 2018, 127, 908–916. [Google Scholar] [CrossRef]
- Pietrak, K.; Wiśniewski, T.S. A review of models for effective thermal conductivity of composite materials. J. Power Technol. 2015, 95, 1. [Google Scholar]
- Liu, X.; Tian, S.; Tao, F.; Yu, W. A review of artificial neural networks in the constitutive modeling of composite materials. Compos. Part B Eng. 2021, 224, 109152. [Google Scholar] [CrossRef]
- Linh, N.T.T.; Pandey, M.; Janizadeh, S.; Bhunia, G.S.; Norouzi, A.; Ali, S.; Ahmadi, K. Flood susceptibility modeling based on new hybrid intelligence model: Optimization of XGboost model using GA metaheuristic algorithm. Adv. Space Res. 2022, 69, 3301–3318. [Google Scholar] [CrossRef]
- Meng, H.; Tao, M.; Huang, R.; Zhao, Y.; Xu, Y. Blasting Mean Fragment Size Prediction Based on XGBoost and Metaheuristic Optimization Algorithms. Nat. Resour. Res. 2025, 1–20. [Google Scholar] [CrossRef]
- Willard, J.; Jia, X.; Xu, S.; Steinbach, M.; Kumar, V. Integrating scientific knowledge with machine learning for engineering and environmental systems. ACM Comput. Surv. 2022, 55, 1–37. [Google Scholar] [CrossRef]
- Schmidt, J.; Marques, M.R.; Botti, S.; Marques, M.A. Recent advances and applications of machine learning in solid-state materials science. npj Comput. Mater. 2019, 5, 83. [Google Scholar] [CrossRef]
- Keshteli, A.N.; Sheikholeslami, M. Nanoparticle enhanced PCM applications for intensification of thermal performance in building: A review. J. Mol. Liq. 2019, 274, 516–533. [Google Scholar] [CrossRef]
- Kıyak, B.; Öztop, H.F.; Ertam, F.; Aksoy, İ.G. An intelligent approach to investigate the effects of container orientation for PCM melting based on an XGBoost regression model. Eng. Anal. Bound. Elem. 2024, 161, 202–213. [Google Scholar] [CrossRef]
- Noh, H.; Lee, S.; Kim, S.M.; Mudawar, I. Utilization of XGBoost algorithm to predict dryout incipience quality for saturated flow boiling in mini/micro-channels. Int. J. Heat Mass Transf. 2024, 231, 125827. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Alahmer, A.; Turner, T.; Al-Dahidi, S.; Alrbai, M. A comprehensive review of optimizing phase change materials in thermal energy storage: The role of nanoparticles, fin configurations, and data-driven approaches. J. Energy Storage 2025, 131, 117464. [Google Scholar] [CrossRef]
- Liu, X.; Liu, T.; Feng, P. Long-term performance prediction framework based on XGBoost decision tree for pultruded FRP composites exposed to water, humidity and alkaline solution. Compos. Struct. 2022, 284, 115184. [Google Scholar] [CrossRef]
- Huang, G.; Guo, Y.; Chen, Y.; Nie, Z. Application of machine learning in material synthesis and property prediction. Materials 2023, 16, 5977. [Google Scholar] [CrossRef]
- Chibani, S.; Coudert, F.X. Machine learning approaches for the prediction of materials properties. APL Mater. 2020, 8, 8. [Google Scholar] [CrossRef]
- Guo, K.; Yang, Z.; Yu, C.H.; Buehler, M.J. Artificial intelligence and machine learning in design of mechanical materials. Mater. Horiz. 2021, 8, 1153–1172. [Google Scholar] [CrossRef]
- Fang, J.; Xie, M.; He, X.; Zhang, J.; Hu, J.; Chen, Y.; Jin, Q. Machine learning accelerates the materials discovery. Mater. Today Commun. 2022, 33, 104900. [Google Scholar] [CrossRef]
- Liu, Y.; Niu, C.; Wang, Z.; Gan, Y.; Zhu, Y.; Sun, S.; Shen, T. Machine learning in materials genome initiative: A review. J. Mater. Sci. Technol. 2020, 57, 113–122. [Google Scholar] [CrossRef]
- Raccuglia, P.; Elbert, K.C.; Adler, P.D.; Falk, C.; Wenny, M.B.; Mollo, A.; Norquist, A.J. Machine-learning-assisted materials discovery using failed experiments. Nature 2016, 533, 73–76. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.C.; Feng, J.W. Development and application of artificial neural network. Wirel. Pers. Commun. 2018, 102, 1645–1656. [Google Scholar] [CrossRef]
- Huang, Y. Advances in artificial neural networks–methodological development and application. Algorithms 2009, 2, 973–1007. [Google Scholar] [CrossRef]
- Samadi, S.H.; Ghobadian, B.; Nosrati, M. Prediction of higher heating value of biomass materials based on proximate analysis using gradient boosted regression trees method. Energy Sources Part A 2021, 43, 672–681. [Google Scholar] [CrossRef]
- Shahmansouri, A.A.; Yazdani, M.; Ghanbari, S.; Bengar, H.A.; Jafari, A.; Ghatte, H.F. Artificial neural network model to predict the compressive strength of eco-friendly geopolymer concrete incorporating silica fume and natural zeolite. J. Clean. Prod. 2021, 279, 123697. [Google Scholar] [CrossRef]
- Li, C.; Wang, C.; Sun, M.; Zeng, Y.; Yuan, Y.; Gou, Q.; Pu, X. Correlated RNN framework to quickly generate molecules with desired properties for energetic materials in the low data regime. J. Chem. Inf. Model. 2022, 62, 4873–4887. [Google Scholar] [CrossRef] [PubMed]
- Unni, R.; Yao, K.; Zheng, Y. Deep convolutional mixture density network for inverse design of layered photonic structures. ACS Photonics 2020, 7, 2703–2712. [Google Scholar] [CrossRef]
- Zhao, X.G.; Zhou, K.; Xing, B.; Zhao, R.; Luo, S.; Li, T.; Zhang, L. JAMIP: An artificial-intelligence aided data-driven infrastructure for computational materials informatics. Sci. Bull. 2021, 66, 1973–1985. [Google Scholar] [CrossRef]
- Javid, A.; Toufigh, V. Utilizing ensemble machine learning and gray wolf optimization to predict the compressive strength of silica fume mixtures. Struct. Concr. 2024, 25, 4048–4074. [Google Scholar] [CrossRef]
- Mahmoodzadeh, A.; Mohammadi, M.; Ibrahim, H.H.; Abdulhamid, S.N.; Salim, S.G.; Ali, H.F.H.; Majeed, M.K. Artificial intelligence forecasting models of uniaxial compressive strength. Transp. Geotech. 2021, 27, 100499. [Google Scholar] [CrossRef]
- Zhou, J.; Chen, Y.; Li, C.; Qiu, Y.; Huang, S.; Tao, M. Machine learning models to predict the tunnel wall convergence. Transp. Geotech. 2023, 41, 101022. [Google Scholar] [CrossRef]
- Wang, Z.; Sun, T.; Sun, Y.; Liu, N. Evaluating the strength properties of high-performance concrete in the form of ensemble and hybrid models using deep learning techniques. Sci. Rep. 2025, 15, 25453. [Google Scholar] [CrossRef]
- Xu, Y.; Afzal, M. Applying machine learning techniques in the form of ensemble and hybrid models to appraise hardness properties of high-performance concrete. J. Intell. Fuzzy Syst. 2024, 46, 903–921. [Google Scholar] [CrossRef]
- Chicco, D.; Warrens, M.J.; Jurman, G. The coefficient of determination R-squared is more informative than SMAPE, MAE, MAPE, MSE and RMSE in regression analysis evaluation. PeerJ. Comput. Sci. 2021, 7, e623. [Google Scholar] [CrossRef]
- Xu, Y.; Goodacre, R. On splitting training and validation set: A comparative study of cross-validation, bootstrap and systematic sampling for estimating the generalization performance of supervised learning. J. Anal. Test. 2018, 2, 249–262. [Google Scholar] [CrossRef]
- Qiu, J. An analysis of model evaluation with cross-validation: Techniques, applications, and recent advances. Adv. Econ. Manag. Polit. Sci. 2024, 99, 69–72. [Google Scholar] [CrossRef]
- Allgaier, J.; Pryss, R. Cross-validation visualized: A narrative guide to advanced methods. Mach. Learn. Knowl. Extr. 2024, 6, 1378–1388. [Google Scholar] [CrossRef]
- Belkin, M.; Hsu, D.; Ma, S.; Mandal, S. Reconciling modern machine-learning practice and the classical bias–variance trade-off. Proc. Natl. Acad. Sci. USA 2019, 116, 15849–15854. [Google Scholar] [CrossRef]
- Ying, X. An overview of overfitting and its solutions. J. Phys. Conf. Ser. 2019, 1168, 022022. [Google Scholar] [CrossRef]
- Hjorth, J.U. Computer Intensive Statistical Methods: Validation, Model Selection, and Bootstrap; Chapman and Hall/CRC: Boca Raton, FL, USA, 2017. [Google Scholar]
- Paleyes, A.; Urma, R.G.; Lawrence, N.D. Challenges in deploying machine learning: A survey of case studies. ACM Comput. Surv. 2022, 55, 1–29. [Google Scholar] [CrossRef]
- Aljarah, I.; Faris, H.; Mirjalili, S. Optimizing connection weights in neural networks using the whale optimization algorithm. Soft Comput. 2018, 22, 1–15. [Google Scholar] [CrossRef]
- Dhiman, G.; Kumar, V. Seagull optimization algorithm: Theory and its applications for large-scale industrial engineering problems. Knowl.-Based Syst. 2019, 165, 169–196. [Google Scholar] [CrossRef]
- Li, C.; Zhou, J.; Du, K.; Dias, D. Stability prediction of hard rock pillar using support vector machine optimized by three metaheuristic algorithms. Int. J. Min. Sci. Technol. 2023, 33, 1019–1036. [Google Scholar] [CrossRef]
- Shariati, M.; Mafipour, M.S.; Ghahremani, B.; Azarhomayun, F.; Ahmadi, M.; Trung, N.T.; Shariati, A. A novel hybrid extreme learning machine–grey wolf optimizer (ELM-GWO) model to predict compressive strength of concrete with partial replacements for cement. Eng. Comput. 2022, 38, 757–779. [Google Scholar] [CrossRef]
- Zhang, N.; Wang, Z. Review of soil thermal conductivity and predictive models. Int. J. Therm. Sci. 2017, 117, 172–183. [Google Scholar] [CrossRef]
- Yadav, C.; Sahoo, R.R. Thermal analysis comparison of nano-additive PCM-based engine waste heat recovery thermal storage systems: An experimental study. J. Therm. Anal. Calorim. 2022, 147, 2785–2802. [Google Scholar] [CrossRef]
- Javadi, F.S.; Metselaar, H.S.C.; Ganesan, P.J.S.E. Performance improvement of solar thermal systems integrated with phase change materials (PCM), a review. Sol. Energy 2020, 206, 330–352. [Google Scholar] [CrossRef]
- Kishore, R.A.; Bianchi, M.V.; Booten, C.; Vidal, J.; Jackson, R. Parametric and sensitivity analysis of a PCM-integrated wall for optimal thermal load modulation in lightweight buildings. Appl. Therm. Eng. 2021, 187, 116568. [Google Scholar] [CrossRef]
- Le, L.T.; Nguyen, H.; Zhou, J.; Dou, J.; Moayedi, H. Estimating the heating load of buildings for smart city planning using a novel artificial intelligence technique PSO-XGBoost. Appl. Sci. 2019, 9, 2714. [Google Scholar] [CrossRef]
- Marani, A.; Zhang, L.; Nehdi, M.L. Design of concrete incorporating microencapsulated phase change materials for clean energy: A ternary machine learning approach based on generative adversarial networks. Eng. Appl. Artif. Intell. 2023, 118, 105652. [Google Scholar] [CrossRef]
- Xiong, S.; Liu, Z.; Min, C.; Shi, Y.; Zhang, S.; Liu, W. Compressive strength prediction of cemented backfill containing phosphate tailings using extreme gradient boosting optimized by whale optimization algorithm. Materials 2022, 16, 308. [Google Scholar] [CrossRef]




















| ML Model | Optimizer | Search Space | Population Size | Iterations | Best Configuration |
|---|---|---|---|---|---|
| SVR | GA | C ∈ [0.1, 100]; γ ∈ [0.001, 1] | 30 | 100 | C = 12–16; γ = 0.01–0.02 |
| PSO | 30 | 100 | C = 13–17; γ = 0.01–0.03 | ||
| WOA | 25 | 120 | C = 17–20; γ = 0.01–0.02 | ||
| GWO | 30 | 150 | C = 13–15; γ = 0.015–0.02 | ||
| FFA | 20 | 100 | C = 11–13; γ = 0.015–0.02 | ||
| RF | GA | n_estimators ∈ [50, 500]; max_depth ∈ [3, 20] | 30 | 100 | n_estimators = 200–240; depth = 11–13 |
| PSO | 25 | 120 | n_estimators = 240–260; depth = 13–15 | ||
| WOA | 30 | 150 | n_estimators = 260–290; depth = 13–14 | ||
| GWO | 20 | 100 | n_estimators = 220–240; depth = 12–13 | ||
| FFA | 25 | 120 | n_estimators = 190–210; depth = 11–12 | ||
| XGBoost | GA | learning_rate ∈ [0.01, 0.3]; n_estimators ∈ [50, 500]; max_depth ∈ [3, 15] | 30 | 100 | learning_rate = 0.07–0.09; n_estimators = 280–320; depth = 9–11 |
| PSO | 25 | 120 | learning_rate = 0.06–0.08; n_estimators = 300–330; depth = 8–10 | ||
| WOA | 30 | 150 | learning_rate = 0.04–0.06; n_estimators = 270–300; depth = 10–12 | ||
| GWO | 20 | 100 | learning_rate = 0.08–0.10; n_estimators = 330–360; depth = 9–11 | ||
| FFA | 25 | 120 | learning_rate = 0.05–0.07; n_estimators = 290–320; depth = 8–10 | ||
| CatBoost | GA | learning_rate ∈ [0.01, 0.3]; depth ∈ [3, 15]; iterations ∈ [100, 1000] | 30 | 100 | learning_rate = 0.04–0.06; depth = 9–11; iterations = 580–620 |
| PSO | 25 | 120 | learning_rate = 0.05–0.07; depth = 8–10; iterations = 620–660 | ||
| WOA | 30 | 150 | learning_rate = 0.04–0.05; depth = 10–12; iterations = 680–720 | ||
| GWO | 20 | 100 | learning_rate = 0.06–0.08; depth = 9–11; iterations = 600–640 | ||
| FFA | 25 | 120 | learning_rate = 0.04–0.06; depth = 8–10; iterations = 560–600 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L.; Sun, W.; Gómez-Zamorano, L.Y.; Liu, Z.; Zhang, W.; Ma, H. From Research Trend to Performance Prediction: Metaheuristic-Driven Machine Learning Optimization for Cement Pastes Containing Bio-Based Phase Change Materials. Polymers 2025, 17, 2541. https://doi.org/10.3390/polym17182541
Li L, Sun W, Gómez-Zamorano LY, Liu Z, Zhang W, Ma H. From Research Trend to Performance Prediction: Metaheuristic-Driven Machine Learning Optimization for Cement Pastes Containing Bio-Based Phase Change Materials. Polymers. 2025; 17(18):2541. https://doi.org/10.3390/polym17182541
Chicago/Turabian StyleLi, Leifa, Wangwen Sun, Lauren Y. Gómez-Zamorano, Zhuangzhuang Liu, Wenzhen Zhang, and Haoran Ma. 2025. "From Research Trend to Performance Prediction: Metaheuristic-Driven Machine Learning Optimization for Cement Pastes Containing Bio-Based Phase Change Materials" Polymers 17, no. 18: 2541. https://doi.org/10.3390/polym17182541
APA StyleLi, L., Sun, W., Gómez-Zamorano, L. Y., Liu, Z., Zhang, W., & Ma, H. (2025). From Research Trend to Performance Prediction: Metaheuristic-Driven Machine Learning Optimization for Cement Pastes Containing Bio-Based Phase Change Materials. Polymers, 17(18), 2541. https://doi.org/10.3390/polym17182541








