Effect of Printing Temperature on the Microstructure and Tensile Properties of Polylactic Acid–Magnetic Iron Composites Manufactured by Material Extrusion
Abstract
1. Introduction
2. Experimental Layout
2.1. Materials and Processes
2.2. Tensile Testing
2.3. Scanning Electron Microscope (SEM)
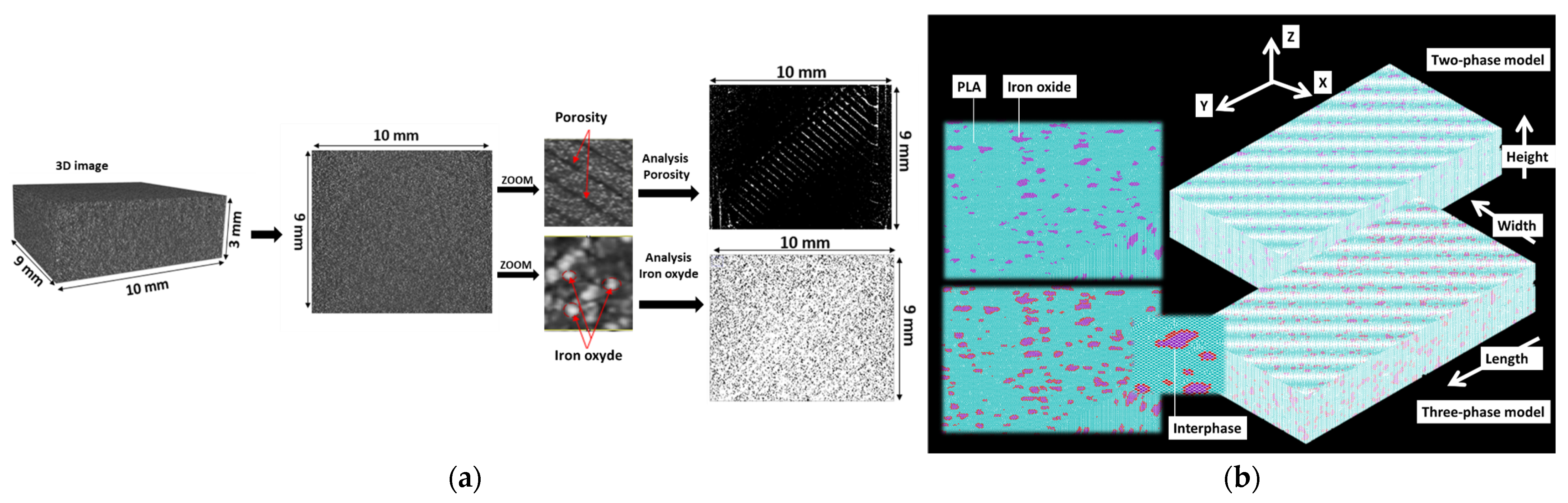
2.4. X-Ray Microtomography Imaging
3. Finite Element Model
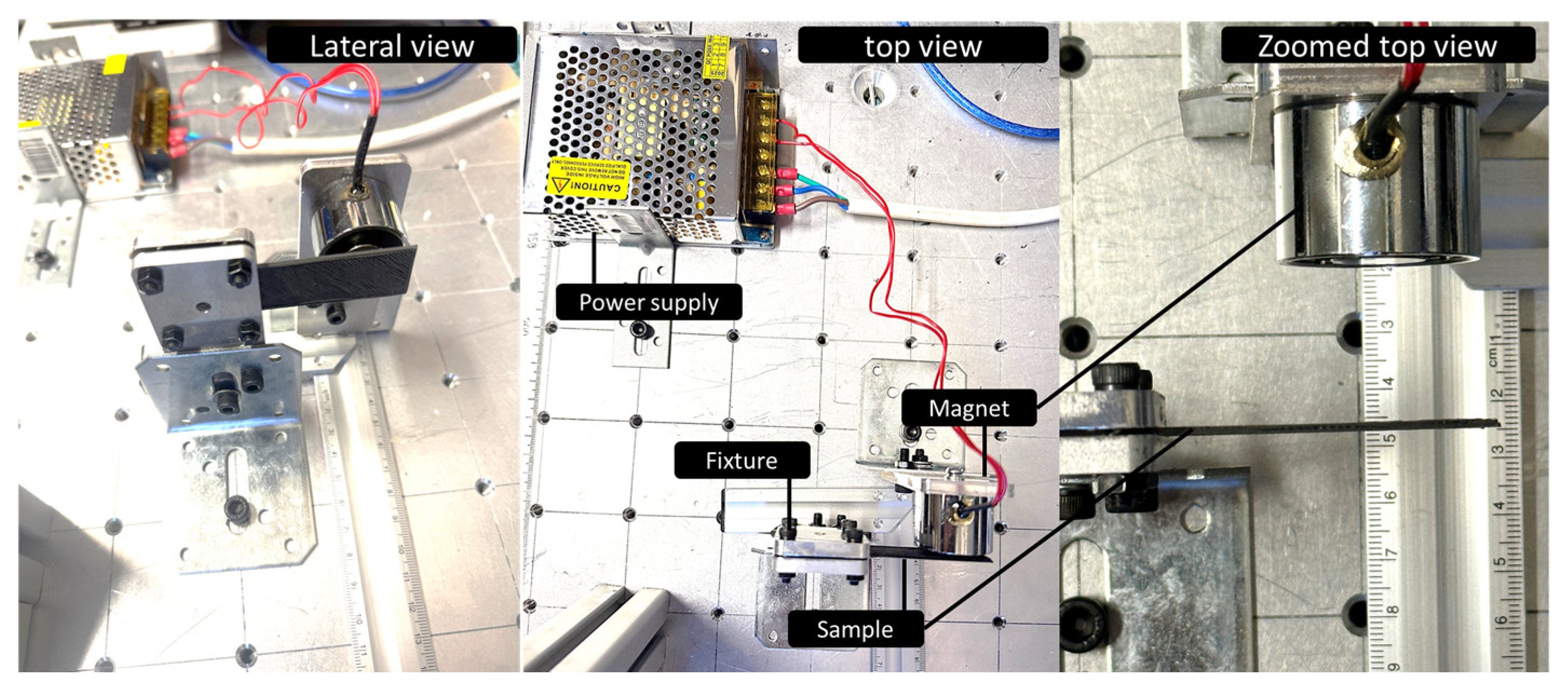
4. Magnetic Actuation Experiment
5. Results and Discussion
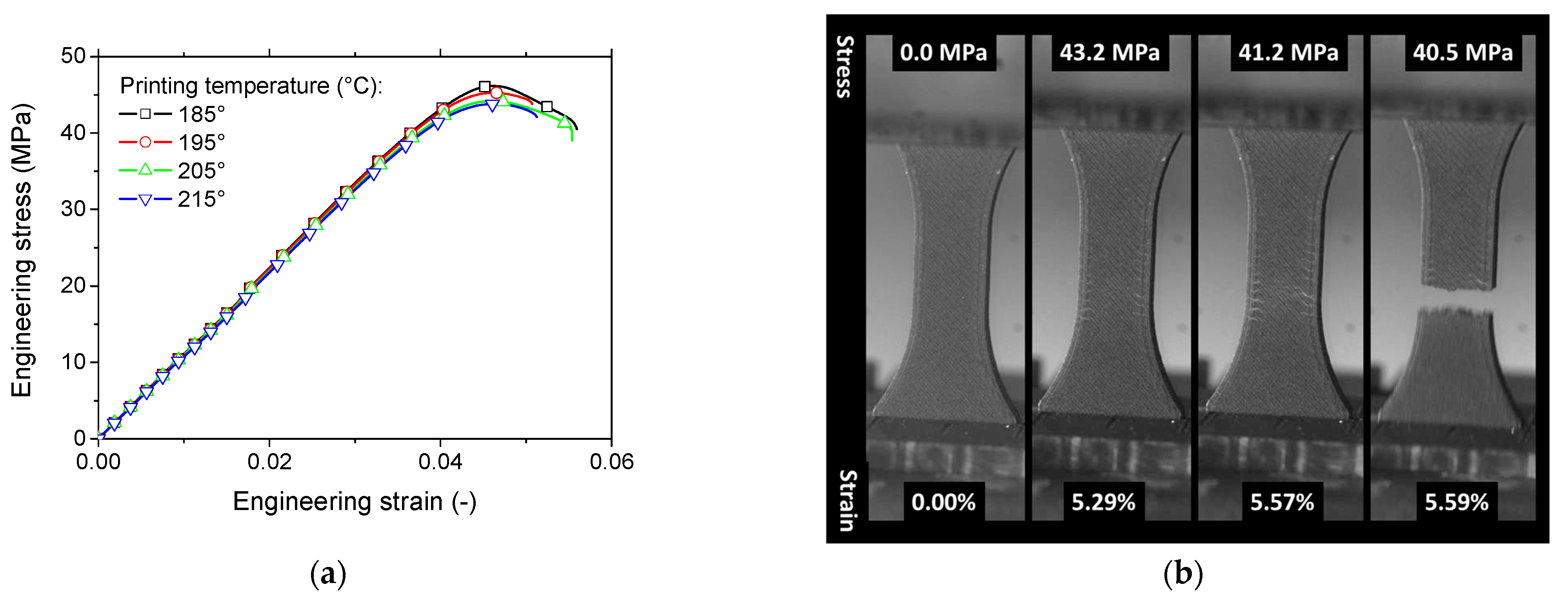
5.1. Mechanical Behaviour of 3D-Printed PLA-Iron Oxide Composites
5.2. Fractography Analysis Using SEM
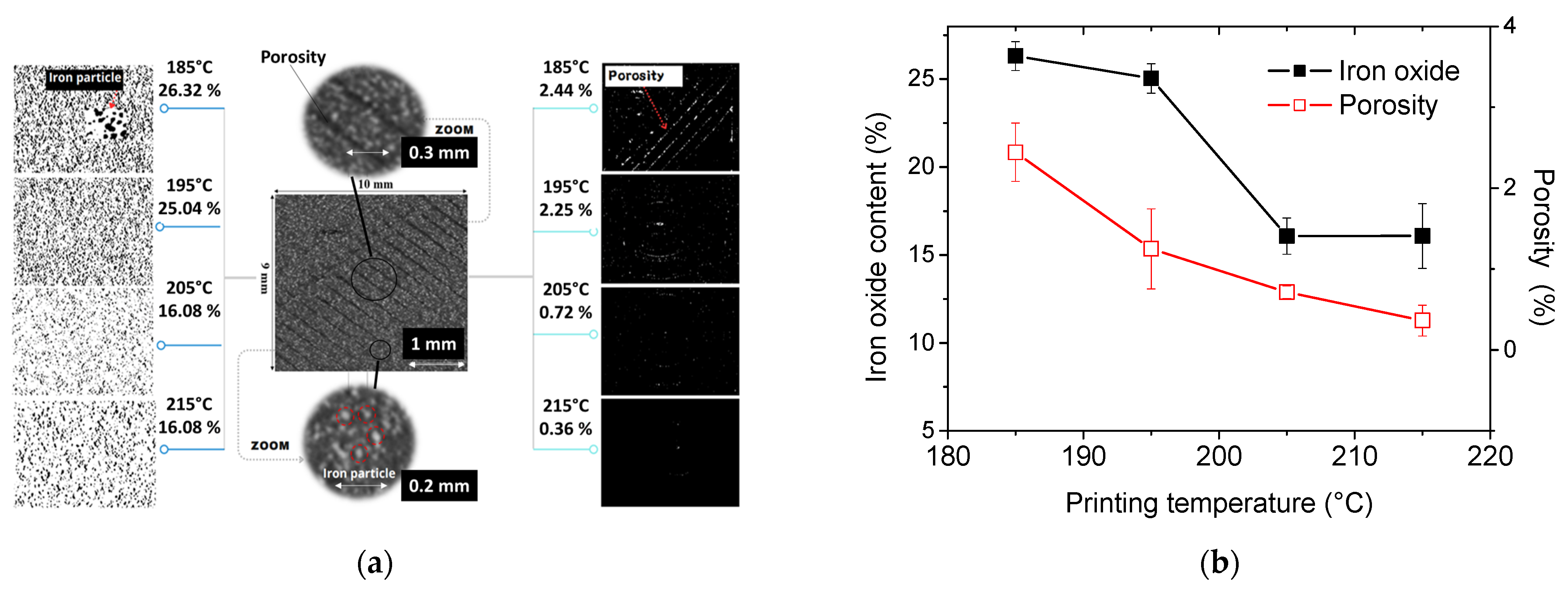
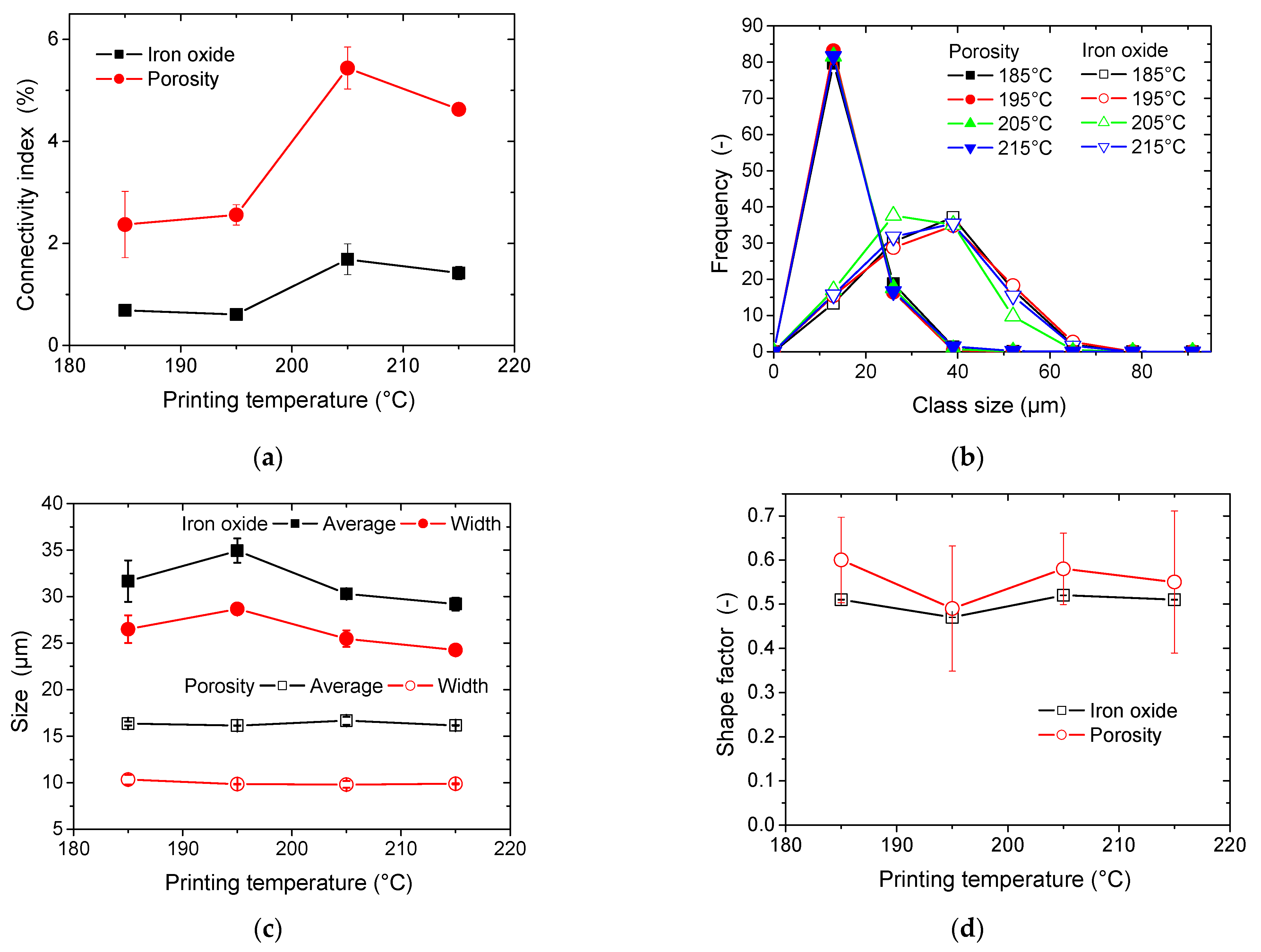
5.3. Microstructural Interpretation
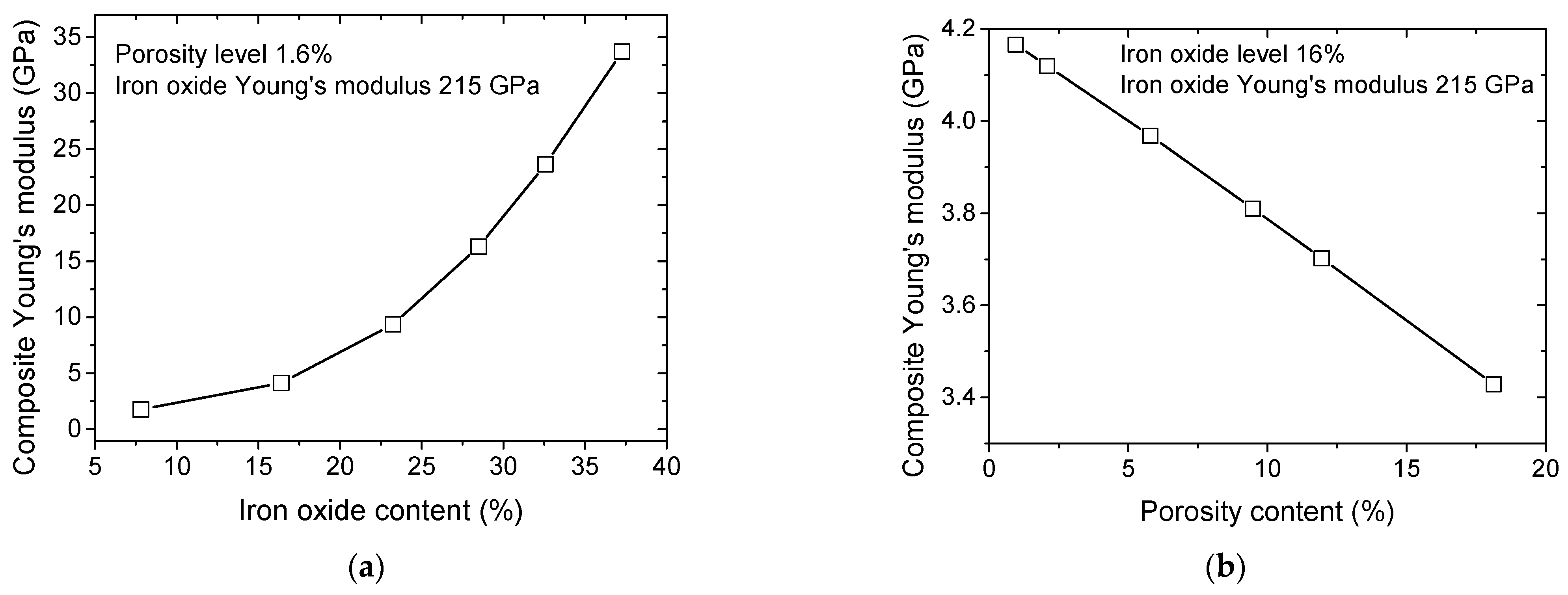
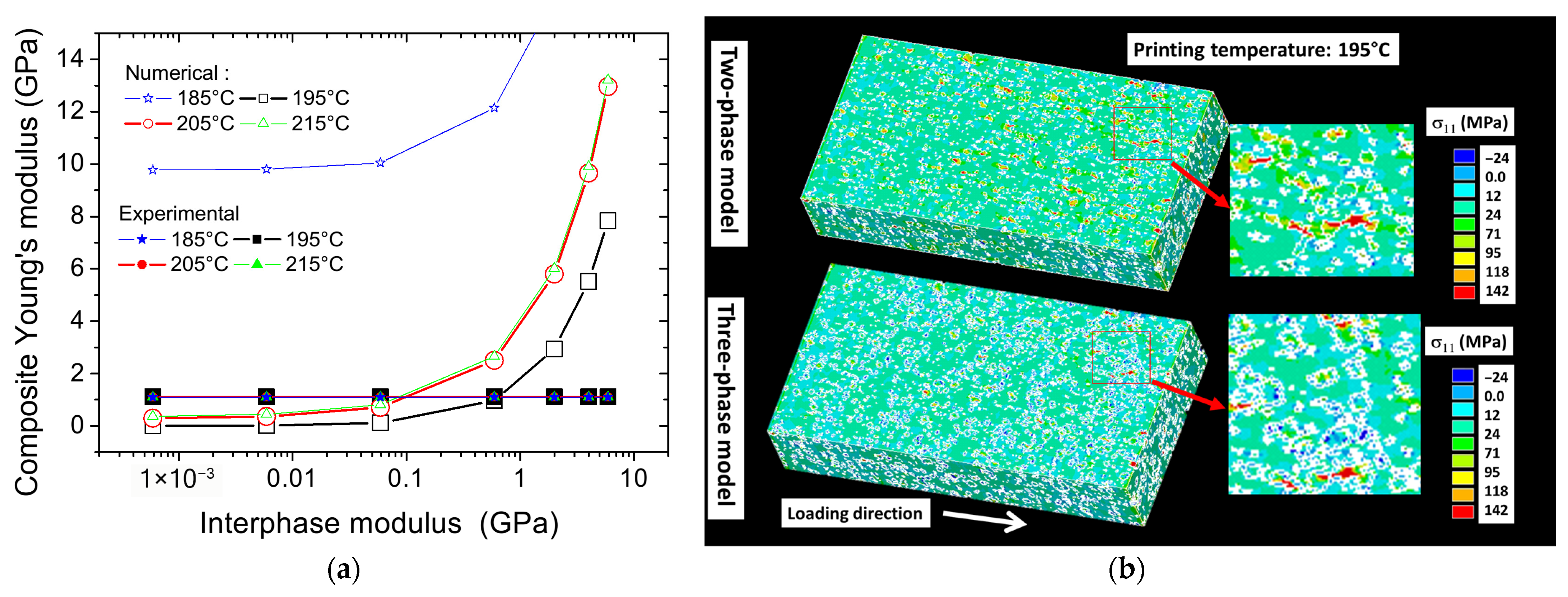
5.4. Finite Element Simulation Results
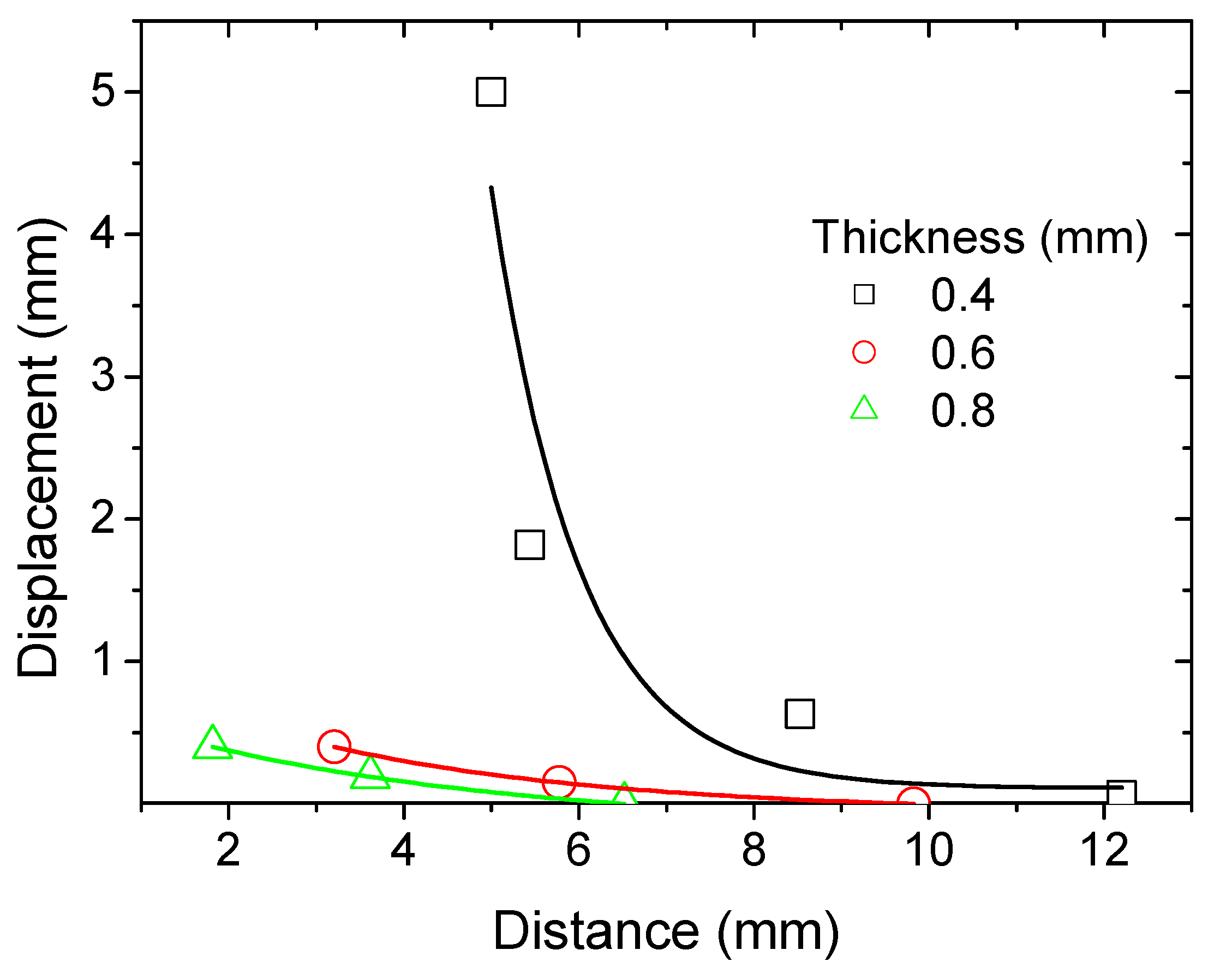
6. Magnetic Actuation of 3D-Printed PLA-Iron Oxide
7. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Prathyusha, A.L.R.; Raghu Babu, G. A review on additive manufacturing and topology optimization process for weight reduction studies in various industrial applications. Mater. Today Proc. 2022, 62, 109–117. [Google Scholar] [CrossRef]
- Praveena, B.A.; Lokesh, N.; Buradi, A.; Santhosh, N.; Praveena, B.L.; Vignesh, R. A comprehensive review of emerging additive manufacturing (3D printing technology): Methods, materials, applications, challenges, trends and future potential. Mater. Today Proc. 2022, 52, 1309–1313. [Google Scholar]
- Guessasma, S.; Zhang, W.; Zhu, J.; Belhabib, S.; Nouri, H. Challenges of additive manufacturing technologies from an optimisation perspective. Int. J. Simul. Multidiscip. Des. Optim. 2016, 6, A9. [Google Scholar] [CrossRef]
- Rasiya, G.; Shukla, A.; Saran, K. Additive manufacturing—A review. Mater. Today Proc. 2021, 47, 6896–6901. [Google Scholar] [CrossRef]
- Beaman, J.J.; Bourell, D.L.; Seepersad, C.C.; Kovar, D. Additive manufacturing review: Early past to current practice. J. Manuf. Sci. Eng. 2020, 142, 110812. [Google Scholar] [CrossRef]
- Conner, B.P.; Manogharan, G.P.; Martof, A.N.; Rodomsky, L.M.; Rodomsky, C.M.; Jordan, D.C.; Limperos, J.W. Making sense of 3-d printing: Creating a map of additive manufacturing products and services. Addit. Manuf. 2014, 1–4, 64–76. [Google Scholar] [CrossRef]
- Zhang, A.; Wang, F.; Chen, L.; Wei, X.; Xue, M.; Yang, F.; Jiang, S. 3D printing hydrogels for actuators: A review. Chin. Chem. Lett. 2021, 32, 2923–2932. [Google Scholar] [CrossRef]
- Germaini, M.-M.; Belhabib, S.; Guessasma, S.; Deterre, R.; Corre, P.; Weiss, P. Additive manufacturing of biomaterials for bone tissue engineering—A critical review of the state of the art and new concepts. Prog. Mater. Sci. 2022, 130, 100963. [Google Scholar] [CrossRef]
- Monteiro, H.; Carmona-Aparicio, G.; Lei, I.; Despeisse, M. Energy and material efficiency strategies enabled by metal additive manufacturing—A review for the aeronautic and aerospace sectors. Energy Rep. 2022, 8, 298–305. [Google Scholar] [CrossRef]
- Siacor, F.D.C.; Chen, Q.; Zhao, J.Y.; Han, L.; Valino, A.D.; Taboada, E.B.; Caldona, E.B.; Advincula, R.C. On the additive manufacturing (3D printing) of viscoelastic materials and flow behavior: From composites to food manufacturing. Addit. Manuf. 2021, 45, 102043. [Google Scholar] [CrossRef]
- Wiese, M.; Kwauka, A.; Thiede, S.; Herrmann, C. Economic assessment for additive manufacturing of automotive end-use parts through digital light processing (dlp). CIRP J. Manuf. Sci. Technol. 2021, 35, 268–280. [Google Scholar] [CrossRef]
- Dörfler, K.; Dielemans, G.; Lachmayer, L.; Recker, T.; Raatz, A.; Lowke, D.; Gerke, M. Additive manufacturing using mobile robots: Opportunities and challenges for building construction. Cem. Concr. Res. 2022, 158, 106772. [Google Scholar] [CrossRef]
- Jadhav, A.; Jadhav, V.S. A review on 3D printing: An additive manufacturing technology. Mater. Today Proc. 2022, 62, 2094–2099. [Google Scholar] [CrossRef]
- Mohd Pu’ad, N.A.S.; Abdul Haq, R.H.; Mohd Noh, H.; Abdullah, H.Z.; Idris, M.I.; Lee, T.C. Review on the fabrication of fused deposition modelling (fdm) composite filament for biomedical applications. Mater. Today Proc. 2020, 29, 228–232. [Google Scholar] [CrossRef]
- Al-Ghamdi, K.A. Sustainable fdm additive manufacturing of abs components with emphasis on energy minimized and time efficient lightweight construction. Int. J. Lightweight Mater. Manuf. 2019, 2, 338–345. [Google Scholar] [CrossRef]
- Subramaniam, S.R.; Samykano, M.; Selvamani, S.K.; Ngui, W.K.; Kadirgama, K.; Sudhakar, K.; Idris, M.S. 3D printing: Overview of pla progress. AIP Conf. Proc. 2019, 2059, 020015. [Google Scholar] [CrossRef]
- Ahn, S.H.; Montero, M.; Odell, D.; Roundy, S.; Wright, P.K. Anisotropic material properties of fused deposition modeling abs. Rapid Prototyp. J. 2002, 8, 248–257. [Google Scholar] [CrossRef]
- Wickramasinghe, S.; Do, T.; Tran, P. Fdm-based 3D printing of polymer and associated composite: A review on mechanical properties, defects and treatments. Polymers 2020, 12, 1529. [Google Scholar] [CrossRef]
- Sun, J.; Ye, D.; Zou, J.; Chen, X.; Wang, Y.; Yuan, J.; Liang, H.; Qu, H.; Binner, J.; Bai, J. A review on additive manufacturing of ceramic matrix composites. J. Mater. Sci. Technol. 2022, 138, 1–16. [Google Scholar] [CrossRef]
- Valvez, S.; Santos, P.; Parente, J.M.; Silva, M.P.; Reis, P.N.B. 3D printed continuous carbon fiber reinforced pla composites: A short review. Procedia Struct. Integr. 2020, 25, 394–399. [Google Scholar] [CrossRef]
- Valino, A.D.; Dizon, J.R.C.; Espera, A.H.; Chen, Q.; Messman, J.; Advincula, R.C. Advances in 3D printing of thermoplastic polymer composites and nanocomposites. Prog. Polym. Sci. 2019, 98, 101162. [Google Scholar] [CrossRef]
- Raju, R.; Manikandan, N.; Binoj, J.S.; Palanisamy, D.; Arulkirubakaran, D.; Thejasree, P.; Pavan Kalyan, A.; Subhash Reddy, G. Optimization and performance evaluation of pla polymer material in situ carbon particles on structural properties. Mater. Today Proc. 2020, 39, 223–229. [Google Scholar] [CrossRef]
- Buj-Corral, I.; Sivatte-Adroer, M. An experimental investigation about the dimensional accuracy and the porosity of copper-filled pla fused filament fabrication parts. Metals 2023, 13, 1608. [Google Scholar] [CrossRef]
- Martinez, L.; Palessonga, D.; Roquefort, P.; Chevalier, A.; Maalouf, A.; Ville, J.; Laur, V. Development of a high temperature printable composite for microwave absorption applications. AIMS Mater. Sci. 2021, 8, 739–747. [Google Scholar] [CrossRef]
- Török, J.; Törökova, M.; Duplakova, D.; Murcinkova, Z.; Duplak, J.; Kascak, J.; Karkova, M. Advanced configuration parameters of post processor influencing tensile testing pla and add-mixtures in polymer matrix in the process of fdm technology. Appl. Sci. 2021, 11, 6212. [Google Scholar] [CrossRef]
- Kumar, J.; Huseynov, O.; Fidan, I.; Rajabali, M. Developing additively manufactured iron powder-filled pla composites. In Proceedings of the 34th Annual International Solid Freeform Fabrication Symposium—An Additive Manufacturing Conference, Austin, TX, USA, 14–16 August 2022; pp. 204–225. [Google Scholar]
- Makridis, A.; Okkalidis, N.; Trygoniaris, D.; Kazeli, K.; Angelakeris, M. Composite magnetic 3D-printing filament fabrication protocol opens new perspectives in magnetic hyperthermia. J. Phys. D Appl. Phys. 2023, 56, 285002. [Google Scholar] [CrossRef]
- Wu, S.; Hu, W.; Ze, Q.; Sitti, M.; Zhao, R. Multifunctional magnetic soft composites: A review. Multifunct. Mater. 2020, 3, 042003. [Google Scholar] [CrossRef] [PubMed]
- Hines, L.; Petersen, K.; Lum, G.Z.; Sitti, M. Soft actuators for small-scale robotics. Adv. Mater. 2017, 29, 1603483. [Google Scholar] [CrossRef]
- Mohd Jani, J.; Leary, M.; Subic, A.; Gibson, M.A. A review of shape memory alloy research, applications and opportunities. Mater. Des. (1980–2015) 2014, 56, 1078–1113. [Google Scholar] [CrossRef]
- Reyssat, E.; Mahadevan, L. Hygromorphs: From pine cones to biomimetic bilayers. J. R. Soc. Interface 2009, 6, 951–957. [Google Scholar] [CrossRef]
- Moradi, M.; Lalegani Dezaki, M.; Kheyri, E.; Rasouli, S.A.; Aghaee Attar, M.; Bodaghi, M. Simultaneous fdm 4d printing and magnetizing of iron-filled polylactic acid polymers. J. Magn. Magn. Mater. 2023, 568, 170425. [Google Scholar] [CrossRef]
- Sood, A.K.; Ohdar, R.K.; Mahapatra, S.S. Parametric appraisal of mechanical property of fused deposition modelling processed parts. Mater. Des. 2010, 31, 287–295. [Google Scholar] [CrossRef]
- Frunzaverde, D.; Cojocaru, V.; Ciubotariu, C.-R.; Miclosina, C.-O.; Ardeljan, D.D.; Ignat, E.F.; Marginean, G. The influence of the printing temperature and the filament color on the dimensional accuracy, tensile strength, and friction performance of fff-printed pla specimens. Polymers 2022, 14, 1978. [Google Scholar] [CrossRef]
- Guessasma, S.; Belhabib, S.; Nouri, H. Understanding the microstructural role of bio-sourced 3D printed structures on the tensile performance. Polym. Test. 2019, 77, 105924. [Google Scholar] [CrossRef]
- Guessasma, S.; Belhabib, S. Infill strategy in 3D printed pla carbon composites: Effect on tensile performance. Polymers 2022, 14, 4221. [Google Scholar] [CrossRef] [PubMed]
- Markl, D.; Zeitler, J.A.; Rasch, C.; Michaelsen, M.H.; Müllertz, A.; Rantanen, J.; Rades, T.; Bøtker, J. Analysis of 3D prints by x-ray computed microtomography and terahertz pulsed imaging. Pharm. Res. 2016, 34, 1037–1052. [Google Scholar] [CrossRef]
- Guessasma, S.; Nouri, H.; Roger, F. Microstructural and mechanical implications of microscaled assembly in droplet-based multi-material additive manufacturing. Polymers 2017, 9, 372. [Google Scholar] [CrossRef]
- Shin, S.; Kim, M.W.; Jin, K.H.; Yi, K.M.; Kohmura, Y.; Ishikawa, T.; Je, J.H.; Park, J. Deep 3D reconstruction of synchrotron x-ray computed tomography for intact lungs. Sci. Rep. 2023, 13, 1738. [Google Scholar] [CrossRef]
- Hamdi, S.E.; Delisée, C.; Malvestio, J.; Da Silva, N.; Le Duc, A.; Beaugrand, J. X-ray computed microtomography and 2d image analysis for morphological characterization of short lignocellulosic fibers raw materials: A benchmark survey. Compos. Part A Appl. Sci. Manuf. 2015, 76, 1–9. [Google Scholar] [CrossRef]
- Swolfs, Y.; Morton, H.; Scott, A.E.; Gorbatikh, L.; Reed, P.A.S.; Sinclair, I.; Spearing, S.M.; Verpoest, I. Synchrotron radiation computed tomography for experimental validation of a tensile strength model for unidirectional fibre-reinforced composites. Compos. Part A Appl. Sci. Manuf. 2015, 77, 106–113. [Google Scholar] [CrossRef]
- Ayadi, A.; Nouri, H.; Guessasma, S.; Roger, F. Large-scale x-ray microtomography analysis of fiber orientation in weld line of short glass fiber reinforced thermoplastic and related elasticity behavior. Macromol. Mater. Eng. 2016, 301, 907–921. [Google Scholar] [CrossRef]
- Moradi, M.; Aminzadeh, A.; Rahmatabadi, D.; Hakimi, A. Experimental investigation on mechanical characterization of 3D printed pla produced by fused deposition modeling (fdm). Mater. Res. Express 2021, 8, 035304. [Google Scholar] [CrossRef]
- Iso 527-1:2019; Plastics Determination of Tensile Properties Part 1: General Principles. ISO: Geneva, Switzerland, 2019. Available online: https://www.iso.org/fr/standard/75824.html (accessed on 20 June 2025).
- Belarbi, Y.E.; Guessasma, S.; Belhabib, S.; Benmahiddine, F.; Hamami, A.E.A. Effect of printing parameters on mechanical behaviour of pla-flax printed structures by fused deposition modelling. Materials 2021, 14, 5883. [Google Scholar] [CrossRef] [PubMed]
- Hedjazi, L.; Belhabib, S.; Stephant, N.; Durand, S.; Guessasma, S. Effects of microstructural arrangement on the mechanical behavior of 3D printed polyamide. Symmetry 2023, 15, 2119. [Google Scholar] [CrossRef]
- Guessasma, S.; Belhabib, S. Effect of the printing angle on the microstructure and tensile performance of iron-reinforced polylactic acid composite manufactured using fused filament fabrication. J. Manuf. Mater. Process. 2024, 8, 65. [Google Scholar] [CrossRef]
- Rasband, W.S. Imagej; National Institutes of Health: Bethesda, MD, USA, 1997. Available online: http://imagej.nih.gov/ij (accessed on 13 August 2025).
- Rjafiallah, S.; Guessasma, S. Three-phase model and digital image correlation to assess the interphase effect on the elasticity of carbohdyrate polymer-based composites reinforced with glass silica beads. Carbohydr. Polym. 2011, 83, 246–256. [Google Scholar] [CrossRef]
- Rjafiallah, S.; Guessasma, S.; Bizot, H. Effect of surface etching on interphase and elastic properties of a biocomposite reinforced using glass-silica particles. Compos. Sci. Technol. 2010, 70, 1272–1279. [Google Scholar] [CrossRef]
- Hanon, M.M.; Marczis, R.; Zsidai, L. Influence of the 3D printing process settings on tensile strength of pla and ht-pla. Period. Polytech. Mech. Eng. 2020, 65, 38–46. [Google Scholar] [CrossRef]
- Hsueh, M.-H.; Lai, C.-J.; Chung, C.-F.; Wang, S.-H.; Huang, W.-C.; Pan, C.-Y.; Zeng, Y.-S.; Hsieh, C.-H. Effect of printing parameters on the tensile properties of 3D-printed polylactic acid (pla) based on fused deposition modeling. Polymers 2021, 13, 2387. [Google Scholar] [CrossRef]
- Delbart, R.; Papasavvas, A.; Robert, C.; Quynh Truong Hoang, T.; Martinez-Hergueta, F. An experimental and numerical study of the mechanical response of 3D printed pla/cb polymers. Compos. Struct. 2023, 319, 117156. [Google Scholar] [CrossRef]










| Tp (°C) | EY (MPa) | σY (MPa) | σM (MPa) | σR (MPa) | εR (%) |
|---|---|---|---|---|---|
| 185 | 1112 ± 5 | 39.3 ± 0.7 | 45.9 ± 0.8 | 41.2 ± 1.0 | 5.4 ± 0.3 |
| 195 | 1102 ± 23 | 38.7 ± 0.6 | 45.1 ± 0.9 | 42.6 ± 1.8 | 5.3 ± 0.4 |
| 205 | 1108 ± 13 | 38.6 ± 0.5 | 45.0 ± 0.8 | 41.8 ± 1.8 | 5.3 ± 0.2 |
| 215 | 1096 ± 16 | 37.9 ± 0.4 | 44.1 ± 0.4 | 41.3 ± 0.9 | 5.2 ± 0.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bouchetara, M.; Belhabib, S.; Melelli, A.; Perrin, J.; Weitkamp, T.; Koubaa, A.; Tahlaiti, M.; Nouri, M.; Guessasma, S. Effect of Printing Temperature on the Microstructure and Tensile Properties of Polylactic Acid–Magnetic Iron Composites Manufactured by Material Extrusion. Polymers 2025, 17, 2485. https://doi.org/10.3390/polym17182485
Bouchetara M, Belhabib S, Melelli A, Perrin J, Weitkamp T, Koubaa A, Tahlaiti M, Nouri M, Guessasma S. Effect of Printing Temperature on the Microstructure and Tensile Properties of Polylactic Acid–Magnetic Iron Composites Manufactured by Material Extrusion. Polymers. 2025; 17(18):2485. https://doi.org/10.3390/polym17182485
Chicago/Turabian StyleBouchetara, Meriem, Sofiane Belhabib, Alessia Melelli, Jonathan Perrin, Timm Weitkamp, Ahmed Koubaa, Mahfoud Tahlaiti, Mustapha Nouri, and Sofiane Guessasma. 2025. "Effect of Printing Temperature on the Microstructure and Tensile Properties of Polylactic Acid–Magnetic Iron Composites Manufactured by Material Extrusion" Polymers 17, no. 18: 2485. https://doi.org/10.3390/polym17182485
APA StyleBouchetara, M., Belhabib, S., Melelli, A., Perrin, J., Weitkamp, T., Koubaa, A., Tahlaiti, M., Nouri, M., & Guessasma, S. (2025). Effect of Printing Temperature on the Microstructure and Tensile Properties of Polylactic Acid–Magnetic Iron Composites Manufactured by Material Extrusion. Polymers, 17(18), 2485. https://doi.org/10.3390/polym17182485










