Optimization of Thermal Conductivity of Bismaleimide/h-BN Composite Materials Based on Molecular Structure Design
Abstract
1. Introduction
2. Experimental
2.1. Materials
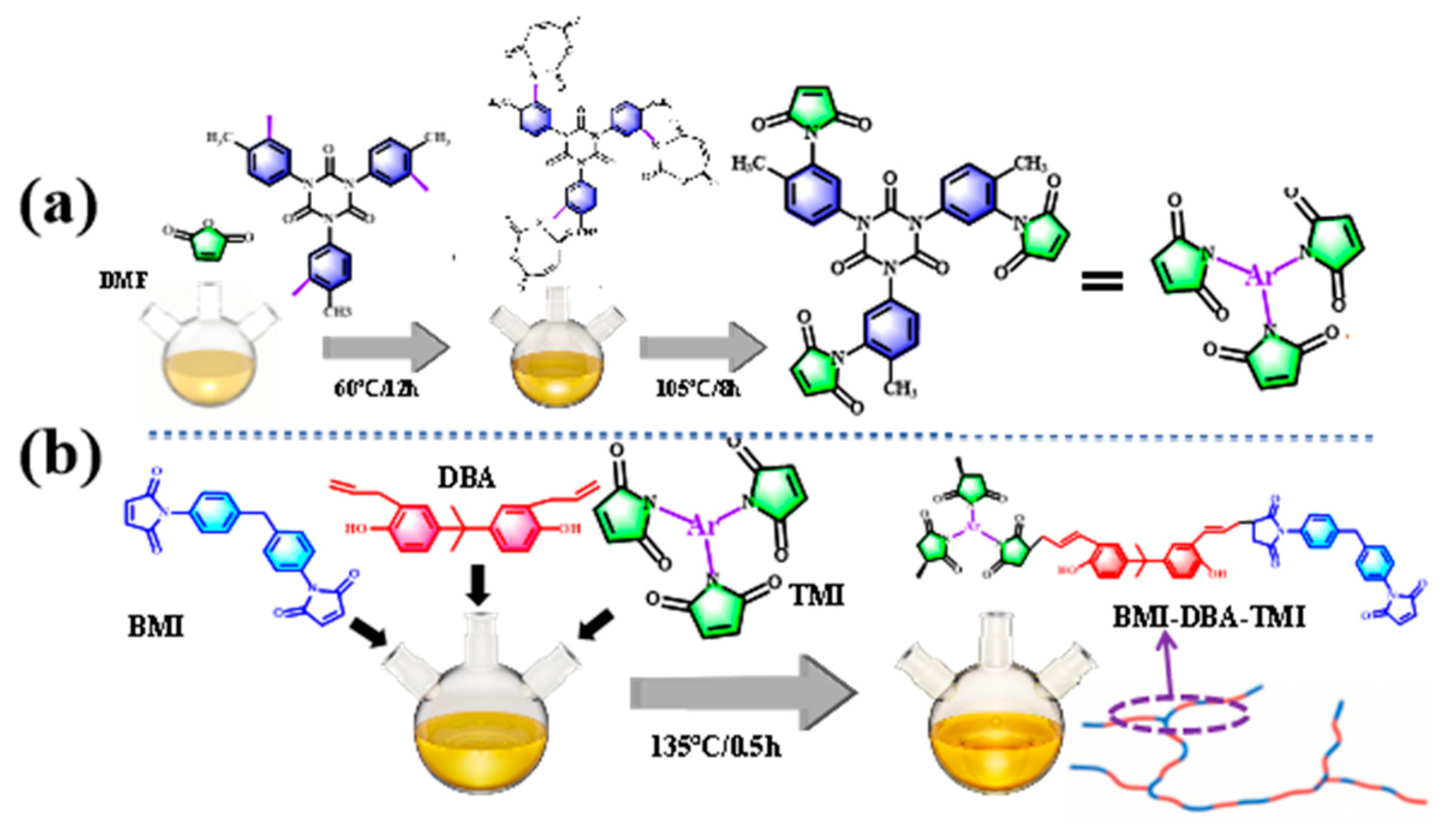
2.2. Preparation of BMI-DBA-TTMI/DMAA/h-BN Composite Material
2.3. Characterization
3. Results and Discussion
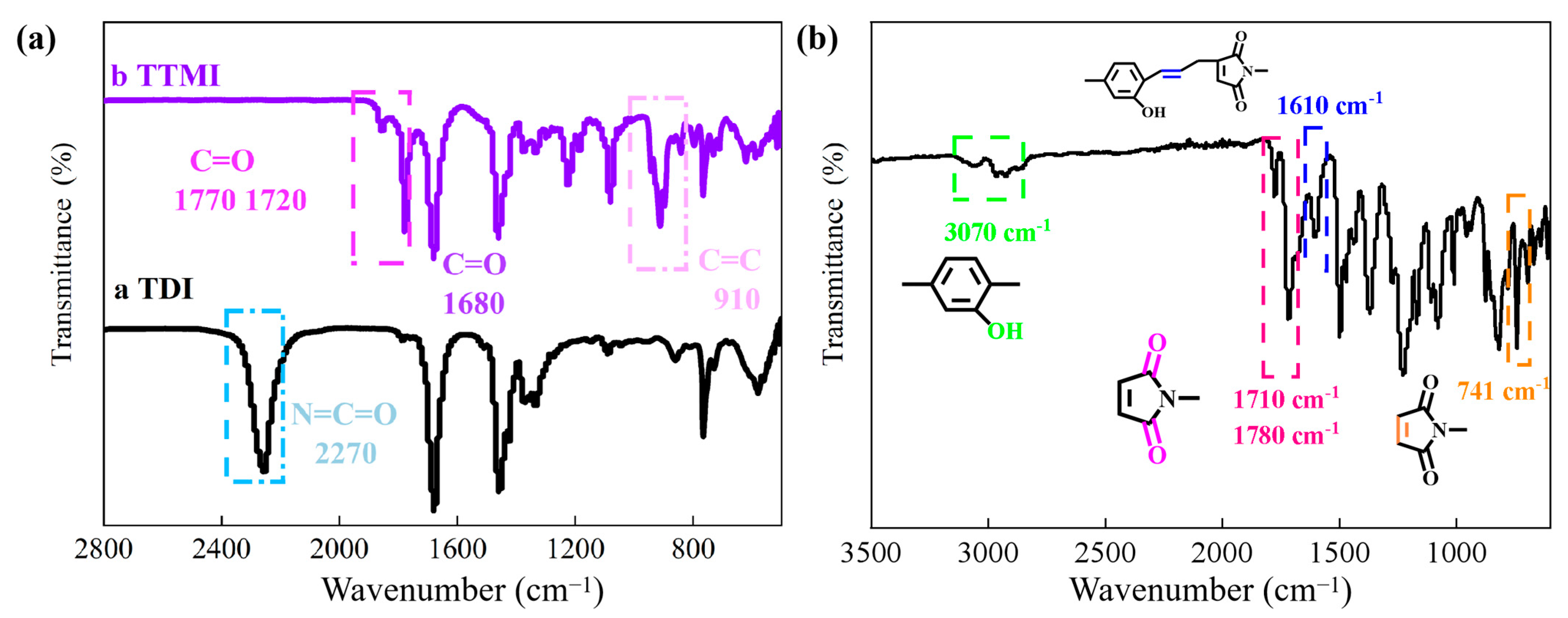
3.1. Structural Characterization of BMI-DBA-TTMI/DMAA
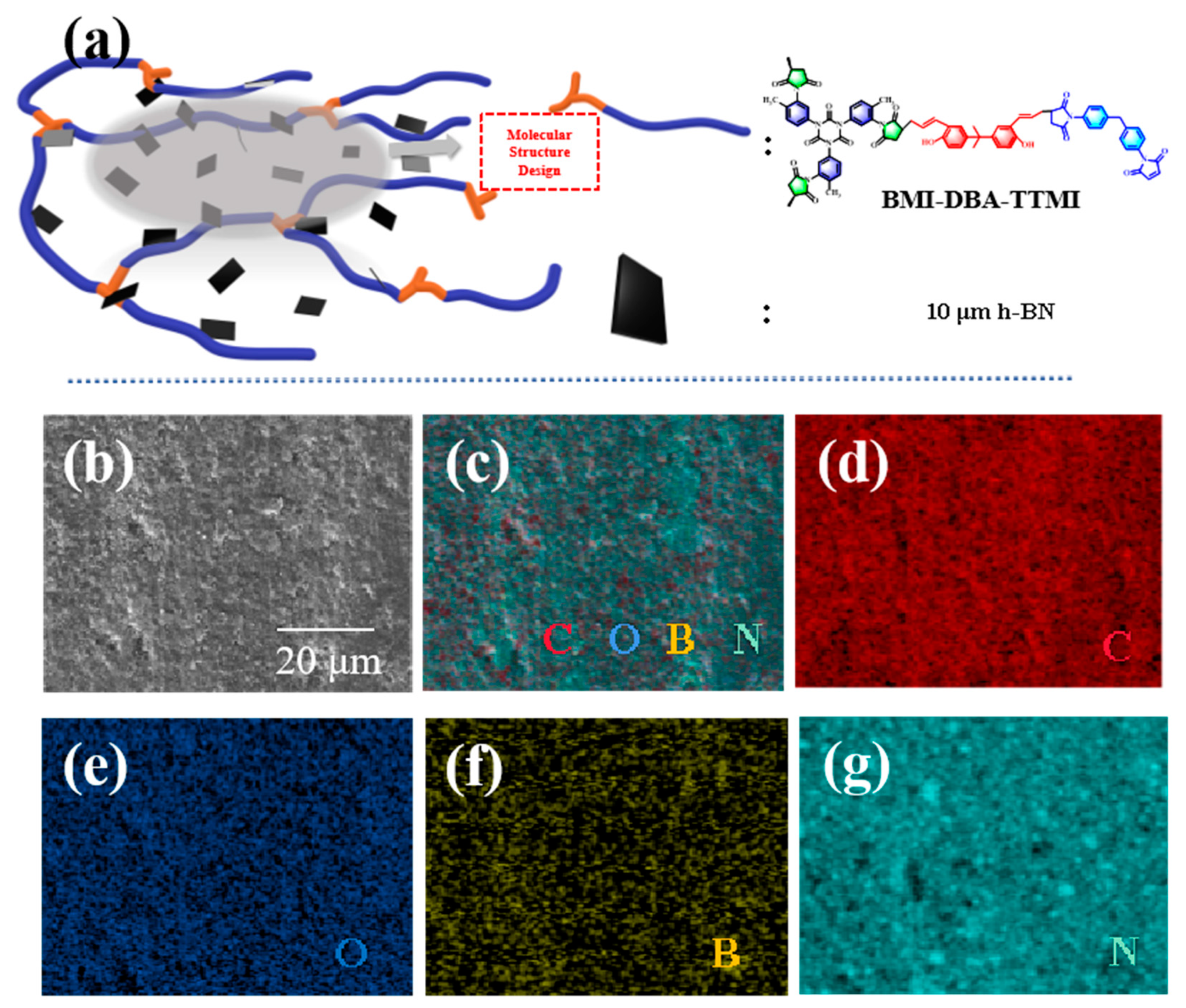
3.2. Microscopic Morphology of BMI-DBA-TTMI/DMAA/h-BN Composite Materials
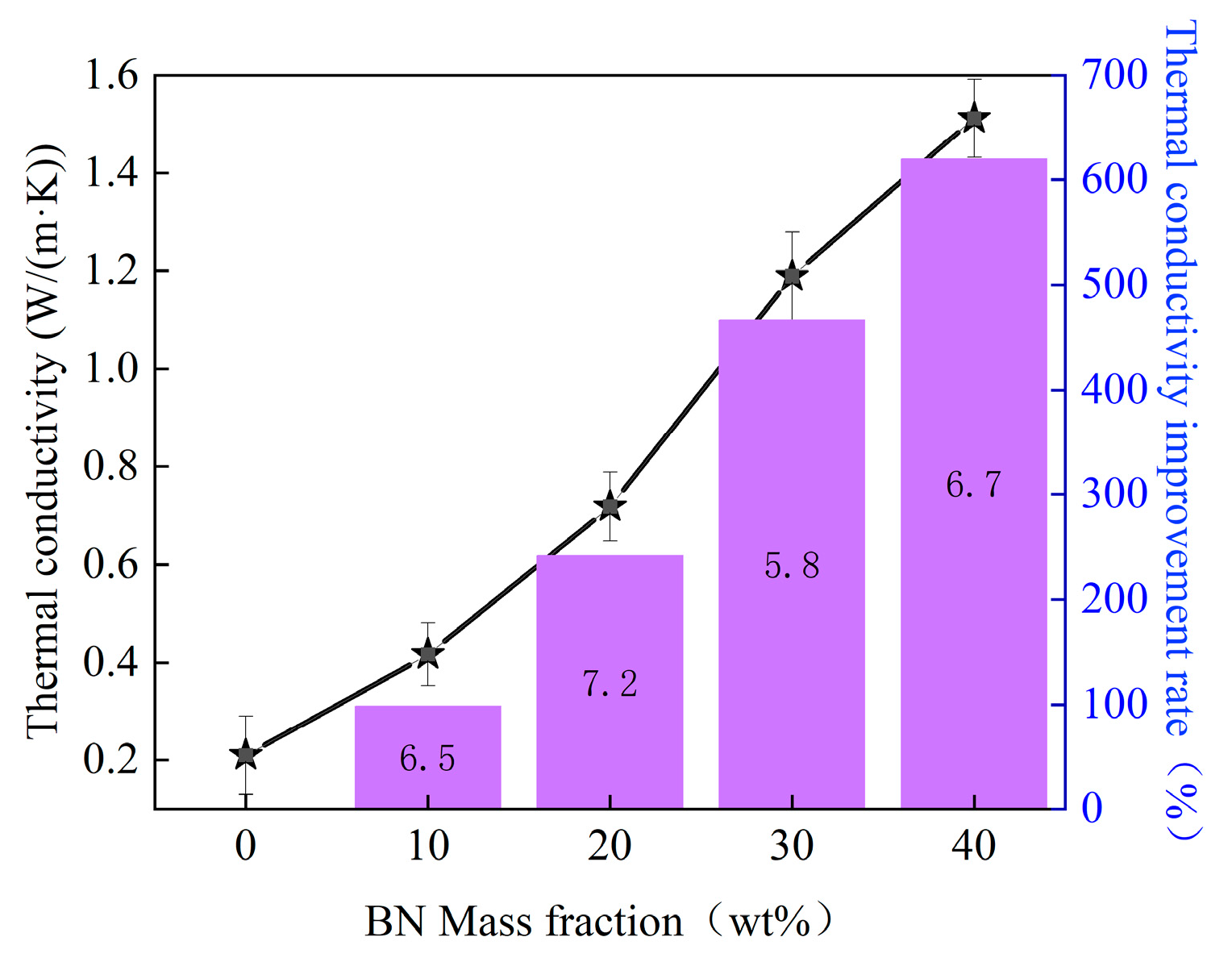
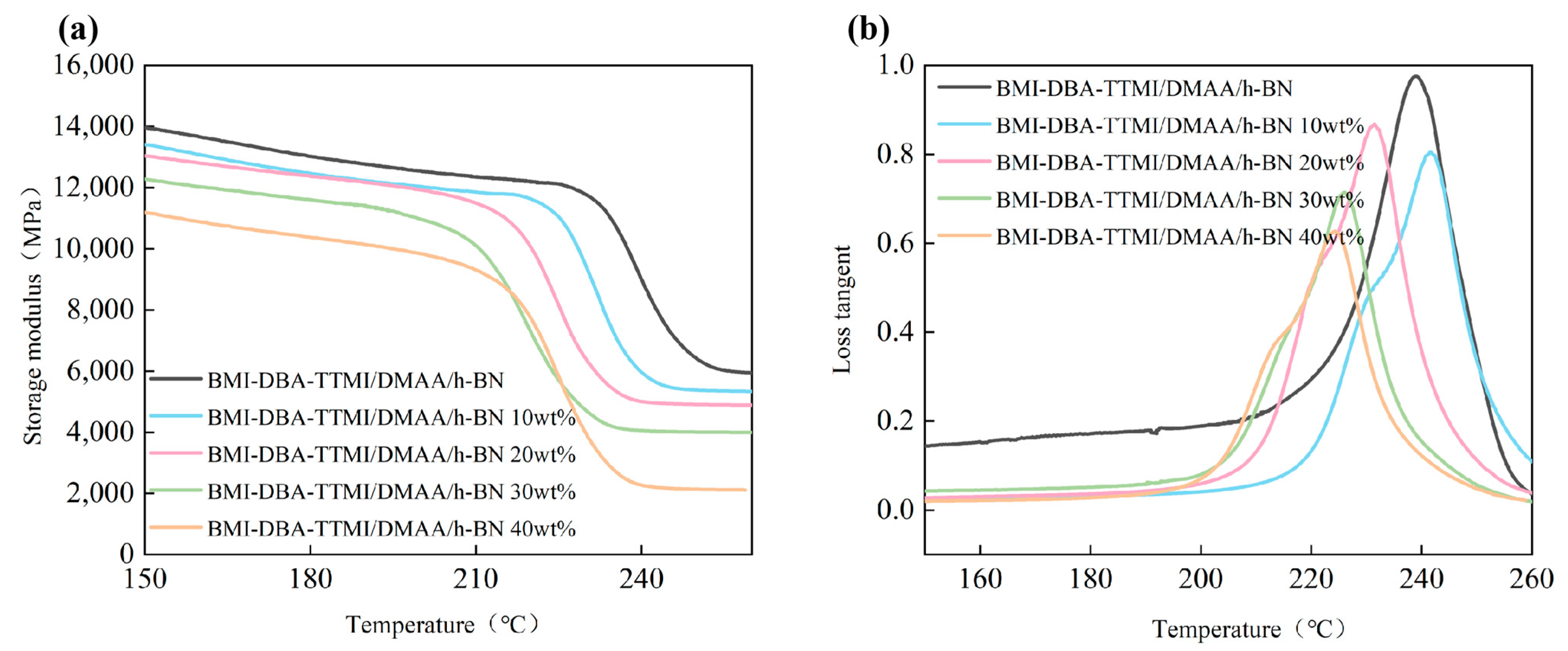
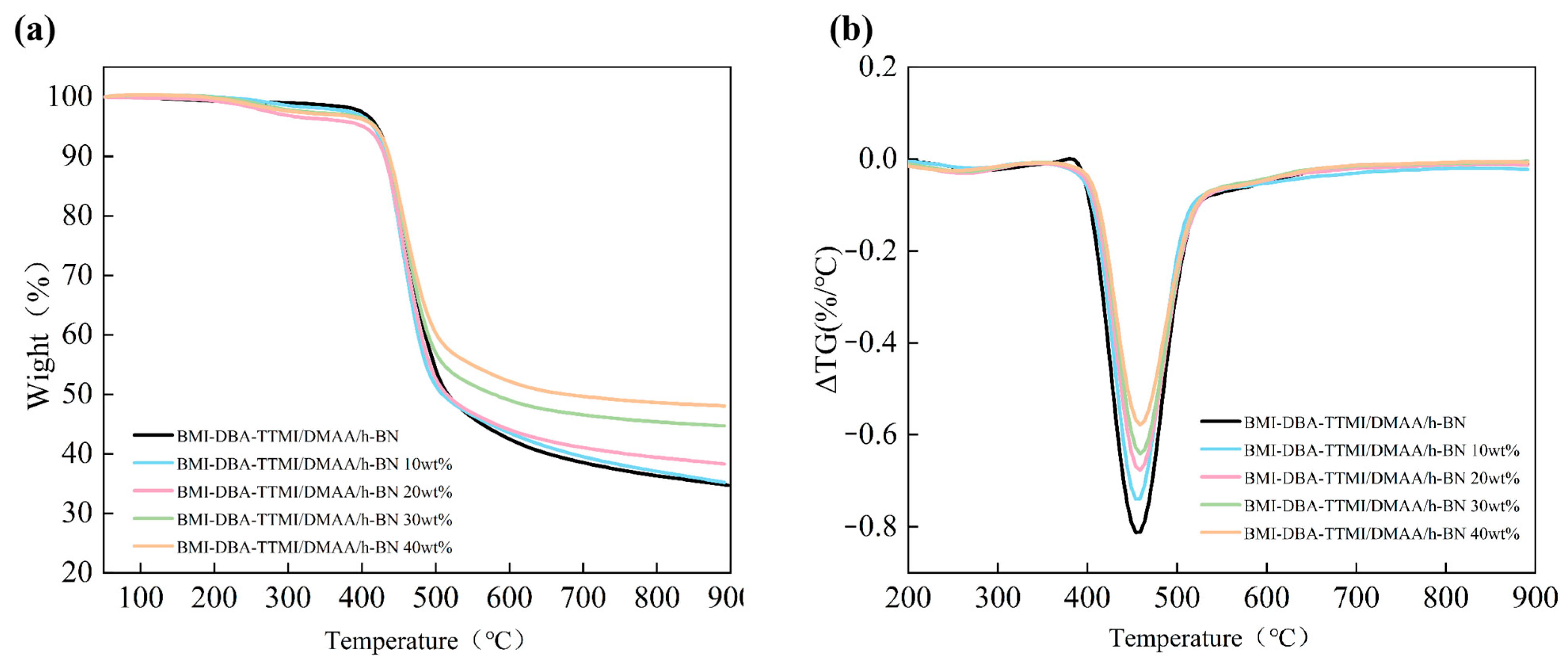
3.3. Thermal Conductivity Characteristics
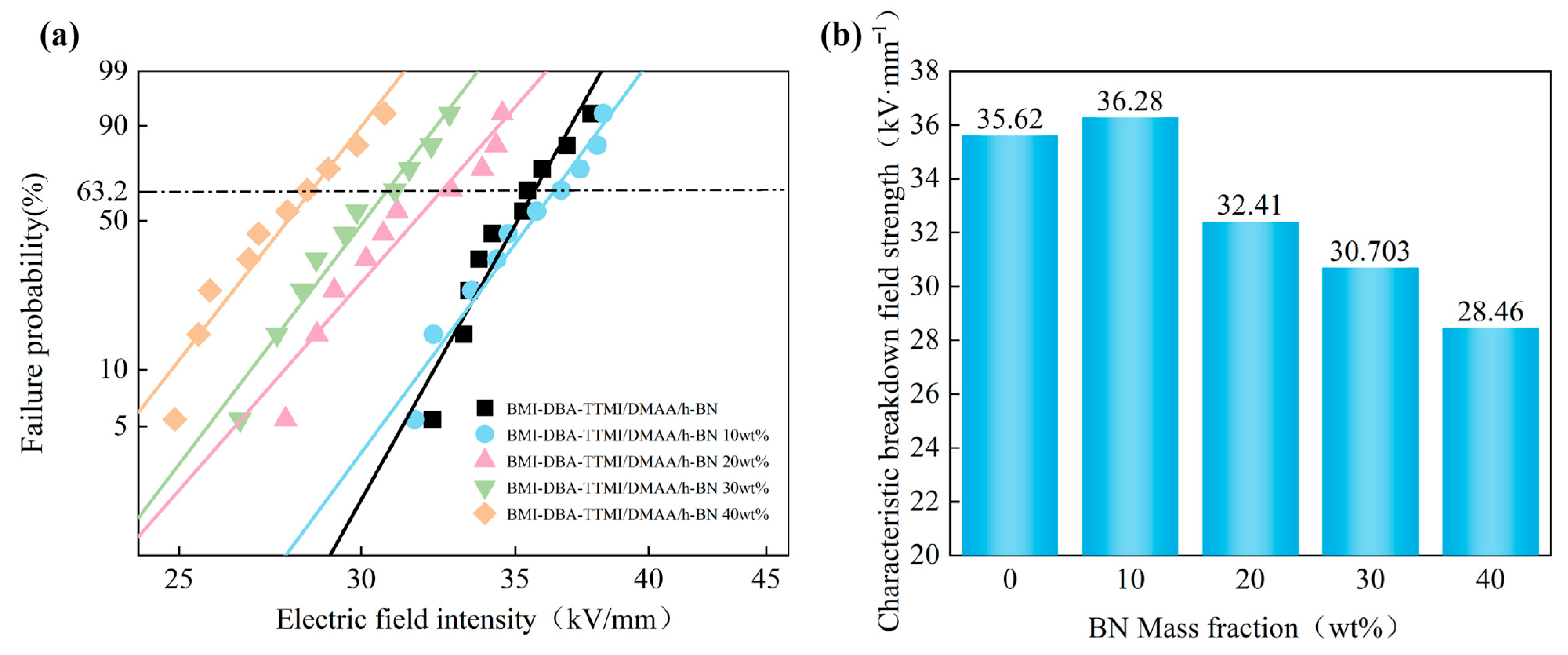
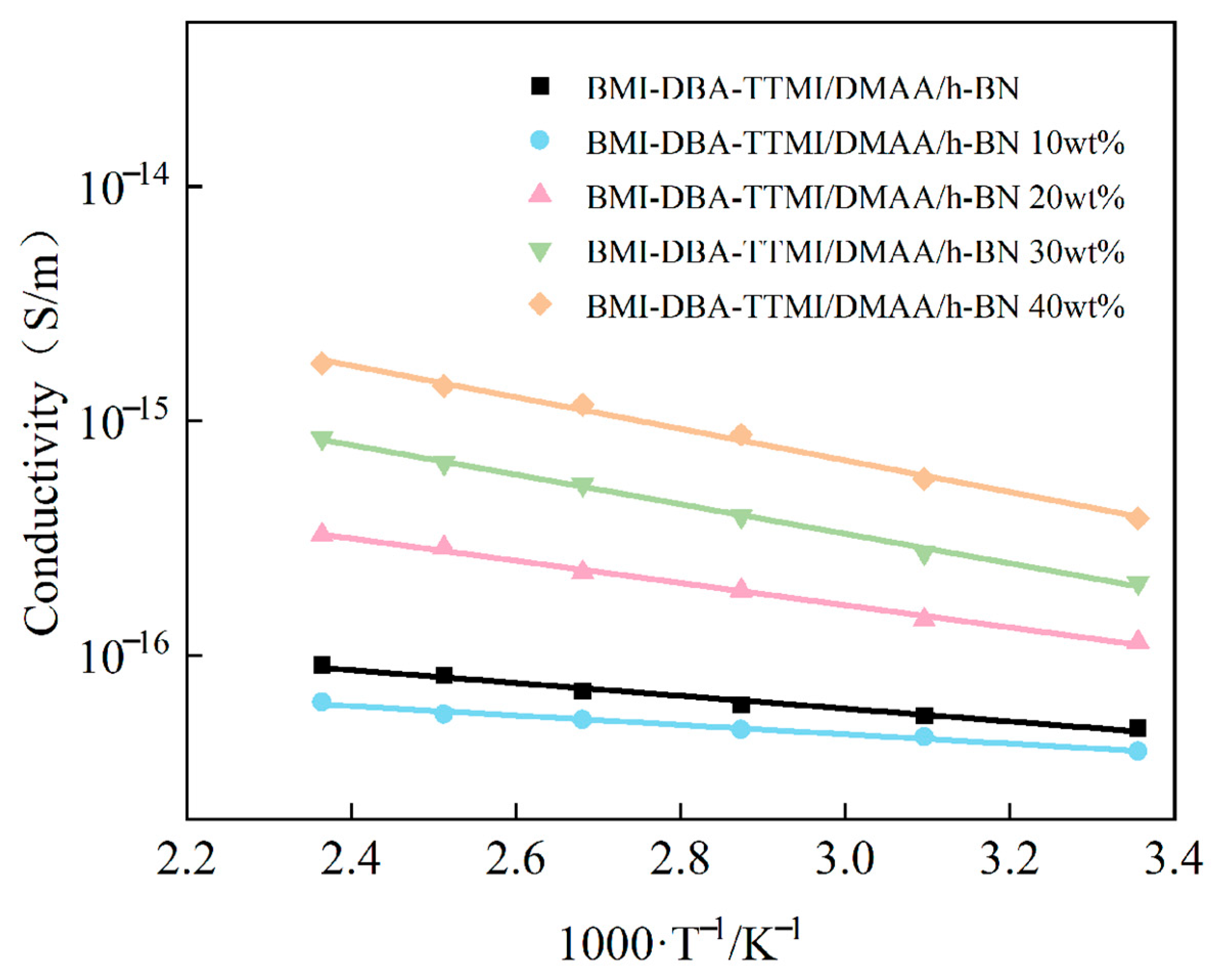
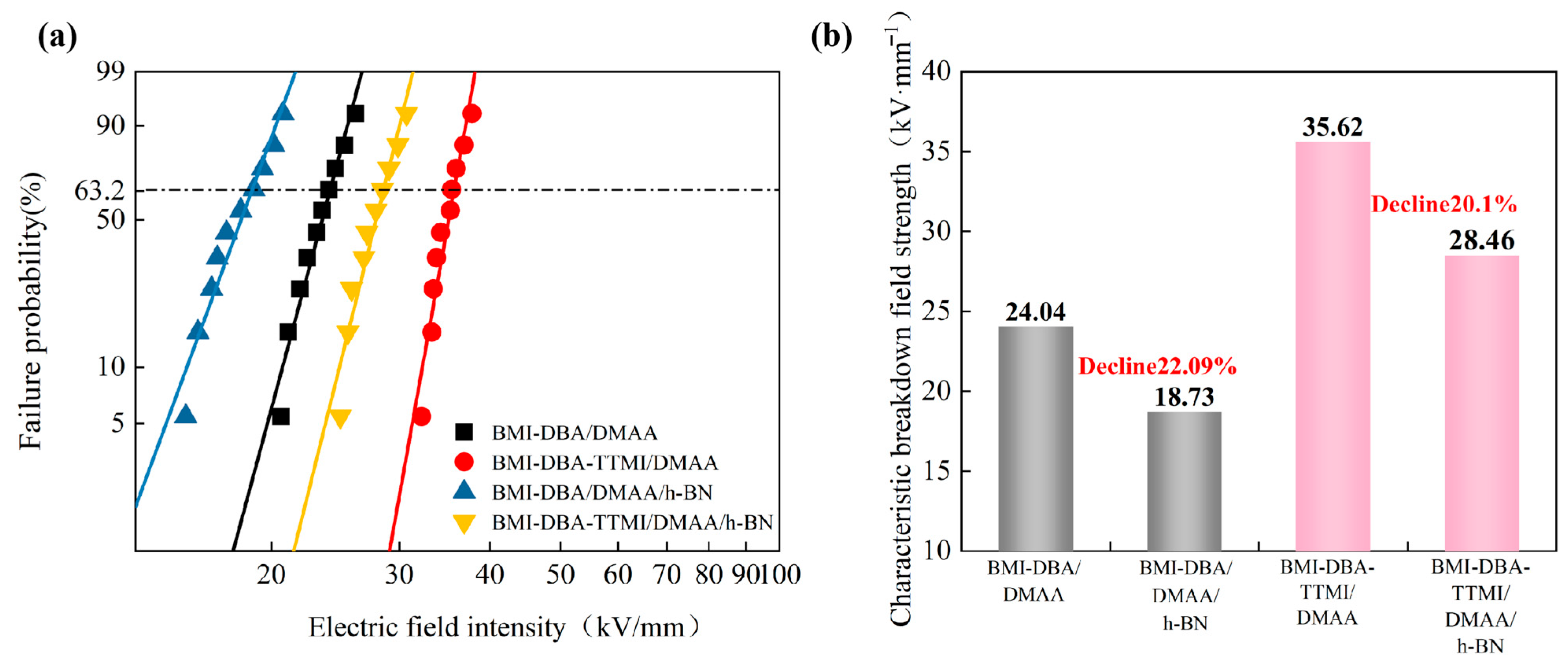
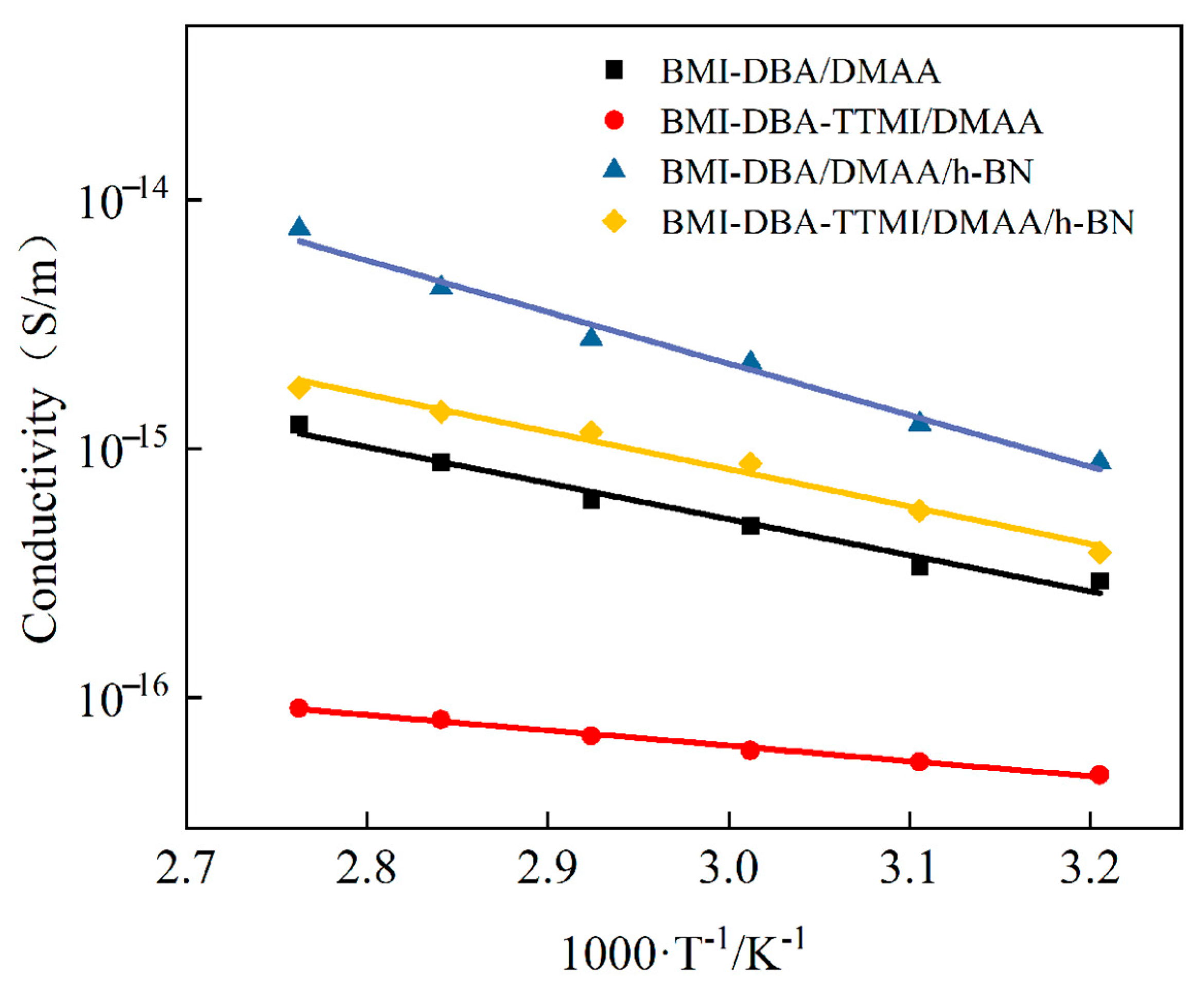
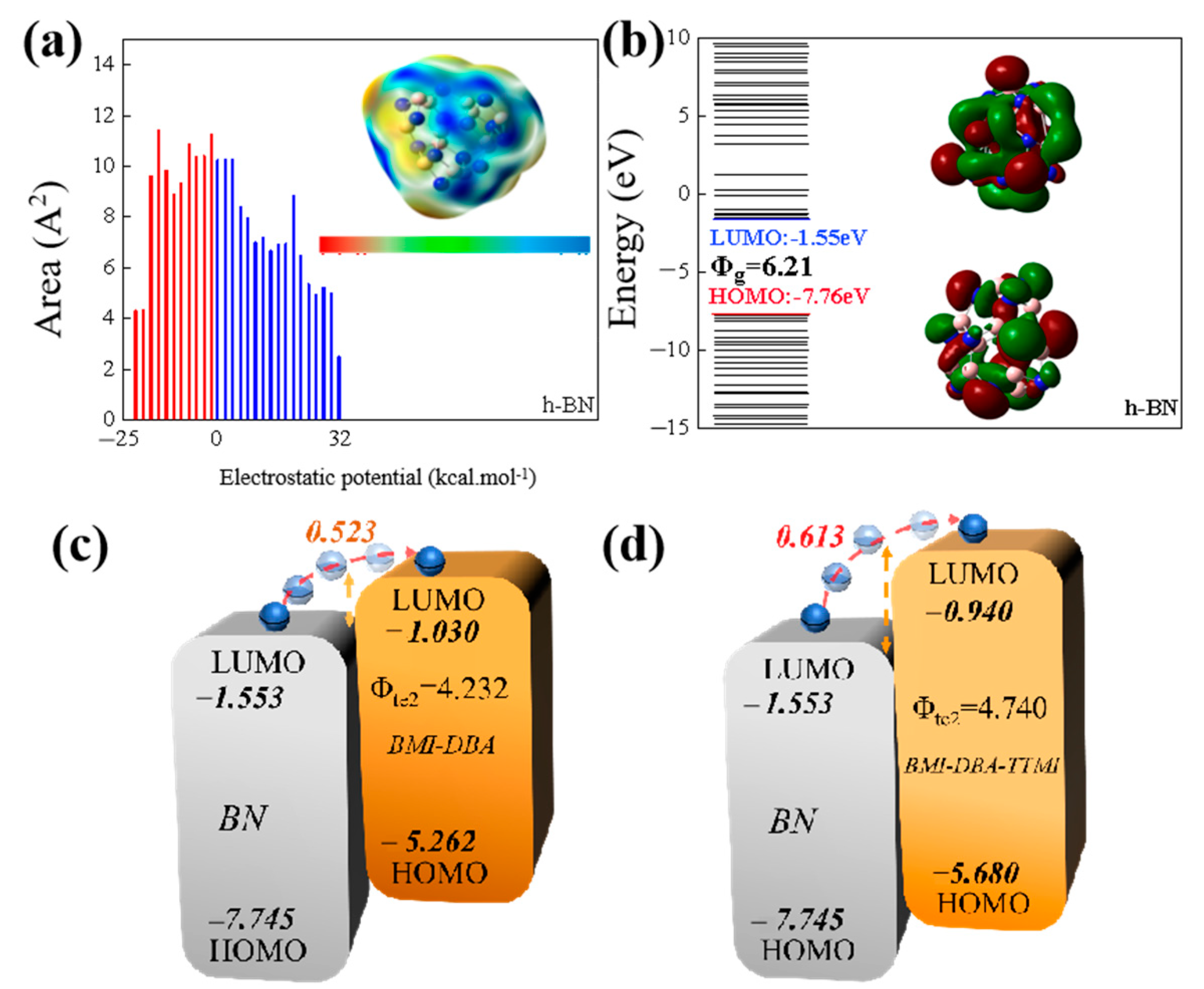
3.4. Insulation Properties
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Bae, J.C.; Cho, H.R.; Yadav, S.; Kim, S.C. Cooling effect of water channel with vortex generators on in-wheel driving motors in electric vehicles. Energies 2022, 15, 722. [Google Scholar] [CrossRef]
- Tang, Y.; Chai, F.; Chen, L. Investigation of open-circuit fault-tolerant strategy in a modular permanent magnet synchronous in-wheel motor based on electromagnetic–thermal analysis. IEEE Trans. Transp. Electrif. 2022, 8, 1085–1093. [Google Scholar] [CrossRef]
- Wang, X.; Li, B.; Gerada, D.; Huang, K.; Stone, I.; Worrall, S.; Yan, Y. A critical review on thermal management technologies for motors in electric cars. Appl. Therm. Eng. 2022, 201, 117758. [Google Scholar] [CrossRef]
- Wang, Q.; Wu, Y.; Niu, S.; Zhao, X. Advances in thermal management technologies of electrical machines. Energies 2022, 15, 3249. [Google Scholar] [CrossRef]
- Guo, C.; Long, L.; Wu, Y.; Xu, K.; Ye, H. Electromagnetic-thermal coupling analysis of a permanent-magnet in-wheel motor with cooling channels in the deepened stator slots. Case Stud. Therm. Eng. 2022, 35, 102158. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, J.; Qu, C.; Zhou, C. Temperature field and demagnetization analysis of in-wheel motors based on magneto-thermal two-way coupling. J. Power Electron. 2024, 24, 227–238. [Google Scholar] [CrossRef]
- Kim, S.; Kim, J.; Kim, M.; Park, J.; Mhin, S.; Kim, D. Physics of failure and high-temperature reliability on Ag sintered ENIG finished die-attachments at 175 °C for integration of in-wheel motor systems. Microelectron. Reliab. 2023, 150, 115090. [Google Scholar] [CrossRef]
- Saleem, A.; Park, M.H.; Ambreen, T.; Kim, S. Optimization of oil flow distribution inside the in-wheel motor assembly of electric vehicles for improved thermal performance. Appl. Therm. Eng. 2022, 201, 117753. [Google Scholar] [CrossRef]
- Liang, P.; Chai, F.; Shen, K.; Liu, W. Water jacket and slot optimization of a water-cooling permanent magnet synchronous in-wheel motor. IEEE Trans. Ind. Appl. 2021, 57, 2431–2439. [Google Scholar] [CrossRef]
- Chen, Q.; Shao, H.; Huang, J.; Sun, H.; Xie, J. Analysis of Temperature Field and Water Cooling of Outer Rotor In-Wheel Motor for Electric Vehicle. IEEE Access 2019, 7, 140142. [Google Scholar] [CrossRef]
- Iredale, R.J.; Ward, C.; Hamerton, I. Modern advances in bismaleimide resin technology: A 21st century perspective on the chemistry of addition polyimides. Prog. Polym. Sci. 2017, 69, 1–21. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, C.; Qiu, S.; Hu, W.; Hu, Y.; Zhang, L. Multifunctional linear polyphosphazene with reactive side groups: Achieving fire resistance and low dielectric bismaleimide. Compos. Part B: Eng. 2025, 296, 112254. [Google Scholar] [CrossRef]
- Zhu, F.; Bao, Y.; Hu, W.; Li, Z.; Fei, X.; Liu, J.; Li, X.; Wei, W. Bismaleimide/epoxy/aromatic diamine ternary resin molding compounds for high-temperature electronic packaging applications. J. Mater. Sci. 2025, 60, 2151–2164. [Google Scholar]
- Guo, J.; Liu, R.; Ding, Z.; Wang, Y.; Wang, J.; Jian, X.; Zong, L. A composite system based on organic-inorganic interface modification: High temperature resistance, high modulus, and low coefficient of thermal expansion. Polymer 2025, 324, 128190. [Google Scholar] [CrossRef]
- Jin, H.; Miller, G.; Pety, S.; Griffin, A.; Stradley, D.; Roach, D.; Sottos, N.; White, S. Fracture behavior of a self-healing, toughened epoxy adhesive. Int. J. Adhes. Adhes. 2013, 44, 157–165. [Google Scholar] [CrossRef]
- Lyu, J.; Ji, B.; Wu, N.; Liao, W.; Yin, C.; Bai, S.; Xing, S. The effect of substituent group in allyl benzoxazine on the thermal, mechanical and dielectric properties of modified bismaleimide. React. Funct. Polym. 2023, 191, 11. [Google Scholar] [CrossRef]
- Zhuo, D.; Gu, A.; Liang, G.; Hu, J.; Yuan, L.; Chen, X. Flame retardancy materials based on a novel fully end-capped hyperbranched polysiloxane and bismaleimide diallylbisphenol A resin with simultaneously improved integrated performance. J. Mater. Chem. 2011, 21, 6584–6594. [Google Scholar] [CrossRef]
- Atinafu, D.G.; Ok, Y.S.; Kua, H.W.; Kin, S. Thermal properties of composite organic phase change materials (PCMs): A critical review on their engineering chemistry. Appl. Therm. Eng. 2020, 181, 115960. [Google Scholar] [CrossRef]
- Wang, W.X.; Li, C.C.; Zeng, X.L.; Chen, J.; Sun, R. Application of polymer-based phase change materials in thermal safety management of power batteries. J. Energy Storage 2022, 55, 105646. [Google Scholar] [CrossRef]
- Yu, X.; Bhatti, M.R.; Ren, X.; Steiner, P.; Di, S.; Dong, M.; Zhang, H.; Papageorgiou, D.; Portale, G.; Kocabas, C.; et al. Dielectric Polymer Composites with Ultra-High Thermal Conductivity and Low Dielectric Loss. Compos. Sci. Technol. 2022, 229, 109695. [Google Scholar] [CrossRef]
- Begum, S.; Ullah, H.; Kausar, A.; Siddiq, M.; Aleem, M. Fabrication of Epoxy Functionalized MWCNTs Reinforced PVDF Nanocomposites with High Dielectric Permittivity, Low Dielectric Loss and High Electrical Conductivity. Compos. Sci. Technol. 2018, 167, 497–506. [Google Scholar] [CrossRef]
- Zeng, X.; Ye, L.; Yu, S.; Sun, R.; Xu, J.; Wong, C. Facile Preparation of Superelastic and Ultralow Dielectric Boron Nitride Nanosheet Aerogels via Freeze-Casting Process. Chem. Mater. 2015, 27, 5849–5855. [Google Scholar] [CrossRef]
- Shi, J.; Wang, X.; Gao, Y.J.; Zhang, X.; Weng, L.; Sun, X. Investigation on the fabrication and mechanism of thermally conductive bismaleimide composites with low dielectric constant via a branched crosslink structure. Mater. Chem. Phys. 2024, 328, 129953. [Google Scholar] [CrossRef]
- Ouyang, Y.; Zhang, X.; Shi, J.; Yu, Y.; Liu, L.; Jia, Z.; Wang, Q.; Xu, H.; Wang, X. Diamine-modified bismaleimide for toughening of UV-cured epoxy acrylate coating. Mater. Chem. Phys. 2024, 313, 128703. [Google Scholar] [CrossRef]
- Sreehari, H.; Gopika, V.; Jayan, J.S.; Sethulekshmi, A.; Staritha, A. A comprehensive review on bio epoxy based IPN: Synthesis, properties and applications. Polymer 2022, 252, 124950. [Google Scholar] [CrossRef]
- Ouyang, Y.; Li, X.; Tian, H.; Bai, L.; Yuan, F. A novel branched Al2O3/silicon rubber composite with improved thermal conductivity and excellent electrical insulation performance. Nanomaterials 2021, 11, 2654. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, Y.; Niu, H.; Wu, L.; He, X.; Xu, T.; Wang, N.; Yao, Y. An electrospinning–electrospraying technique for connecting electrospun fibers to enhance the thermal conductivity of boron nitride/polymer composite films. Compos. Part B: Eng. 2022, 230, 109505. [Google Scholar] [CrossRef]
- Liang, Y.; Liu, B.; Zhang, B.; Liu, Z.; Liu, W. Effects and mechanism of filler surface coating strategy on thermal conductivity of composites: A case study on epoxy/SiO2-coated BN composites. Int. J. Heat Mass Transf. 2021, 164, 120533. [Google Scholar] [CrossRef]
- Zhao, Z.B.; Du, X.Y.; Wang, Y.; Wang, Z.; Zhang, C.; Liu, J.; Yan, C. Preparation of a novel bi-layer modified alumina-based hybrid material and its effect on the thermal conductivity enhancement of polymer composites. Ceram. Int. 2022, 48, 15483–15492. [Google Scholar] [CrossRef]
- Guo, H.; Liu, J.; Wang, Q.; Liu, M.; Du, C.; Li, B.; Feng, L. High thermal conductive poly(vinylidene fluoride)-based composites with well-dispersed carbon nanotubes/graphene three-dimensional network structure via reduced interfacial thermal resistance. Compos. Sci. Technol. 2019, 181, 107713. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, Z.; Yang, J.; Huang, T.; Zhang, N.; Zheng, X.; Wang, Y.; Zhou, Z. Largely enhanced thermal conductivity of poly(vinylidene fluoride)/carbon nanotube composites achieved by adding graphene oxide. Carbon 2015, 90, 242–254. [Google Scholar] [CrossRef]
- Huang, J.; Gao, M.; Pan, T.; Zhang, Y.; Lin, Y. Effective thermal conductivity of epoxy matrix filled with poly(ethyleneimine) functionalized carbon nanotubes. Compos. Sci. Technol. 2014, 95, 16–20. [Google Scholar] [CrossRef]
- Drozdov, A.D.; deClaville Christiansen, J. Modeling thermal conductivity of highly filled polymer composites. Polym. Eng. Sci. 2019, 59, 2174–2179. [Google Scholar] [CrossRef]
- Zare, Y. Development of Halpin-Tsai model for polymer nanocomposites assuming interphase properties and nanofiller size. Polym. Test. 2016, 51, 69–73. [Google Scholar] [CrossRef]
- Tian, F.; Cao, J.; Ma, W. Enhanced thermal conductivity and rheological performance of epoxy and liquid crystal epoxy composites with filled Al2O3 compound. Polym. Test. 2023, 120, 107940. [Google Scholar] [CrossRef]
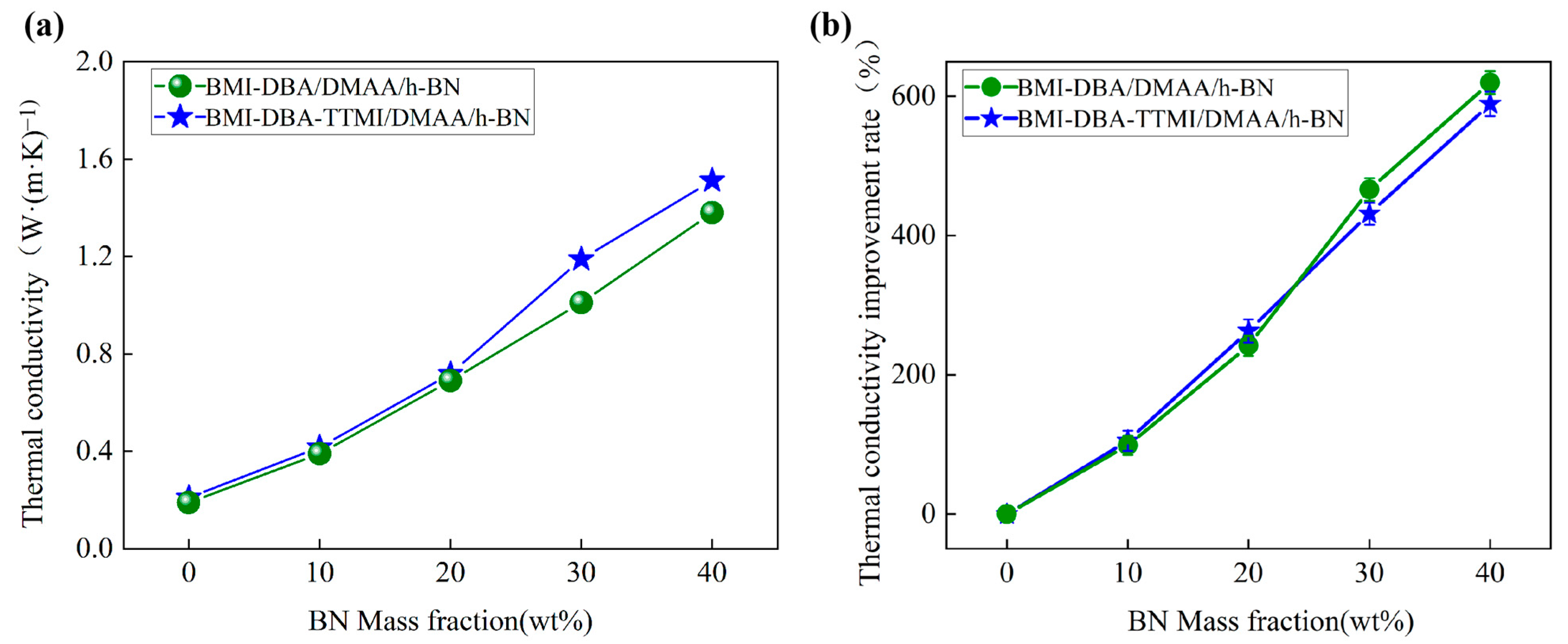
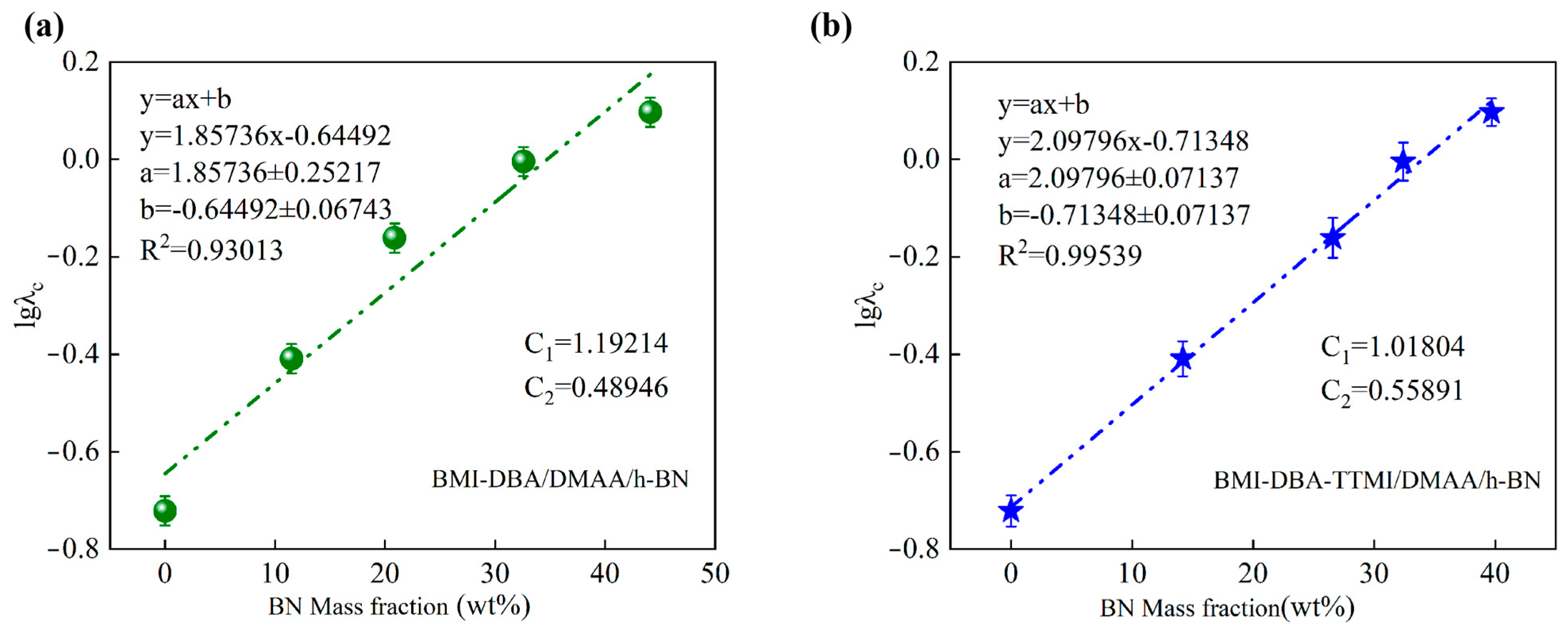
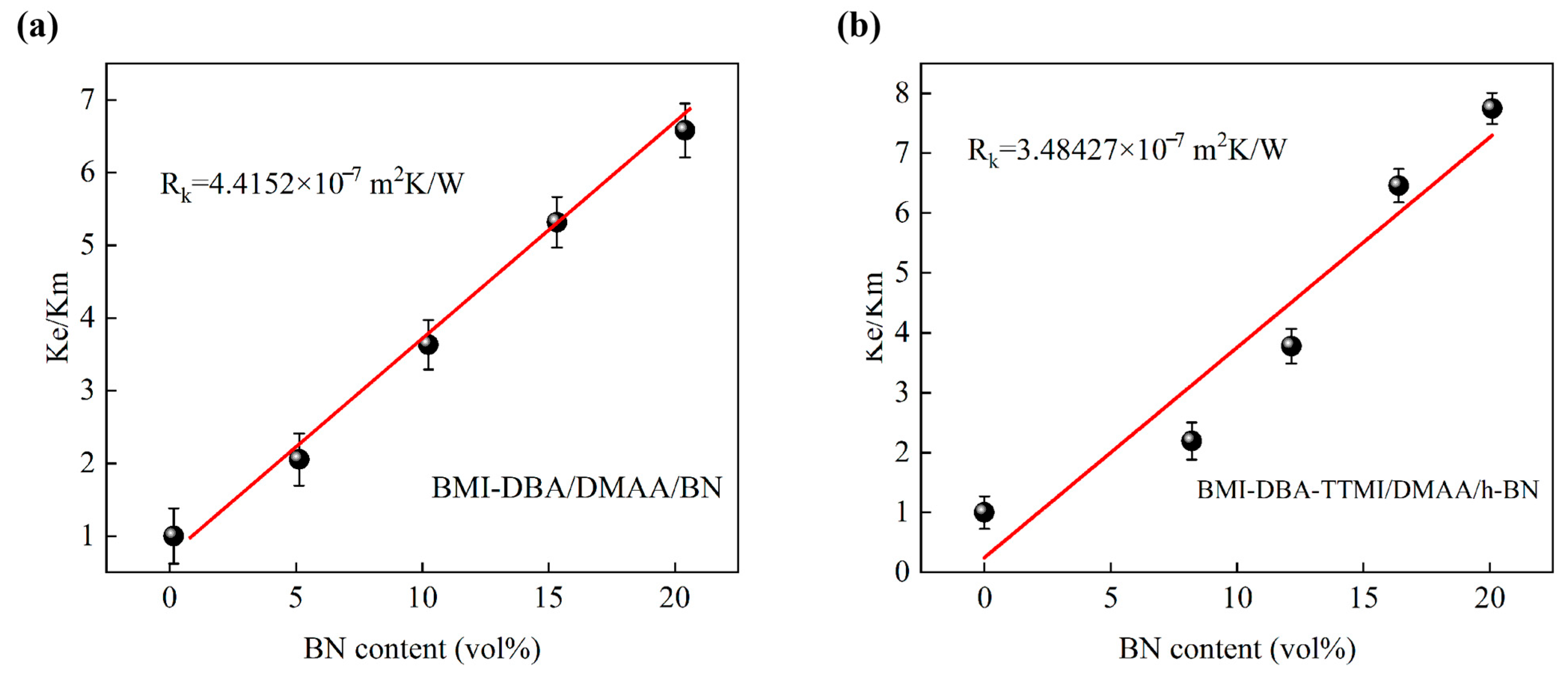
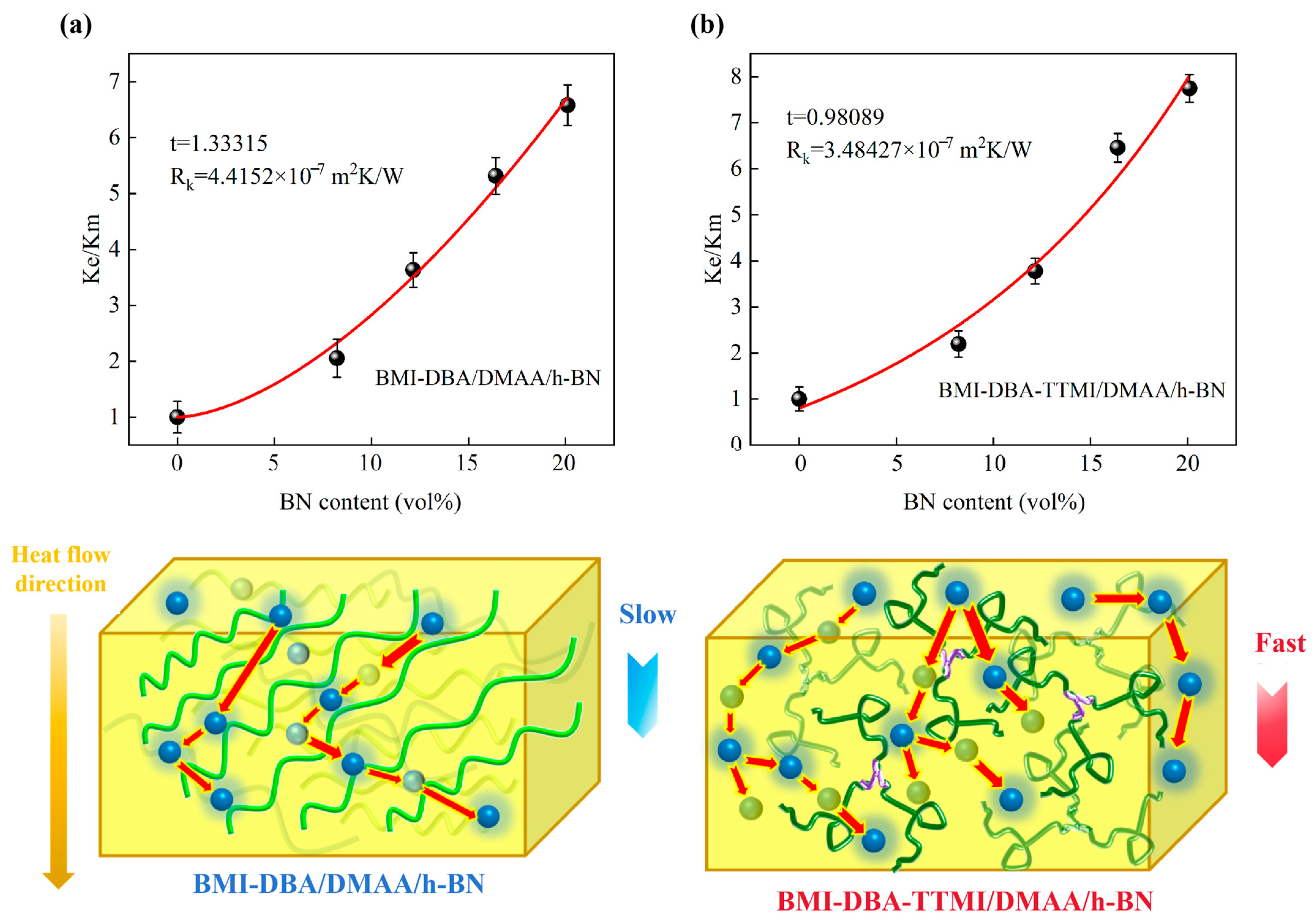
| Sample | C1 | C2 |
|---|---|---|
| BMI-DBA/DMAA/h-BN | 1.192 | 0.489 |
| BMI-DBA-TTMI/DMAA/h-BN | 1.108 | 0.559 |
| Sample | aTg/℃ | bE’r/GPa | cρ/(mol·cm−3) |
|---|---|---|---|
| BMI-DBA-TTMI/DMAA/h-BN | 512 | 5.91 | 0.463 |
| 10 wt%BMI-DBA-TTMI/DMAA/h-BN | 505 | 5.33 | 0.323 |
| 20 wt%BMI-DBA-TTMI/DMAA/h-BN | 504 | 4.88 | 0.298 |
| 30 wt%BMI-DBA-TTMI/DMAA/h-BN | 499 | 3.98 | 0.295 |
| 40 wt%BMI-DBA-TTMI/DMAA/h-BN | 497 | 2.12 | 0.291 |
| Sample | Eb(kV/mm) | β |
|---|---|---|
| BMI-DBA-TTMI/DMAA/h-BN | 35.62 | 22.09 |
| 10 wt%BMI-DBA-TTMI/DMAA/h-BN | 36.28 | 18.85 |
| 20 wt%BMI-DBA-TTMI/DMAA/h-BN | 32.41 | 15.26 |
| 30 wt%BMI-DBA-TTMI/DMAA/h-BN | 30.70 | 17.36 |
| 40 wt%BMI-DBA-TTMI/DMAA/h-BN | 28.46 | 16.31 |
| Sample | Activation Energy (eV) |
|---|---|
| BMI-DBA-TTMI/DMAA/h-BN | 0.236 |
| 10 wt%BMI-DBA-TTMI/DMAA/h-BN | 0.219 |
| 20 wt%BMI-DBA-TTMI/DMAA/h-BN | 0.409 |
| 30 wt%BMI-DBA-TTMI/DMAA/h-BN | 0.498 |
| 40 wt%BMI-DBA-TTMI/DMAA/h-BN | 0.581 |
| Sample | Eb(kV/mm) | β |
|---|---|---|
| BMI-DBA/DMAA/h-BN | 24.04 | 17.13 |
| BMI-DBA-TTMI/DMAA/h-BN | 35.62 | 22.09 |
| 40 wt%BMI-DBA/DMAA/h-BN | 18.73 | 13.25 |
| 40 wt%BMI-DBA-TTMI/DMAA/h-BN | 28.46 | 16.31 |
| Sample | Activation Energy (eV) |
|---|---|
| BMI-DBA/DMAA/h-BN | 0.552 |
| BMI-DBA-TTMI/DMAA/h-BN | 0.236 |
| 40 wt%BMI-DBA/DMAA/h-BN | 0.619 |
| 40 wt%BMI-DBA-TTMI/DMAA/h-BN | 0.581 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, W.; Gu, R.; Wang, X.; Wang, C.; Qu, M.; Wang, X.; Shi, J. Optimization of Thermal Conductivity of Bismaleimide/h-BN Composite Materials Based on Molecular Structure Design. Polymers 2025, 17, 2133. https://doi.org/10.3390/polym17152133
Li W, Gu R, Wang X, Wang C, Qu M, Wang X, Shi J. Optimization of Thermal Conductivity of Bismaleimide/h-BN Composite Materials Based on Molecular Structure Design. Polymers. 2025; 17(15):2133. https://doi.org/10.3390/polym17152133
Chicago/Turabian StyleLi, Weizhuo, Run Gu, Xuan Wang, Chenglong Wang, Mingzhe Qu, Xiaoming Wang, and Jiahao Shi. 2025. "Optimization of Thermal Conductivity of Bismaleimide/h-BN Composite Materials Based on Molecular Structure Design" Polymers 17, no. 15: 2133. https://doi.org/10.3390/polym17152133
APA StyleLi, W., Gu, R., Wang, X., Wang, C., Qu, M., Wang, X., & Shi, J. (2025). Optimization of Thermal Conductivity of Bismaleimide/h-BN Composite Materials Based on Molecular Structure Design. Polymers, 17(15), 2133. https://doi.org/10.3390/polym17152133





