Energy-Based Approach for Fatigue Life Prediction of Additively Manufactured ABS/GNP Composites
Abstract
1. Introduction
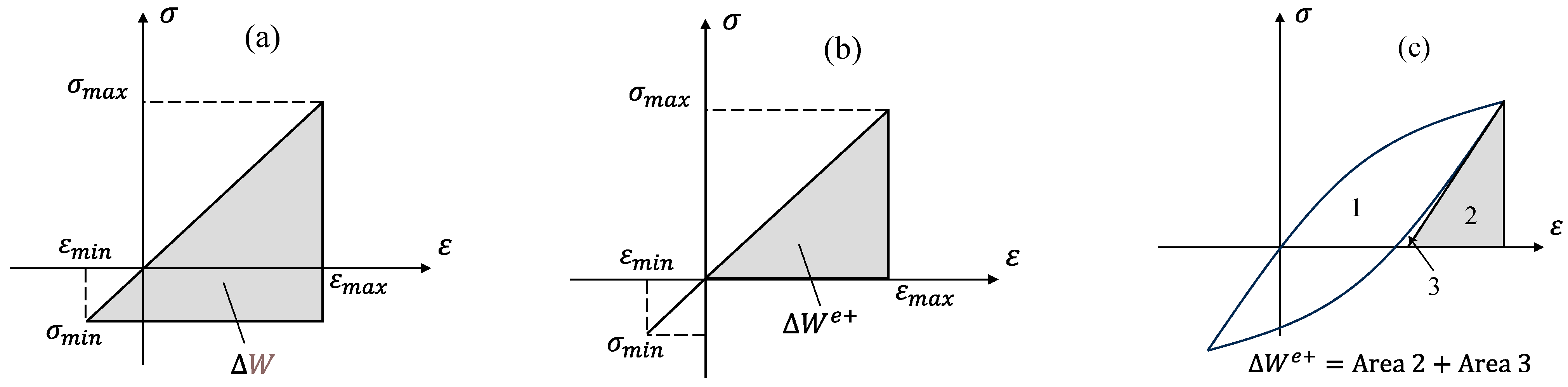
2. Theoretical Background
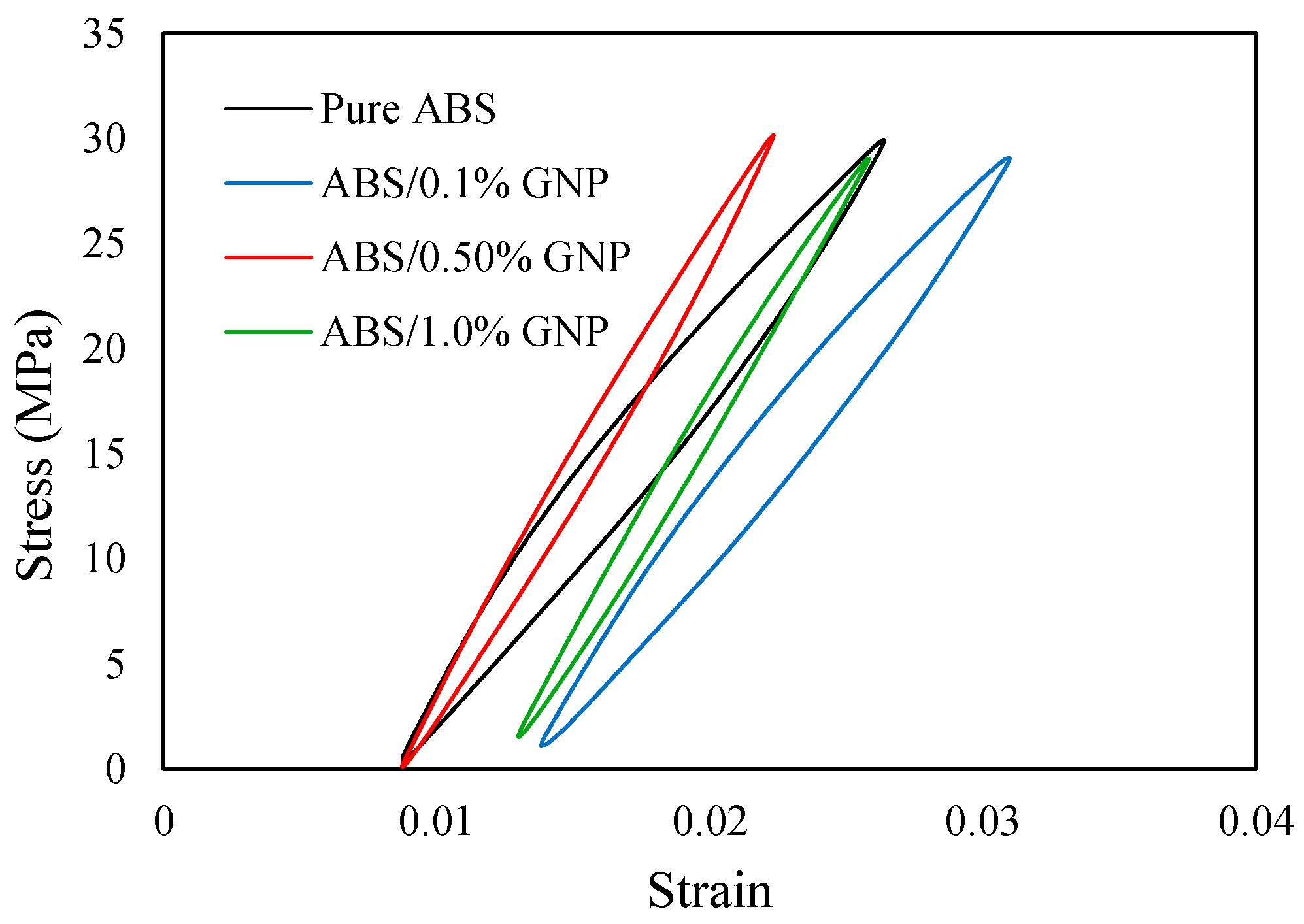
3. Experimental Data
4. Results and Discussion
4.1. Energy-Life Material Properties
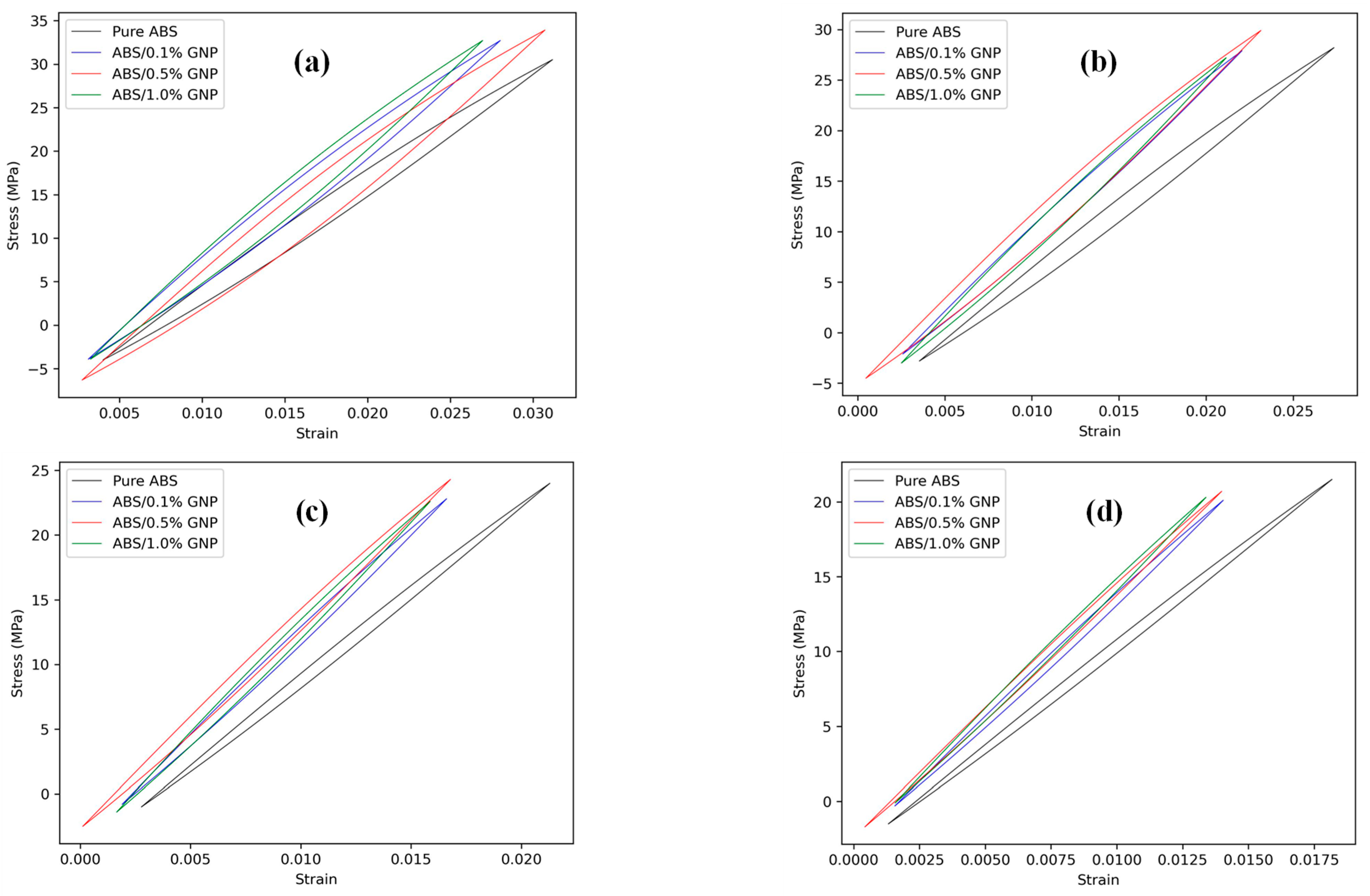
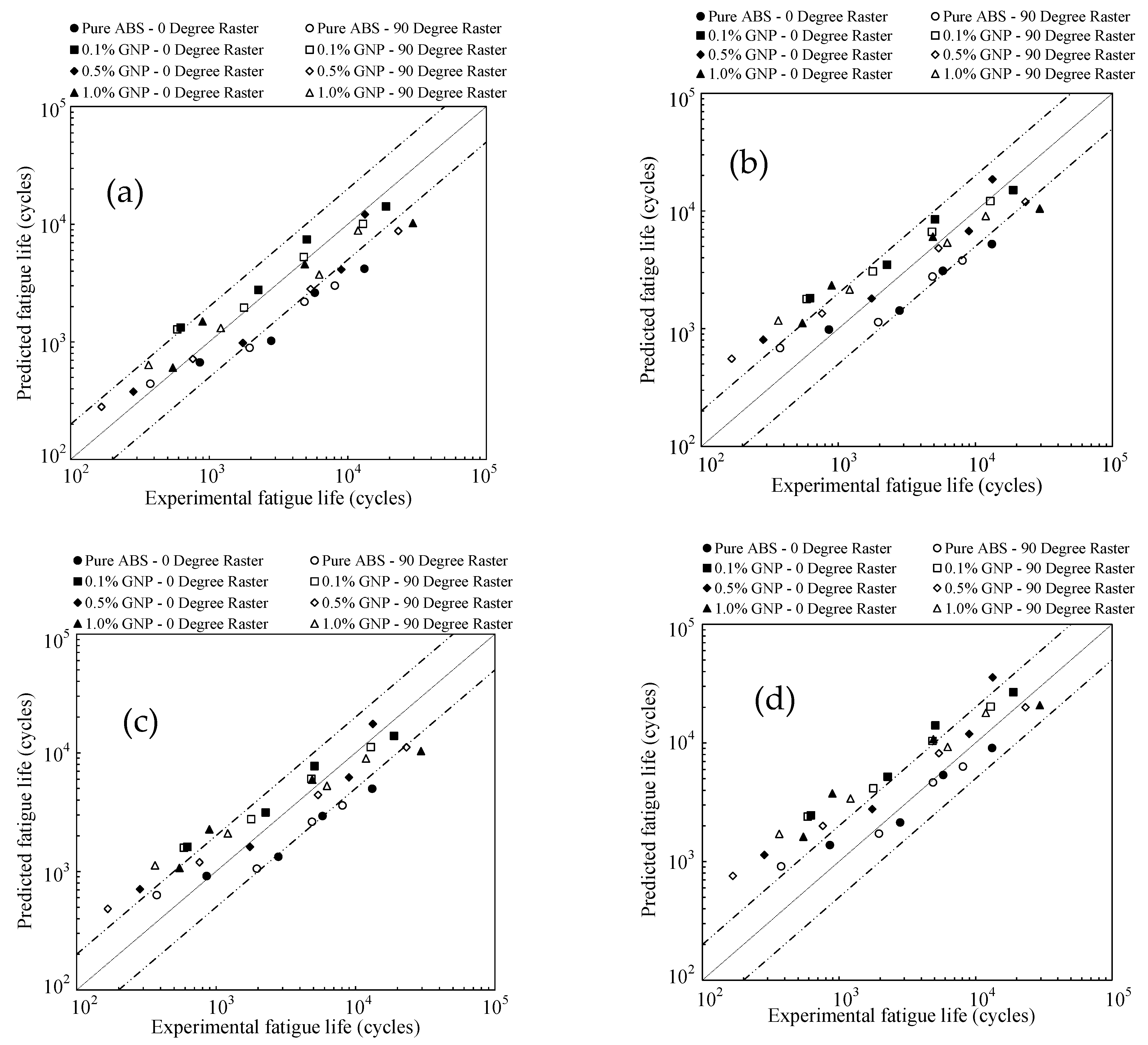
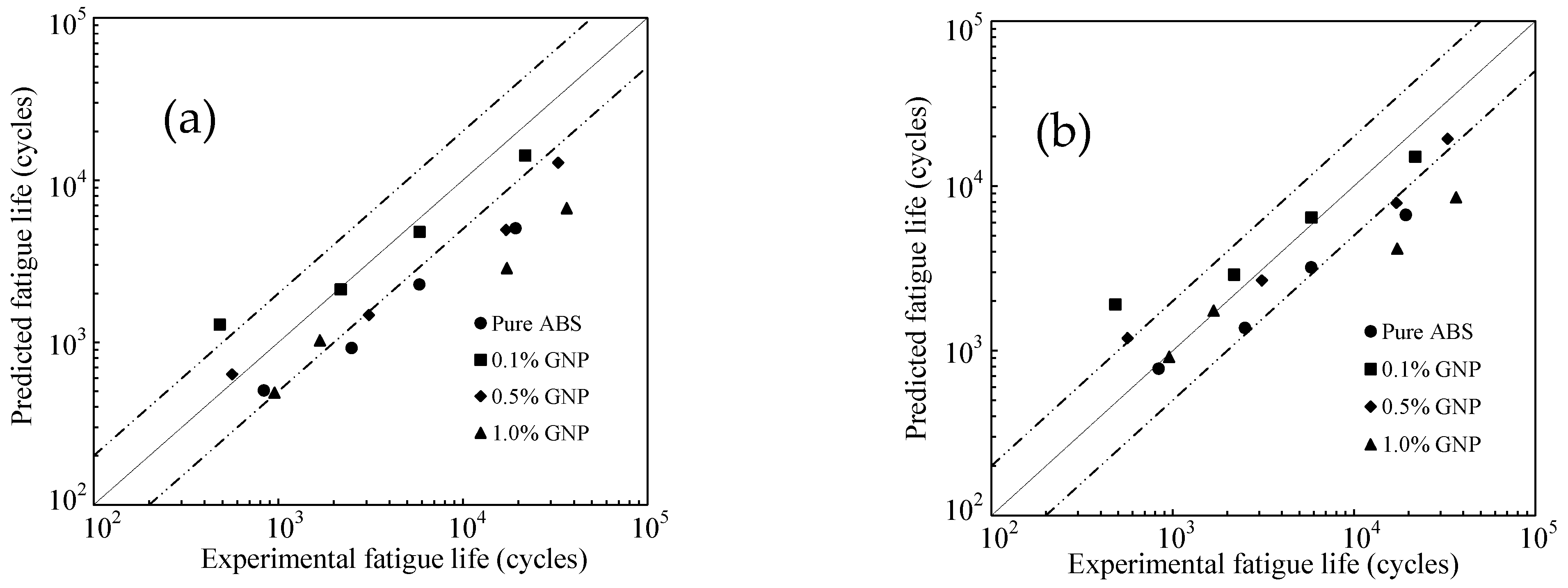
4.2. Application to 0° and 90° Raster Angles
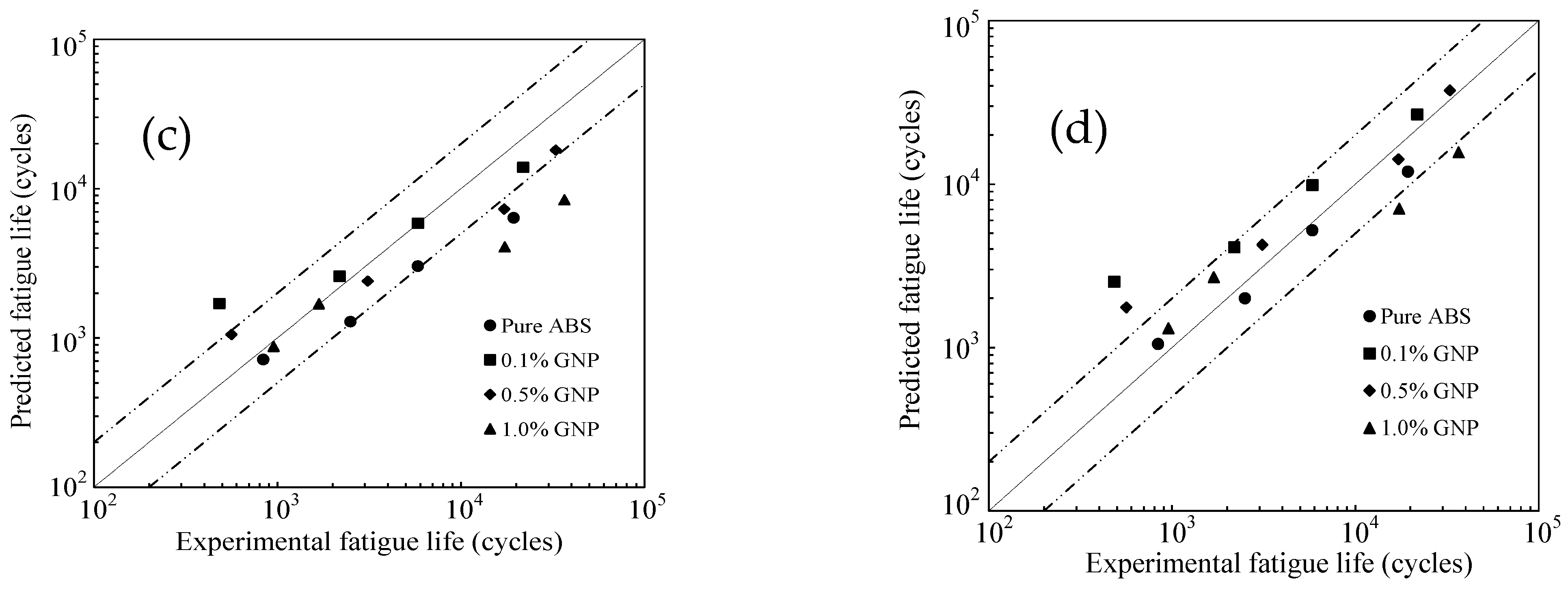
4.3. Application to 45° Raster Angle
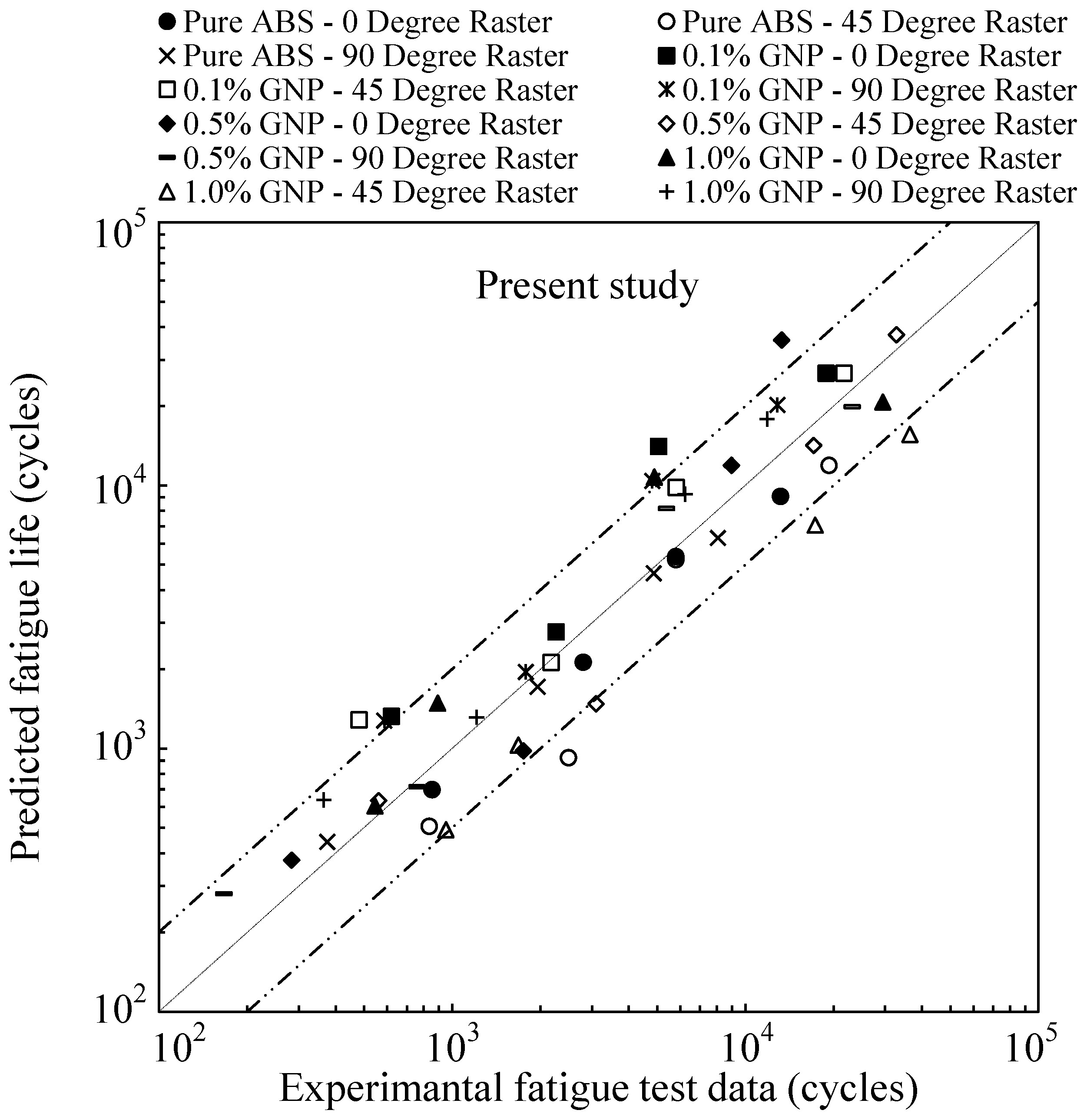
4.4. Proposed Approach
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Daminabo, S.C.; Goel, S.; Grammatikos, S.A.; Nezhad, H.Y.; Thakur, V.K. Fused deposition modeling-based additive manufacturing (3D printing): Techniques for polymer material systems. Mater. Today Chem. 2020, 16, 100248. [Google Scholar] [CrossRef]
- Wolszczak, P.; Lygas, K.; Paszko, M.; Wach, R.A. Heat distribution in material during fused deposition modelling. Rapid Prototyp. J. 2018, 24, 615–622. [Google Scholar] [CrossRef]
- Park, S.; Kun, K. Polymer-based filament feedstock for additive manufacturing. Compos. Sci. Technol. 2021, 213, 108876. [Google Scholar] [CrossRef]
- Ahmed, S.W.; Hussain, G.; Altaf, K.; Ali, S.; Alkahtani, M.; Abidi, M.H.; Alzabidi, A. On the Effects of Process Parameters and Optimization of Interlaminate Bond Strength in 3D Printed ABS/CF-PLA Composite. Polymers 2020, 12, 2155. [Google Scholar] [CrossRef] [PubMed]
- Patel, R.; Jani, S.; Joshi, A. Review on multi-objective optimization of FDM process parameters for composite materials. Int. J. Interact. Des. Manuf. 2023, 17, 2115–2125. [Google Scholar] [CrossRef]
- Bakhtiari, H.; Aamir, M.; Tolouei-Rad, M. Effect of 3D Printing Parameters on the Fatigue Properties of Parts Manufactured by Fused Filament Fabrication: A Review. Appl. Sci. 2023, 13, 904. [Google Scholar] [CrossRef]
- Jap, N.S.F.; Pearce, G.M.; Hellier, A.K.; Russell, N.; Parr, W.C.; Walsh, W.R. The effect of raster orientation on the static and fatigue properties of filament deposited ABS polymer. Int. J. Fatigue 2019, 124, 328–337. [Google Scholar] [CrossRef]
- Spierings, A.B.; Starr, T.L.; Wegener, K. Fatigue performance of additive manufactured metallic parts. Rapid Prototyp. J. 2013, 19, 88–94. [Google Scholar] [CrossRef]
- Yi, M.; Tang, W.; Zhu, Y.; Liang, C.; Tang, Z.; Yin, Y.; He, W.; Sun, S.; Su, S. A holistic review on fatigue properties of additively manufactured metals. J. Mater. Process Technol. 2024, 329, 118425. [Google Scholar] [CrossRef]
- Mirzaei, A.M.; Mirzaei, A.H.; Sapora, A.; Cornetti, P. Strain based finite fracture mechanics for fatigue life prediction of additively manufactured samples. Int. J. Fract. 2025, 249, 44. [Google Scholar] [CrossRef]
- Wang, X.G.; Crupi, V.; Jiang, C.; Feng, E.S.; Guglielmino, E.; Wang, C.S. Energy-based approach for fatigue life prediction of pure copper. Int. J. Fatigue 2017, 104, 243–250. [Google Scholar] [CrossRef]
- Jahed, H.; Varvani-Farahani, A. Upper and lower fatigue life limits model using energy-based fatigue properties. Int. J. Fatigue 2006, 28, 467–473. [Google Scholar] [CrossRef]
- Xiang, D.; Shen, Y.; Sun, X. An energy-based approach for uniaxial fatigue life estimation under asymmetric cyclic loading. Fatigue Fract. Eng. Mater. Struct. 2023, 46, 2411–2423. [Google Scholar] [CrossRef]
- Jahed, H.; Varvani-Farahani, A.; Noban, M.; Khalaji, I. An energy-based fatigue life assessment model for various metallic materials under proportional and non-proportional loading conditions. Int. J. Fatigue 2007, 29, 647–655. [Google Scholar] [CrossRef]
- Lee, K.O.; Hong, S.G.; Lee, S.B. A new energy-based fatigue damage parameter in life prediction of high-temperature structural materials. Mater. Sci. Eng. A 2008, 496, 471–477. [Google Scholar] [CrossRef]
- Benedetti, M.; Berto, F.; Le Bone, L.; Santus, C. A novel Strain-Energy-Density based fatigue criterion accounting for mean stress and plasticity effects on the medium-to-high-cycle uniaxial fatigue strength of plain and notched components. Int. J. Fatigue 2020, 133, 105397. [Google Scholar] [CrossRef]
- Hyuk Park, S.; Hong, S.G.; Ho Lee, B.; Bang, W.; Soo Lee, C. Low-cycle fatigue characteristics of rolled Mg–3Al–1Zn alloy. Int. J. Fatigue 2010, 32, 1835–1842. [Google Scholar] [CrossRef]
- Roostaei, A.A.; Pahlevanpour, A.; Behravesh, S.B.; Jahed, H. On the definition of elastic strain energy density in fatigue modelling. Int. J. Fatigue 2019, 121, 237–242. [Google Scholar] [CrossRef]
- Tao, G.; Xia, Z. Ratcheting behavior of an epoxy polymer and its effect on fatigue life. Polym. Test. 2007, 26, 451–460. [Google Scholar] [CrossRef]
- Algarni, M. Fatigue Behavior of PLA Material and the Effects of Mean Stress and Notch: Experiments and Modeling. Procedia Struct. Integr. 2022, 37, 676–683. [Google Scholar] [CrossRef]
- Hassanifard, S.; Behdinan, K. Effects of voids and raster orientations on fatigue life of notched additively manufactured PLA components. Int. J. Adv. Manuf. Technol. 2022, 120, 6241–6250. [Google Scholar] [CrossRef]
- Santecchia, E.; Hamouda, A.M.S.; Musharavati, F.; Zalnezhad, E.; Cabibbo, M.; El Mehtedi, M.; Spigarelli, S. A Review on Fatigue Life Prediction Methods for Metals. Adv. Mater. Sci. Eng. 2016, 2016, 9573524. [Google Scholar] [CrossRef]
- Ellyin, F.; Golos, K. Multiaxial Fatigue Damage Criterion. J. Eng. Mater. Technol. 1988, 110, 63–68. [Google Scholar] [CrossRef]
- Lukáš, P.; Klesnil, M. Cyclic stress-strain response and fatigue life of metals in low amplitude region. Mater. Sci. Eng. 1973, 11, 345–356. [Google Scholar] [CrossRef]
- Golos, K.; Ellyin, F. A Total Strain Energy Density Theory for Cumulative Fatigue Damage. J. Press. Vessel Technol. 1988, 110, 36–41. [Google Scholar] [CrossRef]
- Koh, S.K. Fatigue damage evaluation of a high pressure tube steel using cyclic strain energy density. Int. J. Press. Vessel Pip. 2002, 79, 791–798. [Google Scholar] [CrossRef]
- Dallmeier, J.; Denk, J.; Huber, O.; Saage, H.; Eigenfeld, K. Deformation Behavior and Fatigue Analysis of Magnesium Wrought Alloys under Variable Amplitude Loading. Mater. Today Proc. 2015, 2, S119–S124. [Google Scholar] [CrossRef]
- Lin, Y.C.; Chen, X.M.; Liu, Z.H.; Chen, J. Investigation of uniaxial low-cycle fatigue failure behavior of hot-rolled AZ91 magnesium alloy. Int. J. Fatigue 2013, 48, 122–132. [Google Scholar] [CrossRef]
- ASTM D638-22; Standard Test Method for Tensile Properties of Plastics. ASTM: West Conshohocken, PA, USA, 2022.
- ASTM D7791-22; Standard Test Method for Uniaxial Fatigue Properties of Plastics. ASTM: West Conshohocken, PA, USA, 2022.
- Hassanifard, S.; Behdinan, K. Fatigue response of multiscale extrusion-based additively manufactured acrylonitrile butadiene styrene-graphene nanoplatelets composites. Compos. B Eng. 2024, 279, 111464. [Google Scholar] [CrossRef]
- Hassanifard, S.; Behdinan, K. Ratcheting strain accumulation of 3D-printed acrylonitrile butadiene styrene-graphene composites. Eng. Fail. Anal. 2023, 154, 107648. [Google Scholar] [CrossRef]
- Zhu, S.P.; Lei, Q.; Huang, H.Z.; Yang, Y.J.; Peng, W. Mean stress effect correction in strain energy-based fatigue life prediction of metals. Int. J. Damage Mech. 2017, 26, 1219–1241. [Google Scholar] [CrossRef]



| GNP Content (%) | E (MPa) | E* (MPa) | Yield Strength (MPa) | UTS (MPa) | ||
|---|---|---|---|---|---|---|
| 0 (Pure ABS) | 1643 | 1438 | 17.8 | 37.0 | 127.3 | 0.31 |
| 0.1 | 1942 | 1760 | 18.2 | 43.8 | 192.4 | 0.38 |
| 0.5 | 2081 | 1751 | 18.1 | 39.8 | 128.7 | 0.31 |
| 1.0 | 2095 | 1867 | 21.1 | 37.8 | 99.4 | 0.24 |
| Material | ||||
|---|---|---|---|---|
| Pure ABS | 2.17 | 67.98 | −0.32 | −0.90 |
| ABS/0.1% GNP | 4.65 | 248.68 | −0.39 | −1.02 |
| ABS/0.5% GNP | 1.94 | 10.24 | −0.29 | −0.64 |
| ABS/1.0% GNP | 2.66 | 10.23 | −0.36 | −0.69 |
| Material | Nominal Stress (MPa) | Raster Angle (°) | Stress/Strain Data | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| R | Lin et al. [28] | Koh [26] | Roostaei et al. [18] | Fan [28] | ||||||||
| Pure ABS | 25 | 0 | 30.5 | 17.2 | −0.13 | 0.0311 | 0.0156 | 323.4 | 411.4 | 262.8 | 338.8 | 53.7 |
| 90 | 33.1 | 19.2 | −0.16 | 0.0357 | 0.0134 | 380.9 | 512.7 | 313.7 | 402.6 | 79.1 | ||
| 20 | 0 | 28.2 | 15.5 | −0.09 | 0.0270 | 0.0117 | 276.5 | 334.1 | 220.4 | 287.5 | 34.9 | |
| 90 | 29.6 | 16.0 | −0.08 | 0.0304 | 0.0123 | 308.7 | 356.0 | 242.5 | 322.7 | 40.7 | ||
| 15 | 0 | 24.0 | 12.5 | −0.04 | 0.0213 | 0.0096 | 200.2 | 217.3 | 154.3 | 205.8 | 14.6 | |
| 90 | 24.5 | 13.0 | −0.06 | 0.0220 | 0.0108 | 208.7 | 235.0 | 162.7 | 214.8 | 17.1 | ||
| 12 | 0 | 21.5 | 11.5 | −0.07 | 0.0182 | 0.0085 | 160.7 | 183.9 | 125.9 | 164.2 | 10.1 | |
| 90 | 22.5 | 12.2 | −0.08 | 0.0198 | 0.0095 | 176.0 | 207 | 139.1 | 180.0 | 13.7 | ||
| ABS/0.1% GNP | 25 | 0 | 32.7 | 18.3 | −0.12 | 0.0280 | 0.0125 | 303.7 | 380.5 | 244.8 | 331.2 | 63.1 |
| 90 | 32.8 | 18.5 | −0.13 | 0.0282 | 0.0128 | 305.6 | 388.9 | 247.5 | 333.3 | 65.1 | ||
| 20 | 0 | 27.9 | 15.5 | −0.11 | 0.0222 | 0.0107 | 221.1 | 255.6 | 173.8 | 236.5 | 31.9 | |
| 90 | 28.5 | 16.5 | −0.16 | 0.0228 | 0.0110 | 230.7 | 309.3 | 189.8 | 247.4 | 41.6 | ||
| 15 | 0 | 22.8 | 11.8 | −0.04 | 0.0168 | 0.0083 | 147.6 | 158.2 | 113.3 | 155.1 | 13.5 | |
| 90 | 24.0 | 12.8 | −0.07 | 0.0178 | 0.0084 | 163.6 | 186.2 | 128.0 | 172.5 | 17.9 | ||
| 12 | 0 | 20.1 | 10.2 | −0.01 | 0.0139 | 0.0070 | 114.7 | 118.2 | 86.9 | 119.4 | 8.0 | |
| 90 | 21.0 | 11.0 | −0.05 | 0.0149 | 0.0071 | 125.2 | 137.5 | 96.8 | 130.7 | 10.5 | ||
| ABS/0.5% GNP | 25 | 0 | 33.9 | 20.1 | −0.19 | 0.0329 | 0.0139 | 328.1 | 484.7 | 273.7 | 351.4 | 92.0 |
| 90 | 35.9 | 21.6 | −0.22 | 0.0367 | 0.0154 | 368.0 | 532.9 | 309.6 | 397.6 | 121.8 | ||
| 20 | 0 | 29.9 | 17.2 | −0.15 | 0.0261 | 0.0113 | 255.2 | 337.9 | 209.2 | 268.9 | 49.7 | |
| 90 | 31.3 | 18.2 | −0.16 | 0.0283 | 0.0122 | 279.7 | 378.3 | 230.7 | 296.3 | 62.2 | ||
| 15 | 0 | 24.4 | 13.4 | −0.10 | 0.0185 | 0.0083 | 168.6 | 205.1 | 134.6 | 174.3 | 18.1 | |
| 90 | 25.8 | 14.2 | −0.10 | 0.0201 | 0.0089 | 187.1 | 233.5 | 150.7 | 194.2 | 23.6 | ||
| 12 | 0 | 20.7 | 11.2 | −0.08 | 0.0145 | 0.0067 | 122.3 | 143.2 | 96.6 | 125.2 | 8.6 | |
| 90 | 22.2 | 12.1 | −0.09 | 0.0161 | 0.0073 | 140.7 | 167.2 | 116.0 | 144.6 | 11.9 | ||
| ABS/1.0% GNP | 25 | 0 | 31.2 | 18.2 | −0.17 | 0.0247 | 0.0107 | 260.6 | 354.8 | 215.4 | 266.0 | 33.3 |
| 90 | 30.9 | 18.0 | −0.17 | 0.0242 | 0.0104 | 255.7 | 347.1 | 211.1 | 260.8 | 31.5 | ||
| 20 | 0 | 27.2 | 15.1 | −0.11 | 0.0191 | 0.0088 | 198.1 | 244.2 | 158.9 | 200.7 | 13.5 | |
| 90 | 27.6 | 15.5 | −0.12 | 0.0196 | 0.0090 | 204.0 | 257.3 | 164.7 | 206.8 | 15.2 | ||
| 15 | 0 | 22.6 | 12.0 | −0.06 | 0.0142 | 0.0066 | 136.7 | 154.2 | 106.7 | 137.8 | 4.3 | |
| 90 | 23.1 | 12.5 | −0.08 | 0.0146 | 0.0073 | 142.9 | 167.3 | 112.8 | 144.0 | 5.2 | ||
| 12 | 0 | 20.3 | 10.2 | 0.00 | 0.0122 | 0.0056 | 110.3 | 111.4 | 83.0 | 110.9 | 1.8 | |
| 90 | 20.9 | 10.5 | 0.00 | 0.0127 | 0.0063 | 116.9 | 118.1 | 88.0 | 117.6 | 2.2 | ||
| Material | Nominal Stress (MPa) | Stress/Strain Data | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| R | Lin et al. [28] | Koh [26] | Roostaei et al. [18] | Fan [28] | |||||||
| Pure ABS | 25 | 32.1 | 18.5 | −0.15 | 0.0342 | 0.0148 | 358.3 | 476.0 | 293.9 | 377.3 | 69.8 |
| 20 | 28.3 | 15.9 | −0.12 | 0.0275 | 0.0122 | 278.4 | 351.6 | 225.0 | 289.6 | 38.0 | |
| 15 | 23.7 | 12.9 | −0.09 | 0.0209 | 0.0096 | 195.3 | 231.4 | 154.7 | 200.6 | 16.2 | |
| 12 | 20.5 | 10.9 | −0.06 | 0.0171 | 0.0080 | 146.1 | 165.2 | 114.1 | 148.9 | 8.1 | |
| ABS/0.1% GNP | 25 | 33.4 | 18.8 | −0.13 | 0.0289 | 0.0128 | 292.7 | 388.9 | 240.2 | 318.4 | 63.4 |
| 20 | 29.1 | 16.1 | −0.11 | 0.0233 | 0.0106 | 240.6 | 294.5 | 192.6 | 258.5 | 40.1 | |
| 15 | 24.1 | 13.1 | −0.09 | 0.0179 | 0.0083 | 165.0 | 195.0 | 130.6 | 174.1 | 19.3 | |
| 12 | 20.1 | 10.2 | −0.01 | 0.0139 | 0.0070 | 114.7 | 118.2 | 86.9 | 119.4 | 8.0 | |
| ABS/0.5% GNP | 25 | 31.9 | 18.6 | −0.17 | 0.0294 | 0.0126 | 290.6 | 395.1 | 240.0 | 308.5 | 67.9 |
| 20 | 28.1 | 16.0 | −0.14 | 0.0235 | 0.0103 | 225.4 | 292.4 | 183.6 | 235.9 | 37.1 | |
| 15 | 23.7 | 13.0 | −0.10 | 0.0177 | 0.0081 | 160.4 | 193.0 | 127.7 | 165.5 | 16.1 | |
| 12 | 20.6 | 11.1 | −0.08 | 0.0144 | 0.0067 | 121.1 | 140.7 | 95.4 | 124.0 | 8.3 | |
| ABS/1.0% GNP | 25 | 32.3 | 19.0 | −0.18 | 0.0265 | 0.0113 | 279.4 | 386.7 | 232.0 | 285.8 | 41.0 |
| 20 | 28.7 | 16.3 | −0.14 | 0.0211 | 0.0093 | 220.6 | 284.6 | 179.4 | 224.1 | 19.5 | |
| 15 | 24.3 | 13.2 | −0.09 | 0.0158 | 0.0073 | 158.1 | 186.6 | 125.1 | 159.6 | 6.9 | |
| 12 | 21.1 | 11.1 | −0.05 | 0.0129 | 0.0061 | 119.2 | 131.9 | 92.4 | 119.9 | 2.9 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hassanifard, S.; Behdinan, K. Energy-Based Approach for Fatigue Life Prediction of Additively Manufactured ABS/GNP Composites. Polymers 2025, 17, 2032. https://doi.org/10.3390/polym17152032
Hassanifard S, Behdinan K. Energy-Based Approach for Fatigue Life Prediction of Additively Manufactured ABS/GNP Composites. Polymers. 2025; 17(15):2032. https://doi.org/10.3390/polym17152032
Chicago/Turabian StyleHassanifard, Soran, and Kamran Behdinan. 2025. "Energy-Based Approach for Fatigue Life Prediction of Additively Manufactured ABS/GNP Composites" Polymers 17, no. 15: 2032. https://doi.org/10.3390/polym17152032
APA StyleHassanifard, S., & Behdinan, K. (2025). Energy-Based Approach for Fatigue Life Prediction of Additively Manufactured ABS/GNP Composites. Polymers, 17(15), 2032. https://doi.org/10.3390/polym17152032







