A Novel Experimental Method and Setup to Quantify Evaporation-Induced Foaming Behavior of Polymer Solutions
Abstract
1. Introduction
2. Theoretical Evolution
2.1. Foam Growth Profile
2.2. Evaluation of Foam Stability
2.3. Bubble Nucleation Mechanism
3. Experiment
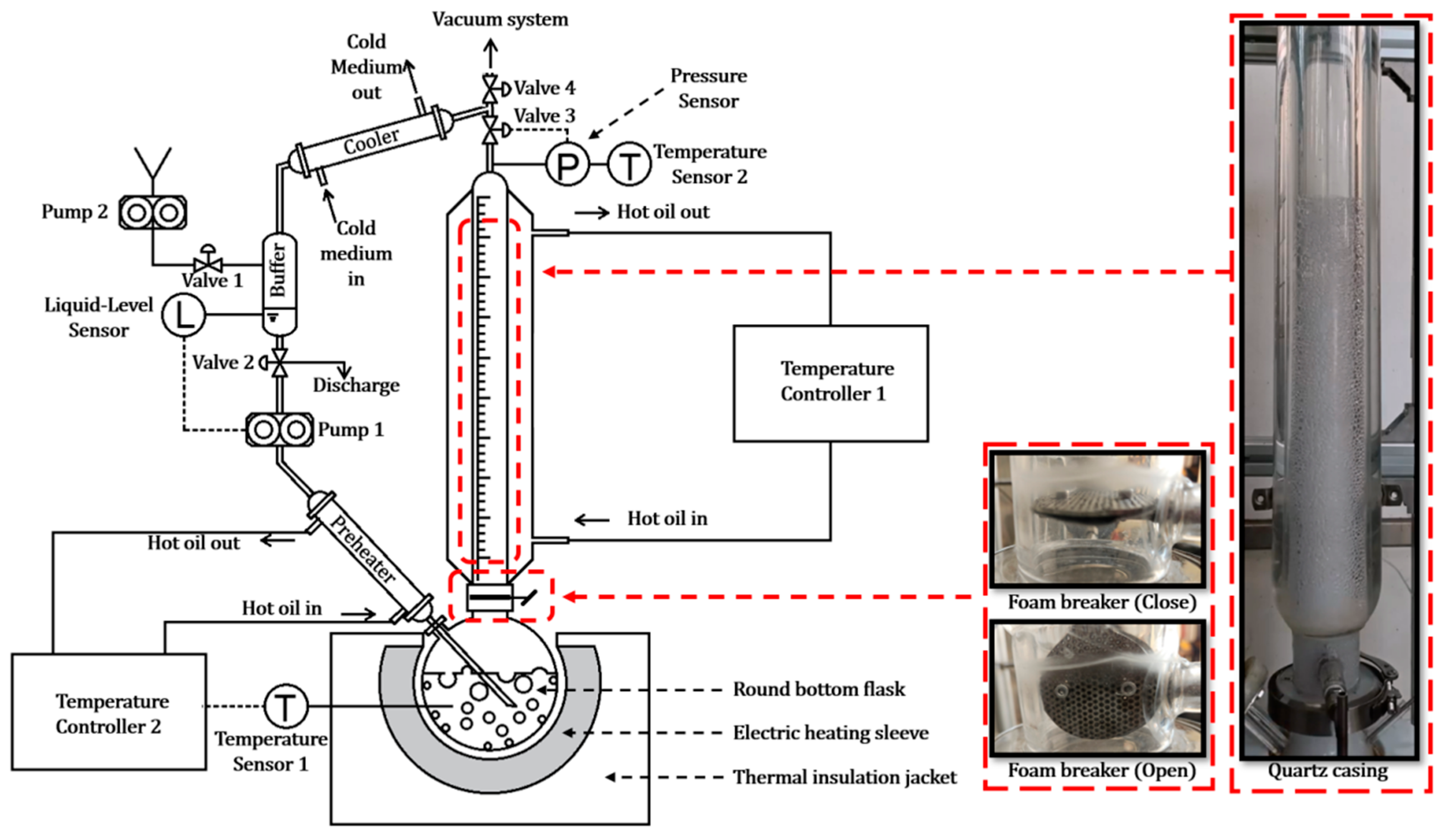
3.1. Experiment Setup
- (1)
- Constant Concentration Control: During the vaporization process, the concentration of the polymer solution in the round-bottom flask increases continuously, which significantly alters the foaming behavior. To maintain a constant concentration throughout the experiment, we incorporated a precisely controlled condensation reflux module into the system.
- (2)
- Reheating of Refluxed Liquid: The refluxed liquid must be reheated to near boiling before re-entering the round-bottom flask. If the condensate is too cold, it will absorb a portion of the heating energy from the electric heating sleeve—energy that is intended solely for vaporizing the solution. This would reduce the effective vaporization heat and compromise the experimental accuracy.
- (3)
- Pressure Control: To investigate the influence of pressure on the bubbling and foaming behavior of polymer solutions, we introduced Valve 3, a gas-phase back-pressure regulator, between the quartz casing and the cooler. This valve allows precise adjustment of the upstream pressure, ensuring that the pressure within the round-bottom flask and quartz casing remains stable at the target experimental value.
- (4)
- Foam Layer Dynamics Observation: Studying foam dynamics requires capturing the time-dependent growth of the foam layer. This necessitates initiating observations from a steady state where the system has reached thermal equilibrium, but foam formation has not yet begun. To achieve this, we innovatively installed a foam breaker between the round-bottom flask and the quartz casing. The foam breaker consists of three intricately designed porous sieves with staggered capillary channels. These allow vapor generated in the flask to pass freely, while intercepting foam carried by the vapor. This design enables the establishment of a reflux equilibrium with the foam breaker closed. Once equilibrium is achieved, opening the foam breaker allows immediate observation of the foam entering and growing in the quartz casing.
3.2. Experimental Steps
4. Results and Discussion
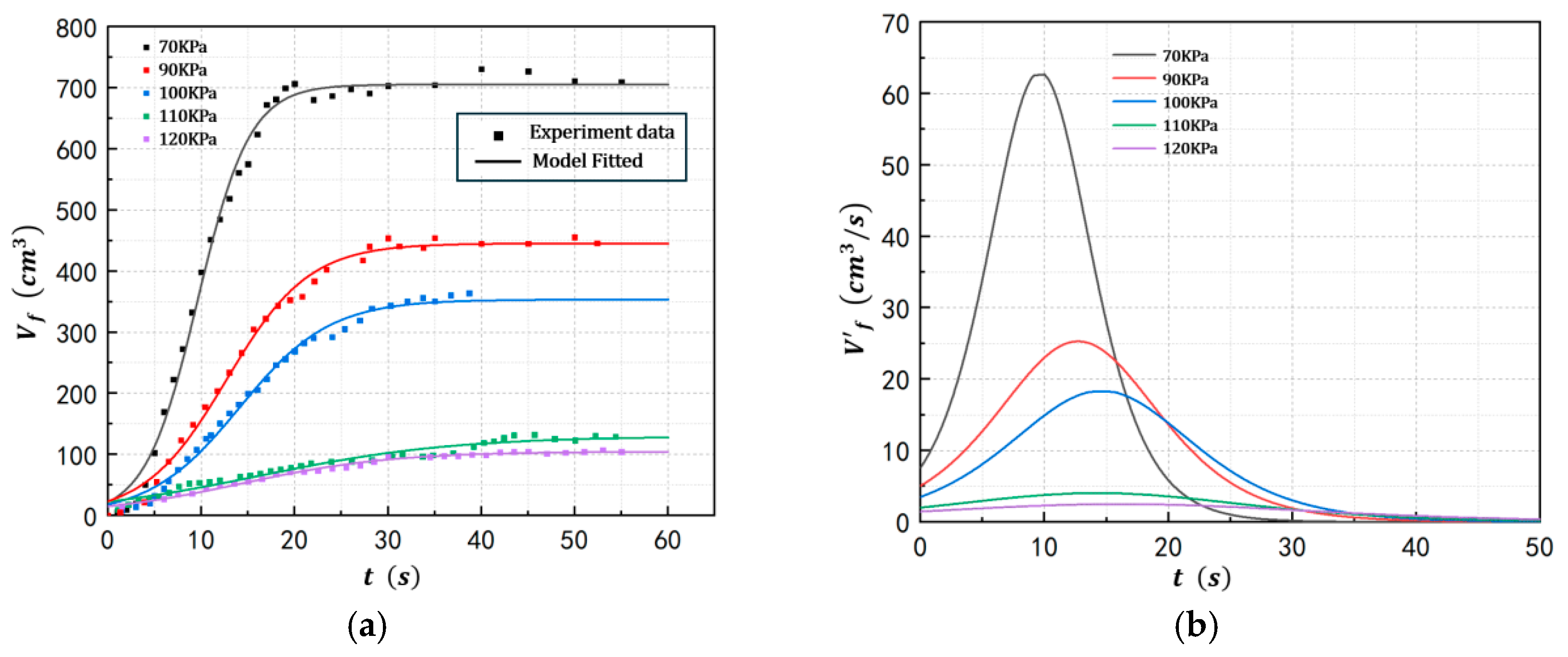
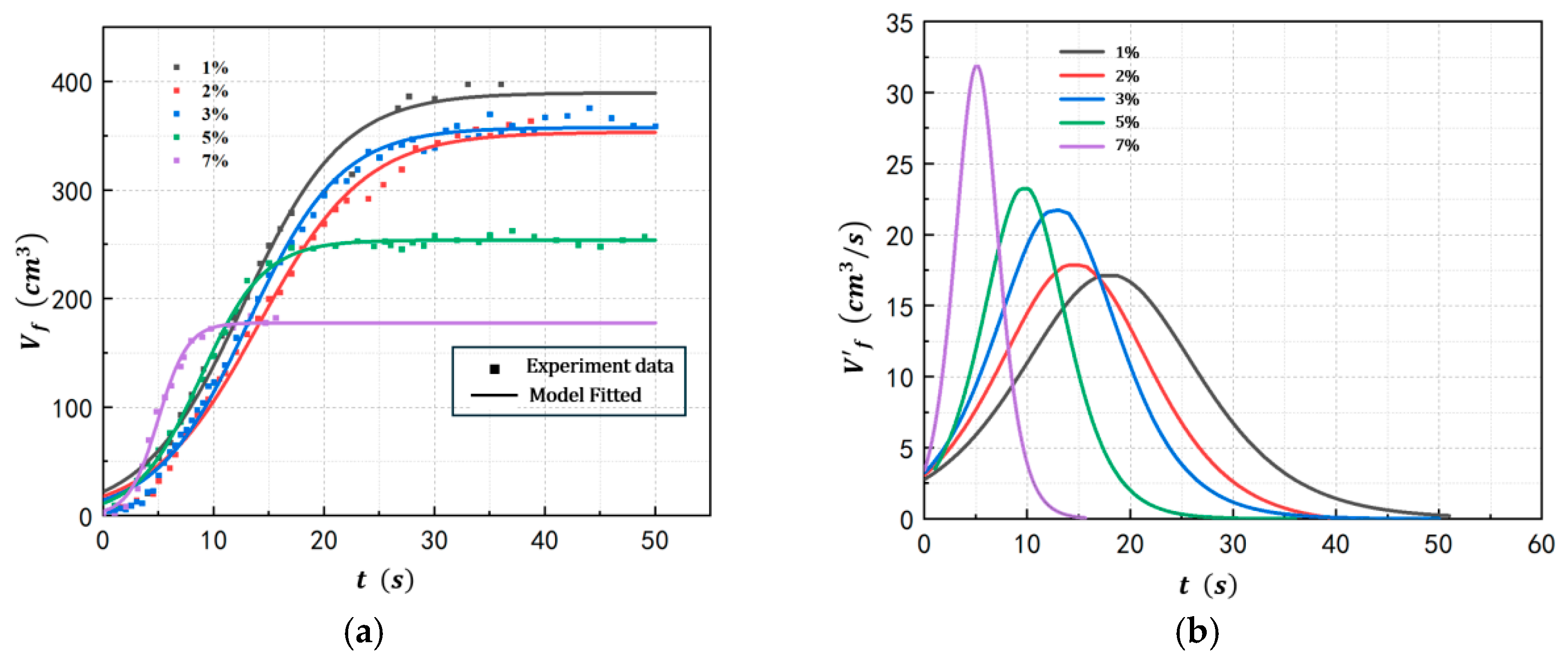
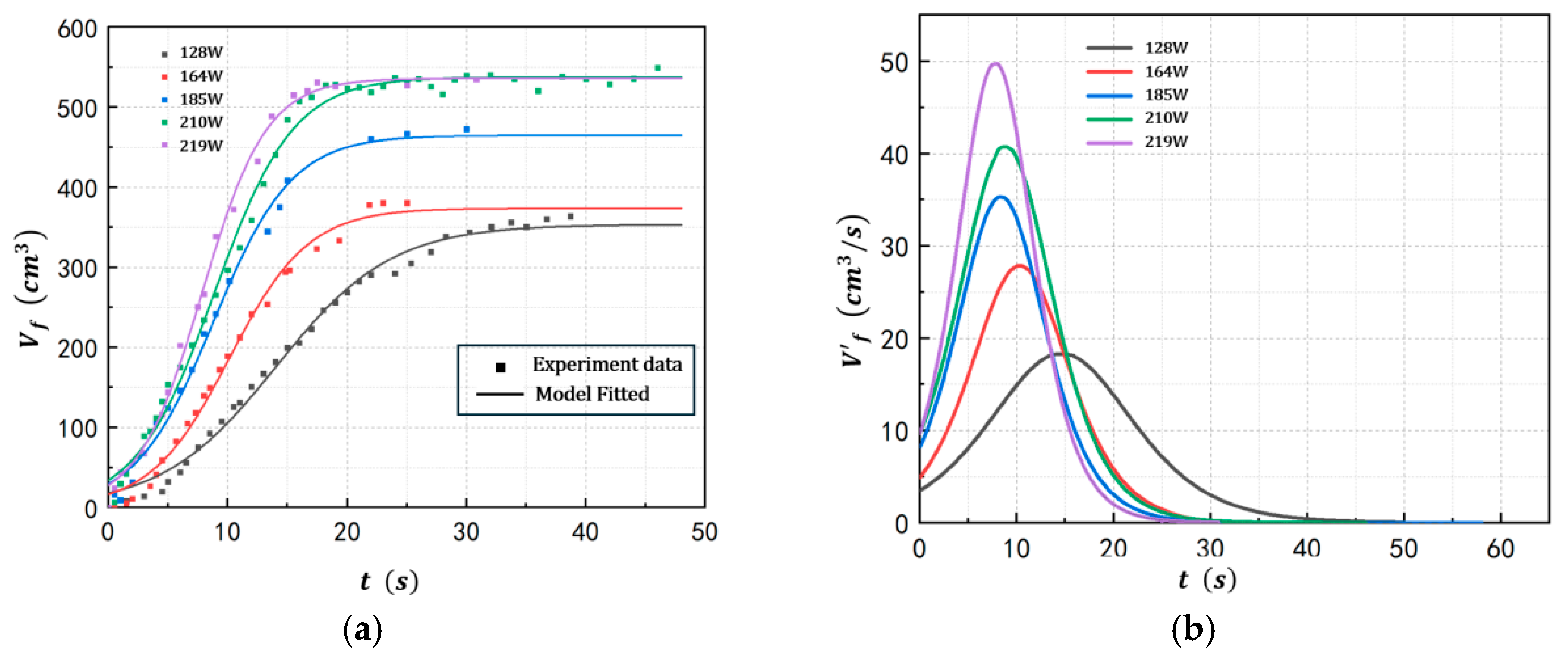
4.1. Foam Growth Profile of POE/n-Hexane PSMS in Different Conditions
4.2. Comprehensive Evaluation of Foaming Stability in Different Conditions
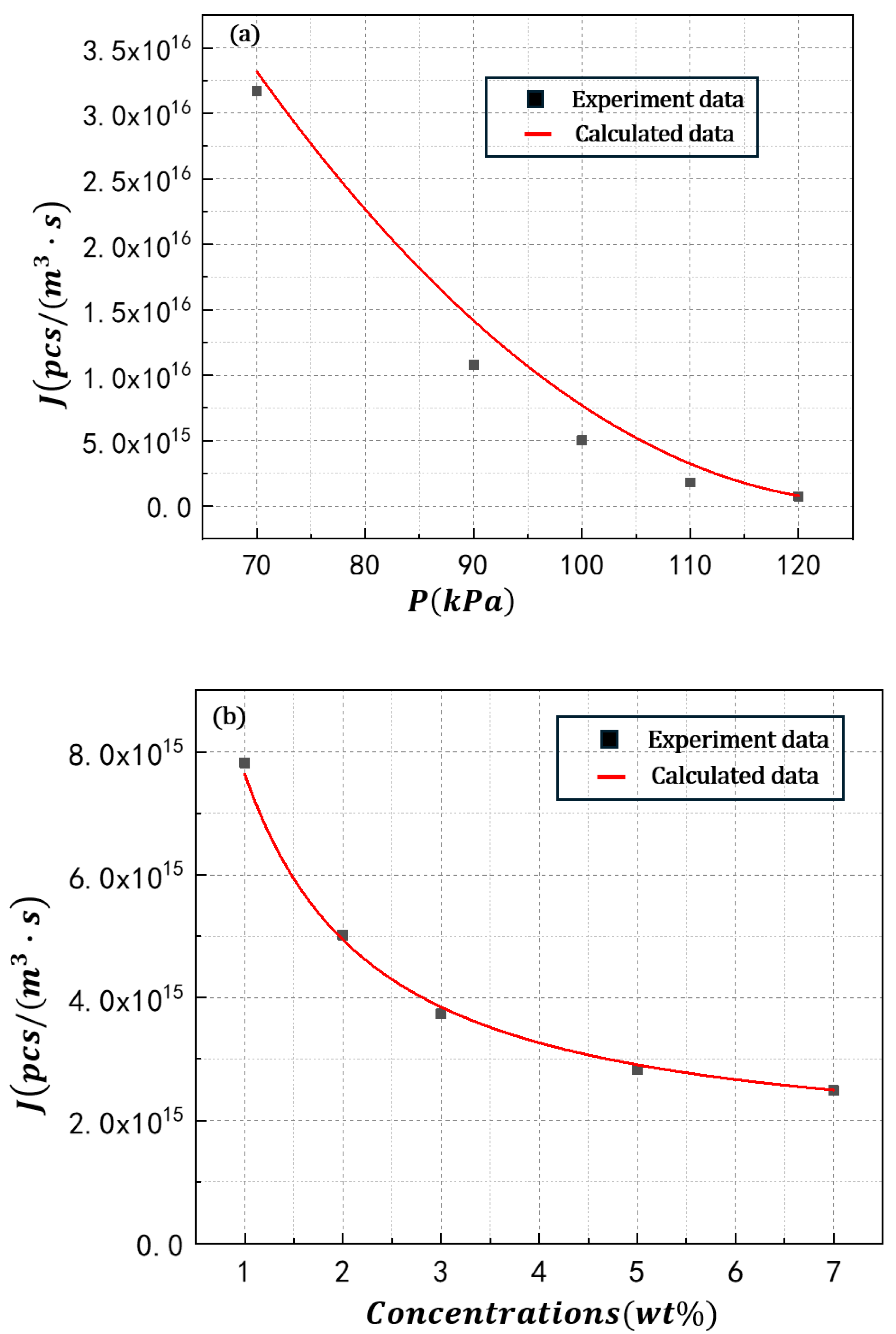
4.3. Bubble Nucleation Rate of POE/N-Hexane PSMS
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- McKenna, T.F.L. Condensed Mode Cooling of Ethylene Polymerization in Fluidized Bed Reactors. Macromol. React. Eng. 2019, 13, 1800026. [Google Scholar] [CrossRef]
- Utikar, R.P.; Harshe, Y.M.; Mehra, A.; Ranade, V.V. Modeling of a fluidized bed propylene polymerization reactor operated in condensed mode. J. Appl. Polym. Sci. 2008, 108, 2067–2076. [Google Scholar] [CrossRef]
- Pan, H.; Liang, X.F.; Luo, Z.H. CFD modeling of the gas-solid two-fluid flow in polyethylene FBRs: From traditional operation to super-condensed mode. Adv. Powder Technol. 2016, 27, 1494–1505. [Google Scholar] [CrossRef]
- Pelz, P.; Noß, J.; von Harbou, E.; Bart, H.J. Whey protein fouling on polymeric heat exchangers. Heat Transf. 2024, 53, 2948–2964. [Google Scholar] [CrossRef]
- Liu, G.Y.; Chen, Y.C.; Hou, E.F.; Ma, C.F. Experimental Study of Antifouling Effect of Ultrasonic/Magnetic Compound Treatment in Heat Transfer. Heat Transf. Eng. 2023, 44, 24–38. [Google Scholar] [CrossRef]
- Javad, H.; Nayef, M.G.; Wan. Effects of the temperature and mixing rate on foaming in a polymerization reaction to produce fatty polyamides in the presence of catalyst. Ind. Eng. Chem. Res. 2004, 43, 6048–6054. [Google Scholar] [CrossRef]
- Meier, G.B.; Weickert, G.; van Swaaij, W.P.M. FBR for catalytic propylene polymerization: Controlled mixing and reactor modeling. AIChE J. 2002, 48, 1268–1283. [Google Scholar] [CrossRef]
- Yates, J.G.; Lettieri, P. Fluidized-Bed Reactors: Processes and Operating Conditions; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Ji, E.; Zhou, H.; Xu, G.; Wang, X.; Wang, L.; Gao, J.; Yan, J. Insights into heterogeneous surface induced bubble nucleation mechanisms in cellulose reinforced polylactic acid foams. Int. J. Biol. Macromol. 2024, 268, 131659. [Google Scholar] [CrossRef] [PubMed]
- Cowman, M.K. Mutual macromolecular crowding as the basis for polymer solution non-ideality. Polym. Adv. Technol. 2017, 28, 1000–1004. [Google Scholar] [CrossRef]
- Kezios, P.S.; Schowalter, W.R. Rapid growth and collapse of single bubbles in polymer solutions undergoing shear. Phys. Fluids 1986, 29, 3172–3181. [Google Scholar] [CrossRef]
- Zhang, J.; Manglik, R.M. Nucleate pool boiling of aqueous polymer solutions on a cylindrical heater. J. Non-Newton. Fluid Mech. 2005, 125, 185–196. [Google Scholar] [CrossRef]
- Dehghani, R.; Bayat, A.E.; Sarvestani, M.T.; Behnood, M. A comprehensive review on key mechanisms and parameters affecting foam stability. J. Mol. Liq. 2024, 416, 126477. [Google Scholar] [CrossRef]
- Karimzadeh, F.; Ebrahimi, N.; Sadeghi, R. Vapor-liquid equilibria behavior of binary and ternary polymer-polymer alcoholic solutions. Fluid Phase Equilibria 2023, 573 (Suppl. C), 113856. [Google Scholar] [CrossRef]
- Li, H.T.; Cui, C.Z.; Guo, L.L.; Yuan, F.Q.; Xu, Z.C.; Gong, Q.T.; Jin, Z.Q. Dynamic interfacial tensions of sulfobetaine and polymers solutions: Effect of structures. J. Mol. Liq. 2022, 356, 119018. [Google Scholar] [CrossRef]
- Yang, H.E.; Bae, Y.C. Thermodynamic analysis of phase equilibrium and surface tension of ternary polymer solutions. AIChE J. 2019, 65, e16679. [Google Scholar] [CrossRef]
- Bikerman, J.J. Foams; Springer: Berlin/Heidelberg, Germany, 1973. [Google Scholar] [CrossRef]
- Strodtmann, L.; Staud, R.; Klinke, T.; Jasch, K.; Scholl, S. Quantification of evaporation-induced foaming ability. Chem. Eng. Res. Des. 2022, 179, 502–509. [Google Scholar] [CrossRef]
- Blander, M.; Katz, J.L. Bubble nucleation in liquids. AIChE J. 1975, 21, 833–848. [Google Scholar] [CrossRef]
- Amon, M.; Denson, C.D. A study of the dynamics of foam growth: Analysis of the growth of closely spaced spherical bubbles. Polym. Eng. Sci. 1984, 24, 1026–1034. [Google Scholar] [CrossRef]
- Saye, R.I.; Sethian, J.A. Multiscale Modeling of Membrane Rearrangement Drainage, and Rupture in Evolving Foams. Science 2013, 340, 720–724. [Google Scholar] [CrossRef] [PubMed]
- Wu, S.; He, L.; Zhang, C.; Gong, W.; He, Y.; Luo, Y. Visualization observation of cells growth in low-density polyethylene foaming processes. Polym. Test. 2017, 63, 367–374. [Google Scholar] [CrossRef]
- Bartsch, O. Ueber Schaumbildungsfähigkeit und Oberflächenspannung. Kolloid-Zeitschrift 1926, 38, 177–179. [Google Scholar] [CrossRef]
- Miles, G.D.; Ross, J. Foam Stability of Solutions of Soaps of Pure Fatty Acids. J. Phys. Chem. 1944, 48, 280–290. [Google Scholar] [CrossRef]
- Dai, C.; Ding, Q.; Zhao, M.; Zhao, J.; Fang, J.; Li, H. Construction and performance evaluation of a highly efficient mixed foaming system. RSC Adv. 2015, 35, 27978–27985. [Google Scholar] [CrossRef]
- Du, L.; Wang, S.; Zhang, T.; Xu, C. Molecular dynamics simulation of the effect of calcium ions on the foamability of anionic surfactants. Colloids Surf. A Physicochem. Eng. Asp. 2025, 707, 135819. [Google Scholar] [CrossRef]
- Amankeldi, F.; Issakhov, M.; Pourafshary, P.; Ospanova, Z.; Gabdullin, M.; Miller, R. Foam stabilization by surfactant/SiO2 composite nanofluids. Colloids Interfaces 2023, 7, 57. [Google Scholar] [CrossRef]
- Yekeen, N.; Idris, A.K.; Manan, M.A.; Samin, A.M. Experimental study of the influence of silica nanoparticles on the bulk stability of SDS-foam in the presence of oil. J. Dispers. Sci. Technol. 2017, 38, 416–424. [Google Scholar] [CrossRef]
- Han, J.H.; Han, C.D. Bubble nucleation in polymeric liquids. I. Bubble nucleation in concentrated polymer solutions. J. Polym. Sci. Part B Polym. Phys. 1990, 28, 711–741. [Google Scholar] [CrossRef]
- Han, J.H.; Han, C.D. Bubble nucleation in polymeric liquids. II. theoretical considerations. J. Polym. Sci. 1990, 28, 743–761. [Google Scholar] [CrossRef]


| Nomenclature | Concentration | Pressure | Temperature | Energy Input Power |
|---|---|---|---|---|
| (%wt) | (kPa) | (℃) | (kW) | |
| Exp 1 | 1 | 100 | 68.2 | 128 |
| Exp 2 | 2 | 100 | 68.3 | 128 |
| Exp 3 | 3 | 100 | 68.4 | 128 |
| Exp 4 | 5 | 100 | 68.4 | 128 |
| Exp 5 | 7 | 100 | 68.5 | 128 |
| Exp 6 | 2 | 70 | 57.5 | 128 |
| Exp 7 | 2 | 90 | 65.1 | 128 |
| Exp 8 | 2 | 110 | 71.5 | 128 |
| Exp 9 | 2 | 120 | 74.4 | 128 |
| Exp 10 | 2 | 100 | 68.3 | 164 |
| Exp 11 | 2 | 100 | 68.4 | 185 |
| Exp 12 | 2 | 100 | 68.4 | 210 |
| Exp 13 | 2 | 100 | 68.3 | 219 |
| Nomenclature | (kPa(a)) | (cm3) | (cm3/s) | (-) | (s) | (cm3/s) |
|---|---|---|---|---|---|---|
| Exp 6 | 70 | 705.4 | 62.69 | 0.358 | 9.69 | 7.611 |
| Exp 7 | 90 | 445.3 | 25.29 | 0.227 | 12.7 | 5.057 |
| Exp 2 | 100 | 353.4 | 18.28 | 0.207 | 14.1 | 3.513 |
| Exp 8 | 110 | 129.8 | 4.035 | 0.124 | 14.3 | 2.002 |
| Exp 9 | 120 | 104.7 | 2.196 | 0.095 | 16.2 | 1.448 |
| Nomenclature | (w/w) | (cm3) | (cm3/s) | (s) | (cm3/s) | |
|---|---|---|---|---|---|---|
| Exp 1 | 1% | 378.2 | 17.15 | 0.223 | 17.2 | 2.799 |
| Exp 2 | 2% | 353.4 | 18.28 | 0.207 | 14.1 | 3.513 |
| Exp 3 | 3% | 336.6 | 21.75 | 0.375 | 13.0 | 3.521 |
| Exp 4 | 5% | 244.1 | 23.26 | 0.397 | 9.59 | 3.523 |
| Exp 5 | 7% | 177.3 | 31.88 | 0.823 | 5.22 | 3.532 |
| Nomenclature | (W) | (cm3) | (cm3/s) | (s) | (cm3/s) | |
|---|---|---|---|---|---|---|
| Exp 2 | 128 | 353.4 | 18.28 | 0.207 | 14.1 | 3.513 |
| Exp 10 | 164 | 357.7 | 27.83 | 0.294 | 10.3 | 4.945 |
| Exp 11 | 185 | 407.3 | 35.30 | 0.326 | 8.37 | 8.219 |
| Exp 12 | 210 | 500.8 | 40.73 | 0.304 | 8.85 | 9.712 |
| Exp 13 | 219 | 504.6 | 49.71 | 0.375 | 7.79 | 9.727 |
| Nomenclature | (kPa(a)) | (cm3/s) | (cm3/s) | |
|---|---|---|---|---|
| Exp 6 | 70 | 184.34 | 62.69 | 0.340 |
| Exp 7 | 90 | 146.69 | 25.29 | 0.172 |
| Exp 2 | 100 | 133.33 | 18.28 | 0.137 |
| Exp 8 | 110 | 122.30 | 4.035 | 0.033 |
| Exp 9 | 120 | 113.04 | 2.196 | 0.019 |
| Nomenclature | (w/w) | (cm3/s) | (cm3/s) | |
|---|---|---|---|---|
| Exp 1 | 1% | 133.33 | 17.15 | 0.129 |
| Exp 2 | 2% | 136.58 | 18.28 | 0.134 |
| Exp 3 | 3% | 139.13 | 21.75 | 0.156 |
| Exp 4 | 5% | 144.39 | 23.26 | 0.161 |
| Exp 5 | 7% | 149.76 | 31.88 | 0.213 |
| Nomenclature | (W) | (cm3/s) | (cm3/s) | |
|---|---|---|---|---|
| Exp 2 | 128 | 133.33 | 18.28 | 0.137 |
| Exp 10 | 164 | 171.43 | 27.83 | 0.162 |
| Exp 11 | 185 | 193.14 | 35.30 | 0.183 |
| Exp 12 | 210 | 219.42 | 40.73 | 0.186 |
| Exp 13 | 219 | 228.57 | 49.71 | 0.217 |
| Nomenclature | (cm3/s) | (um) |
|---|---|---|
| Exp 1 | 2.799 | 1.02 |
| Exp 2 | 3.513 | 1.28 |
| Exp 3 | 3.521 | 1.41 |
| Exp 4 | 3.523 | 1.55 |
| Exp 5 | 3.532 | 1.62 |
| Exp 6 | 7.611 | 0.89 |
| Exp 7 | 5.057 | 1.12 |
| Exp 8 | 2.002 | 1.49 |
| Exp 9 | 1.448 | 1.79 |
| Exp 10 | 4.945 | 1.02 |
| Exp 11 | 8.219 | 0.77 |
| Exp 12 | 9.712 | 0.61 |
| Exp 13 | 9.727 | 0.49 |
| Variables | (No./m3) | |
|---|---|---|
| Pressure | 8.20 × 108 | 2.85 × 10−8 |
| Concentration | 1.41 × 108 | 7.04 × 10−9 |
| Energy input power | 1.33 × 109 | 4.44 × 10−8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiu, X.; Cui, Z.; Zhao, M.; Jiang, J.; Guo, W.; Zhao, L.; Xi, Z.; Yuan, W. A Novel Experimental Method and Setup to Quantify Evaporation-Induced Foaming Behavior of Polymer Solutions. Polymers 2025, 17, 2025. https://doi.org/10.3390/polym17152025
Qiu X, Cui Z, Zhao M, Jiang J, Guo W, Zhao L, Xi Z, Yuan W. A Novel Experimental Method and Setup to Quantify Evaporation-Induced Foaming Behavior of Polymer Solutions. Polymers. 2025; 17(15):2025. https://doi.org/10.3390/polym17152025
Chicago/Turabian StyleQiu, Xiaoyi, Zhaoqi Cui, Ming Zhao, Jie Jiang, Wenze Guo, Ling Zhao, Zhenhao Xi, and Weikang Yuan. 2025. "A Novel Experimental Method and Setup to Quantify Evaporation-Induced Foaming Behavior of Polymer Solutions" Polymers 17, no. 15: 2025. https://doi.org/10.3390/polym17152025
APA StyleQiu, X., Cui, Z., Zhao, M., Jiang, J., Guo, W., Zhao, L., Xi, Z., & Yuan, W. (2025). A Novel Experimental Method and Setup to Quantify Evaporation-Induced Foaming Behavior of Polymer Solutions. Polymers, 17(15), 2025. https://doi.org/10.3390/polym17152025







