Molecular Simulations of Interface-Driven Crosslinked Network Formation and Mechanical Response in Composite Propellants
Abstract
1. Introduction
2. Materials and Methods
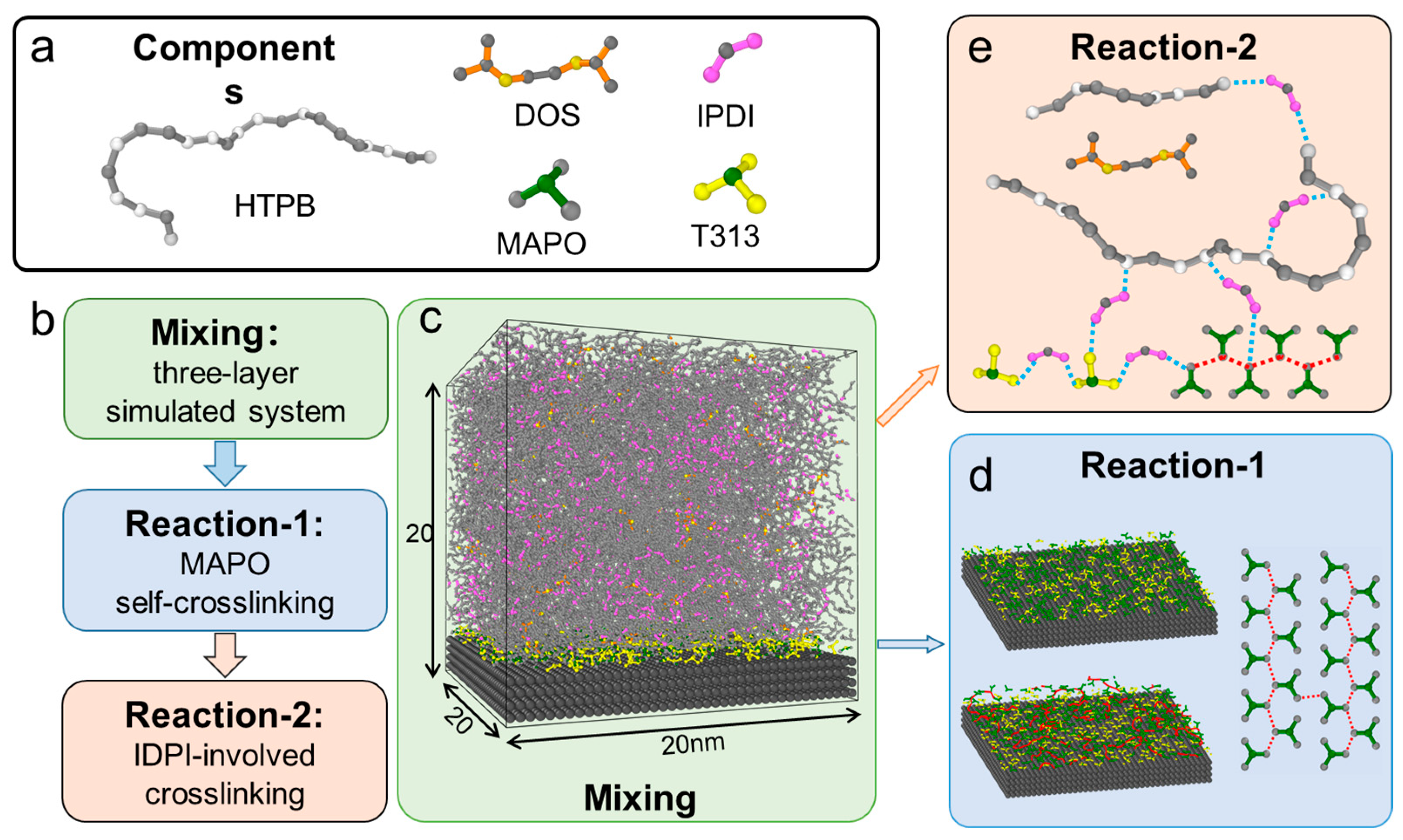
2.1. Coarse-Grained Models for Simulations
2.2. Simulations System Setup and Workflow
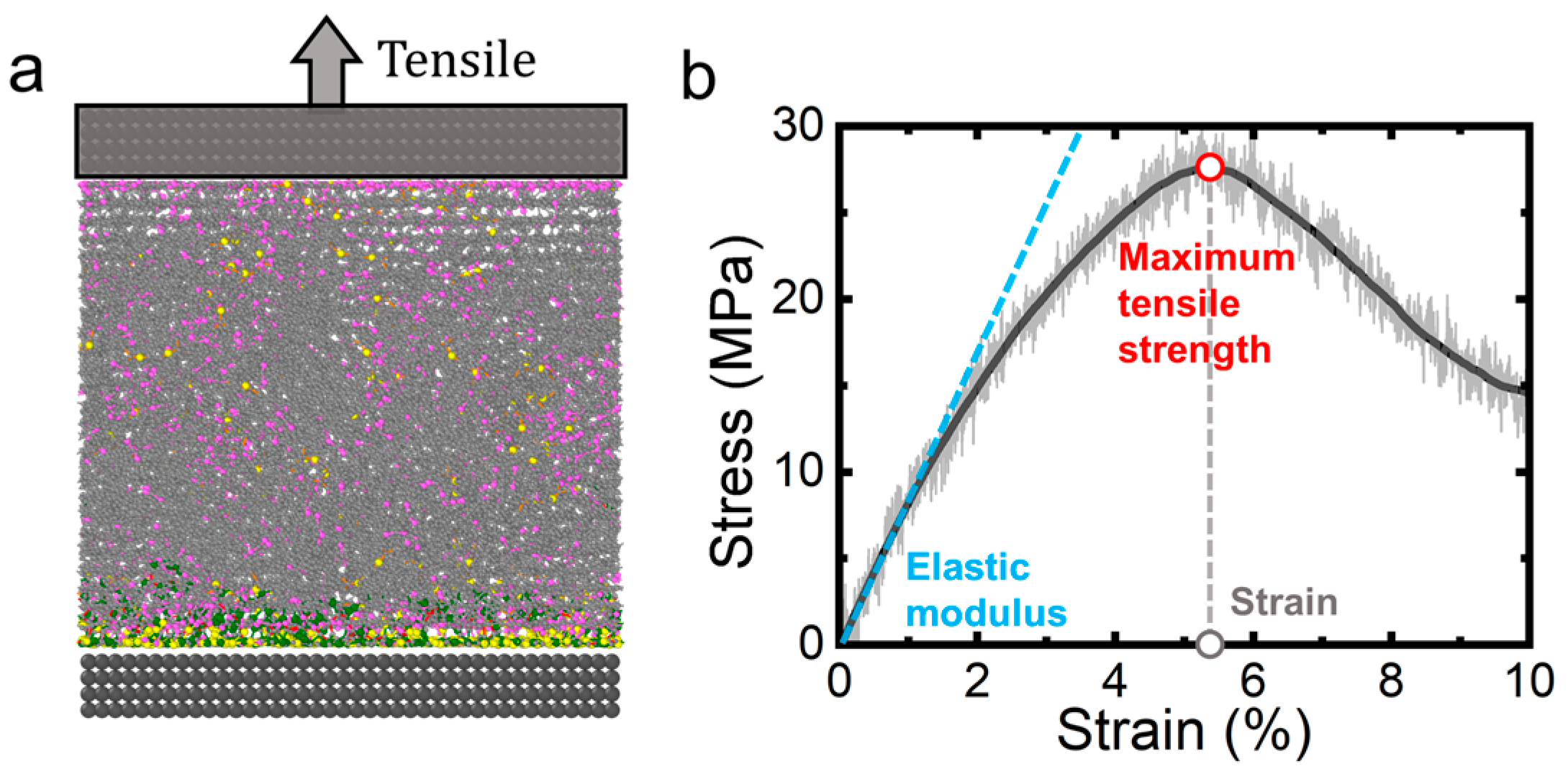
2.3. Mechanical Characterization Through Tensile Simulations
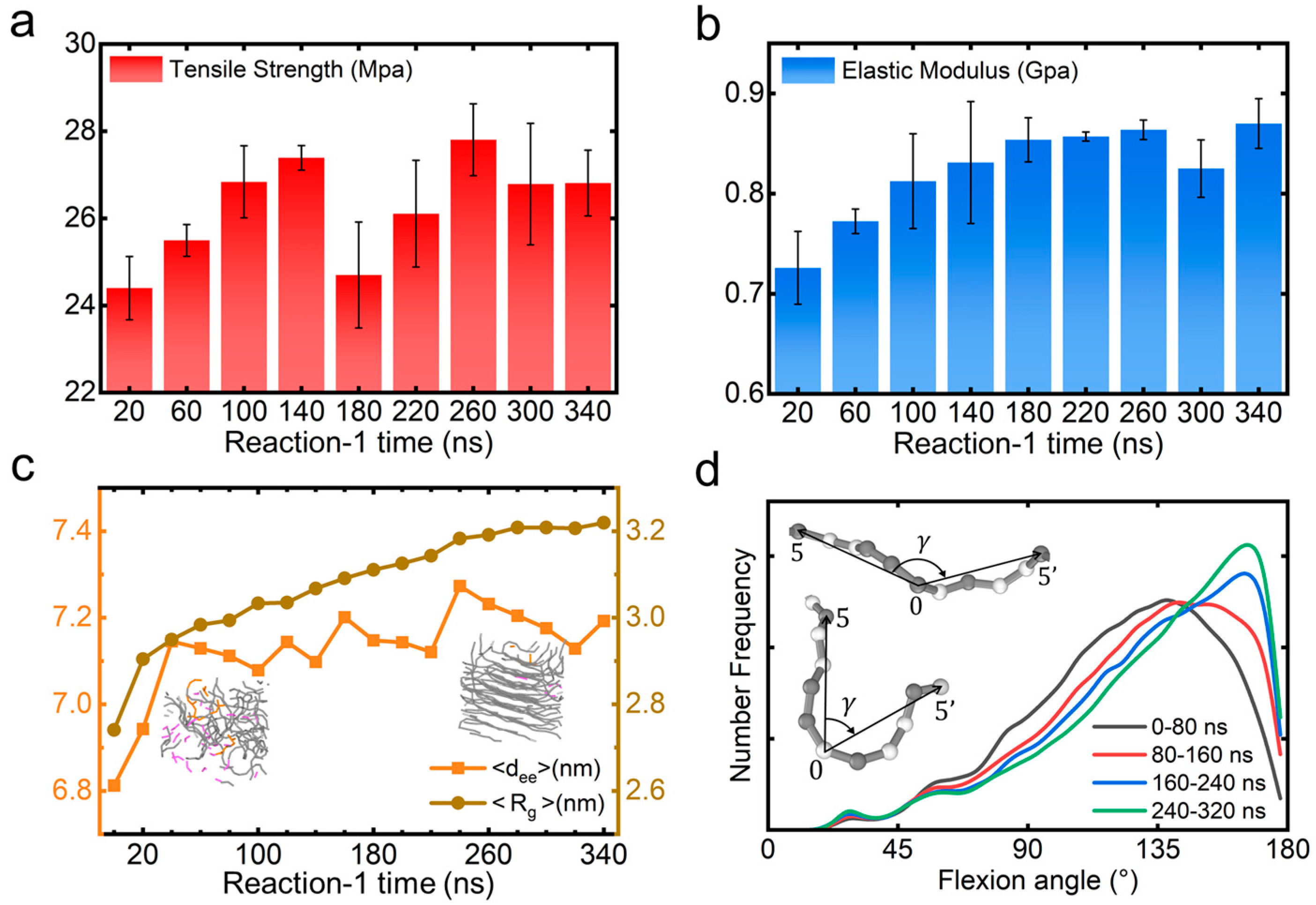
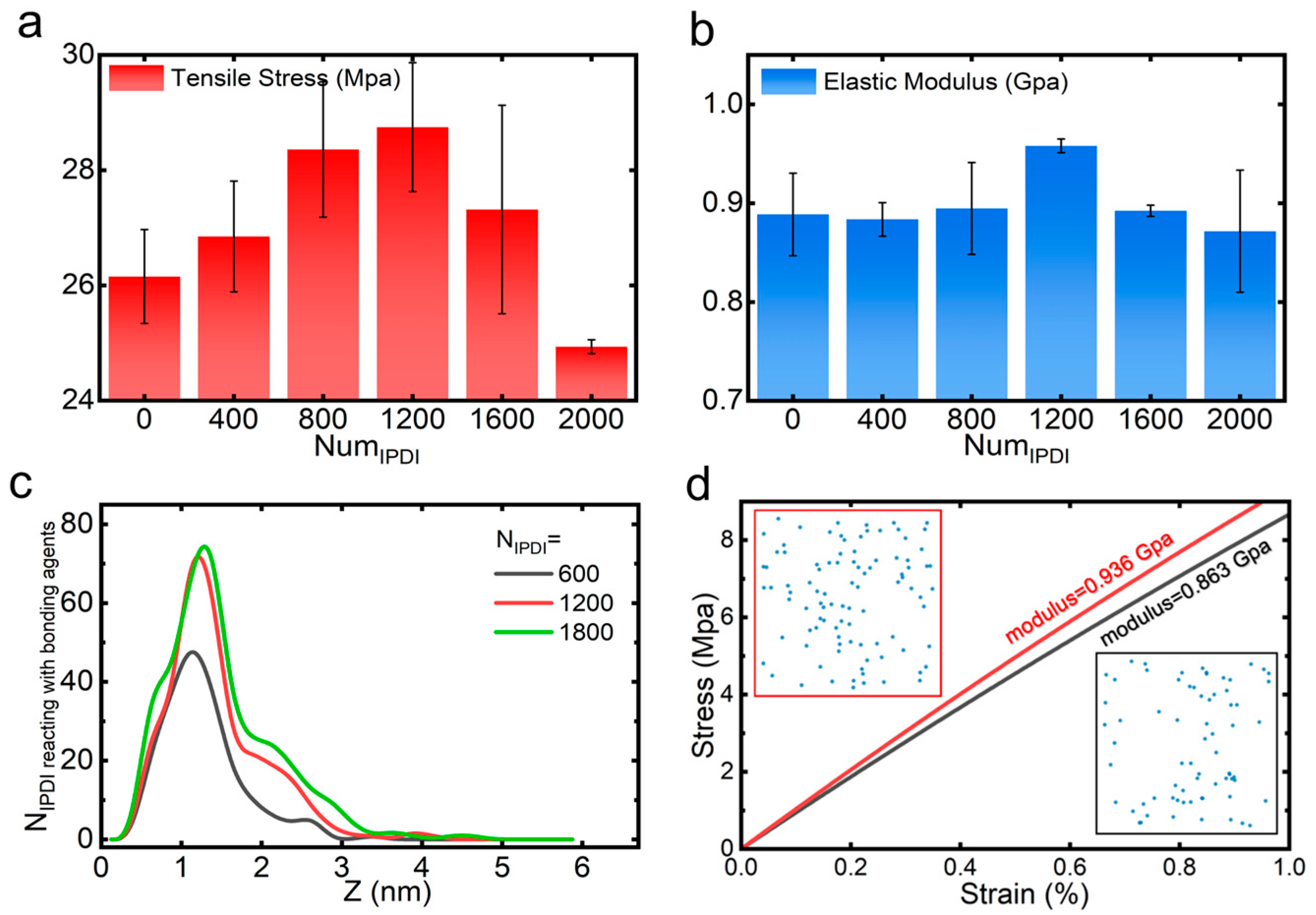
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Yadav, A.; Pant, C.S.; Das, S. Research Advances in Bonding Agents for Composite Propellants. Propell. Explos. Pyrot. 2020, 45, 695–704. [Google Scholar] [CrossRef]
- Yadav, N.; Srivastava, P.K.; Varma, M. Recent Advances in Catalytic Combustion of AP-Based Composite Solid Propellants. Def. Technol. 2021, 17, 1013–1031. [Google Scholar] [CrossRef]
- Galavotti, A.; Noè, C.; Polizzi, G.; Antonaci, P.; Maggi, F.; Masseni, F.; Pastrone, D. Solid Rocket Propellant Photo-Polymerization with an In-House LED-UV Prototype. Polymers 2023, 15, 1633. [Google Scholar] [CrossRef]
- Hua, C.; Ye, B.; Yin, S.; Qiu, M.; Wang, J.; An, C. Interfacial Engineering Endowing Ammonium Perchlorate with High Mechanical Properties and Energy-Release Efficiency. Ceram. Int. 2024, 50, 30316–30325. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, M.; Miao, Y.; Wang, H.; Chen, T.; Fan, X.; Chang, H. Dynamic Mechanical Response and Damage Mechanism of HTPB Propellant under Impact Loading. Materials 2020, 13, 3031. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Fan, Y.; Chen, X.; Wen, J.; Wang, Q.; Huang, J. Low/Intermediate Speed Impact-Induced Ignition and Damage of a Novel High-Energy Solid Propellant. Propell. Explos. Pyrot. 2023, 48, e202300056. [Google Scholar] [CrossRef]
- Yıldırım, H.C.; Özüpek, Ş. Structural Assessment of a Solid Propellant Rocket Motor: Effects of Aging and Damage. Aerosp. Sci. Technol. 2011, 15, 635–641. [Google Scholar] [CrossRef]
- Liu, Y.; He, J.; Xian, W.; Li, Y. Impact Velocity and Temperature Effects on the Shock Wave Propagation and Spallation of Hydroxyl-Terminated Polybutadiene: A Molecular Dynamics Study. ACS Appl. Polym. Mater. 2023, 5, 8937–8948. [Google Scholar] [CrossRef]
- Yin, S.; Lu, Z.; Bai, H.; Liu, X.; Li, H.; Hu, Y. Functionalized GO/Hydroxy-Terminated Polybutadiene Composites with High Anti-Migration and Ablation Resistance Performance. Polymers 2022, 14, 3315. [Google Scholar] [CrossRef]
- Zhang, Y.; Tian, Y.; Zhang, Y.; Fu, X.; Li, H.; Lu, Z.; Zhang, T.; Hu, Y. Improvement in Migration Resistance of Hydroxyl-Terminated Polybutadiene (HTPB) Liners by Using Graphene Barriers. Polymers 2022, 14, 5213. [Google Scholar] [CrossRef]
- Marimuthu, R.; Rao, B.N. Development of Efficient Finite Elements for Structural Integrity Analysis of Solid Rocket Motor Propellant Grains. Int. J. Pres. Ves. Pip. 2013, 111–112, 131–145. [Google Scholar] [CrossRef]
- Badgujar, D.M.; Talawar, M.B.; Asthana, S.N.; Mahulikar, P.P. Advances in Science and Technology of Modern Energetic Materials: An Overview. J. Hazard. Mater. 2008, 151, 289–305. [Google Scholar] [CrossRef] [PubMed]
- Zhang, P.; Sun, L.; Yuan, J.; Deng, J. Synthesis of Multifunctional Additives for Solid Propellants: Structure, Properties and Mechanism. Def. Technol. 2024, 33, 308–316. [Google Scholar] [CrossRef]
- Wu, C.; Liu, Y.; Hu, S.; Lu, Y.; Guo, C.; Li, H.; Qu, H.; Fu, X.; Li, H. Correlation between Microstructural Evolution and Mechanical Properties of CMDB Propellant during Uniaxial Tension. Propell. Explos. Pyrot. 2023, 48, e202300117. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, Z.; Yuan, B.; Yang, K. Surface Wetting Behaviors of Hydroxyl-Terminated Polybutadiene: Molecular Mechanism and Modulation. Polymers 2024, 16, 3085. [Google Scholar] [CrossRef] [PubMed]
- Liang, J.; Nie, J.; Zhang, H.; Guo, X.; Yan, S.; Han, M. Interaction Mechanism of Composite Propellant Components under Heating Conditions. Polymers 2023, 15, 2485. [Google Scholar] [CrossRef]
- Zhang, X.; Deng, Z.; Xu, W.; Jiang, L.; Xu, H.; Tang, Q.; Zheng, Q.; Li, J. Influence of Process Aids on Solid–Liquid Interfacial Properties of Three-Component Hydroxyl-Terminated Polybutadiene Propellants. Polymers 2025, 17, 286. [Google Scholar] [CrossRef]
- Liu, J.; Yu, H.; Wang, D.; Sun, S.; Li, F. Application of Spherical Ultrafine CuO@AP with Core–Shell in AP/HTPB Composite Solid Propellant. J. Therm. Anal. Calorim. 2023, 148, 5235–5246. [Google Scholar] [CrossRef]
- Deng, S.; Wang, J.; Sun, Y.; Luo, G.; Huan, F.; Mao, C.; Wang, J. Effect of Bonding Agent on Interfacial Strength of AP/T313/PBT in PBT-Based Composite Solid Propellants by Molecular Dynamics Simulation. Mater. Today Commun. 2025, 45, 112291. [Google Scholar] [CrossRef]
- Zhang, J.; Luo, P. Molecular-Level Insights into the Improvement Mechanism of the Bonding Agent MAPO on the Mechanical Properties of the AP/HTPB-TDI Cross-Linked System. Ind. Eng. Chem. Res. 2023, 62, 20689–20701. [Google Scholar] [CrossRef]
- Maimaitituersun, W.; Wu, Y.; Hou, X.; Wang, N. Numerical investigations on mesoscopic structure parameters affecting mechanical responses of propellant. fhclxb 2022, 39, 2949–2961. [Google Scholar] [CrossRef]
- Lai, G.D.; Sang, L.P.; Bian, Y.L.; Xie, H.L.; Liu, J.H.; Chai, H.W. Interfacial Debonding and Cracking in a Solid Propellant Composite under Uniaxial Tension: An In Situ Synchrotron X-Ray Tomography Study. Compos. Sci. Technol. 2024, 256, 110743. [Google Scholar] [CrossRef]
- Kim, J.; Zhang, G.; Shi, M.; Suo, Z. Fracture, Fatigue, and Friction of Polymers in Which Entanglements Greatly Outnumber Cross-Links. Science 2021, 374, 212–216. [Google Scholar] [CrossRef]
- Lian, Q.; Chen, H.; Luo, Y.; Li, Y.; Cheng, J.; Liu, Y. Toughening Mechanism Based on the Physical Entanglement of Branched Epoxy Resin in the Non-Phase-Separated Inhomogeneous Crosslinking Network: An Experimental and Molecular Dynamics Simulation Study. Polymer 2022, 247, 124754. [Google Scholar] [CrossRef]
- Guo, Z.; Lu, X.; Wang, X.; Li, X.; Li, J.; Sun, J. Engineering of Chain Rigidity and Hydrogen Bond Cross-Linking toward Ultra-Strong, Healable, Recyclable, and Water-Resistant Elastomers. Adv. Mater. 2023, 35, 2300286. [Google Scholar] [CrossRef] [PubMed]
- Cui, K.; Ma, Z.; Tian, N.; Su, F.; Liu, D.; Li, L. Multiscale and Multistep Ordering of Flow-Induced Nucleation of Polymers. Chem. Rev. 2018, 118, 1840–1886. [Google Scholar] [CrossRef]
- Wen, J.-L.; Ming, Y.-Q.; Zhang, A.-F.; Li, J.-L.; Du, X.-Y.; Shuai, L.; Nie, Y.-J. Interplay between Hydrogen Bond Network and Entangled Network in Polymers During Stretching Based on Molecular Simulations. Chin. J. Polym. Sci. 2024, 42, 2069–2080. [Google Scholar] [CrossRef]
- Berezkin, A.V.; Kudryavtsev, Y.V. Effect of Cross-Linking on the Structure and Growth of Polymer Films Prepared by Interfacial Polymerization. Langmuir 2015, 31, 12279–12290. [Google Scholar] [CrossRef]
- Zhu, Y.-L.; Liu, H.; Li, Z.-W.; Qian, H.-J.; Milano, G.; Lu, Z.-Y. GALAMOST: GPU-Accelerated Large-Scale Molecular Simulation Toolkit. J. Comput. Chem. 2013, 34, 2197–2211. [Google Scholar] [CrossRef]
- Martyna, G.J.; Tobias, D.J.; Klein, M.L. Constant Pressure Molecular Dynamics Algorithms. J. Chem. Phys. 1994, 101, 4177–4189. [Google Scholar] [CrossRef]
- Sardon, H.; Irusta, L.; Fernández-Berridi, M.J. Synthesis of Isophorone Diisocyanate (IPDI) Based Waterborne Polyurethanes: Comparison between Zirconium and Tin Catalysts in the Polymerization Process. Prog. Org. Coat. 2009, 66, 291–295. [Google Scholar] [CrossRef]
- Nawaz, S.; Carbone, P. Coarse-Graining Poly(Ethylene Oxide)–Poly(Propylene Oxide)–Poly(Ethylene Oxide) (PEO–PPO–PEO) Block Copolymers Using the MARTINI Force Field. J. Phys. Chem. B 2014, 118, 1648–1659. [Google Scholar] [CrossRef] [PubMed]
- Lee, H.; Choi, J.S.; Larson, R.G. Molecular Dynamics Studies of the Size and Internal Structure of the PAMAM Dendrimer Grafted with Arginine and Histidine. Macromolecules 2011, 44, 8681–8686. [Google Scholar] [CrossRef]
- Alessandri, R.; Grünewald, F.; Marrink, S.J. The Martini Model in Materials Science. Adv. Mater. 2021, 33, 2008635. [Google Scholar] [CrossRef] [PubMed]
- Grunewald, F.; Rossi, G.; de Vries, A.H.; Marrink, S.J.; Monticelli, L. Transferable MARTINI Model of Poly (Ethylene Oxide). J. Phys. Chem. B 2018, 122, 7436–7449. [Google Scholar] [CrossRef]
- Milani, A.; Casalegno, M.; Castiglioni, C.; Raos, G. Coarse-Grained Simulations of Model Polymer Nanofibres. Macromol. Theor. Simul. 2011, 20, 305–319. [Google Scholar] [CrossRef]
- Giuntoli, A.; Hansoge, N.K.; van Beek, A.; Meng, Z.; Chen, W.; Keten, S. Systematic Coarse-Graining of Epoxy Resins with Machine Learning-Informed Energy Renormalization. npj Comput. Mater. 2021, 7, 168. [Google Scholar] [CrossRef]
- Jacobs, R.; Morgan, D.; Attarian, S.; Meng, J.; Shen, C.; Wu, Z.; Xie, C.Y.; Yang, J.H.; Artrith, N.; Blaiszik, B.; et al. A Practical Guide to Machine Learning Interatomic Potentials—Status and Future. Curr. Opin. Solid State Mater. Sci. 2025, 35, 101214. [Google Scholar] [CrossRef]
- Stukowski, A. Visualization and Analysis of Atomistic Simulation Data with OVITO–the Open Visualization Tool. Modelling Simul. Mater. Sci. Eng. 2009, 18, 015012. [Google Scholar] [CrossRef]
- Zou, Z.; Qiang, H.; Zhou, J.; Zhang, F.; Wang, X.; Li, Y. Research on Microscopic Structure–Activity Relationship of AP Particle–Matrix Interface in HTPB Propellant. e-Polymers 2024, 24, 20240073. [Google Scholar] [CrossRef]
- Ma, L.; Zhu, X.; Zhang, W.; Zhang, H.; Wang, J.; Qu, J. Study on the Preparation and Performance Comparison of Side-Chain Hydroxyl-Terminated Polybutadiene Derivatives with Narrowly Molecular Weight Distribution Used for Polyurethane. Polym. Test. 2021, 104, 107389. [Google Scholar] [CrossRef]
- Liu, H.; Zhu, Y.-L.; Lu, Z.-Y.; Müller-Plathe, F. A Kinetic Chain Growth Algorithm in Coarse-Grained Simulations. J. Comput. Chem. 2016, 37, 2634–2646. [Google Scholar] [CrossRef]
- Yang, B.; Liu, S.; Ma, J.; Yang, Y.; Li, J.; Jiang, B.-P.; Ji, S.; Shen, X.-C. Monte Carlo Simulation of Surface-Initiated Polymerization: Heterogeneous Reaction Environment. Macromolecules 2022, 55, 1970–1980. [Google Scholar] [CrossRef]
- Ma, J.; Li, J.; Yang, B.; Liu, S.; Jiang, B.-P.; Ji, S.; Shen, X.-C. A Simple Stochastic Reaction Model for Heterogeneous Polymerizations. Polymers 2022, 14, 3269. [Google Scholar] [CrossRef]
- Quagliano Amado, J.C.; Ross, P.G.; Mattos Silva Murakami, L.; Narciso Dutra, J.C. Properties of Hydroxyl-Terminal Polybutadiene (HTPB) and Its Use as a Liner and Binder for Composite Propellants: A Review of Recent Advances. Propellants Explos. Pyrotech. 2022, 47, e202100283. [Google Scholar] [CrossRef]
- Yoon, S.; Lee, S.; Lee, J. Comprehensive Review on Post-Polymerization Modification of Hydroxyl-Terminated Polybutadiene (HTPB). Elastomers Compos. 2024, 59, 108–120. [Google Scholar] [CrossRef]
- Nie, Y.; Gao, H.; Wu, Y.; Hu, W. Thermodynamics of Strain-Induced Crystallization of Random Copolymers. Soft Matter 2013, 10, 343–347. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Yu, Y.; Guo, Y.; Luo, W.; Hu, W. Roles of Repeating-Unit Interactions in the Stress Relaxation Process of Bulk Amorphous Polymers. Polymer 2021, 224, 123740. [Google Scholar] [CrossRef]
- Zheng, T.; Wang, S.; Zhou, L.; Li, X.; Zhang, H. The Disentanglement and Shear Properties of Amorphous Polyethylene during Friction: Insights from Molecular Dynamics Simulations. Appl. Surf. Sci. 2022, 580, 152301. [Google Scholar] [CrossRef]
- Choi, J.B.; Nguyen, P.C.H.; Sen, O.; Udaykumar, H.S.; Baek, S. Artificial Intelligence Approaches for Energetic Materials by Design: State of the Art, Challenges, and Future Directions. Propell. Explos. Pyrot. 2023, 48, e202200276. [Google Scholar] [CrossRef]
- Han, R.; Fu, X.; Qu, B.; Shi, L.; Liu, Y. Deep-Neural-Networks-Based Data-Driven Methods for Characterizing the Mechanical Behavior of Hydroxyl-Terminated Polyether Propellants. Polymers 2025, 17, 660. [Google Scholar] [CrossRef] [PubMed]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ling, C.; Zhang, X.; Li, X.; Mou, G.; Guo, X.; Yuan, B.; Yang, K. Molecular Simulations of Interface-Driven Crosslinked Network Formation and Mechanical Response in Composite Propellants. Polymers 2025, 17, 1863. https://doi.org/10.3390/polym17131863
Ling C, Zhang X, Li X, Mou G, Guo X, Yuan B, Yang K. Molecular Simulations of Interface-Driven Crosslinked Network Formation and Mechanical Response in Composite Propellants. Polymers. 2025; 17(13):1863. https://doi.org/10.3390/polym17131863
Chicago/Turabian StyleLing, Chen, Xinke Zhang, Xin Li, Guozhu Mou, Xiang Guo, Bing Yuan, and Kai Yang. 2025. "Molecular Simulations of Interface-Driven Crosslinked Network Formation and Mechanical Response in Composite Propellants" Polymers 17, no. 13: 1863. https://doi.org/10.3390/polym17131863
APA StyleLing, C., Zhang, X., Li, X., Mou, G., Guo, X., Yuan, B., & Yang, K. (2025). Molecular Simulations of Interface-Driven Crosslinked Network Formation and Mechanical Response in Composite Propellants. Polymers, 17(13), 1863. https://doi.org/10.3390/polym17131863






