Creep Compliance of Carbon Black-Filled Rubber Converted from Storage Modulus by Use of Collocation Method: Numerical and Experimental Validation
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. DMA Tests
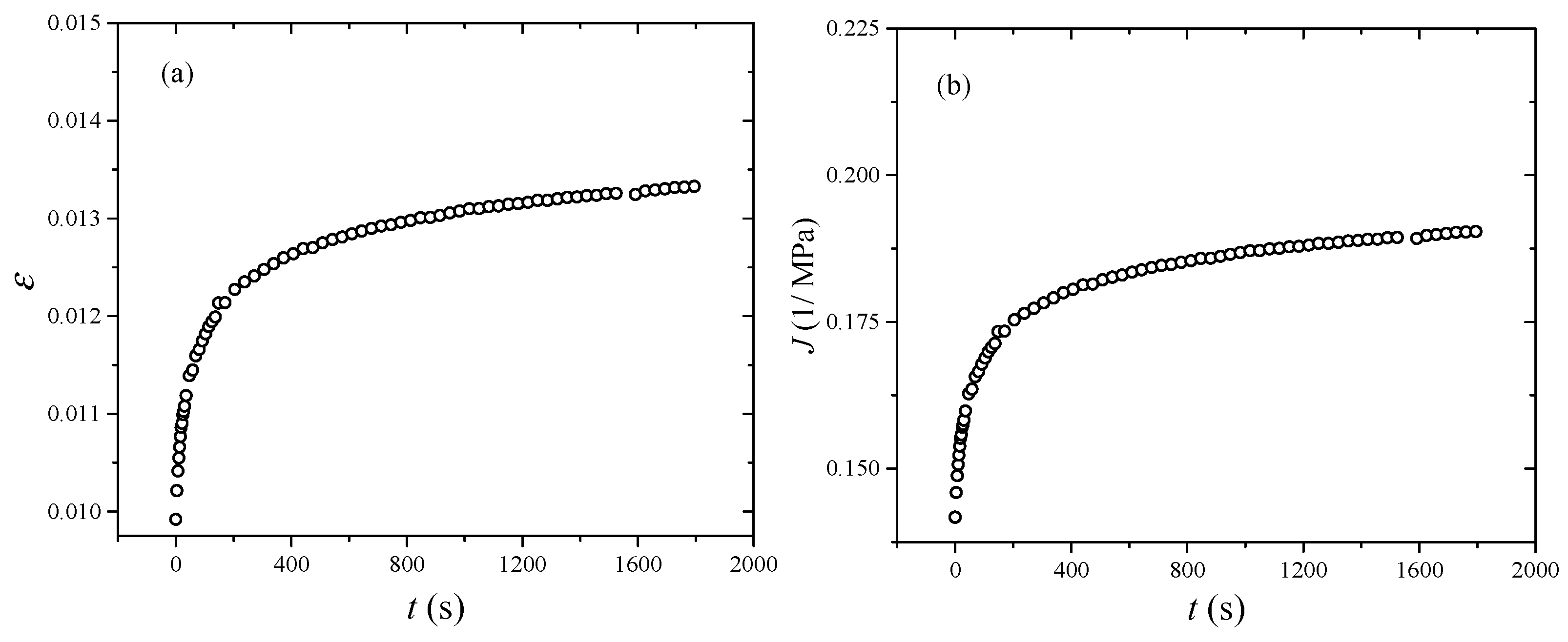
2.3. Creep Tests
2.4. General Theory
2.4.1. Generalized Kelvin Model
2.4.2. Superposition Principle
3. Results and Discussion
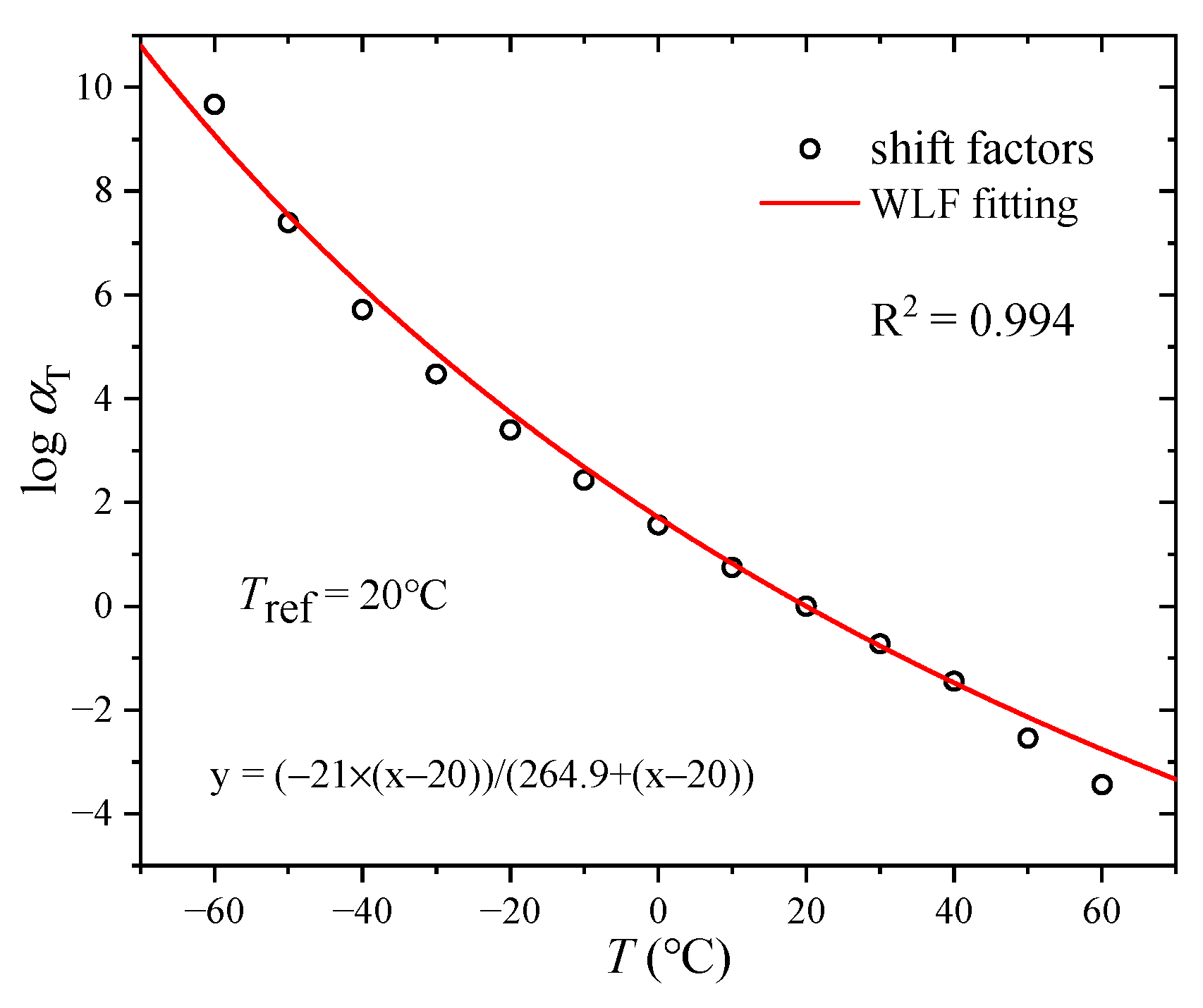
3.1. Dynamic Mechanical Property
3.2. Creep Behavior
3.3. Creep Compliance Converted from Storage Modulus
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CB | Carbon black |
| TTSP | Time-temperature superposition principle |
| WLF | Williams–Landel–Ferry |
| DMA | Dynamic mechanical analysis |
References
- Chen, P.; Wang, B.; Zhang, Z.; Li, T.; Dai, K. A generalized model of lead rubber bearing considering large strain stiffening and degradation. Eng. Struct. 2023, 275, 115264. [Google Scholar] [CrossRef]
- Ansari, A.; Mohanty, T.R.; Sarkar, S.; Ramakrishnan, S.; Amarnath, S.K.P.; Singha, N.K. Epoxy modified styrene butadiene rubber (SBR) in green tire application. Eur. Polym. J. 2024, 213, 113069. [Google Scholar] [CrossRef]
- Shafik, E.S.; Tharwat, C.; Abd-El-Messieh, S.L. Utilization study on red brick waste as novel reinforcing and economical filler for acrylonitrile butadiene rubber composite. Clean Technol. Environ. 2023, 25, 1605–1615. [Google Scholar] [CrossRef]
- Srivabut, C.; Homkhiew, C.; Petdee, T.; Rawangwong, S. Possibility of using bio-based polymer blends for producing children’s toys: Effects of polylactic acid (PLA) grades and contents. Fiber. Polym. 2025, 26, 983–994. [Google Scholar] [CrossRef]
- Urtekin, G.; Ullah, M.S.; Yildirim, R.; Ozkoc, G.; Kodal, M. A comprehensive review of the recent developments in thermoplastics and rubber blends-based composites and nanocomposites. Polym. Compos. 2023, 44, 8303–8329. [Google Scholar] [CrossRef]
- Nitta, K.H.; Maeda, H. Creep behavior of high density polyethylene under a constant true stress. Polym. Test. 2010, 29, 60–65. [Google Scholar] [CrossRef]
- Gent, A.N. Relaxation processes in vulcanized rubber. I. Relation among stress relaxation, creep, recovery, and hysteresis. J. Appl. Polym. Sci. 1962, 6, 433–441. [Google Scholar] [CrossRef]
- Luo, R.K.; Zhou, X.; Tang, J. Numerical prediction and experiment on rubber creep and stress relaxation using time-dependent hyperelastic approach. Polym. Test. 2016, 52, 246–253. [Google Scholar] [CrossRef]
- Ferry, J.D. Viscoelastic Properties of Polymers; Wiley: Hoboken, NJ, USA, 1980. [Google Scholar]
- Houwink, R. Slipping of molecules during the deformation of reinforced rubber. Rubber Chem. Tech. 1956, 29, 888–893. [Google Scholar] [CrossRef]
- Cui, Y.; Campbell, J.E.; Burley, M.; Patel, M.; Hunt, K.; Clyne, T.W. Effects of temperature and filler content on the creep behaviour of a polyurethane rubber. Mech. Mater. 2020, 148, 103461. [Google Scholar] [CrossRef]
- Banerjee, S.S.; Bhowmick, A.K. High-temperature thermoplastic elastomers from rubber-plastic blends: A state-of-the-art review. Rubber Chem. Tech. 2017, 90, 1–36. [Google Scholar] [CrossRef]
- Ramachandran, P.; Dutta, J.; Chatterjee, T.; Nando, G.B.; Naskar, K. Investigation of different cross-linking methods of EOC: PDMS thermoplastic elastomers for cable insulation application with special reference to thermal, rheological, creep, and electrical properties. Rubber Chem. Tech. 2017, 90, 585–610. [Google Scholar] [CrossRef]
- Yin, B.; Hu, X.; Song, K. Evaluation of classic and fractional models as constitutive relations for carbon black-filled rubber. J. Elastom. Plast. 2018, 50, 463–477. [Google Scholar] [CrossRef]
- Zhang, B.; Jin, X.; Yu, T.; Yu, X.; Gu, C. Fatigue and Creep Properties of Carbon Nanotube/Aramid Fiber Synergistically-Reinforced Rubber Sealing Composites. Fiber. Polym. 2023, 24, 2401–2409. [Google Scholar] [CrossRef]
- Cai, W.; Wang, P.; Zhang, Y. Fractional-order model for temperature-dependent rheological behaviors of polymeric materials. Mech. Adv. Mater. Struct. 2024, 31, 4069–4080. [Google Scholar] [CrossRef]
- Xiao, R.; Sun, H.; Chen, W. An equivalence between generalized Maxwell model and fractional Zener model. Mech. Mater. 2016, 100, 148–153. [Google Scholar] [CrossRef]
- Lv, H.; Ye, W.; Tan, Y.; Zhang, D. Inter-conversion of the generalized Kelvin and generalized Maxwell model parameters via a continuous spectrum method. Constr. Build. Mater. 2022, 351, 128963. [Google Scholar] [CrossRef]
- Mandlekar, N.; Rana, B.; Maurya, P.; Butola, B.S.; Joshi, M. Long-term prediction of creep and stress-relaxation behaviour in synthetic fabrics using the time–temperature superposition principle. Fiber. Polym. 2023, 24, 2195–2207. [Google Scholar] [CrossRef]
- Zhang, W.; Cui, B.; Gu, X.; Dong, Q. Comparison of relaxation modulus converted from frequency-and time-dependent viscoelastic functions through numerical methods. Appl. Sci. 2018, 8, 2447. [Google Scholar] [CrossRef]
- Zhao, Y.; Ni, Y.; Zeng, W. A consistent approach for characterising asphalt concrete based on generalised Maxwell or Kelvin model. Road Mater. Pavement Des. 2014, 15, 674–690. [Google Scholar] [CrossRef]
- Luo, R.; Lv, H.; Liu, H. Development of Prony series models based on continuous relaxation spectrums for relaxation moduli determined using creep tests. Constr. Build. Mater. 2018, 168, 758–770. [Google Scholar] [CrossRef]
- Forough, S.A.; Nejad, F.M.; Khodaii, A. Comparing various fitting models to construct the tensile relaxation modulus master curve of asphalt mixes. Int. J. Pavement Eng. 2016, 17, 314–330. [Google Scholar] [CrossRef]
- Sun, Y.; Huang, B.; Chen, J. A unified procedure for rapidly determining asphalt concrete discrete relaxation and retardation spectra. Constr. Build. Mater. 2015, 93, 35–48. [Google Scholar] [CrossRef]
- Fang, Y.; Jiao, X.; Yin, B. Evaluation of converted relaxation modulus obtained from dynamic modulus of carbon black filled rubber: Numerical modeling and experimental validation. J. Mater. Sci. 2025, 60, 9957–9968. [Google Scholar] [CrossRef]
- ISO 4664-1:2022; Rubber, Vulcanized or Thermoplastic-Determination of Dynamic Properties-Part1: General Guidance. International Organization for Standardization: Geneva, Switzerland, 2022.
- ISO 2285:2019; Rubber, Vulcanized or Thermoplastic-Determination of Tension Set Under Constant Elongation, and of Tension Set, Elongation and Creep Under Constant Tensile Load. International Organization for Standardization: Geneva, Switzerland, 2019.
- Yin, B.; Jiao, X.; Fang, Y.; Sun, H. Dynamic viscoelasticity and hysteresis loss of carbon black filled rubber: Measurements and prediction. Polym. Compos. 2025. [Google Scholar] [CrossRef]
- Mallamace, D.; Mensitieri, G.; Salzano de Luna, M.; Mallamace, F. The time-temperature superposition of polymeric rubber gels treated by means of the mode-coupling theory. Gels 2024, 10, 313. [Google Scholar] [CrossRef]
- Irfan, M.S.; Gill, Y.Q.; Hashmi, M.; Ullah, S.; Saeed, F.; Qaiser, A.A. Long-term stress relaxation behavior of Polyaniline-EPDM blends using the time-temperature-strain superposition method. Mater. Res. Express 2018, 6, 025318. [Google Scholar] [CrossRef]
- Yao, Q.; Dong, P.; Zhao, Z.; Li, Z.; Wei, T.; Wu, J.; Qiu, J.; Li, W. Temperature dependent tensile fracture strength model of rubber materials based on Mooney-Rivlin model. Eng. Fract. Mech. 2023, 292, 109646. [Google Scholar] [CrossRef]
- Liu, X.; Zhu, D.; Lin, J.; Zhang, Y. Temperature and frequency dependence of the dynamic viscoelastic properties of silicone rubber. Polymers 2023, 15, 3005. [Google Scholar] [CrossRef]
- Park, S.W.; Kim, Y.R. Interconversion between relaxation modulus and creep compliance for viscoelastic solids. J. Mater. Civ. Eng. 1999, 11, 76–82. [Google Scholar] [CrossRef]
- Park, S.W.; Schapery, R.A. Methods of interconversion between linear viscoelastic material functions. Part I—A numerical method based on Prony series. Int. J. Solids Struct. 1999, 36, 1653–1675. [Google Scholar] [CrossRef]







| i | 1/Ei | i | 1/Ei | ||
|---|---|---|---|---|---|
| 1 | 5 × 10−13 | 5.833 × 10−5 | 11 | 5 × 10−3 | 1.613 × 10−2 |
| 2 | 5 × 10−12 | 7.937 × 10−5 | 12 | 5 × 10−2 | 1.587 × 10−2 |
| 3 | 5 × 10−11 | 9.016 × 10−5 | 13 | 5 × 10−1 | 1.493 × 10−2 |
| 4 | 5 × 10−10 | 4.684 × 10−4 | 14 | 5 × 100 | 1.449 × 10−2 |
| 5 | 5 × 10−9 | 1.873 × 10−3 | 15 | 5 × 101 | 1.389 × 10−2 |
| 6 | 5 × 10−8 | 1.204 × 10−2 | 16 | 5 × 102 | 1.299 × 10−2 |
| 7 | 5 × 10−7 | 1.923 × 10−2 | 17 | 5 × 103 | 1.250 × 10−2 |
| 8 | 5 × 10−6 | 2.500 × 10−2 | 18 | 5 × 104 | 1.111 × 10−2 |
| 9 | 5 × 10−5 | 2.128 × 10−2 | 1/E0 | 4.212 × 10−4 | |
| 10 | 5 × 10−4 | 1.694 × 10−2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, B.; Zhao, B.; Tang, W.; Wang, R.; Yin, B. Creep Compliance of Carbon Black-Filled Rubber Converted from Storage Modulus by Use of Collocation Method: Numerical and Experimental Validation. Polymers 2025, 17, 1809. https://doi.org/10.3390/polym17131809
Zhou B, Zhao B, Tang W, Wang R, Yin B. Creep Compliance of Carbon Black-Filled Rubber Converted from Storage Modulus by Use of Collocation Method: Numerical and Experimental Validation. Polymers. 2025; 17(13):1809. https://doi.org/10.3390/polym17131809
Chicago/Turabian StyleZhou, Bo, Bin Zhao, Wei Tang, Rongyong Wang, and Boyuan Yin. 2025. "Creep Compliance of Carbon Black-Filled Rubber Converted from Storage Modulus by Use of Collocation Method: Numerical and Experimental Validation" Polymers 17, no. 13: 1809. https://doi.org/10.3390/polym17131809
APA StyleZhou, B., Zhao, B., Tang, W., Wang, R., & Yin, B. (2025). Creep Compliance of Carbon Black-Filled Rubber Converted from Storage Modulus by Use of Collocation Method: Numerical and Experimental Validation. Polymers, 17(13), 1809. https://doi.org/10.3390/polym17131809





