Experimental Evaluation and Machine Learning-Based Prediction of Laser Cutting Quality in FFF-Printed ABS Thermoplastics
Abstract
1. Introduction
2. Materials and Methods
2.1. ABS Parts Manufacturing with Fused Filament Fabrication (FFF)
2.2. CO2 Laser Cutting Process
2.3. Measurement of Performance Indicators
3. Machine Learning Models
3.1. Long Short-Term Memory (LSTM)
3.2. LSTM-Gated Recurrent Unit (LSTM-GRU)
3.3. LSTM-Extreme Gradient Boosting (LSTM-XGBoost)
3.4. Extreme Gradient Boosting (XGBoost)
3.5. Linear Regression (LR)
3.6. Random Forest (RF)
3.7. Support Vector Regression (SVR)
3.8. Evaluation Metrics
4. Results and Discussion
4.1. Assessment of Laser Cutting Performance Indicators
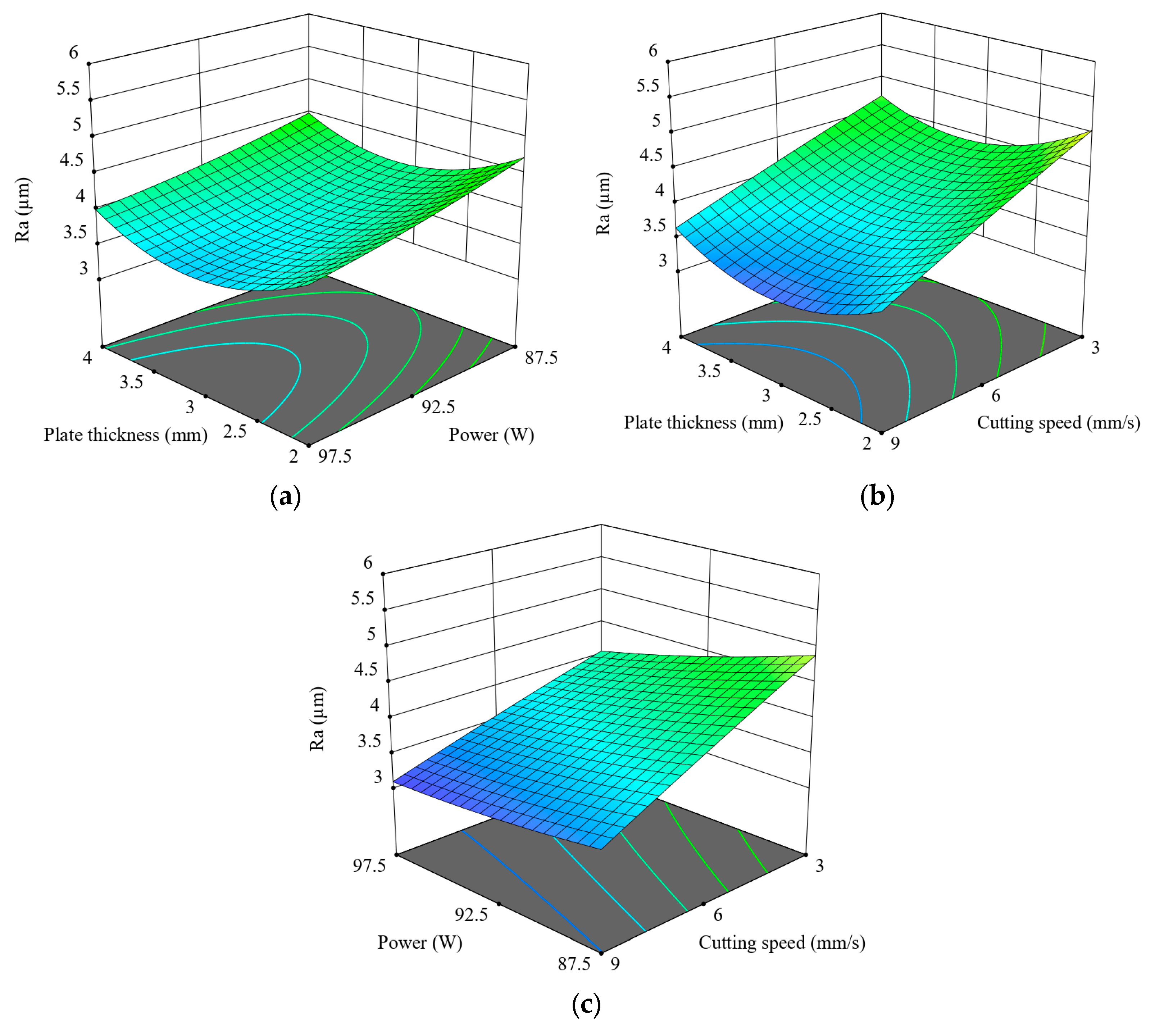
4.1.1. Surface Roughness
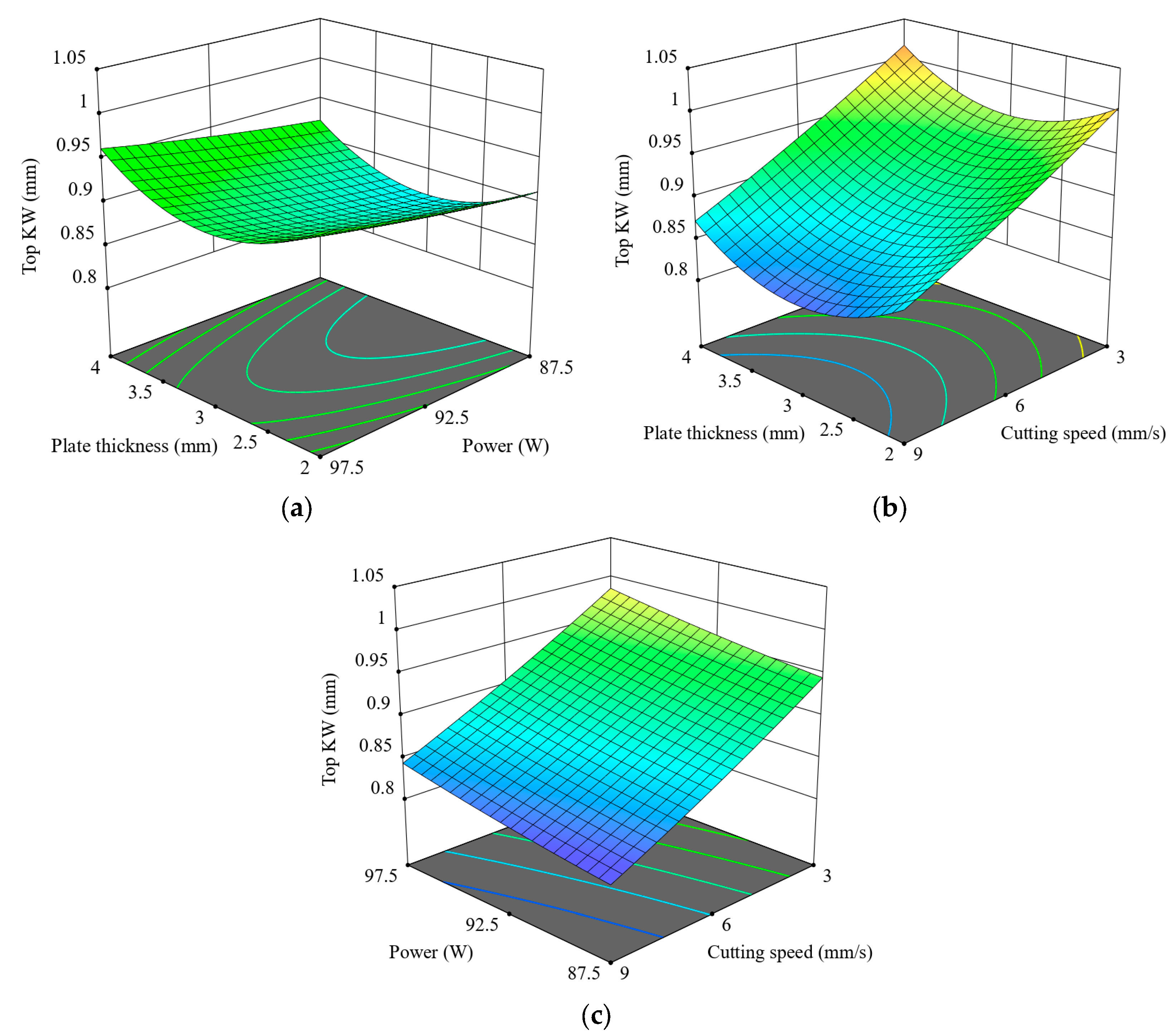
4.1.2. Top Kerf Width
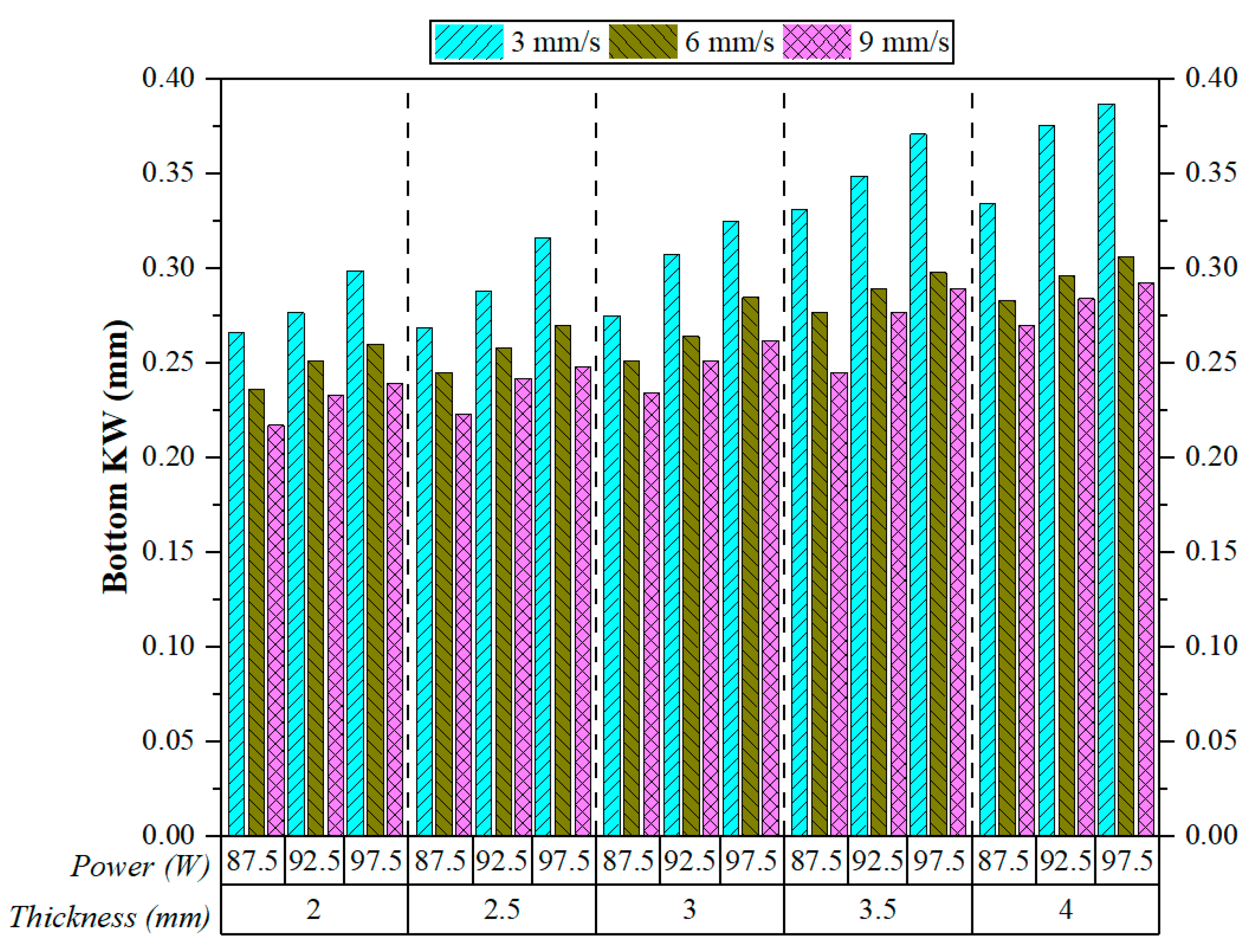
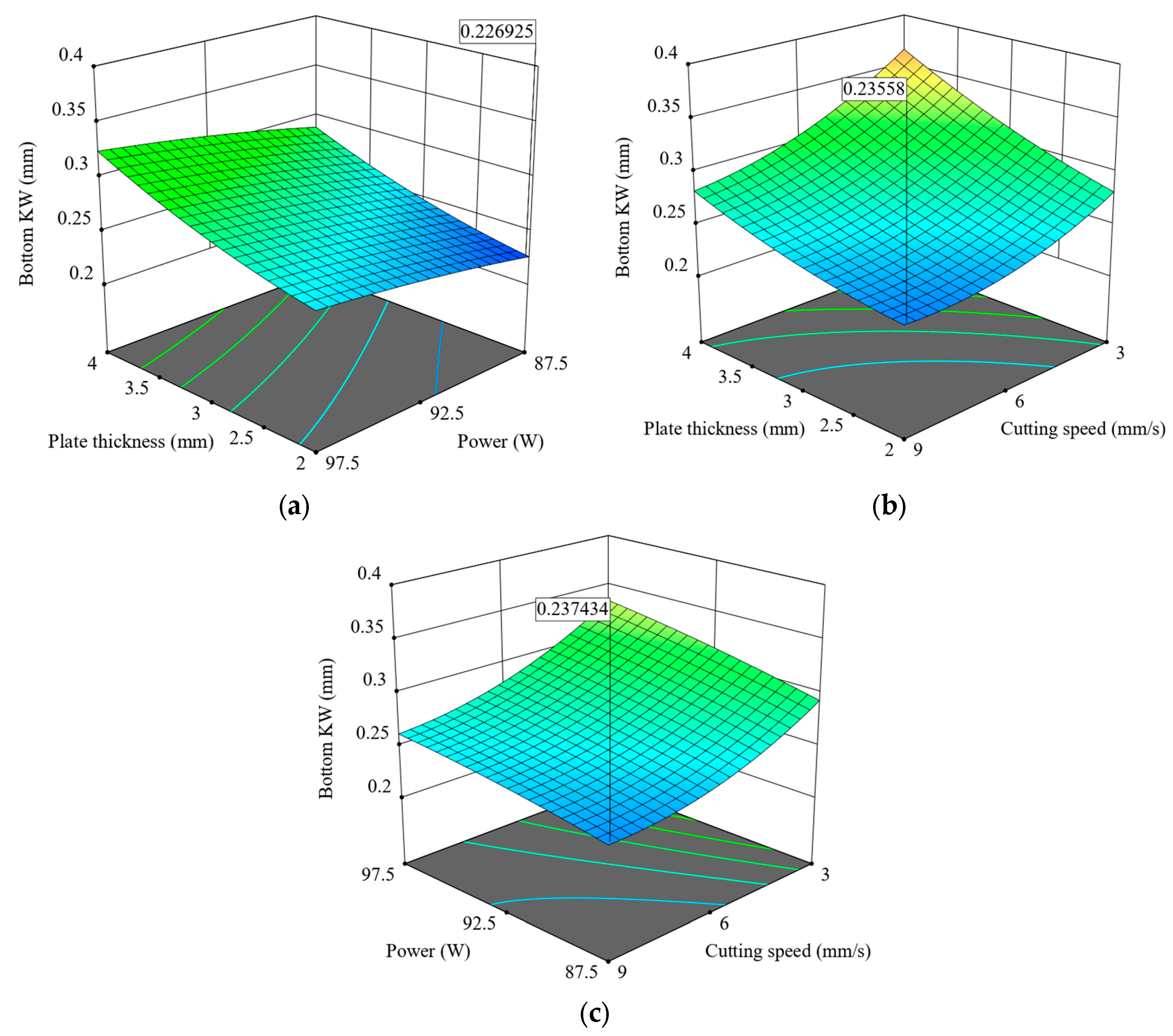
4.1.3. Bottom Kerf Width
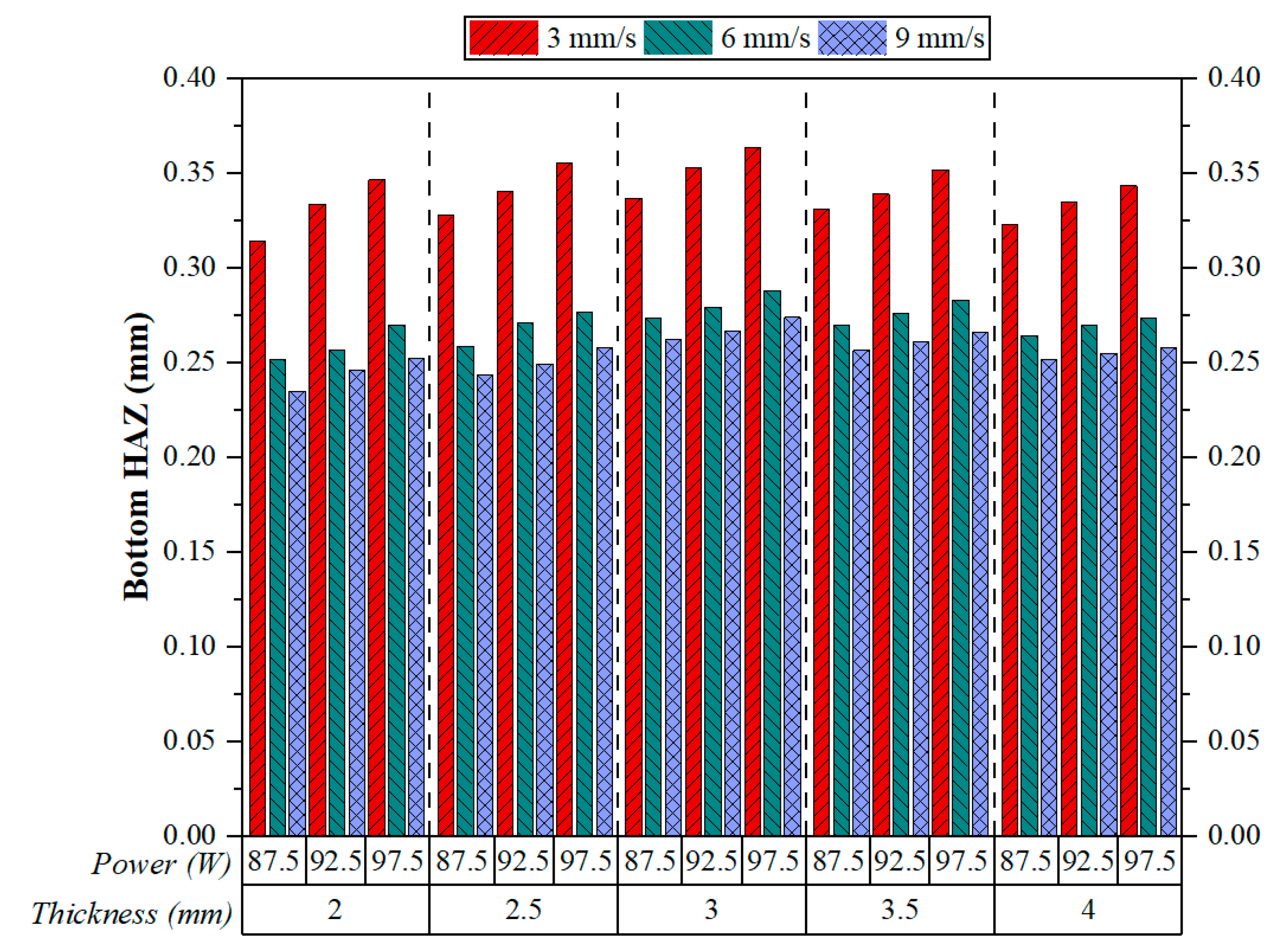
4.1.4. Bottom HAZ
4.2. ANOVA Results
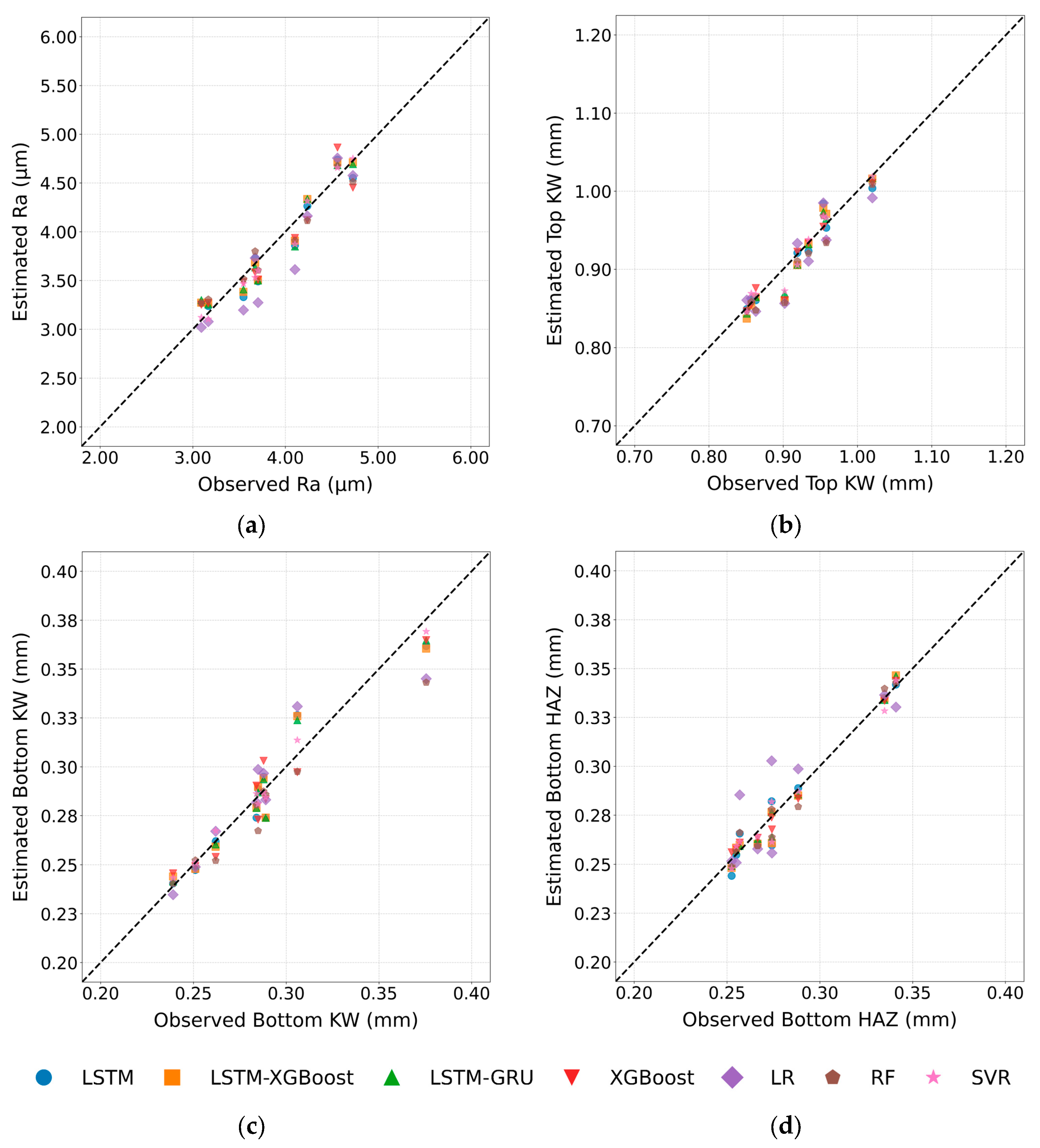
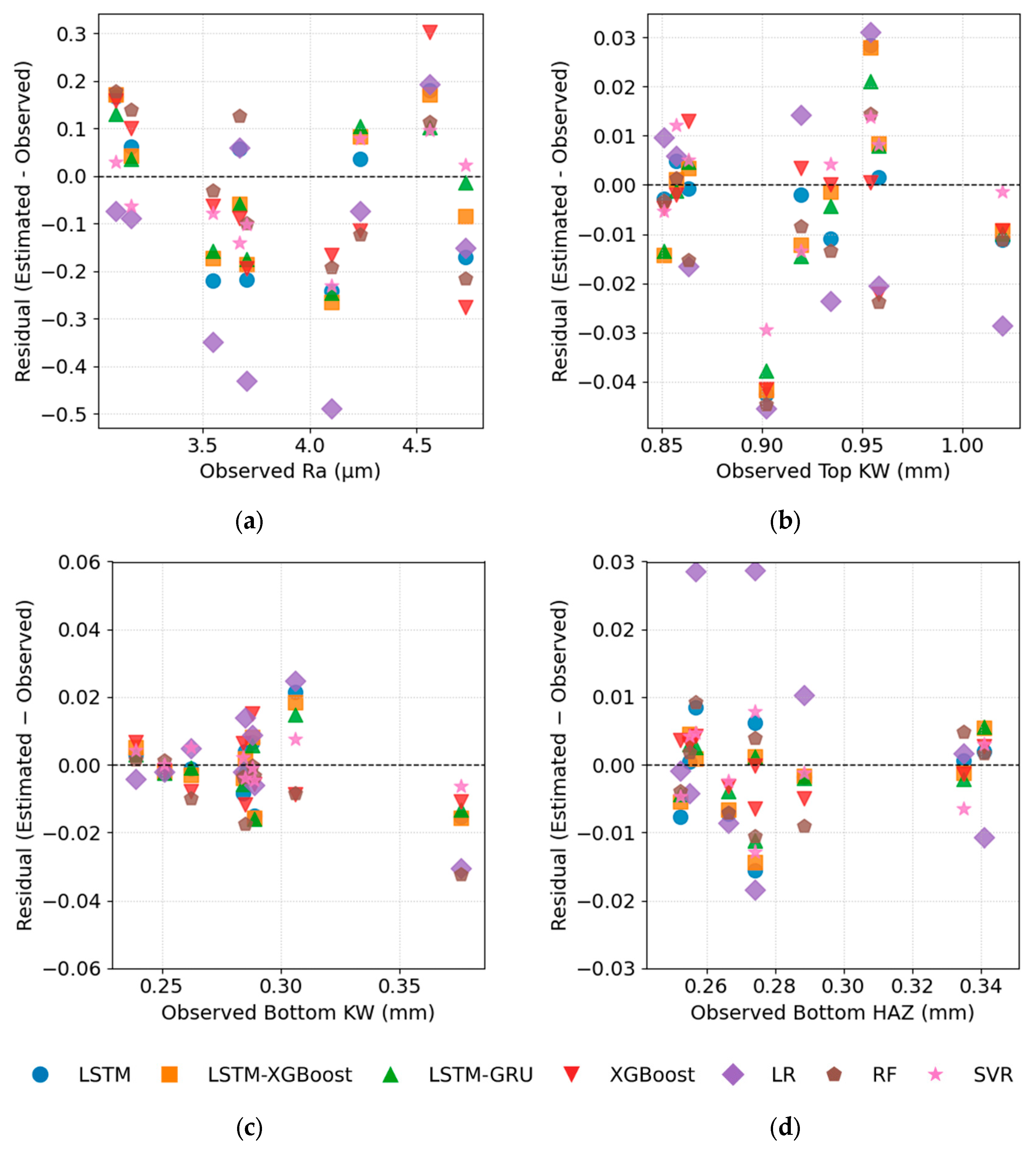
4.3. Machine Learning Modelling Results
5. Conclusions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Darıcık, F.; Delibaş, H.; Canbolat, G.; Topcu, A. Effects of Short-Term Thermal Aging on the Fracture Behavior of 3D-Printed Polymers. J. Mater. Eng. Perform. 2021, 30, 8851–8858. [Google Scholar] [CrossRef]
- Basar, G.; Der, O.; Guvenc, M.A. AI-Powered Hybrid Metaheuristic Optimization for Predicting Surface Roughness and Kerf Width in CO2 Laser Cutting of 3D-Printed PLA-CF Composites. J. Thermoplast. Compos. Mater. 2025. [Google Scholar] [CrossRef]
- Tuli, N.T.; Khatun, S.; Rashid, A. Bin Unlocking the Future of Precision Manufacturing: A Comprehensive Exploration of 3D Printing with Fiber-Reinforced Composites in Aerospace, Automotive, Medical, and Consumer Industries. Heliyon 2024, 10, e27328. [Google Scholar] [CrossRef] [PubMed]
- Beg, S.; Almalki, W.H.; Malik, A.; Farhan, M.; Aatif, M.; Rahman, Z.; Alruwaili, N.K.; Alrobaian, M.; Tarique, M.; Rahman, M. 3D Printing for Drug Delivery and Biomedical Applications. Drug. Discov. Today 2020, 25, 1668–1681. [Google Scholar] [CrossRef]
- Garmabi, M.M.; Shahi, P.; Tjong, J.; Sain, M. 3D Printing of Polyphenylene Sulfide for Functional Lightweight Automotive Component Manufacturing through Enhancing Interlayer Bonding. Addit. Manuf. 2022, 56, 102780. [Google Scholar] [CrossRef]
- Tonelli, A.; Candiani, A.; Sozzi, M.; Zucchelli, A.; Foresti, R.; Dall’Asta, C.; Selleri, S.; Cucinotta, A. The Geek and the Chemist: Antioxidant Capacity Measurements by DPPH Assay in Beverages Using Open Source Tools, Consumer Electronics and 3D Printing. Sens. Actuators B 2019, 282, 559–566. [Google Scholar] [CrossRef]
- Siddique, T.H.M.; Sami, I.; Nisar, M.Z.; Naeem, M.; Karim, A.; Usman, M. Low Cost 3D Printing for Rapid Prototyping and Its Application. In Proceedings of the 2019 Second International Conference on Latest trends in Electrical Engineering and Computing Technologies (INTELLECT), Karachi, Pakistan, 13–14 November 2019. [Google Scholar]
- Cicek, U.I.; Johnson, A.A. Multi-Objective Optimization of FDM Process Parameters for 3D-Printed Polycarbonate Using Taguchi-Based Gray Relational Analysis. Int. J. Adv. Manuf. Technol. 2025, 137, 3709–3725. [Google Scholar] [CrossRef]
- Kahya, Ç.; Tunçel, O.; Çavuşoğlu, O.; Tüfekci, K. Thermal Annealing Optimization for Improved Mechanical Performance of PLA Parts Produced via 3D Printing. Polym. Test. 2025, 144, 108735. [Google Scholar] [CrossRef]
- Solomon, I.J.; Sevvel, P.; Gunasekaran, J. A Review on the Various Processing Parameters in FDM. Mater. Today Proc. 2021, 37, 509–514. [Google Scholar] [CrossRef]
- Ebrahimi, F.; Xu, H.; Fuenmayor, E.; Major, I. A Comparison of Droplet Deposition Modelling, Fused Filament Fabrication, and Injection Moulding for the Production of Oral Dosage Forms Containing Hydrochlorothiazide. Int. J. Pharm. 2023, 645, 123400. [Google Scholar] [CrossRef]
- Kantaros, A.; Katsantoni, M.; Ganetsos, T.; Petrescu, N. The Evolution of Thermoplastic Raw Materials in High-Speed FFF/FDM 3D Printing Era: Challenges and Opportunities. Materials 2025, 18, 1220. [Google Scholar] [CrossRef] [PubMed]
- Ordu, M.; Der, O. Polymeric Materials Selection for Flexible Pulsating Heat Pipe Manufacturing Using a Comparative Hybrid MCDM Approach. Polymers 2023, 15, 2933. [Google Scholar] [CrossRef] [PubMed]
- Khosravani, M.R.; Schüürmann, J.; Berto, F.; Reinicke, T. On the Post-Processing of 3D-Printed ABS Parts. Polymers 2021, 13, 1559. [Google Scholar] [CrossRef] [PubMed]
- Der, O.; Başar, G. Investigation of The Effects of Process Parameters on Machining Performance in Laser Cutting of 3D-Printed PLA. Int. J. 3D Print. Technol. Digit. Ind. 2025, 9, 9–20. [Google Scholar] [CrossRef]
- Der, O.; Edwardson, S.; Bertola, V. Manufacturing Low-Cost Fluidic and Heat Transfer Devices with Polymer Materials by Selective Transmission Laser Welding. In Encyclopedia of Materials: Plastics and Polymers; Elsevier: Amsterdam, The Netherlands, 2022; pp. 370–378. [Google Scholar]
- Der, O.; Ordu, M.; Basar, G. Optimization of Cutting Parameters in Manufacturing of Polymeric Materials for Flexible Two-Phase Thermal Management Systems. Mater. Test. 2024, 66, 1700–1719. [Google Scholar] [CrossRef]
- Kechagias, J.D.; Ninikas, K.; Zaoutsos, S.; Tzounis, L.; Stavropoulos, P. On Optimizing CO2 Laser Cutting of 3D-Printed PA12/CNTs Composite Sheet Kerf Characteristics. Int. J. Adv. Manuf. Technol. 2025, 138, 1307–1322. [Google Scholar] [CrossRef]
- Der, O.; Edwardson, S.; Marengo, M.; Bertola, V. Engineered Composite Polymer Sheets with Enhanced Thermal Conductivity. IOP Conf. Ser. Mater. Sci. Eng. 2019, 613, 012008. [Google Scholar] [CrossRef]
- Kechagias, J.D.; Ninikas, K.; Petousis, M.; Vidakis, N. Laser Cutting of 3D Printed Acrylonitrile Butadiene Styrene Plates for Dimensional and Surface Roughness Optimization. Int. J. Adv. Manuf. Technol. 2022, 119, 2301–2315. [Google Scholar] [CrossRef]
- Sabri, H.; Mehrabi, O.; Khoran, M.; Moradi, M. Leveraging CO2 Laser Cutting for Enhancing Fused Deposition Modeling (FDM) 3D Printed PETG Parts through Postprocessing. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2024. [Google Scholar] [CrossRef]
- Moradi, M.; Karami Moghadam, M.; Shamsborhan, M.; Bodaghi, M.; Falavandi, H. Post-Processing of FDM 3D-Printed Polylactic Acid Parts by Laser Beam Cutting. Polymers 2020, 12, 550. [Google Scholar] [CrossRef]
- Kechagias, J.D.; Fountas, N.A.; Ninikas, K.; Petousis, M.; Vidakis, N.; Vaxevanidis, N. Surface Characteristics Investigation of 3D-Printed PET-G Plates during CO2 Laser Cutting. Mater. Manuf. Processes 2022, 37, 1347–1357. [Google Scholar] [CrossRef]
- Kechagias, J.D.; Ninikas, K.; Petousis, M.; Vidakis, N.; Vaxevanidis, N. An Investigation of Surface Quality Characteristics of 3D Printed PLA Plates Cut by CO2 Laser Using Experimental Design. Mater. Manuf. Processes 2021, 36, 1544–1553. [Google Scholar] [CrossRef]
- Adugna, T.; Xu, W.; Fan, J. Comparison of Random Forest and Support Vector Machine Classifiers for Regional Land Cover Mapping Using Coarse Resolution FY-3C Images. Remote Sens. 2022, 14, 574. [Google Scholar] [CrossRef]
- Malashin, I.; Tynchenko, V.; Gantimurov, A.; Nelyub, V.; Borodulin, A. Applications of Long Short-Term Memory (LSTM) Networks in Polymeric Sciences: A Review. Polymers 2024, 16, 2607. [Google Scholar] [CrossRef]
- García-Ávila, J.; Torres Serrato, D.d.J.; Rodriguez, C.A.; Martínez, A.V.; Cedillo, E.R.; Martínez-López, J.I. Predictive Modeling of Soft Stretchable Nanocomposites Using Recurrent Neural Networks. Polymers 2022, 14, 5290. [Google Scholar] [CrossRef]
- Kumshe, U.M.M.; Abdulhamid, Z.M.; Mala, B.A.; Muazu, T.; Muhammad, A.U.; Sangary, O.; Ba, A.F.; Tijjani, S.; Adam, J.M.; Ali, M.A.H.; et al. Improving Short-Term Daily Streamflow Forecasting Using an Autoencoder Based CNN-LSTM Model. Water Resour. Manag. 2024, 38, 5973–5989. [Google Scholar] [CrossRef]
- Zhang, G.-Y.; Zhang, C.-X.; Zhang, J.-S. Out-of-Bag Estimation of the Optimal Hyperparameter in SubBag Ensemble Method. Commun. Stat.-Simul. Comput. 2010, 39, 1877–1892. [Google Scholar] [CrossRef]
- Chang, E.-C.; Sun, Y.-J.; Cheng, C.-A. A New and Improved Sliding Mode Control Design Based on a Grey Linear Regression Model and Its Application in Pure Sine Wave Inverters for Photovoltaic Energy Conversion Systems. Micromachines 2025, 16, 377. [Google Scholar] [CrossRef]
- Senoussaoui, M.E.A.; Brahami, M.; Fofana, I. Transformer Oil Quality Assessment Using Random Forest with Feature Engineering. Energies 2021, 14, 1809. [Google Scholar] [CrossRef]
- Al-Anazi, A.F.; Gates, I.D. Support Vector Regression for Porosity Prediction in a Heterogeneous Reservoir: A Comparative Study. Comput. Geosci. 2010, 36, 1494–1503. [Google Scholar] [CrossRef]
- Üstün, İ.; Üneş, F.; Mert, İ.; Karakuş, C. A Comparative Study of Estimating Solar Radiation Using Machine Learning Approaches: DL, SMGRT, and ANFIS. Energy Sources Part A 2022, 44, 10322–10345. [Google Scholar] [CrossRef]
- Karim, F.K.; Khafaga, D.S.; Eid, M.M.; Towfek, S.K.; Alkahtani, H.K. A Novel Bio-Inspired Optimization Algorithm Design for Wind Power Engineering Applications Time-Series Forecasting. Biomimetics 2023, 8, 321. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Wang, L. Optimization of Site Investigation Program for Reliability Assessment of Undrained Slope Using Spearman Rank Correlation Coefficient. Comput. Geotech. 2023, 155, 105208. [Google Scholar] [CrossRef]
- Kechagias, J.D.; Ninikas, K.; Vakouftsi, F.; Fountas, N.A.; Palanisamy, S.; Vaxevanidis, N.M. Optimization of Laser Beam Parameters during Processing of ASA 3D-Printed Plates. Int. J. Adv. Manuf. Technol. 2024, 130, 527–539. [Google Scholar] [CrossRef]
- Tamrin, K.F.; Nukman, Y.; Choudhury, I.A.; Shirley, S. Multiple-Objective Optimization in Precision Laser Cutting of Different Thermoplastics. Opt. Lasers Eng. 2015, 67, 57–65. [Google Scholar] [CrossRef]
- Kechagias, J.D.; Fountas, N.A.; Ninikas, K.; Vaxevanidis, N.M. Kerf Geometry and Surface Roughness Optimization in CO2 Laser Processing of FFF Plates Utilizing Neural Networks and Genetic Algorithms Approaches. J. Manuf. Mater. Process. 2023, 7, 77. [Google Scholar] [CrossRef]
- Moghadasi, K.; Tamrin, K. Multi-Pass Laser Cutting of Carbon/Kevlar Hybrid Composite: Prediction of Thermal Stress, Heat-Affected Zone, and Kerf Width by Thermo-Mechanical Modeling. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2020, 234, 1228–1241. [Google Scholar] [CrossRef]
- Der, O.; Başar, G.; Ordu, M. Statistical Investigation of the Effect of CO2 Laser Cutting Parameters on Kerf Width and Heat Affected Zone in Thermoplastic Materials. J. Mater. Mechatron. A 2023, 4, 459–474. [Google Scholar] [CrossRef]
- Basar, G.; Der, O. Multi-Objective Optimization of Process Parameters for Laser Cutting Polyethylene Using Fuzzy AHP-Based MCDM Methods. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2025. [Google Scholar] [CrossRef]
- Kechagias, J.D.; Vidakis, N.; Ninikas, K.; Petousis, M.; Vaxevanidis, N.M. Hybrid 3D Printing of Multifunctional Polylactic Acid/Carbon Black Nanocomposites Made with Material Extrusion and Post-Processed with CO2 Laser Cutting. Int. J. Adv. Manuf. Technol. 2023, 124, 1843–1861. [Google Scholar] [CrossRef]
- Mehrabi, O.; Malekshahi Beiranvand, Z.; Rasoul, F.A.; Moradi, M. Enhancing the Quality and Sustainability of Laser Cutting Processes in Laser-Assisted Manufacturing Using a Box–Behnken Design. Processes 2025, 13, 1279. [Google Scholar] [CrossRef]
- Kameyama, N.; Yoshida, H.; Fukagawa, H.; Yamada, K.; Fukuda, M. Thin-Film Processing of Polypropylene and Polystyrene Sheets by a Continuous Wave CO2 Laser with the Cu Cooling Base. Polymers 2021, 13, 1448. [Google Scholar] [CrossRef] [PubMed]
- Masoud, F.; Sapuan, S.M.; Ariffin, M.K.A.M.; Nukman, Y.; Bayraktar, E. Experimental Analysis of Heat-Affected Zone (HAZ) in Laser Cutting of Sugar Palm Fiber Reinforced Unsaturated Polyester Composites. Polymers 2021, 13, 706. [Google Scholar] [CrossRef] [PubMed]
- Jia, Y.; Wu, Z.; Xu, Y.; Ke, D.; Su, K. Long Short-Term Memory Projection Recurrent Neural Network Architectures for Piano’s Continuous Note Recognition. J. Rob. 2017, 2017, 2061827. [Google Scholar] [CrossRef]
- Kumar, P.; Suresh, S. Deep Learning Models for Recognizing the Simple Human Activities Using Smartphone Accelerometer Sensor. IETE J. Res. 2023, 69, 5148–5158. [Google Scholar] [CrossRef]
- Biswas, K.; Kumar, S.; Banerjee, S.; Pandey, A.K. Smooth Maximum Unit: Smooth Activation Function for Deep Networks Using Smoothing Maximum Technique. In Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 18–24 June 2022. [Google Scholar]
- Tanaka, M. Weighted Sigmoid Gate Unit for an Activation Function of Deep Neural Network. Pattern Recognit. Lett. 2020, 135, 354–359. [Google Scholar] [CrossRef]
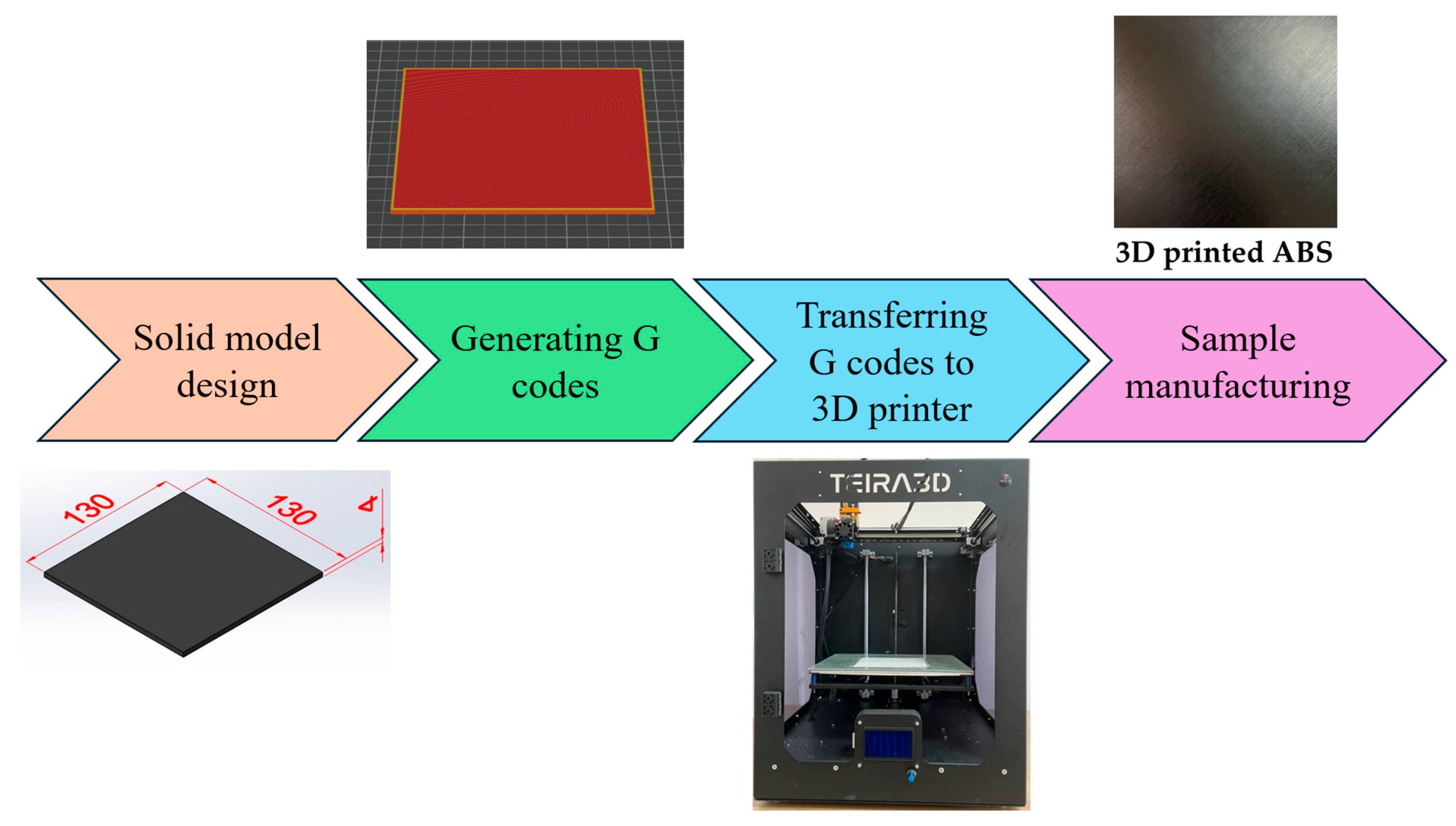


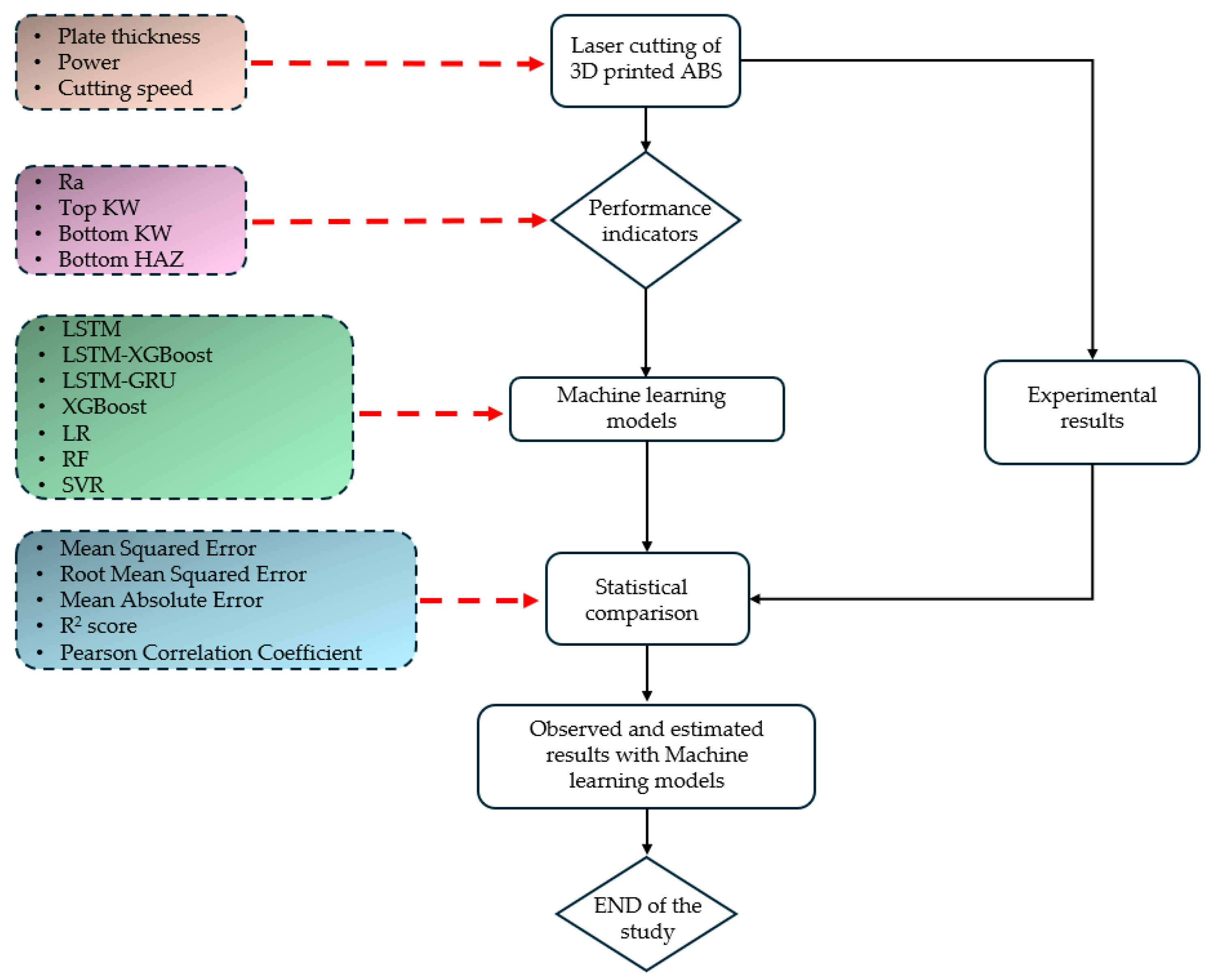








| Properties | Value |
|---|---|
| Manufacturer | Filameon |
| Filament | ABS |
| Print temperature (°C) | 230–260 |
| Diameter (mm) | 1.75 |
| Density (g/cm3) | 1.04 |
| Tensile strength (MPa) | 45 |
| Elongation (%) | 10 |
| Flexural strength (MPa) | 73 |
| Rockwell hardness (R scale) | 108 |
| Glass transition temperature (°C) | 85 |
| Melt flow index (220 °C/10 kg) | 23 |
| Parameter | Value |
|---|---|
| Printing orientation (Degree) | ±45 |
| Layer thickness (mm) | 0.24 |
| Bed temperature (°C) | 100 |
| Extrusion temperature (°C) | 250 |
| Infill pattern | line |
| Wall line count | 3 |
| Top solid layer | 5 |
| Bottom solid layer | 4 |
| Fill density (%) | 100 |
| Printing speed (mm/s) | 40 |
| Fan speed | 100 |
| Factors | Level | ||||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | |
| Plate thickness (mm) | 2 | 2.5 | 3 | 3.5 | 4 |
| Cutting speed (mm/s) | 3 | 6 | 9 | - | - |
| Power (W) | 87.5 | 92.5 | 97.5 | - | - |
| Source | DF | Seq SS | Adj SS | Adj MS | F-Value | p-Value | Contribution (%) |
|---|---|---|---|---|---|---|---|
| Ra (µm) | |||||||
| Plate thickness (mm) | 4 | 2.0414 | 2.0414 | 0.51035 | 26.37 | p < 0.001 | 12.25 |
| Power (W) | 2 | 2.4072 | 2.4072 | 1.20358 | 62.20 | p < 0.001 | 14.45 |
| Cutting speed (mm/s) | 2 | 11.5144 | 11.5144 | 5.75721 | 297.52 | p < 0.001 | 69.12 |
| Error | 36 | 0.6966 | 0.6966 | 0.01935 | 4.18 | ||
| Total | 44 | 16.6596 | 100 | ||||
| R2 = 95.82%, R2 (adj) = 94.89%, R2 (pred) = 93.47% | |||||||
| Top KW (mm) | |||||||
| Plate thickness (mm) | 4 | 0.020361 | 0.020361 | 0.005090 | 93.86 | p < 0.001 | 10.99 |
| Power (W) | 2 | 0.011908 | 0.011908 | 0.005954 | 109.78 | p < 0.001 | 6.43 |
| Cutting speed (mm/s) | 2 | 0.150989 | 0.150989 | 0.075495 | 1392.00 | p < 0.001 | 81.52 |
| Error | 36 | 0.001952 | 0.001952 | 0.000054 | 1.05 | ||
| Total | 44 | 0.185211 | 100 | ||||
| R2 = 98.95%, R2 (adj) = 98.71%, R2 (pred) = 98.35% | |||||||
| Bottom KW (mm) | |||||||
| Plate thickness (mm) | 4 | 0.025151 | 0.025151 | 0.006288 | 62.82 | p < 0.001 | 35.99 |
| Power (W) | 2 | 0.008082 | 0.008082 | 0.004041 | 40.37 | p < 0.001 | 11.56 |
| Cutting speed (mm/s) | 2 | 0.033052 | 0.033052 | 0.016526 | 165.10 | p < 0.001 | 47.29 |
| Error | 36 | 0.003604 | 0.003604 | 0.000100 | 5.16 | ||
| Total | 44 | 0.069888 | 100 | ||||
| R2 = 94.84%, R2 (adj) = 93.70%, R2 (pred) = 91.94% | |||||||
| Bottom HAZ (mm) | |||||||
| Plate thickness (mm) | 4 | 0.002301 | 0.002301 | 0.000575 | 33.33 | p < 0.001 | 3.51 |
| Power (W) | 2 | 0.002291 | 0.002291 | 0.001146 | 66.37 | p < 0.001 | 3.50 |
| Cutting speed (mm/s) | 2 | 0.060266 | 0.060266 | 0.030133 | 1745.89 | p < 0.001 | 92.04 |
| Error | 36 | 0.000621 | 0.000621 | 0.000017 | 0.95 | ||
| Total | 44 | 0.065480 | 100 | ||||
| R2 = 99.05%, R2 (adj) = 98.84%, R2 (pred) = 95.52% | |||||||
| Model | Architecture | Optimisation |
|---|---|---|
| LSTM | Single layer with 64 neurons | Adam (LR = 0.001) |
| LSTM-XGBoost (Hybrid) | LSTM (32 units) + Dense (16 units) | Adam (LR = 0.001) |
| LSTM-GRU (Hybrid) | LSTM (32 units) + GRU (32 units) | Adam (LR = 0.001) |
| XGBoost | 100 trees, learning_rate = 0.1 | Gradient Boosting |
| LR | Least squares method | – |
| RF | 100 decision trees | Bootstrap Aggregating (Bagging) |
| SVR | RBF kernel, C = 100, gamma = 0.1 | Kernel Trick |
| Feature | Model | MSE | MAE | RMSE | R2 | Pearson |
|---|---|---|---|---|---|---|
| Ra (µm) | LSTM | 0.052600 | 0.193600 | 0.229300 | 0.921000 | 0.960000 |
| LSTM-XGBoost | 0.044900 | 0.178900 | 0.211900 | 0.933000 | 0.966000 | |
| LSTM-GRU | 0.039100 | 0.167200 | 0.197700 | 0.942000 | 0.971000 | |
| XGBoost | 0.063200 | 0.213400 | 0.251400 | 0.902000 | 0.950000 | |
| LR | 0.096500 | 0.263800 | 0.310600 | 0.850000 | 0.922000 | |
| RF | 0.048300 | 0.185500 | 0.219800 | 0.928000 | 0.963000 | |
| SVR | 0.045800 | 0.180300 | 0.214000 | 0.931000 | 0.965000 | |
| Top KW (mm) | LSTM | 0.000380 | 0.015600 | 0.019500 | 0.986000 | 0.993000 |
| LSTM-XGBoost | 0.000450 | 0.017200 | 0.021200 | 0.983000 | 0.992000 | |
| LSTM-GRU | 0.000420 | 0.016500 | 0.020500 | 0.984000 | 0.992000 | |
| XGBoost | 0.000340 | 0.014800 | 0.018400 | 0.987000 | 0.994000 | |
| LR | 0.001100 | 0.027600 | 0.033200 | 0.958000 | 0.979000 | |
| RF | 0.000390 | 0.016000 | 0.019700 | 0.985000 | 0.993000 | |
| SVR | 0.000470 | 0.017800 | 0.021700 | 0.982000 | 0.991000 | |
| Bottom KW (mm) | LSTM | 0.000193 | 0.011845 | 0.013899 | 0.938421 | 0.968724 |
| LSTM-XGBoost | 0.000185 | 0.011623 | 0.013607 | 0.940982 | 0.970045 | |
| LSTM-GRU | 0.000179 | 0.011412 | 0.013384 | 0.943012 | 0.971096 | |
| XGBoost | 0.000214 | 0.012462 | 0.014632 | 0.931845 | 0.965308 | |
| LR | 0.000287 | 0.014438 | 0.016941 | 0.908523 | 0.953158 | |
| RF | 0.000201 | 0.012036 | 0.014178 | 0.935672 | 0.967302 | |
| SVR | 0.000183 | 0.011539 | 0.013527 | 0.942157 | 0.970651 | |
| Bottom HAZ (mm) | LSTM | 0.000267 | 0.013700 | 0.016300 | 0.928000 | 0.963000 |
| LSTM-XGBoost | 0.000216 | 0.012300 | 0.014700 | 0.942000 | 0.971000 | |
| LSTM-GRU | 0.000198 | 0.011700 | 0.014100 | 0.947000 | 0.973000 | |
| XGBoost | 0.000289 | 0.014500 | 0.017000 | 0.922000 | 0.960000 | |
| LR | 0.000912 | 0.025800 | 0.030200 | 0.753000 | 0.868000 | |
| RF | 0.000242 | 0.013000 | 0.015600 | 0.935000 | 0.967000 | |
| SVR | 0.000219 | 0.012400 | 0.014800 | 0.941000 | 0.970000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Basar, G. Experimental Evaluation and Machine Learning-Based Prediction of Laser Cutting Quality in FFF-Printed ABS Thermoplastics. Polymers 2025, 17, 1728. https://doi.org/10.3390/polym17131728
Basar G. Experimental Evaluation and Machine Learning-Based Prediction of Laser Cutting Quality in FFF-Printed ABS Thermoplastics. Polymers. 2025; 17(13):1728. https://doi.org/10.3390/polym17131728
Chicago/Turabian StyleBasar, Gokhan. 2025. "Experimental Evaluation and Machine Learning-Based Prediction of Laser Cutting Quality in FFF-Printed ABS Thermoplastics" Polymers 17, no. 13: 1728. https://doi.org/10.3390/polym17131728
APA StyleBasar, G. (2025). Experimental Evaluation and Machine Learning-Based Prediction of Laser Cutting Quality in FFF-Printed ABS Thermoplastics. Polymers, 17(13), 1728. https://doi.org/10.3390/polym17131728







