Recent Progress of Artificial Intelligence Application in Polymer Materials
Abstract
1. Introduction
2. The Application of AI in Polymer Materials
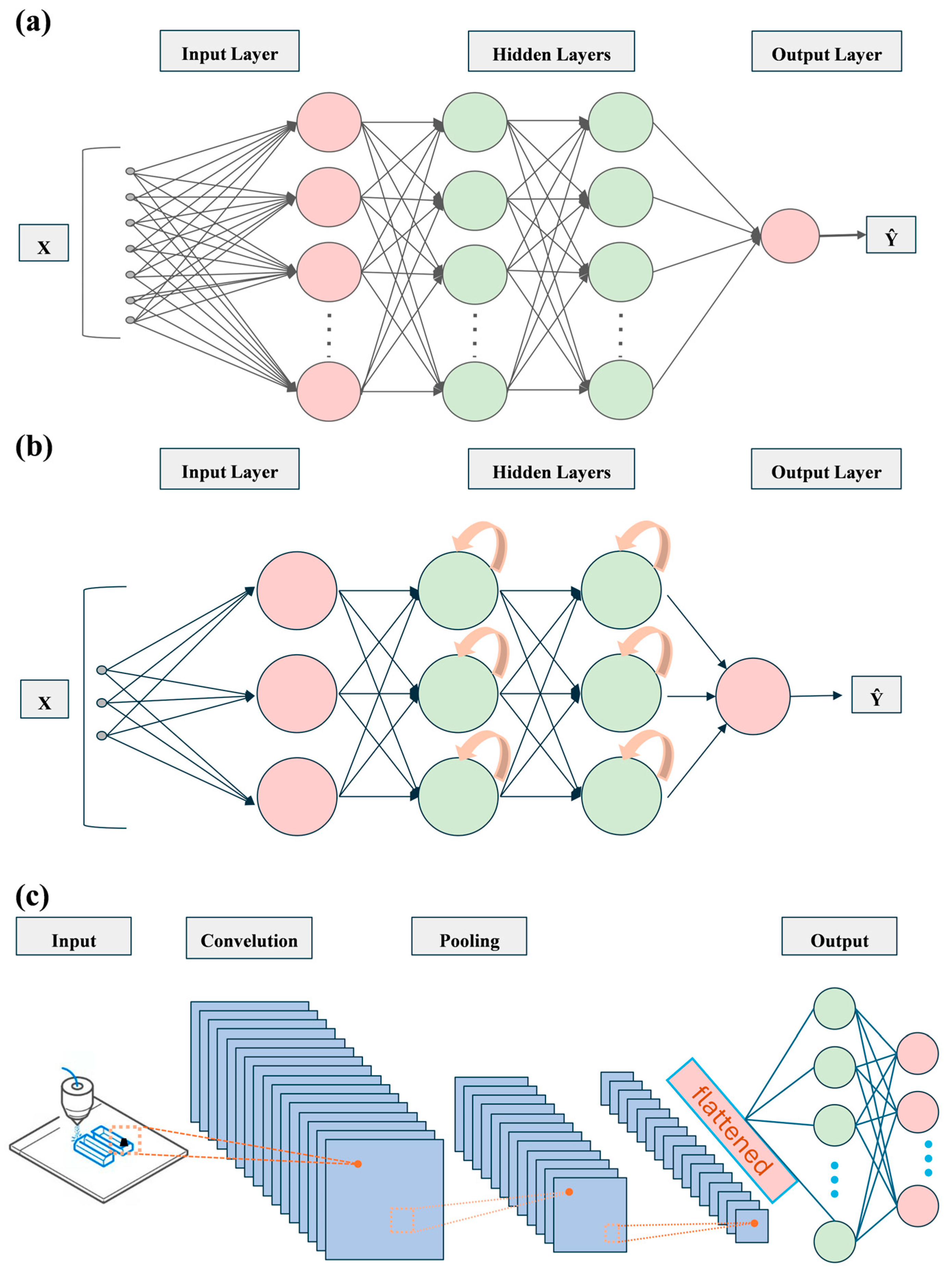
2.1. Foundations and Applications of Machine Learning in Materials Science
2.2. The Exploration of Property and Structure Relationship for Polymer Materials
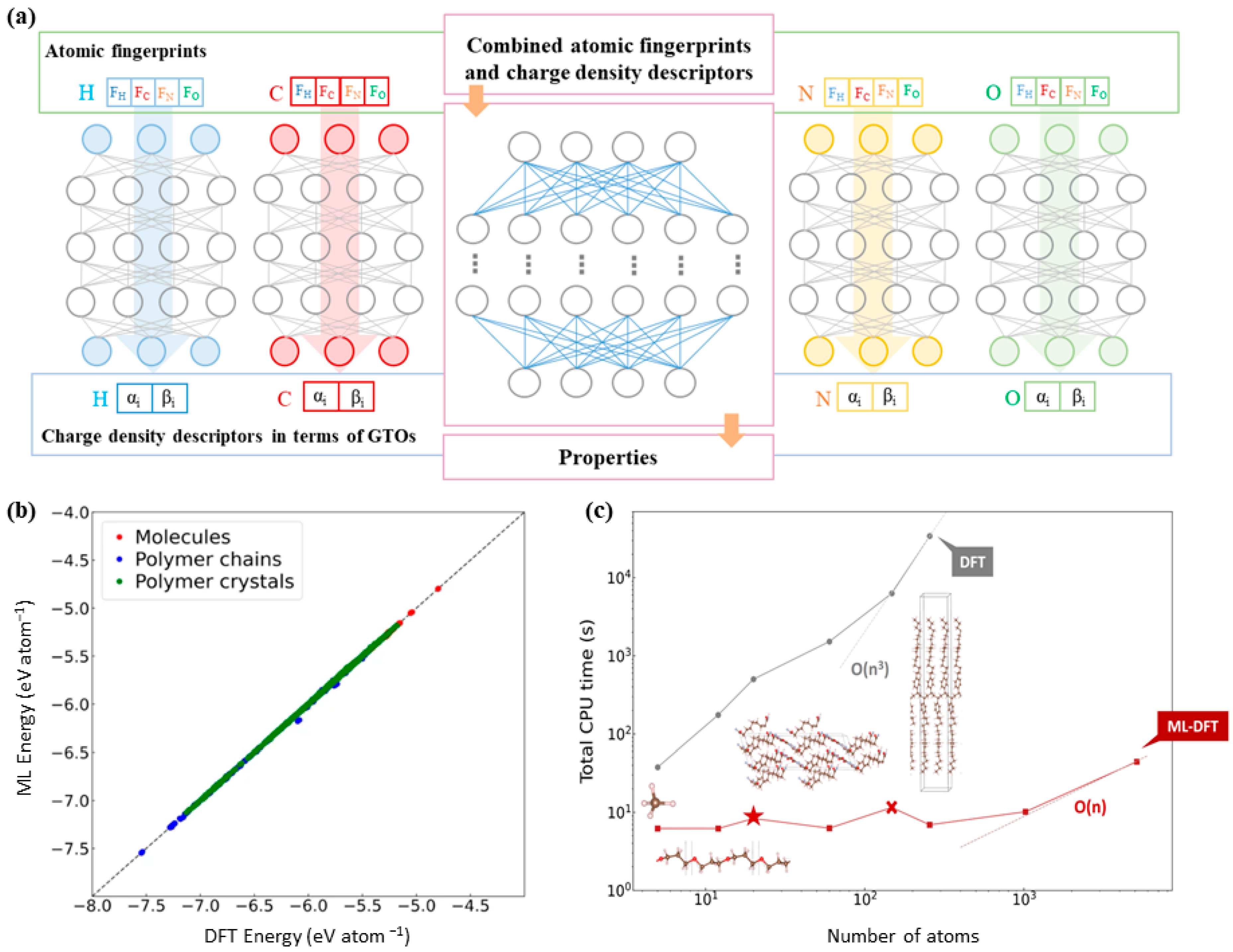
2.2.1. Machine Learning Interatomic Potentials
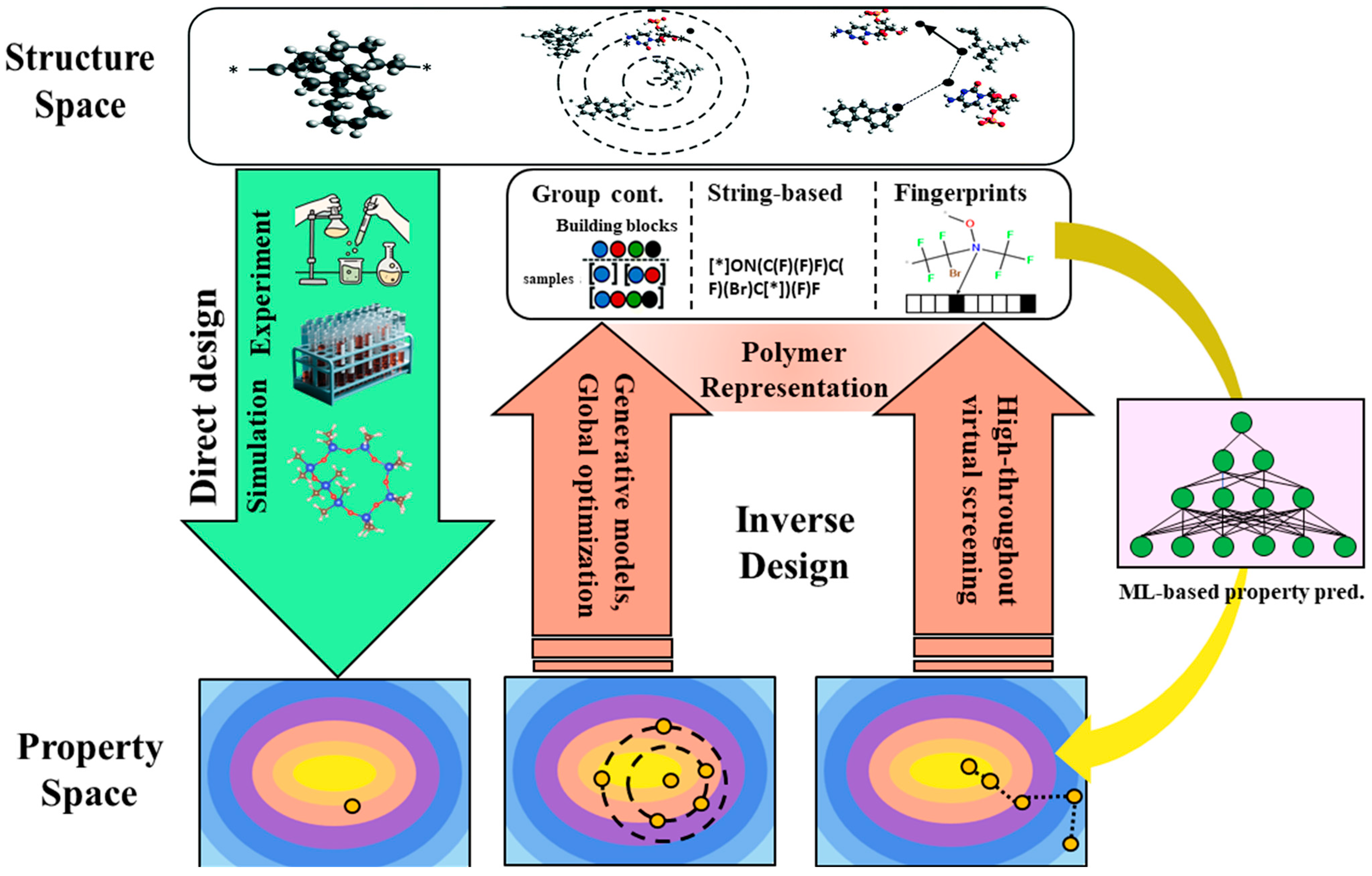
2.2.2. Structure–Property Modeling and Inverse Design of Polymers
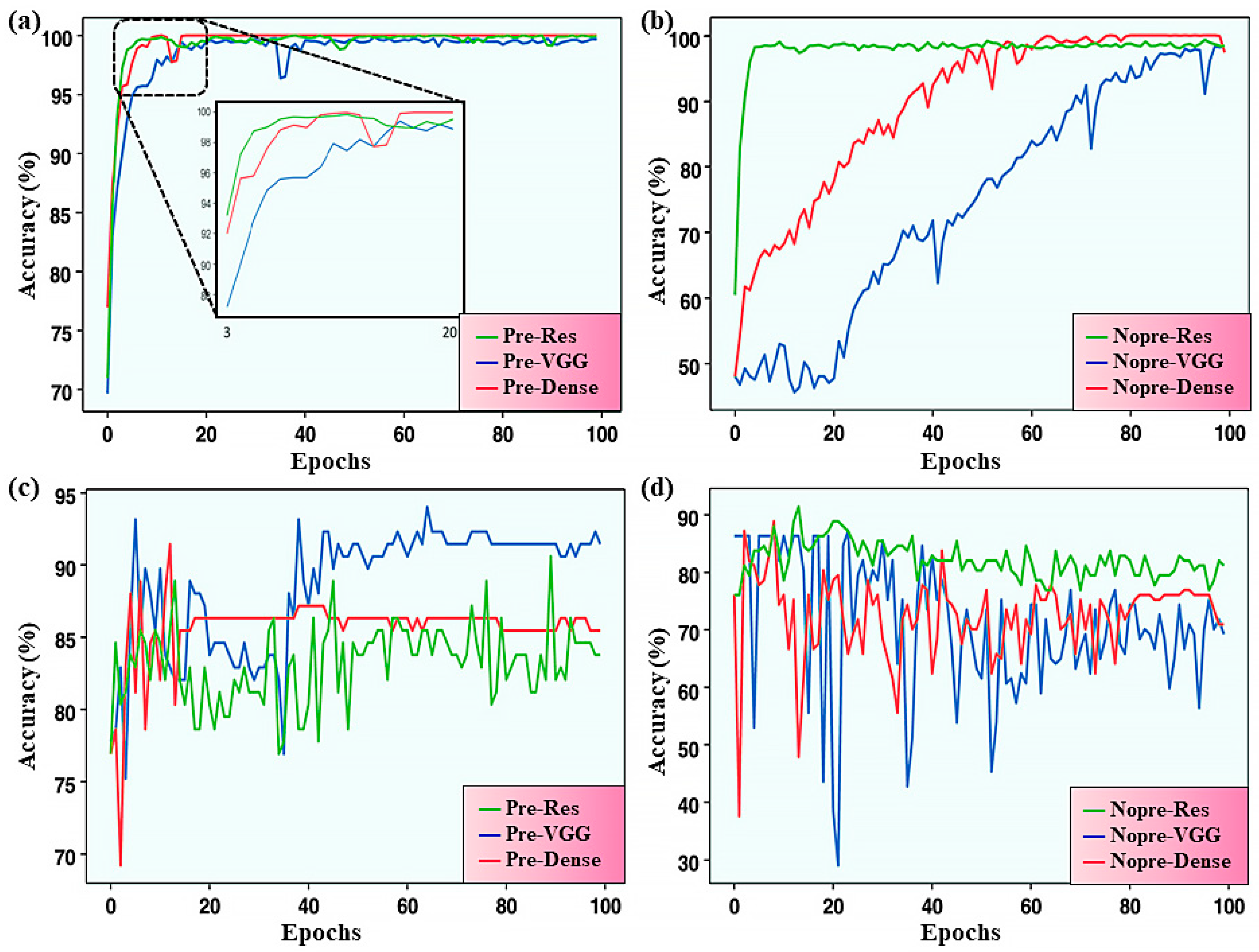
2.2.3. Properties Prediction Model
2.3. Polymer Process Optimization
2.3.1. Parameter Optimization of the Process
2.3.2. Process Iteration and Experimental Closed-Loop Systems
3. Challenges and Feasible Solutions
3.1. Databases
3.2. Descriptors
3.3. Task-Orientated Algorithm
4. Summary and Prospect
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Nandi, A.K.; Chatterjee, D.P. Hybrid Polymer Gels for Energy Applications. J. Mater. Chem. A 2023, 11, 12593–12642. [Google Scholar] [CrossRef]
- Alam, A.U.; Qin, Y.; Nambiar, S.; Yeow, J.T.W.; Howlader, M.M.R.; Hu, N.-X.; Deen, M.J. Polymers and Organic Materials-Based pH Sensors for Healthcare Applications. Prog. Mater. Sci. 2018, 96, 174–216. [Google Scholar] [CrossRef]
- Liles, D.; Lin, F. Silicone Elastomeric Particles in Skin Care Applications. ACS Symp. Ser. 2010, 1053, 207–219. [Google Scholar] [CrossRef]
- Sionkowska, A. Current Research on the Blends of Natural and Synthetic Polymers as New Biomaterials: Review. Prog. Polym. Sci. 2011, 36, 1254–1276. [Google Scholar] [CrossRef]
- Pfleger, J.; Cimrová, V. Polymers for Electronics and Photonics: Science for Applications. Chem. Pap. 2018, 72, 1561–1562. [Google Scholar] [CrossRef]
- Huan, T.D.; Boggs, S.; Teyssedre, G.; Laurent, C.; Cakmak, M.; Kumar, S.; Ramprasad, R. Advanced Polymeric Dielectrics for High Energy Density Applications. Prog. Mater. Sci. 2016, 83, 236–269. [Google Scholar] [CrossRef]
- Li, J.; Liu, X.; Feng, Y.; Yin, J. Recent Progress in Polymer/Two-Dimensional Nanosheets Composites with Novel Performances. Prog. Polym. Sci. 2022, 126, 101505. [Google Scholar] [CrossRef]
- Zhang, G.; Cheng, X.; Wang, Y.; Zhang, W. Supramolecular Chiral Polymeric Aggregates: Construction and Applications. Aggregate 2023, 4, e262. [Google Scholar] [CrossRef]
- Geyer, R.; Jambeck, J.R.; Law, K.L. Production, Use, and Fate of All Plastics Ever Made. Sci. Adv. 2017, 3, e1700782. [Google Scholar] [CrossRef] [PubMed]
- Jayaraman, A.; Klok, H.-A. ACS Polymers Au’s Grand Challenges in Polymer Science. ACS Polym. Au 2023, 3, 1–4. [Google Scholar] [CrossRef]
- Kumar, S.K.; Krishnamoorti, R. Nanocomposites: Structure, Phase Behavior, and Properties. Annu. Rev. Chem. Biomol. Eng. 2010, 1, 37–58. [Google Scholar] [CrossRef]
- Sarkar, B.; Alexandridis, P. Block Copolymer–Nanoparticle Composites: Structure, Functional Properties, and Processing. Prog. Polym. Sci. 2015, 40, 33–62. [Google Scholar] [CrossRef]
- Correa-Baena, J.-P.; Hippalgaonkar, K.; van Duren, J.; Jaffer, S.; Chandrasekhar, V.R.; Stevanovic, V.; Wadia, C.; Guha, S.; Buonassisi, T. Accelerating Materials Development via Automation, Machine Learning, and High-Performance Computing. Joule 2018, 2, 1410–1420. [Google Scholar] [CrossRef]
- Sha, W.; Guo, Y.; Yuan, Q.; Tang, S.; Zhang, X.; Lu, S.; Guo, X.; Cao, Y.-C.; Cheng, S. Artificial Intelligence to Power the Future of Materials Science and Engineering. Adv. Intell. Syst. 2020, 2, 1900143. [Google Scholar] [CrossRef]
- Papadimitriou, I.; Gialampoukidis, I.; Vrochidis, S.; Kompatsiaris, I. AI Methods in Materials Design, Discovery and Manufacturing: A Review. Comput. Mater. Sci. 2024, 235, 112793. [Google Scholar] [CrossRef]
- Kalidindi, S.R. Feature Engineering of Material Structure for AI-Based Materials Knowledge Systems. J. Appl. Phys. 2020, 128, 041103. [Google Scholar] [CrossRef]
- Hattrick-Simpers, J.R.; Choudhary, K.; Corgnale, C. A Simple Constrained Machine Learning Model for Predicting High-Pressure-Hydrogen-Compressor Materials. Mol. Syst. Des. Eng. 2018, 3, 509–517. [Google Scholar] [CrossRef]
- Choudhary, K.; Bercx, M.; Jiang, J.; Pachter, R.; Lamoen, D.; Tavazza, F. Accelerated Discovery of Efficient Solar Cell Materials Using Quantum and Machine-Learning Methods. Chem. Mater. 2019, 31, 5900–5908. [Google Scholar] [CrossRef]
- Chun, S.; Roy, S.; Nguyen, Y.T.; Choi, J.B.; Udaykumar, H.S.; Baek, S.S. Deep Learning for Synthetic Microstructure Generation in a Materials-by-Design Framework for Heterogeneous Energetic Materials. Sci. Rep. 2020, 10, 13307. [Google Scholar] [CrossRef]
- Jiao, P.; Alavi, A.H. Artificial Intelligence-Enabled Smart Mechanical Metamaterials: Advent and Future Trends. Int. Mater. Rev. 2021, 66, 365–393. [Google Scholar] [CrossRef]
- Guo, K.; Yang, Z.; Yu, C.-H.; Buehler, M.J. Artificial Intelligence and Machine Learning in Design of Mechanical Materials. Mater. Horiz. 2021, 8, 1153–1172. [Google Scholar] [CrossRef]
- Gu, G.X.; Chen, C.-T.; Richmond, D.J.; Buehler, M.J. Bioinspired Hierarchical Composite Design Using Machine Learning: Simulation, Additive Manufacturing, and Experiment. Mater. Horiz. 2018, 5, 939–945. [Google Scholar] [CrossRef]
- Zhang, G.; Ali, Z.H.; Aldlemy, M.S.; Mussa, M.H.; Salih, S.Q.; Hameed, M.M.; Al-Khafaji, Z.S.; Yaseen, Z.M. Reinforced Concrete Deep Beam Shear Strength Capacity Modelling Using an Integrative Bio-Inspired Algorithm with an Artificial Intelligence Model. Eng. Comput. 2022, 38, 15–28. [Google Scholar] [CrossRef]
- Shen, S.C.; Buehler, M.J. Nature-Inspired Architected Materials Using Unsupervised Deep Learning. Commun. Eng. 2022, 1, 37. [Google Scholar] [CrossRef]
- Ishiwatari, Y.; Yokoyama, T.; Kojima, T.; Banno, T.; Arai, N. Machine Learning Prediction of Self-Assembly and Analysis of Molecular Structure Dependence on the Critical Packing Parameter. Mol. Syst. Des. Eng. 2024, 9, 20–28. [Google Scholar] [CrossRef]
- Wei, J.; Chu, X.; Sun, X.-Y.; Xu, K.; Deng, H.-X.; Chen, J.; Wei, Z.; Lei, M. Machine Learning in Materials Science. InfoMat 2019, 1, 338–358. [Google Scholar] [CrossRef]
- Zhou, T.; Song, Z.; Sundmacher, K. Big Data Creates New Opportunities for Materials Research: A Review on Methods and Applications of Machine Learning for Materials Design. Engineering 2019, 5, 1017–1026. [Google Scholar] [CrossRef]
- Goswami, L.; Deka, M.K.; Roy, M. Artificial Intelligence in Material Engineering: A Review on Applications of Artificial Intelligence in Material Engineering. Adv. Eng. Mater. 2023, 25, 2300104. [Google Scholar] [CrossRef]
- Yu, C.-H.; Qin, Z.; Buehler, M.J. Artificial Intelligence Design Algorithm for Nanocomposites Optimized for Shear Crack Resistance. Nano Futures 2019, 3, 035001. [Google Scholar] [CrossRef]
- Gu, G.H.; Noh, J.; Kim, I.; Jung, Y. Machine Learning for Renewable Energy Materials. J. Mater. Chem. A 2019, 7, 17096–17117. [Google Scholar] [CrossRef]
- Yang, K.; Xu, X.; Yang, B.; Cook, B.; Ramos, H.; Krishnan, N.M.A.; Smedskjaer, M.M.; Hoover, C.; Bauchy, M. Predicting the Young’s Modulus of Silicate Glasses Using High-Throughput Molecular Dynamics Simulations and Machine Learning. Sci. Rep. 2019, 9, 8739. [Google Scholar] [CrossRef]
- Venkatraman, V.; Evjen, S.; Knuutila, H.K.; Fiksdahl, A.; Alsberg, B.K. Predicting Ionic Liquid Melting Points Using Machine Learning. J. Mol. Liq. 2018, 264, 318–326. [Google Scholar] [CrossRef]
- Qu, N.; Liu, Y.; Liao, M.; Lai, Z.; Zhou, F.; Cui, P.; Han, T.; Yang, D.; Zhu, J. Ultra-High Temperature Ceramics Melting Temperature Prediction via Machine Learning. Ceram. Int. 2019, 45, 18551–18555. [Google Scholar] [CrossRef]
- Chen, L.; Tran, H.; Batra, R.; Kim, C.; Ramprasad, R. Machine Learning Models for the Lattice Thermal Conductivity Prediction of Inorganic Materials. Comput. Mater. Sci. 2019, 170, 109155. [Google Scholar] [CrossRef]
- Luo, Y.; Li, M.; Yuan, H.; Liu, H.; Fang, Y. Predicting Lattice Thermal Conductivity via Machine Learning: A Mini Review. NPJ Comput. Mater. 2023, 9, 4. [Google Scholar] [CrossRef]
- Chen, Z.; Andrejevic, N.; Drucker, N.C.; Nguyen, T.; Xian, R.P.; Smidt, T.; Wang, Y.; Ernstorfer, R.; Tennant, D.A.; Chan, M.; et al. Machine Learning on Neutron and X-Ray Scattering and Spectroscopies. Chem. Phys. Rev. 2021, 2, 031301. [Google Scholar] [CrossRef]
- Anker, A.S.; Butler, K.T.; Selvan, R.; Jensen, K.M.Ø. Machine Learning for Analysis of Experimental Scattering and Spectroscopy Data in Materials Chemistry. Chem. Sci. 2023, 14, 14003–14019. [Google Scholar] [CrossRef]
- Deagen, M.E.; Walsh, D.J.; Audus, D.J.; Kroenlein, K.; de Pablo, J.J.; Aou, K.; Chard, K.; Jensen, K.F.; Olsen, B.D. Networks and Interfaces as Catalysts for Polymer Materials Innovation. Cell Rep. Phys. Sci. 2022, 3, 101126. [Google Scholar] [CrossRef]
- Lutz, J.-F.; Lehn, J.-M.; Meijer, E.W.; Matyjaszewski, K. From Precision Polymers to Complex Materials and Systems. Nat. Rev. Mater. 2016, 1, 16024. [Google Scholar] [CrossRef]
- Meijer, H.E.H.; Govaert, L.E. Mechanical Performance of Polymer Systems: The Relation between Structure and Properties. Prog. Polym. Sci. 2005, 30, 915–938. [Google Scholar] [CrossRef]
- Gurnani, R.; Kuenneth, C.; Toland, A.; Ramprasad, R. Polymer Informatics at Scale with Multitask Graph Neural Networks. Chem. Mater. 2023, 35, 1560–1567. [Google Scholar] [CrossRef] [PubMed]
- Patra, T.K. Data-Driven Methods for Accelerating Polymer Design. ACS Polym. Au 2022, 2, 8–26. [Google Scholar] [CrossRef]
- Tran, H.; Gurnani, R.; Kim, C.; Pilania, G.; Kwon, H.-K.; Lively, R.P.; Ramprasad, R. Design of Functional and Sustainable Polymers Assisted by Artificial Intelligence. Nat. Rev. Mater. 2024, 9, 866–886. [Google Scholar] [CrossRef]
- Egrioglu, E.; Bas, E. A New Deep Neural Network for Forecasting: Deep Dendritic Artificial Neural Network. Artif. Intell. Rev. 2024, 57, 171. [Google Scholar] [CrossRef]
- Zhou, J.; Cui, G.; Hu, S.; Zhang, Z.; Yang, C.; Liu, Z.; Wang, L.; Li, C.; Sun, M. Graph Neural Networks: A Review of Methods and Applications. AI Open 2020, 1, 57–81. [Google Scholar] [CrossRef]
- Yoo, H.; Byun, H.E.; Han, D.; Lee, J.H. Reinforcement Learning for Batch Process Control: Review and Perspectives. Annu. Rev. Control 2021, 52, 108–119. [Google Scholar] [CrossRef]
- Martin, T.B.; Audus, D.J. Emerging Trends in Machine Learning: A Polymer Perspective. ACS Polym. Au 2023, 3, 239–258. [Google Scholar] [CrossRef]
- Liu, N.; Jafarzadeh, S.; Lattimer, B.Y.; Ni, S.; Lua, J.; Yu, Y. Large Language Models, Physics-Based Modeling, Experimental Measurements: The Trinity of Data-Scarce Learning of Polymer Properties. arXiv 2024, arXiv:2407.02770. [Google Scholar]
- Schmid, F. Understanding and Modeling Polymers: The Challenge of Multiple Scales. ACS Polym. Au 2023, 3, 28–58. [Google Scholar] [CrossRef]
- Xu, B.; Yang, G. Interpretability Research of Deep Learning: A Literature Survey. Inf. Fusion. 2025, 115, 102721. [Google Scholar] [CrossRef]
- Pugliese, R.; Regondi, S.; Marini, R. Machine Learning-Based Approach: Global Trends, Research Directions, and Regulatory Standpoints. Data Sci. Manag. 2021, 4, 19–29. [Google Scholar] [CrossRef]
- Unke, O.T.; Chmiela, S.; Sauceda, H.E.; Gastegger, M.; Poltavsky, I.; Schütt, K.T.; Tkatchenko, A.; Müller, K.-R. Machine Learning Force Fields. Chem. Rev. 2021, 121, 10142–10186. [Google Scholar] [CrossRef] [PubMed]
- Xu, P.; Chen, H.; Li, M.; Lu, W. New Opportunity: Machine Learning for Polymer Materials Design and Discovery. Adv. Theory Simul. 2022, 5, 2100565. [Google Scholar] [CrossRef]
- Badini, S.; Regondi, S.; Pugliese, R. Unleashing the Power of Artificial Intelligence in Materials Design. Materials 2023, 16, 5927. [Google Scholar] [CrossRef]
- Jain, A.; Ong, S.P.; Hautier, G.; Chen, W.; Richards, W.D.; Dacek, S.; Cholia, S.; Gunter, D.; Skinner, D.; Ceder, G.; et al. Commentary: The Materials Project: A Materials Genome Approach to Accelerating Materials Innovation. APL Mater. 2013, 1, 011002. [Google Scholar] [CrossRef]
- Curtarolo, S.; Setyawan, W.; Wang, S.; Xue, J.; Yang, K.; Taylor, R.H.; Nelson, L.J.; Hart, G.L.W.; Sanvito, S.; Buongiorno-Nardelli, M.; et al. AFLOWLIB.ORG: A Distributed Materials Properties Repository from High-Throughput Ab. Initio Calculations. Comput. Mater. Sci. 2012, 58, 227–235. [Google Scholar] [CrossRef]
- Kirklin, S.; Saal, J.E.; Meredig, B.; Thompson, A.; Doak, J.W.; Aykol, M.; Rühl, S.; Wolverton, C. The Open Quantum Materials Database (OQMD): Assessing the Accuracy of DFT Formation Energies. NPJ Comput. Mater. 2015, 1, 15010. [Google Scholar] [CrossRef]
- Chanussot, L.; Das, A.; Goyal, S.; Lavril, T.; Shuaibi, M.; Riviere, M.; Tran, K.; Heras-Domingo, J.; Ho, C.; Hu, W.; et al. Open Catalyst 2020 (OC20) Dataset and Community Challenges. ACS Catal. 2021, 11, 6059–6072. [Google Scholar] [CrossRef]
- Otsuka, S.; Kuwajima, I.; Hosoya, J.; Xu, Y.; Yamazaki, M. PoLyInfo: Polymer Database for Polymeric Materials Design. In Proceedings of the 2011 International Conference on Emerging Intelligent Data and Web Technologies, Tirana, Albania, 7–9 September 2011; pp. 22–29. [Google Scholar] [CrossRef]
- Graziano, G. Fingerprints of Molecular Reactivity. Nat. Rev. Chem. 2020, 4, 227. [Google Scholar] [CrossRef]
- Zhao, Y.; Mulder, R.J.; Houshyar, S.; Le, T.C. A Review on the Application of Molecular Descriptors and Machine Learning in Polymer Design. Polym. Chem. 2023, 14, 3325–3346. [Google Scholar] [CrossRef]
- Lee, D.E.; Song, S.-O.; Yoon, E.S. Weighted Support Vector Machine for Quality Estimation in Polymerization Processes. Korean J. Chem. Eng. 2004, 21, 1103–1107. [Google Scholar] [CrossRef]
- Malashin, I.; Tynchenko, V.; Gantimurov, A.; Nelyub, V.; Borodulin, A. Support Vector Machines in Polymer Science: A Review. Polymers 2025, 17, 491. [Google Scholar] [CrossRef]
- Savage, N. Neural Net Worth. Commun. ACM 2019, 62, 10–12. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Orsenigo, C.; Vercellis, C. Kernel Ridge Regression for Out-of-Sample Mapping in Supervised Manifold Learning. Expert. Syst. Appl. 2012, 39, 7757–7762. [Google Scholar] [CrossRef]
- Wang, X.; Huang, F.; Cheng, Y. Computational Performance Optimization of Support Vector Machine Based on Support Vectors. Neurocomputing 2016, 211, 66–71. [Google Scholar] [CrossRef]
- Tolles, J.; Meurer, W.J. Logistic Regression: Relating Patient Characteristics to Outcomes. JAMA 2016, 316, 533–534. [Google Scholar] [CrossRef]
- Schulz, E.; Speekenbrink, M.; Krause, A. A Tutorial on Gaussian Process Regression: Modelling, Exploring, and Exploiting Functions. J. Math. Psychol. 2018, 85, 1–16. [Google Scholar] [CrossRef]
- Jakob, P.; Madan, M.; Schmid-Schirling, T.; Valada, A. Multi-Perspective Anomaly Detection. Sensors 2021, 21, 5311. [Google Scholar] [CrossRef] [PubMed]
- Ertefaie, A.; McKay, J.R.; Oslin, D.; Strawderman, R.L. Robust Q-Learning. J. Am. Stat. Assoc. 2021, 116, 368–381. [Google Scholar] [CrossRef]
- Rodemann, J.; Augustin, T. Imprecise Bayesian Optimization. Knowl.-Based Syst. 2024, 300, 112186. [Google Scholar] [CrossRef]
- Yu, C.; Yao, W.; Bai, X. Robust Linear Regression: A Review and Comparison. arXiv 2014. [Google Scholar] [CrossRef]
- He, Z.; Wu, Z.; Xu, G.; Liu, Y.; Zou, Q. Decision Tree for Sequences. IEEE Trans. Knowl. Data Eng. 2023, 35, 251–263. [Google Scholar] [CrossRef]
- Safavian, S.R.; Landgrebe, D. A Survey of Decision Tree Classifier Methodology. IEEE Trans. Syst. Man. Cybern. 1991, 21, 660–674. [Google Scholar] [CrossRef]
- Valkenborg, D.; Rousseau, A.-J.; Geubbelmans, M.; Burzykowski, T. Support Vector Machines. Am. J. Orthod. Dentofac. Orthop. 2023, 164, 754–757. [Google Scholar] [CrossRef]
- Zhao, Z.; Fitzsimons, J.K.; Fitzsimons, J.F. Quantum-Assisted Gaussian Process Regression. Phys. Rev. A 2019, 99, 052331. [Google Scholar] [CrossRef]
- Boloix-Tortosa, R.; Murillo-Fuentes, J.J.; Payán-Somet, F.J.; Pérez-Cruz, F. Complex Gaussian Processes for Regression. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 5499–5511. [Google Scholar] [CrossRef]
- Aldana-Bobadila, E.; Kuri-Morales, A.; Lopez-Arevalo, I.; Rios-Alvarado, A.B. An Unsupervised Learning Approach for Multilayer Perceptron Networks. Soft Comput. 2019, 23, 11001–11013. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar] [CrossRef]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.-Y. LightGBM: A Highly Efficient Gradient Boosting Decision Tree. In Advances in Neural Information Processing Systems; Curran Associates, Inc.: Red Hook, NY, USA, 2017; Volume 30. [Google Scholar]
- Hancock, J.T.; Khoshgoftaar, T.M. CatBoost for Big Data: An Interdisciplinary Review. J. Big Data 2020, 7, 94. [Google Scholar] [CrossRef]
- Arik, S.Ö.; Pfister, T. TabNet: Attentive Interpretable Tabular Learning. Proc. AAAI Conf. Artif. Intell. 2021, 35, 6679–6687. [Google Scholar] [CrossRef]
- Tan, L.; Wu, S.; Zhou, W.; Huang, X. Weighted Neural Tangent Kernel: A Generalized and Improved Network-Induced Kernel. Mach. Learn. 2023, 112, 2871–2901. [Google Scholar] [CrossRef]
- Yoder, J.; and Priebe, C.E. Semi-Supervised k-Means++. J. Stat. Comput. Simul. 2017, 87, 2597–2608. [Google Scholar] [CrossRef]
- Cohen-addad, V.; Kanade, V.; Mallmann-trenn, F.; Mathieu, C. Hierarchical Clustering: Objective Functions and Algorithms. J. ACM 2019, 66, 1–42. [Google Scholar] [CrossRef]
- Greenacre, M.; Groenen, P.J.F.; Hastie, T.; D’Enza, A.I.; Markos, A.; Tuzhilina, E. Principal Component Analysis. Nat. Rev. Methods Primers 2022, 2, 100. [Google Scholar] [CrossRef]
- Sainburg, T.; McInnes, L.; Gentner, T.Q. Parametric UMAP Embeddings for Representation and Semisupervised Learning. Neural Comput. 2021, 33, 2881–2907. [Google Scholar] [CrossRef]
- Wei, X.; Zhang, Z.; Huang, H.; Zhou, Y. An Overview on Deep Clustering. Neurocomputing 2024, 590, 127761. [Google Scholar] [CrossRef]
- Geadah, V.; Barello, G.; Greenidge, D.; Charles, A.S.; Pillow, J.W. Sparse-Coding Variational Autoencoders. Neural Comput. 2024, 36, 2571–2601. [Google Scholar] [CrossRef]
- Joo, W.; Lee, W.; Park, S.; Moon, I.-C. Dirichlet Variational Autoencoder. Pattern Recognit. 2020, 107, 107514. [Google Scholar] [CrossRef]
- Wang, J.; Yang, J.; He, J.; Peng, D. Multi-Augmentation-Based Contrastive Learning for Semi-Supervised Learning. Algorithms 2024, 17, 91. [Google Scholar] [CrossRef]
- He, K.; Fan, H.; Wu, Y.; Xie, S.; Girshick, R. Momentum Contrast for Unsupervised Visual Representation Learning. arXiv 2020, arXiv:1911.05722. [Google Scholar]
- Amini, M.-R.; Feofanov, V.; Pauletto, L.; Hadjadj, L.; Devijver, É.; Maximov, Y. Self-Training: A Survey. Neurocomputing 2025, 616, 128904. [Google Scholar] [CrossRef]
- Ning, X.; Wang, X.; Xu, S.; Cai, W.; Zhang, L.; Yu, L.; Li, W. A Review of Research on Co-Training. Concurr. Comput. Pract. Exp. 2023, 35, e6276. [Google Scholar] [CrossRef]
- Zhou, D.; Bousquet, O.; Lal, T.; Weston, J.; Schölkopf, B. Learning with Local and Global Consistency. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2003; Volume 16. [Google Scholar]
- Sohn, K.; Berthelot, D.; Li, C.-L.; Zhang, Z.; Carlini, N.; Cubuk, E.D.; Kurakin, A.; Zhang, H.; Raffel, C. FixMatch: Simplifying Semi-Supervised Learning with Consistency and Confidence. arXiv 2020, arXiv:2001.07685. [Google Scholar]
- Berthelot, D.; Carlini, N.; Goodfellow, I.; Papernot, N.; Oliver, A.; Raffel, C. MixMatch: A Holistic Approach to Semi-Supervised Learning. arXiv 2019, arXiv:1905.02249. [Google Scholar]
- Lee, D.H. Pseudo-label: The simple and efficient semi-supervised learning method for deep neural networks. Workshop Chall. Represent. Learn. 2013, 3, 896. [Google Scholar]
- Ratner, A.; Bach, S.H.; Ehrenberg, H.; Fries, J.; Wu, S.; Ré, C. Snorkel: Rapid Training Data Creation with Weak Supervision. Proc. VLDB Endow. 2017, 11, 269–282. [Google Scholar] [CrossRef] [PubMed]
- Fan, Y.; Kukleva, A.; Schiele, B. Revisiting Consistency Regularization for Semi-Supervised Learning. arXiv 2021, arXiv:2112.05825. [Google Scholar]
- Derry, A.; Krzywinski, M.; Altman, N. Convolutional Neural Networks. Nat. Methods 2023, 20, 1269–1270. [Google Scholar] [CrossRef]
- Zaremba, W.; Sutskever, I.; Vinyals, O. Recurrent Neural Network Regularization. arXiv 2015, arXiv:1409.2329. [Google Scholar]
- Van Houdt, G.; Mosquera, C.; Nápoles, G. A Review on the Long Short-Term Memory Model. Artif. Intell. Rev. 2020, 53, 5929–5955. [Google Scholar] [CrossRef]
- Cai, Z.; Xiong, Z.; Xu, H.; Wang, P.; Li, W.; Pan, Y. Generative Adversarial Networks: A Survey Toward Private and Secure Applications. ACM Comput. Surv. 2021, 54, 1–38. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention Is All You Need. arXiv 2023, arXiv:1706.03762. [Google Scholar]
- Song, J.; Meng, C.; Ermon, S. Denoising Diffusion Implicit Models. arXiv 2020, arXiv:2010.02502. [Google Scholar]
- Graph Neural Networks. Nat. Rev. Methods Primers 2024, 4, 18. [CrossRef]
- Watkins, C.J.C.H.; Dayan, P. Q-Learning. Mach. Learn. 1992, 8, 279–292. [Google Scholar] [CrossRef]
- Liu, Q.; Cui, C.; Fan, Q. Self-Adaptive Constrained Multi-Objective Differential Evolution Algorithm Based on the State–Action–Reward–State–Action Method. Mathematics 2022, 10, 813. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Graves, A.; Antonoglou, I.; Wierstra, D.; Riedmiller, M. Playing Atari with Deep Reinforcement Learning. arXiv 2013, arXiv:1312.5602. [Google Scholar]
- Betancourt, M. The Convergence of Markov Chain Monte Carlo Methods: From the Metropolis Method to Hamiltonian Monte Carlo. Ann. Der Phys. 2019, 531, 1700214. [Google Scholar] [CrossRef]
- Okada, M.; Taniguchi, T. DreamingV2: Reinforcement Learning with Discrete World Models without Reconstruction. arXiv 2022, arXiv:2203.00494. [Google Scholar]
- Liashchynskyi, P.; Liashchynskyi, P. Grid Search, Random Search, Genetic Algorithm: A Big Comparison for NAS. arXiv 2019, arXiv:1912.06059. [Google Scholar]
- Wang, X.; Jin, Y.; Schmitt, S.; Olhofer, M. Recent Advances in Bayesian Optimization. ACM Comput. Surv. 2023, 55, 1–36. [Google Scholar] [CrossRef]
- Baymurzina, D.; Golikov, E.; Burtsev, M. A Review of Neural Architecture Search. Neurocomputing 2022, 474, 82–93. [Google Scholar] [CrossRef]
- Li, L.; Jamieson, K.; DeSalvo, G.; Rostamizadeh, A.; Talwalkar, A. Hyperband: Bandit-based configuration evaluation for hyperparameter optimization. J. Mach. Learn. Res. 2017, 18, 1–52. [Google Scholar]
- Finn, C.; Abbeel, P.; Levine, S. Model-Agnostic Meta-Learning for Fast Adaptation of Deep Networks. arXiv 2017, arXiv:1703.03400. [Google Scholar]
- Behl, H.S.; Baydin, A.G.; Torr, P.H.S. Alpha MAML: Adaptive Model-Agnostic Meta-Learning. arXiv 2019, arXiv:1905.07435. [Google Scholar]
- Jose, S.T.; Simeone, O. Information-Theoretic Generalization Bounds for Meta-Learning and Applications. Entropy 2021, 23, 126. [Google Scholar] [CrossRef]
- Long, T.; Li, J.; Wang, C.; Wang, H.; Cheng, X.; Lu, H.; Zhang, Y.; Zhou, C. Polymers Simulation Using Machine Learning Interatomic Potentials. Polymer 2024, 308, 127416. [Google Scholar] [CrossRef]
- Patel, R.A.; Borca, C.H.; Webb, M.A. Featurization Strategies for Polymer Sequence or Composition Design by Machine Learning. Mol. Syst. Des. Eng. 2022, 7, 661–676. [Google Scholar] [CrossRef]
- Zhang, B.; Li, X.; Zeng, M.; Cao, J. COMFO: Integrated Deep Learning Model Facilitates Discovery of Multifunctional Polyimide Materials. Polymer 2025, 320, 128081. [Google Scholar] [CrossRef]
- del Rio, B.G.; Phan, B.; Ramprasad, R. A Deep Learning Framework to Emulate Density Functional Theory. NPJ Comput. Mater. 2023, 9, 158. [Google Scholar] [CrossRef]
- Yao, K.; Herr, J.E.; Parkhill, J. The Many-Body Expansion Combined with Neural Networks. J. Chem. Phys. 2017, 146, 014106. [Google Scholar] [CrossRef] [PubMed]
- Gautham, S.M.B.; Patra, T.K. Deep Learning Potential of Mean Force between Polymer Grafted Nanoparticles. Soft Matter 2022, 18, 7909–7916. [Google Scholar] [CrossRef]
- Shi, J.; Quevillon, M.J.; Amorim Valença, P.H.; Whitmer, J.K. Predicting Adhesive Free Energies of Polymer–Surface Interactions with Machine Learning. ACS Appl. Mater. Interfaces 2022, 14, 37161–37169. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.; Zhao, C.; Ren, J.; Zheng, K.; Shao, Z.; Ling, S. Acquiring Structural and Mechanical Information of a Fibrous Network through Deep Learning. Nanoscale 2022, 14, 5044–5053. [Google Scholar] [CrossRef]
- Fang, X.; Murphy, E.A.; Kohl, P.A.; Li, Y.; Hawker, C.J.; Bates, C.M.; Gu, M. Universal Phase Identification of Block Copolymers From Physics-Informed Machine Learning. J. Polym. Sci. 2025, 63, 1433–1440. [Google Scholar] [CrossRef]
- Nguyen, D.; Tao, L.; Li, Y. Integration of Machine Learning and Coarse-Grained Molecular Simulations for Polymer Materials: Physical Understandings and Molecular Design. Front. Chem. 2022, 9, 820417. [Google Scholar] [CrossRef]
- Li, H.; Collins, C.R.; Ribelli, T.G.; Matyjaszewski, K.; Gordon, G.J.; Kowalewski, T.; Yaron, D.J. Tuning the Molecular Weight Distribution from Atom Transfer Radical Polymerization Using Deep Reinforcement Learning. Mol. Syst. Des. Eng. 2018, 3, 496–508. [Google Scholar] [CrossRef]
- Kranthiraja, K.; Saeki, A. Machine Learning: Experiment-Oriented Machine Learning of Polymer:Non-Fullerene Organic Solar Cells (Adv. Funct. Mater. 23/2021). Adv. Funct. Mater. 2021, 31, 2170168. [Google Scholar] [CrossRef]
- Webb, M.A.; Jackson, N.E.; Gil, P.S.; de Pablo, J.J. Targeted Sequence Design Within the Coarse-Grained Polymer Genome|Science Advances. Sci. Adv. 2020, 6, eabc6216. [Google Scholar] [CrossRef]
- Hiraide, K.; Oya, Y.; Suzuki, M.; Muramatsu, M. Inverse Design of Polymer Alloys Using Deep Learning Based on Self-Consistent Field Analysis and Finite Element Analysis. Mater. Today Commun. 2023, 37, 107233. [Google Scholar] [CrossRef]
- Zhu, C.; Zhang, J. Inferential Estimation of Polymer Melt Index Using Deep Belief Networks. In Proceedings of the 2018 24th International Conference on Automation and Computing (ICAC), Newcastle Upon Tyne, UK, 6–7 September 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Sattari, K.; Xie, Y.; Lin, J. Data-Driven Algorithms for Inverse Design of Polymers. Soft Matter 2021, 17, 7607–7622. [Google Scholar] [CrossRef] [PubMed]
- Queen, O.; McCarver, G.A.; Thatigotla, S.; Abolins, B.P.; Brown, C.L.; Maroulas, V.; Vogiatzis, K.D. Polymer Graph Neural Networks for Multitask Property Learning. NPJ Comput. Mater. 2023, 9, 90. [Google Scholar] [CrossRef]
- Pilania, G.; Iverson, C.N.; Lookman, T.; Marrone, B.L. Machine-Learning-Based Predictive Modeling of Glass Transition Temperatures: A Case of Polyhydroxyalkanoate Homopolymers and Copolymers. J. Chem. Inf. Model. 2019, 59, 5013–5025. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.-K.; Lu, C.; Yu, Y.; Sun, Q.; Hsieh, C.-Y.; Zhang, S.; Liu, Q.; Shi, L. Transfer Learning with Graph Neural Networks for Optoelectronic Properties of Conjugated Oligomers. J. Chem. Phys. 2021, 154, 024906. [Google Scholar] [CrossRef]
- Kuenneth, C.; Lalonde, J.; Marrone, B.L.; Iverson, C.N.; Ramprasad, R.; Pilania, G. Bioplastic Design Using Multitask Deep Neural Networks. Commun. Mater. 2022, 3, 96. [Google Scholar] [CrossRef]
- Phan, B.K.; Shen, K.-H.; Gurnani, R.; Tran, H.; Lively, R.; Ramprasad, R. Gas Permeability, Diffusivity, and Solubility in Polymers: Simulation-Experiment Data Fusion and Multi-Task Machine Learning. NPJ Comput. Mater. 2024, 10, 186. [Google Scholar] [CrossRef]
- Himanshu; Chakraborty, K.; Patra, T.K. Developing Efficient Deep Learning Model for Predicting Copolymer Properties. Phys. Chem. Chem. Phys. 2023, 25, 25166–25176. [Google Scholar] [CrossRef]
- Liang, Z.; Tan, Z.; Hong, R.; Ouyang, W.; Yuan, J.; Zhang, C. Automatically Predicting Material Properties with Microscopic Images: Polymer Miscibility as an Example. J. Chem. Inf. Model. 2023, 63, 5971–5980. [Google Scholar] [CrossRef]
- Kim, C.; Chandrasekaran, A.; Huan, T.D.; Das, D.; Ramprasad, R. Polymer Genome: A Data-Powered Polymer Informatics Platform for Property Predictions. J. Phys. Chem. C 2018, 122, 17575–17585. [Google Scholar] [CrossRef]
- Upadhya, R.; Tamasi, M.; Di Mare, E.; Murthy, S.; Gormley, A. Data-Driven Design of Protein-Like Single-Chain Polymer Nanoparticles. ChemRxiv 2022. [Google Scholar] [CrossRef]
- Doan Tran, H.; Kim, C.; Chen, L.; Chandrasekaran, A.; Batra, R.; Venkatram, S.; Kamal, D.; Lightstone, J.P.; Gurnani, R.; Shetty, P.; et al. Machine-Learning Predictions of Polymer Properties with Polymer Genome. J. Appl. Phys. 2020, 128, 171104. [Google Scholar] [CrossRef]
- Hong, X.; Yang, Q.; Liao, K.; Pei, J.; Chen, M.; Mo, F.; Lu, H.; Zhang, W.-B.; Zhou, H.; Chen, J.; et al. AI for Organic and Polymer Synthesis. Sci. China Chem. 2024, 67, 2461–2496. [Google Scholar] [CrossRef]
- Khanzadeh, M.; Rao, P.; Jafari-Marandi, R.; Smith, B.K.; Tschopp, M.A.; Bian, L. Quantifying Geometric Accuracy With Unsupervised Machine Learning: Using Self-Organizing Map on Fused Filament Fabrication Additive Manufacturing Parts. J. Manuf. Sci. Eng.-Trans. ASME 2018, 140, 031011. [Google Scholar] [CrossRef]
- Roy, M.; Wodo, O. Data-Driven Modeling of Thermal History in Additive Manufacturing. Addit. Manuf. 2020, 32, 101017. [Google Scholar] [CrossRef]
- Zhu, Y.; Kwok, T.; Haug, J.C.; Guo, S.; Chen, X.; Xu, W.; Ravichandran, D.; Tchoukalova, Y.D.; Cornella, J.L.; Yi, J.; et al. 3D Printable Hydrogel with Tunable Degradability and Mechanical Properties as a Tissue Scaffold for Pelvic Organ Prolapse Treatment. Adv. Mater. Technol. 2023, 8, 2201421. [Google Scholar] [CrossRef]
- Edlim, F.W.; Mafazy, M.M.; Ansori, D.B.; Klemm, S.F.; Purwitasari, D. Failure Detection on 3D Printing Images with Color-Based Data Augmentation. In Proceedings of the 2024 International Conference on Smart Computing, IoT and Machine Learning (SIML), Surakarta, Indonesia, 6–7 June 2024; pp. 68–73. [Google Scholar] [CrossRef]
- Lee, X.Y.; Saha, S.K.; Sarkar, S.; Giera, B. Automated Detection of Part Quality during Two-Photon Lithography via Deep Learning. Addit. Manuf. 2020, 36, 101444. [Google Scholar] [CrossRef]
- Sassaman, D.; Phillips, T.; Milroy, C.; Ide, M.; Beaman, J. A Method for Predicting Powder Flowability for Selective Laser Sintering. JOM 2022, 74, 1102–1110. [Google Scholar] [CrossRef]
- Satterlee, N.; Torresani, E.; Olevsky, E.; Kang, J.S. Comparison of Machine Learning Methods for Automatic Classification of Porosities in Powder-Based Additive Manufactured Metal Parts. Int. J. Adv. Manuf. Technol. 2022, 120, 6761–6776. [Google Scholar] [CrossRef]
- Nasrin, T.; Pourkamali-Anaraki, F.; Peterson, A.M. Application of Machine Learning in Polymer Additive Manufacturing: A Review. J. Polym. Sci. 2024, 62, 2639–2669. [Google Scholar] [CrossRef]
- Chen, F.; Wang, J.; Guo, Z.; Jiang, F.; Ouyang, R.; Ding, P. Machine Learning and Structural Design to Optimize the Flame Retardancy of Polymer Nanocomposites with Graphene Oxide Hydrogen Bonded Zinc Hydroxystannate. ACS Appl. Mater. Interfaces 2021, 13, 53425–53438. [Google Scholar] [CrossRef]
- Li, C.; Rubín de Celis Leal, D.; Rana, S.; Gupta, S.; Sutti, A.; Greenhill, S.; Slezak, T.; Height, M.; Venkatesh, S. Rapid Bayesian Optimisation for Synthesis of Short Polymer Fiber Materials. Sci. Rep. 2017, 7, 5683. [Google Scholar] [CrossRef] [PubMed]
- Takasuka, S.; Ito, S.; Oikawa, S.; Harashima, Y.; Takayama, T.; Nag, A.; Wakiuchi, A.; Ando, T.; Sugawara, T.; Hatanaka, M.; et al. Bayesian Optimization of Radical Polymerization Reactions in a Flow Synthesis System. ChemRxiv 2024, 4, 2425178. [Google Scholar] [CrossRef]
- Qi, Y.; Hu, D.; Jiang, Y.; Wu, Z.; Zheng, M.; Chen, E.X.; Liang, Y.; Sadi, M.A.; Zhang, K.; Chen, Y.P. Recent Progresses in Machine Learning Assisted Raman Spectroscopy. Adv. Opt. Mater. 2023, 11, 2203104. [Google Scholar] [CrossRef]
- Ranjan, N.; Kumar, R.; Kumar, R.; Kaur, R.; Singh, S. Investigation of Fused Filament Fabrication-Based Manufacturing of ABS-Al Composite Structures: Prediction by Machine Learning and Optimization. J. Mater. Eng. Perform. 2023, 32, 4555–4574. [Google Scholar] [CrossRef]
- Aizawa, T. New Design Method for Fabricating Multilayer Membranes Using CO2-Assisted Polymer Compression Process. Molecules 2020, 25, 5786. [Google Scholar] [CrossRef]
- Barnett, J.W.; Bilchak, C.R.; Wang, Y.; Benicewicz, B.C.; Murdock, L.A.; Bereau, T.; Kumar, S.K. Designing Exceptional Gas-Separation Polymer Membranes Using Machine Learning. Sci. Adv. 2020, 6, eaaz4301. [Google Scholar] [CrossRef]
- Sbrana, A.; de Almeida, A.G.; de Oliveira, A.M.; Neto, H.S.; Rimes, J.P.C.; Belli, M.C. Plastic Classification With NIR Hyperspectral Images and Deep Learning. IEEE Sens. Lett. 2023, 7, 1–4. [Google Scholar] [CrossRef]
- Rizkin, B.A.; Shkolnik, A.S.; Ferraro, N.J.; Hartman, R.L. Combining Automated Microfluidic Experimentation with Machine Learning for Efficient Polymerization Design. Nat. Mach. Intell. 2020, 2, 200–209. [Google Scholar] [CrossRef]
- Cao, L.; Russo, D.; Lapkin, A.A. Automated Robotic Platforms in Design and Development of Formulations. AIChE J. 2021, 67, e17248. [Google Scholar] [CrossRef]
- Knox, S.T.; Parkinson, S.J.; Wilding, C.Y.P.; Bourne, R.A.; Warren, N.J. Autonomous Polymer Synthesis Delivered by Multi-Objective Closed-Loop Optimisation. Polym. Chem. 2022, 13, 1576–1585. [Google Scholar] [CrossRef]
- Gong, Y.; Shao, H.; Luo, J.; Li, Z. A Deep Transfer Learning Model for Inclusion Defect Detection of Aeronautics Composite Materials. Compos. Struct. 2020, 252, 112681. [Google Scholar] [CrossRef]
- Cheng, J.; Tan, W.; Yuan, Y.; Zhao, Z.; Cheng, Y. Research on Defect Detection Method for Composite Materials Based on Deep Learning Networks. Appl. Sci. 2024, 14, 4161. [Google Scholar] [CrossRef]
- Gao, L.; Lin, J.; Wang, L.; Du, L. Machine Learning-Assisted Design of Advanced Polymeric Materials. Acc. Mater. Res. 2024, 5, 571–584. [Google Scholar] [CrossRef]
- Han, L.; Peng, X.F.; Li, L.X. Entire-Region Constitutive Relation for Treloar’s Data. Rubber Chem. Technol. 2021, 95, 119–127. [Google Scholar] [CrossRef]
- Meyer, T.A.; Ramirez, C.; Tamasi, M.J.; Gormley, A.J. A User’s Guide to Machine Learning for Polymeric Biomaterials. ACS Polym. Au 2023, 3, 141–157. [Google Scholar] [CrossRef]
- Zhang, H.; Chen, W.; Rondinelli, J.M.; Chen, W. ET-AL: Entropy-Targeted Active Learning for Bias Mitigation in Materials Data. Appl. Phys. Rev. 2023, 10, 021403. [Google Scholar] [CrossRef]
- Ma, X.; Chen, H.; He, R.; Yu, Z.; Prokhorenko, S.; Wen, Z.; Zhong, Z.; Íñiguez-González, J.; Bellaiche, L.; Wu, D.; et al. Active Learning of Effective Hamiltonian for Super-Large-Scale Atomic Structures. NPJ Comput. Mater. 2025, 11, 70. [Google Scholar] [CrossRef]
- Yang, Z.; Li, S.; Li, S.; Yang, J.; Liu, D. A Two-Step Data Augmentation Method Based on Generative Adversarial Network for Hardness Prediction of High Entropy Alloy. Comput. Mater. Sci. 2023, 220, 112064. [Google Scholar] [CrossRef]
- Chen, X.; Wang, T.; Guo, T.; Guo, K.; Zhou, J.; Li, H.; Song, Z.; Gao, X.; Zhang, X. Unveiling the Power of Language Models in Chemical Research Question Answering. Commun. Chem. 2025, 8, 4. [Google Scholar] [CrossRef]
- Yan, R.; Jiang, X.; Wang, W.; Dang, D.; Su, Y. Materials Information Extraction via Automatically Generated Corpus. Sci. Data 2022, 9, 401. [Google Scholar] [CrossRef]
- Hu, B. Data Curation of a Findable, Accessible, Interoperable, Reusable Polymer Nanocomposites Data Resource—MaterialsMine. Ph.D. Thesis, Duke University, Durham, NC, USA, 2022. Available online: https://www.proquest.com/docview/2773518516/abstract/E55EDA9E16E247CDPQ/1 (accessed on 25 September 2024).
- Brinson, L.C.; Deagen, M.; Chen, W.; McCusker, J.; McGuinness, D.L.; Schadler, L.S.; Palmeri, M.; Ghumman, U.; Lin, A.; Hu, B. Polymer Nanocomposite Data: Curation, Frameworks, Access, and Potential for Discovery and Design. ACS Macro Lett. 2020, 9, 1086–1094. [Google Scholar] [CrossRef] [PubMed]
- Yu, T.; Sun, Z.-B.; Sang, J.-P.; Huang, S.-Y.; Zou, X.-W. Structural Class Tendency of Polypeptide: A New Conception in Predicting Protein Structural Class. Phys. A Stat. Mech. Its Appl. 2007, 386, 581–589. [Google Scholar] [CrossRef]
- Niu, J.; Miao, B.; Guo, J.; Ding, Z.; He, Y.; Chi, Z.; Wang, F.; Ma, X. Leveraging Deep Neural Networks for Estimating Vickers Hardness from Nanoindentation Hardness. Materials 2024, 17, 148. [Google Scholar] [CrossRef]
- Lee, F.L.; Park, J.; Goyal, S.; Qaroush, Y.; Wang, S.; Yoon, H.; Rammohan, A.; Shim, Y. Comparison of Machine Learning Methods towards Developing Interpretable Polyamide Property Prediction. Polymers 2021, 13, 3653. [Google Scholar] [CrossRef]
- Bahoria, B.V.; Pande, P.B.; Dhengare, S.W.; Raut, J.M.; Bhagat, R.M.; Shelke, N.M.; Uparkar, S.S.; Vairagade, V.S. Predictive Models for Properties of Hybrid Blended Modified Sustainable Concrete Incorporating Nano-Silica, Basalt Fibers, and Recycled Aggregates: Application of Advanced Artificial Intelligence Techniques. Nano-Struct. Nano-Objects 2024, 40, 101373. [Google Scholar] [CrossRef]
- Tao, Q.; Yang, X.; Bao, L.; Zhou, Y.; Yang, T.; Zhao, Y.; Shi, R.; Yao, Z.; Liu, X. Transforming Machine Learning Model Knowledge into Material Insights for Multi-Principal-Element Superalloy Phase Design. NPJ Comput. Mater. 2025, 11, 99. [Google Scholar] [CrossRef]
- Yang, Z.; Shan, X.; Zhang, W. Discovery of Knowledge of Wall-Bounded Turbulence via Symbolic Regression. arXiv 2024, arXiv:2406.08950. [Google Scholar]
- Ouyang, R.; Curtarolo, S.; Ahmetcik, E.; Scheffler, M.; Ghiringhelli, L.M. SISSO: A Compressed-Sensing Method for Identifying the Best Low-Dimensional Descriptor in an Immensity of Offered Candidates. Phys. Rev. Mater. 2018, 2, 083802. [Google Scholar] [CrossRef]



| Class of Algorithm | Classic Important Algorithms | Latest Development Algorithm | |
|---|---|---|---|
| Machine learning | Supervised learning | Linear model [73], logistic regression [68], decision tree [74,75], support vector machine [76], random forest [65], gaussian process regression [77,78], multilayer perceptron [79] | XGBoost [80], LightGBM [81], CatBoost [82], TabNet [83], Neural Tangent Kernel [84] |
| Unsupervised learning | K-means [85], hierarchical clustering [86], principal component analysis [87] | UMAP [88], Deep clustering [89], Variational autoencoder [90,91], learning contrast (SimCLR [92], MoCo [93]) | |
| Semi-supervised learning | Self-training [94], co-training [95], label propagation [96] | FixMatch [97], MixMatch [98], Pseudo-labeling [99], Snorkel [100], Consistency Regularization [101] | |
| Deep learning | Convolutional neural network [102], recurrent neural network [103], long short-term memory [104], generative adversarial network [105] | Transformer [106] (BERT, GPT, Vision Transformer), Diffusion model [107], Graph Neural Networks [108] | |
| Reinforcement learning | Q-learning [109], state-action-reward-state-action [110], deep q-network [111], Monte Carlo method [112] | DreamerV2 [113] | |
| Meta learning/Auto ML | Grid search [114], random search [114], Bayesian optimization [115] | Neural architecture search [116], Hyperband [117], Meta-Learning [118] (MAML [119], Reptile [120]) |
| No. | Database | Origin of Data | Description | URL |
|---|---|---|---|---|
| 1 | Khazazna | computational | thermoplastic; mechanical, thermal, electrical properties | https://khazana.gatech.edu/dataset/ (accessed on 18 February 2020) |
| 2 | PolyInfo | empirical | thermoplastic; mechanical, optical, thermal, rheological properties | https://polymer.nims.go.jp/ (accessed on 22 January 2021) |
| 3 | Polymer property predictor and database | empirical | Flory–Huggins parameter, glass transition temperature, binary polymer solution cloud point | https://pppdb.uchicago.edu/ (accessed on 30 March 2016) |
| 4 | Material properties database | empirical/computational | thermoplastic, thermoset, rubber; mechanical, thermal, electrical properties | https://www.makeitfrom.com/ (accessed on 16 April 2020) |
| 5 | CROW polymer properties database | empirical/computational | thermoplastic, rubber, fiber; physical, thermal properties | https://polymerdatabase.com/ (accessed on 2 March 2019) |
| 6 | PI1M | computational | virtual polymers; physical, thermal, electrical properties | https://github.com/RUIMINMA1996/PI1M (accessed on 11 December 2020) |
| 7 | Dortmund database | computational | physical properties, phase equilibrium data | https://ddbst.com/ (accessed on 7 October 2020) |
| 8 | AI plus Polymers | empirical/computational | thermoset, thermoplastic; physical, mechanical, thermal, electrical properties | https://polymergenome.ecust.edu.cn/ (accessed on 23 March 2019) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Long, T.; Pang, Q.; Deng, Y.; Pang, X.; Zhang, Y.; Yang, R.; Zhou, C. Recent Progress of Artificial Intelligence Application in Polymer Materials. Polymers 2025, 17, 1667. https://doi.org/10.3390/polym17121667
Long T, Pang Q, Deng Y, Pang X, Zhang Y, Yang R, Zhou C. Recent Progress of Artificial Intelligence Application in Polymer Materials. Polymers. 2025; 17(12):1667. https://doi.org/10.3390/polym17121667
Chicago/Turabian StyleLong, Teng, Qianqian Pang, Yanyan Deng, Xiteng Pang, Yixuan Zhang, Rui Yang, and Chuanjian Zhou. 2025. "Recent Progress of Artificial Intelligence Application in Polymer Materials" Polymers 17, no. 12: 1667. https://doi.org/10.3390/polym17121667
APA StyleLong, T., Pang, Q., Deng, Y., Pang, X., Zhang, Y., Yang, R., & Zhou, C. (2025). Recent Progress of Artificial Intelligence Application in Polymer Materials. Polymers, 17(12), 1667. https://doi.org/10.3390/polym17121667






