Influence of Temperature on Hyperelastic Mechanical Behavior of Accelerated Aged EPDM Rubber
Abstract
1. Introduction
2. Materials and Methods
2.1. Material and Specimen
2.2. Accelerated Aging Test and Time–Temperature Equivalent Principle
2.3. Temperature-Dependent Uniaxial Compression Test
3. Results and Discussion
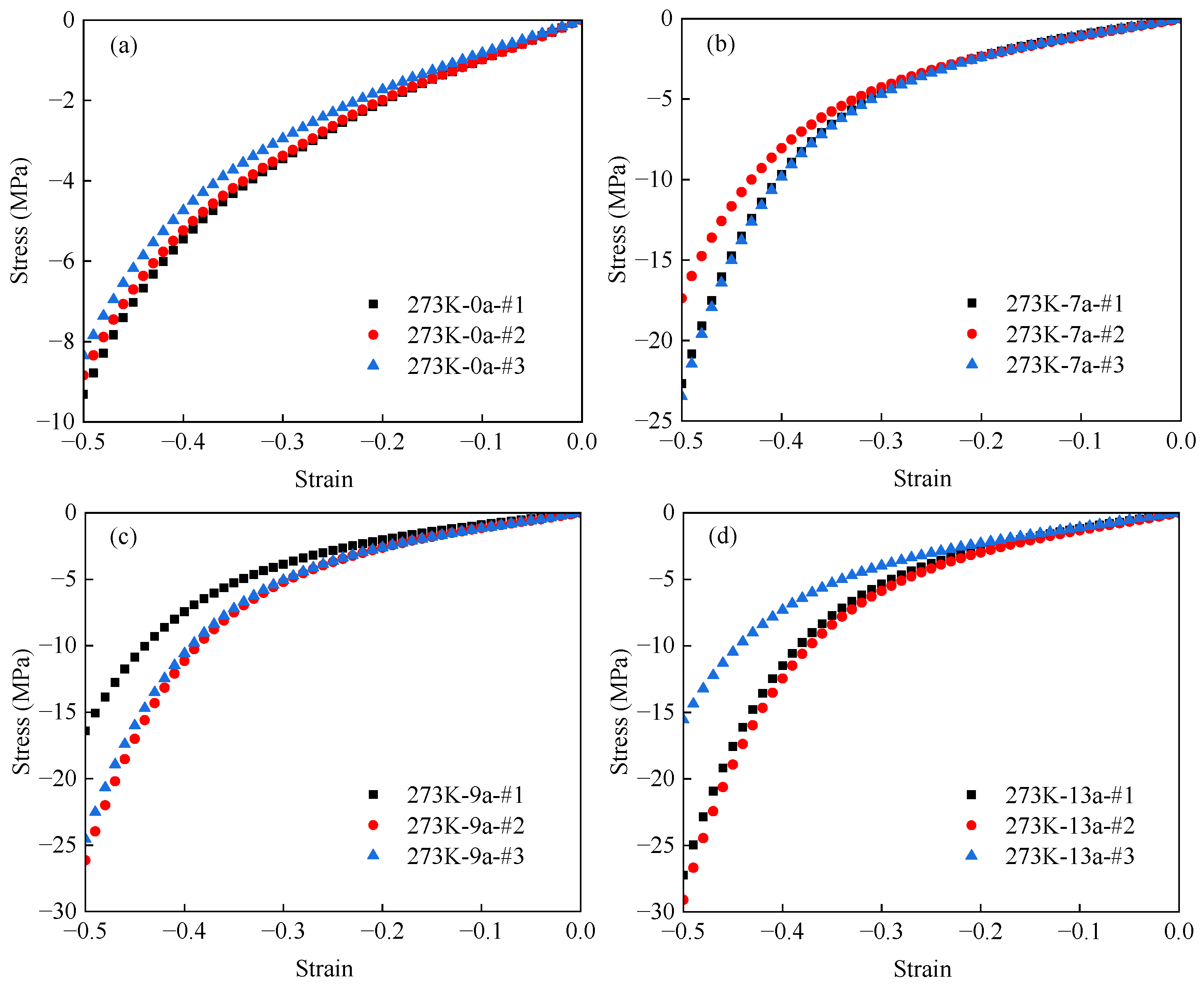
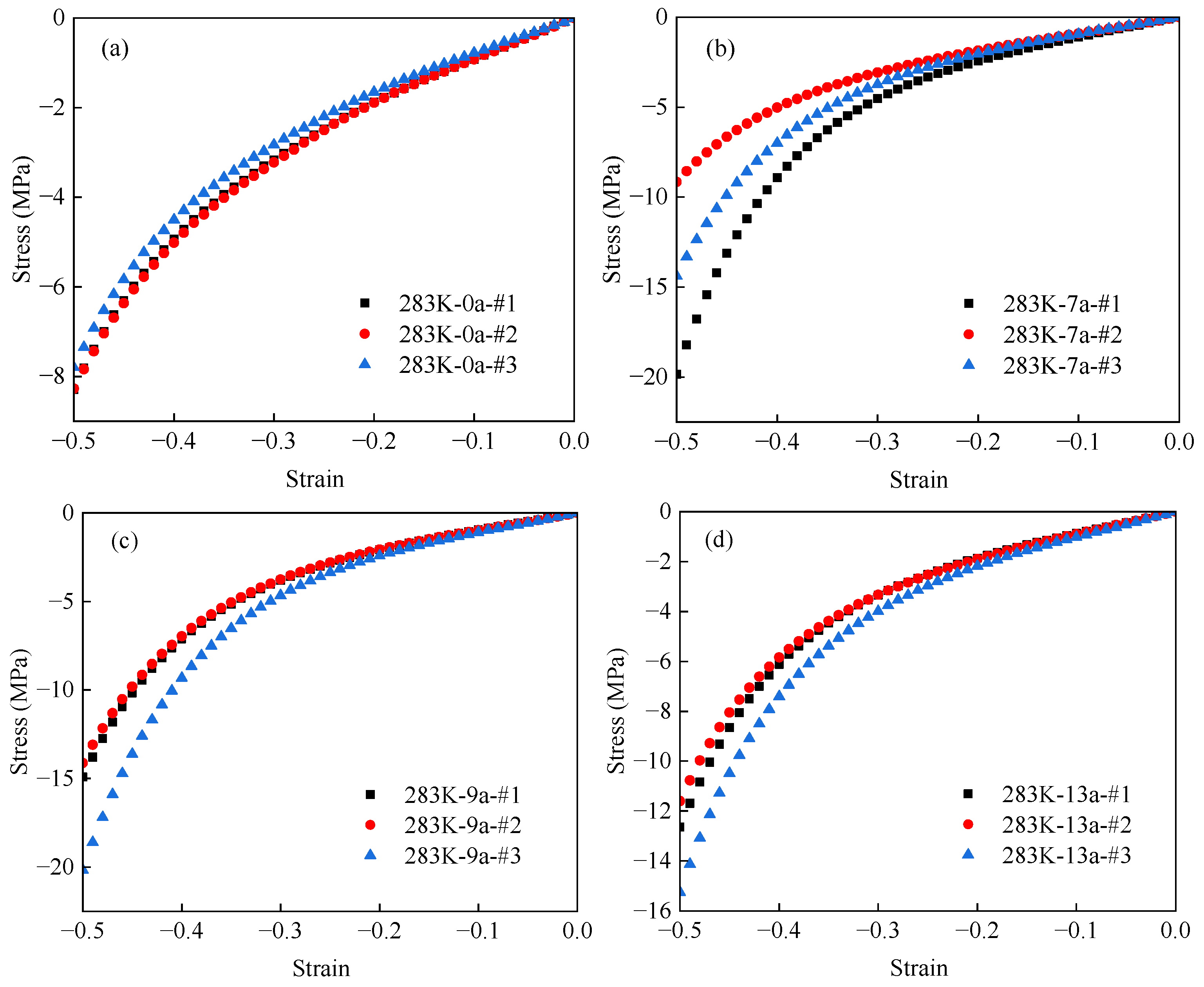
3.1. Test Results of Accelerated Aged EPDM Rubber at Different Temperatures
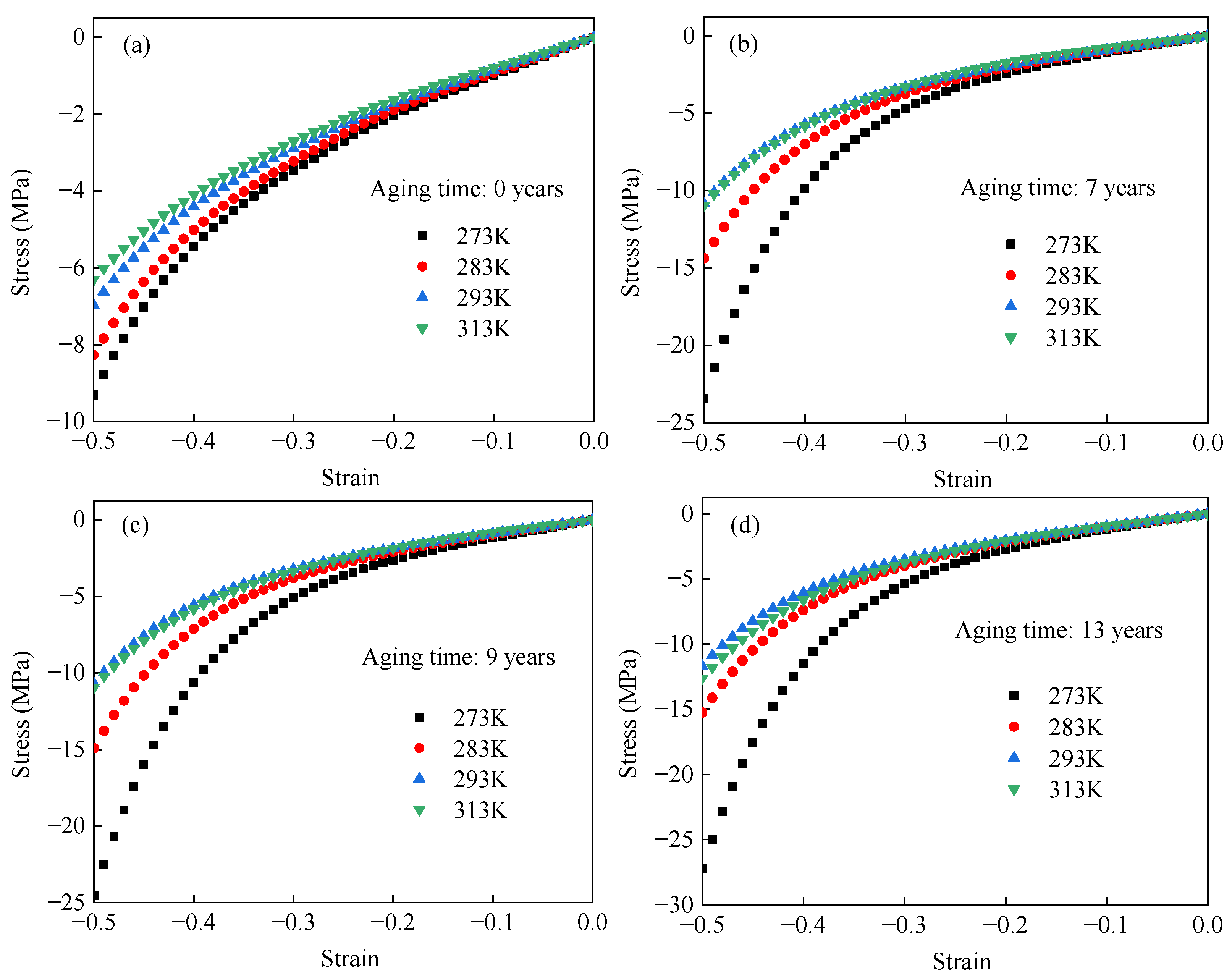
3.2. Test Results of Different Accelerated Aged EPDM Rubber Specimens at Constant Temperatures
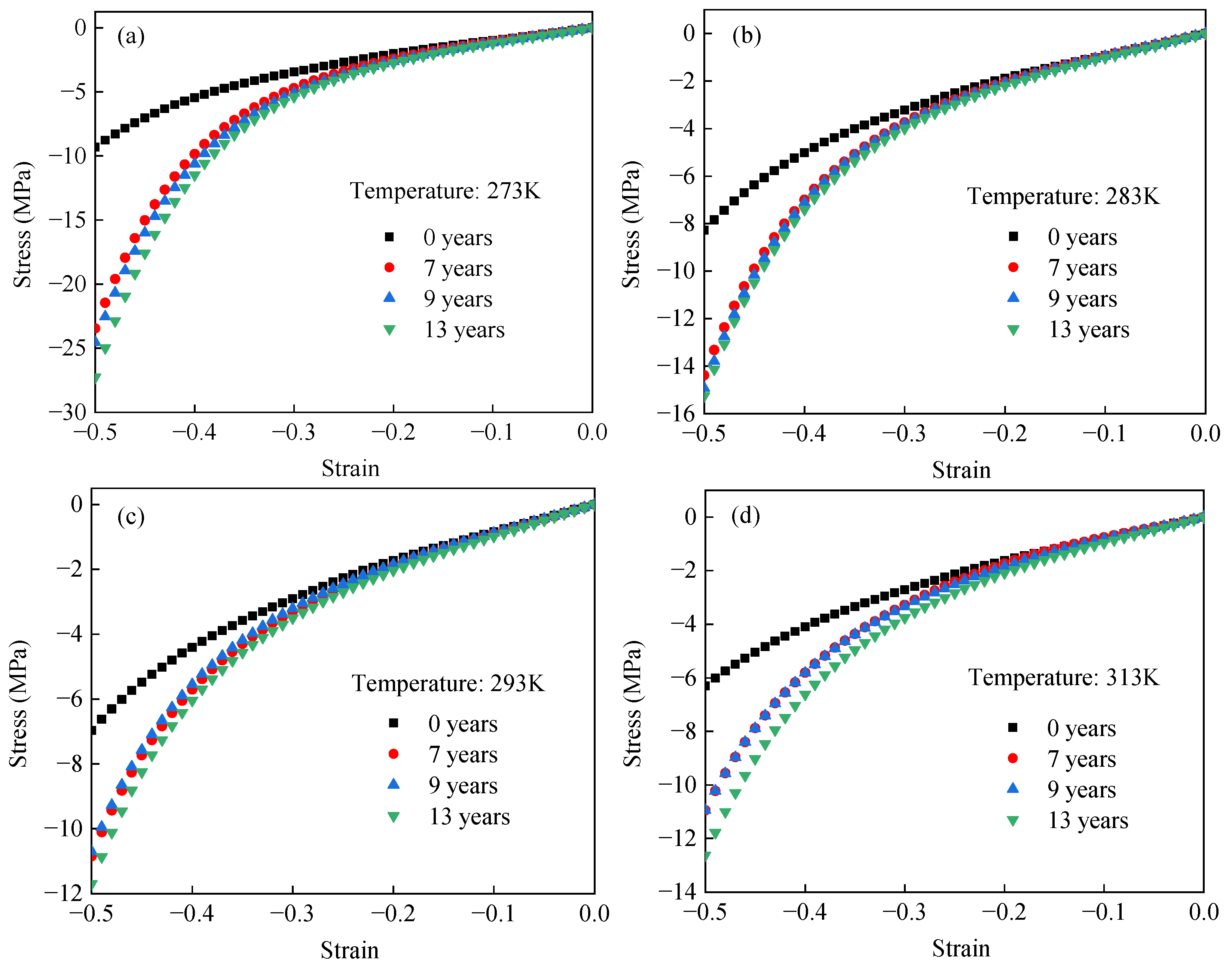
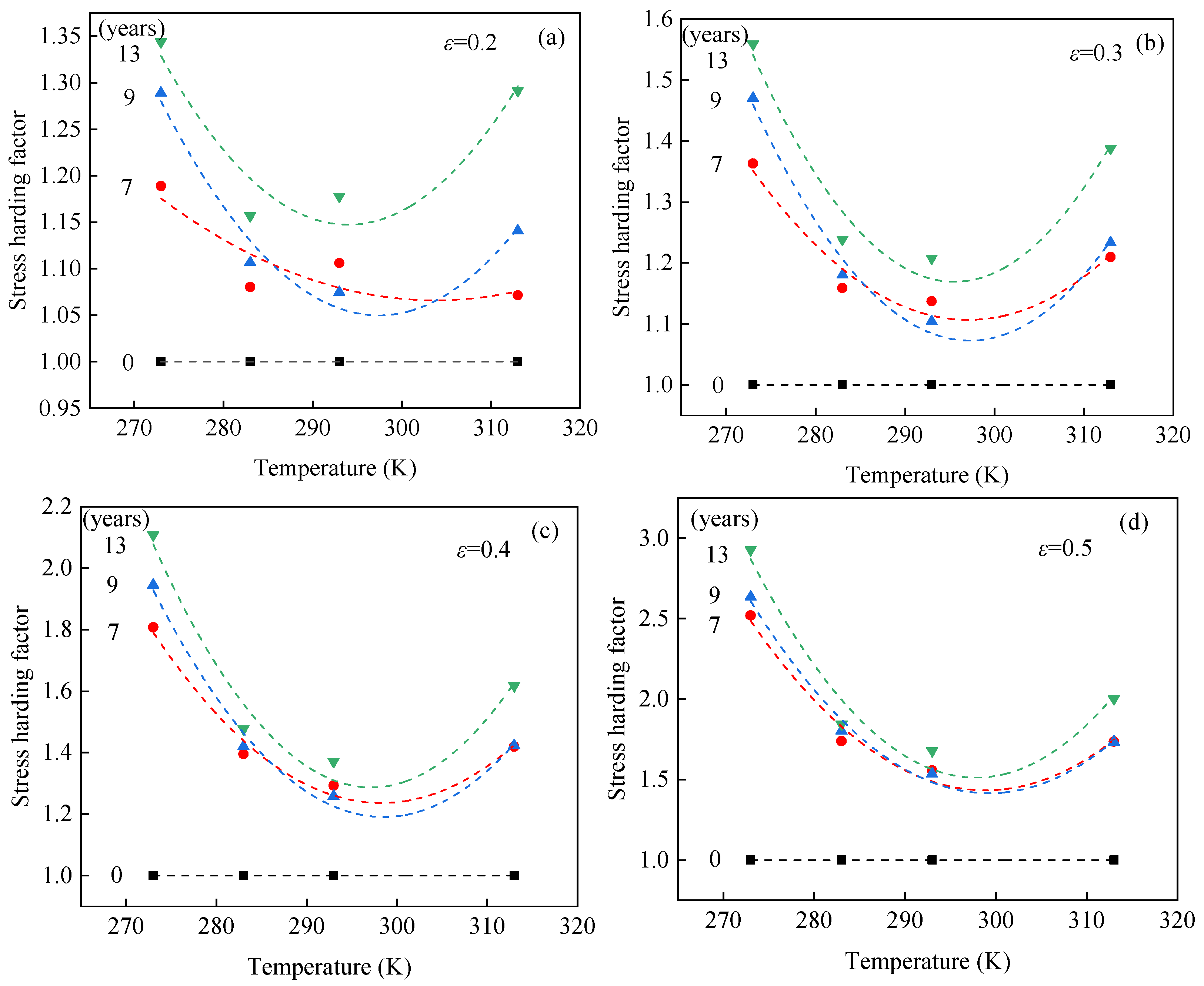
3.3. Discussion on Relationship Between Accelerated Aging and Service Temperature
4. Constitutive Modeling
4.1. Hyperelastic Constitutive Relation
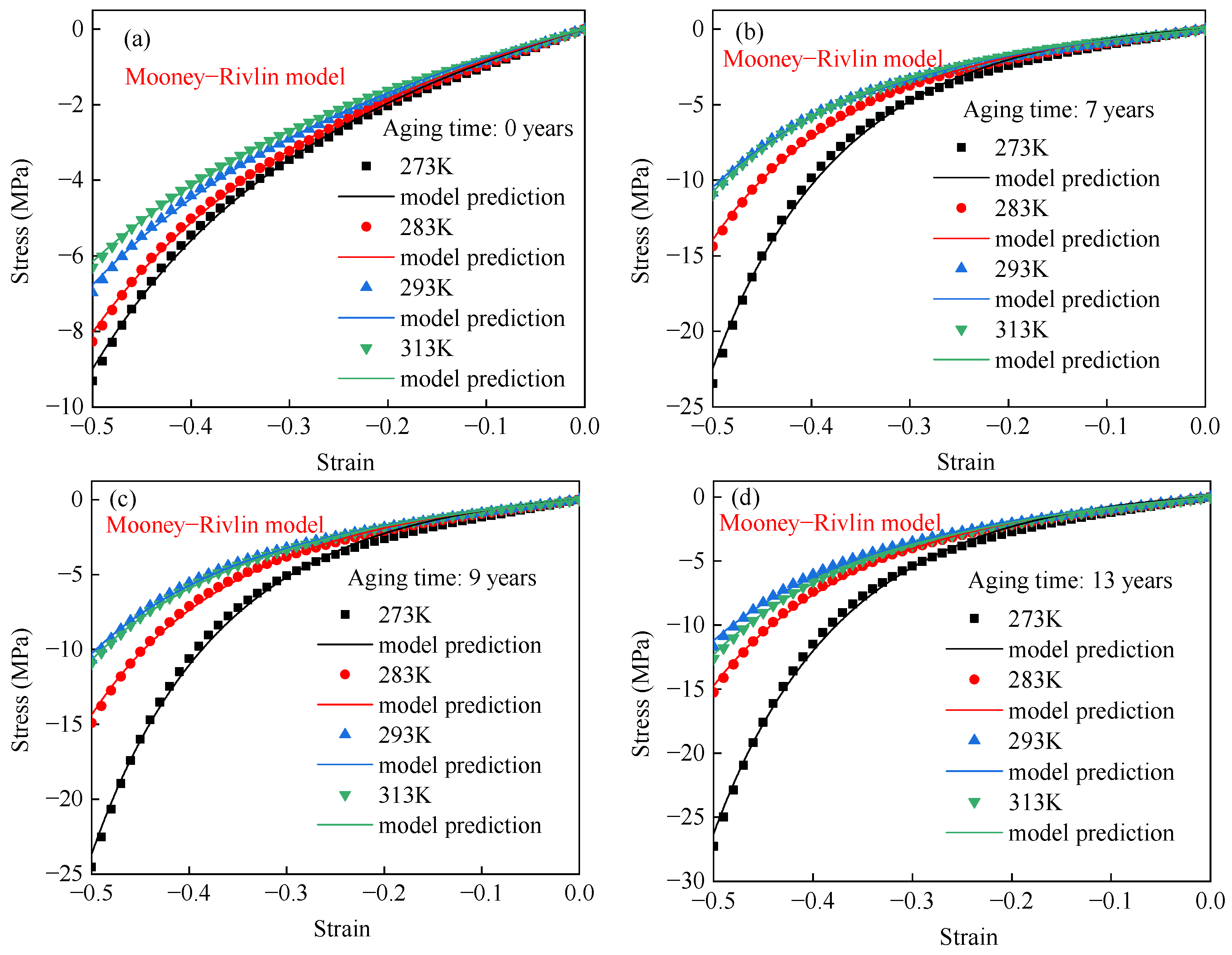
4.2. Hyperelastic Constitutive Model for EPDM Rubber
4.2.1. Model Evaluation Method
4.2.2. Evaluation of Rivlin Models of Different Orders
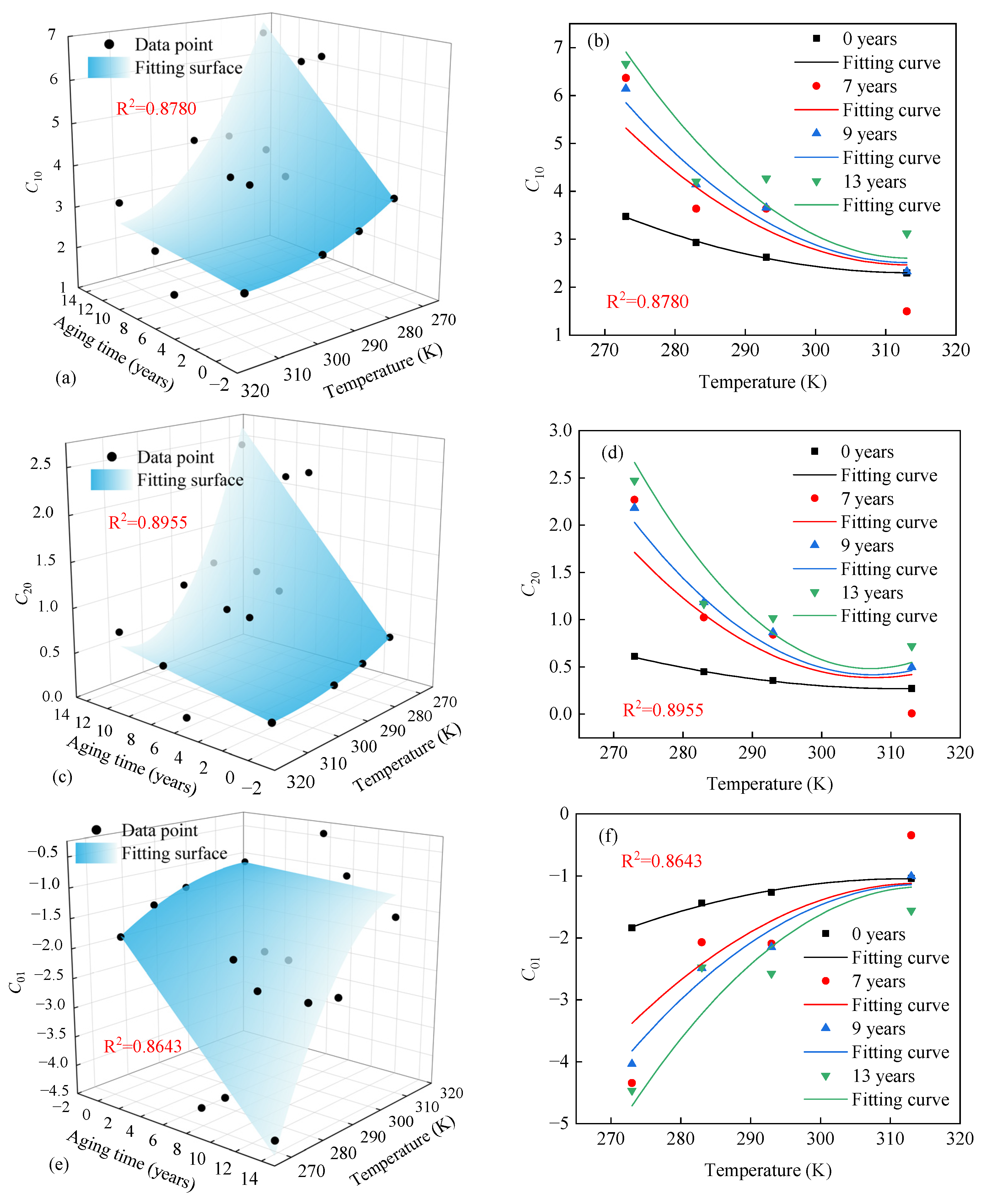
4.3. Effects of Temperature and Accelerated Aging on Model Parameters
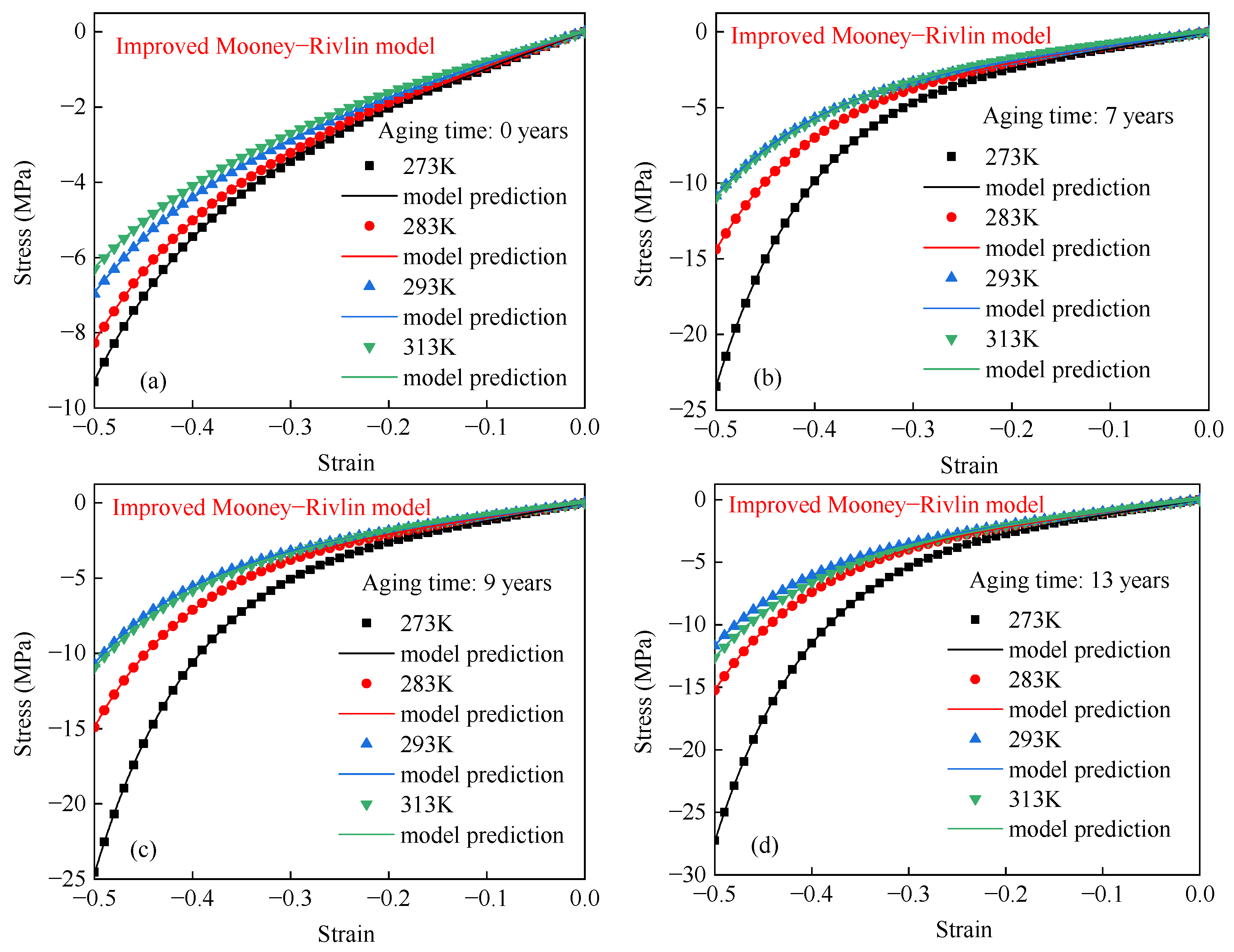
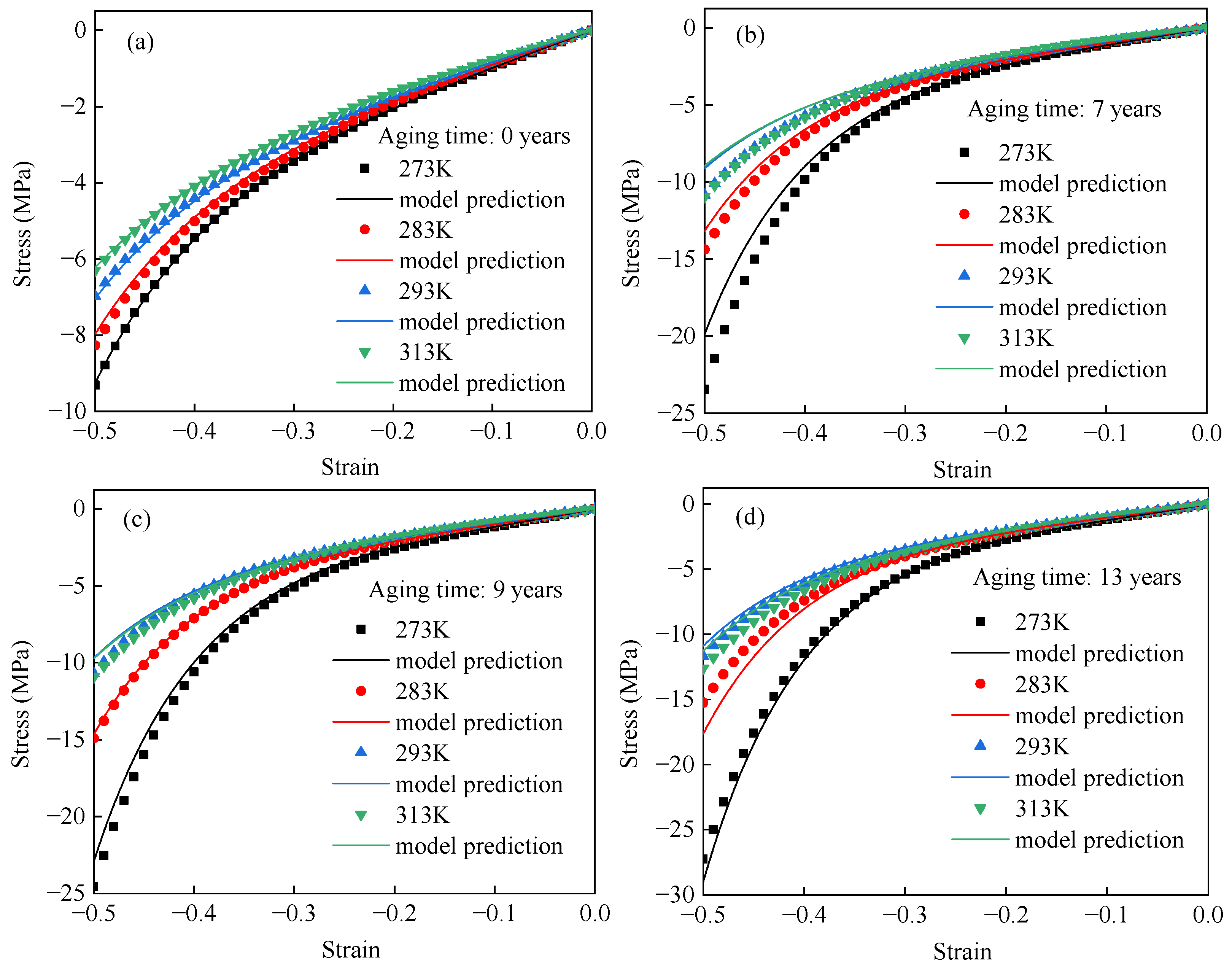
4.4. Model Verification
5. Conclusions
- (1)
- The experimental data shows that the stiffness of EPDM rubber aged for different times initially decreases and then increases with increasing temperature. The critical transition temperature decreases with increasing aging time. In addition, the stiffness of EPDM rubber increases approximately linearly with aging time at different temperatures.
- (2)
- The stress hardening factor is defined to characterize the effects of temperature on the aging effects of EPDM rubber. The results indicate that the stress hardening factor initially decreases and then increases with testing temperature.
- (3)
- The temperature-dependent hyperelastic behavior of aged rubber is analyzed using the Neo–Hooke model, the Mooney–Rivlin model, and an improved Mooney–Rivlin model. The results show that the improved Mooney–Rivlin model can accurately describe temperature-dependent hyperelastic behavior.
- (4)
- The parameters of the improved Mooney–Rivlin model were extended to incorporate the effects of temperature and aging time. Moreover, the experimental data were used to validate the proposed model, and the results show that the model can accurately capture the compression response of both unaged and aged EPDM rubber, particularly within the compression strain range of 50%.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Temperature (K) | Specimen Number | Diameter (mm) | Height (mm) |
|---|---|---|---|
| 273 K | 273K-0a-#1 | 28.48 | 12.35 |
| 273K-0a-#2 | 28.63 | 12.13 | |
| 273K-0a-#2 | 28.81 | 12.32 | |
| 283 K | 283K-0a-#1 | 28.66 | 12.31 |
| 283K-0a-#2 | 28.67 | 12.14 | |
| 283K-0a-#3 | 28.84 | 12.30 | |
| 293 K | 293K-0a-#1 | 29.02 | 12.27 |
| 293K-0a-#2 | 29.00 | 12.25 | |
| 293K-0a-#3 | 28.76 | 12.17 | |
| 313 K | 313K-0a-#1 | 28.85 | 12.30 |
| 313K-0a-#2 | 28.54 | 12.13 |
| Temperature (K) | Specimen Number | Diameter (mm) | Height (mm) |
|---|---|---|---|
| 273 K | 273K-7a-#1 | 30.53 | 10.90 |
| 273K-7a-#2 | 30.03 | 11.61 | |
| 273K-7a-#2 | 30.45 | 11.43 | |
| 283 K | 283K-7a-#1 | 30.44 | 11.03 |
| 283K-7a-#2 | 30.41 | 11.05 | |
| 283K-7a-#3 | 30.59 | 10.92 | |
| 293 K | 293K-7a-#1 | 30.27 | 11.03 |
| 293K-7a-#2 | 29.61 | 11.56 | |
| 293K-7a-#3 | 30.38 | 10.93 | |
| 313 K | 313K-7a-#1 | 30.49 | 11.20 |
| 313K-7a-#2 | 30.59 | 10.88 | |
| 313K-7a-#3 | 30.57 | 11.01 |
| Temperature (K) | Specimen Number | Diameter (mm) | Height (mm) |
|---|---|---|---|
| 273 K | 273K-9a-#1 | 30.38 | 11.00 |
| 273K-9a-#2 | 30.56 | 11.01 | |
| 273K-9a-#2 | 30.71 | 10.99 | |
| 283 K | 283K-9a-#1 | 30.45 | 11.06 |
| 283K-9a-#2 | 30.88 | 10.91 | |
| 283K-9a-#3 | 31.00 | 11.03 | |
| 293 K | 293K-9a-#1 | 30.59 | 10.82 |
| 293K-9a-#2 | 30.54 | 10.86 | |
| 293K-9a-#3 | 30.40 | 10.89 | |
| 313 K | 313K-9a-#1 | 30.67 | 10.91 |
| 313K-9a-#2 | 30.65 | 10.85 | |
| 313K-9a-#3 | 30.72 | 11.25 |
| Temperature (K) | Specimen Number | Diameter (mm) | Height (mm) |
|---|---|---|---|
| 273 K | 273K-13a-#1 | 31.03 | 10.80 |
| 273K-13a-#2 | 30.66 | 11.04 | |
| 273K-13a-#2 | 29.83 | 11.49 | |
| 283 K | 283K-13a-#1 | 30.49 | 11.20 |
| 283K-13a-#2 | 30.37 | 10.77 | |
| 283K-13a-#3 | 30.87 | 10.76 | |
| 293 K | 293K-13a-#1 | 30.50 | 10.71 |
| 293K-13a-#2 | 30.82 | 10.78 | |
| 293K-13a-#3 | 30.75 | 11.01 | |
| 313 K | 313K-13a-#1 | 30.69 | 11.04 |
| 313K-13a-#2 | 30.81 | 10.82 | |
| 313K-13a-#3 | 31.17 | 10.97 |
Appendix B


References
- Hough, P.; van der Aar, N.; Qiu, Z. Compounding and Mixing Methodology for Good Performance of EPDM in Tire Sidewalls. Tire Sci. Technol. 2020, 48, 2–21. [Google Scholar] [CrossRef]
- Wang, R.; Zhang, Y.; Wang, N.; Wu, Y. Rate-Dependent Tensile Properties of Aluminum-Hydroxide-Enhanced Ethylene Propylene Diene Monomer Coatings for Solid Rocket Motors. Materials 2024, 17, 3790. [Google Scholar] [CrossRef] [PubMed]
- Guo, M.; Li, J.; Xi, K.; Liu, Y.; Ji, J. Effect of Multi-Walled Carbon Nanotubes On Thermal Stability and Ablation Properties of EPDM Insulation Materials for Solid Rocket Motors. Acta Astronaut. 2019, 159, 508–516. [Google Scholar] [CrossRef]
- Xie, Z.; Chen, J.; Zhang, K. Lifetime Prediction of EPDM Sealing Materials with Thermal Aging Under Constant Compression. J. Phys. Conf. Ser. 2024, 2842, 012008. [Google Scholar] [CrossRef]
- Huang, X.; Gu, J.; Li, M.; Yu, X.; Liu, Y.; Xu, G. A Leakage Prediction Model for Sealing Performance Assessment of EPDM O-Rings under Irradiation Conditions. Polymers 2023, 15, 3073. [Google Scholar] [CrossRef]
- Zhou, Y.; Qiu, L.; Xu, Z.; Huang, S.; Nie, J.; Yin, H.; Tu, F.; Zhao, Z. Thermal Oxidative Aging and Service Life Prediction of Commercial Ethylene–Propylene–Diene Monomer Spacer Damping Composites for High-Voltage Transmission Lines. Polymers 2024, 16, 1186. [Google Scholar] [CrossRef]
- Hu, Q.; Chen, Q.; Song, P.; Gong, X.; Chen, J.; Zhao, Y. Performance of Thermal-Oxidative Aging on the Structure and Properties of Ethylene Propylene Diene Monomer (EPDM) Vulcanizates. Polymers 2023, 15, 2329. [Google Scholar] [CrossRef]
- Jost, C.; Lacuve, M.; Haller, S.; Espuche, E.; Colin, X. Influence of Thermo-Oxidative Aging On the Structure and the Water Transport Properties of Sulfur-Crosslinked EPDM. Polym. Degrad. Stab. 2025, 234, 111210. [Google Scholar] [CrossRef]
- Assink, R.A.; Gillen, K.T.; Sanderson, B. Monitoring the Degradation of a Thermally Aged EPDM Terpolymer by 1 H NMR Relaxation Measurements of Solvent Swelled Samples. Polymer 2002, 43, 1349–1355. [Google Scholar] [CrossRef]
- Yeoh, O.H. Characterization of Elastic Properties of Carbon-Black-Filled Rubber Vulcanizates. Rubber Chem. Technol. 1990, 63, 792–805. [Google Scholar] [CrossRef]
- Ogden, R.W. Large Deformation Isotropic Elasticity: On the Correlation of Theory and Experiment for Compressible Rubberlike Solids. Proc. R. Soc. A 1972, 328, 567–583. [Google Scholar] [CrossRef]
- Mooney, M. A Theory of Large Elastic Deformation. J. Appl. Phys. 1940, 11, 582–592. [Google Scholar] [CrossRef]
- Arruda, E.M.; Boyce, M.C. A Three-Dimensional Constitutive Model for the Large Stretch Behavior of Rubber Elastic Materials. J. Mech. Phys. Solids 1993, 41, 389–412. [Google Scholar] [CrossRef]
- Miehe, C. A Micro-Macro Approach to Rubber-Like Materials–Part I: The Non-Affine Micro-Sphere Model of Rubber Elasticity. J. Mech. Phys. Solids 2004, 52, 2617–2660. [Google Scholar] [CrossRef]
- Treloar, L.R.G. The Elasticity of a Network of Long-Chain Molecules-II. Trans. Faraday Soc. 1943, 39, 241–246. [Google Scholar] [CrossRef]
- He, H.; Zhang, Q.; Zhang, Y.; Chen, J.; Zhang, L.; Li, F. A Comparative Study of 85 Hyperelastic Constitutive Models for Both Unfilled Rubber and Highly Filled Rubber Nanocomposite Material. Nano Mater. Sci. 2022, 4, 64–82. [Google Scholar] [CrossRef]
- Dal, H.; Açıkgöz, K.; Badienia, Y. On the Performance of Isotropic Hyperelastic Constitutive Models for Rubber-Like Materials: A State of the Art Review. Appl. Mech. Rev. 2021, 73, 020802. [Google Scholar] [CrossRef]
- Beda, T. An Approach for Hyperelastic Model-Building and Parameters Estimation a Review of Constitutive Models. Eur. Polym. J. 2014, 50, 97–108. [Google Scholar] [CrossRef]
- Steinmann, P.; Hossain, M.; Possart, G. Hyperelastic Models for Rubber-Like Materials: Consistent Tangent Operators and Suitability for Treloar’s Data. Arch. Appl. Mech. 2012, 82, 1183–1217. [Google Scholar] [CrossRef]
- Lion, A. On the Large Deformation Behaviour of Reinforced Rubber at Different Temperatures. J. Mech. Phys. Solids 1997, 45, 1805–1834. [Google Scholar] [CrossRef]
- Holzapfel, G.A.; Simo, J.C. Entropy Elasticity of Isotropic Rubber-Like Solids at Finite Strains. Comput. Methods Appl. Mech. Eng. 1996, 132, 17–44. [Google Scholar] [CrossRef]
- Lu, S.C.H.; Pister, K.S. Decomposition of Deformation and Representation of the Free Energy Function for Isotropic Thermoelastic Solids. Int. J. Solids Struct. 1975, 11, 927–934. [Google Scholar] [CrossRef]
- Huang, Z. A Novel Constitutive Formulation for Rubberlike Materials in Thermoelasticity. J. Appl. Mech. 2014, 81, 041013. [Google Scholar] [CrossRef]
- Yao, X.; Wang, Z.; Ma, L.; Miao, Z.; Su, M.; Han, X.; Yang, J. Temperature Dependence of Rubber Hyper-Elasticity Based On Different Constitutive Models and their Prediction Ability. Polymers 2022, 14, 3521. [Google Scholar] [CrossRef]
- Fu, X.; Wang, Z.; Ma, L. Ability of Constitutive Models to Characterize the Temperature Dependence of Rubber Hyperelasticity and to Predict the Stress-Strain Behavior of Filled Rubber Under Different Defomation States. Polymers 2021, 13, 369. [Google Scholar] [CrossRef]
- Fu, X.; Wang, Z.; Ma, L.; Zou, Z.; Zhang, Q.; Guan, X. Temperature-Dependence of Rubber Hyperelasticity Based On the Eight-Chain Model. Polymers 2020, 12, 932. [Google Scholar] [CrossRef]
- Huang, Y.; Li, Y.; Zhao, H.; Wen, H. Research On Constitutive Models of Hydrogenated Nitrile Butadiene Rubber for Packer at Different Temperatures. J. Mech. Sci. Technol. 2020, 34, 155–164. [Google Scholar] [CrossRef]
- Li, X.; Dong, Y.; Li, Z.; Xia, Y. Experimental Study On the Temperature Dependence of Hyperelastic Behavior of Tire Rubbers Under Moderate Finite Deformation. Rubber Chem. Technol. 2011, 84, 215–228. [Google Scholar] [CrossRef]
- Jin, L.; Xue, Z.; Wang, Z.; Li, R.; Liu, J. Mechanical Response of the Sealing Packer Based On Two Rubber Materials at High Temperatures. Polym. Test. 2023, 124, 108073. [Google Scholar] [CrossRef]
- Ovalle Rodas, C.; Zaïri, F.; Naït-Abdelaziz, M.; Charrier, P. Temperature and Filler Effects On the Relaxed Response of Filled Rubbers: Experimental Observations On a Carbon-Filled SBR and Constitutive Modeling. Int. J. Solids Struct. 2015, 58, 309–321. [Google Scholar] [CrossRef]
- Li, X.; Bai, T.; Li, Z.; Liu, L. Influence of the Temperature On the Hyper-Elastic Mechanical Behavior of Carbon Black Filled Natural Rubbers. Mech. Mater. 2016, 95, 136–145. [Google Scholar] [CrossRef]
- Jiang, D.; Wang, Z.; Wang, X. A General Hyperelastic Model for Rubber-Like Materials Incorporating Strain-Rate and Temperature. J. Elastomers Plast. 2024, 56, 624–651. [Google Scholar] [CrossRef]
- Yan, S.; Jia, D.; Yu, Y.; Wang, L.; Qiu, Y.; Wan, Q. Influence of Γ-Irradiation On Mechanical Behaviors of Poly Methyl-Vinyl Silicone Rubber Foams at Different Temperatures. Mech. Mater. 2020, 151, 103639. [Google Scholar] [CrossRef]
- Korba, A.G.; Kumar, A.; Barkey, M. A Hyper-Elastic Thermal Aging Constitutive Model for Rubber-Like Materials. J. Elastomers Plast. 2020, 52, 677–700. [Google Scholar] [CrossRef]
- Lou, W.; Xie, C.; Guan, X. Thermal-Aging Constitutive Model for a Silicone Rubber Foam Under Compression. Polym. Degrad. Stab. 2022, 198, 109873. [Google Scholar] [CrossRef]
- Li, Q.; Xu, Z.D.; Tong, Q.S.; Dong, Y.R.; Xu, Y.S.; Lu, Y. Mechanical Properties of Viscoelastic Materials Subjected to Thermal-Oxidative Aging: An Experimental and Theoretical Study. J. Appl. Polym. Sci. 2023, 140, e54667. [Google Scholar] [CrossRef]
- Li, Q.; Xu, Z.; Dong, Y.; He, Z.; He, J.; Yan, X. Hyperelastic Hybrid Molecular Chain Model of Thermal-Oxidative Aging Viscoelastic Damping Materials Based on Physical–Chemical Process. J. Eng. Mech. 2023, 149, 04022099. [Google Scholar] [CrossRef]
- Ha-Anh, T.; Vu-Khanh, T. Prediction of Mechanical Properties of Polychloroprene During Thermo-Oxidative Aging. Polym. Test. 2005, 24, 775–780. [Google Scholar] [CrossRef]
- Hu, X.; Yang, X.; Jiang, X.; Song, K. Constitutive Model for Thermal-Oxygen-Aged EPDM Rubber Based on the Arrhenius Law. Polymers 2024, 16, 2608. [Google Scholar] [CrossRef]
- Xie, Z.; Huang, X.; Zhang, K.; Yan, S.; Chen, J.; He, R.; Li, J.; Zhong, W. Thermo-Oxidative Aging Effects on Hyperelastic Behavior of EPDM Rubber: A Constitutive Modeling Approach. Materials 2025, 18, 2236. [Google Scholar] [CrossRef]
- Shakiba, M.; Najmeddine, A. Physics-Based Constitutive Equation for Thermochemically Aged Elastomers Based On Crosslink Density Evolution. J. Mech. Mater. Struct. 2022, 17, 229–246. [Google Scholar] [CrossRef]
- Zhi, J.; Wang, Q.; Zhang, M.; Zhou, Z.; Liu, A.; Jia, Y. Coupled Analysis On Hyper-Viscoelastic Mechanical Behavior and Macromolecular Network Alteration of Rubber During Thermo-Oxidative Aging Process. Polymer 2019, 171, 15–24. [Google Scholar] [CrossRef]
- Li, K.; Zheng, J.; Zhi, J.; Zhang, K. Aging Constitutive Model of Hydroxyl-Terminated Polybutadiene Coating in Solid Rocket Motor. Acta Astronaut. 2018, 151, 555–562. [Google Scholar] [CrossRef]
- Du, Y.; Zheng, J.; Xiong, C. Cross-Linking Density and Aging Constitutive Model of HTPB Coating Under Prestrain Thermal Accelerated Aging. Def. Technol. 2020, 16, 439–446. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, Q.; Liu, R.; Chen, M.; Zhang, C.; Li, X.; Li, W.; Wang, H. Compressive Stress-Hydrothermal Aging Behavior and Constitutive Model of Shield Tunnel EPDM Rubber Material. Constr. Build. Mater. 2022, 320, 126298. [Google Scholar] [CrossRef]
- Wang, S.; Xu, J.; Li, H.; Liu, J.; Zhou, C. The Effect of Thermal Aging On the Mechanical Properties of Ethylene Propylene Diene Monomer Charge Coating. Mech. Time-Depend. Mater. 2022, 28, 321–336. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, F.; Guo, J.; Xue, J.; Yi, Z. Sealing Properties of EPDM Intercalation Composite Rings in High Temperature. Lubr. Eng. 2014, 39, 107–109. (In Chinese) [Google Scholar]
- Gong, C.; Xie, C.; Zhu, H.; Ding, W.; Song, J.; Ge, Y. Time-Varying Compressive Properties and Constitutive Model of EPDM Rubber Materials for Tunnel Gasketed Joint. Constr. Build. Mater. 2024, 433, 136734. [Google Scholar] [CrossRef]
- Celina, M.; Gillen, K.T.; Assink, R.A. Accelerated Aging and Lifetime Prediction: Review of non-Arrhenius Behaviour Due to Two Competing Processes. Polym. Degrad. Stab. 2005, 90, 395–404. [Google Scholar] [CrossRef]
- Cui, Z.; Liu, W.; Tan, L.; Sun, G.; Hu, X. Evidence for non-Arrhenius Behavior of EPDM Rubber by Combining Arrhenius and Time–Temperature Superposition (TTS) Extrapolations. RSC Adv. 2024, 14, 5216–5221. [Google Scholar] [CrossRef]
- Ben Hassine, M.; Naït-Abdelaziz, M.; Zaïri, F.; Colin, X.; Tourcher, C.; Marque, G. Time to Failure Prediction in Rubber Components Subjected to Thermal Ageing: A Combined Approach Based upon the Intrinsic Defect Concept and the Fracture Mechanics. Mech. Mater. 2014, 79, 15–24. [Google Scholar] [CrossRef]
- Lee, J.H.; Bae, J.W.; Kim, J.S.; Hwang, T.J.; Park, S.D.; Park, S.H.; Yeo, T.M.; Kim, W.; Jo, N. Life-Time Prediction of a Chloroprene Rubber (CR) O-ring Using Intermittent Compression Stress Relaxation (CSR) and Time-Temperature Superposition (TTS) Principle. Macromol. Res. 2011, 19, 555–562. [Google Scholar] [CrossRef]
- Bouaziz, R.; Ahose, K.D.; Lejeunes, S.; Eyheramendy, D.; Sosson, F. Characterization and Modeling of Filled Rubber Submitted to Thermal Aging. Int. J. Solids Struct. 2019, 169, 122–140. [Google Scholar] [CrossRef]
- Guo, J.; Xu, P.; Lv, J.; Han, X.; Sun, Y.; Hou, D.; Yuan, Z.; Li, C. Ageing Behaviour and Molecular/Network Structure Evolution of EPDM/carbon Black Composites Under Compression and in Thermal-Oxidative Environments. Polym. Degrad. Stab. 2023, 214, 110417. [Google Scholar] [CrossRef]






| Ingredients | Value [phr] |
|---|---|
| EPDM EPT4045 | 100 |
| Carbon black N330 | 30 |
| Organo-modified montmorillonite | 25 |
| Compatibilizer EPDM-g-MAH | 10 |
| Zinc oxide | 5 |
| Antioxidant poly(1,2-dihydro-2,2,4-trimethyl-quinoline) | 3 |
| Vulcanizator 2,5-Dimethyl-2,5-di(tert-butylperoxy) hexane | 3 |
| Aging Time (Years) | Temperature (K) | Neo–Hooke Model | Mooney–Rivlin Model | Improved Mooney–Rivlin Model | |||
|---|---|---|---|---|---|---|---|
| R2 (%) | The Maximum Relative Error (%) | R2 (%) | The Maximum Relative Error (%) | R2 (%) | The Maximum Relative Error (%) | ||
| 0 | 273 | 99.83 | 12.90 | 99.83 | 12.99 | 99.99 | 2.08 |
| 283 | 99.82 | 14.98 | 99.88 | 11.33 | 99.99 | 2.13 | |
| 293 | 99.44 | 19.25 | 99.90 | 10.11 | 99.99 | 2.06 | |
| 313 | 99.18 | 19.66 | 99.93 | 8.16 | 99.99 | 1.67 | |
| 7 | 273 | 91.33 | 60.14 | 99.60 | 38.41 | 1.00 | 5.44 |
| 283 | 96.36 | 27.56 | 99.80 | 22.43 | 1.00 | 0.87 | |
| 293 | 98.64 | 11.63 | 99.76 | 19.24 | 1.00 | 1.08 | |
| 313 | 98.26 | 24.68 | 99.97 | 8.16 | 1.00 | 2.42 | |
| 9 | 273 | 92.02 | 56.23 | 99.68 | 36.20 | 1.00 | 2.06 |
| 283 | 96.06 | 27.80 | 99.75 | 23.55 | 1.00 | 2.19 | |
| 293 | 98.48 | 12.44 | 99.74 | 19.64 | 1.00 | 1.91 | |
| 313 | 98.59 | 16.00 | 99.92 | 10.97 | 1.00 | 2.58 | |
| 13 | 273 | 91.02 | 65.04 | 99.66 | 38.98 | 1.00 | 3.52 |
| 283 | 96.47 | 26.45 | 99.77 | 23.41 | 1.00 | 0.97 | |
| 293 | 98.47 | 12.54 | 99.70 | 21.00 | 1.00 | 1.15 | |
| 313 | 98.32 | 15.85 | 99.88 | 15.10 | 1.00 | 1.31 | |
| Aging Time (Years) | Temperature (K) | C10 | C20 | C01 |
|---|---|---|---|---|
| 0 | 273 | 3.475 | 0.610 | −1.838 |
| 283 | 2.930 | 0.449 | −1.439 | |
| 293 | 2.625 | 0.355 | −1.262 | |
| 313 | 2.297 | 0.270 | −1.038 | |
| 7 | 273 | 6.366 | 2.268 | −4.344 |
| 283 | 3.638 | 1.023 | −2.070 | |
| 293 | 3.636 | 0.841 | −2.095 | |
| 313 | 1.496 | 0.301 | −0.345 | |
| 9 | 273 | 6.144 | 2.181 | −4.038 |
| 283 | 4.144 | 1.183 | −2.487 | |
| 293 | 3.661 | 0.864 | −2.150 | |
| 313 | 2.329 | 0.497 | −1.006 | |
| 13 | 273 | 6.661 | 2.471 | −4.464 |
| 283 | 4.205 | 1.168 | −2.472 | |
| 293 | 4.272 | 1.016 | −2.574 | |
| 313 | 3.124 | 0.719 | −1.560 |
| Aging-Related | Unaged-Related | ||
|---|---|---|---|
| Parameter | Value | Parameter | Value |
| a11 | 1.4797 × 10−4 | a01 | 7.0118 × 10−4 |
| b11 | −0.0928 | b01 | −0.4399 |
| c11 | 14.5606 | c01 | 71.3091 |
| a12 | 1.2734 × 10−4 | a02 | 2.2128 × 10−4 |
| b12 | −0.0781 | b02 | −0.1380 |
| c12 | 11.9758 | c02 | 21.7822 |
| a13 | −1.1580 × 10−4 | a03 | −5.0176 × 10−4 |
| b13 | 0.07315 | b03 | 0.3135 |
| c13 | −11.5622 | c03 | −50.0245 |
| Aging Time (Years) | Temperature (K) | The Maximum Relative Error (%) |
|---|---|---|
| 0 | 273 | 2.38 |
| 283 | 3.73 | |
| 293 | 3.00 | |
| 313 | 1.48 | |
| 7 | 273 | 15.21 |
| 283 | 8.43 | |
| 293 | 15.92 | |
| 313 | 18.25 | |
| 9 | 273 | 7.00 |
| 283 | 4.90 | |
| 293 | 9.20 | |
| 313 | 11.02 | |
| 13 | 273 | 6.43 |
| 283 | 15.71 | |
| 293 | 6.80 | |
| 313 | 10.58 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, Z.; Jia, D.; Huang, X.; Zhang, K.; Yan, S.; Chen, J.; Li, J.; Zhong, W. Influence of Temperature on Hyperelastic Mechanical Behavior of Accelerated Aged EPDM Rubber. Polymers 2025, 17, 1626. https://doi.org/10.3390/polym17121626
Xie Z, Jia D, Huang X, Zhang K, Yan S, Chen J, Li J, Zhong W. Influence of Temperature on Hyperelastic Mechanical Behavior of Accelerated Aged EPDM Rubber. Polymers. 2025; 17(12):1626. https://doi.org/10.3390/polym17121626
Chicago/Turabian StyleXie, Zhaonan, Dong Jia, Xicheng Huang, Kai Zhang, Shunping Yan, Junhong Chen, Jiaxing Li, and Weizhou Zhong. 2025. "Influence of Temperature on Hyperelastic Mechanical Behavior of Accelerated Aged EPDM Rubber" Polymers 17, no. 12: 1626. https://doi.org/10.3390/polym17121626
APA StyleXie, Z., Jia, D., Huang, X., Zhang, K., Yan, S., Chen, J., Li, J., & Zhong, W. (2025). Influence of Temperature on Hyperelastic Mechanical Behavior of Accelerated Aged EPDM Rubber. Polymers, 17(12), 1626. https://doi.org/10.3390/polym17121626







