Investigation of Thermomechanical Properties of Hollow Glass Microballoon-Filled Composite Materials Developed by Additive Manufacturing with Machine Learning Validation
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Preparation of the Samples
2.3. Mechanical Testing
2.4. Dynamic Mechanical Analysis (DMA)
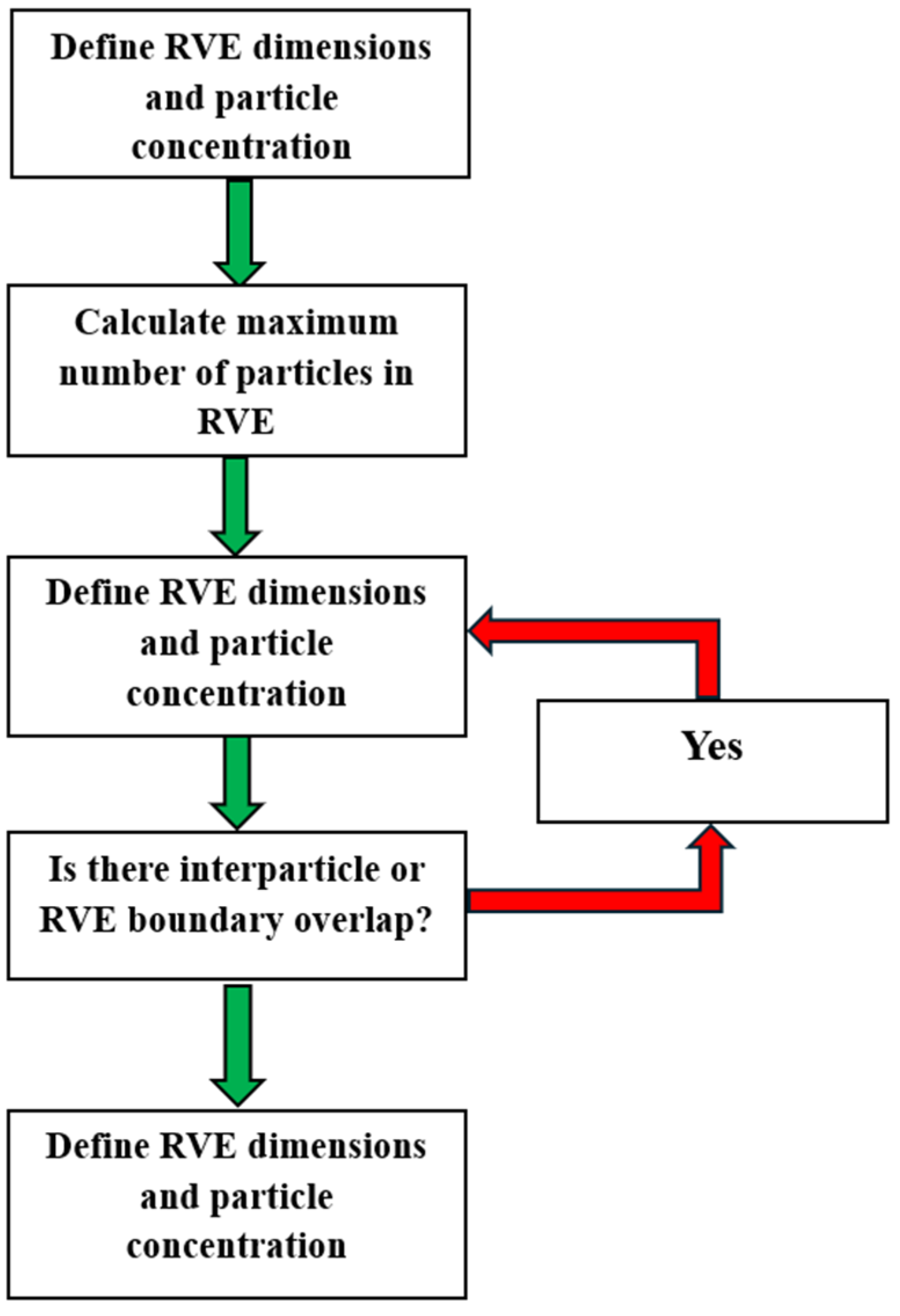
2.5. Numerical Analysis
2.6. Analysis by Machine Learning Model
- is the number of data points
- is the actual value
- is the predicted value
- is the mean of the actual values
3. Results and Discussion
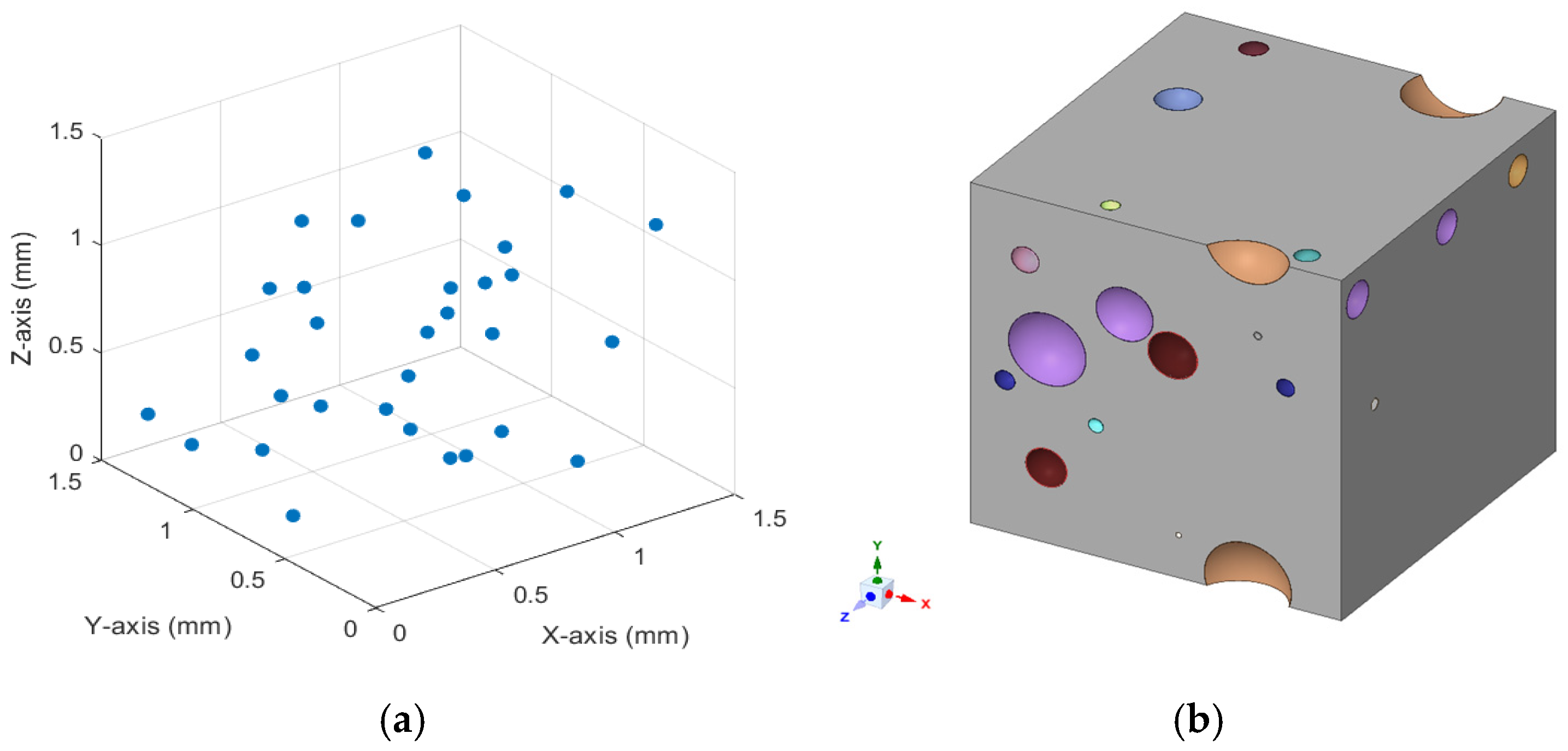
3.1. Microstructural Characterization
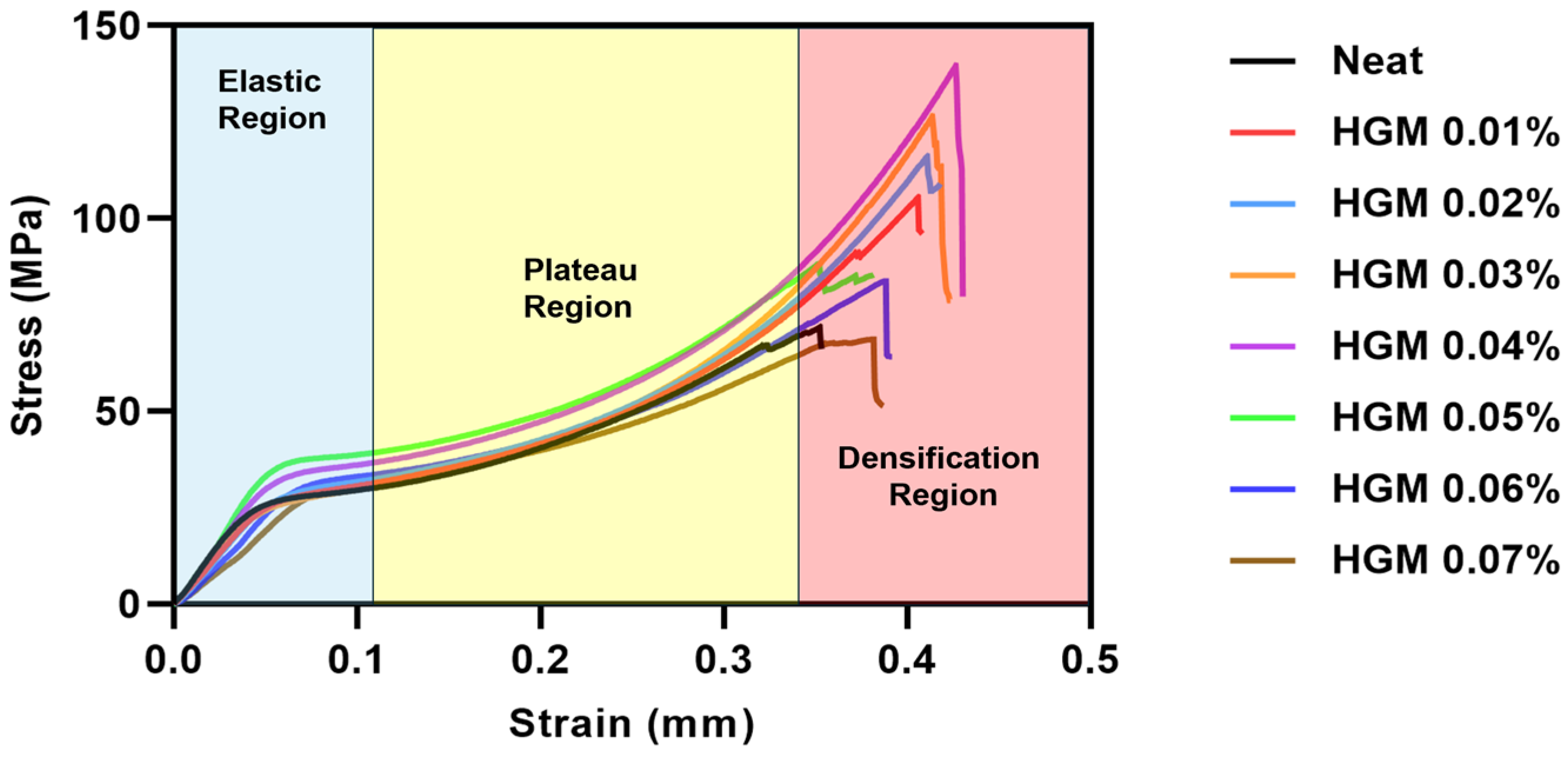
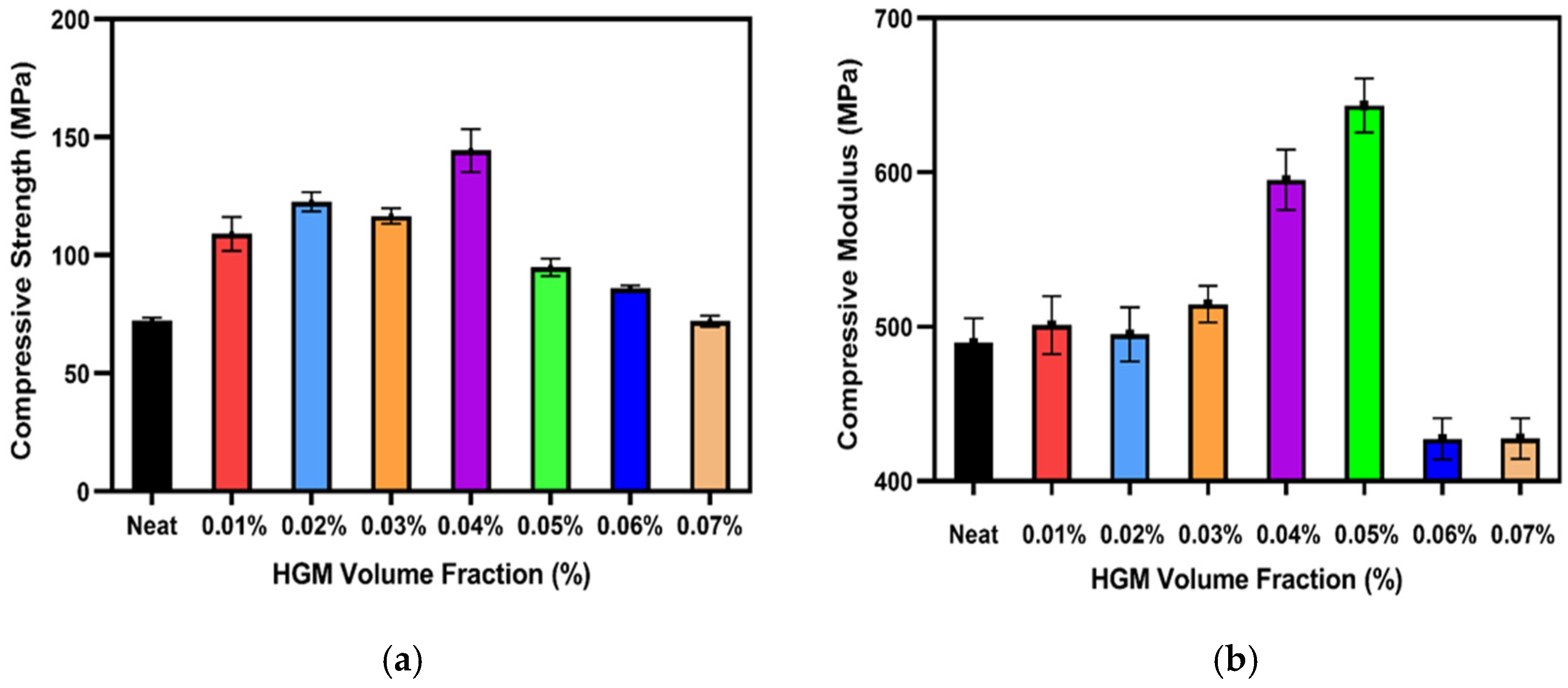
3.2. Mechanical Properties
3.3. Failure Mechanism
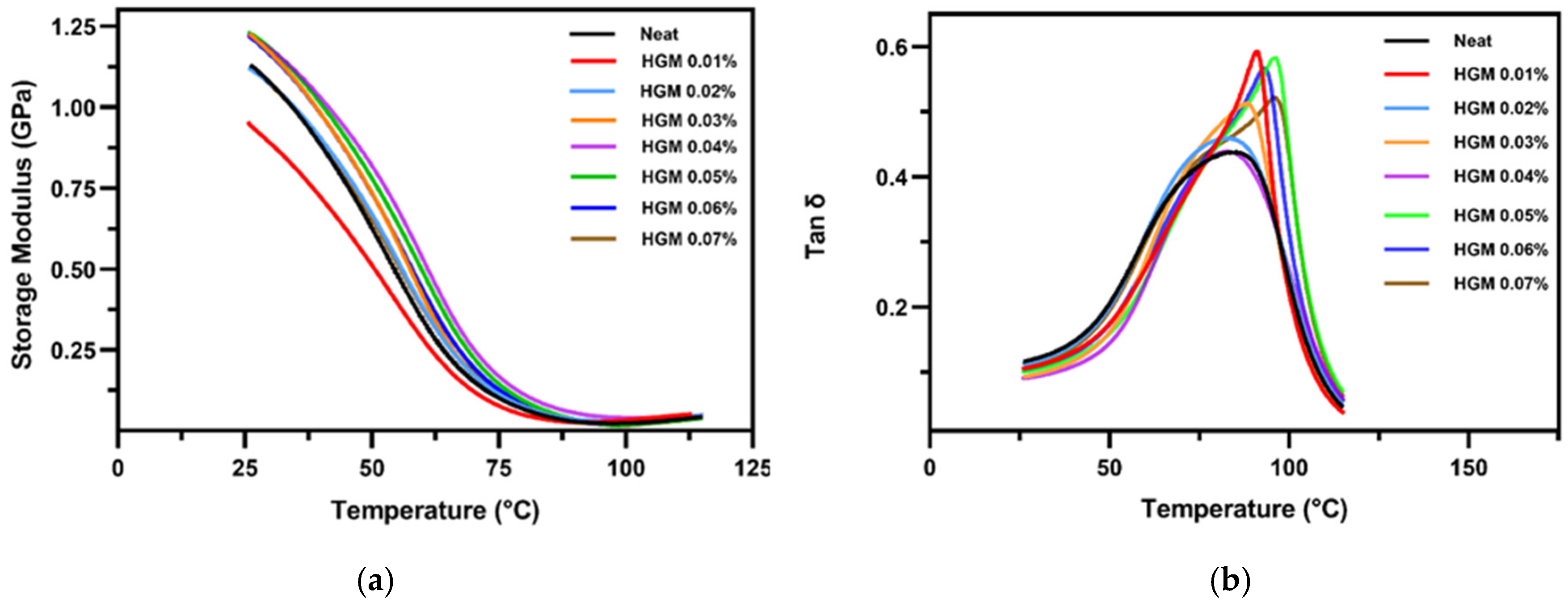
3.4. Dynamic Mechanical Analysis Results
3.5. Numerical Simulation with ANSYS
3.6. Prediction with ML Model
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Afolabi, L.O.; Ariff, Z.M.; Hashim, S.F.S.; Alomayri, T.; Mahzan, S.; Kamarudin, K.-A.; Muhammad, I.D. Syntactic foams formulations, production techniques, and industry applications: A review. J. Mater. Res. Technol. 2020, 9, 10698–10718. [Google Scholar] [CrossRef]
- Chitrakar, R.; Hossain, M.S.; Nilufar, S. The Effect of Microballoon Volume Fraction on the Elastic and Viscoelastic Properties of Hollow Microballoon-Filled Epoxy Composites. Materials 2023, 16, 7554. [Google Scholar] [CrossRef] [PubMed]
- Nawafleh, N.; Wright, W.; Dariavach, N.; Celik, E. 3D-printed thermoset syntactic foams with tailorable mechanical performance. J. Mater. Sci. 2020, 55, 16048–16057. [Google Scholar] [CrossRef]
- Kumar, B.B.; Doddamani, M.; Zeltmann, S.E.; Gupta, N.; Ramesh, M.; Ramakrishna, S. Processing of cenosphere/HDPE syntactic foams using an industrial scale polymer injection molding machine. Mater. Des. 2016, 92, 414–423. [Google Scholar] [CrossRef]
- Spratt, M.; Newkirk, J.W.; Chandrashekhara, K. Aluminum Matrix Syntactic Foam Fabricated with Additive Manufacturing. 2017. Available online: https://scholarsmine.mst.edu/cgi/viewcontent.cgi?article=3243&context=matsci_eng_facwork (accessed on 25 May 2025).
- Myers, K.; Cortes, P.; Conner, B.; Wagner, T.; Hetzel, B.; Peters, K. Structure property relationship of metal matrix syntactic foams manufactured by a binder jet printing process. Addit. Manuf. 2015, 5, 54–59. [Google Scholar] [CrossRef]
- Shah, D.M.; Morris, J.; Plaisted, T.A.; Amirkhizi, A.V.; Hansen, C.J. Highly filled resins for DLP-based printing of low density, high modulus materials. Addit. Manuf. 2021, 37, 101736. [Google Scholar] [CrossRef]
- Nawafleh, N.; Chabot, J.; Aljaghtham, M.; Oztan, C.; Dauer, E.; Gorguluarslan, R.M.; Demir, T.; Celik, E. Additive manufacturing of Kevlar reinforced epoxy composites. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Salt Lake City, UT, USA, 11–14 November 2019; p. V02AT02A067. [Google Scholar]
- Tagliavia, G.; Porfiri, M.; Gupta, N. Analysis of flexural properties of hollow-particle filled composites. Compos. Part B Eng. 2010, 41, 86–93. [Google Scholar] [CrossRef]
- Zhong, W.; Li, F.; Zhang, Z.; Song, L.; Li, Z. Short fiber reinforced composites for fused deposition modeling. Mater. Sci. Eng. A 2001, 301, 125–130. [Google Scholar] [CrossRef]
- Lawrence, J. Effects of Print Process Parameters on Droplet-Powder Interaction in Binder Jet Additive Manufacturing. Master’s Thesis, Brigham Young University, Provo, UT, USA, 2024. [Google Scholar]
- Nath, S.D.; Nilufar, S. An Overview of Additive Manufacturing of Polymers and Associated Composites. Polymers 2020, 12, 2719. [Google Scholar] [CrossRef]
- Jacobs, P.F. Fundamentals of Stereolithography. 1992. Available online: https://repositories.lib.utexas.edu/server/api/core/bitstreams/03e894c8-0920-41fe-a42c-9e91539cebc4/content (accessed on 25 May 2025).
- Melchels, F.P.; Feijen, J.; Grijpma, D.W. A review on stereolithography and its applications in biomedical engineering. Biomaterials 2010, 31, 6121–6130. [Google Scholar] [CrossRef]
- McMenamin, P.G.; Quayle, M.R.; McHenry, C.R.; Adams, J.W. The production of anatomical teaching resources using three-dimensional (3D) printing technology. Anat. Sci. Educ. 2014, 7, 479–486. [Google Scholar] [CrossRef] [PubMed]
- Ngo, T.D.; Kashani, A.; Imbalzano, G.; Nguyen, K.T.; Hui, D. Additive manufacturing (3D printing): A review of materials, methods, applications and challenges. Compos. Part B Eng. 2018, 143, 172–196. [Google Scholar] [CrossRef]
- Bártolo, P.J. Stereolithography: Materials, Processes and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Ligon, S.C.; Liska, R.; Stampfl, J.; Gurr, M.; Mulhaupt, R. Polymers for 3D printing and customized additive manufacturing. Chem. Rev. 2017, 117, 10212–10290. [Google Scholar] [CrossRef] [PubMed]
- Dizon, J.R.C.; Espera Jr, A.H.; Chen, Q.; Advincula, R.C. Mechanical characterization of 3D-printed polymers. Addit. Manuf. 2018, 20, 44–67. [Google Scholar] [CrossRef]
- Zhu, W.; Ma, X.; Gou, M.; Mei, D.; Zhang, K.; Chen, S. 3D printing of functional biomaterials for tissue engineering. Curr. Opin. Biotechnol. 2016, 40, 103–112. [Google Scholar] [CrossRef]
- Guo, N.; Leu, M.C. Additive manufacturing: Technology, applications and research needs. Front. Mech. Eng. 2013, 8, 215–243. [Google Scholar] [CrossRef]
- Afolabi, O.A. Hybrid Syntactic Foam Core Cased Natural-Glass Fibre Sandwich Composite; Durban University of Technology: Durban, South Africa, 2023. [Google Scholar]
- Singh, A.K.; Deptula, A.J.; Anawal, R.; Doddamani, M.; Gupta, N. Additive manufacturing of three-phase syntactic foams containing glass microballoons and air pores. JOM 2019, 71, 1520–1527. [Google Scholar] [CrossRef]
- Pack, R.C.; Romberg, S.K.; Badran, A.A.; Hmeidat, N.S.; Yount, T.; Compton, B.G. Carbon fiber and syntactic foam hybrid materials via core–shell material extrusion additive manufacturing. Adv. Mater. Technol. 2020, 5, 2000731. [Google Scholar] [CrossRef]
- Mummareddy, B.; Burden, E.; Carrillo, J.; Myers, K.; MacDonald, E.; Cortes, P. Mechanical performance of lightweight ceramic structures via binder jetting of microspheres. SN Appl. Sci. 2021, 3, 402. [Google Scholar] [CrossRef]
- Senthooran, V.; Weng, Z.; Wu, L. Enhancing Mechanical and Thermal Properties of 3D-Printed Samples Using Mica-Epoxy Acrylate Resin Composites—Via Digital Light Processing (DLP). Polymers 2024, 16, 1148. [Google Scholar] [CrossRef]
- Spoerk, M.; Savandaiah, C.; Arbeiter, F.; Sapkota, J.; Holzer, C. Optimization of mechanical properties of glass-spheres-filled polypropylene composites for extrusion-based additive manufacturing. Polym. Compos. 2019, 40, 638–651. [Google Scholar] [CrossRef]
- Bharath, H.; Bonthu, D.; Prabhakar, P.; Doddamani, M. Three-dimensional printed lightweight composite foams. ACS Omega 2020, 5, 22536. [Google Scholar]
- Galvagnini, F.; Fredi, G.; Dorigato, A.; Fambri, L.; Pegoretti, A. Mechanical behaviour of multifunctional epoxy/hollow glass microspheres/paraffin microcapsules syntactic foams for thermal management. Polymers 2021, 13, 2896. [Google Scholar] [CrossRef]
- Boaretto, J.; Cruz, R.C.D.; Vannucchi de Camargo, F.; Cordeiro, G.L.; Fragassa, C.; Bergmann, C.P. Using Thermomechanical Properties to Reassess Particles’ Dispersion in Nanostructured Polymers: Size vs. Content. Polymers 2023, 15, 3707. [Google Scholar] [CrossRef]
- Bharath, H.; Sawardekar, A.; Waddar, S.; Jeyaraj, P.; Doddamani, M. Mechanical behavior of 3D printed syntactic foam composites. Compos. Struct. 2020, 254, 112832. [Google Scholar] [CrossRef]
- Verheyen, C.A.; Uzel, S.G.; Kurum, A.; Roche, E.T.; Lewis, J.A. Integrated data-driven modeling and experimental optimization of granular hydrogel matrices. Matter 2023, 6, 1015–1036. [Google Scholar] [CrossRef]
- Szymanik, B. An Evaluation of 3D-Printed Materials’ Structural Properties Using Active Infrared Thermography and Deep Neural Networks Trained on the Numerical Data. Materials 2022, 15, 3727. [Google Scholar] [CrossRef]
- Rezapour Sarabi, M.; Alseed, M.M.; Karagoz, A.A.; Tasoglu, S. Machine learning-enabled prediction of 3D-printed microneedle features. Biosensors 2022, 12, 491. [Google Scholar] [CrossRef]
- Mohammad, S.; Akand, R.; Cook, K.M.; Nilufar, S.; Chowdhury, F. Leveraging Deep Learning and Generative AI for Predicting Rheological Properties and Material Compositions of 3D Printed Polyacrylamide Hydrogels. Gels 2024, 10, 660. [Google Scholar] [CrossRef]
- Cho, Y.J.; Lee, W.; Park, Y.H. Finite element modeling of tensile deformation behaviors of iron syntactic foam with hollow glass microspheres. Materials 2017, 10, 1201. [Google Scholar] [CrossRef]
- Antunes, F.; Ferreira, J.; Capela, C. Numerical modelling of the Young’s modulus of syntactic foams. Finite Elem. Anal. Des. 2011, 47, 78–84. [Google Scholar] [CrossRef]
- Nguyen, N.Q.; Gupta, N. Analyzing the effect of fiber reinforcement on properties of syntactic foams. Mater. Sci. Eng. A 2010, 527, 6422–6428. [Google Scholar] [CrossRef]
- Gupta, N.; Woldesenbet, E.; Mensah, P. Compression properties of syntactic foams: Effect of cenosphere radius ratio and specimen aspect ratio. Compos. Part A Appl. Sci. Manuf. 2004, 35, 103–111. [Google Scholar] [CrossRef]
- Ali, M.; Rubel, R.; Yusuf, S.; Siddique, M.A. A review on syntactic foams processing, preparation and applications. In Proceedings of the International Conference on Mechanical Engineering and Renewable Energy, Chittagong, Bangladesh, 11–13 December 2019. [Google Scholar]
- Li, G.; Jones, N. Development of rubberized syntactic foam. Compos. Part A Appl. Sci. Manuf. 2007, 38, 1483–1492. [Google Scholar] [CrossRef]
- Huang, R.; Li, P.; Liu, T. X-ray microtomography and finite element modelling of compressive failure mechanism in cenosphere epoxy syntactic foams. Compos. Struct. 2016, 140, 157–165. [Google Scholar] [CrossRef]
- Huang, R.; Li, P. Elastic behaviour and failure mechanism in epoxy syntactic foams: The effect of glass microballoon volume fractions. Compos. Part B Eng. 2015, 78, 401–408. [Google Scholar] [CrossRef]
- ASTM D695-15; Standard Test Method for Compressive Properties of Rigid Plastics. ASTM International: West Conshohocken, PA, USA, 2015.
- Nath, S.D.; Nilufar, S. Performance evaluation of sandwich structures printed by vat photopolymerization. Polymers 2022, 14, 1513. [Google Scholar] [CrossRef]
- ASTM D7028-15; Standard Test Method for Glass Transition Temperature (DMA Tg) of Polymer Matrix Composites by Dynamic Mechanical Analysis (DMA). ASTM International: West Conshohocken, PA, USA, 2015.
- Carolan, D.; Mayall, A.; Dear, J.; Fergusson, A. Micromechanical modelling of syntactic foam. Compos. Part B Eng. 2020, 183, 107701. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Harris, C.R.; Millman, K.J.; Van Der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.J. Array programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef]
- McKinney, W. Pandas: A Foundational Python Library for Data Analysis and Statistics. 2011. Available online: https://www.researchgate.net/publication/265194455_pandas_a_Foundational_Python_Library_for_Data_Analysis_and_Statistics (accessed on 25 May 2025).
- Fabian, P. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825. [Google Scholar]
- Hunter, J.D. Matplotlib: A 2D graphics environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]
- Saha, M.C.; Nilufar, S. Nanoclay-reinforced syntactic foams: Flexure and thermal behavior. Polym. Compos. 2010, 31, 1332–1342. [Google Scholar] [CrossRef]
- Pagliocca, N.; Youssef, G.; Koohbor, B. In-Plane mechanical and failure responses of honeycombs with syntactic foam cell walls. Compos. Struct. 2022, 295, 115866. [Google Scholar] [CrossRef]
- Wang, X.; Jiang, M.; Zhou, Z.; Gou, J.; Hui, D. 3D printing of polymer matrix composites: A review and prospective. Compos. Part B Eng. 2017, 110, 442–458. [Google Scholar] [CrossRef]
- Saha, M.C.; Nilufar, S.; Major, M.; Jeelani, S. Processing and performance evaluation of hollow microspheres filled epoxy composites. Polym. Compos. 2008, 29, 293–301. [Google Scholar] [CrossRef]
- Ullas, A.; Kumar, D.; Roy, P.K. Epoxy-Glass Microballoon Syntactic Foams: Rheological Optimization of the Processing Window. Adv. Polym. Technol. 2019, 2019, 9180302. [Google Scholar] [CrossRef]
- Huffman, B.; Singh, A.; Koohbor, B.; Youssef, G. Vat Photopolymerization 3D Printing of Glass Microballoon-Reinforced TPMS Meta-Structures. Compos. Part B Eng. 2024, 287, 111799. [Google Scholar] [CrossRef]
- Huang, C.; Huang, Z.; Qin, Y.; Ding, J.; Lv, X. Mechanical and dynamic mechanical properties of epoxy syntactic foams reinforced by short carbon fiber. Polym. Compos. 2016, 37, 1960–1970. [Google Scholar] [CrossRef]
- Turi, E. Thermal Characterization of Polymeric Materials; Academic Press: New York, NY, USA, 2012. [Google Scholar]
- Jawaid, M.; Khalil, H.A.; Alattas, O.S. Woven hybrid biocomposites: Dynamic mechanical and thermal properties. Compos. Part A Appl. Sci. Manuf. 2012, 43, 288–293. [Google Scholar] [CrossRef]
- Vaezi, M.; Seitz, H.; Yang, S. A review on 3D micro-additive manufacturing technologies. Int. J. Adv. Manuf. Technol. 2013, 67, 1721–1754. [Google Scholar] [CrossRef]
- Mohan, N.; Senthil, P.; Vinodh, S.; Jayanth, N. A review on composite materials and process parameters optimisation for the fused deposition modelling process. Virtual Phys. Prototyp. 2017, 12, 47–59. [Google Scholar] [CrossRef]
- Sankaran, S.; Sekhar, K.R.; Raju, G.; Kumar, M.J. Characterization of epoxy syntactic foams by dynamic mechanical analysis. J. Mater. Sci. 2006, 41, 4041–4046. [Google Scholar] [CrossRef]
- Menard, K.P.; Menard, N. Dynamic Mechanical Analysis; CRC Press: Boca Raton, FL, USA, 2020. [Google Scholar]
- Islam, M.T.; Chowdhury, S.A.; Islam, M.T.; Hossain, M.S. A comparative study of heat formation in various metals due to different types of stresses using finite element analysis. In Proceedings of the AIP Conference, Dhaka, Bangladesh, 19–21 December 2018. [Google Scholar]





| Samples | Composition |
|---|---|
| Neat | Resin without any glass microballoon |
| HGM 0.01% | 0.01 vol% glass microballoon with neat resin |
| HGM 0.02% | 0.02 vol% glass microballoon with neat resin |
| HGM 0.03% | 0.03 vol% glass microballoon with neat resin |
| HGM 0.04% | 0.04 vol% glass microballoon with neat resin |
| HGM 0.05% | 0.05 vol% glass microballoon with neat resin |
| HGM 0.06% | 0.06 vol% glass microballoon with neat resin |
| HGM 0.07% | 0.07 vol% glass microballoon with neat resin |
| Parameter | Value |
|---|---|
| Slice thickness | 100 µm |
| Number of base layers | 5 |
| Bottom exposure time | 30 s |
| Curing time of the layers | 10 s |
| Lifting distance | 6 mm |
| Lifting speed | 60 mm/min |
| Retraction speed | 150 mm/min |
| Samples | E′ at 30 °C (GPa) | E′ at 105 °C (GPa) | Tg | E″ at 105 °C (GPa) |
|---|---|---|---|---|
| Neat | 1.074 | 0.028 | 85 | 0.004 |
| HGM 0.01% | 0.887 | 0.041 | 91 | 0.005 |
| HGM 0.02% | 1.070 | 0.036 | 82 | 0.005 |
| HGM 0.03% | 1.169 | 0.034 | 88 | 0.004 |
| HGM 0.04% | 1.179 | 0.041 | 82 | 0.007 |
| HGM 0.05% | 1.180 | 0.026 | 96 | 0.006 |
| HGM 0.06% | 1.162 | 0.033 | 93 | 0.006 |
| HGM 0.07% | 1.067 | 0.024 | 96 | 0.005 |
| Samples | MSE | MAE | R2 Score |
|---|---|---|---|
| Neat | 0.0212 | 0.0858 | 0.9999 |
| HGM 0.01% | 0.0237 | 0.1083 | 1.0000 |
| HGM 0.02% | 0.0185 | 0.0999 | 1.0000 |
| HGM 0.03% | 0.0430 | 0.1324 | 0.9999 |
| HGM 0.04% | 0.1259 | 0.1452 | 0.9999 |
| HGM 0.05% | 0.0281 | 0.0925 | 0.9999 |
| HGM 0.06% | 0.0170 | 0.0834 | 1.0000 |
| HGM 0.07% | 0.1282 | 0.1056 | 0.9996 |
| MSE | MAE | R2 Score | ||||
|---|---|---|---|---|---|---|
| Samples | Storage Modulus | tan δ | Storage Modulus | tan δ | Storage Modulus | tan δ |
| Neat | 0.0000 | 0.0000 | 0.0017 | 0.00 | 0.9999 | 0.9997 |
| HGM 0.01% | 0.0000 | 0.0000 | 0.0012 | 0.0015 | 0.9999 | 0.9993 |
| HGM 0.02% | 0.0000 | 0.0000 | 0.0014 | 0.0010 | 0.9999 | 0.9997 |
| HGM 0.03% | 0.0000 | 0.0000 | 0.0016 | 0.0012 | 0.9999 | 0.9997 |
| HGM 0.04% | 0.0000 | 0.0000 | 0.0015 | 0.0010 | 0.9999 | 0.9997 |
| HGM 0.05% | 0.0000 | 0.0000 | 0.0016 | 0.0017 | 0.9999 | 0.9994 |
| HGM 0.06% | 0.0000 | 0.0000 | 0.0015 | 0.0012 | 0.9999 | 0.9996 |
| HGM 0.07% | 0.0000 | 0.0000 | 0.0012 | 0.0011 | 0.9999 | 0.9995 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hossain, M.S.; Rabi, S.N.; Mohammad, S.; Cook, K.; Chowdhury, F.; Nilufar, S. Investigation of Thermomechanical Properties of Hollow Glass Microballoon-Filled Composite Materials Developed by Additive Manufacturing with Machine Learning Validation. Polymers 2025, 17, 1495. https://doi.org/10.3390/polym17111495
Hossain MS, Rabi SN, Mohammad S, Cook K, Chowdhury F, Nilufar S. Investigation of Thermomechanical Properties of Hollow Glass Microballoon-Filled Composite Materials Developed by Additive Manufacturing with Machine Learning Validation. Polymers. 2025; 17(11):1495. https://doi.org/10.3390/polym17111495
Chicago/Turabian StyleHossain, Md Sakhawat, Sazid Noor Rabi, Sakib Mohammad, Kaden Cook, Farhan Chowdhury, and Sabrina Nilufar. 2025. "Investigation of Thermomechanical Properties of Hollow Glass Microballoon-Filled Composite Materials Developed by Additive Manufacturing with Machine Learning Validation" Polymers 17, no. 11: 1495. https://doi.org/10.3390/polym17111495
APA StyleHossain, M. S., Rabi, S. N., Mohammad, S., Cook, K., Chowdhury, F., & Nilufar, S. (2025). Investigation of Thermomechanical Properties of Hollow Glass Microballoon-Filled Composite Materials Developed by Additive Manufacturing with Machine Learning Validation. Polymers, 17(11), 1495. https://doi.org/10.3390/polym17111495








