Effect of Elasticity on Heat and Mass Transfer of Highly Viscous Non-Newtonian Fluids Flow in Circular Pipes
Abstract
1. Introduction
2. Materials and Methods
2.1. Typical Polymer and Its Rheological Constitutive Equation
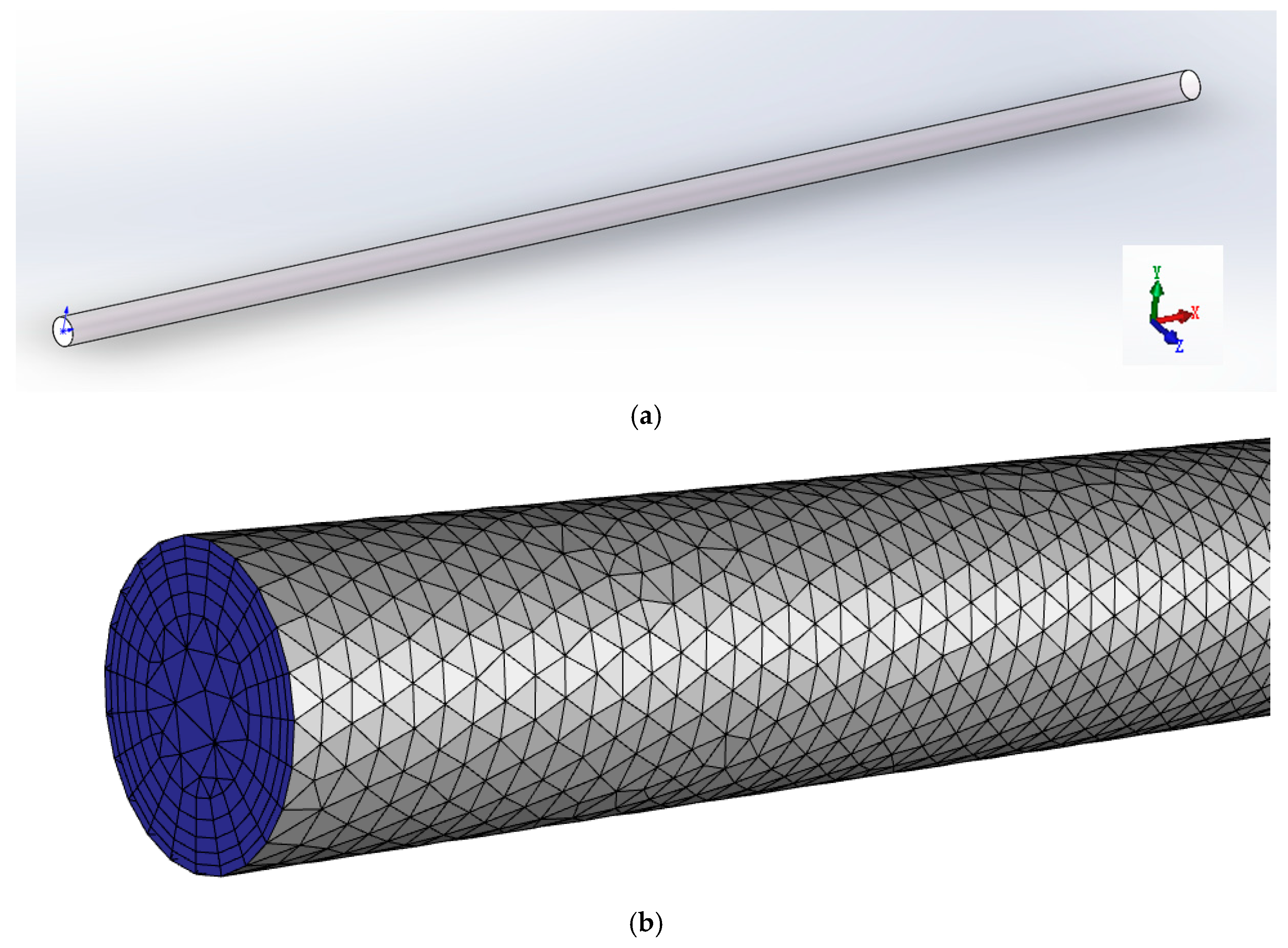
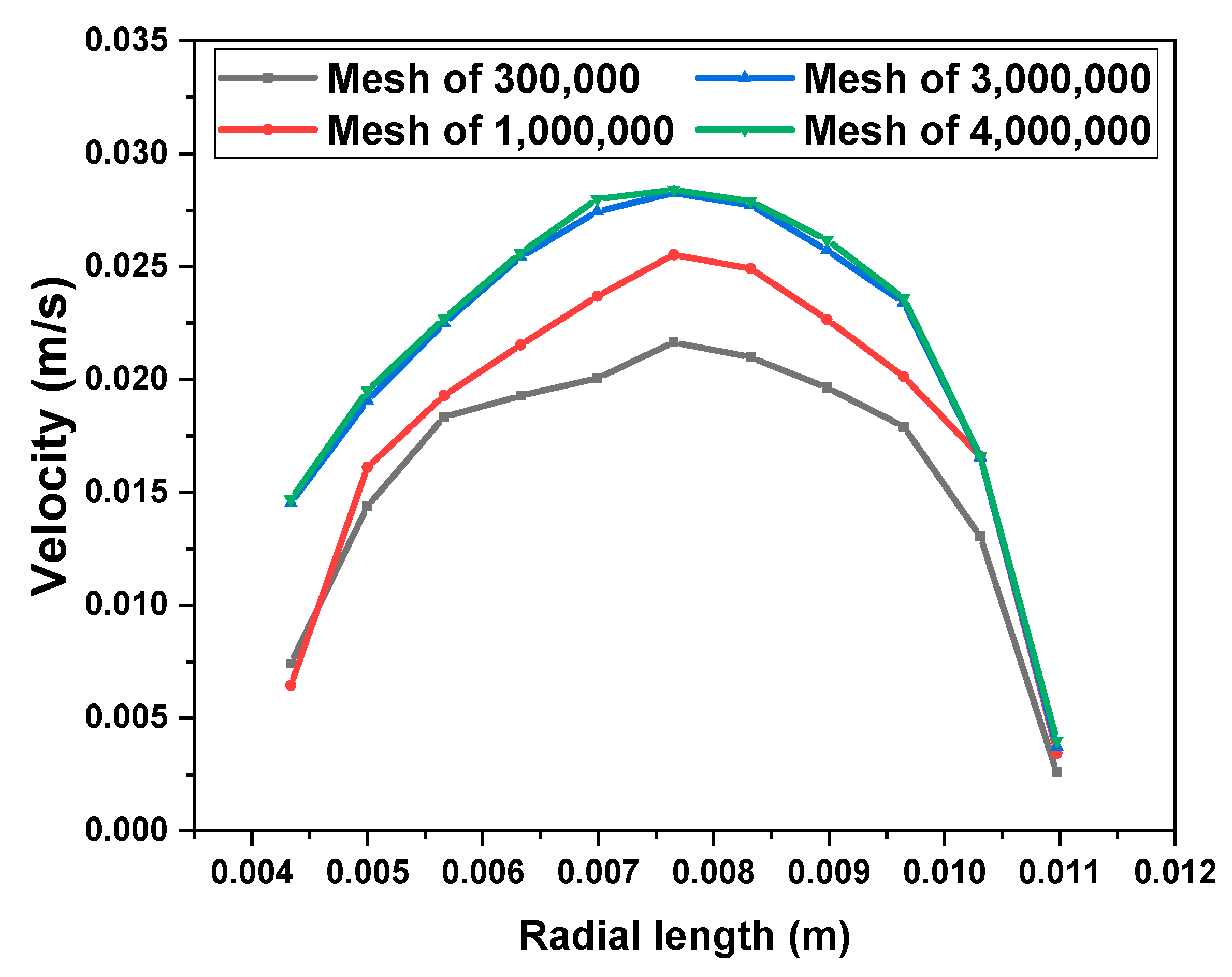
2.2. CFD Simulation Details
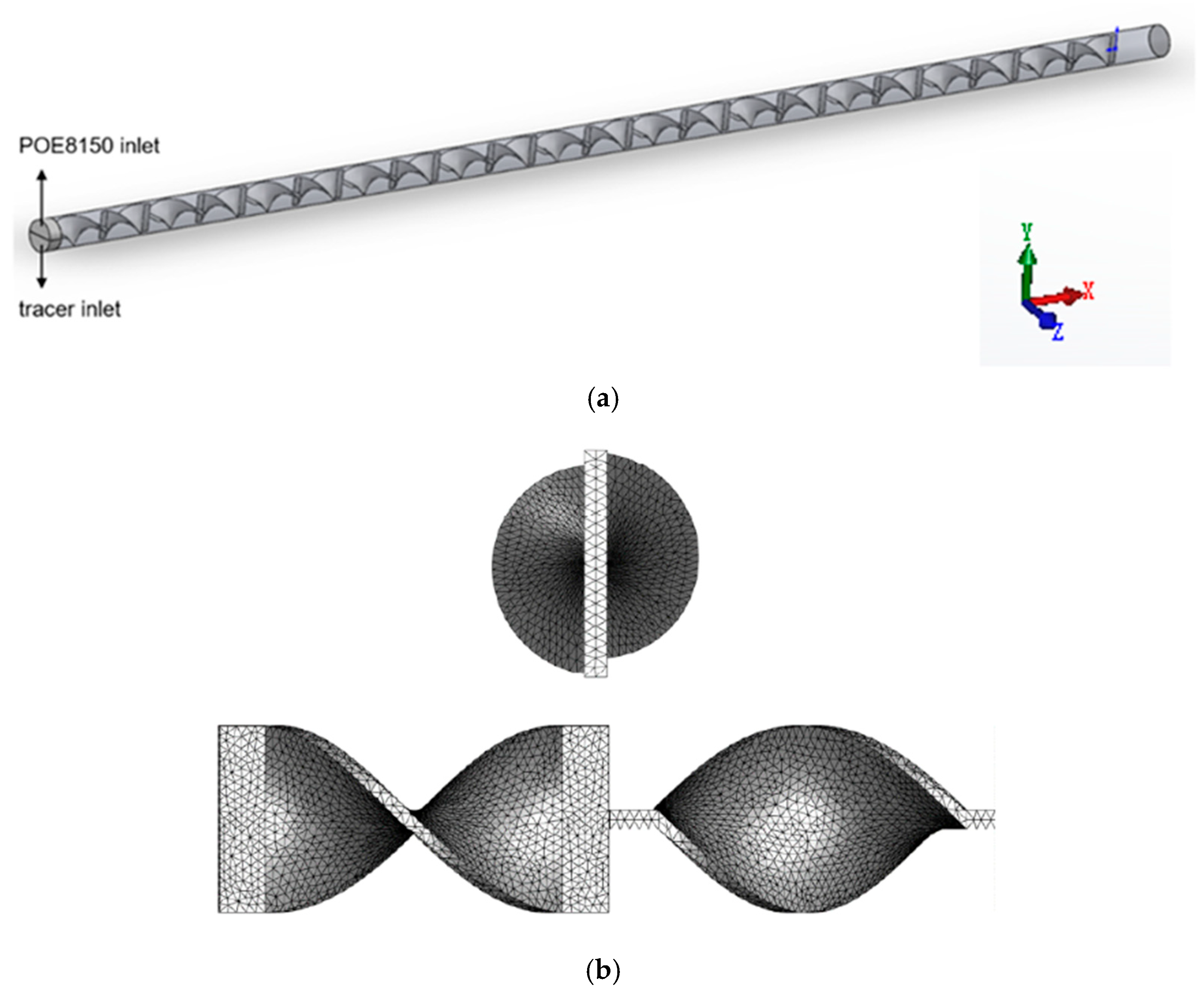
2.3. Pipeline Flowing Experiments
3. Results and Discussion
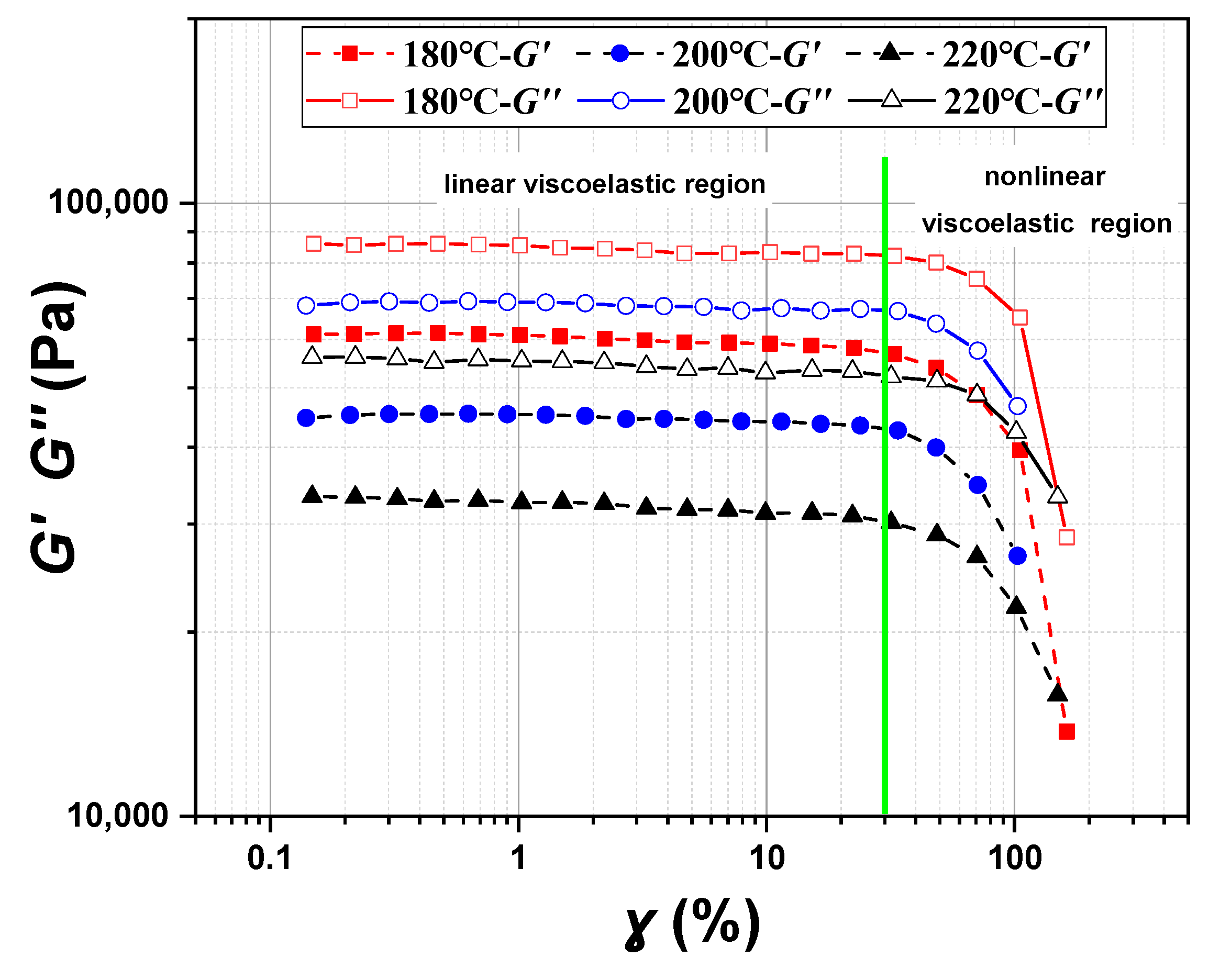
3.1. Rheological Behavior of POE Melt
3.2. Fitting of Constitutive Equations for POE Melt
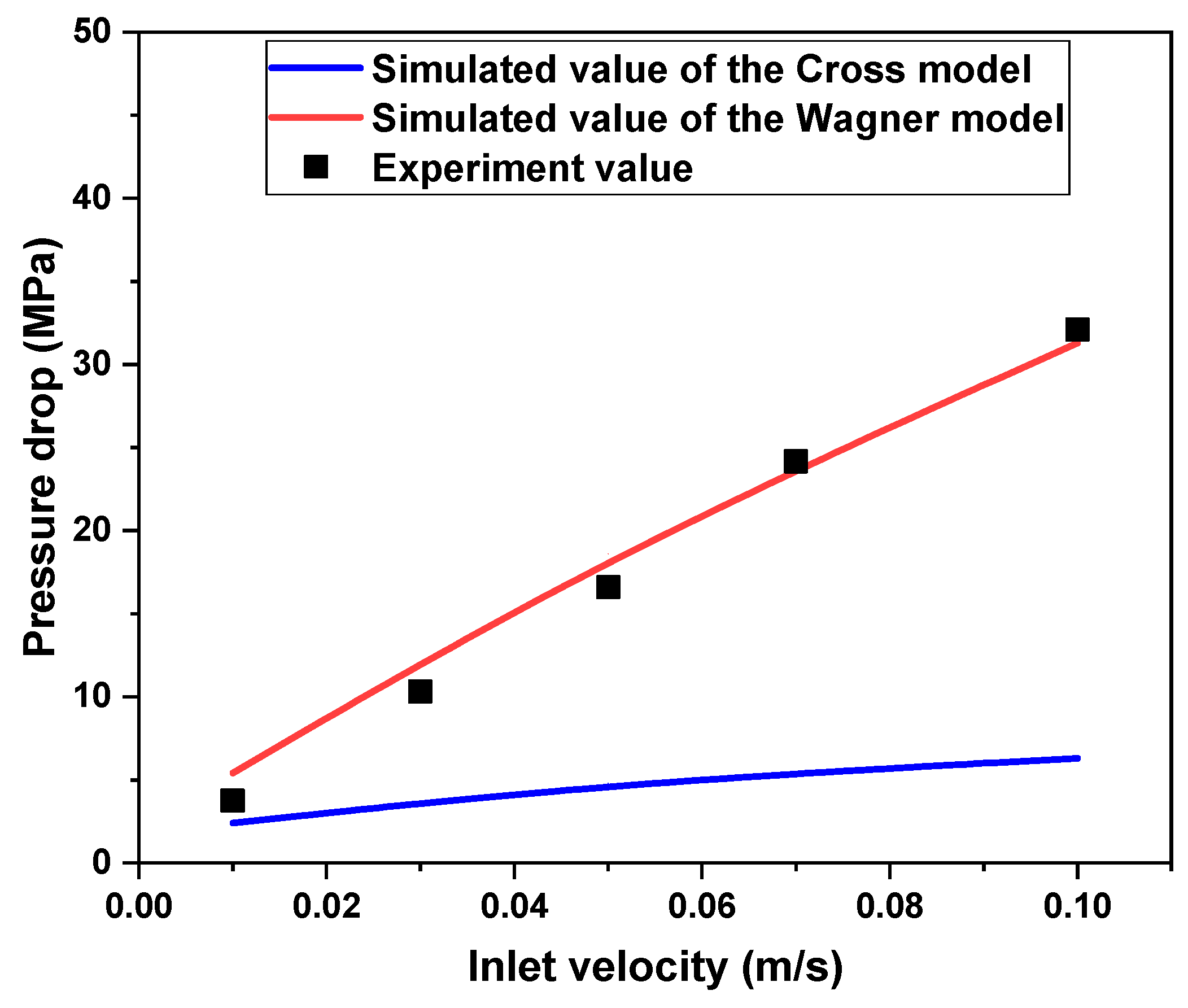
3.3. Differences in Pressure Drop Simulated by Two Models in the Empty Tube
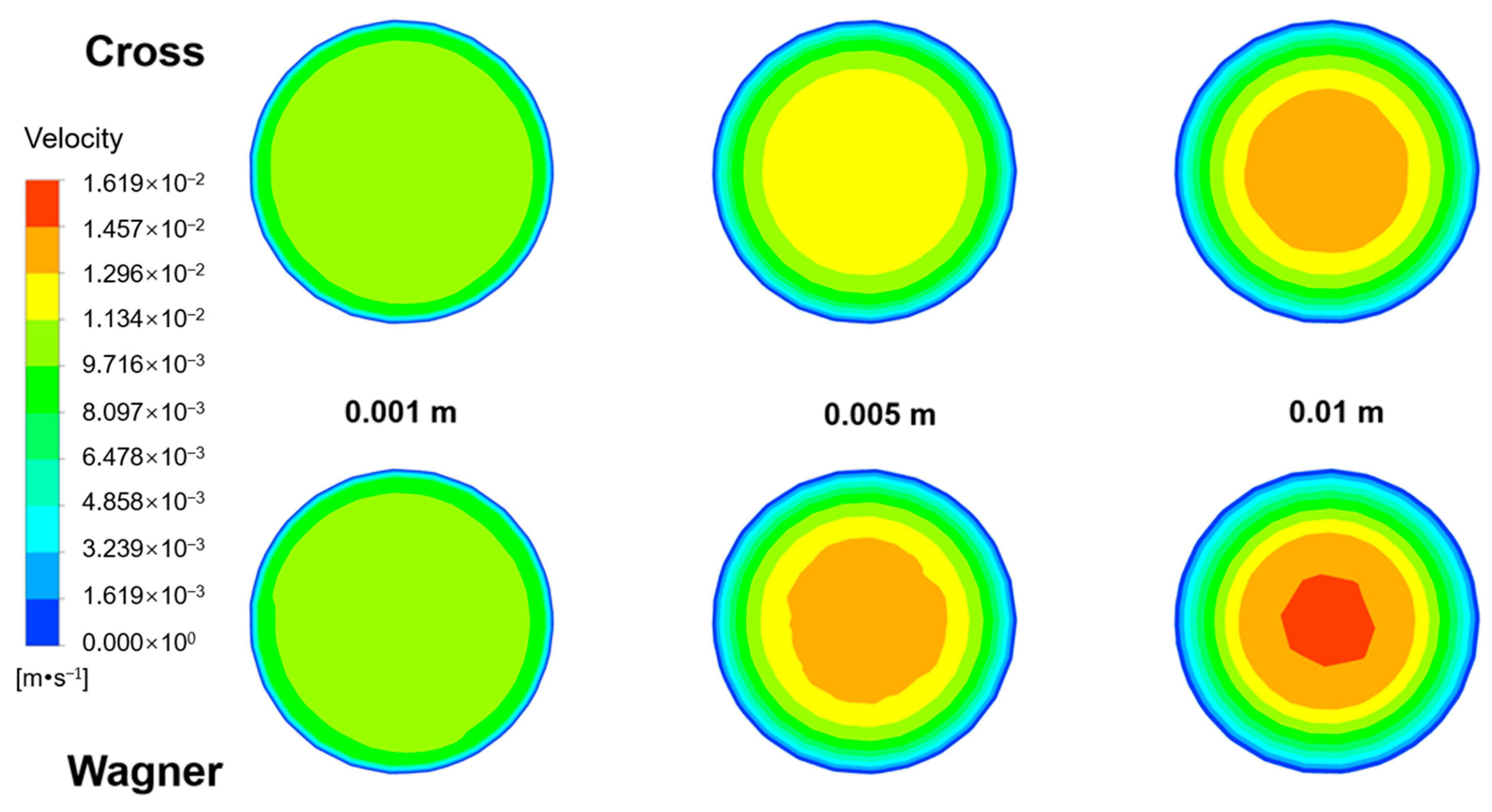
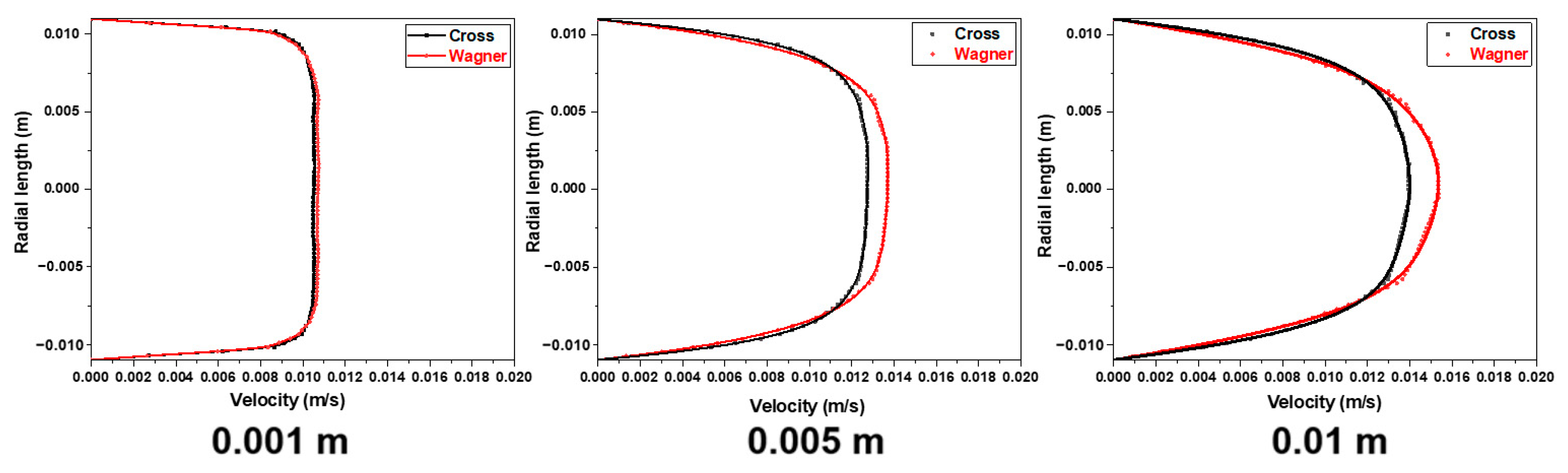
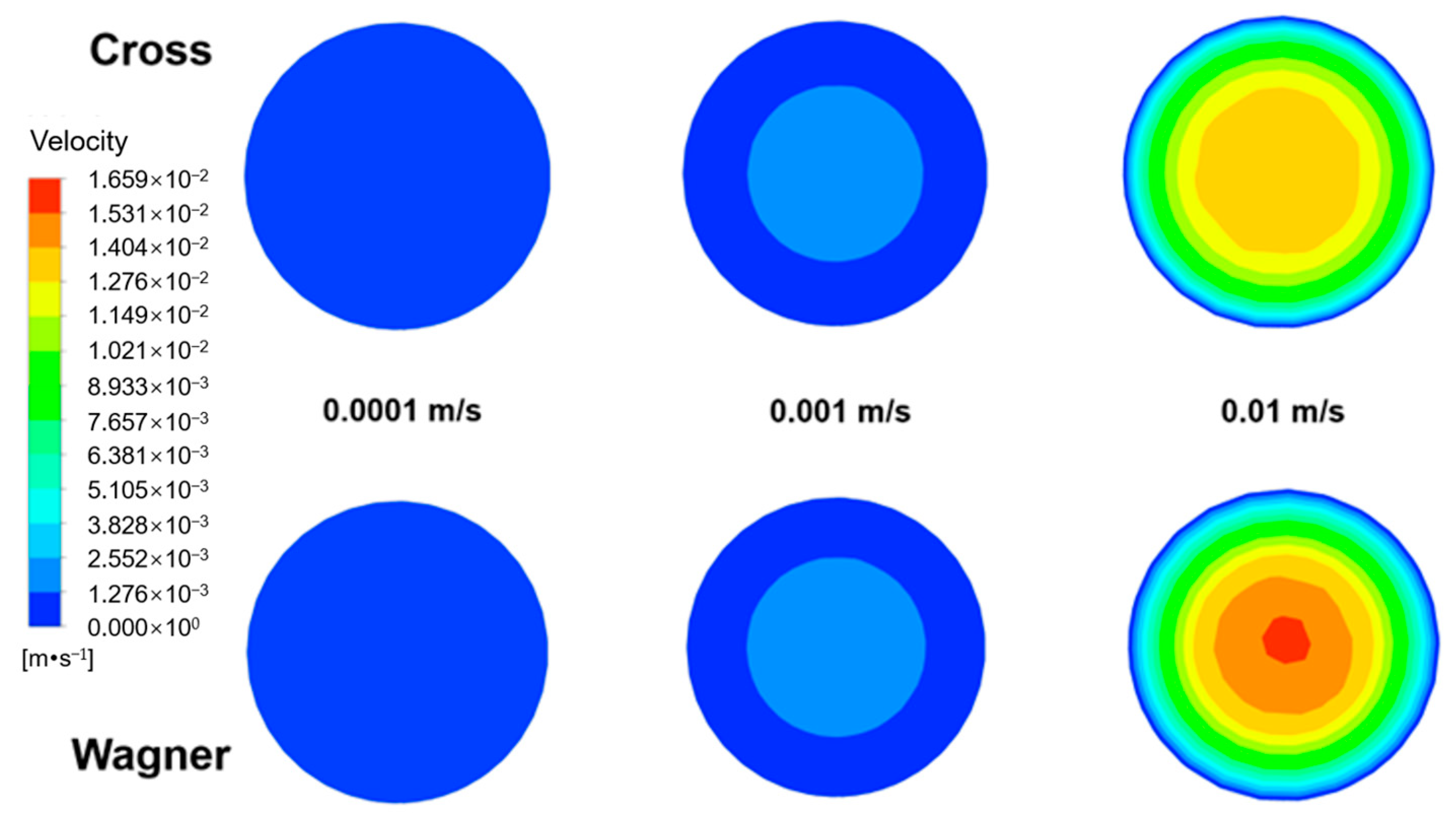
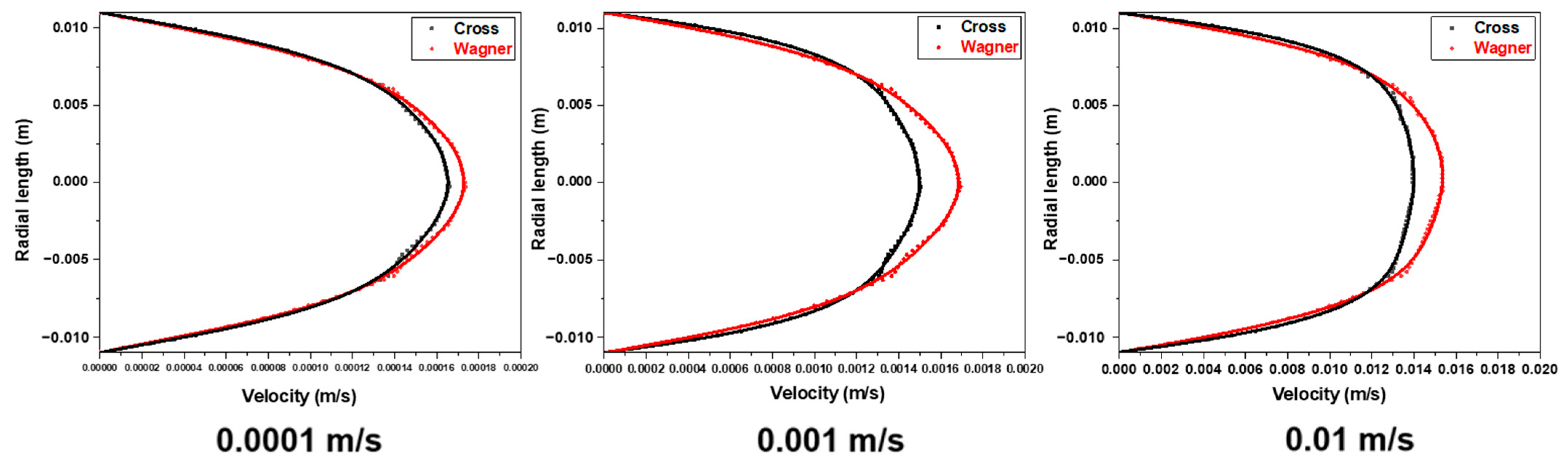
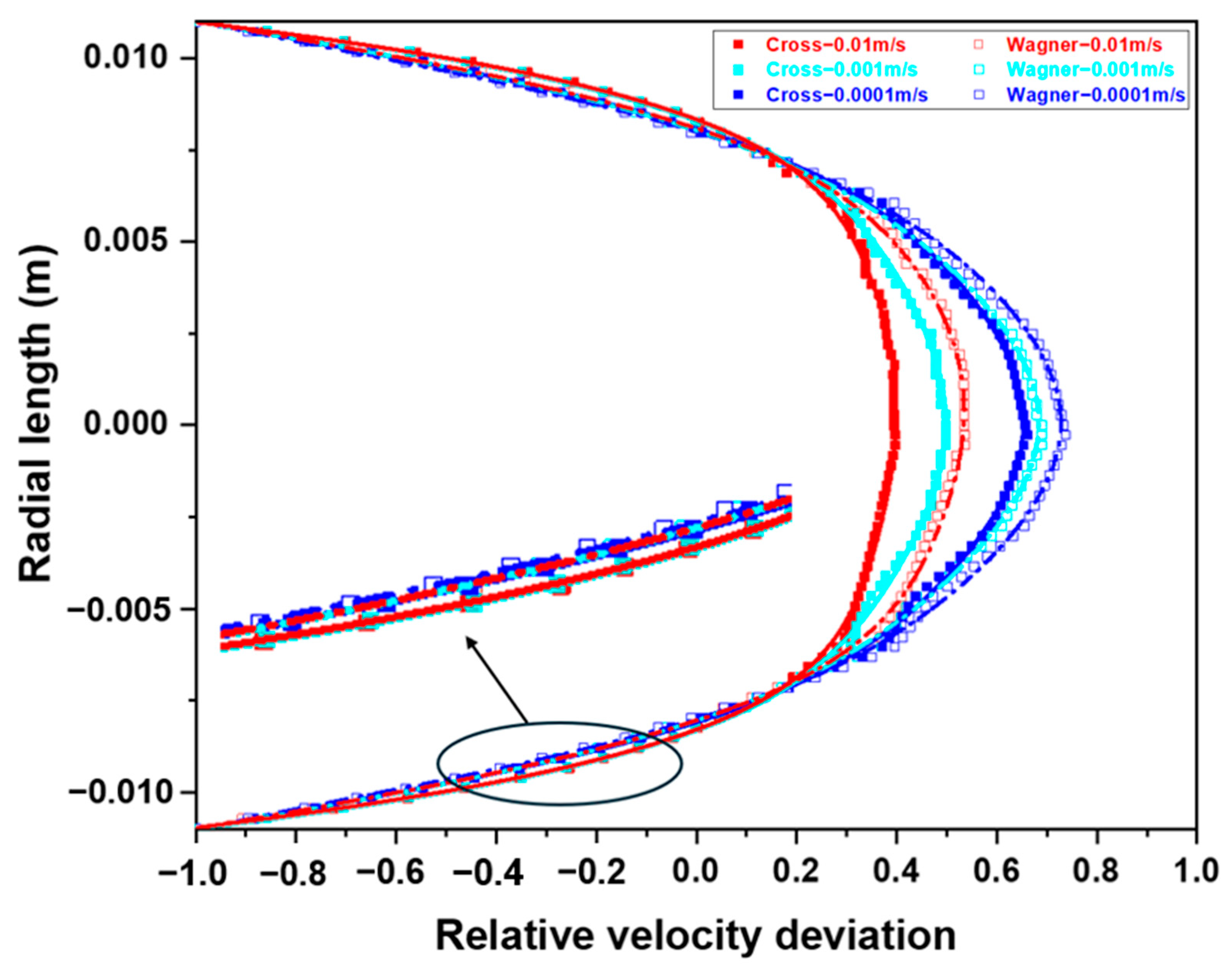
3.4. Differences in Velocity Field Simulated by Two Models in the Empty Tube
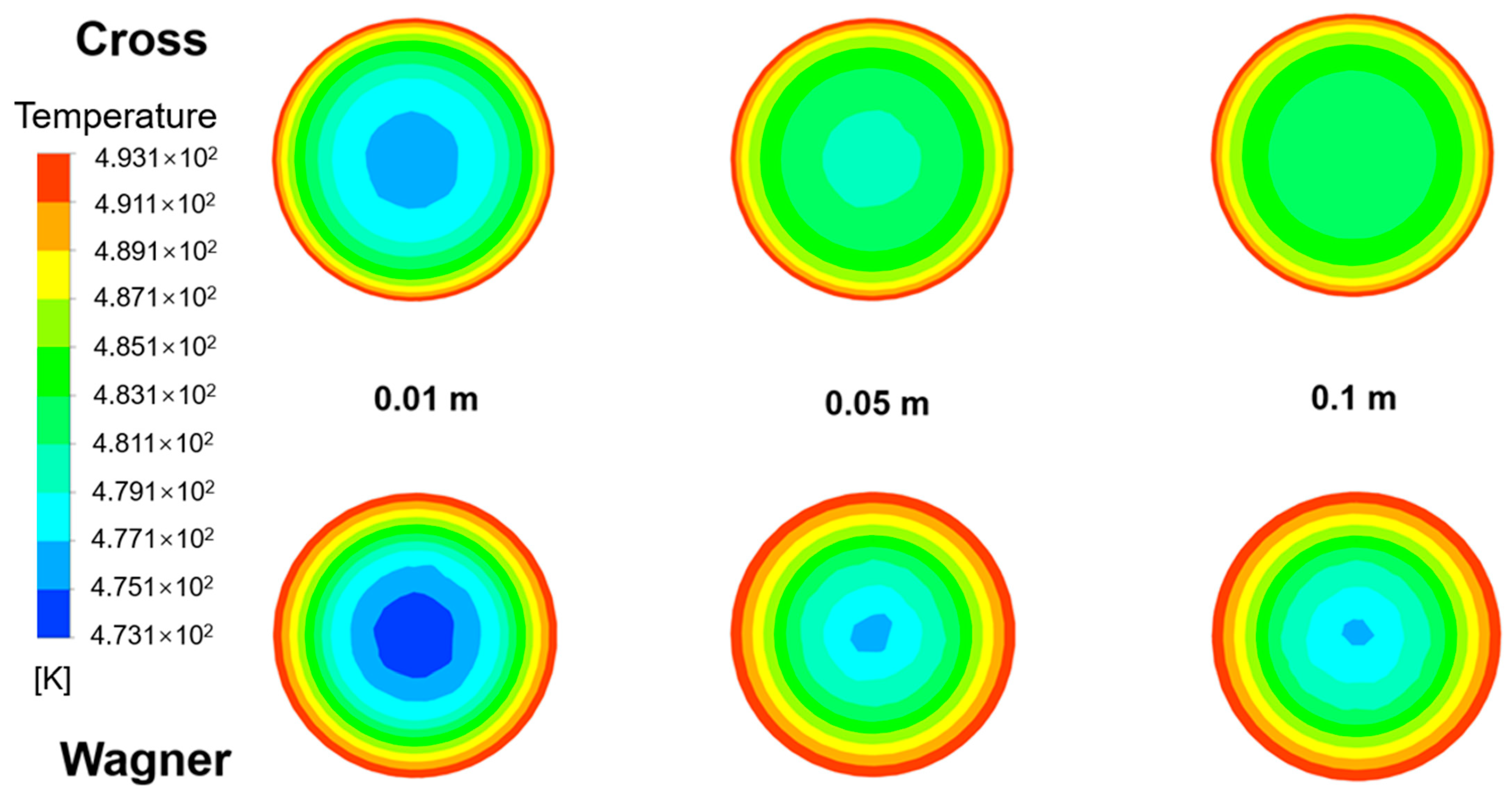
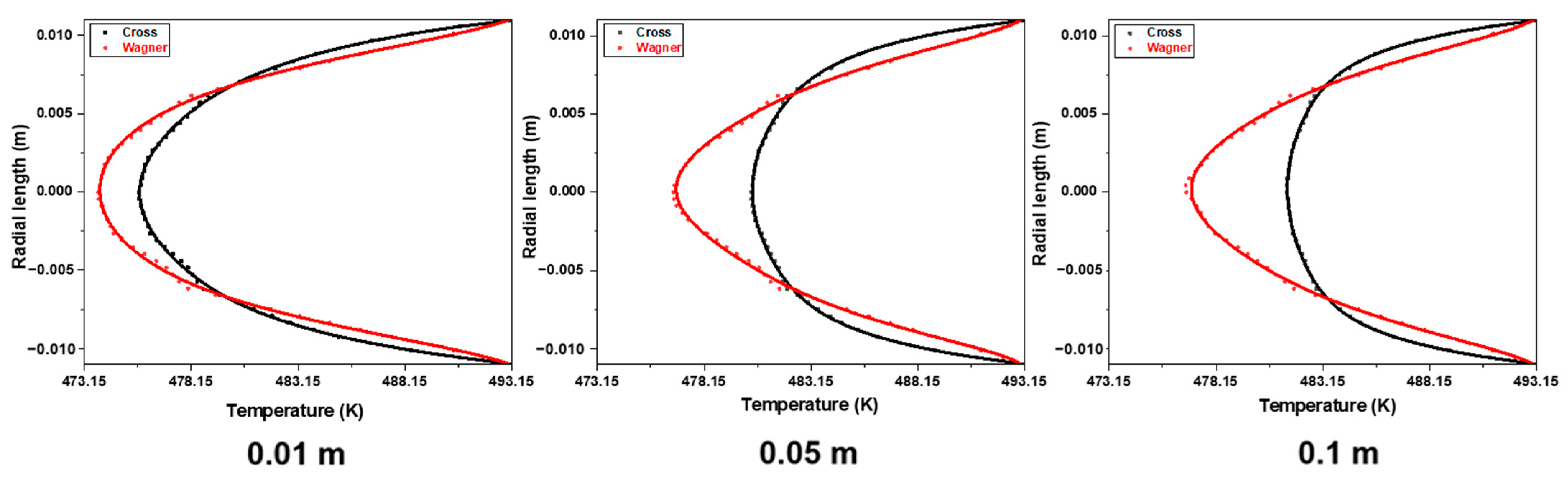
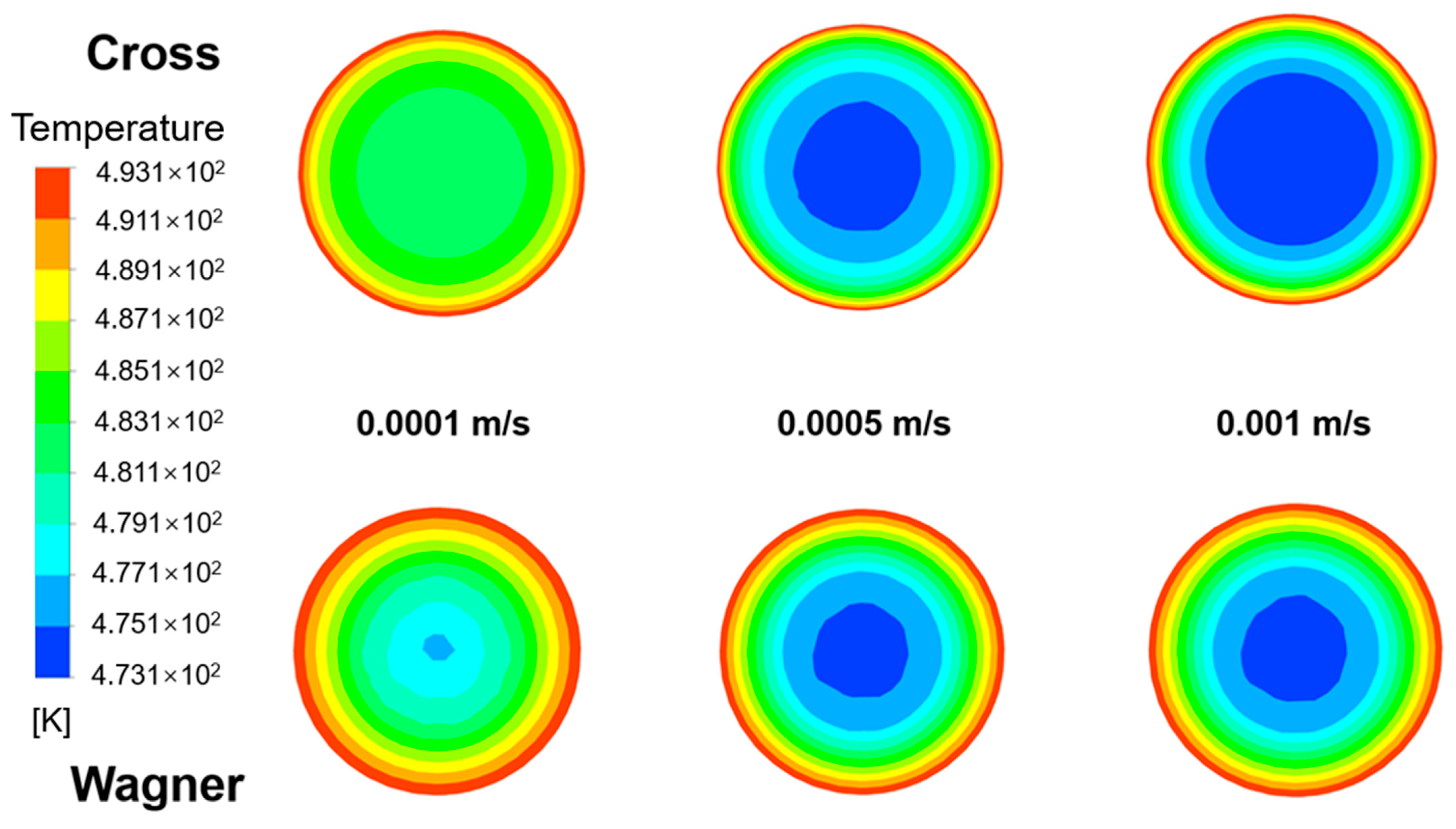
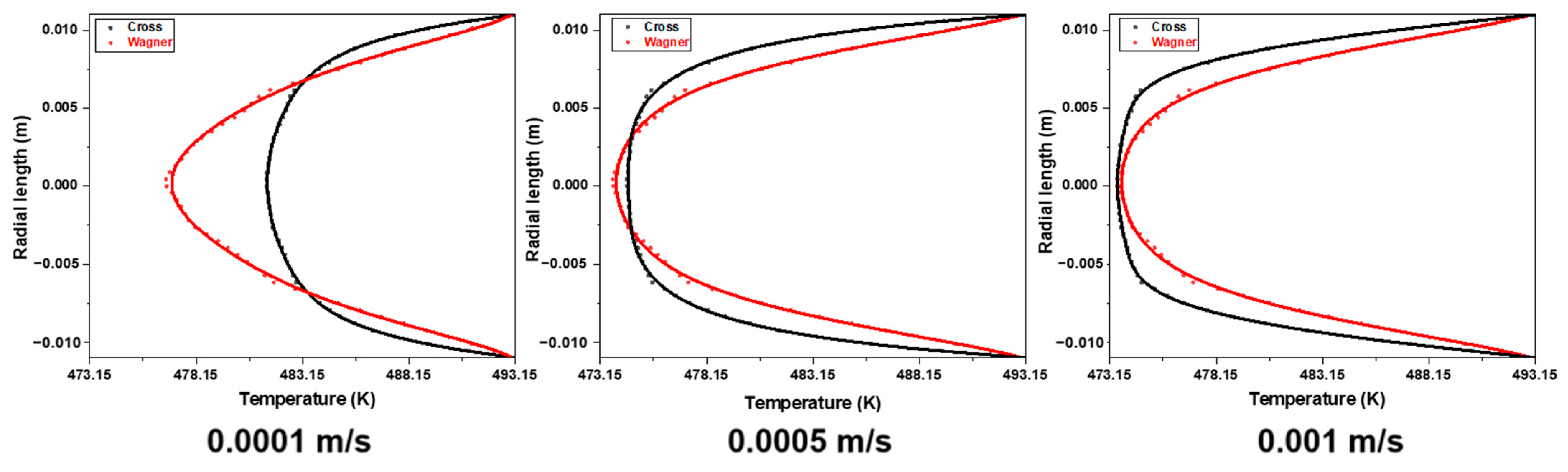
3.5. Differences in Temperature Field Simulated by Two Models in the Empty Tube
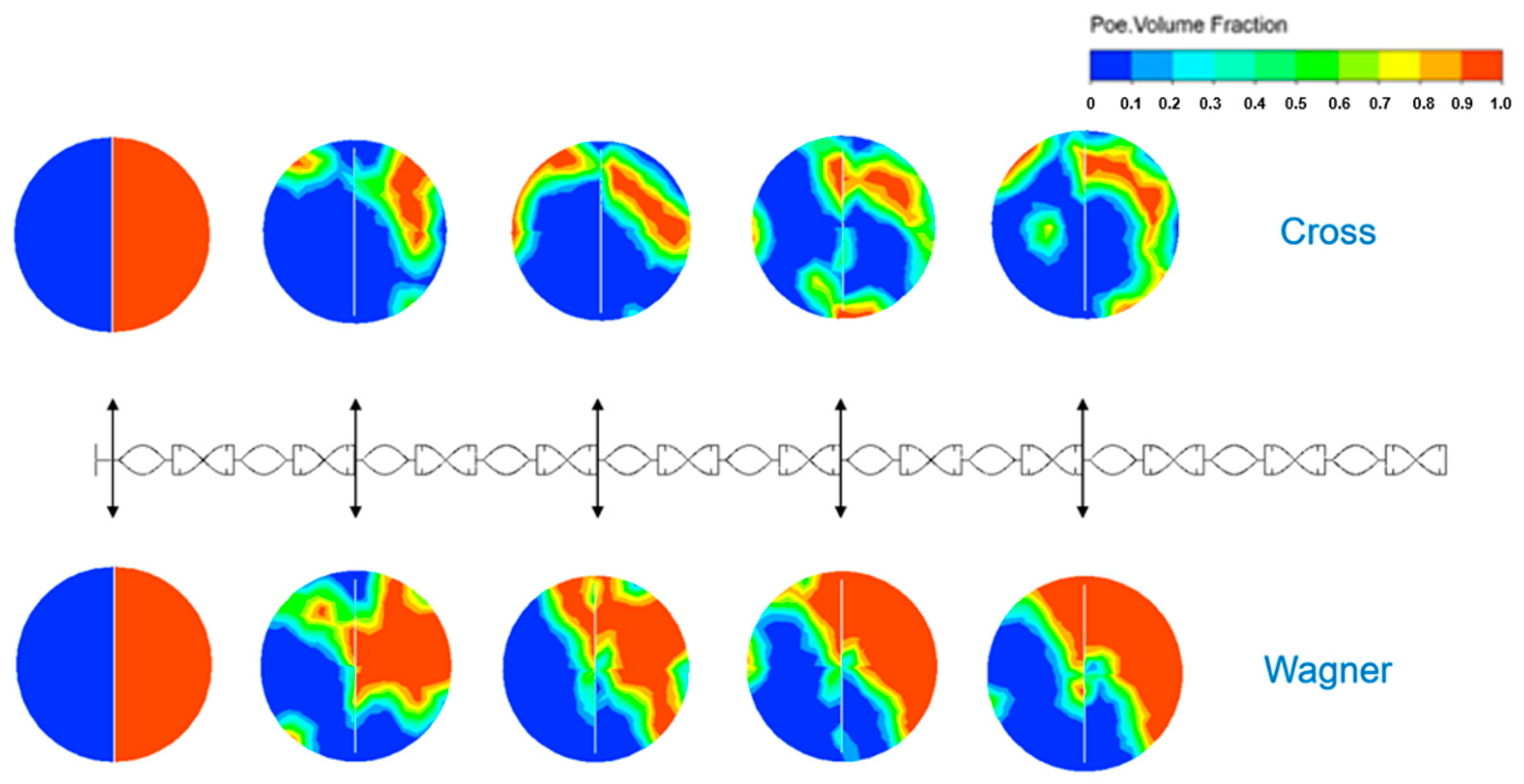
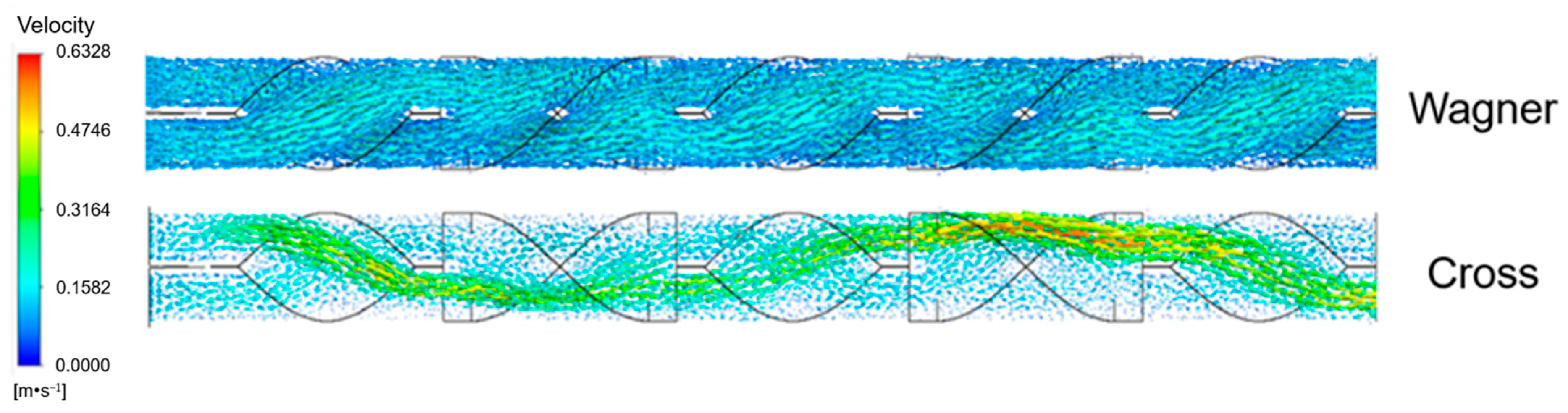
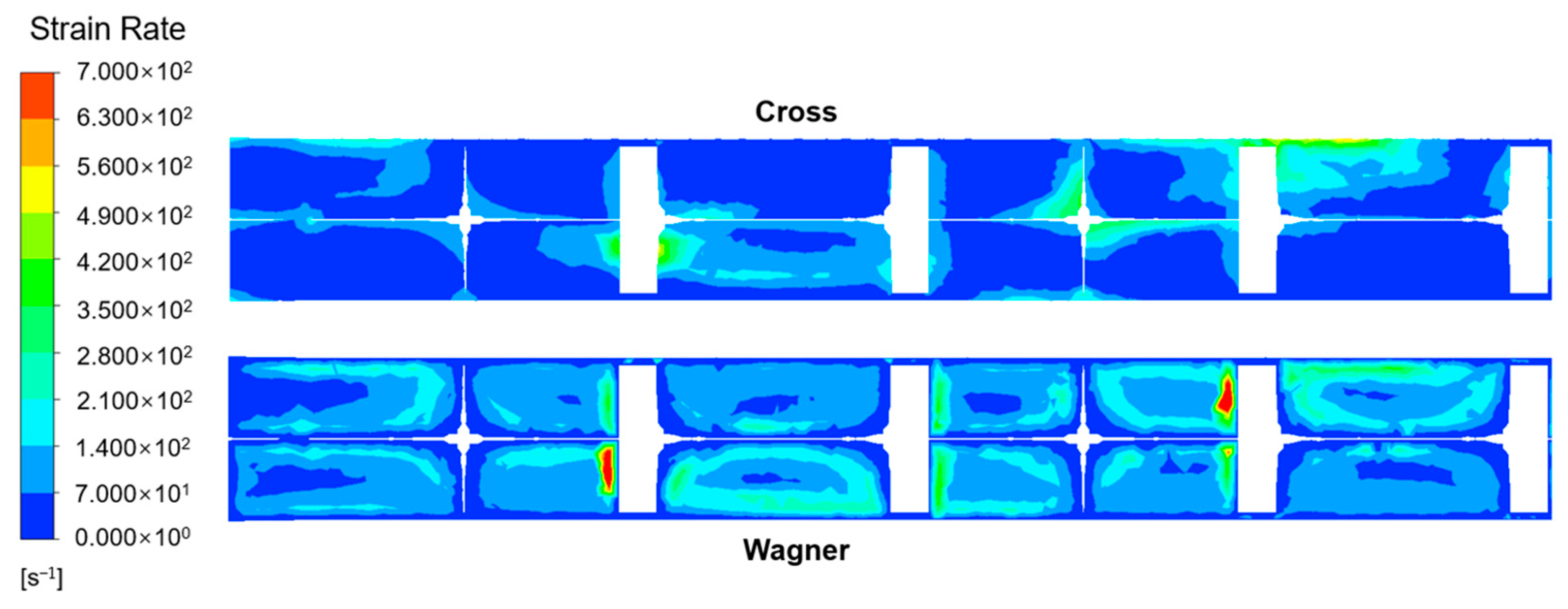
3.6. Differences in Mixing Field Simulated by Two Models in the Static Mixer
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| η | The viscosity of the fluid |
| η0 | The viscosity of the first Newtonian region |
| η∞ | The viscosity of the second Newtonian region |
| λ | The characteristic time, which is directly related to the material properties |
| m | The fluid behavior index, which is related to the material properties |
| The shear rate | |
| γ | The strain of the fluid |
| m(t − t′) | The memory function, which is time derivative of relaxation modulus |
| h(γ) | The damping function, which can be used for describing the nonlinear rheological response |
| γ(t, t′) | The deformation history from time t′ to t |
| gi | The relaxation modulus |
| λi | The relaxation time |
| N | The number of the Maxwell models |
| G′(ω) | The storage modulus of the fluid |
| G″(ω) | The loss modulus of the fluid |
| G(t) | The linear stress relaxation modulus |
| G(t,γ) | The nonlinear stress relaxation modulus |
| γc | The critical strain of the fluid |
| α | The fitting parameter of the damping function |
| ω | The oscillation frequency |
References
- Kang, Q.Q.; Liu, J.F.; Feng, X.; Yang, C.; Wang, J.T. Isolated mixing regions and mixing enhancement in a high-viscosity laminar stirred tank. Chin. J. Chem. Eng. 2021, 41, 176–192. [Google Scholar] [CrossRef]
- Yang, L.; Du, K. A comprehensive review on the natural, forced, and mixed convection of non-Newtonian fluids (nanofluids) inside different cavities. J. Therm. Anal. Calorim. 2020, 140, 2033–2054. [Google Scholar] [CrossRef]
- Kaempfe, M.; Fischer, M.; Kuehnert, I.; Wießner, S. Process-Relevant Flow Characteristics of Styrene-Based Thermoplastic Elastomers and Their Representation by Rheometric Data. Polymers 2023, 15, 3537. [Google Scholar] [CrossRef]
- Patel, D.; Ein-Mozaffari, F.; Mehrvar, M. Effect of rheological parameters on non-ideal flows in the continuous-flow mixing of biopolymer solutions. Chem. Eng. Res. Des. 2015, 100, 126–134. [Google Scholar] [CrossRef]
- Schlichting, H.; Gersten, K. Boundary-Layer Theory; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Shinohara, A.; Pan, C.; Guo, Z.; Zhou, L.; Liu, Z.; Du, L.; Yan, Z.; Stadler, F.J.; Wang, L.; Nakanishi, T. Viscoelastic Conjugated Polymer Fluids. Angew. Chem. 2019, 131, 9581–9585. [Google Scholar] [CrossRef]
- Prokunin, A.N. On the description of viscoelastic flows of polymer fluids. Rheol. Acta 1989, 28, 38–47. [Google Scholar] [CrossRef]
- Lemou, M.; Picasso, M.; Degond, P. Viscoelastic Fluid Models Derived from Kinetic Equations for Polymers. Siam J. Appl. Math. 2002, 62, 1501–1519. [Google Scholar] [CrossRef]
- Centa, U.G.; Oseli, A.; Mihelčič, M.; Kralj, A.; Žnidaršič, M.; Halilovič, M.; Perše, L.S. Long-Term Viscoelastic Behavior of Polyisobutylene Sealants before and after Thermal Stabilization. Polymers 2024, 16, 22. [Google Scholar] [CrossRef]
- Billon, N.; Castellani, R.; Bouvard, J.L.; Rival, G. Viscoelastic Properties of Polypropylene during Crystallization and Melting: Experimental and Phenomenological Modeling. Polymers 2023, 15, 3846. [Google Scholar] [CrossRef]
- Hooshyar, S.; Germann, N. The investigation of shear banding polymer solutions in die extrusion geometry. J. Non-Newton. Fluid Mech. 2019, 272, 104161. [Google Scholar] [CrossRef]
- Southwick, J.G.; Manke, C.W. Molecular Degradation, Injectivity, and Elastic Properties of Polymer Solutions. Spe Reserv. Eng. 1988, 3, 1193–1201. [Google Scholar] [CrossRef]
- Figueiredo, R.; Oishi, C.; Afonso, A.; Tasso, I.; Cuminato, J. A two-phase solver for complex fluids: Studies of the Weissenberg effect. Int. J. Multiph. Flow 2016, 84, 98–115. [Google Scholar] [CrossRef]
- Jegatheeswaran, S.; Ein-Mozaffari, F.; Wu, J.N. Laminar mixing of non-Newtonian fluids in static mixers: Process intensification perspective. Rev. Chem. Eng. 2018, 36, 423–436. [Google Scholar] [CrossRef]
- Kulichikhin, V.G.; Malkin, A.Y. The Role of Structure in Polymer Rheology: Review. Polymers 2022, 14, 1262. [Google Scholar] [CrossRef]
- Cherizol, R.; Sain, M.; Tjong, J. Review of Non-Newtonian Mathematical Models for Rheological Characteristics of Viscoelastic Composites. Green Sustain. Chem. 2015, 5, 6–14. [Google Scholar] [CrossRef]
- Tan, D.H.; Zhou, C.; Ellison, C.J.; Kumar, S.; Macosko, C.W.; Bates, F.S. Meltblown fibers: Influence of viscosity and elasticity on diameter distribution. J. Non-Newton. Fluid Mech. 2010, 165, 892–900. [Google Scholar] [CrossRef]
- Pereira, J.O.; Farias, T.M.; Castro, A.M.; Secchi, A.R.; Cardozo, N.S.M. Estimation of the nonlinear parameters of viscoelastic constitutive models using CFD and multipass rheometer data. J. Non-Newton. Fluid Mech. 2020, 281, 104284. [Google Scholar] [CrossRef]
- Cha, J.; Kim, M.; Park, D.; Go, J.S. Experimental determination of the viscoelastic parameters of K-BKZ model and the influence of temperature field on the thickness distribution of ABS thermoforming. Int. J. Adv. Manuf. Technol. 2019, 103, 985–995. [Google Scholar] [CrossRef]
- Tseng, H.C. A revisitation of White−Metzner viscoelastic fluids. Phys. Fluids 2021, 33, 057115. [Google Scholar] [CrossRef]
- Zheng, Q.; Wang, W.; Yu, Q.; Yu, J.; He, L.; Tan, H. Nonlinear viscoelastic behavior of styrene-[ethylene-(ethylene-propylene)]-styrene block copolymer. J. Polym. Sci. Part B-Polym. Phys. 2006, 44, 1309–1319. [Google Scholar] [CrossRef]
- Wagner, M.H. Analysis of time-dependent non-linear stress-growth data for shear and elongational flow of low-density branched polyethylene melt. Rheol. Acta 1976, 15, 136–142. [Google Scholar] [CrossRef]
- Mahammedi, A.; Tayeb, N.N.; Kim, K.K.; Hossain, S. Mixing Enhancement of Non-Newtonian Shear-Thinning Fluid for a Kenics Micromixer. Micromachines 2021, 12, 1494. [Google Scholar] [CrossRef]
- Nazemi, A.; Baou, M.; Jabari-Moghadam, A.; Norouzi, M. A numerical study on viscoelastic boundary layer on flat plate. J. Braz. Soc. Mech. Sci. Eng. 2020, 42, 11. [Google Scholar] [CrossRef]
- Gambaryan-Roisman, T. Dynamics of free liquid films during formation of polymer foams. Colloids Surf. A Physicochem. Eng. Asp. 2011, 382, 113–117. [Google Scholar] [CrossRef]
- Vilalta, G.; Silva, M.; Blanco, A. Influence Study of the Viscoelastic Fluids Features in Drag Reduction in Laminar Regime Flow in Pipeline. MATEC Web Conf. 2016, 70, 7001. [Google Scholar] [CrossRef]
- Faroughi, S.A.; Del Giudice, F. Microfluidic Rheometry and Particle Settling: Characterizing the Effect of Polymer Solution Elasticity. Polymers 2022, 14, 657. [Google Scholar] [CrossRef]
- Jegatheeswaran, S.; Ein-Mozaffari, F.; Wu, J. Efficient Mixing of Yield-Pseudoplastic Fluids at Low Reynolds Numbers in the Chaotic SMX Static Mixer. Chem. Eng. J. 2017, 317, 215–231. [Google Scholar] [CrossRef]
- Guer, Y.L.; Omari, K.E. Chaotic Advection for Thermal Mixing. Adv. Appl. Mech. 2012, 45, 189–237. [Google Scholar]
- Madhuranthakam, C.; Pan, Q.; Rempel, G.L. Residence time distribution and liquid holdup in Kenics KMX static mixer with hydrogenated nitrile butadiene rubber solution and hydrogen gas system. Chem. Eng. Sci. 2009, 64, 3320–3328. [Google Scholar] [CrossRef]
- Migliozzi, S.; Mazzei, L.; Angeli, P. Viscoelastic flow instabilities in static mixers: Onset and effect on the mixing efficiency. Phys. Fluids 2021, 33, 013104. [Google Scholar] [CrossRef]
- Ramsay, J.; Simmons, M.; Ingram, A.; Stitt, E. Mixing performance of viscoelastic fluids in a Kenics KM in-line static mixer. Chem. Eng. Res. Des. 2016, 115, 310–324. [Google Scholar] [CrossRef]
- Arratia, P.E.; Voth, G.A.; Gollub, J.P. Stretching and mixing of non-Newtonian fluids in time-periodic flows. Phys. Fluids 2005, 17, 053102(1)–053102(10). [Google Scholar] [CrossRef]
- Caserta, S.; Preziosi, V.; Pommella, A.; Guido, S. Non-Newtonian Liquid-Liquid Fluids in Kenics Static Mixers. Chem. Eng. Trans. 2013, 32, 1477–1482. [Google Scholar]
- Mack, C. Deformation mechanism of nonlinear viscoelasticity. J. Rheol. 1969, 13, 59–82. [Google Scholar] [CrossRef]


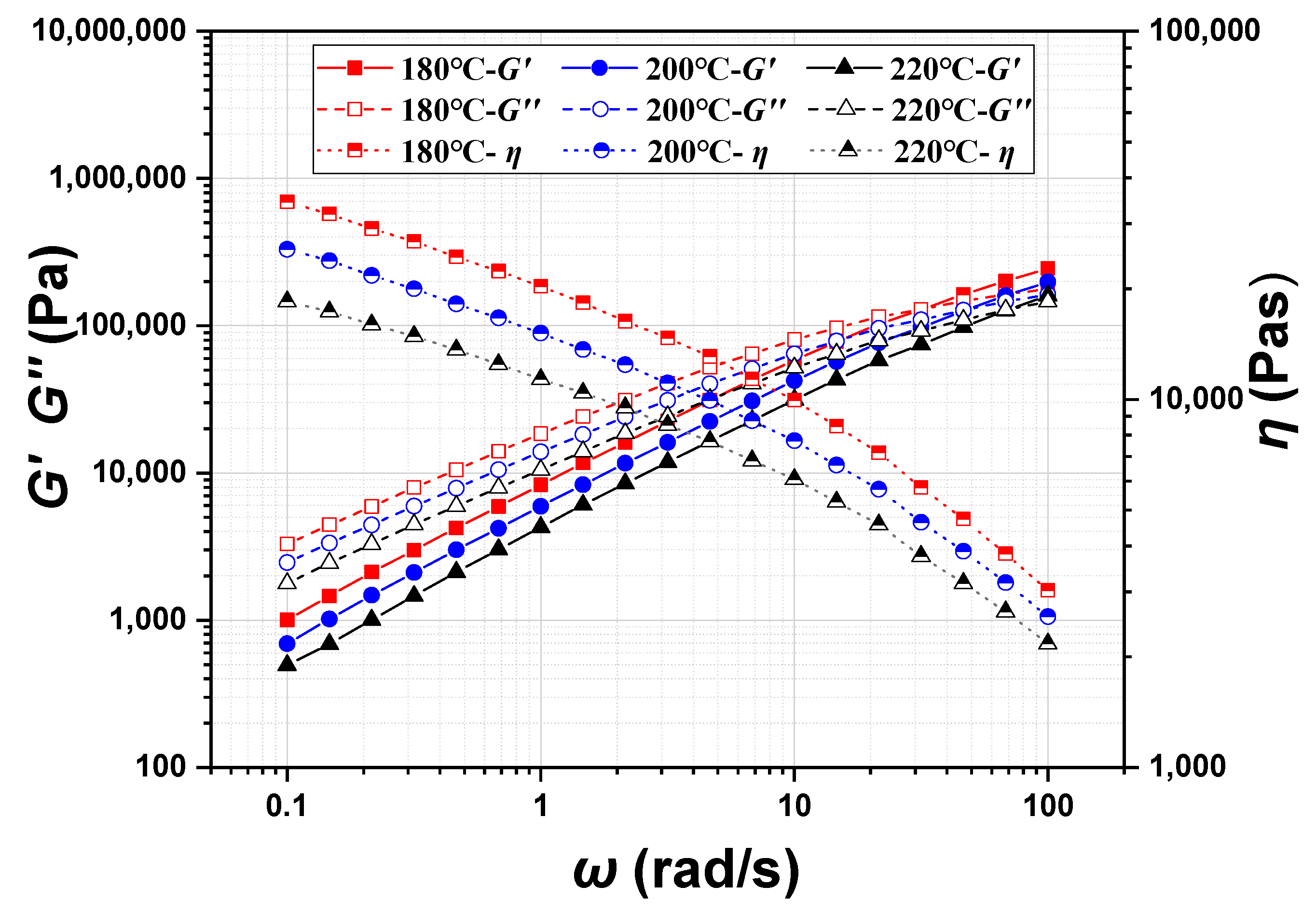

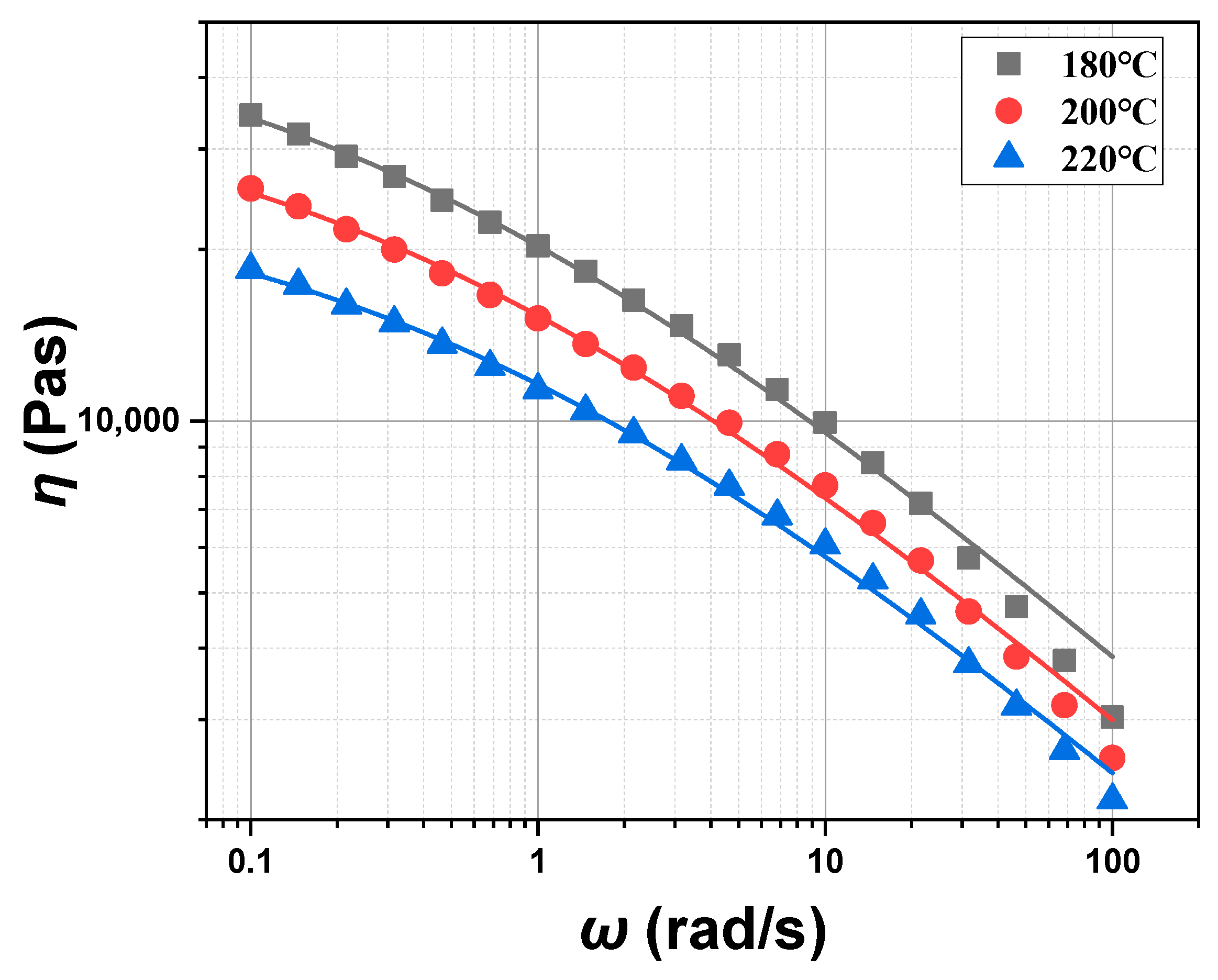
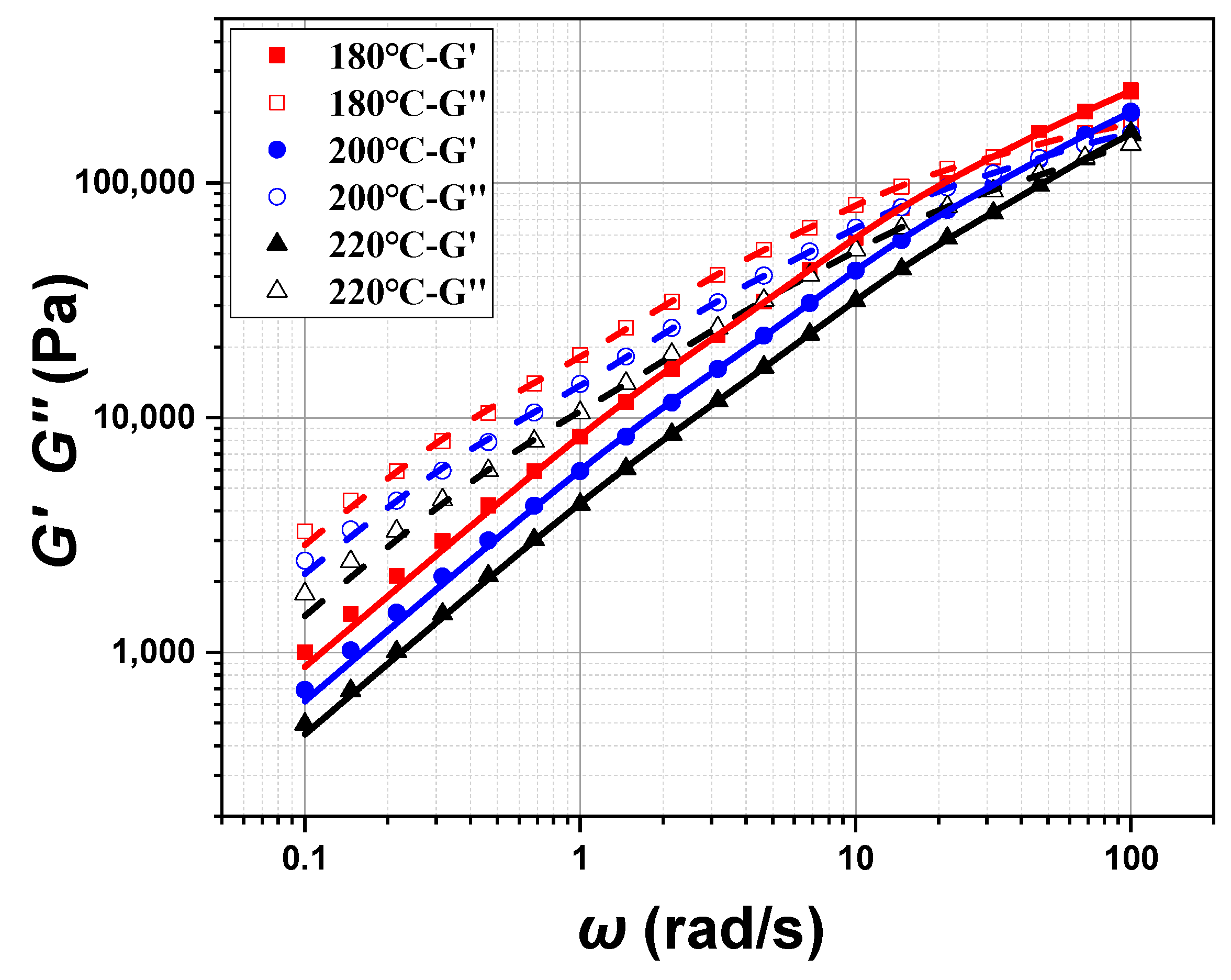
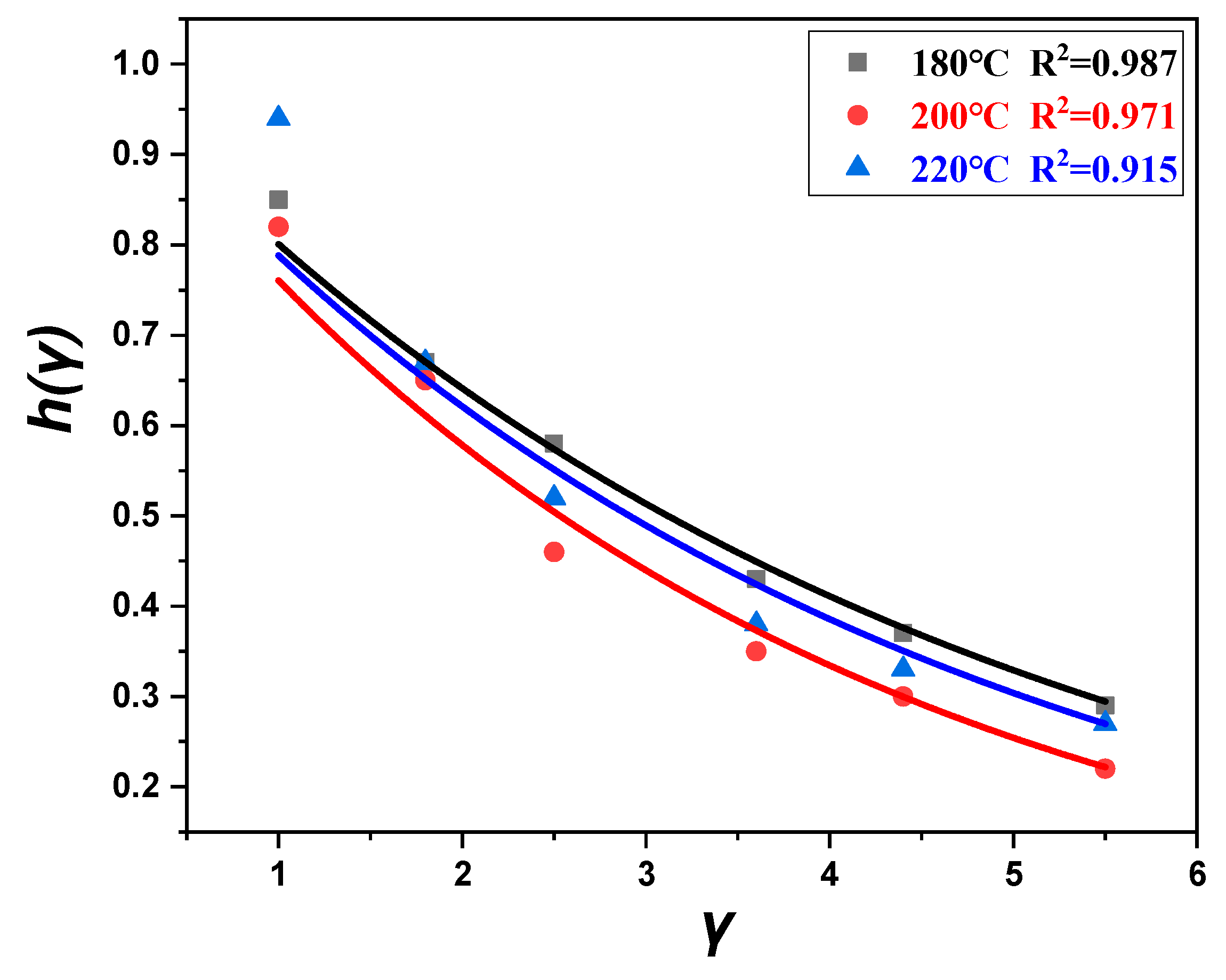
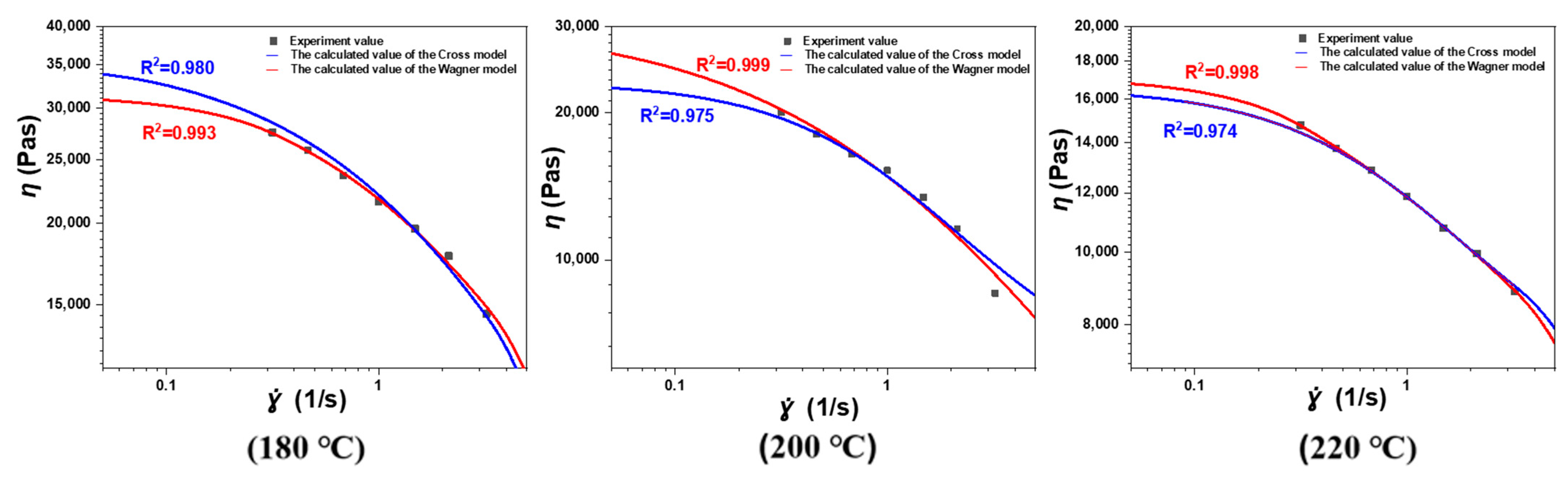

| T/°C | η0/Pa·s | η∞/Pa·s | λ/s | m |
|---|---|---|---|---|
| 180 | 77,430.7 | 0 | 18.910 | 0.35512 |
| 200 | 56,063.8 | 0 | 16.558 | 0.35512 |
| 220 | 35,867.3 | 0 | 8.489 | 0.35512 |
| i | λi | gi | ||||
|---|---|---|---|---|---|---|
| 180 °C | 200 °C | 220 °C | 180 °C | 200 °C | 220 °C | |
| 1 | 1.00 × 10−5 | 1.00 × 10−5 | 1.00 × 10−5 | 1.00 × 106 | 1.00 × 106 | 1.01 × 106 |
| 2 | 1.00 × 10−3 | 0.0010 | 1.07 × 10−3 | 2.46 × 105 | 1.00 × 105 | 2.93 × 105 |
| 3 | 8.65 × 10−3 | 0.0093 | 0.010 | 1.03 × 105 | 9.98 × 104 | 8.10 × 104 |
| 4 | 8.67 × 10−3 | 0.0093 | 0.011 | 1.04 × 105 | 9.98 × 104 | 8.11 × 104 |
| 5 | 0.028 | 0.023 | 0.069 | 7.61 × 104 | 9.90 × 104 | 4.61 × 104 |
| 6 | 0.087 | 0.027 | 0.37 | 6.44 × 104 | 9.90 × 104 | 1.16 × 104 |
| 7 | 3.84 | 0.072 | 2.90 | 4719.00 | 9021.00 | 2951.00 |
| 8 | 0.43 | 1.66 | 0.024 | 1.98 × 104 | 9410.00 | 1.58 × 104 |
| T/°C | α |
|---|---|
| 180 | 0.222 |
| 200 | 0.274 |
| 220 | 0.238 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Qiu, X.; Zhang, X.; Zhao, L.; Xi, Z. Effect of Elasticity on Heat and Mass Transfer of Highly Viscous Non-Newtonian Fluids Flow in Circular Pipes. Polymers 2025, 17, 1393. https://doi.org/10.3390/polym17101393
Wang X, Qiu X, Zhang X, Zhao L, Xi Z. Effect of Elasticity on Heat and Mass Transfer of Highly Viscous Non-Newtonian Fluids Flow in Circular Pipes. Polymers. 2025; 17(10):1393. https://doi.org/10.3390/polym17101393
Chicago/Turabian StyleWang, Xuesong, Xiaoyi Qiu, Xincheng Zhang, Ling Zhao, and Zhenhao Xi. 2025. "Effect of Elasticity on Heat and Mass Transfer of Highly Viscous Non-Newtonian Fluids Flow in Circular Pipes" Polymers 17, no. 10: 1393. https://doi.org/10.3390/polym17101393
APA StyleWang, X., Qiu, X., Zhang, X., Zhao, L., & Xi, Z. (2025). Effect of Elasticity on Heat and Mass Transfer of Highly Viscous Non-Newtonian Fluids Flow in Circular Pipes. Polymers, 17(10), 1393. https://doi.org/10.3390/polym17101393







