Non-Stationary Viscoelastic Modeling of Compression Creep Behavior in Composite Bolted Joints
Abstract
1. Introduction
2. Materials and Methods
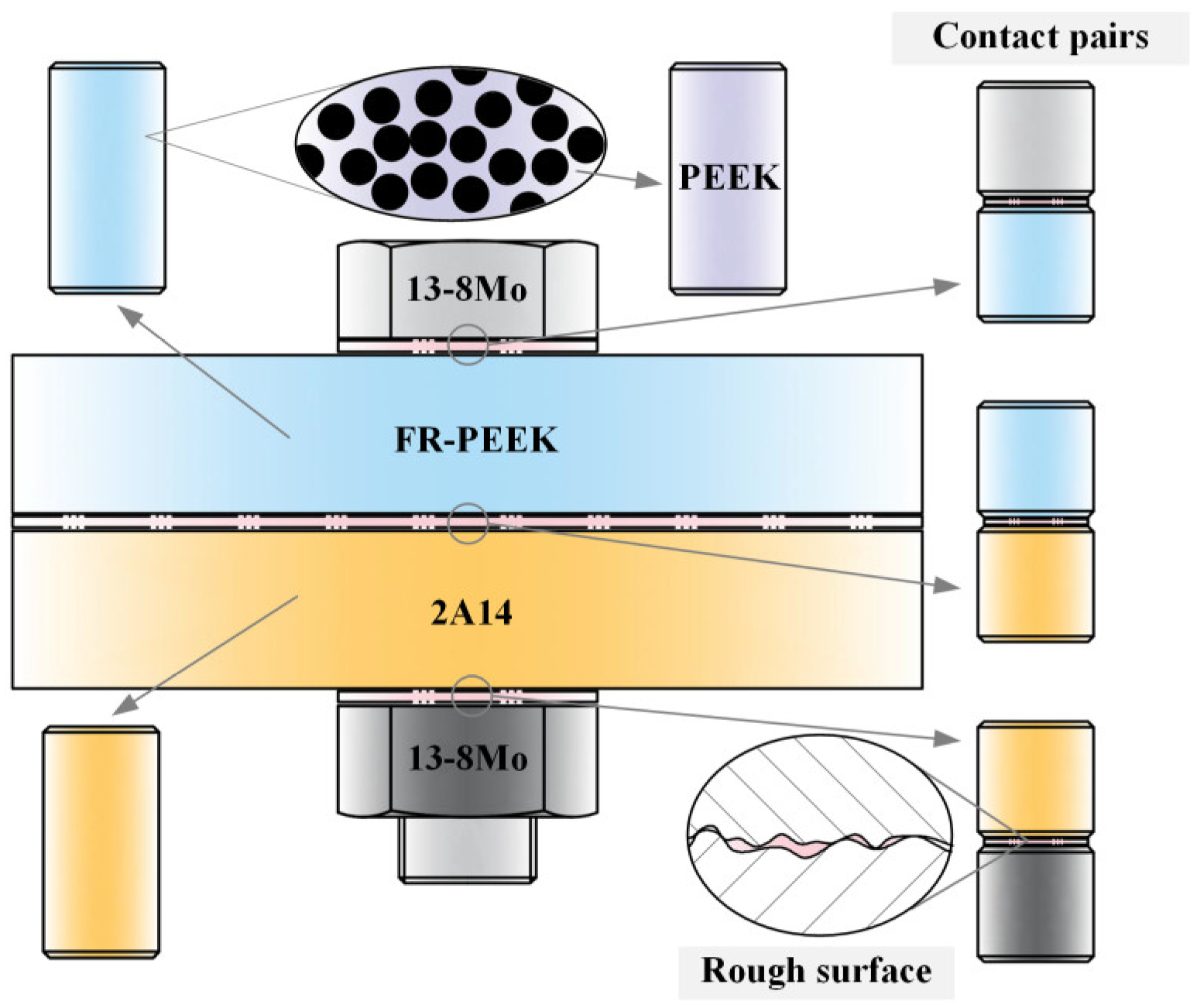
2.1. Materials
2.2. Non-Stationary Burgers Model
2.3. Numerical Implementation
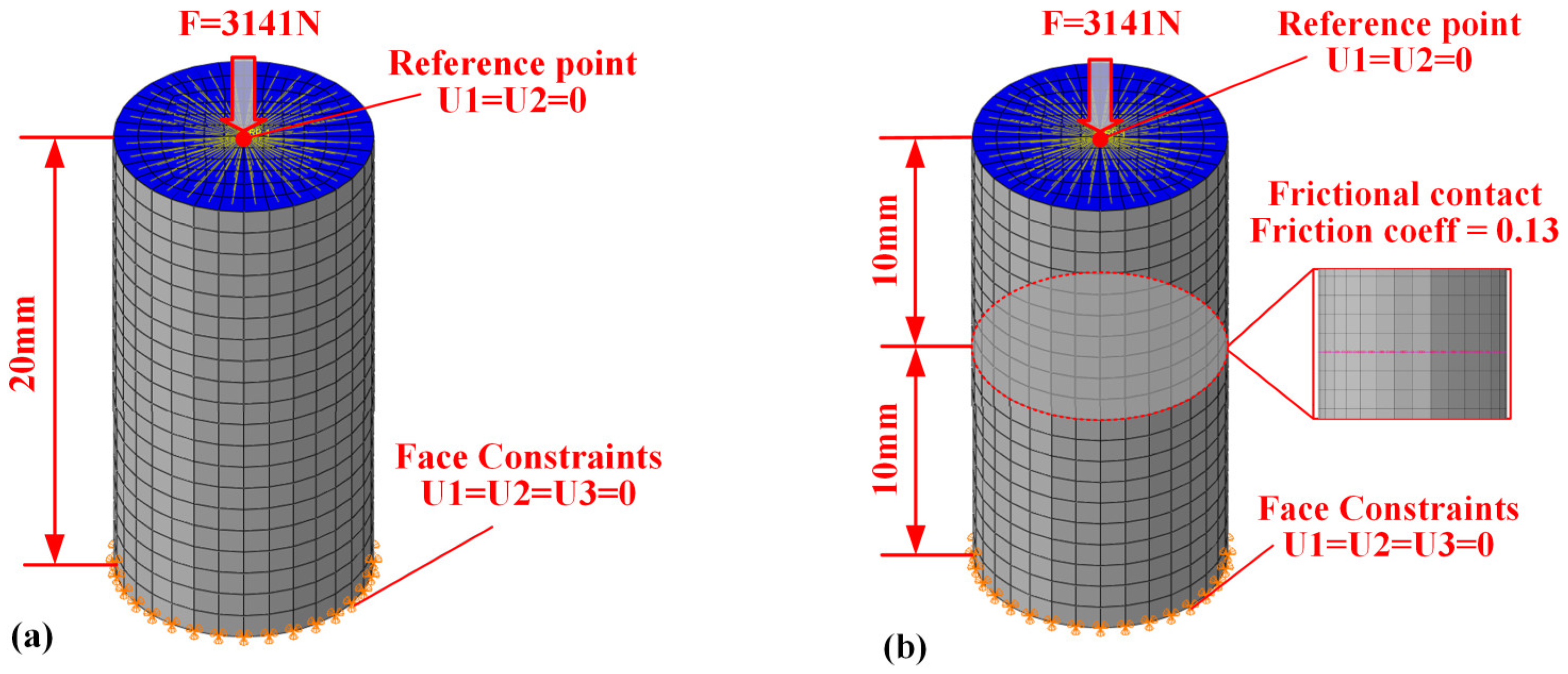
2.4. Finite Element Model
3. Experimental Tests
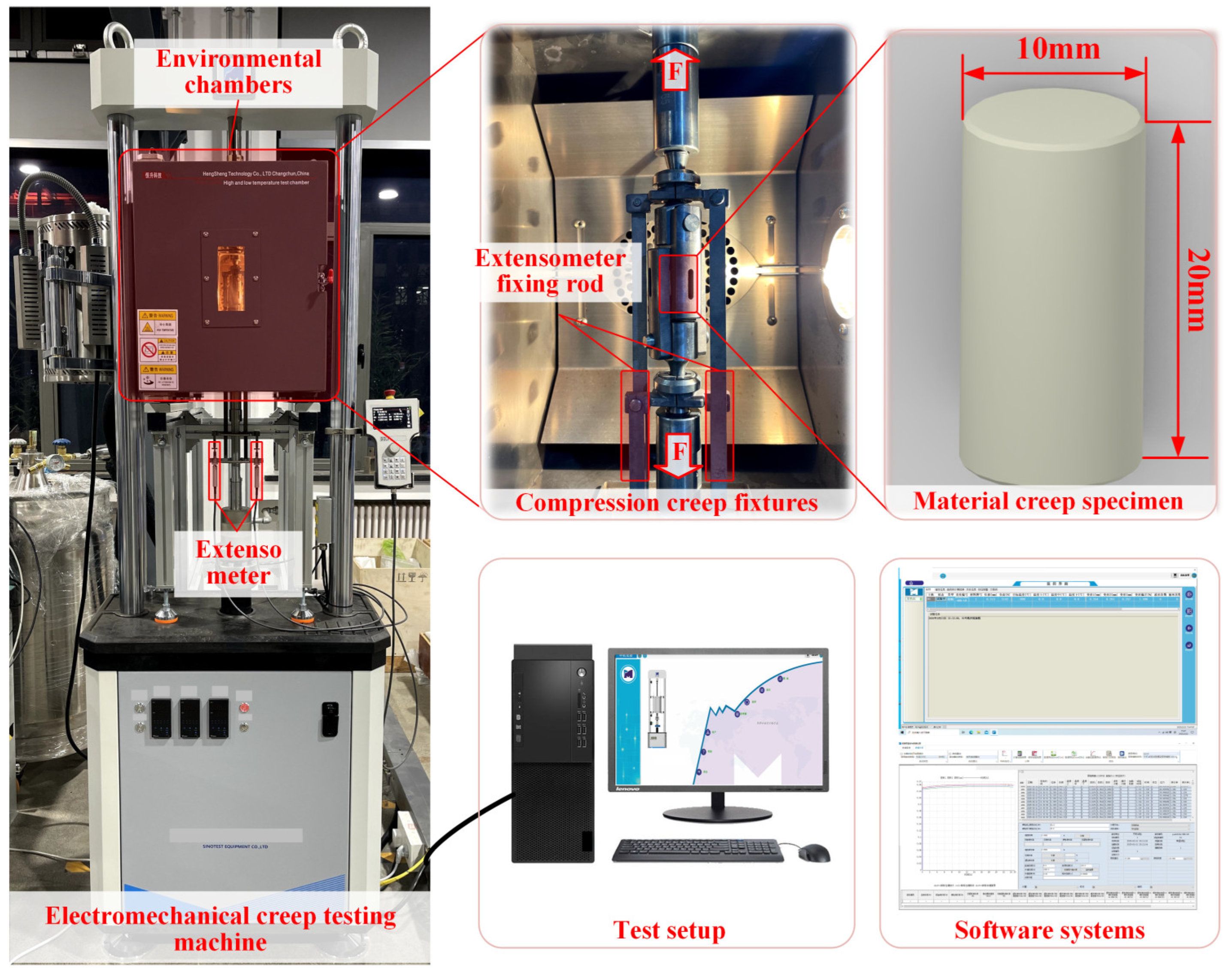
3.1. Problem Statement
3.2. Compression Creep Testing Setup
4. Results and Discussion
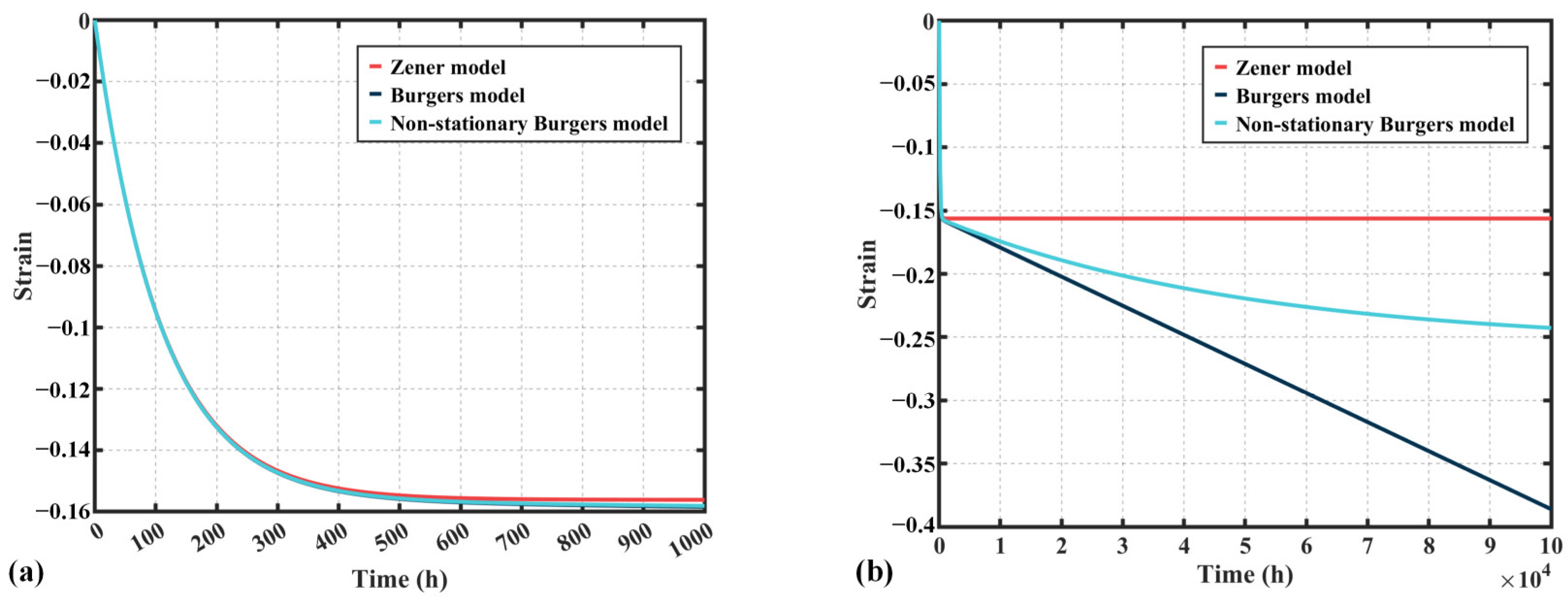
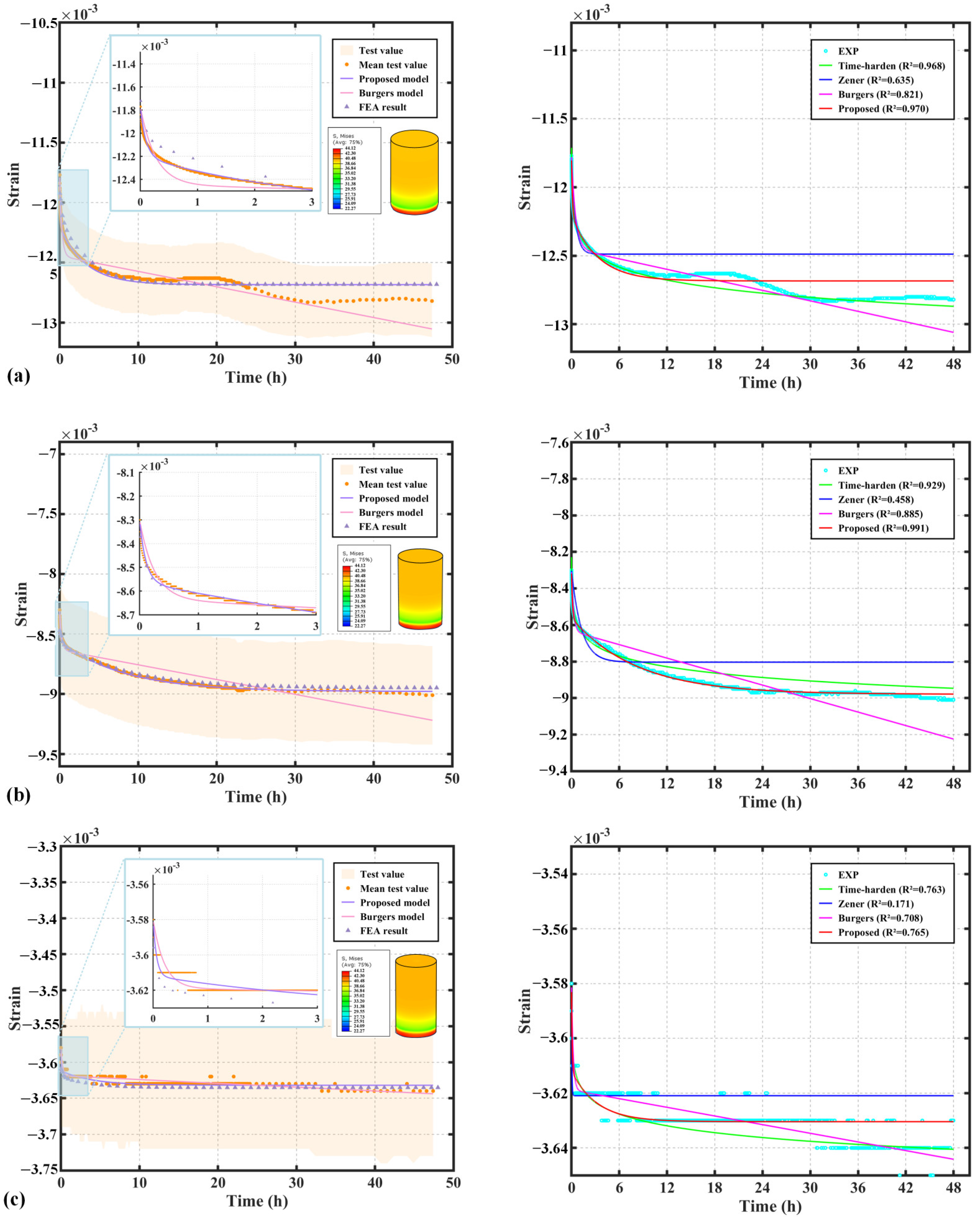
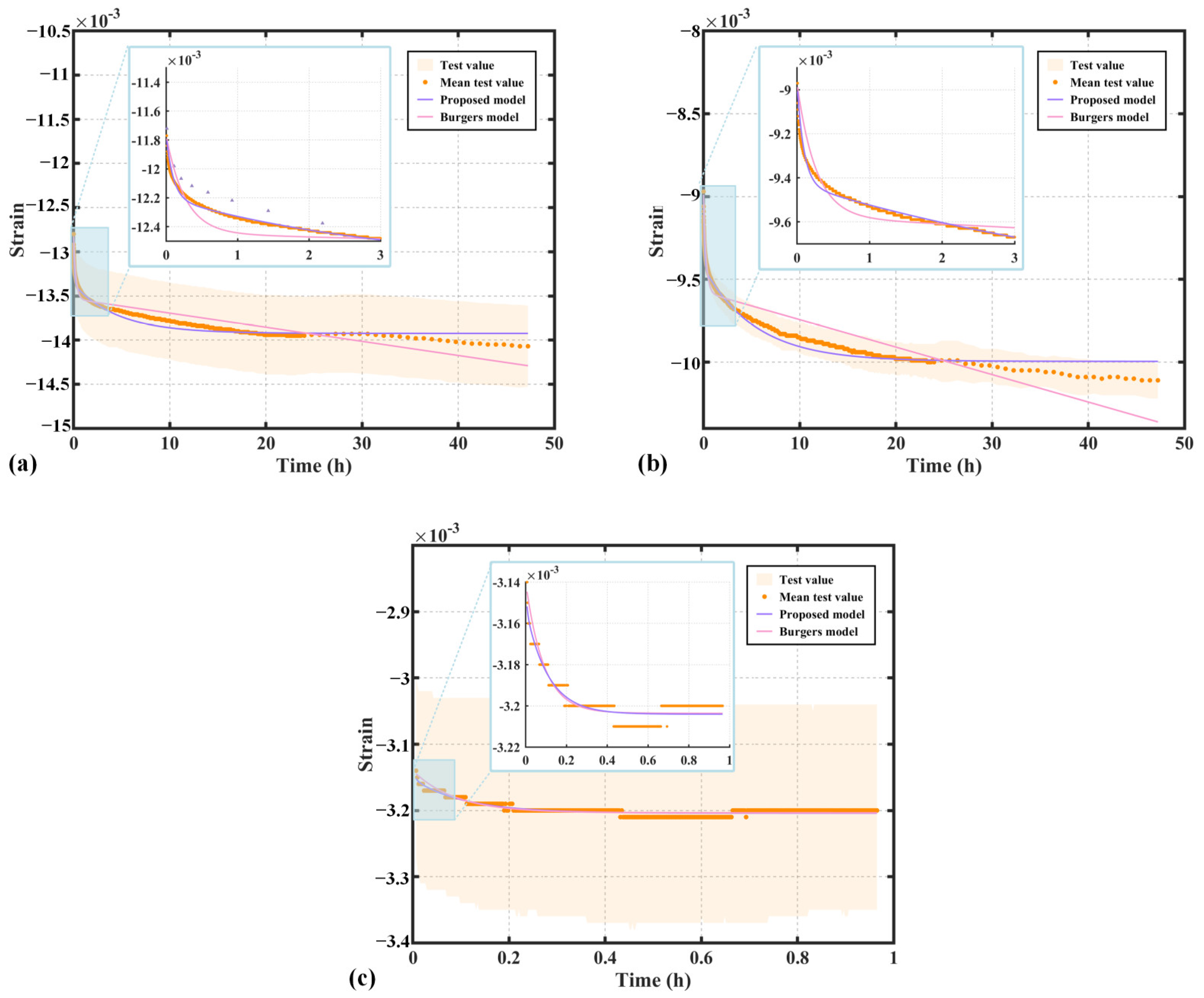
4.1. Parameter Determination and Model Validation
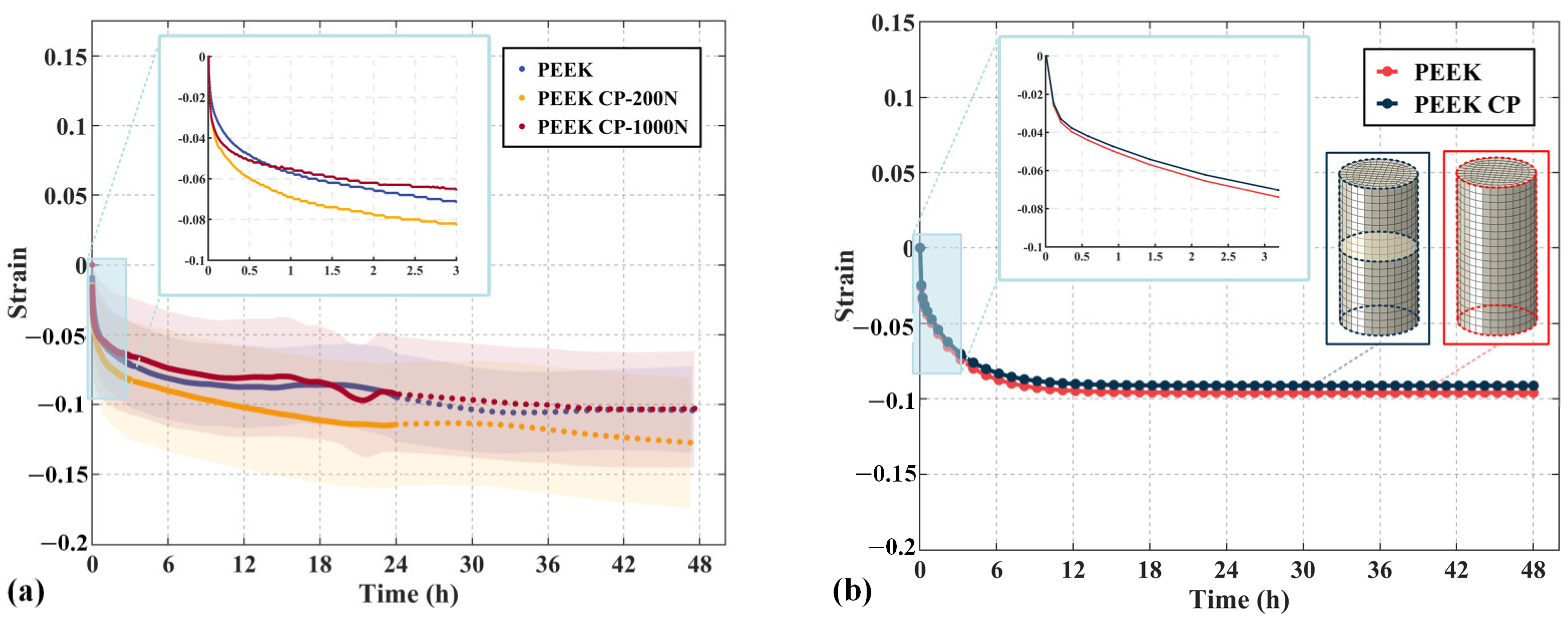
4.2. Creep of Contact Pairs
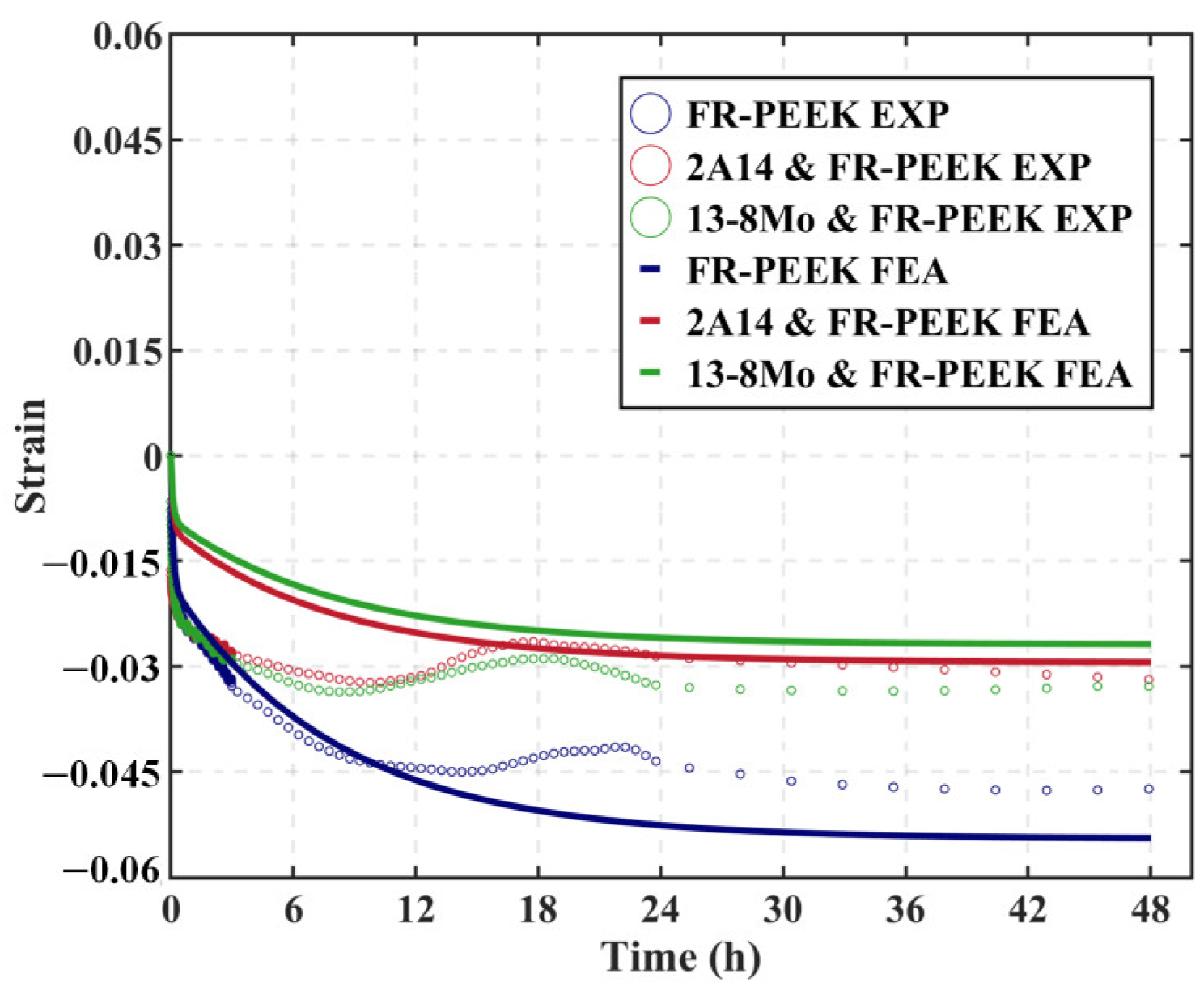
4.3. Localized Loading
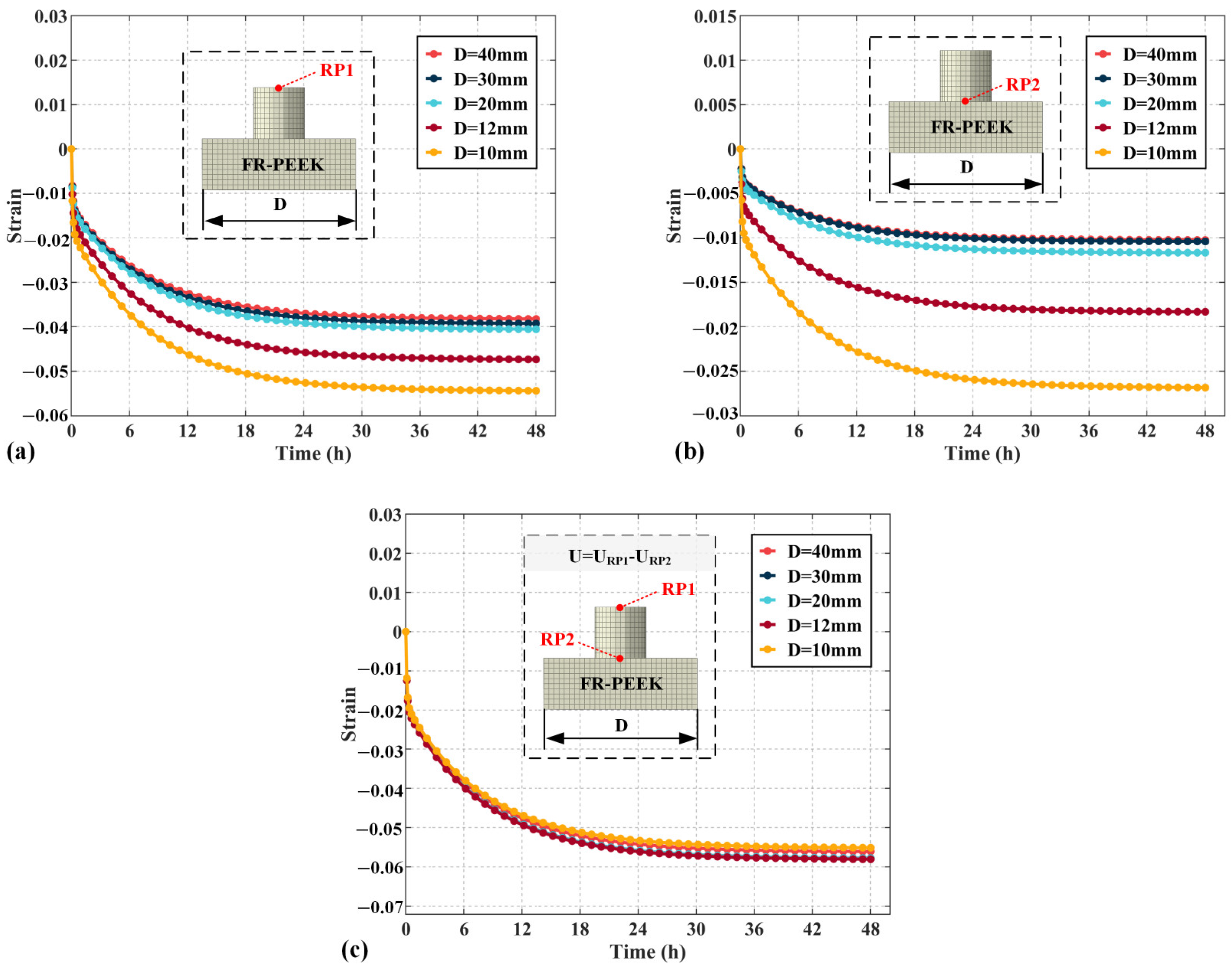
4.4. Structural Parameters
5. Conclusions
- (1)
- A non-stationary Burgers model, based on a nonlinear viscoelastic correction term, was developed. The model parameters for PEEK, FR-PEEK, and 2A14 were fitted using nonlinear least squares, with results showing satisfactory performance compared to the classical Burgers model.
- (2)
- A UMAT subroutine for the non-stationary Burgers model was developed in ABAQUS. Simulations using the fitted parameters showed that numerical results align with experimental data, confirming the subroutine’s correctness.
- (3)
- Compression creep tests indicate that an increased initial load significantly enhances the structure’s resistance to creep. Moreover, the initial load exerts a considerable influence on the preload relaxation behavior of both FRP composites and metals.
- (4)
- The strain was significantly smaller than under uniform loading under localized loading. If the loaded area is sufficiently small, strain can decrease by over 60%. Consequently, structural parameters significantly affect preload relaxation.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| FRP | Fiber-reinforced polymer |
| FEA | Finite element analysis |
| PEEK | Polyetheretherketone |
| FR-PEEK | Fiber-reinforced polyetheretherketone |
| UMAT | User-defined material subroutine |
References
- Zhang, J.; Lin, G.; Vaidya, U.; Wang, H. Past, Present and Future Prospective of Global Carbon Fibre Composite Developments and Applications. Compos. Part B Eng. 2023, 250, 110463. [Google Scholar] [CrossRef]
- Song, Z.-G.; Li, F.-M.; Carrera, E.; Hagedorn, P. A New Method of Smart and Optimal Flutter Control for Composite Laminated Panels in Supersonic Airflow under Thermal Effects. J. Sound Vib. 2018, 414, 218–232. [Google Scholar] [CrossRef]
- Mallick, P.K. Fiber-Reinforced Composites: Materials, Manufacturing, and Design, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2007; ISBN 978-0-429-12206-4. [Google Scholar]
- An, N.; Jia, Q.; Jin, H.; Ma, X.; Zhou, J. Multiscale Modeling of Viscoelastic Behavior of Unidirectional Composite Laminates and Deployable Structures. Mater. Des. 2022, 219, 110754. [Google Scholar] [CrossRef]
- Miyano, Y.; Nakada, M. Accelerated Testing Methodology for Durability of CFRP. Compos. Part B Eng. 2020, 191, 107977. [Google Scholar] [CrossRef]
- Marsh, G. Airbus A350 XWB Update. Reinf. Plast. 2010, 54, 20–24. [Google Scholar] [CrossRef]
- Shan, M.; Zhao, L.; Hong, H.; Liu, F.; Zhang, J. A Progressive Fatigue Damage Model for Composite Structures in Hygrothermal Environments. Int. J. Fatigue 2018, 111, 299–307. [Google Scholar] [CrossRef]
- Pramanik, A.; Basak, A.K.; Dong, Y.; Sarker, P.K.; Uddin, M.S.; Littlefair, G.; Dixit, A.R.; Chattopadhyaya, S. Joining of Carbon Fibre Reinforced Polymer (CFRP) Composites and Aluminium Alloys—A Review. Compos. Part A Appl. Sci. Manuf. 2017, 101, 1–29. [Google Scholar] [CrossRef]
- Ucsnik, S.; Scheerer, M.; Zaremba, S.; Pahr, D.H. Experimental Investigation of a Novel Hybrid Metal–Composite Joining Technology. Compos. Part A Appl. Sci. Manuf. 2010, 41, 369–374. [Google Scholar] [CrossRef]
- Kabche, J.-P.; Caccese, V.; Berube, K.A.; Bragg, R. Experimental Characterization of Hybrid Composite-to-Metal Bolted Joints under Flexural Loading. Compos. Part B Eng. 2007, 38, 66–78. [Google Scholar] [CrossRef]
- Thoppul, S.D.; Finegan, J.; Gibson, R.F. Mechanics of Mechanically Fastened Joints in Polymer–Matrix Composite Structures—A Review. Compos. Sci. Technol. 2009, 69, 301–329. [Google Scholar] [CrossRef]
- Starikov, R.; Schön, J. Quasi-Static Behaviour of Composite Joints with Countersunk Composite and Metal Fasteners. Compos. Part B Eng. 2001, 32, 401–411. [Google Scholar] [CrossRef]
- Galińska, A. Mechanical Joining of Fibre Reinforced Polymer Composites to Metals—A Review. Part I: Bolted Joining. Polymers 2020, 12, 2252. [Google Scholar] [CrossRef]
- Cao, Z.; Cardew-Hall, M. Interference-Fit Riveting Technique in Fiber Composite Laminates. Aerosp. Sci. Technol. 2006, 10, 327–330. [Google Scholar] [CrossRef]
- Liu, F.; Yao, W.; Zhao, L.; Wu, H.; Zhang, X.; Zhang, J. An Improved 2D Finite Element Model for Bolt Load Distribution Analysis of Composite Multi-Bolt Single-Lap Joints. Compos. Struct. 2020, 253, 112770. [Google Scholar] [CrossRef]
- Zuo, Y.; Wang, Z.; Jiao, Y.; Pei, X. Progressive Damage and Stiffness Degradation Assessments of Double-lap CFRP/Ti Interference Fit Bolted Joints under Quasi-static Tensile Load. Polym. Compos. 2025, 46, 794–808. [Google Scholar] [CrossRef]
- Li, C.; Xian, G. Novel Wedge-Shaped Bond Anchorage System for Pultruded CFRP Plates. Mater. Struct. 2018, 51, 162. [Google Scholar] [CrossRef]
- Khashaba, U.A.; Sallam, H.E.M.; Al-Shorbagy, A.E.; Seif, M.A. Effect of Washer Size and Tightening Torque on the Performance of Bolted Joints in Composite Structures. Compos. Struct. 2006, 73, 310–317. [Google Scholar] [CrossRef]
- Li, H.; Shi, J.; Zhao, J.; Zheng, Y.; Duan, Y.; Li, C. Tensile Behavior Analysis of CFRP (Carbon-Fiber-Reinforced-Polymer)–Titanium Joint under Preload. Polym. Compos. 2023, 44, 2205–2221. [Google Scholar] [CrossRef]
- Horn, W.; Schmitt, R. Relaxation in bolted thermoplastic compositejoints. In Proceedings of the 34th Structures, Structural Dynamics and Materials Conference, La Jolla, CA, USA, 19–22 April 1993; American Institute of Aeronautics and Astronautics: La Jolla, CA, USA, 1993. [Google Scholar]
- Mara, V.; Haghani, R.; Al-Emrani, M. Improving the Performance of Bolted Joints in Composite Structures Using Metal Inserts. J. Compos. Mater. 2016, 50, 3001–3018. [Google Scholar] [CrossRef]
- Gong, H.; Ding, X.; Liu, J.; Feng, H. Review of Research on Loosening of Threaded Fasteners. Friction 2022, 10, 335–359. [Google Scholar] [CrossRef]
- Gong, H.; Liu, J.; Feng, H. Research Review on Loosening Mechanisms and Anti-Loosening Methods of Threaded Fasteners. J. Mech. Eng. 2022, 58, 326. [Google Scholar] [CrossRef]
- Friedrich, C.; Hubbertz, H. Friction Behavior and Preload Relaxation of Fastening Systems with Composite Structures. Compos. Struct. 2014, 110, 335–341. [Google Scholar] [CrossRef]
- Caccese, V.; Berube, K.A.; Fernandez, M.; Daniel Melo, J.; Kabche, J.P. Influence of Stress Relaxation on Clamp-up Force in Hybrid Composite-to-Metal Bolted Joints. Compos. Struct. 2009, 89, 285–293. [Google Scholar] [CrossRef]
- Finck, D.; Seidel, C.; Hausmann, J.; Rief, T. Rief Creep-Induced Screw Preload Loss of Carbon-Fiber Sheet Molding Compound at Elevated Temperature. Materials 2019, 12, 3598. [Google Scholar] [CrossRef]
- Liu, G.; Wu, Q.; Wang, Z.; Luo, Y.; Qi, Y. Preload Relaxation Analysis and Reliable Life Prediction of Space Connection and Separation Device Based on Accelerated Degradation Tests. Chin. J. Aeronaut. 2023, 36, 202–211. [Google Scholar] [CrossRef]
- Wang, S.; Stratford, T.; Reynolds, T.P.S. Linear Creep of Bonded FRP-Strengthened Metallic Structures at Warm Service Temperatures. Constr. Build. Mater. 2021, 283, 122699. [Google Scholar] [CrossRef]
- Lal, H.M.; Uthaman, A.; Li, C.; Xian, G.; Thomas, S. Combined Effects of Cyclic/Sustained Bending Loading and Water Immersion on the Interface Shear Strength of Carbon/Glass Fiber Reinforced Polymer Hybrid Rods for Bridge Cable. Constr. Build. Mater. 2022, 314, 125587. [Google Scholar] [CrossRef]
- Bažant, Z.P.; Yunping, X. Drying Creep of Concrete: Constitutive Model and New Experiments Separating Its Mechanisms. Mater. Struct. 1994, 27, 3–14. [Google Scholar] [CrossRef]
- Jin, S.; Harmuth, H.; Gruber, D. Compressive Creep Testing of Refractories at Elevated Loads—Device, Material Law and Evaluation Techniques. J. Eur. Ceram. Soc. 2014, 34, 4037–4042. [Google Scholar] [CrossRef]
- Yang, J.; DeWolf, J.T. Mathematical Model for Relaxation in High-Strength Bolted Connections. J. Struct. Eng. 1999, 125, 803–809. [Google Scholar] [CrossRef]
- Shivakumar, K.; Crews, J., Jr. Bolt Clampup Relaxation in a Graphite/Epoxy Laminate. In Long-Term Behavior of Composites; O’Brien, T., Ed.; ASTM International: West Conshohocken, PA, USA, 1983; Volume STP813-EB, ISBN 978-0-8031-0252-1. [Google Scholar]
- Bouzid, A.; Chaaban, A.; Bazergui, A. The Effect of Gasket Creep-Relaxation on the Leakage Tightness of Bolted Flanged Joints. J. Press. Vessel Technol. 1995, 117, 71–78. [Google Scholar] [CrossRef]
- Bouzid, A.; Chaaban, A. An Accurate Method of Evaluating Relaxation in Bolted Flanged Connections. J. Press. Vessel Technol. 1997, 119, 10–17. [Google Scholar] [CrossRef]
- Kallmeyer, A.; Stephens, R. Creep Elongation of Bolt Holes Subjected to Bearing Loads in a Polymer Matrix Composite Laminate. In Composite Materials: Fatigue and Fracture (Sixth Volume); Armanios, E., Ed.; ASTM International: West Conshohocken, PA, USA, 1997; pp. 452–466. ISBN 978-0-8031-2411-0. [Google Scholar]
- Nechache, A.; Bouzid, A.-H. Creep Analysis of Bolted Flange Joints. Int. J. Press. Vessel. Pip. 2007, 84, 185–194. [Google Scholar] [CrossRef]
- Scattina, A.; Roncato, D.; Belingardi, G.; Martino, G. Investigation of Creep Phenomenon on Composite Material for Bolt Connections. Compos. Struct. 2015, 134, 378–383. [Google Scholar] [CrossRef]
- Findley, W.N.; Lai, J.S.; Onaran, K. (Eds.) Chapter 5. In Creep and Relaxation of Nonlinear Viscoelastic Materials; North-Holland Series in Applied Mathematics and Mechanics; North-Holland: Amsterdam, The Netherland, 1976; Volume 18, pp. 50–107. [Google Scholar]
- Epaarachchi, J.A. 17—The Effect of Viscoelasticity on Fatigue Behaviour of Polymer Matrix Composites. In Creep and Fatigue in Polymer Matrix Composites; Guedes, R.M., Ed.; Woodhead Publishing Series in Composites Science and Engineering; Woodhead Publishing: Sawston, UK, 2011; pp. 492–513. ISBN 978-1-84569-656-6. [Google Scholar]
- Abboud, A.; Nassar, S.A. Viscoelastic Strain Hardening Model for Gasket Creep Relaxation. J. Press. Vessel Technol. 2013, 135, 031201. [Google Scholar] [CrossRef]
- Wang, J.; Li, Y.; Dai, F. A Micromechanical Relaxation Model of Composite Bolted Connections Based on Viscoelastic Theory. Compos. Struct. 2016, 146, 14–25. [Google Scholar] [CrossRef]
- Hu, J.; Zhang, K.; Cheng, H.; Qi, Z. Mechanism of Bolt Pretightening and Preload Relaxation in Composite Interference-Fit Joints under Thermal Effects. J. Compos. Mater. 2020, 54, 4929–4946. [Google Scholar] [CrossRef]
- Li, Y.; Wang, Y.; Liu, Z.; Yang, X.; Zhang, C.; Cheng, Y. A Combined Theoretical and Experimental Study on Contact Creep-Induced Clamping Force Relaxation of Bolted Joints at Ambient Temperature. Mar. Struct. 2022, 85, 103263. [Google Scholar] [CrossRef]
- Lv, J.; Xiao, Y.; Xue, Y. Time–Temperature-Dependent Response and Analysis of Preload Relaxation in Bolted Composite Joints. J. Reinf. Plast. Compos. 2018, 37, 460–474. [Google Scholar] [CrossRef]
- Lv, J.; Xiao, Y.; Zhou, Y.; Xie, Y. Characterization and Modeling of the Creep Behavior of Fiber Composites with Tension and Compression Asymmetry. Int. J. Mech. Sci. 2020, 170, 105340. [Google Scholar] [CrossRef]
- Xie, Y.; Xiao, Y.; Lv, J.; Zhang, Z.; Zhou, Y.; Xue, Y. Influence of Creep on Preload Relaxation of Bolted Composite Joints: Modeling and Numerical Simulation. Compos. Struct. 2020, 245, 112332. [Google Scholar] [CrossRef]
- ISO 527-1:2019; Plastics—Determination of Tensile Properties—Part 1: General Principles. International Standards Organization: Geneva, Switzerland, 2019. Available online: https://www.iso.org/obp/ui/en/#iso:std:iso:527:-1:ed-3:v1:en (accessed on 14 May 2025).
- ISO 604:2002; Plastics—Determination of Compressive Properties. International Standards Organization: Geneva, Switzerland, 2002. Available online: https://www.iso.org/standard/31261.html (accessed on 14 May 2025).
- ISO 11357-1:2023; Plastics—Differential Scanning Calorimetry (DSC)—Part 1: General Principles. International Standards Organization: Geneva, Switzerland, 2023. Available online: https://www.iso.org/standard/83904.html (accessed on 14 May 2025).
- ISO 75-2:2013; Plastics—Determination of Temperature of Deflection Under Load—Part 2: Plastics and ebonite. International Standards Organization: Geneva, Switzerland, 2013. Available online: https://www.iso.org/standard/55653.html (accessed on 14 May 2025).
- Wang, Y.; Wang, D.; Li, G.; Wang, L.; Zhu, C.; Du, Y.; Zhou, Z. Three-Dimensional Nonlinear Model of Rock Creep under Freeze–Thaw Cycles. PLoS ONE 2023, 18, e0287605. [Google Scholar] [CrossRef] [PubMed]
- D20 Committee ASTM International; Test Methods for Tensile, Compressive, and Flexural Creep and Creep-Rupture of Plastics. ASTM International: West Conshohocken, PA, USA, 2017. [CrossRef]



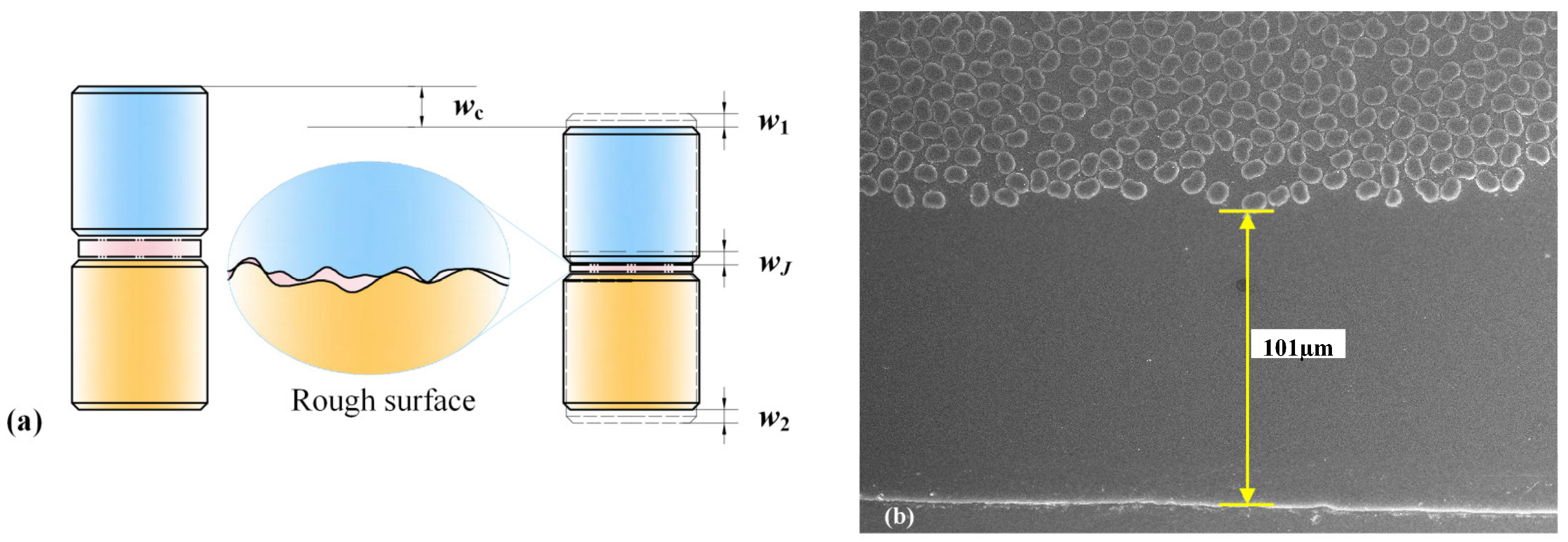
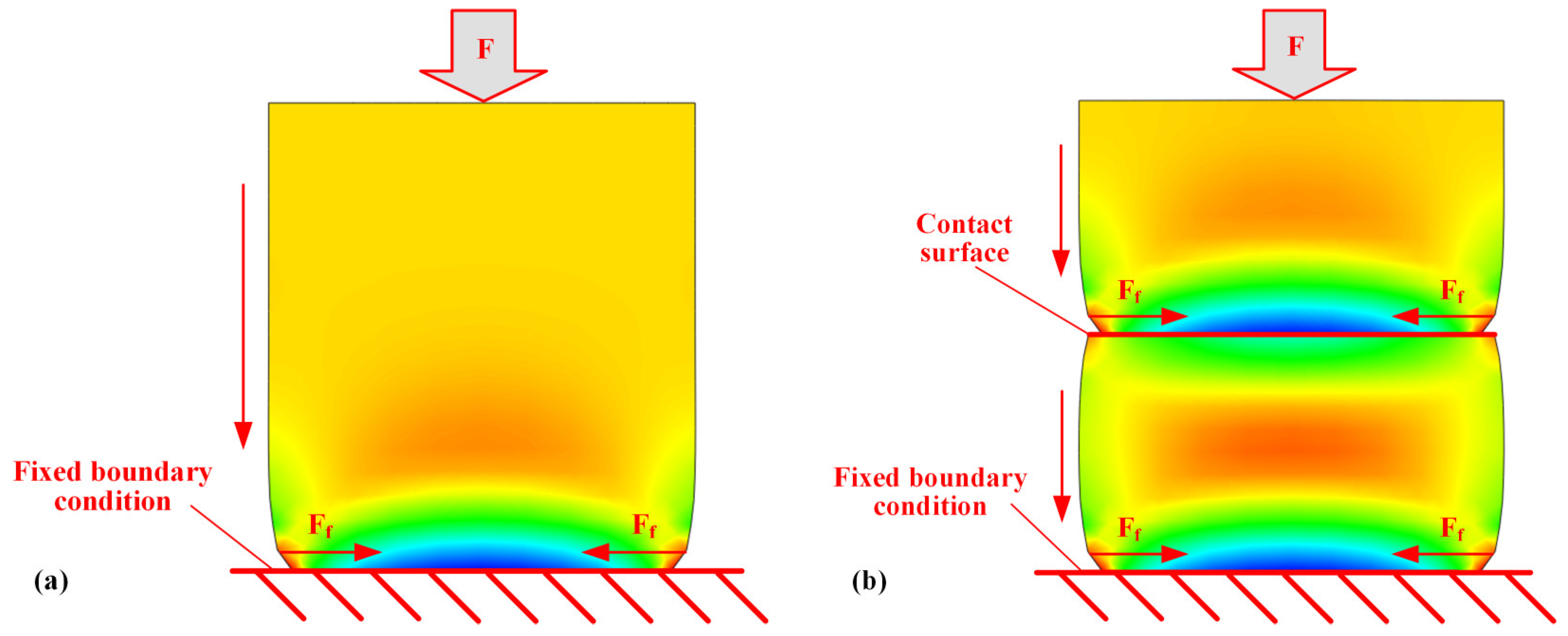
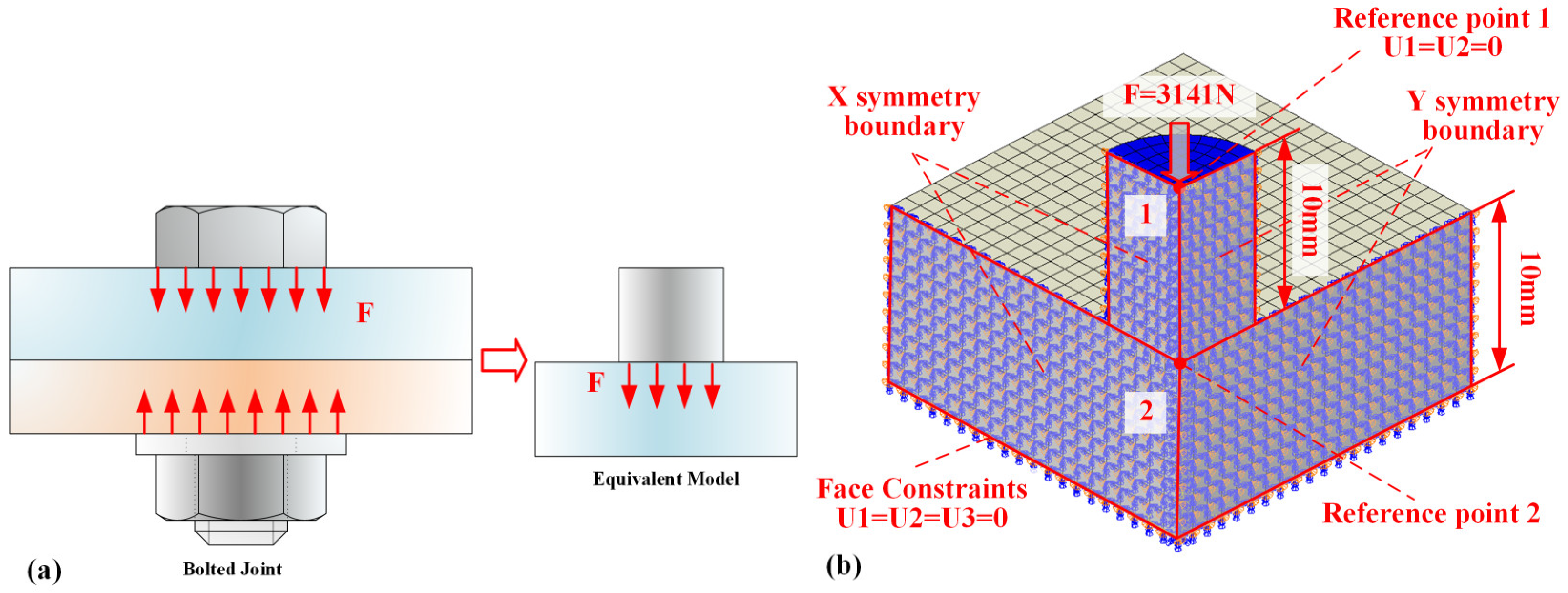
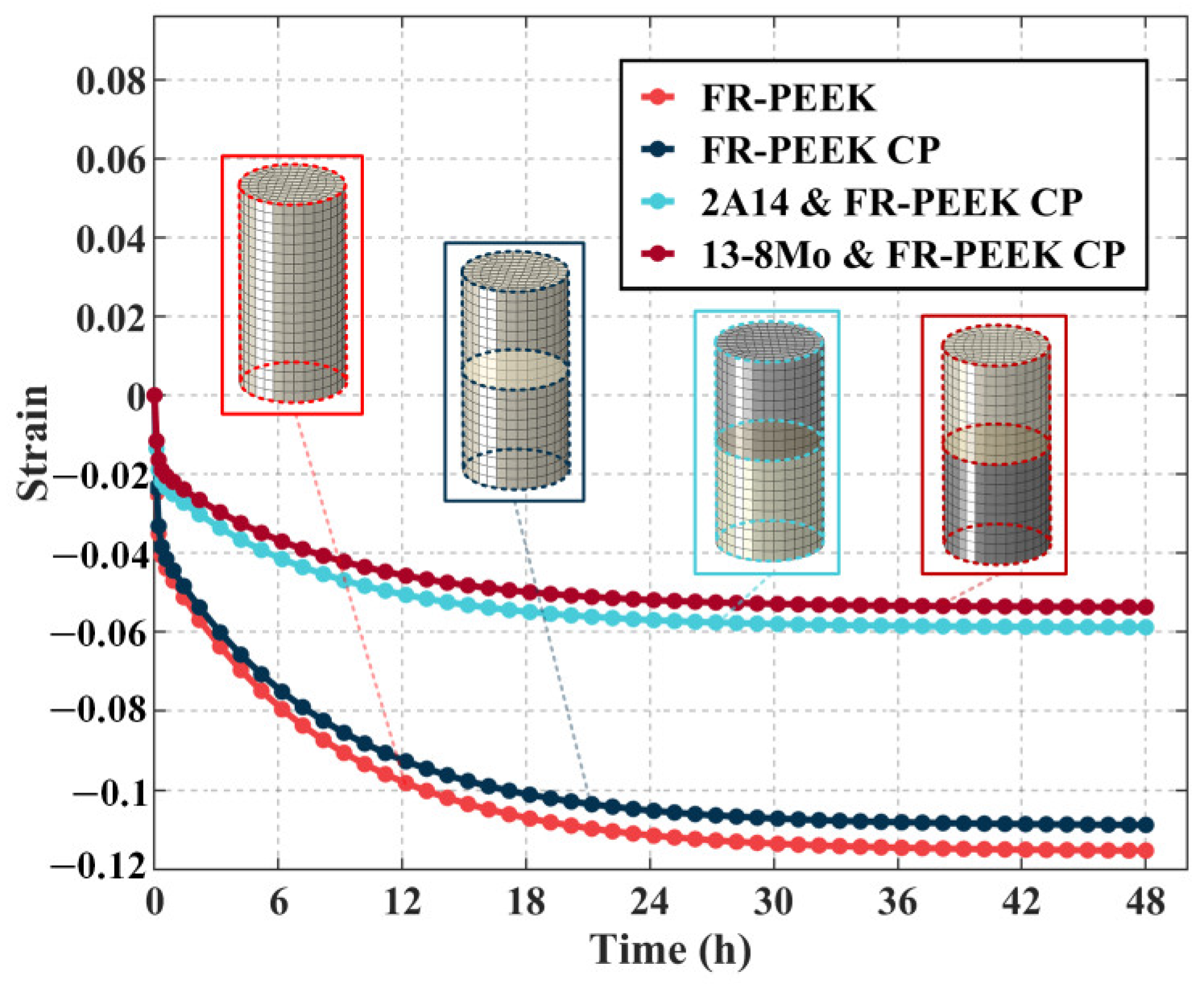



| Properties | Unit | Standard | PEEK | FR-PEEK |
|---|---|---|---|---|
| Tensile strength at yield | MPa | ISO 527 [48] | 95 | - |
| Elongation at yield | % | ISO 527 | 5 | - |
| Tensile strength at break | MPa | ISO 527 | - | 113 |
| Elongation at break | % | ISO 527 | 25 | 5 |
| Modulus of elasticity in tension | MPa | ISO 527 | 4200 | 6300 |
| Compression modulus | MPa | ISO 604 [49] | 3400 | - |
| Compression strength | MPa | ISO 604 | 23/43/102 | 29/52/120 |
| Glass transition temperature | °C | ISO 11357 [50] | 150 | 147 |
| Heat distortion temperature HDT, Method A | °C | ISO-R 75 Method A [51] | 162 | - |
| Density | g/cm3 | - | 1.31 | 1.53 |
| Model | Material | E1/GPa | η1/GPa·h | A/GPa·h | B |
|---|---|---|---|---|---|
| The classical Burgers model | PEEK | 54 | 13 | 2499 | - |
| FR-PEEK | 66 | 17 | 2408 | - | |
| 2A14 | 630 | 56 | 290457 | - | |
| The non-stationary Burgers model | PEEK | 71 | 6 | 329 | 0.321 |
| FR-PEEK | 87 | 8 | 379 | 9.365 | |
| 2A14 | 3058 | 18 | 86 | 0.312 |
| Model | Material | E1/GPa | η1/GPa·h | A/GPa·h | B | R2 |
|---|---|---|---|---|---|---|
| The classical Burgers model | PEEK | 54 | 13 | 2499 | - | 0.8765 |
| FR-PEEK | 66 | 17 | 2408 | - | 0.8846 | |
| 2A14 | 630 | 56 | 290,457 | - | 0.8252 | |
| The non-stationary Burgers model | PEEK | 71 | 6 | 329 | 0.218 | 0.9679 |
| FR-PEEK | 87 | 8 | 379 | 0.186 | 0.9803 | |
| 2A14 | 3058 | 18 | 86 | 9.087 | 0.8530 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, J.; Wang, S.; Lu, H.; Yuan, Z.; Mu, X.; Sun, Q.; Yuan, B. Non-Stationary Viscoelastic Modeling of Compression Creep Behavior in Composite Bolted Joints. Polymers 2025, 17, 1382. https://doi.org/10.3390/polym17101382
Yang J, Wang S, Lu H, Yuan Z, Mu X, Sun Q, Yuan B. Non-Stationary Viscoelastic Modeling of Compression Creep Behavior in Composite Bolted Joints. Polymers. 2025; 17(10):1382. https://doi.org/10.3390/polym17101382
Chicago/Turabian StyleYang, Jingwen, Shuai Wang, Hongli Lu, Zhiwei Yuan, Xiaokai Mu, Qingchao Sun, and Bo Yuan. 2025. "Non-Stationary Viscoelastic Modeling of Compression Creep Behavior in Composite Bolted Joints" Polymers 17, no. 10: 1382. https://doi.org/10.3390/polym17101382
APA StyleYang, J., Wang, S., Lu, H., Yuan, Z., Mu, X., Sun, Q., & Yuan, B. (2025). Non-Stationary Viscoelastic Modeling of Compression Creep Behavior in Composite Bolted Joints. Polymers, 17(10), 1382. https://doi.org/10.3390/polym17101382









