Determination of Tensile Characteristics and Electrical Resistance Variation of Cables Used for Charging Electric Vehicles
Abstract
1. Introduction
- -
- Common test methods for insulating and sheathing materials of electric cables and optical cables: Part 202: General tests—Measurement of thickness of non-metallic sheath (IEC 60811-202, [5]);
- -
- Power cables with extruded insulation and their accessories (IEC 60502-1, [6]);
- -
- Tests on electrical cables and optical fiber cables under fire conditions (IEC 60332-1-2, [7]);
- -
- Charging cables for electric vehicles for rated voltages up to and including 0.6/1 kV: Part 1: general requirements (IEC 62893-1, [8]);
- -
- Electric cables: charging cables for electric vehicles (EN 50520:2020/A1;2021, [9]);
- -
- Electric and optical fiber cables: test methods for non-metallic materials (EN 60811-100, [10]).
2. Materials and Methods
2.1. Materials Used for Static Tensile Testing
2.2. Description of the Cable Configuration and Materials Introduced in the Finite Element Analysis
2.3. Method and Device Used for Tensile Tests
3. Results Obtained from the Static Tensile Test of Cables
3.1. Advantages of Using the Universal Testing Machine Attachment Device
- -
- It is provided with a system of transverse guidance of the rollers so that cables of different diameters can be tested while maintaining axiality between the geometrical axis of the cables and that of the testing machine. For this purpose, the rollers over which the wire is passed are movable in such a way that the geometrical axis of the wire between the two rollers always corresponds to the stress axis on which the equal and opposite forces applied from the testing machine are arranged. The displacement of the rollers shall be affected by means of screws and guided on the rectangular groove in each of the base plates.
- -
- On the outside of the rollers, a circular polyamide cover has been fitted, which can be easily replaced. This sleeve has a certain radius to the outside; therefore, it will not have a linear generator. Under these conditions the squeezing effect of the cable by the metal cylinder at the contact between the two components— the cylinder and cable—will be reduced. Depending on the diameter of the cable, the polyamide cover wheels with the corresponding radius are changed.
- -
- The test system contains two metal guide rods between the upper and lower (semi-device) parts of the device in order to balance the moments that lead to the rotation of one or the other part (Figure 4b). The rods rest on two cylindrical guides, one for each semi-device, designed so that the moments developed from the asymmetry of forces in each semi-device cancel each other out, given their opposite direction. If these rods did not exist, the rotations arising from the eccentricity of the two forces on the load cylinders would result in a rotational moment about the load axis for both the upper and lower parts of the device. These moments should be taken over by the testing machine, which is not convenient. By mounting the two guide rods, the rotating moments from the two semi-devices cancel each other, having different directions.
3.2. Results Obtained from the Static Tensile Test
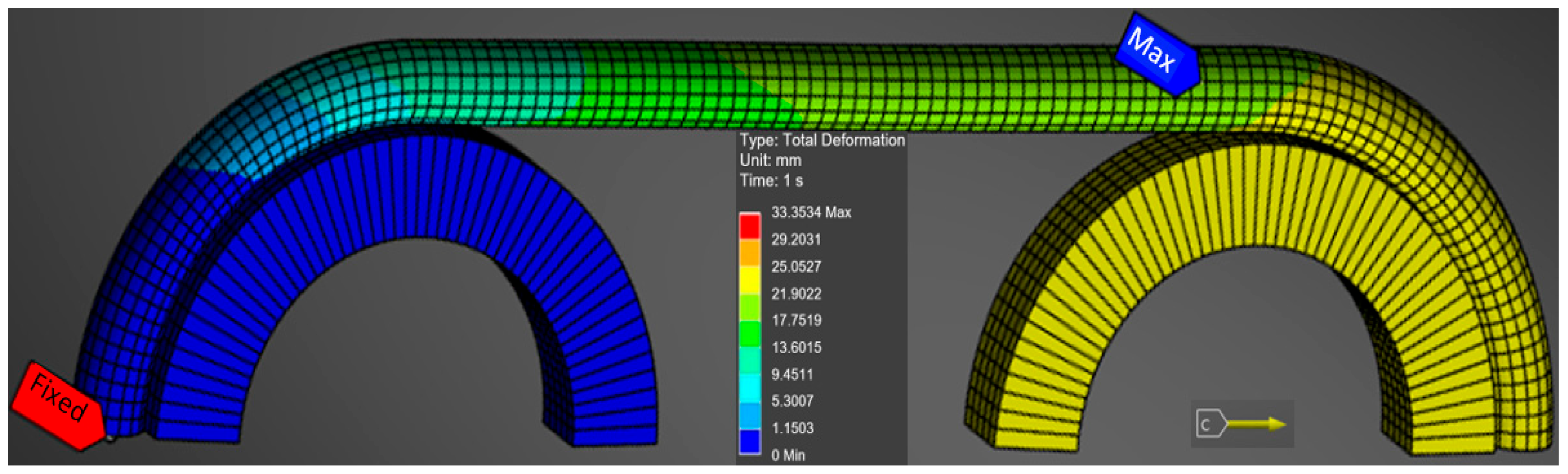
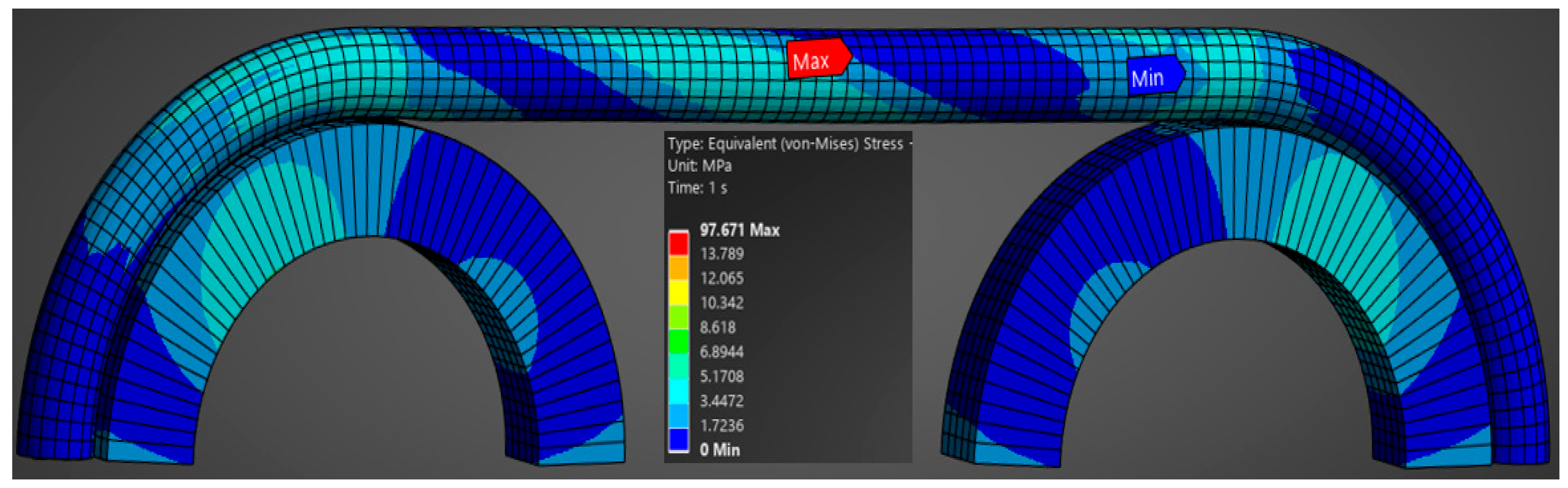
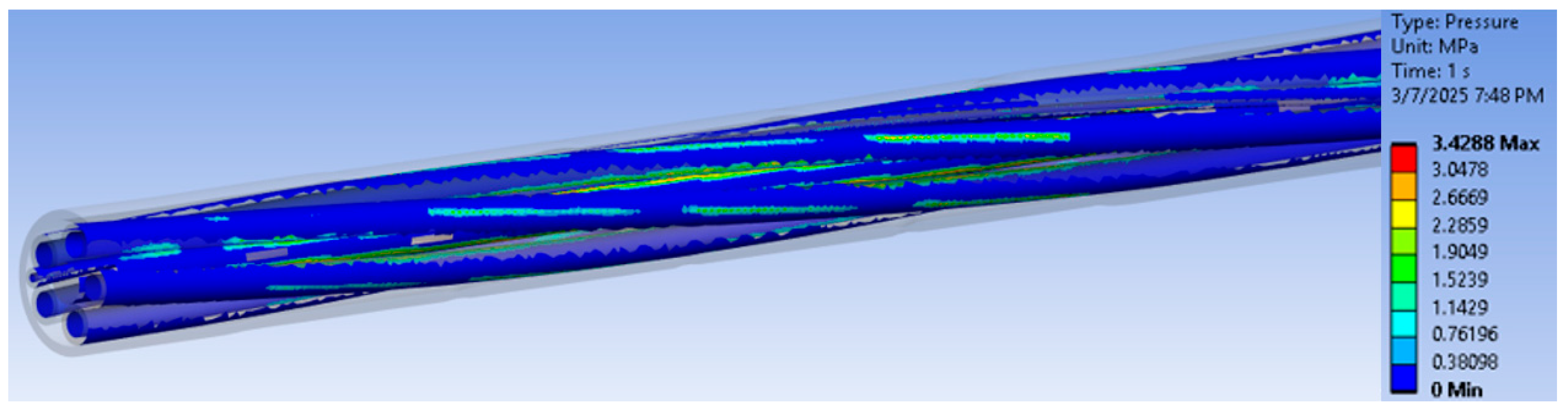
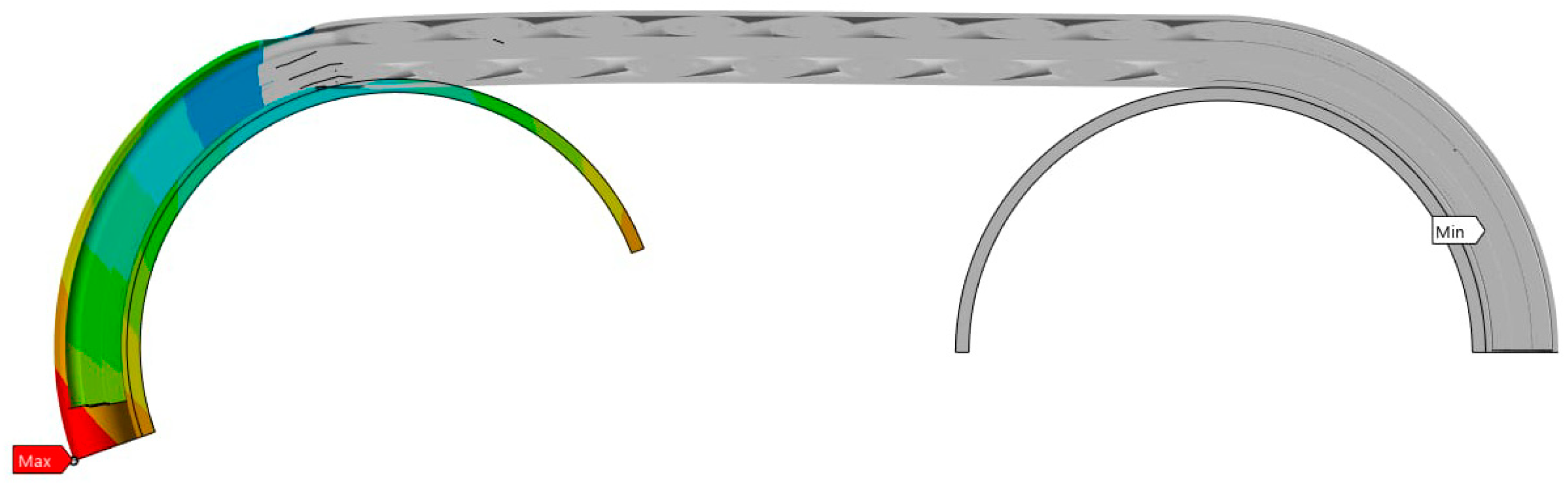
3.3. Results Obtained from Finite Element Analysis of Tensile Loading of 16 mm Outer Diameter Cable
3.4. Results Obtained from Tensile Test, Recording the Change in Electrical Resistance of a Single Conductor
3.4.1. Electrical Circuit Bonding Mode
- A cable with an outer diameter of 12 mm, having six inner electrical wires/conductors, five of which are approx. 3.2 mm in diameter and the sixth approx. 1.7 mm in diameter, and a textile wire;
- An aluminum plate, to which a 120-ohm resistance tensiometer strain gauge has been glued;
- A measuring device with a dual function: to check the initial resistance and to feed the electrical circuit to measure the resistance;
- A National Instruments NI-USB-6009 data acquisition board;
- A laptop on which Labview software (NI Labview, version 19, 64 bit), used for data acquisition, is installed.
3.4.2. Mechanical Clamping and Electrical Connections
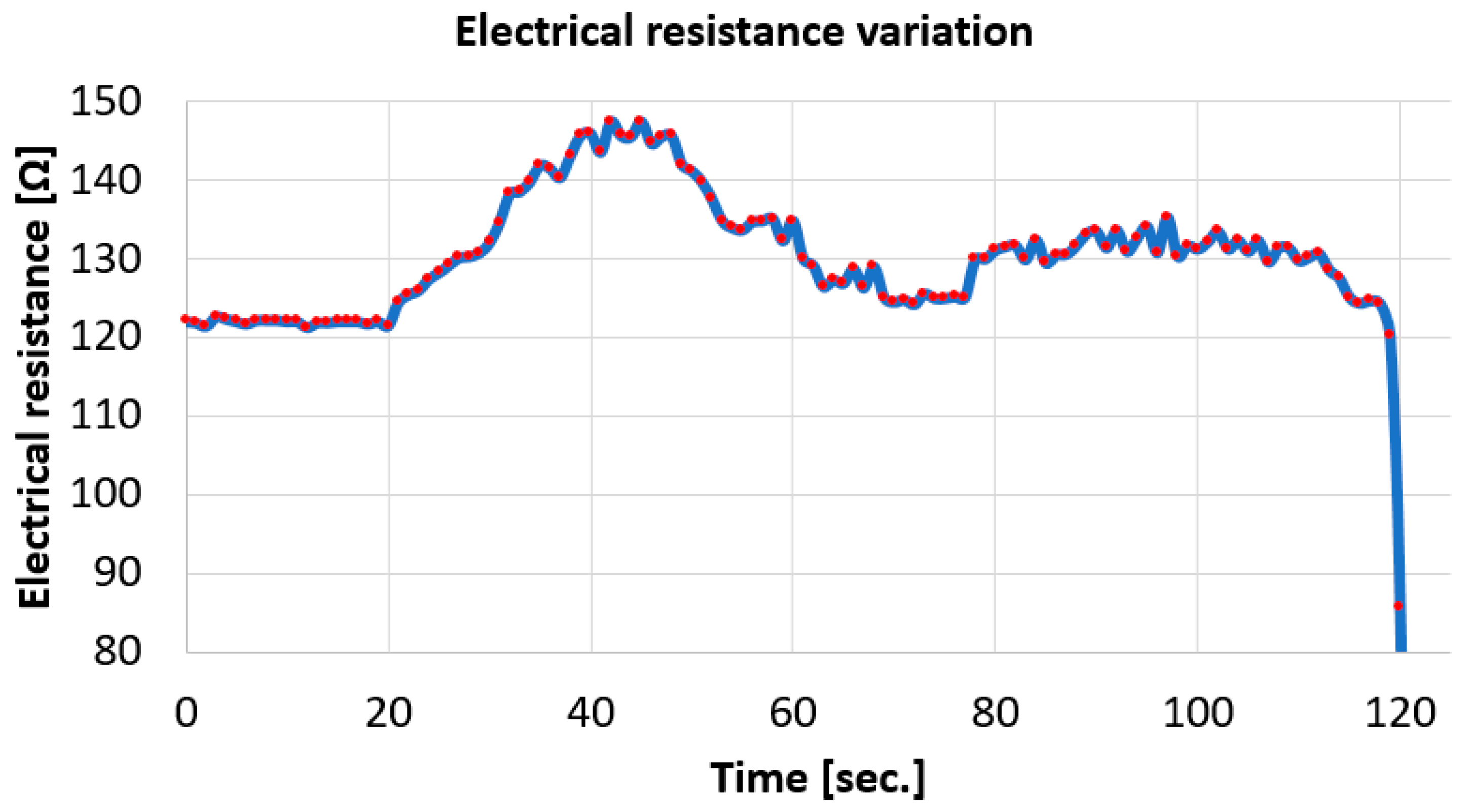
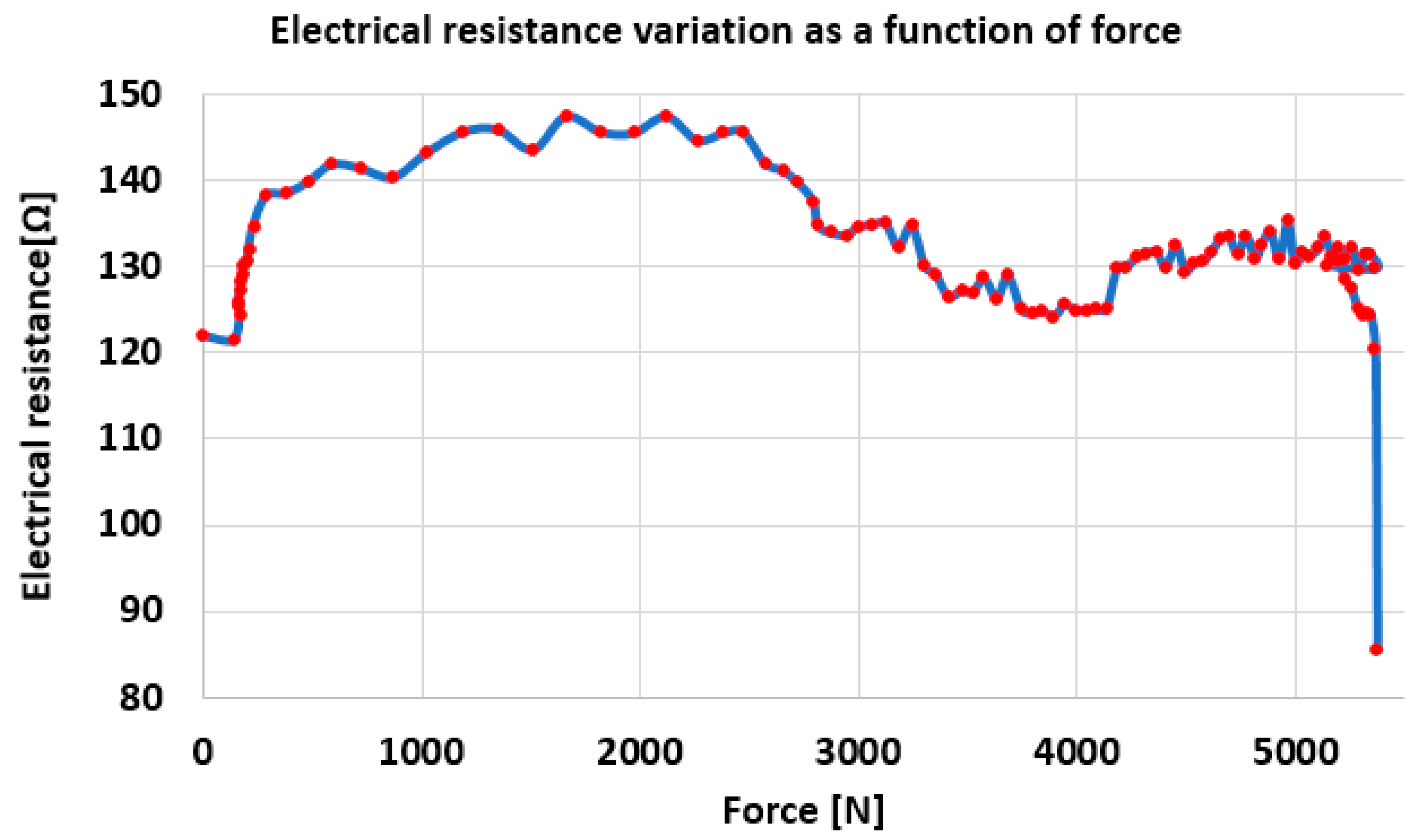
3.4.3. Experimental Data Processing and Conclusions Drawn from the Acquisition of Electrical Resistance Variation
- Initially, the total resistance of the monitored circuit has a value of approx. 121 ohms, given that the resistance of the strain gauge used in the circuit is 120 ohms;
- The initial area with constant resistance at approx. 121 ohms is before the start of the tensile test, given that data acquisition was started first, and then the tensile test was started (after approx. 20 s);
- At the beginning of the test, an increase in resistance is observed: the largest increase was approx. 28 ohms.
- After approx. 45 s, although the tensile test continues, the resistance begins to decrease. This happens because the thin copper conductors that make up the brown conductor begin to break. In fact, sudden drops in resistance are also observed before, caused by the failure of the copper conductors.
- Between the times of 60 s and approx. 120 s, the value of the electrical resistance varies less, with temporary increases and decreases. This is attributed to the achievement of a relative balance between the increase in resistance produced by the elongation of the thin copper conductors and the breakage of some of them. In this interval, two levels can be observed: between 62 and 77 s and between 78 and 113 s. Between these, respectively, between seconds 77 and 78, the resistance increases as a result of the fact that the stretching of the copper conductors occurs without the breakage of other conductors.
- After approx. 120 s from the beginning of the acquisition (approx. 97 s from the beginning of the test, all the thin copper conductors within the brown conductor break.
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Bernstein, B.S. Cable Testing: Can we do better? IEEE Electr. Insul. Mag. 1994, 10, 33–38. [Google Scholar] [CrossRef]
- Chaohe, T.; Chengyu, L. Standardization analysis of electric vehicle charging cable. Electr. Ind. 2013, 11, 60–63. [Google Scholar]
- Yiyan, C. Simulation of tensile mechanical behavior of high strength composite cable. Mater. Dev. Appl. 2017, 32, 47–52. [Google Scholar]
- Linshu, L.; Jie, Y.; Hu Yongle, H. FEM and Simulation of bending of DC charging cable of electric vehicle. Wire Cable 2019, 2, 12–15. [Google Scholar]
- IEC 60811-202:2012; Electric and Optical Fibre Cables—Test Methods for Non-Metallic Materials—Part 202: General Tests—Measurement of Thickness of Non-Metallic Sheath, IEC Technical Committee 20: Electric Cables. International Electrotechnical Commission: Geneva, Switzerland, 2012.
- IEC 60502-1; Power Cables with Extruded Insulation and Their Accessories for Rated Voltages from 1 kV (Um = 1,2 kV) up to 30 kV (Um = 36 kV)—Part 1: Cables for Rated Voltages of 1 kV (Um = 1,2 kV) and 3 kV (Um = 3,6 kV). IEC Technical Committee 20: Electric Cables. International Electrotechnical Commission: Geneva, Switzerland, 2021.
- IEC60332-1-2; Tests on Electric and Optical Fibre Cables Under Fire Conditions—Part 1-2: Test for Vertical Flame Propagation for a Single Insulated Wire or Cable. International Electrotechnical Commission: Geneva, Switzerland, 2015.
- IEC 62893-1; Charging Cables for Electric Vehicles for Rated Voltages up to and Including 0.6/1 kV—Part 1: General Requirements, EC Technical Committee 20: Electric Cables. International Electrotechnical Commission: Geneva, Switzerland, 2020.
- EN 50520:2020/A1:2021; Cover Plates and Cover Tapes for the Protection and Location Warning of Buried Cables or Buried Conduits in Underground Installations, EU Technical Committee—CLC/TC 213—Cable Management Systems. European Committee for Electrotechnical Standardization: Brussels, Belgium, 2021.
- EN 60811-100; Electric and Optical Fibre Cables—Test Methods for Non-Metallic Materials—Part 100: General, EU Technical Committee—CLC/TC 20—Electric Cables. European Committee for Electrotechnical Standardization: Brussels, Belgium, 2012.
- Singh, A.; Vishnuram, P.; Alagarsamy, S.; Bajaj, M.; Blazek, V.; Damaj, I.; Rathore, R.S.; Al-Wesabi, F.N.; Othman, K. Electric vehicle charging technologies, infrastructure expansion, grid integration strategies, and their role in promoting sustainable. Alex. Eng. J. 2024, 105, 300–330. [Google Scholar] [CrossRef]
- Lin, L.; Xiao Zhiyong, X.; Guiping, L. Finite Element Modeling and Simulation of Mechanical Properties of DC Charging Cables for Electric Vehicles. In Proceedings of IncoME-V & CEPE Net; Springer: Cham, Switzerland, 2021. [Google Scholar] [CrossRef]
- Lin, L.; Xiao Zhiyong, X.; Guiping, L. Mechanical Performance Test and Analysis of DC Charging Cable for Electric Vehicle. E3S Web Conf. 2020, 185, 01070. [Google Scholar] [CrossRef]
- Jin, C.; Tang, J.; Ghosh, P. Optimizing Electric Vehicle Charging with Energy Storage in the Electricity Market. IEEE Trans. Smart Grid 2013, 4, 311–320. [Google Scholar] [CrossRef]
- Xiao, Z.; Lu, G.; Zhong, Z. Design and Research of New-Type Clamping Fixture Based on Tensile Test of Wire and Cable Materials. In Advances in Asset Management and Condition Monitoring. Smart Innovation, Systems and Technologies; Ball, A., Gelman, L., Rao, B., Eds.; Springer: Berlin/Heidelberg, Germany, 2020; p. 166. [Google Scholar] [CrossRef]
- Stevens, A.; Bilotti, E.; Peijs, T.; Busfield, J.C.J. Development of a novel fatigue test method for cord-rubber composites. Polym. Test. 2018, 71, 238–247. [Google Scholar]
- Jingle Jabha, D.F.; Selvi, K.; Joselin, R. Determination of Tensile Strength and Dielectric Strength in XLPE Power Cables Using Acoustic Emission Technique. Non-Destr. Eval. 2016, 22, 162–168. [Google Scholar]
- Kuzmanov, N.; Borisov, B.; Muhtarov, I. Tensile testing of Inconel 600 wire at high temperatures. IOP Conf. Ser. Mater. Sci. Eng. 2020, 878, 012057. [Google Scholar] [CrossRef]
- Anderson, P.; Bror Person, B. Performance of Cables Subjected to Elevates Temperatures. Brandforsk Project 625-001. Available online: https://publications.iafss.org/publications/fss/8/1121/view/fss_8-1121.pdf (accessed on 18 March 2025).
- Du, Y.; Peng, J.Z.; Yuen, J.; Liew, R.; Li, G.Q. Mechanical properties of high tensile steel cables at elevated temperatures. Constr. Build. Mater. 2018, 182, 52–65. [Google Scholar] [CrossRef]
- Zhang, Z.; Xu, Y.; Huang, Y.; Wei Chen, W.W.; Ni, Y.; Ye, J.; Jiang, J. Experiment study on the mechanical properties and constitutive model of grade 1960 steel wires under and after elevated temperatures. J. Build. Eng. 2024, 82, 108318. [Google Scholar] [CrossRef]
- Rickman, S.L.; Furst, B.; Johnson, K.L. Thermal Testing and Analysis Techniques for Wires and Wire Bundles. J. Phys. Conf. 2021, 2116, 012075. [Google Scholar] [CrossRef]
- Guo, Z.; Dai, C.; Qin, J.; Zhou, C.; Li, J.; Yu, W.; Liu, F.; Yang, D.; Huang, C.; Li, L.; et al. Research on mechanical properties of high-performance cable-in-conduit conductors with different design. Supercond. Sci. Technol. 2020, 33, 4. [Google Scholar] [CrossRef]
- IEC 60228:2023; Conductors of Insulated Cables. International Electrotechnical Commission: Geneva, Switzerland, 2023.
- Zhao, Y.; Hu, J.; Song, S.; Zhang, T.; Li, P.; Xiong, G. Global Stability Behavior of Pre-Cast Cable-Stiffened Steel Columns. Buildings 2024, 14, 2485. [Google Scholar] [CrossRef]
- Li, P.; Zhao, X.; Qiu, J.; Qian, J.; Zhu, Z.; Zhang, Z.; Meng, L. Experimental and Numerical Investigation into the Stability Behaviour of Cable-Stiffened Steel Columns. Materials 2022, 15, 8813. [Google Scholar] [CrossRef] [PubMed]





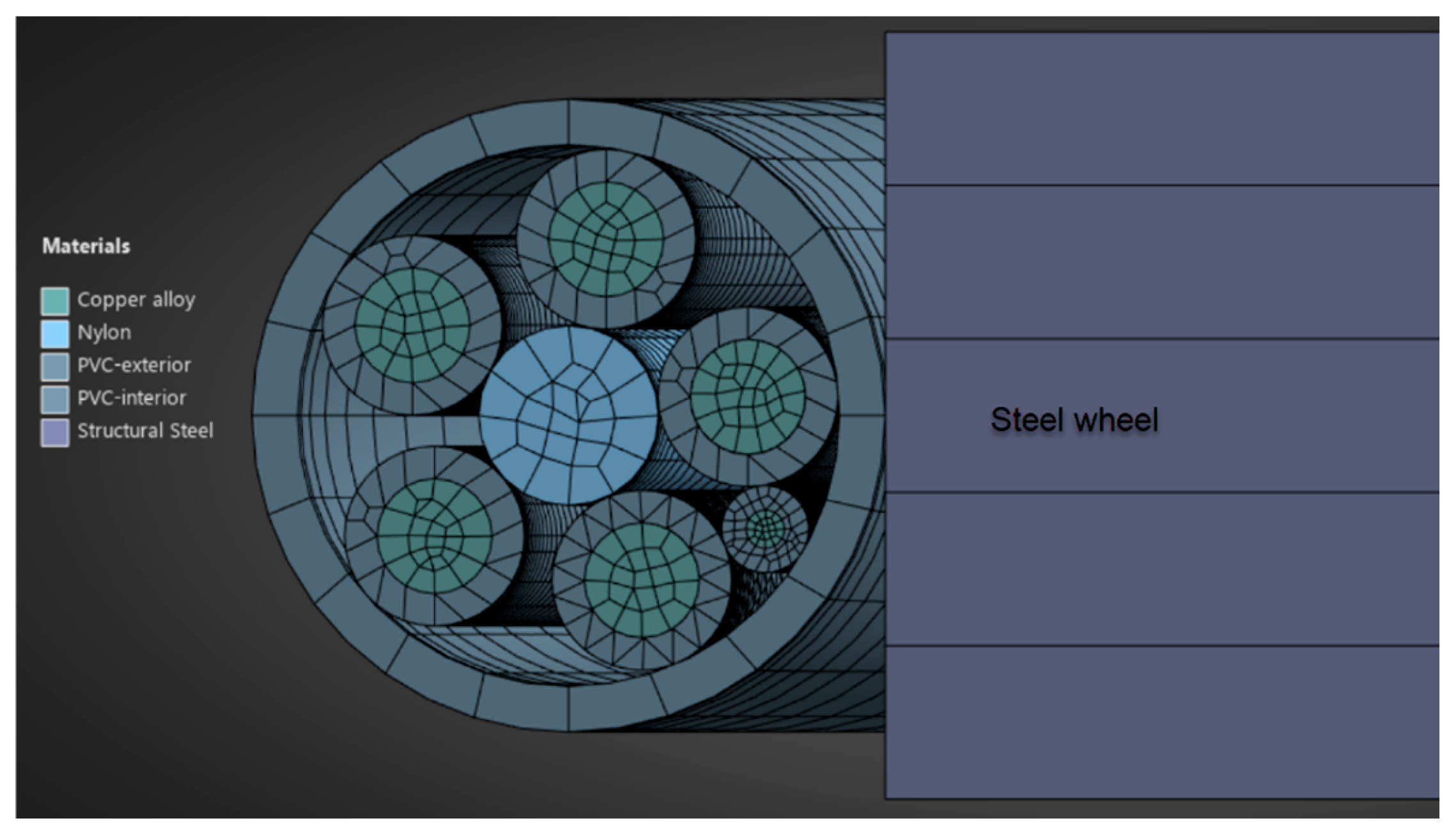


| Young’s Modulus | Poisson’s Ratio | Yield Strength | Tangential Modulus | |
|---|---|---|---|---|
| Material | [MPa] | [MPa] | [MPa] | |
| Copper | 110,000 | 0.34 | 150 | 1150 |
| Outside cover | 1100 | 0.42 | 4 | 0 |
| Inside cover | 1100 | 0.42 | 2.5 | 0 |
| Textile wire | 3500 | 0.39 | 50 | 0 |
| Steel | 2.1 × 105 | 0.3 | 360 | 4400 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cosau, E.R.; Goanta, V.; Blanari, I.; Alkisswani, L.; Samara, F. Determination of Tensile Characteristics and Electrical Resistance Variation of Cables Used for Charging Electric Vehicles. Polymers 2025, 17, 1317. https://doi.org/10.3390/polym17101317
Cosau ER, Goanta V, Blanari I, Alkisswani L, Samara F. Determination of Tensile Characteristics and Electrical Resistance Variation of Cables Used for Charging Electric Vehicles. Polymers. 2025; 17(10):1317. https://doi.org/10.3390/polym17101317
Chicago/Turabian StyleCosau, Elena Roxana, Viorel Goanta, Igor Blanari, Layth Alkisswani, and Fayez Samara. 2025. "Determination of Tensile Characteristics and Electrical Resistance Variation of Cables Used for Charging Electric Vehicles" Polymers 17, no. 10: 1317. https://doi.org/10.3390/polym17101317
APA StyleCosau, E. R., Goanta, V., Blanari, I., Alkisswani, L., & Samara, F. (2025). Determination of Tensile Characteristics and Electrical Resistance Variation of Cables Used for Charging Electric Vehicles. Polymers, 17(10), 1317. https://doi.org/10.3390/polym17101317






