Low-Frequency Resonant Magnetoelectric Effect in a Piezopolymer-Magnetoactive Elastomer Layered Structure at Different Magnetization Geometries
Abstract
1. Introduction
2. Materials and Methods
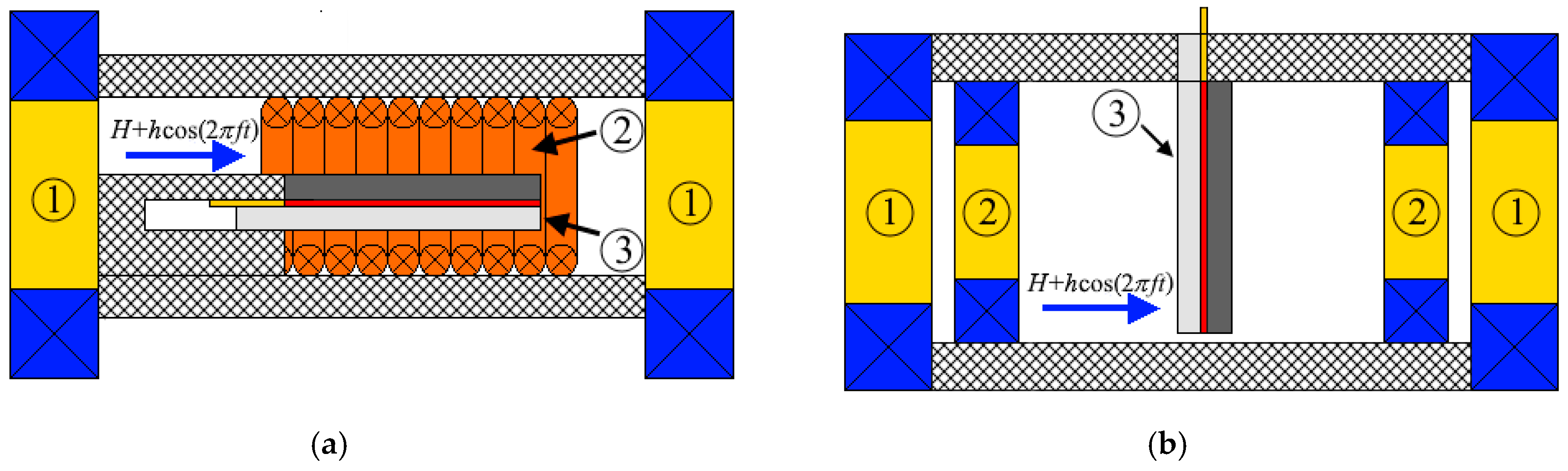
2.1. Composite Structure
2.2. Geometry 1 (L-T)
2.3. Geometry 2 (T-T)
3. Results
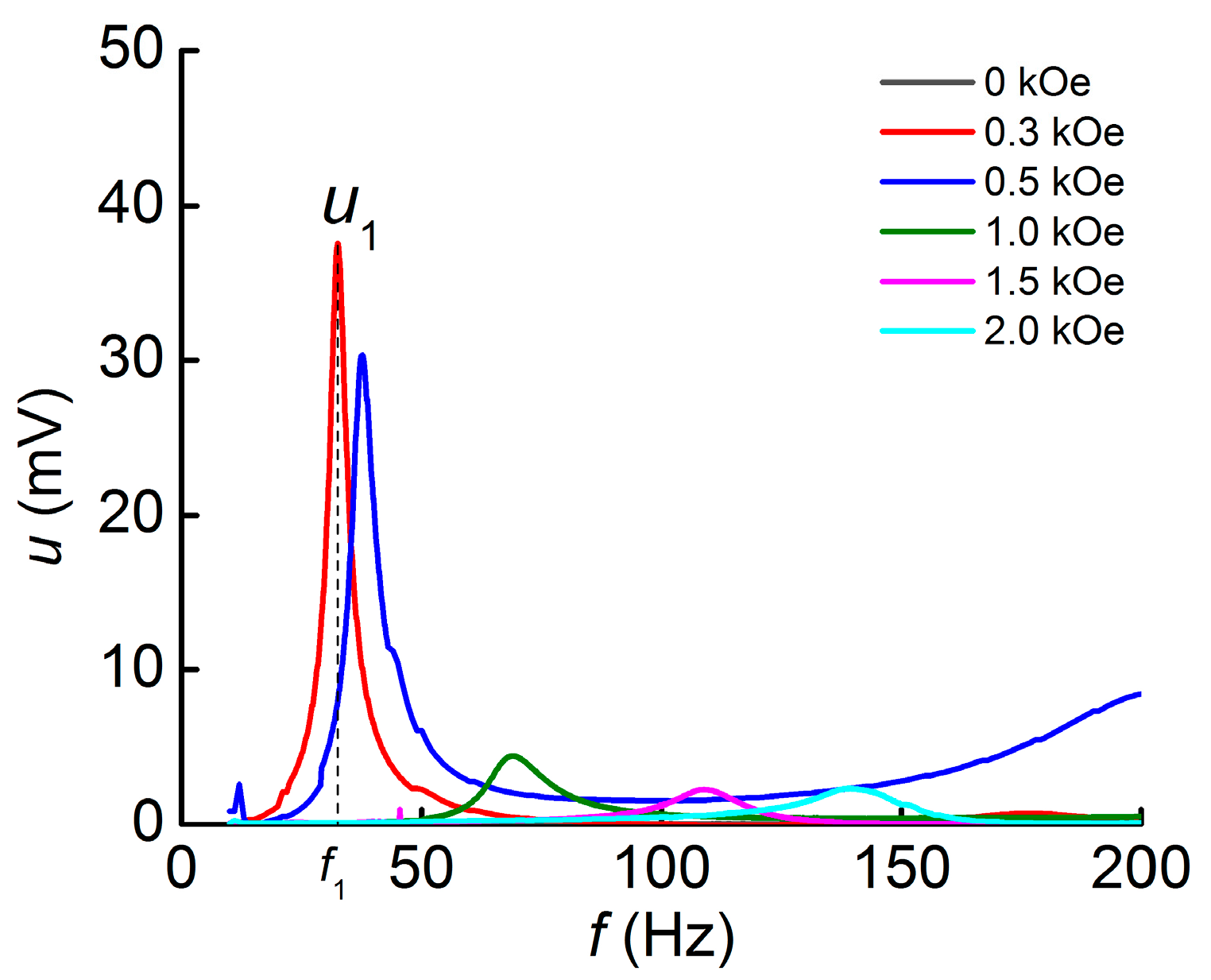
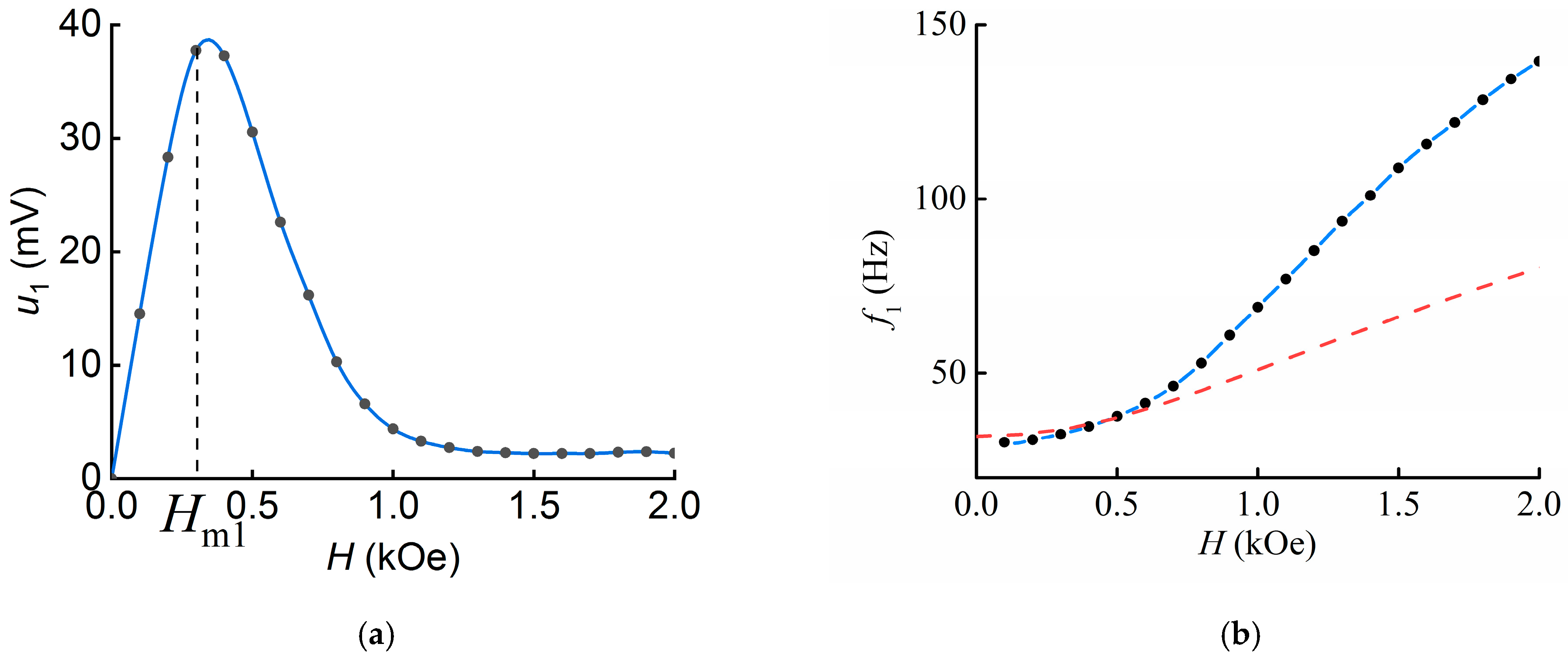
3.1. ME Effect in Geometry 1 (L-T)
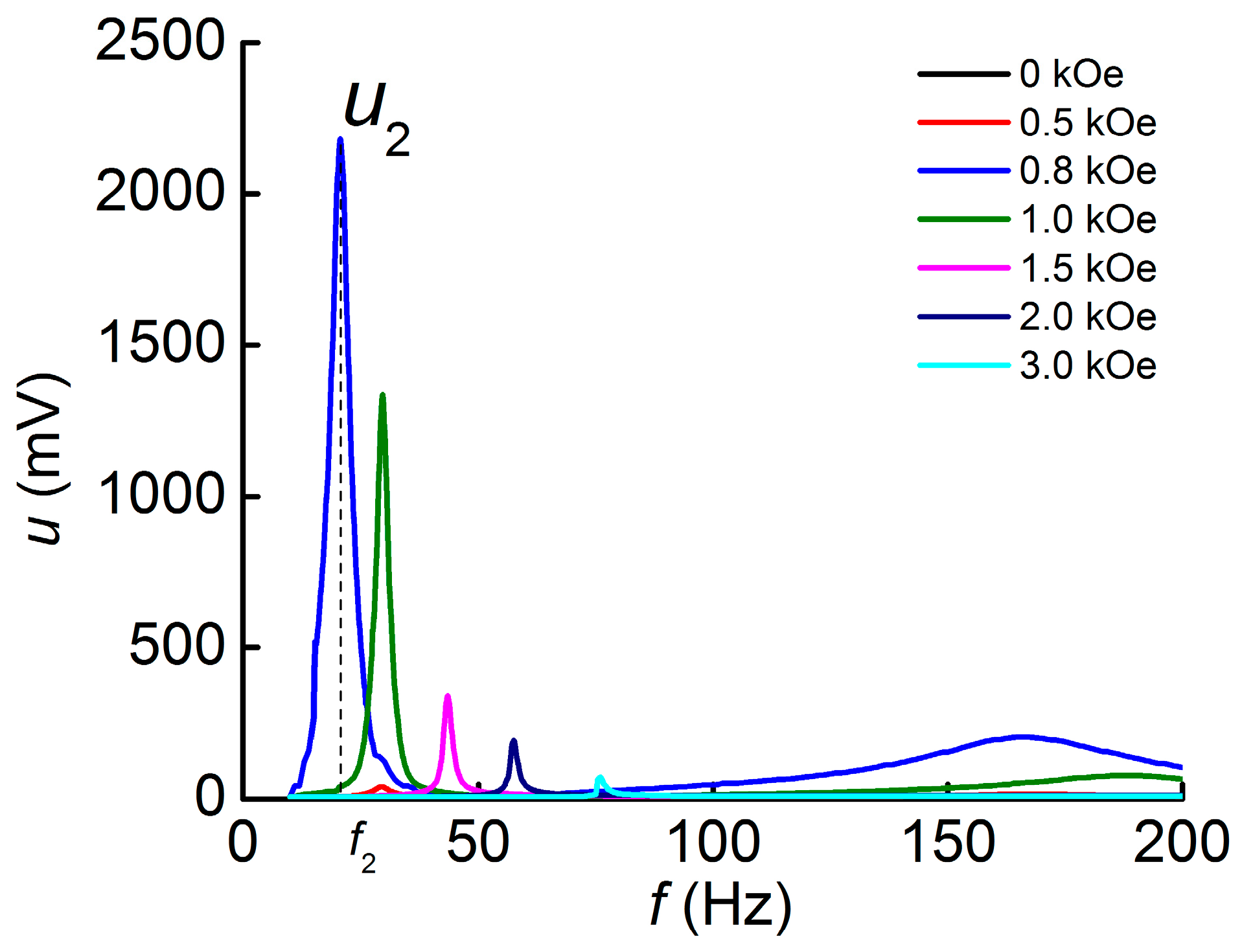
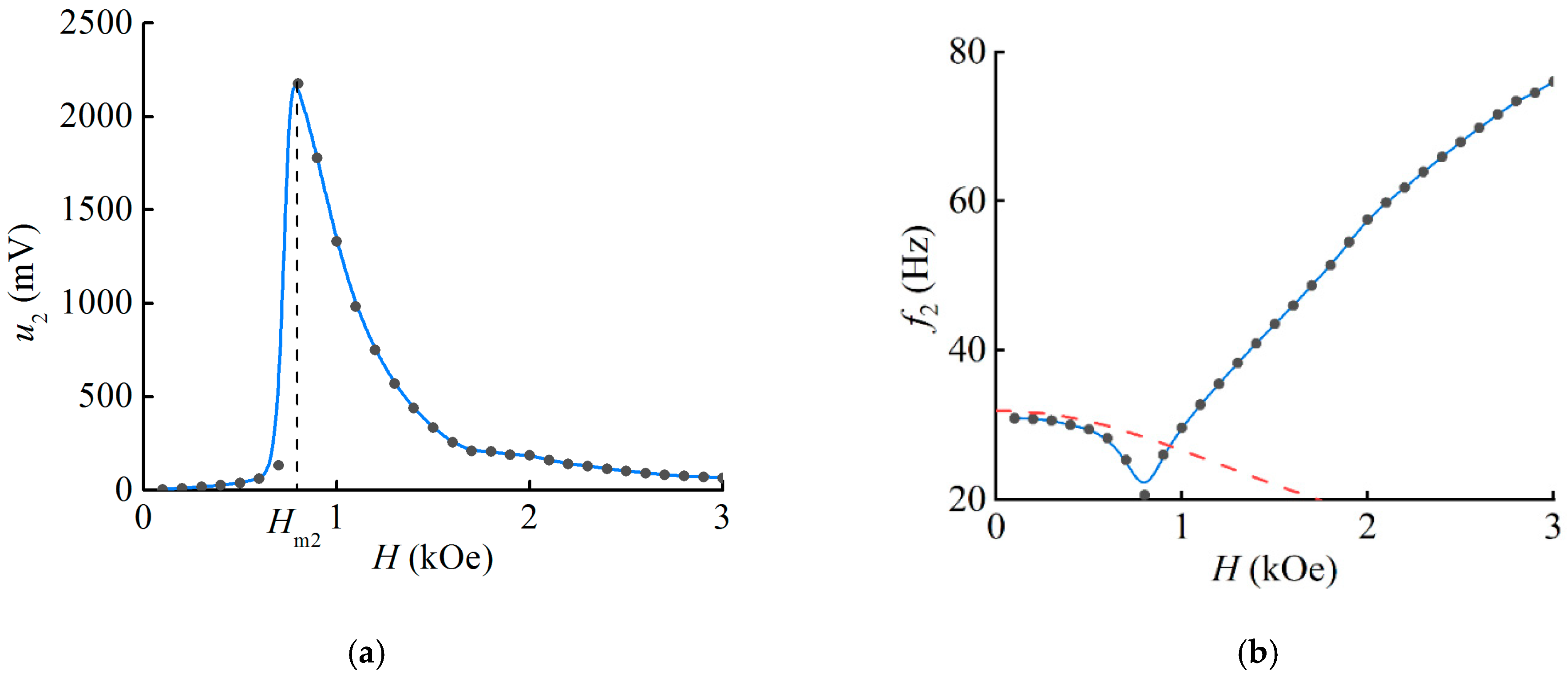
3.2. ME Effect Geometry 2 (T-T)
4. Discussion
4.1. Influence of the Magnetic Field Direction on the ME Voltage
4.2. Influence of the Magnetic Field on the Resonance Frequency
4.3. Calculation of the Resonant Frequency in Magnetic Field
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liang, X.; Matyushov, A.; Hayes, P.; Schell, V.; Dong, C.; Chen, H.; He, Y.; Will-Cole, A.; Quandt, E.; Martins, P.; et al. Roadmap on Magnetoelectric Materials and Devices. IEEE Trans. Magn. 2021, 57, 400157. [Google Scholar] [CrossRef]
- Pereira, N.; Lima, A.C.; Lanceros-Mendez, S.; Martins, P. Magnetoelectrics: Three centuries of research heading towards the 4.0 industrial revolution. Materials 2020, 13, 4033. [Google Scholar] [CrossRef]
- Dong, C.; He, Y.; Li, M.; Tu, C.; Chu, Z.; Liang, X.; Chen, H.; Wei, Y.; Zaeimbashi, M.; Wang, X.; et al. A portable very low frequency (VLF) communication system based on acoustically actuated magnetoelectric antennas. IEEE Antennas Wirel. Propag. Lett. 2020, 19, 398–402. [Google Scholar] [CrossRef]
- Li, M.; Dong, C.; Zhou, H.; Wang, Z.; Wang, X.; Liang, X.; Lin, Y.; Sun, N.X. Highly sensitive DC magnetic field sensor based on nonlinear ME effect. IEEE Sens. Lett. 2017, 1, 2501104. [Google Scholar] [CrossRef]
- Lin, H.; Lou, J.; Gao, Y.; Hasegawa, R.; Liu, M.; Howe, B.; Jones, J.; Brown, G.; Sun, N.X. Voltage tunable magnetoelectric inductors with improved operational frequency and quality factor for power electronics. IEEE Trans. Magn. 2015, 51, 4002705. [Google Scholar] [CrossRef]
- Lin, H.; Nan, T.; Qian, Z.; Gao, Y.; Hui, Y.; Wang, X.; Guo, R.; Belkessam, A.; Shi, W.; Rinaldi, M.; et al. Tunable RF band-pass filters based on NEMS magnetoelectric resonators. In Proceedings of the 2016 IEEE/MTT-S International Microwave Symposium (IMS), San Francisco, CA, USA, 22–27 May 2016; pp. 1–4. [Google Scholar]
- Nan, C.-W.; Bichurin, M.I.; Dong, S.; Viehland, D.; Srinivasan, G. Multiferroic magnetoelectric composites: Historical perspective, status, and future directions. J. Appl. Phys. 2008, 103, 031101. [Google Scholar] [CrossRef]
- Fiebig, M. Revival of the magnetoelectric effect. J. Phys. D Appl. Phys. 2005, 38, R123–R152. [Google Scholar] [CrossRef]
- Turutin, A.V.; Vidal, J.V.; Kubasov, I.V.; Kislyuk, A.M.; Malinkovich, M.D.; Parkhomenko, Y.N.; Kobeleva, S.P.; Pakhomov, O.V.; Kholkin, A.L.; Sobolev, N.A.; et al. Magnetoelectric metglas/bidomain y+ 140-cut lithium niobate composite for sensing fT magnetic fields. Appl. Phys. Lett. 2018, 112, 262906. [Google Scholar] [CrossRef]
- Sun, C.; Yang, W.; Zhang, Y. A Symmetrical Quartz-Based Magnetoelectric Sensor for Pico-Tesla Magnetic Field Detection. Symmetry 2022, 14, 2130. [Google Scholar] [CrossRef]
- Su, J.; Niekiel, F.; Fichtner, S.; Thormaehlen, L.; Kirchhof, C.; Meyners, D.; Quandt, E.; Wagner, B.; Lofink, F. AlScN-Based MEMS Magnetoelectric Sensor. Appl. Phys. Lett. 2020, 117, 132903. [Google Scholar] [CrossRef]
- Costa, C.M.; Cardoso, V.F.; Martins, P.; Correia, D.M.; Gonçalves, R.; Costa, P.; Correia, V.; Ribeiro, C.; Fernandes, M.M.; Martins, P.M.; et al. Smart and multifunctional materials based on electroactive poly (vinylidene fluoride): Recent advances and opportunities in sensors, actuators, energy, environmental, and biomedical applications. Chem. Rev. 2023, 123, 11392–11487. [Google Scholar] [CrossRef] [PubMed]
- Fernández, C.S.L.; Pereira, N.; Lanceros-Méndez, S.; Martins, P. Evaluation and optimization of the magnetoelectric response of CoFe2O4/poly(vinylidene fluoride) composite spheres by computer simulation. Compos. Sci. Technol. 2017, 146, 119–130. [Google Scholar] [CrossRef]
- Pereira, N.; Lima, A.C.; Correia, V.; Pe, N.; Lanceros-Mendez, S.; Martins, P. Magnetic proximity sensor based on magnetoelectric composites and printed coils. Materials 2020, 13, 1729. [Google Scholar] [CrossRef] [PubMed]
- Martins, P.; Lanceros-Méndez, S. Polymer-based magnetoelectric materials. Adv. Funct. Mater. 2013, 23, 3371–3385. [Google Scholar] [CrossRef]
- Ribeiro, C.; Costa, C.; Correia, D.; Nunes-Pereira, J.; Oliveira, J.; Martins, P.; Gonçalves, R.; Cardoso, V.F.; Lanceros-Méndez, S. Electroactive poly(vinylidene fluoride)-based structures for advanced applications. Nat. Protoc. 2018, 13, 681–704. [Google Scholar] [CrossRef] [PubMed]
- Martins, P.; Lanceros-Méndez, S. Polymer-based magnetoelectric materials: To be or not to be. Appl. Mater. Today 2019, 15, 558–561. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, J.; Xia, X.; Fang, C.; Weng, G.J. Nonlinear magnetoelectric effects of polymer-based hybrid magnetoelectric composites with chain-like terfenold-D/epoxy and PVDF multilayers. Compos. Sci. Technol. 2021, 216, 109069. [Google Scholar] [CrossRef]
- Cai, N.; Nan, C.W.; Zhai, J.; Lin, Y. Large high-frequency magnetoelectric response in laminated composites of piezoelectric ceramics, rare-earth iron alloys and polymer. Appl. Phys. Lett. 2004, 84, 3516–3518. [Google Scholar] [CrossRef]
- Fetisov, L.Y.; Chashin, D.V.; Saveliev, D.V.; Afanas’ev, M.S.; Simonov-Emel’yanov, I.D.; Vopson, M.M.; Fetisov, Y.K. Magnetoelectric direct and converse resonance effects in a flexible ferromagnetic-piezoelectric polymer structure. J. Magn. Magn. Mater. 2019, 485, 251–256. [Google Scholar] [CrossRef]
- Kulkarni, A.; Meurisch, K.; Teliban, I.; Jahns, R.; Strunskus, T.; Piorra, A.; Knöchel, R.; Faupel, F. Giant magnetoelectric effect at low frequencies in polymer-based thin film composites. Appl. Phys. Lett. 2014, 104, 022904. [Google Scholar] [CrossRef]
- Reis, S.; Silva, M.P.; Castro, N.; Correia, V.; Rocha, J.G.; Martins, P.; Lasheras, A.; Gutierrez, J.; Lanceros-Mendez, S. Electronic optimization for an energy harvesting system based on magnetoelectric metglas/poly(vinylidene fluoride)/metglas composites. Smart Mater. Struct. 2016, 25, 085028. [Google Scholar] [CrossRef]
- Lasheras, A.; Gutiérrez, J.; Reis, S.; Sousa, D.; Silva, M.; Martins, P.; Lanceros-Mendez, S.; Barandiarán, J.M.; Shishkin, D.A.; Potapov, A.P. Energy harvesting device based on a metallic glass/PVDF magnetoelectric laminated composite. Smart Mater. Struct. 2015, 24, 065024. [Google Scholar] [CrossRef]
- Lasheras, A.; Saiz, P.G.; Porro, J.M.; Quintana, I.; Polak, C.; Lopes, A.C. Enhanced performance of magnetoelectric laminated composites by geometry engineering for high frequency applications. J. Alloys Compd. 2021, 884, 161065. [Google Scholar] [CrossRef]
- Tan, K.; Wen, X.; Deng, Q.; Shen, S.; Liu, L.; Sharma, P. Soft rubber as a magnetoelectric materal—Generating electricity from the remote action of a magnetic field. Mater. Today 2021, 43, 8–16. [Google Scholar] [CrossRef]
- Channagoudra, G.; Dayal, V. Magnetoelectric coupling in ferromagnetic/ferroelectric heterostructures: A survey and perspective. J. Alloys Compd. 2022, 928, 167181. [Google Scholar] [CrossRef]
- Timoshenko, S. Vibration Problems in Engineering, 2nd ed.; D. van Nostrand Company: Toronto, ON, Canada, 1955. [Google Scholar]
- Abramchuk, S.; Kramarenko, E.; Grishin, D.; Stepanov, G.; Nikitin, L.V.; Filipcsei, G.; Khokhlov, A.R.; Zrínyi, M. Novel highly elastic magnetic materials for dampers and seals: Part II. Material behavior in a magnetic field. Polym. Adv. Technol. 2007, 18, 513–518. [Google Scholar] [CrossRef]
- Makarova, L.A.; Alekhina, Y.A.; Isaev, D.A.; Khairullin, M.F.; Perov, N.S. Tunable layered composites based on magnetoactive elastomers and piezopolymer for sensors and energy harvesting devices. J. Phys. D Appl. Phys. 2020, 54, 015003. [Google Scholar] [CrossRef]
- Glavan, G.; Belyaeva, I.A.; Ruwisch, K.; Wollschläger, J.; Shamonin, M. Magnetoelectric response of laminated cantilevers comprising a magnetoactive elastomer and a piezoelectric polymer, in pulsed uniform magnetic field. Sensors 2021, 21, 6390. [Google Scholar] [CrossRef]
- Glavan, G.; Belyaeva, I.A.; Shamonin, M. Multiferroic cantilevers containing a magnetoactive elastomer: Magnetoelectric response to low-frequency magnetic fields of triangular and sinusoidal waveform. Sensors 2022, 22, 3791. [Google Scholar] [CrossRef]
- Saveliev, D.V.; Glavan, G.; Belan, V.O.; Belyaeva, I.A.; Fetisov, L.Y.; Shamonin, M. Resonant Magnetoelectric Effect at Low Frequencies in Layered Polymeric Cantilevers Containing a Magnetoactive Elastomer. Appl. Sci. 2022, 12, 2102. [Google Scholar] [CrossRef]
- Makarova, L.A.; Alekhina, I.A.; Khairullin, M.F.; Makarin, R.A.; Perov, N.S. Dynamic magnetoelectric effect of the soft layered composites with magnetic elastomer. Polymers 2023, 15, 2262. [Google Scholar] [CrossRef]
- Burdin, D.A.; Chashin, D.V.; Ekonomov, N.A.; Fetisov, L.Y.; Preobrazhensky, V.L.; Fetisov, Y.K. Low-frequency resonant magnetoelectric effects in layered heterostructures antiferromagnet-piezoelectric. Sensors 2023, 23, 5901. [Google Scholar] [CrossRef]
- Zabel, S.; Kirchhof, C.; Yarar, E.; Meyners, D.; Quandt, E.; Faupel, F. Phase modulated magnetoelectric delta-E effect sensor for sub-nano tesla magnetic fields. Appl. Phys. Lett. 2015, 107, 152402. [Google Scholar] [CrossRef]
- Spetzler, B.; Su, J.; Friedrich, R.-M.; Niekiel, F.; Fichtner, S.; Lofink, F.; Faupel, F. Influence of the piezoelectric material on the signal and noise of magnetoelectric magnetic field sensors based on the delta-E effect. APL Mater. 2021, 9, 031108. [Google Scholar] [CrossRef]
- Raikher, Y.L.; Stolbov, O.V.; Stepanov, G.V. Deformation of a circular ferroelastic membrane in a uniform magnetic field. Tech. Phys. 2008, 53, 1169–1176. [Google Scholar] [CrossRef]
- Kalita, V.M.; Dzhezherya, Y.I.; Cherepov, S.V.; Skirta, Y.B.; Bodnaruk, A.V.; Levchenko, G.G. Critical bending and shape memory effect in magnetoactive elastomers. Smart Mater. Struct. 2021, 30, 025020. [Google Scholar] [CrossRef]
- Silva, M.P.; Martins, P.; Lasheras, A.; Gutiérrez, J.; Barandiarán, J.M.; Lanceros-Mendez, S. Size effects on the magnetoelectric response on PVDF/Vitrovac 4040 laminate composites. J. Magn. Magn. Mater. 2015, 377, 29–33. [Google Scholar] [CrossRef]
- Reis, S.; Silva, M.P.; Castro, N.; Correia, V.; Gutierrez, J.; Lasheras, A.; Lanceros-Mendez, S.; Martins, P. Optimized anisotropic magnetoelectric response of Fe61.6Co16.4Si10.8B11.2/PVDF/Fe61.6Co16.4Si10.8B11.2 laminates for AC/DC magnetic field sensing. Smart Mater. Struct. 2016, 25, 055050. [Google Scholar] [CrossRef]
- Lu, S.G.; Jin, J.Z.; Zhou, X.; Fang, Z.; Wang, Q.; Zhang, Q.M. Large magnetoelectric coupling coefficient in poly(vinylidene fluoride-hexafluoropropylene)/Metglas laminates. J. Appl. Phys. 2011, 110, 104103. [Google Scholar] [CrossRef]
- Filippov, D.A.; Laletsin, V.M.; Poddubnaya, N.N.; Galichyan, A.; Zhang, J.; Srinivasan, G. Magnetoelectric and magnetostriction characteristics of symmetric three layered structures of nickel-lead zirconate titanate–nickel and permendure–lead zirconate titanate–permendure. In IOP Conference Series: Materials Science and Engineering, Proceedings of the III International Scientific and Practical Conference on Innovations in Engineering and Technology, Veliky Novgorod, Russia, 25–26 June 2020; IOP Publishing: Bristol, UK, 2020; Volume 939, p. 012023. [Google Scholar]
- Feng, M.; Wang, J.-J.; Hu, J.-M.; Wang, J.; Ma, J.; Li, H.-B.; Shen, Y.; Lin, Y.-H.; Chen, L.-Q.; Nan, C.-W. Optimizing direct magnetoelectric coupling in Pb(Zr,Ti)O3/Ni multiferroic film heterostructures. Appl. Phys. Lett. 2015, 106, 072901. [Google Scholar] [CrossRef]
- Yu, S.; Huang, H.; Zhou, L.; Ye, Y.; Ke, S. Structure and properties of PMN–PT/NZFO laminates and composites. Ceram. Int. 2008, 34, 701–704. [Google Scholar] [CrossRef]
- Liu, Y.; Xu, G.; Xie, Y.; Lv, H.; Huang, C.; Chen, Y.; Tong, Z.; Shi, J.; Xiong, R. Magnetoelectric behaviors in BaTiO3/CoFe2O4/BaTiO3 laminated ceramic composites prepared by spark plasma sintering. Ceram. Int. 2018, 44, 9649–9655. [Google Scholar] [CrossRef]
- Yang, N.; Wu, H.; Wang, S.; Yuan, G.; Zhang, J.; Sokolov, O.; Bichurin, M.I.; Wang, K.; Wang, Y. Ultrasensitive flexible magnetoelectric sensor. APL Mater. 2021, 9, 021123. [Google Scholar] [CrossRef]
- Filippov, D.; Liu, Y.; Zhou, P.; Ge, B.; Liu, J.; Zhang, J.; Zhang, T.; Srinivasan, G. Low-frequency magnetoelectric effects in magnetostrictive–piezoelectric bilayers: Longitudinal and bending deformations. J. Compos. Sci. 2021, 5, 287. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Savelev, D.V.; Burdin, D.A.; Fetisov, L.Y.; Fetisov, Y.K.; Perov, N.S.; Makarova, L.A. Low-Frequency Resonant Magnetoelectric Effect in a Piezopolymer-Magnetoactive Elastomer Layered Structure at Different Magnetization Geometries. Polymers 2024, 16, 928. https://doi.org/10.3390/polym16070928
Savelev DV, Burdin DA, Fetisov LY, Fetisov YK, Perov NS, Makarova LA. Low-Frequency Resonant Magnetoelectric Effect in a Piezopolymer-Magnetoactive Elastomer Layered Structure at Different Magnetization Geometries. Polymers. 2024; 16(7):928. https://doi.org/10.3390/polym16070928
Chicago/Turabian StyleSavelev, Dmitrii V., Dmitri A. Burdin, Leonid Y. Fetisov, Yuri K. Fetisov, Nikolai S. Perov, and Liudmila A. Makarova. 2024. "Low-Frequency Resonant Magnetoelectric Effect in a Piezopolymer-Magnetoactive Elastomer Layered Structure at Different Magnetization Geometries" Polymers 16, no. 7: 928. https://doi.org/10.3390/polym16070928
APA StyleSavelev, D. V., Burdin, D. A., Fetisov, L. Y., Fetisov, Y. K., Perov, N. S., & Makarova, L. A. (2024). Low-Frequency Resonant Magnetoelectric Effect in a Piezopolymer-Magnetoactive Elastomer Layered Structure at Different Magnetization Geometries. Polymers, 16(7), 928. https://doi.org/10.3390/polym16070928









