Directed Self-Assembly of Cylinder-Forming Block Copolymers Using Pillar Topographic Patterns
Abstract
1. Introduction
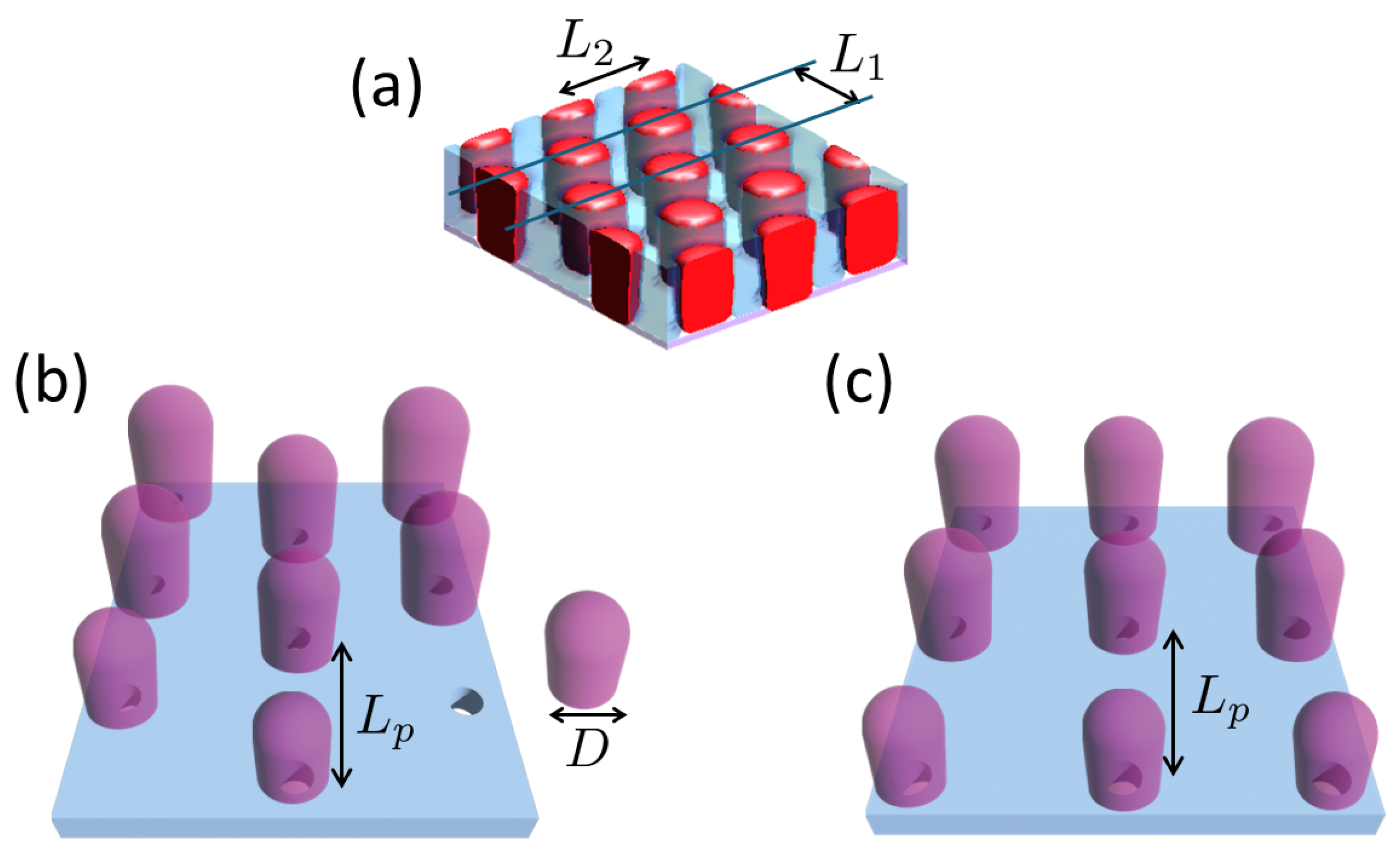
2. Simulation Methods
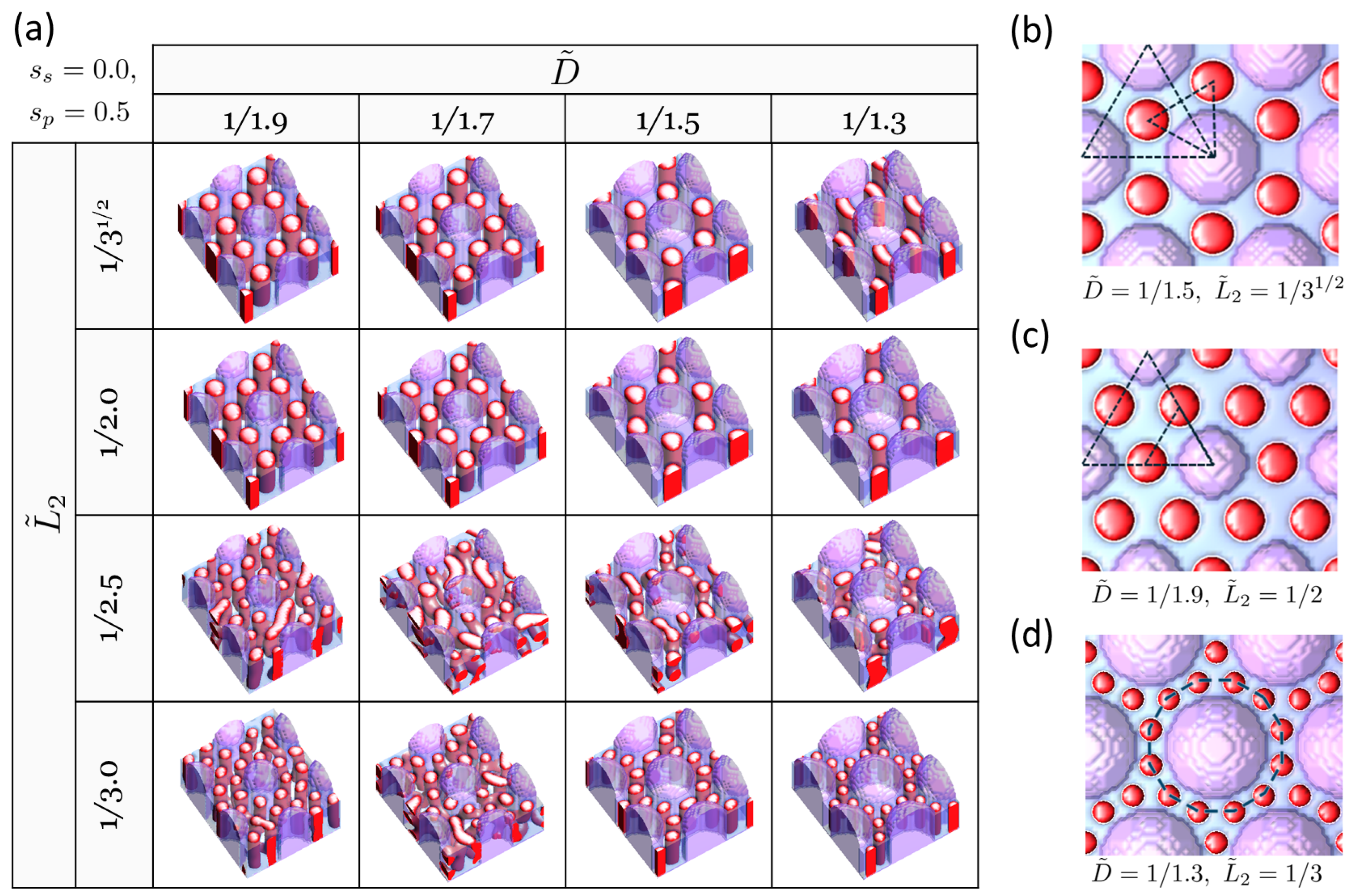
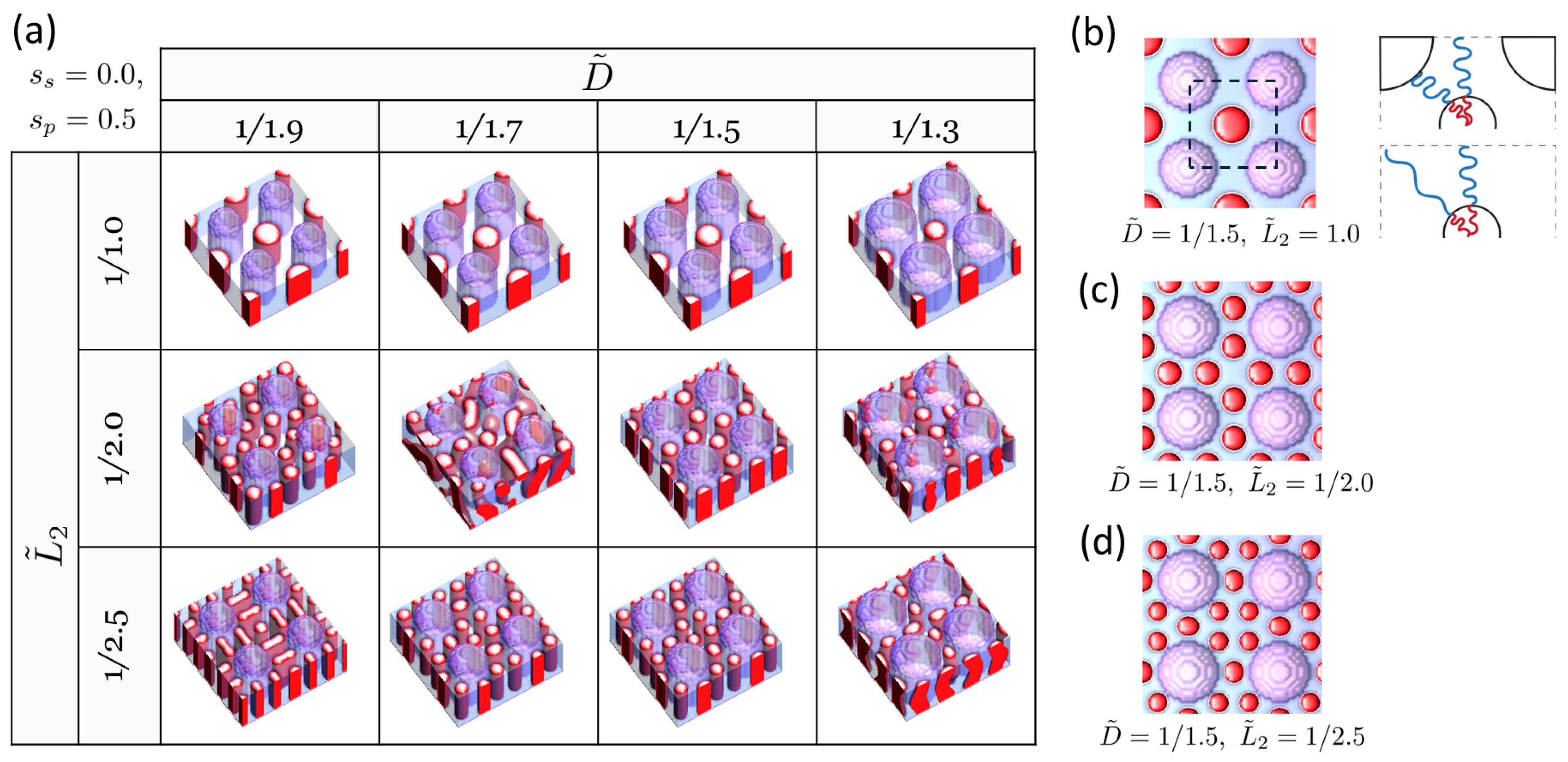
3. Results
4. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ji, S.; Wan, L.; Liu, C.-C.; Nealey, P.F. Directed self-assembly of block copolymers on chemical patterns: A platform for nanofabrication. Prog. Polym. Sci. 2016, 54–55, 76–127. [Google Scholar] [CrossRef]
- Cummins, C.; Lundy, R.; Walsh, J.J.; Ponsinet, V.; Fleury, G.; Morris, M.A. Enabling future nanomanufacturing through block copolymer self-assembly: A review. Nano Today 2020, 35, 100936. [Google Scholar] [CrossRef]
- Nicaise, S.M.; Tavakkoli, S.M.; Berggren, K.K. Self-assembly of block copolymers by graphoepitaxy. In Directed Self-Assembly of Block Co-Polymers for Nano-Manufacturing; Gronheid, R., Nealey, P., Eds.; Elsevier: Amsterdam, The Netherlands, 2015; pp. 199–232. [Google Scholar]
- Seino, Y.; Kasahara, Y.; Sato, H.; Kobayashi, K.; Miyagi, K.; Minegishi, S.; Kodera, K.; Kanai, H.; Tobana, T.; Kihara, N.; et al. A novel simple sub-15 nm line-and-space patterning process flow using directed self-assembly technology. Microelectron. Eng. 2015, 134, 27–32. [Google Scholar] [CrossRef]
- Giammaria, T.J.; Gharbi, A.; Paquet, A.; Nealey, P.; Tiron, R. Resist-Free Directed Self-Assembly Chemo-Epitaxy Approach for Line/Space Patterning. Polymers 2020, 10, 2443. [Google Scholar] [CrossRef]
- Yi, H.; Bao, X.-Y.; Tiberio, R.; Wong, H.-S.P. A General Design Strategy for Block Copolymer Directed Self-Assembly Patterning of Integrated Circuits Contact Holes using anAlphabet Approach. Nano Lett. 2015, 15, 805–812. [Google Scholar] [CrossRef] [PubMed]
- Yi, H.; Bao, X.-Y.; Zhang, J.; Bencher, C.; Chang, L.-W.; Chen, X.; Tiberio, R.; Conway, J.; Dai, H.; Chen, Y.; et al. Flexible Control of Block Copolymer Directed SelfAssembly using Small, Topographical Templates: Potential Lithography Solution for Integrated Circuit Contact Hole Patterning. Adv. Mater. 2012, 24, 3107–3114. [Google Scholar] [CrossRef]
- Hu, X.-H.; Zhang, R.; Zhang, X.; Wu, Z.; Zhou, J.; Li, W.; Xiong, S. Focused solar annealing for block copolymer fast self-assembly. Heliyon 2024, 10, e24016. [Google Scholar] [CrossRef] [PubMed]
- Wu, H.; Lou, J.J.-C.; Xiao, H.; Cai, Y.; Yang, Y. Advanced IC Manufacturing Processes. In Handbook of Integrated Circuit Industry; Wang, Y., Chi, M.-H., Lou, J.J.-C., Chen, C.-Z., Eds.; Springer: Singapore, 2023; pp. 1865–1872. [Google Scholar]
- Griffiths, R.A.; Williams, A.; Oakland, C.; Roberts, J.; Vijayaraghavan, A.; Thomson, T. Directed self-assembly of block copolymers for use in bit patterned media fabrication. J. Phys. D Appl. Phys. 2013, 46, 503001. [Google Scholar] [CrossRef]
- Gronheid, R.; Singh, A.; Younkin, T.R.; Delgadillo, P.R.; Nealey, P.; Chan, B.T.; Nafus, K.; Negreira, A.R.; Somervell, M. Rectification of EUV-patterned contact holes using directed self-assembly. In Proceedings of the Advances in Resist Materials and Processing Technology XXX, San Jose, CA, USA, 24–28 February 2013; Volume 8682. [Google Scholar]
- Guo, J.; Janes, D.W.; Mignot, Y.; Johnson, R.C.; Chi, C.; Liu, C.-C.; Meli, L.; Kuroda, T.; DiPaola, D.A.; Tanaka, Y.; et al. LCDU improvement of EUV-patterned vias with DSA. In Proceedings of the Novel Patterning Technologies for Semiconductors, MEMS/NEMS, and MOEMS 2019, San Jose, CA, USA, 24–28 February 2019; Volume 10958. [Google Scholar]
- Mulkens, J.; Slachter, B.; Kubis, M.; Tel, W.; Hinnen, P.; Maslow, M.; Dillen, H.; Ma, E.; Chou, K.; Liu, X.; et al. Holistic approach for overlay and edge placement error to meet the 5 nm technology node requirements. In Proceedings of the Metrology, Inspection, and Process Control for Microlithography XXXII, San Jose, CA, USA, 25 February–1 March 2018; Volume 10585. [Google Scholar]
- De Bisschop, P. Stochastic effects in EUV lithography: Random, local CD variability, and printing failures. J. Micro/Nanolithogr. MEMS MOEMS 2017, 16, 041013. [Google Scholar]
- De Bisschop, P. Stochastic printing failures in extreme ultraviolet lithography. J. Micro/Nanolithogr. MEMS MOEMS 2018, 17, 041011. [Google Scholar] [CrossRef]
- Verstraete, L.; Suh, H.S.; van Bel, J.; Timi, P.H.; Vallat, R.; Bezard, P.; Vandereyken, J.; Beggiato, M.; Tamaddon, A.-H.; Beral, C.; et al. Mitigating stochastics in EUV lithography by directed self-assembly. In Proceedings of the Novel Patterning Technologies 2023, San Jose, CA, USA, 26 February–2 March 2023; Volume 12497. [Google Scholar]
- Tinck, S.; Altamirano-Sanchez, E.; De Schepper, P.; Bogaerts, A. Formation of a Nanoscale SiO2 Capping Layer on Photoresist Lines with an Ar/SiCl4/O2 Inductively Coupled Plasma: A Modeling Investigation. J. Plasma Process. Polym. 2014, 11, 52–62. [Google Scholar] [CrossRef]
- He, Y.; Che, Y.; Que, L. A Top–Down Fabrication Process for Vertical Hollow Silicon Nanopillars. J. Microelectromech. Syst. 2016, 25, 662–667. [Google Scholar] [CrossRef]
- Wi, J.-S.; Lee, H.-S.; Lim, K.; Nam, S.-W.; Kim, H.-M.; Park, S.-Y.; Lee, J.J.; Hong, C.D.; Jin, S.; Kim, K.-B. Fabrication of Silicon Nanopillar Teradot Arrays by Electron-Beam Patterning for Nanoimprint Molds. Small 2008, 4, 2118–2122. [Google Scholar] [CrossRef] [PubMed]
- Barrios, C.A.; Canalejas-Tejero, V. A top-down approach for fabricating three-dimensional closed hollow nanostructures with permeable thin metal walls. Beilstein J. Nanotechnol. 2017, 8, 1231–1237. [Google Scholar] [CrossRef] [PubMed]
- Pinna, M.; Guo, X.; Zvelindovsky, A.V. Block Copolymer Nanocontainers. ACS Nano 2010, 4, 2845–2855. [Google Scholar] [CrossRef] [PubMed]
- Huh, J.; Jung, J.Y.; Lee, J.U.; Cho, H.; Park, S.; Park, C.; Jo, W.H. Supramolecular Assembly of End-Functionalized Polymer Mixtures Confined in Nanospheres. ACS Nano 2011, 5, 115–122. [Google Scholar] [CrossRef] [PubMed]
- Leibler, L. Theory of Microphase Separation in Block Copolymers. Macromolecules 1980, 13, 1602–1617. [Google Scholar] [CrossRef]
- Fredrickson, G.H. Surface Ordering Phenomena in Block Copolymer Melts. Macromolecules 1987, 20, 2535–2542. [Google Scholar] [CrossRef]
- Mayes, A.M.; Olvera de la Cruz, M.; McMullen, W.E. Asymptotic Properties of Higher-Order Vertex Functions for Block Copolymer Melts. Macromolecules 1993, 26, 4050–4051. [Google Scholar] [CrossRef]
- Oono, Y.; Puri, S. A Study of phase-separation dynamics by use of cell dynamical systems. I. Modeling. Phys. Rev. A 1988, 38, 434–453. [Google Scholar] [CrossRef]
- Oono, Y.; Puri, S. A Study of phase-separation dynamics by use of cell dynamical systems. II. Two-dimensional demonstrations. Phys. Rev. A 1988, 38, 1542–1565. [Google Scholar] [CrossRef] [PubMed]
- Roths, T.; Friedrich, C.; Marth, M.; Honerkamp, J. Dynamics and rheology of the morphology of immiscible polymer blends-on modeling and simulation. Rheol. Acta 2002, 38, 211–222. [Google Scholar] [CrossRef]
- Ginzburg, V.V. Nanoparticle/Polymer Blends: Theory and Modeling. In Encyclopedia of Polymer Blends; Isayev, A.I., Ed.; Wiley-VCH: Weinheim, Germany, 2010; pp. 233–268. [Google Scholar]
- Pinna, M.; Zvelindovsky, A.V. Large scale simulation of block copolymers with cell dynamics. Eur. Phys. J. B 2012, 85, 210. [Google Scholar] [CrossRef]
- Diazm, J.; Pinna, M.; Zvelindovsky, A.V.; Asta, A.; Pagonabarraga, I. Cell Dynamic Simulations of Diblock Copolymer/Colloid Systems. Macromol. Theory Simul. 2017, 26, 1600050. [Google Scholar] [CrossRef]
- Teixeira, P.I.C.; Mulder, B.M. Comment on “Study of phase-separation dynamics by use of cell dynamical systems. I. Modeling”. Phys. Rev. E 1997, 55, 3789–3791. [Google Scholar] [CrossRef]
- Han, E.; Stuen, K.O.; Leolukman, M.; Liu, C.-C.; Nealey, P.F.; Gopalan, P. Perpendicular Orientation of Domains in Cylinder-Forming Block Copolymer Thick Films by Controlled Interfacial Interactions for Block Copolymer Melts. Macromolecules 2009, 42, 4896–4901. [Google Scholar] [CrossRef]
- Kim, S.-W.; Kim, E.; Lee, H.; Berry, B.C.; Kim, H.-C.; Ryu, D.Y. Thickness-dependent ordering of perpendicularly oriented lamellae in PS-b-PMMA thin films. Polymer 2015, 74, 63–69. [Google Scholar] [CrossRef]
- Tang, C.; Lennon, E.M.; Fredrickson, G.H.; Kramer, E.J.; Hawker, C.J. Evolution of Block CopolymerLithography to Highly OrderedSquare Arrays. Science 2008, 332, 429–432. [Google Scholar] [CrossRef]
- Vayer, M.; Guliyeva, A.; Warmont, F.; Takano, A.; Matsushita, Y.; Sinturel, C. Transition between tetragonal and hexagonal pattern in binary blends of ABC block copolymers with different chain lengths. Eur. Polym. J. 2020, 138, 109986. [Google Scholar] [CrossRef]
- Singh, A.; Chan, B.T.; Cao, Y.; Lin, G.; Gronheid, R. Using chemo-epitaxial directed self-assembly for repair and frequency multiplication of EUVL contact hole patterns. In Proceedings of the Alternative Lithographic Technologies VI, San Jose, CA, USA, 23–27 February 2014; Volume 9049. [Google Scholar]
- Kim, E. Personal Communication; Samsung Electronics: Suwon, Republic of Korea, 2017. [Google Scholar]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huh, J. Directed Self-Assembly of Cylinder-Forming Block Copolymers Using Pillar Topographic Patterns. Polymers 2024, 16, 881. https://doi.org/10.3390/polym16070881
Huh J. Directed Self-Assembly of Cylinder-Forming Block Copolymers Using Pillar Topographic Patterns. Polymers. 2024; 16(7):881. https://doi.org/10.3390/polym16070881
Chicago/Turabian StyleHuh, June. 2024. "Directed Self-Assembly of Cylinder-Forming Block Copolymers Using Pillar Topographic Patterns" Polymers 16, no. 7: 881. https://doi.org/10.3390/polym16070881
APA StyleHuh, J. (2024). Directed Self-Assembly of Cylinder-Forming Block Copolymers Using Pillar Topographic Patterns. Polymers, 16(7), 881. https://doi.org/10.3390/polym16070881






