Numerical Simulation of Polyacrylamide Hydrogel Prepared via Thermally Initiated Frontal Polymerization
Abstract
1. Introduction
2. Methods
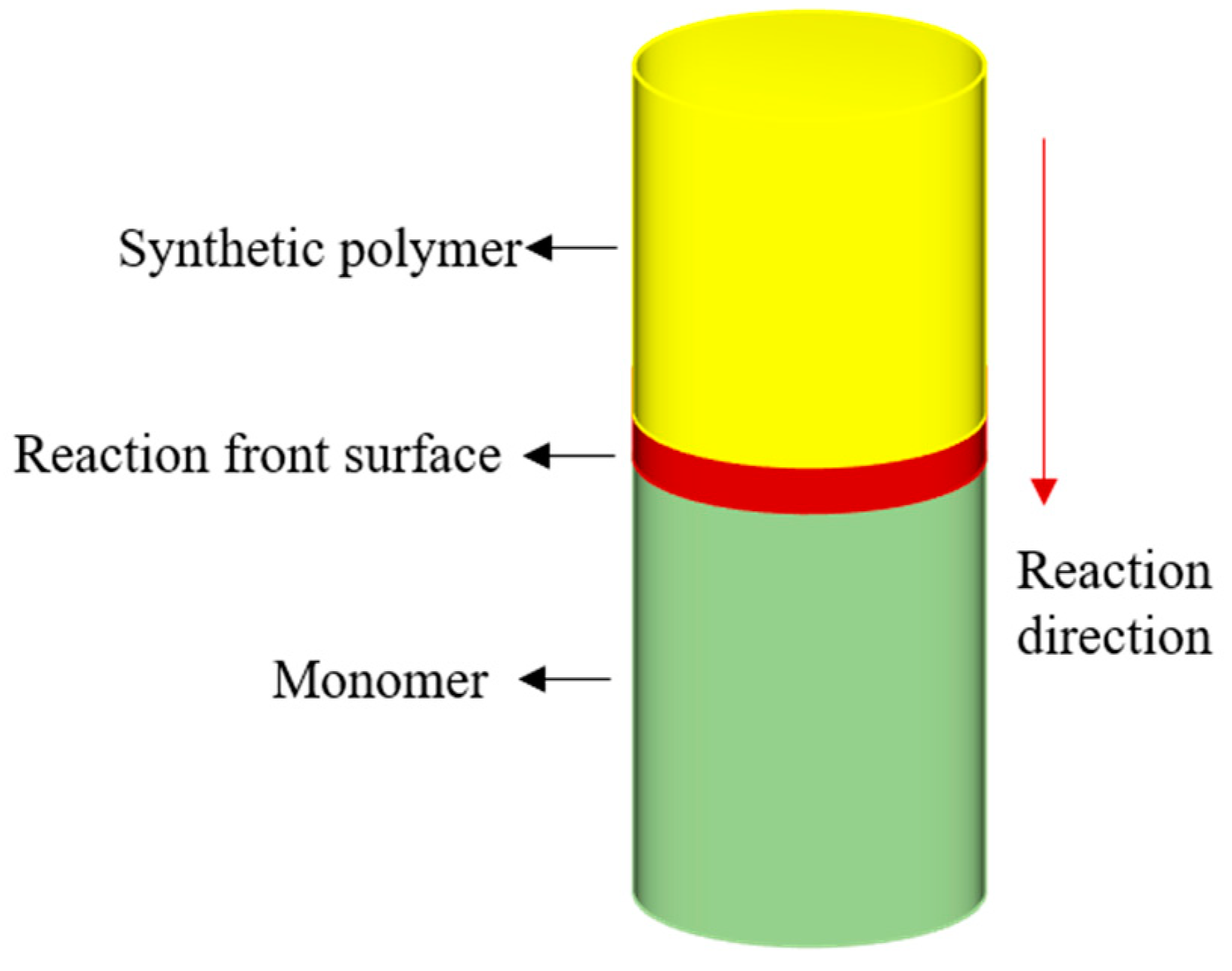
2.1. Basic Mechanism of FP Communication
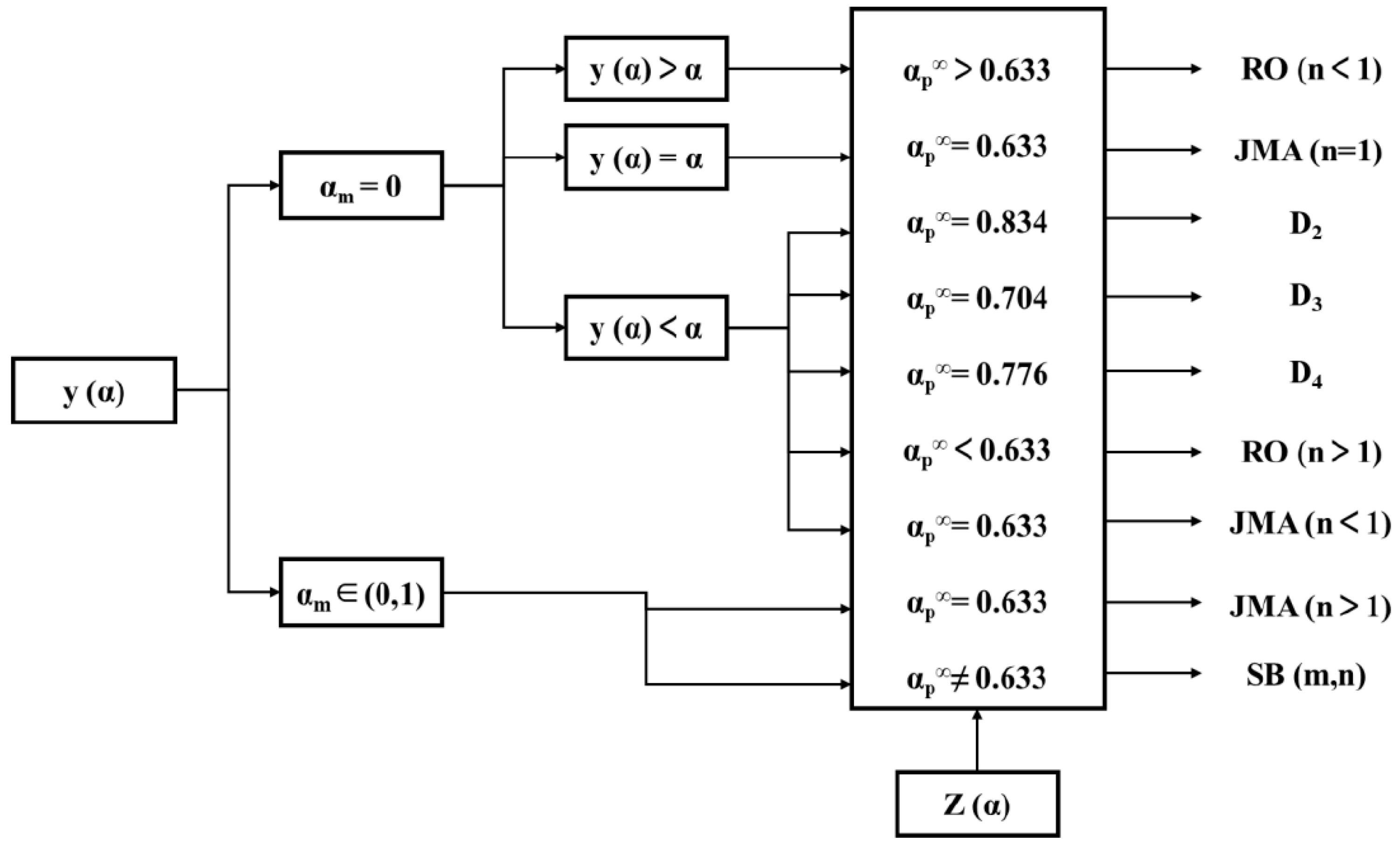
2.2. Curing Kinetics Model
- (1)
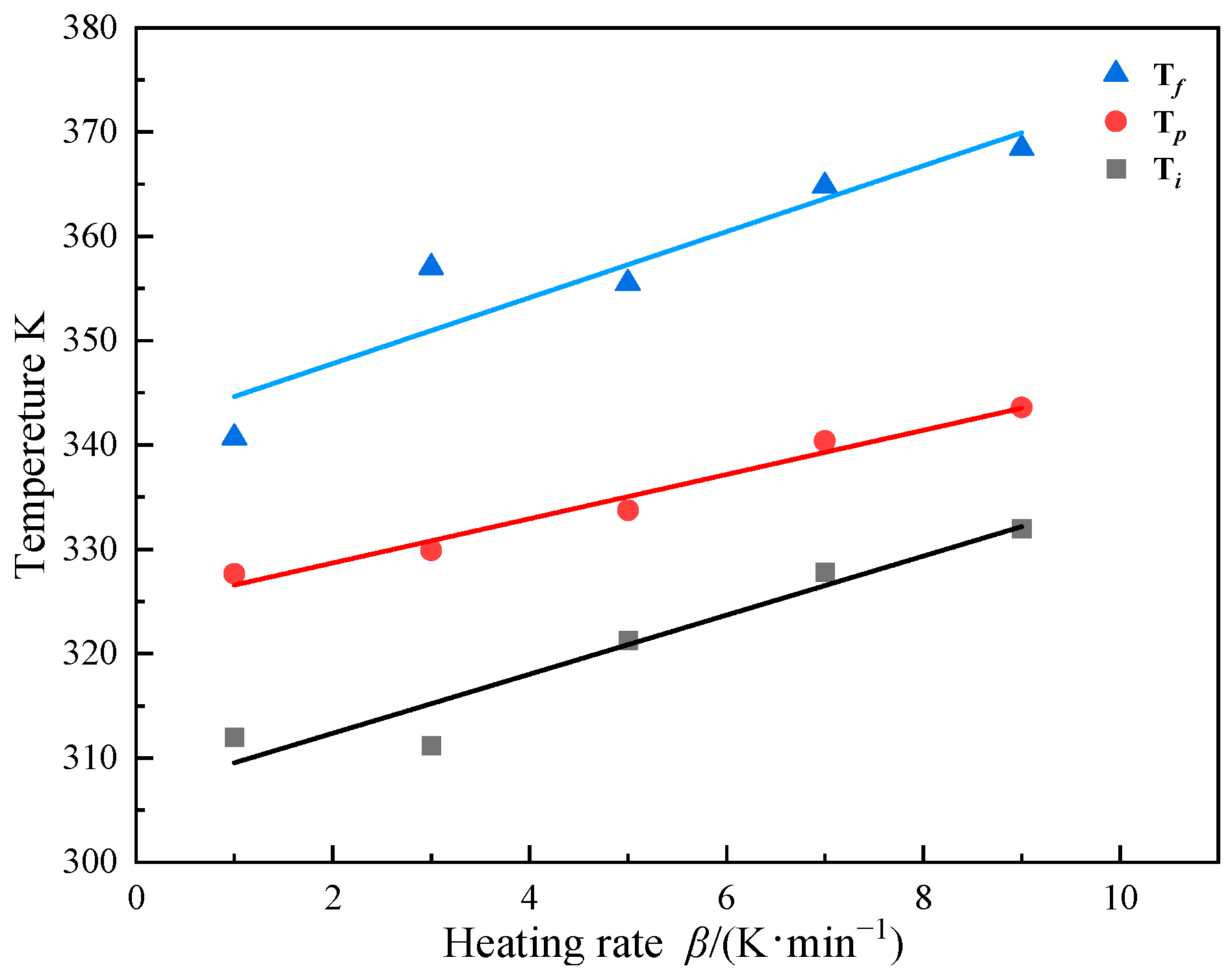
- Use the isoconversional method to determine the activation energy Ea;
- (2)
- Determine the form of the reaction kinetics mechanism function f(α) based on the shape and corresponding characteristic values of the defined functions and transformed from experimental data;
- (3)
- Based on the kinetic mechanism function, choose the appropriate formula to calculate the kinetic power indices n, m, etc.;
- (4)
- Calculate the pre-exponential factor A.
2.3. Heat Diffusion Transfer Model
3. Experiment and Discussion
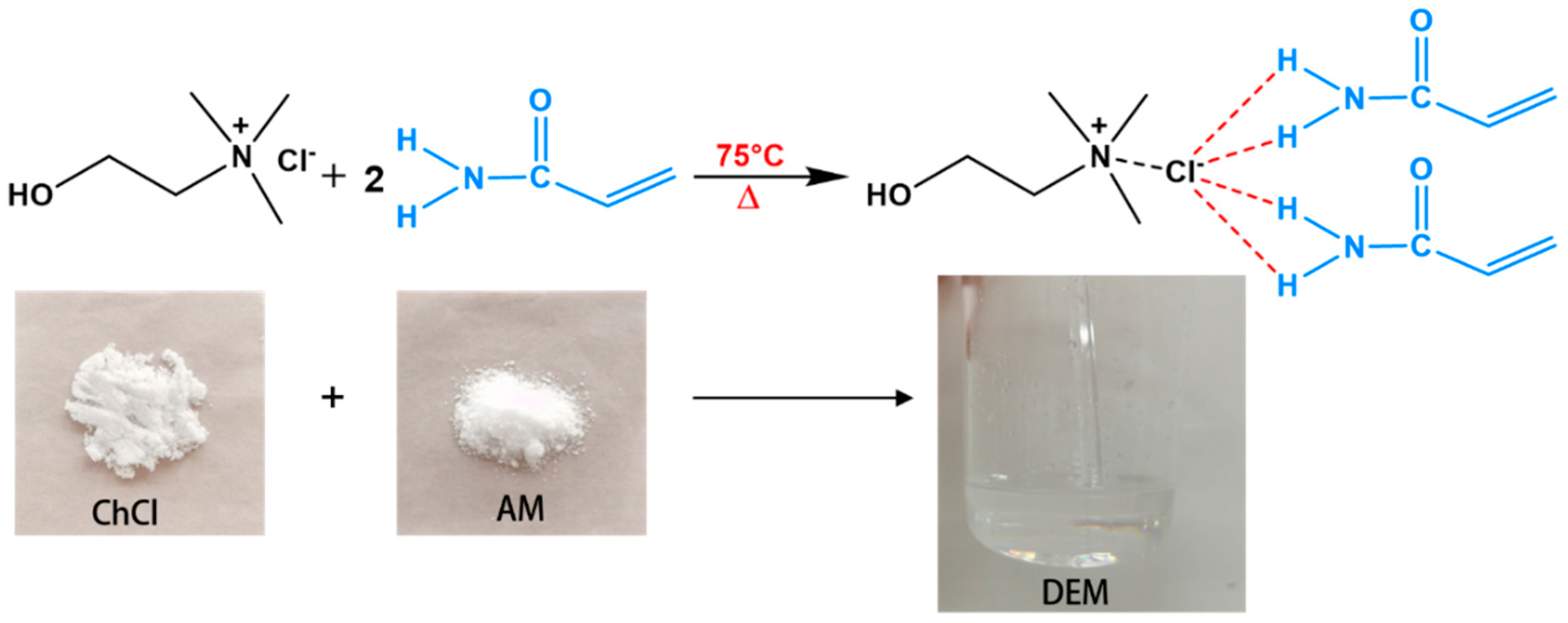
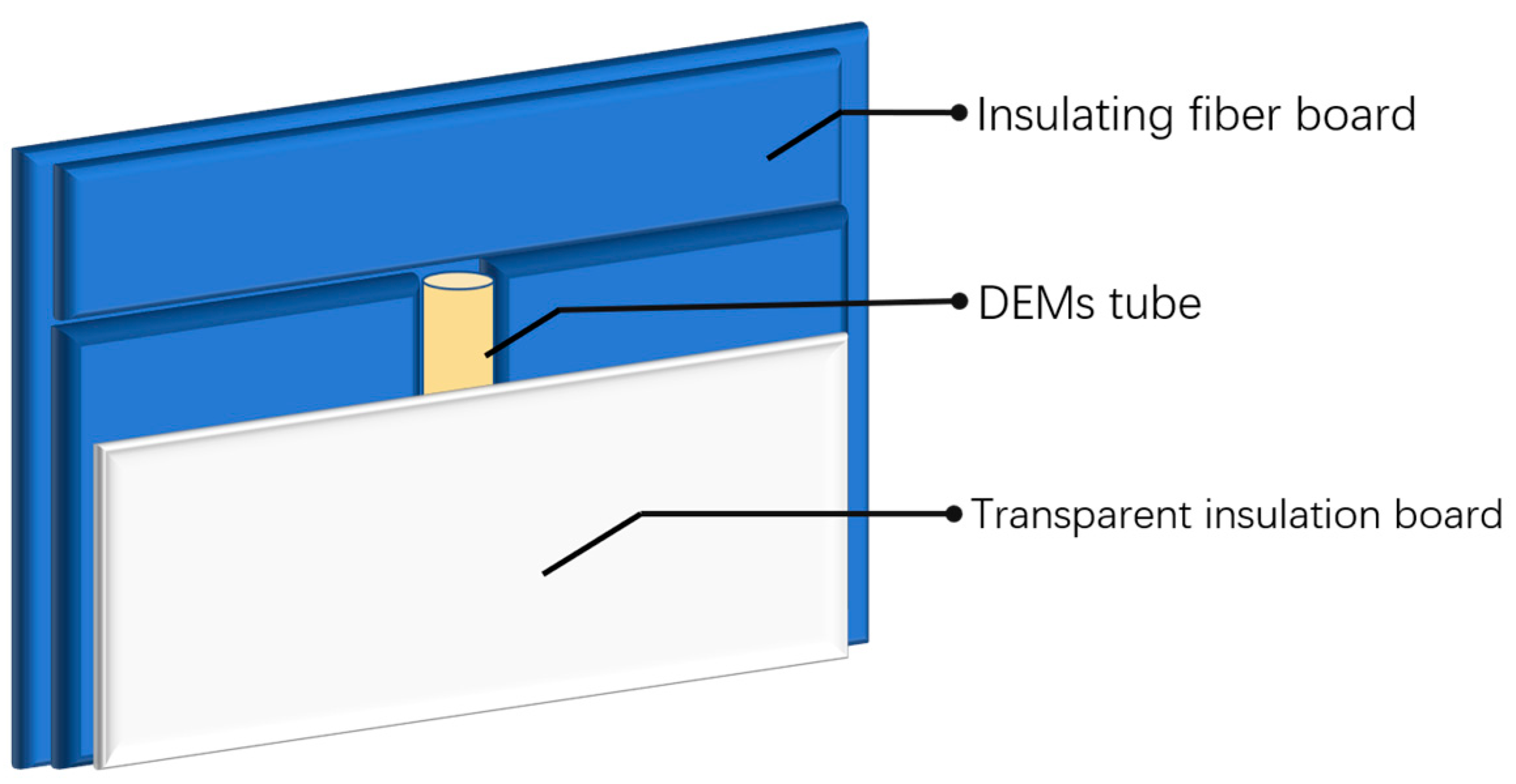
3.1. Material Preparation
3.2. Non-Isothermal Isothermal DSC Experiment
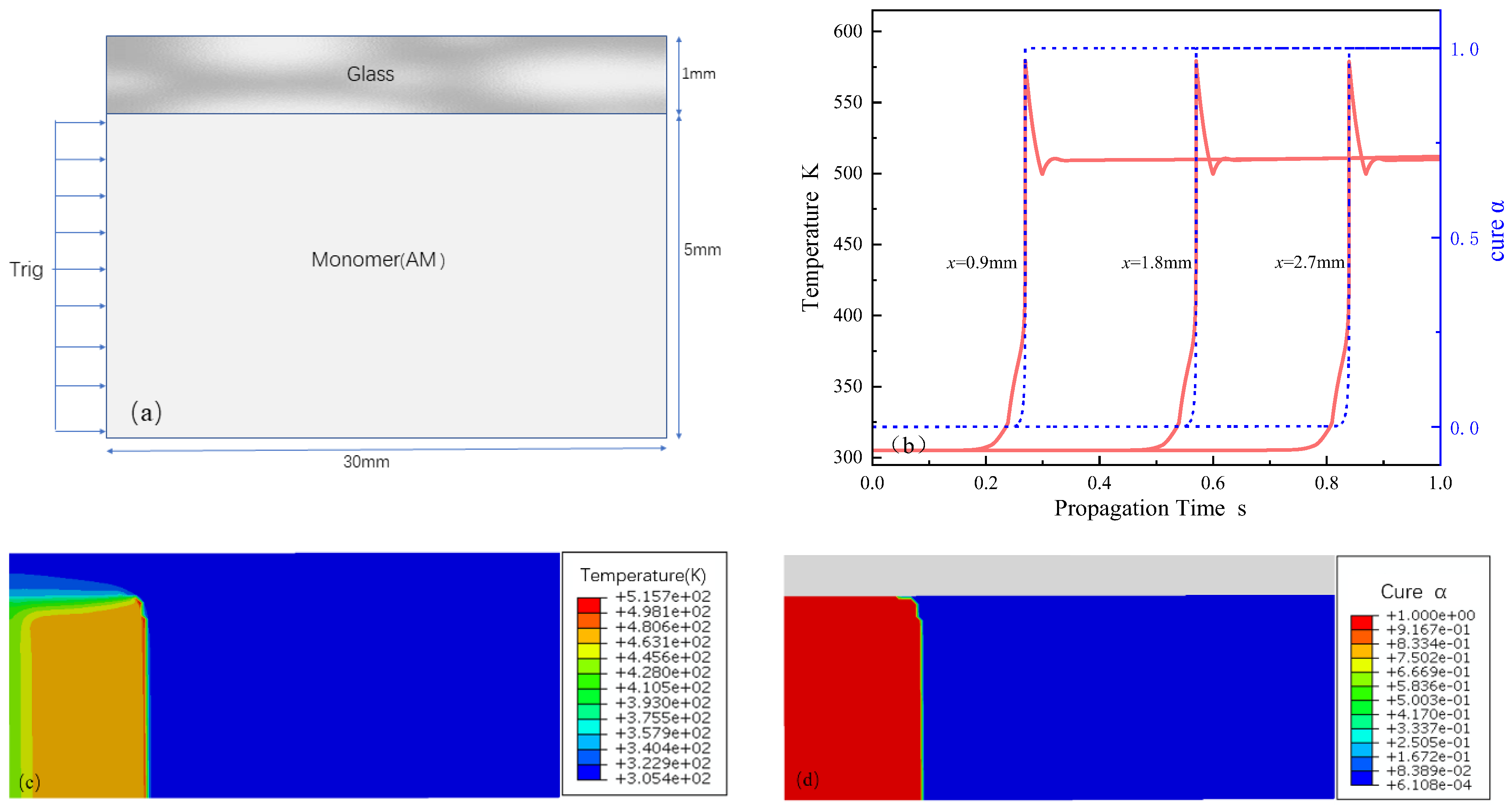
3.3. Numerical Simulation
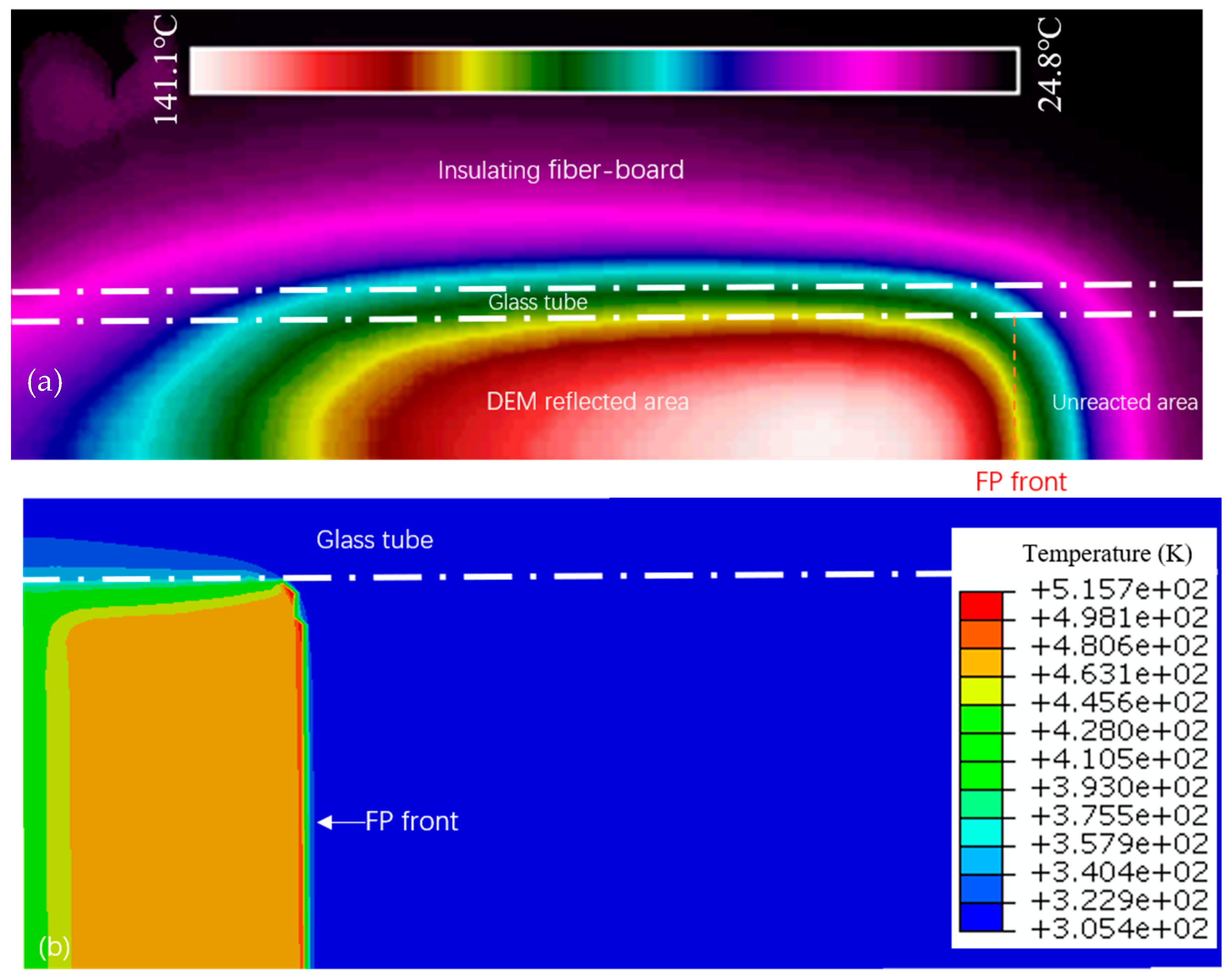
3.4. Model Validation
4. Conclusions
- (1)
- A kinetic model of the curing process for acrylamide-based deep eutectic solvents was successfully developed using Differential Scanning Calorimetry under non-isothermal conditions. The model was validated through a comparison with empirical data, demonstrating that the nth-order autocatalytic model exhibits reliability and accuracy in curing kinetics for DEM-based synthesis. This finding underscores the model’s potential applicability in the predictive analysis of polymerization kinetics within similar systems.
- (2)
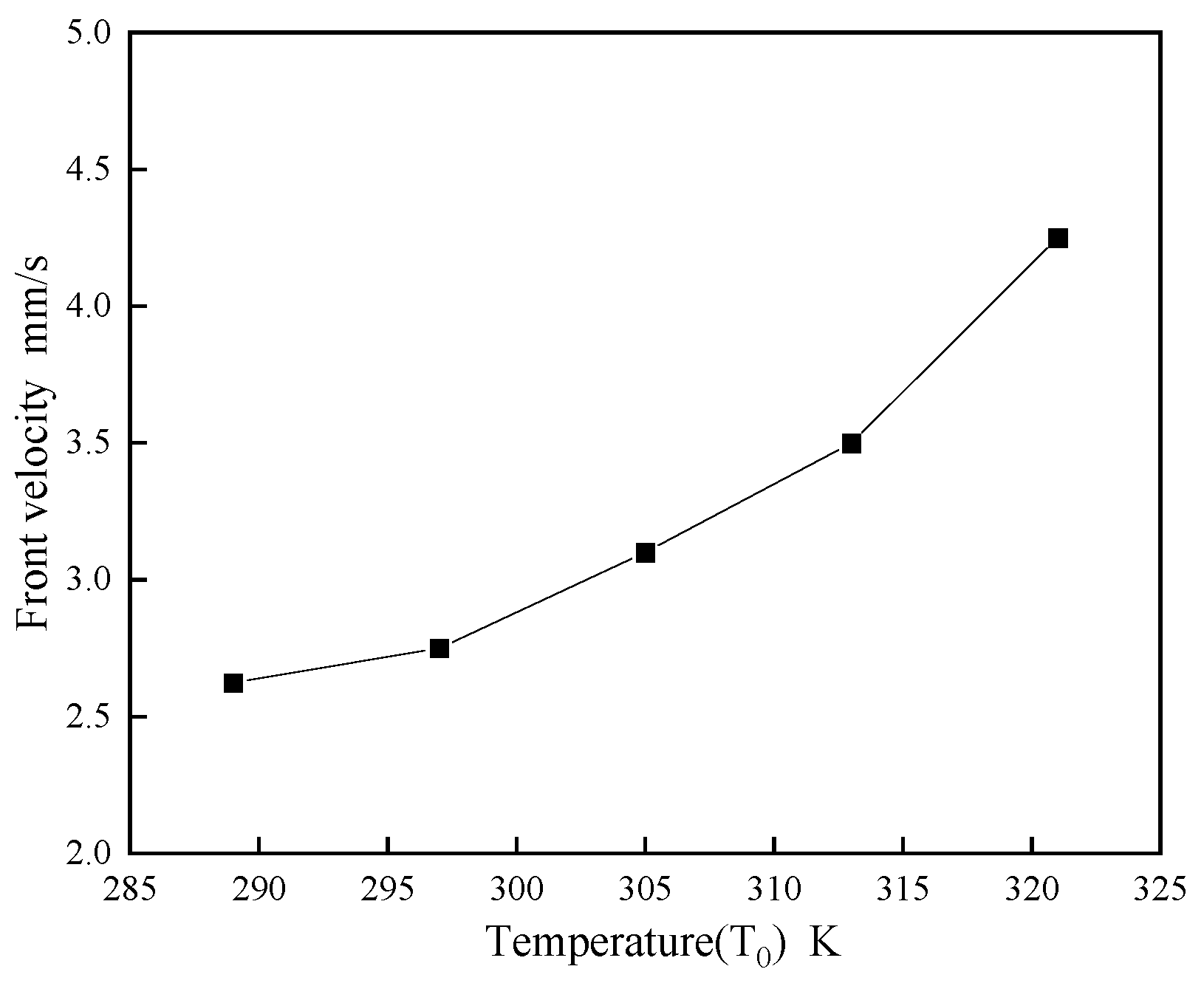
- Finite element numerical simulations were employed to elucidate factors influencing the characteristic temperature and velocity of the frontal polymerization (FP) process, examining the regulatory role of temperature within the FP reaction. The results indicate that both the duration of and increase in the triggering temperature momentarily elevate the front velocity before it stabilizes, while the initial temperature of the liquid substantially affects the front velocity. This observation provides valuable insights into the thermal dynamics governing FP and informs reaction condition optimization.
- (3)
- When comparing numerical simulation predictions with experimental outcomes, discrepancies predominantly attributed to experimental measurement errors, as well as the susceptibility of experiments to temperature control, were noted, resulting in higher predictive values overall. However, the overall temperature distribution and peak temperature characteristics exhibited remarkably similar trends between simulations and experiments. This congruence affirms the accuracy of numerical simulations and their reliability in forecasting the rapid curing process of hydrogel composites synthesized via FP. Consequently, these simulations serve as an essential reference for experimental design and optimization, facilitating advancements in the efficient fabrication of high-performance hydrogel composites. This indicates that under the strict control of experimental conditions, there is still some space to optimize the model in order to improve its accuracy.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Abliz, D.; Duan, Y.; Steuernagel, L.; Xie, L.; Li, D.; Ziegmann, G. Curing methods for advanced polymer composites—A review. Polym. Polym. Compos. 2013, 21, 341–348. [Google Scholar] [CrossRef]
- Davtyan, S.P.; Berlin, A.A.; Tonoyan, A.O. Advances and problems of frontal polymerization processes. Rev. J. Chem. 2011, 1, 56–92. [Google Scholar] [CrossRef]
- Robertson, I.D.; Yourdkhani, M.; Centellas, P.J.; Aw, J.E.; Ivanoff, D.G.; Goli, E.; Lloyd, E.M.; Dean, L.M.; Sottos, N.R.; Geubelle, P.H.; et al. Rapid energy-efficient manufacturing of polymers and composites via frontal polymerization. Nature 2018, 557, 223–227. [Google Scholar] [CrossRef]
- Mariani, A.; Bidali, S.; Fiori, S.; Sangermano, M.; Malucelli, G.; Bongiovanni, R.; Priola, A. Uv-ignited frontal polymerization of an epoxy resin. J. Polym. Sci. Part A Polym. Chem. 2004, 42, 2066–2072. [Google Scholar] [CrossRef]
- Frulloni, E.; Salinas, M.M.; Torre, L.; Mariani, A.; Kenny, J.M. Numerical modeling and experimental study of the frontal polymerization of the diglycidyl ether of bisphenol a/diethylenetriamine epoxy system. J. Appl. Polym. Sci. 2005, 96, 1756–1766. [Google Scholar] [CrossRef]
- Scognamillo, S.; Bounds, C.; Thakuri, S.; Mariani, A.; Wu, Q.; Pojman, J.A. Frontal cationic curing of epoxy resins in the presence of defoaming or expanding compounds. J. Appl. Polym. Sci. 2014, 131. [Google Scholar] [CrossRef]
- McFarland, B.; Popwell, S.; Pojman, J.A. Free-radical frontal polymerization with a microencapsulated initiator: Characterization of microcapsules and their effect on pot life, front velocity, and mechanical properties. Macromolecules 2006, 39, 55–63. [Google Scholar] [CrossRef]
- Nason, C.; Roper, T.; Hoyle, C.; Pojman, J.A. Uv-induced frontal polymerization of multifunctional (meth)acrylates. Macromolecules 2005, 38, 5506–5512. [Google Scholar] [CrossRef]
- Goldfeder, P.M.; Volpert, V.A.; Ilyashenko, V.M.; Khan, A.M.; Pojman, J.A.; Solovyov, S.E. Mathematical modeling of free-radical polymerization fronts. J. Phys. Chem. B 1997, 101, 3474–3482. [Google Scholar] [CrossRef]
- Mariani, A.; Bidali, S.; Fiori, S.; Malucelli, G.; Sanna, E. Synthesis and characterization of a polyurethane prepared by frontal polymerization. e-Polymers 2003, 3, 44. [Google Scholar] [CrossRef][Green Version]
- Chen, S.; Sui, J.; Chen, L.; Pojman, J.A. Polyurethane–nanosilica hybrid nanocomposites synthesized by frontal polymerization. J. Polym. Sci. Part A Polym. Chem. 2005, 43, 1670–1680. [Google Scholar] [CrossRef]
- Fiori, S.; Mariani, A.; Ricco, L.; Russo, S. First synthesis of a polyurethane by frontal polymerization. Macromolecules 2003, 36, 2674–2679. [Google Scholar] [CrossRef]
- Robertson, I.D.; Pruitt, E.L.; Moore, J.S. Frontal ring-opening metathesis polymerization of exo-dicyclopentadiene for low catalyst loadings. ACS Macro Lett. 2016, 5, 593–596. [Google Scholar] [CrossRef] [PubMed]
- Alzari, V.; Nuvoli, D.; Sanna, D.; Ruiu, A.; Mariani, A. Effect of limonene on the frontal ring opening metathesis polymerization of dicyclopentadiene. J. Polym. Sci. Part A Polym. Chem. 2016, 54, 63–68. [Google Scholar] [CrossRef]
- Ruiu, A.; Sanna, D.; Alzari, V.; Nuvoli, D.; Mariani, A. Advances in the frontal ring opening metathesis polymerization of dicyclopentadiene. J. Polym. Sci. Part A Polym. Chem. 2014, 52, 2776–2780. [Google Scholar] [CrossRef]
- Sennakesavan, G.; Mostakhdemin, M.; Dkhar, L.K.; Seyfoddin, A.; Fatihhi, S.J. Acrylic acid/acrylamide based hydrogels and its properties—A review. Polym. Degrad. Stab. 2020, 180, 109308. [Google Scholar] [CrossRef]
- Chen, Y.; Yan, S.; Li, S.; Zou, T. Preparation of Macroporous Hydrogel by Frontal Polymerization of Deep Eutectic Solvent and Its Swelling and Adsorption Performance. Polym. Mater. Sci. Eng. 2021, 37, 141–148. [Google Scholar]
- Jiang, Y.; Li, S.; Chen, Y.; Yan, S.; Tao, M.; Wen, P. Facile and green preparation of superfast responsive macroporous polyacrylamide hydrogels by frontal polymerization of polymerizable deep eutectic monomers. Ind. Eng. Chem. Res. 2020, 59, 1526–1533. [Google Scholar] [CrossRef]
- Viner, V.G.; Pojman, J.A.; Golovaty, D. The effect of phase change materials on the frontal polymerization of a triacrylate. Phys. D Nonlinear Phenom. 2010, 239, 838–847. [Google Scholar] [CrossRef]
- Goli, E.; Robertson, I.D.; Geubelle, P.H.; Moore, J.S. Frontal polymerization of dicyclopentadiene: A numerical study. J. Phys. Chem. B 2018, 122, 4583–4591. [Google Scholar] [CrossRef]
- Lu, C.; Huang, X.; He, Y.; Zhang, Y. Preparation of mesoporous—Molecular -sieve/polydicyclopentadiene composites. Acta Mater. Compos. Sin. 2012, 29, 65–72. [Google Scholar]
- Kobayashi, S. Encyclopedia of Polymeric Nanomaterials; Springer: Berlin/Heidelberg, Germany, 2015; pp. 1654–1658. [Google Scholar]
- Senum, G.; Yang, R. Rational approximations of the integral of the arrhenius function. J. Therm. Anal. 1977, 11, 445–447. [Google Scholar] [CrossRef]
- Málek, J. Kinetic analysis of crystallization processes in amorphous materials. Thermochim. Acta 2000, 355, 239–253. [Google Scholar] [CrossRef]
- Goli, E.; Parikh, N.A.; Yourdkhani, M.; Hibbard, N.G.; Moore, J.S.; Sottos, N.R.; Geubelle, P.H. Frontal polymerization of unidirectional carbon-fiber-reinforced composites. Compos. Part A Appl. Sci. Manuf. 2020, 130, 105689. [Google Scholar] [CrossRef]
- Hayaty, M.; Honarkar, H.; Beheshty, M.H. Curing behavior of dicyandiamide/epoxy resin system using different accelerators. Iran. Polym. J. 2013, 22, 591–598. [Google Scholar] [CrossRef]
- Saad, G.R.; Abdallah, H.M.; Aziz, M.S.A.; Mohamed, N.A.; Sabaa, M.W. Cure kinetics and thermal stability of maleimide modified epoxy tgic/cpe powder coating system. Thermochim. Acta 2015, 617, 191–199. [Google Scholar] [CrossRef]
- Mafi, R.; Mirabedini, S.; Naderi, R.; Attar, M. Effect of curing characterization on the corrosion performance of polyester and polyester/epoxy powder coatings. Corros. Sci. 2008, 50, 3280–3286. [Google Scholar] [CrossRef]
- Popescu, C. Integral method to analyze the kinetics of heterogeneous reactions under non-isothermal conditions a variant on the ozawa-flynn-wall method. Thermochim. Acta 1996, 285, 309–323. [Google Scholar] [CrossRef]
- Jouyandeh, M.; Paran, S.M.R.; Jannesari, A.; Puglia, D.; Saeb, M.R. Protocol for nonisothermal cure analysis of thermoset composites. Prog. Org. Coat. 2019, 131, 333–339. [Google Scholar] [CrossRef]
- Choe, Y.; Kim, W. Cure reactions of epoxy/anhydride/(polyamide copolymer) blends. Macromol. Res. 2002, 10, 259–265. [Google Scholar] [CrossRef]

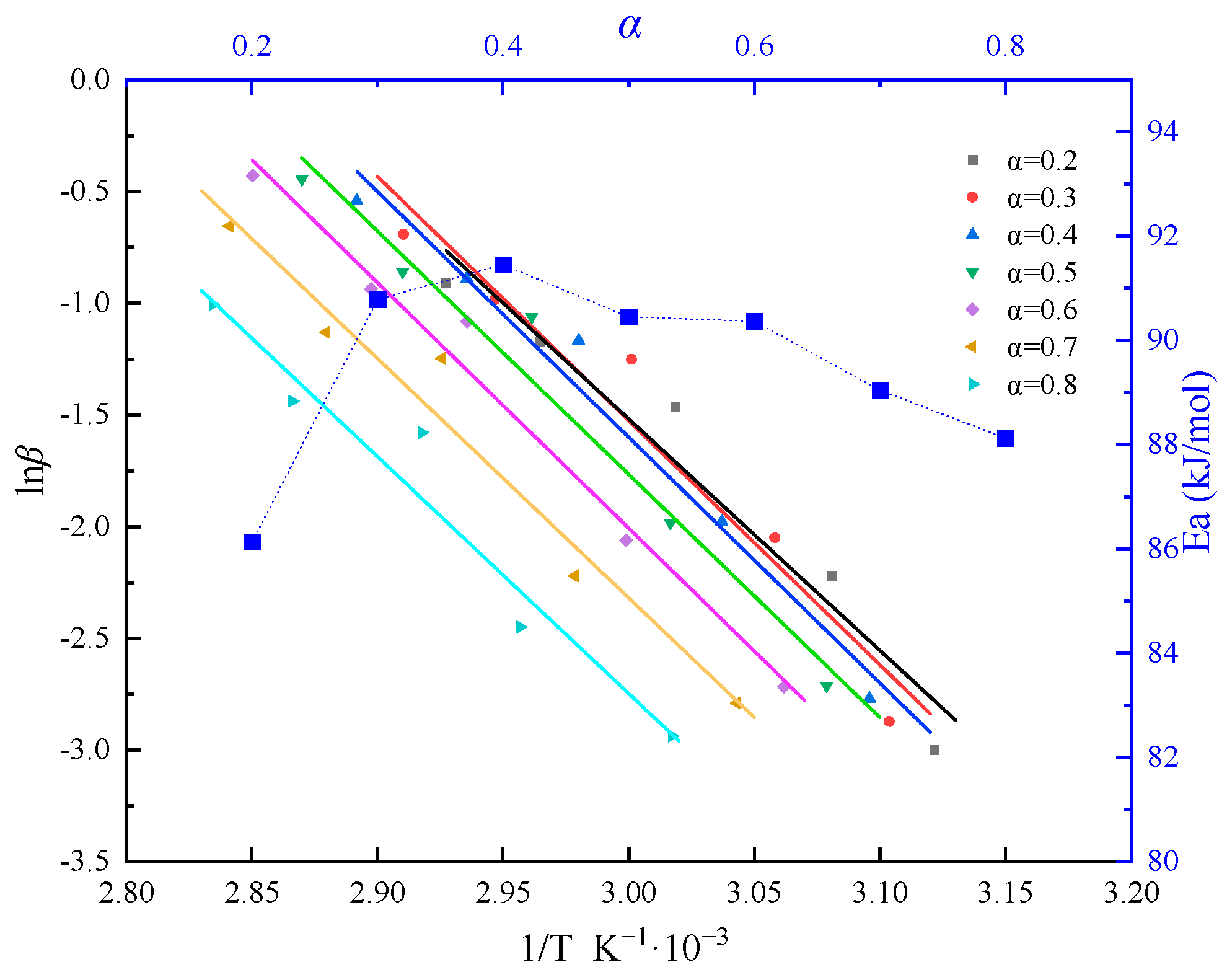

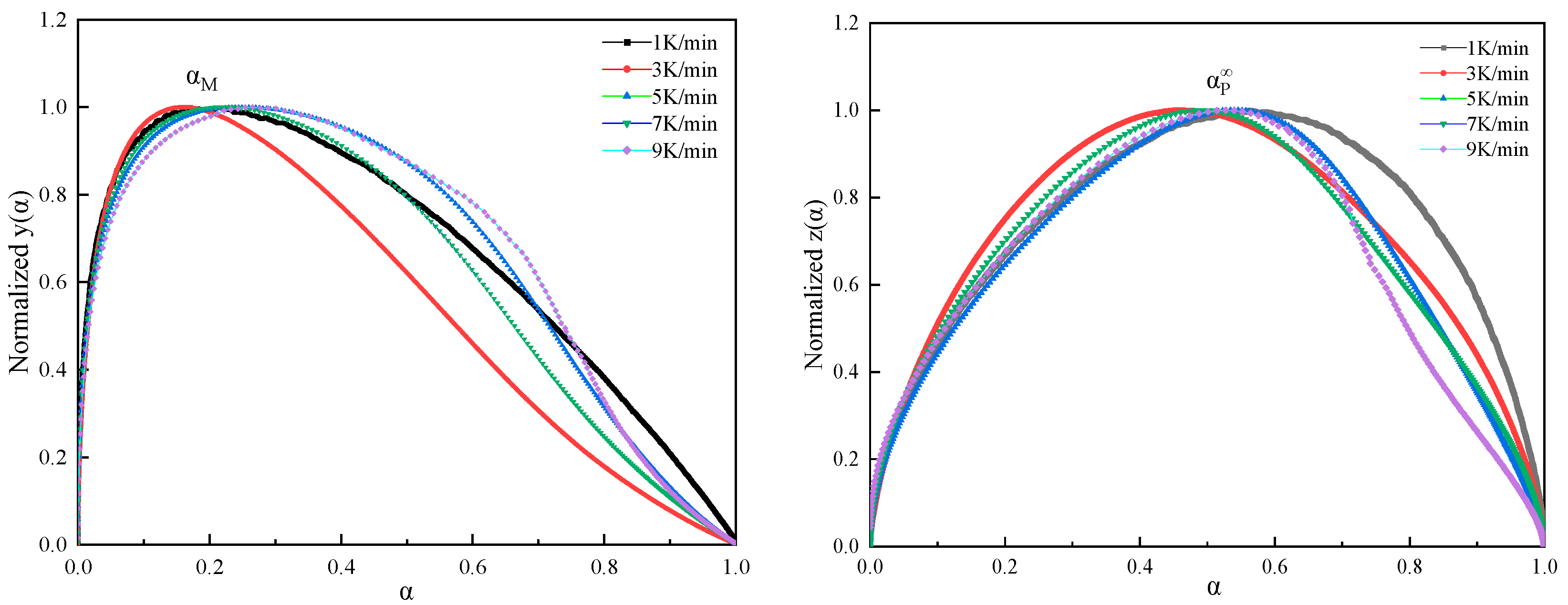

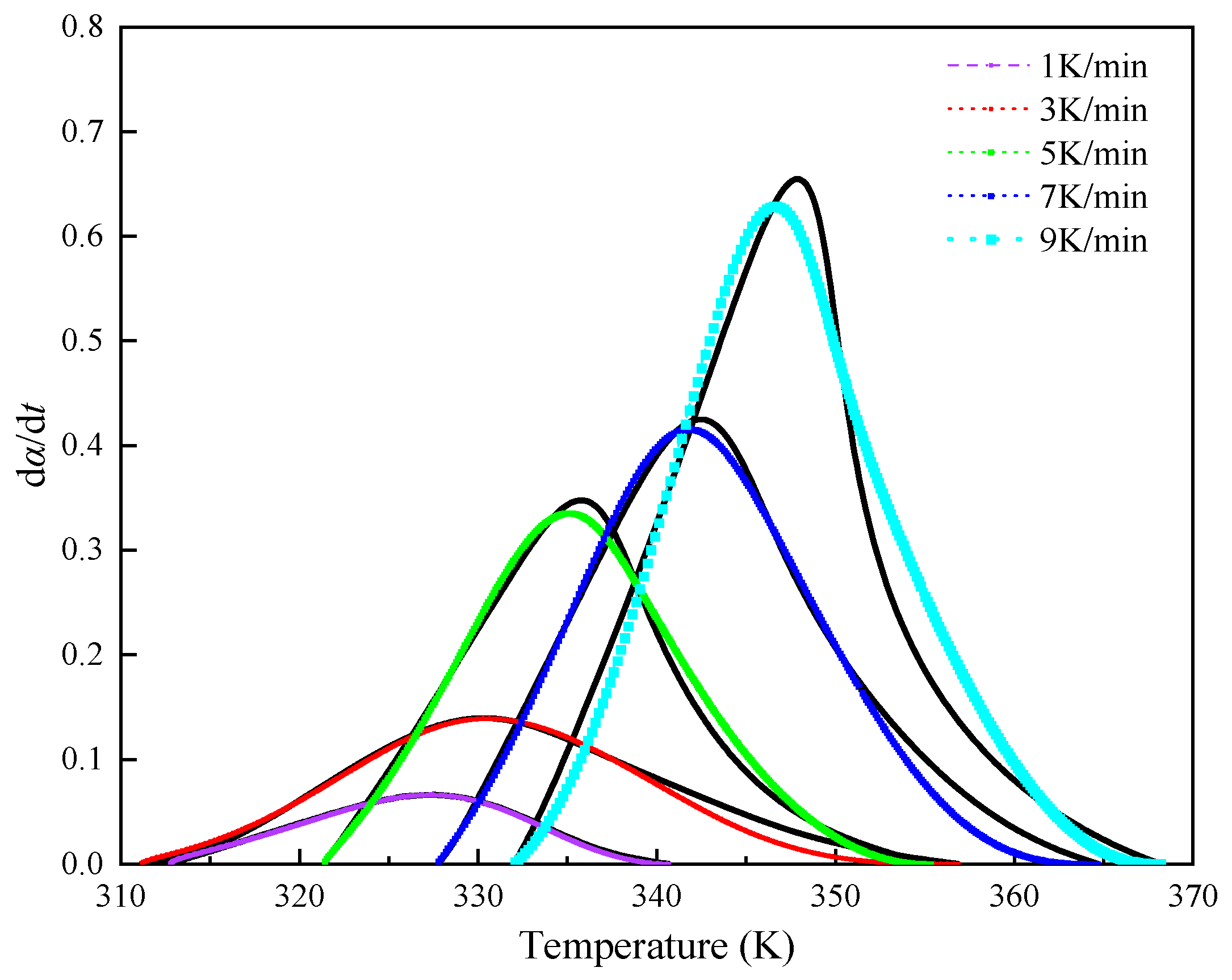


| β | αp | αm | αp∞ | n | m | lnA |
|---|---|---|---|---|---|---|
| 1 | 0.561 | 0.214 | 0.561 | 0.883 | 0.240 | 31.035 |
| 3 | 0.478 | 0.189 | 0.468 | 1.490 | 0.347 | 31.725 |
| 5 | 0.534 | 0.249 | 0.540 | 1.133 | 0.376 | 32.073 |
| 7 | 0.485 | 0.222 | 0.489 | 1.357 | 0.386 | 31.750 |
| 9 | 0.556 | 0.267 | 0.527 | 1.309 | 0.476 | 31.927 |
| mean | 0.523 | 0.223 | 0.517 | 1.234 | 0.365 | 31.702 |
| Monomer | (W/m·k) | ρ (kg/m3) | Hr (J/g) | T0 (K) | |
|---|---|---|---|---|---|
| AM | 0.25 | 900 | 1990 | 406.05 | 305 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yi, X.; Li, S.; Wen, P.; Yan, S. Numerical Simulation of Polyacrylamide Hydrogel Prepared via Thermally Initiated Frontal Polymerization. Polymers 2024, 16, 873. https://doi.org/10.3390/polym16070873
Yi X, Li S, Wen P, Yan S. Numerical Simulation of Polyacrylamide Hydrogel Prepared via Thermally Initiated Frontal Polymerization. Polymers. 2024; 16(7):873. https://doi.org/10.3390/polym16070873
Chicago/Turabian StyleYi, Xiong, Shengfang Li, Pin Wen, and Shilin Yan. 2024. "Numerical Simulation of Polyacrylamide Hydrogel Prepared via Thermally Initiated Frontal Polymerization" Polymers 16, no. 7: 873. https://doi.org/10.3390/polym16070873
APA StyleYi, X., Li, S., Wen, P., & Yan, S. (2024). Numerical Simulation of Polyacrylamide Hydrogel Prepared via Thermally Initiated Frontal Polymerization. Polymers, 16(7), 873. https://doi.org/10.3390/polym16070873







